Parameter identification method of time-domain stable discrete rational approximation for frequency response of foundations
-
摘要: 离散时间有理近似函数是建立基础动力分析模型的重要方法之一。而有理函数的稳定性和精度决定了动力时程分析的稳定性和精度。目前关于离散时间有理近似函数的研究主要集中于时域分析模型建立,而无法同时保证辨识函数的稳定性、精度及计算效率。基于系统稳定性理论,将有理近似函数看成一阶与二阶系统的组合,并根据其根的稳定条件推导了被辨识参数的稳定界限。在此基础上,利用遗传算法与序列二次规划算法提出了时域稳定的参数识别方法。通过对不同基础频响函数的数值仿真,验证了该方法辨识参数的稳定性与精度。由于该方法限制了参数取值范围,其计算效率也得到了大幅度提高。Abstract: The discrete-time rational approximation function is one of the important methods for establishing dynamic analysis model for foundations. The stability and accuracy of the rational function determine those of dynamic time history analysis. At present, the researches on the discrete-time rational approximation function mainly focus on the establishment of time-domain analysis model, but they cannot guarantee the stability, accuracy and calculation efficiency of the identification function at the same time. Based on the theory of system stability, the rational approximation function is regarded as the combination of first-order and second-order systems, and the stability boundary of identification parameters is derived according to the stability condition of its roots. On this basis, a time-domain stable parameter identification method is proposed by using the genetic algorithm and the sequential quadratic programming algorithm. The stability and accuracy of parameter identification are verified through numerical simulation of different frequency response functions for foundations. Due to the boundary of parameter range, the calculation efficiency is also greatly improved.
-
0. 引言
吸力基础具有制作简便、安装速度快、造价低等优点,常用做海洋工程结构物的基础。吸力基础沉贯至预定位置,是正常使用的前提。当吸力基础在砂土沉贯时,土体中发生渗流作用,导致基础端部有效应力和尖阻力大幅降低,甚至降为零[1-2],此时沉贯阻力主要由基础内外壁摩阻力组成[3]。准确预测基础侧壁摩阻力,对确定工程中沉贯所需吸力值有重要意义。对于吸力基础而言,其沉贯过程中基础–土体界面相互作用力学特性决定其沉贯侧壁摩阻力的大小。
国内外学者对吸力基础吸力沉贯特性和基础–土体界面相互作用开展了一系列研究。Houlsby等[4-5]提出吸力基础在砂土和黏性土中沉贯阻力以及所需吸力的计算公式。Mehravar等[6]发现不同尺寸的吸力基础沉贯过程中,所需吸力的变化曲线是相似的,所需吸力随基础尺寸增加逐渐增大。李大勇等[7-8]基于滑移线理论,提出了计算吸力沉贯最大、最小吸力值的计算方法。Chen等[9]研究发现,吸力沉贯时内壁摩阻力和端阻力显著降低,而外壁摩阻力基本保持不变,并建立了所需吸力的新的预测方法。Harireche等[10]研究了不同深度处土体渗透系数值对沉贯阻力和所需吸力的影响,认为土体渗透性恒定的传统理论会使吸力的预测过于保守。闫澍旺等[11]开展模型试验,阐明黏性土中吸力基础内部土塞随吸力发展规律。Liu等[12]开展模型试验,发现任一沉贯深度处,吸力基础界面摩擦系数为对应压力贯入条件下的0.5倍。
相比传统结构–土体界面力学研究,吸力基础沉贯过程中基础–土体界面力学特性研究较少,反映了这方面研究还不成熟,传统结构如桩基础等结构与土体界面相互作用的研究可为吸力基础界面力学特性研究提供借鉴。
Nardelli等[13]使用大型直剪仪,研究混凝土材料-砂土界面剪切特性,发现界面摩擦角与土体摩擦角之比随砂土密实程度的降低逐渐增大。Tiwari等[14]采用直剪仪,开展了界面剪切试验,发现砂土–结构界面摩擦角与土体内摩擦角之比随着砂土密实程度的增大逐渐降低;界面抗剪强度包络线并非为一条直线,同时指出大多数规范中计算土体–结构界面摩阻力的方法是相当保守的。Tejchman等[15]通过开展直剪试验,发现钢材–砂土界面摩擦角随着砂土密实程度增加逐渐增大,砂土与粗糙界面摩擦角近似等于土体内摩擦角。Jitsangiam等[16]利用直剪仪进行单调直剪试验和循环直剪试验,发现抗剪强度随土体密实程度的提高而增大,且在循环剪切后施加剪切荷载得到的界面摩擦系数大于单调直剪试验得到的摩擦系数。郭聚坤等[17]利用改进直剪仪研究了混凝土桩与黏性土界面剪切特性,发现固结时间对界面摩擦角影响较小。
对于吸力基础,其在砂土中沉贯安装过程与传统桩基础存在显著差别:吸力沉贯时,基础内外侧土体发生渗流作用,基础内侧土体有效应力降低,外侧有效应力增加,最终导致基础内外壁–土体界面法向应力、摩擦系数、摩阻力量值均有较大差异。目前计算吸力基础沉贯摩阻力的方法普遍采用假定系数,将基础内、外壁与土体界面侧摩阻系数假设为一定值kf[18],但该方法未能体现界面摩擦系数随沉贯深度和砂土相对密实度等因素的变化规律。
开展界面剪切试验研究饱和砂土–吸力基础沉贯界面力学特性,讨论了相对密实度和沉贯深度的影响规律,得到界面摩擦系数的变化趋势,分析了吸力基础沉贯时桶壁摩阻力的变化趋势,为揭示吸力沉贯基础–砂土界面相互作用机理、确定摩阻力提供借鉴。结合试验现象,阐述了吸力基础沉贯导致的土体置换和侧向挤出现象。
1. 试验仪器及流程
1.1 试验仪器
图 1为吸力基础–砂土沉贯界面剪切试验的GDS界面仪,图 2为不锈钢制压杆,压杆界面粗糙度Ra=0.3 μm。吸力基础–土体接触面为圆形,试验过程中不锈钢制压杆固定不动,通过底部步进电机控制底座旋转,带动环刀及内部砂土试样转动,从而模拟吸力基础沉贯过程。采用此种设计可以保证剪切过程中界面面积恒定。界面仪法向压力由电机控制,通过设置不同法向压力,模拟实际工程中不同沉贯深度处侧壁受到的法向压力作用。采用干装法向环刀内填装土样,砂土试样直径为70 mm,高度为20 mm。图 3为电控直剪残剪仪,用于土体直剪试验。
1.2 试验材料
试验海砂取自青岛金沙滩。其物理参数和级配曲线见表 1和图 4。
表 1 试验用砂相关物理参数Table 1. Relevant physical parameters of sand for tests试验用砂 Cu Cc D50/mm emax emin 细砂 2.33 0.98 0.18 0.980 0.560 1.3 试验方案
界面仪底座在剪切扭矩作用下匀速旋转,从而在结构–土体界面产生剪应力。利用式(1)和式(2),可将作用于界面的扭矩以及界面旋转角位移换算为吸力沉贯界面剪应力和剪切位移:
τ=M∫R02πr2dr=3M2πR3, (1) 式中,τ为剪应力,M为扭矩,R为轴向应力杆底面半径。
s=π180vr′t, (2) 式中,s为剪切位移,r′为平均半径,计算公式见式(3),v为剪切角速度,t为剪切时间。采用平均半径的作用是消除剪切过程中界面剪应力和剪切位移分布不均的情况。
r′=∫R02πr2drπR2=23R。 (3) 为了使试验结果更好地反映工程实际,试验剪切速率参考天津港北大防波堤、大港油田等吸力基础实际工程,沉贯速率分别为0.17和1.2 cm/min[19],因此,本文的沉贯速率介于二者之间,设置为1 cm/min。
此外,吸力基础在砂土中沉贯时,基础内部及周围土体形成由外向内的渗流作用,使得基础内部土体有效应力降低、外部土体有效应力增加,导致作用于基础外壁的侧向压力大于作用于内壁的侧向压力。目前,针对吸力基础在砂土中沉贯时内外渗流场的分布以及对界面特性影响的研究尚不完善,但可以通过研究不同深度处土压力分布以正确反映沉贯渗流作用。Liu等[12]以长径比为1.0的吸力基础为研究对象,得到了吸力沉贯过程中,作用于基础内壁和外壁的法向应力(即土压力)分布规律。试验结果综合考虑了渗流作用以及挤土作用。对上述法向应力分布进行拟合,可以得出作用于基础的土压力与沉贯深度的关系:
pi=19.70l−0.806, (4) po=40.28l−4.147, (5) 式中,pi为内壁土压力,po为外壁土压力,l为沉贯深度。
通过式(4),(5)可得高度为5 m,长径比为1.0的吸力基础在不同外壁土压力(即试验法向应力)条件下对应的贯入深度,见表 2。吸力基础沉贯时,作用于基础内外壁的土压力受桶壁粗糙度等因素影响显著。界面剪切试验研究需进一步与吸力基础模型试验相结合,探讨基础沉贯内外壁土压力值的影响因素。
表 2 法向应力与沉贯深度对应关系Table 2. Normal stresses under various penetration depths土压力/kPa 10 20 30 50 100 150 200 对应外壁沉贯深度/m 0.35 0.60 0.83 1.30 2.50 3.70 5.00 对应内壁沉贯深度/m 0.55 1.06 1.56 2.58 5.00 — — 本文试验设计了不同初始密实程度状态的砂土:松散(Dr =0.3)、中密(Dr =0.5)和密实(Dr =0.7,0.9,1)。表 3给出了各试验工况对应的法向应力和初始相对密实度。
表 3 试验工况Table 3. Experimental programs剪切类型 相对密实度 法向应力/kPa 界面剪切 0.3, 0.5, 0.7, 0.9, 1.0 10, 20, 30, 50, 100, 150, 200 直剪 0.3, 0.5, 0.7, 0.9, 1.0 2. 结果分析
2.1 剪应力–剪切位移曲线
图 5给出了砂土–基础界面剪应力随剪切位移变化规律,界面剪应力及剪切位移分别由式(1),(2)计算得到。由图 5可知,法向应力为10,20,30,50 kPa时,界面剪应力首先迅速增长至峰值,随后骤然减小至稳定值。法向应力为100,150,200 kPa时,界面剪应力首先随剪切位移线性增长至最大值,随后减小至稳定值。最大剪应力值对应的剪切位移为0.37~1 mm。
此外,从图 5中可以看出,界面抗剪强度随土体密实程度的增大显著增加,这与Jitsangiam等[16]的界面抗剪强度随相对密实度变化的结论一致。法向应力较小时(10~20 kPa),密实状态砂土–基础界面抗剪强度较中密状态提高幅度最大,分别提高了10.8%,4.7%,14.1%;当法向应力为30~200 kPa时,砂土相对密实度由松散变为中密时的界面抗剪强度增幅最为明显,分别增加了10.7%,10.9%,13.9%和8.8%。
图 6给出了直剪试验中,不同密实程度砂土中剪应力–剪切位移关系,砂土剪应力和剪切位移分别由直剪仪水平力传感器和水平位移传感器测得(如图 3所示)。试验砂土抗剪强度随密实程度的提高逐渐增加。当土体密实程度由松散变为中密时,其抗剪强度提高幅度最大,法向应力10,50,100,200 kPa对应的抗剪强度分别提高了16.3%,27.6%,33.7%,12.4%。不同法向应力下,随土体密实程度增大,峰值剪应力对应的位移逐渐减小。其原因为高密实程度砂土中,土体颗粒排列紧密,咬合力增强,粒间摩擦力变大,导致需要克服更大的颗粒翻滚、移动阻力。
2.2 竖向位移–剪切位移变化规律
图 7为不同相对密实度下,界面法向位移与剪切位移关系,界面竖向位移由GDS界面剪切仪的竖向位移传感器测得(图 1所示),剪切位移由式(2)计算得到。各法向应力下,砂土的体积表现出剪缩特征(即竖向位移不断减小)。由图 7(a)可以看出,曲线变化可分3阶段:①第Ⅰ阶段,法向位移随剪切位移增加呈线性减小趋势,同一法向应力下曲线斜率基本相同,如50 kPa下,Dr=0.3,0.5,0.7,0.9,1.0的砂土中曲线斜率分别为1.63,1.69,1.79,1.65,1.63;②第Ⅱ阶段,曲线斜率减小;③第Ⅲ阶段,曲线基本平缓,竖向位移降低至恒定值。第Ⅰ,Ⅱ阶段分界点对应的剪切位移值随相对密实度和法向应力的增加而增大,变化范围为0~1 mm。不同法向应力下,试验结束时,界面法向位移量与土体密实程度成正相关的关系。竖向位移增大的原因包括:①法向应力作用下,导致土体孔隙压缩;②剪切过程中,界面–土体相互作用造成的土体颗粒挤出(图 9所示);③界面剪切过程中,土体颗粒破碎。
对试验结束后的砂土试样烘干,进行颗粒筛分试验,得到剪切试验之后砂土的颗粒级配曲线,如图 8所示,界面剪切后的颗粒级配曲线较剪切前的颗粒级配曲线向左偏移,因此,剪切试验完成后,砂土颗粒发生破碎。
从图 9可以看出,一定法向应力下,试验过程中界面处砂土颗粒由于基础–土体相互作用被逐渐挤出环刀,此过程主要发生在第Ⅰ,Ⅱ阶段剪切初期,此时剪切位移较小,但土体挤出量相对较大。此外,相同剪切位移下砂土挤出量随着法向应力和相对密实度的增大而增加。此现象可用于解释吸力基础沉贯过程中,桶壁贯入造成的砂土置换侧向挤出现象。从图 7可以看出,由于不同法向应力代表不同沉贯深度,一定深度处的砂土挤出仅发生在基础贯入该深度后的小位移范围内。相对密实度为1.0,法向应力为10 kPa的试验完成后没有砂土挤出,法向应力为100,200 kPa的试验完成后砂土的挤出量分别占砂土总量的0.38%和0.54%。由此可得,相对密实度为1.0,法向应力较小时,竖向位移主要由土体颗粒剪切破碎产生的,法向应力较大时,竖向位移的变化是砂土挤出和颗粒剪切破碎的共同作用,且法向应力越大,砂土挤出量越多。相对密实度为0.5,法向应力为100 kPa和200 kPa的试验完成后,砂土挤出量非常小,此时,土体竖向位移的变化主要是由于土体孔隙压缩和剪切过程中颗粒破碎共同引起。
2.3 界面和土体强度参数变化规律
图 10为界面剪切试验和直剪试验得到的强度包络线。法向应力越大,抗剪强度越大。界面抗剪强度与法向应力的关系可以用式(6)表示,用于评估界面抗剪强度。
τ=a×σ′2+b×σ′+c, (6) 式中,τ为抗剪强度,σ′为法向应力,a,b,c为系数,其值见表 4。由表 4可知,抗剪强度与法向应力关系与拟合曲线较为吻合。利用式(6)以及表 4中的数据可以计算出任意法向应力下的界面抗剪强度。
表 4 抗剪强度–法向应力线性回归方程Table 4. Shear strength–linear regression equations for vertical pressure相对密实度 a b c R2 1.0 0.00021 0.3050 -0.1190 0.997 0.9 0.00015 0.2871 -0.1090 0.999 0.7 0.00027 0.2885 -0.6047 0.999 0.5 0.00060 0.2741 -0.8873 0.999 0.3 0.00018 0.2206 -0.1780 0.997 图 10所示,相同法向应力下,界面抗剪强度、饱和土体抗剪强度随土体密实程度的提高,均显著增加。法向应力确定的情况下,土体密实程度对土体抗剪强度的影响大于对界面抗剪强度的影响。吸力基础实际工程设计时,假定抗剪强度与法向应力呈线性关系,但所得的抗剪强度与法向应力呈二次曲线关系,因此,如果实际工程采用线性关系设计,会使得出的结果偏于危险。
表 5给出了法向应力为100 kPa时界面摩擦角和土体内摩擦角之间的关系。定义参数m为界面摩擦角与土体内摩擦角的比值。从表 5可知,砂土内摩擦角、界面摩擦角与土体密实程度成正相关的关系。试验工况下,界面摩擦角的变化范围为14.05°~18.12°,土体内摩擦角的变化范围为39.15°~54.07°,可见相对密实度对土体内摩擦角的影响比对界面摩擦角的影响更加显著,这与Tejchman等[15]界面摩擦角的变化规律一致。m随相对密实度的提高而减小。图 11给出了界面摩擦角随砂土内摩擦角变化的规律,土体–基础界面摩擦角随土体内摩擦角增加显著增大。
表 5 不同相对密实度下砂土抗剪强度指标Table 5. Parameters of sand under different relative densitiesDr 界面摩擦角δ/(°) 内摩擦角φ/(°) m 1.0 18.12 54.07 0.335 0.9 17.23 50.89 0.338 0.7 16.13 47.20 0.342 0.5 15.51 43.50 0.357 0.3 14.05 39.15 0.359 2.4 砂土–基础界面摩擦系数
界面摩擦系数为剪应力和法向应力的比值。由图 12可知,界面摩擦系数随法向应力及相对密实度的增加逐渐增大。当法向应力由50 kPa增大至100 kPa时,砂土–基础界面摩擦系数变化幅度最大,相对密实度为0.3,0.5,0.7,0.9,1.0的土体界面摩擦系数分别提高了13.7%,9.3%,8.7%,15.2%,15.0%。当竖向压力为150 kPa时,砂土密实程度对土体–界面摩擦系数影响最为显著。
2.5 沉贯过程中吸力基础阻力变化
式(7)和(8)给出了沉贯过程中,吸力基础内壁和外壁摩阻力计算公式:
Fo=μπDo∫h0po(l)dl, (7) Fi=μπDi∫h0pi(l)dl, (8) 式中,Fi,Fo分别为吸力基础内、外壁总摩阻力,μ为界面摩擦系数,可从表 4,5进行取值,Di,Do分别为吸力基础内、外直径,h为吸力基础长度。
结合式(1),(2)以及式(4),(5),得到基础沉贯时内壁及外壁土压力(法向压力)随沉贯深度的变化,将界面剪切试验得到的相应深度处摩擦系数代入公式(7),(8),从而得到基础不同沉贯深度出内外壁摩阻力(如图 13所示)。
由图 13可知,内外壁摩阻力与沉贯深度呈指数形式增长趋势,基础内壁摩阻力明显小于外壁摩阻力。当吸力沉贯深度为5.0 m时,相对密实度为0.3,0.5,0.7,0.9,1.0的砂土中,外壁摩阻力量值为内壁摩阻力的2.08,2.07,2.06,2.08和2.12倍。此外,从图中可以看出,基础内外壁摩阻力随土体密实程度的增大逐渐增加。
3. 结论
以吸力基础为研究对象,开展界面剪切试验,研究了基础吸力沉贯过程中基础–砂土界面相互作用。讨论了相对密实度对界面摩擦角和界面摩擦系数的影响,得到了基础沉贯过程中内外壁阻力的演化规律,得出以下结论:
(1)不同相对密实度下,砂土–基础界面剪应力随剪切位移增加表现出软化趋势,界面抗剪强度随相对密实度的增加而提高;本文试验工况下,砂土–吸力基础界面抗剪强度对应的剪切位移随相对密实度的提高而增加,剪切位移为0.37~1 mm。
(2)界面剪切试验中,砂土发生明显挤出现象,砂土挤出主要发生在剪切初期,对应剪切位移较小。此现象可揭示吸力基础沉贯过程中,桶壁贯入造成的砂土置换侧向挤出。一定沉贯深度处的砂土挤出仅发生在基础贯入该深度后的小位移范围内。
(3)界面剪切过程中,砂土颗粒破碎,细小颗粒填入土体孔隙,是界面剪切试验竖向位移变化的重要影响因素。
(4)随相对密实度增加,砂土–基础界面摩擦角与摩擦系数均增大。相同密实程度条件下,界面摩擦角为内摩擦角的0.37~0.41倍,相对密实度对土体内摩擦角的影响比对界面摩擦角的影响更加显著。不同相对密实度下,试验工况条件下,摩擦系数变化范围为0.20~0.34。
(5)沉贯过程中,吸力基础外壁摩阻力大于内壁摩阻力。沉贯完成时(法向应力200 kPa时),试验工况下,最大外壁摩阻力值为内壁摩阻力值的2.12倍。随着土体密实程度增加,基础内外壁摩阻力均提高。
4. 讨论
吸力基础沉贯设计中,首先需要计算沉贯阻力,进而确定所需沉贯吸力以及合理的沉贯抽水速率,确保基础顺利贯入至预定位置。由本文试验分析可知,侧壁摩阻力显著影响吸力基础的沉贯过程及最终贯入深度。当侧摩阻力预测值小于实际值时,施加预设吸力无法将基础贯入至设计深度;当侧摩阻力预测值大于实际值,导致施加吸力过大,引起基础内部形成较高“土塞”,基础无法沉贯至设计深度。因此需要准确预测吸力基础沉贯侧摩阻力。
开展界面剪切试验,讨论了相对密实度和法向应力对砂土–吸力基础界面强度以及界面摩擦系数、摩擦角的影响,分析了侧壁摩阻力变化规律。结合本文试验阐述了实际工程中吸力基础沉贯过程中挤土现象。本文是在单一界面粗糙度条件下开展的研究,界面粗糙程度对剪切特性的影响是今后研究的主要内容之一。
-
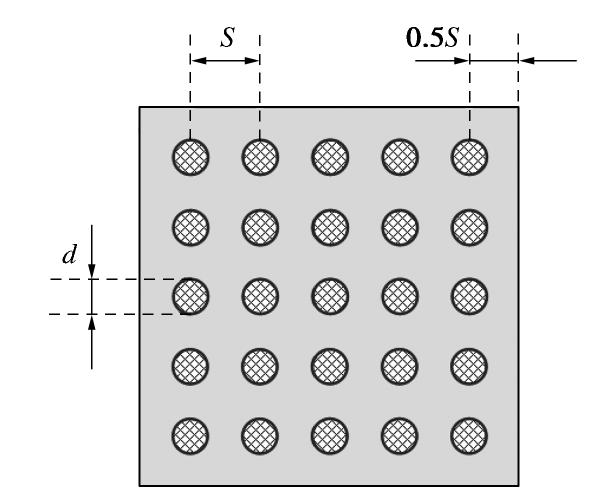
表 1 3×3群桩基础辨识效率
Table 1 Identification efficiency of foundation with 3×3 pile groups
阶次 3 4 5 6 7 本文方法/s 1.82 2.24 2.24 2.86 2.92 罚函数法/s 3.53 4.67 8.41 16.17 33.67 表 2 5×5群桩基础拟合精度与效率
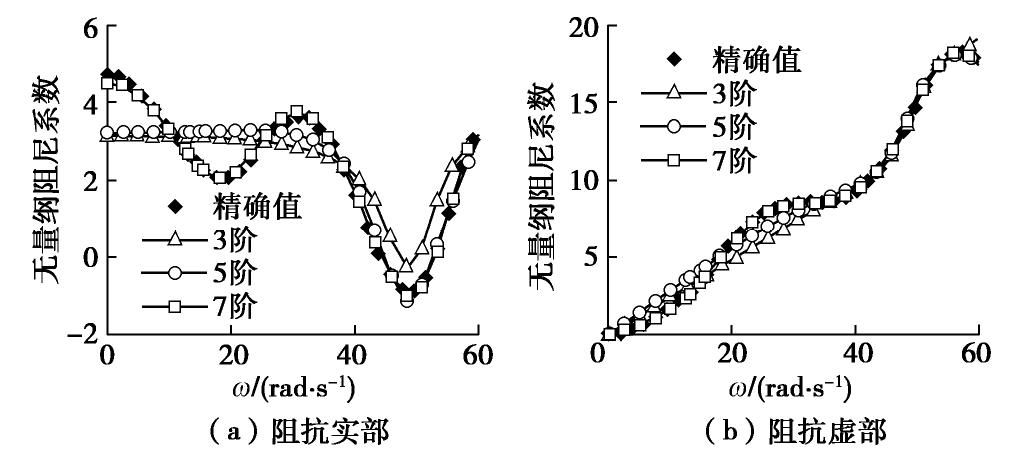
Table 2 Identification accuracy and efficiency of foundation with 5×5 pile groups
阶次 3 4 5 6 7 误差/% 18.80 18.23 13.02 2.03 1.97 时间/s 9.02 8.15 9.81 13.74 16.46 表 3 圆形基础拟合精度与效率
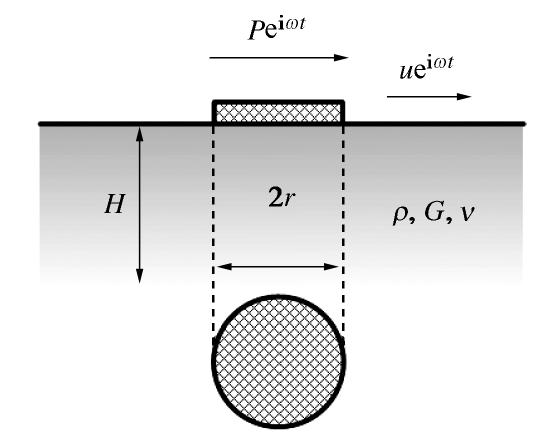
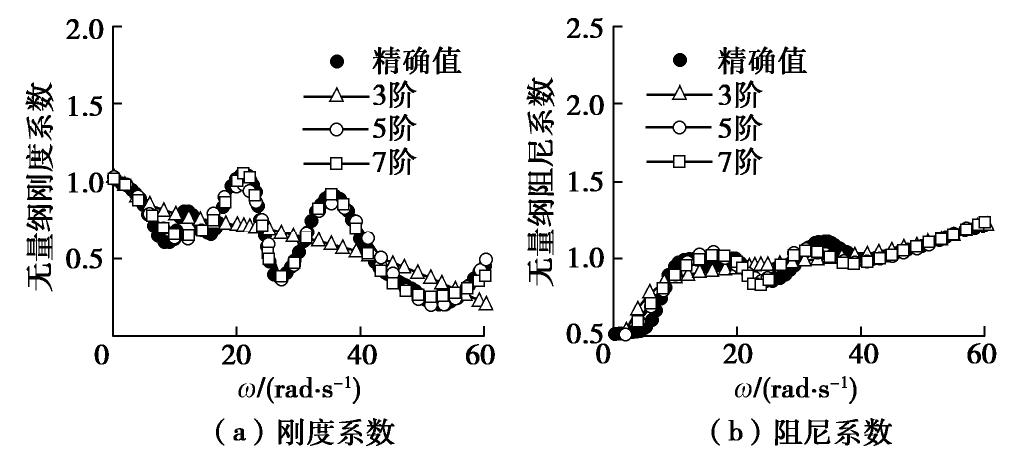
Table 3 Identification accuracy and efficiency of circular foundation
阶次 3 5 7 9 11 误差/% 16.82 12.29 7.49 6.74 6.62 时间/s 4.46 4.19 5.79 7.12 8.66 -
[1] 崔春义, 孟坤, 武亚军, 等. 考虑竖向波动效应的径向非均匀黏性阻尼土中管桩纵向振动响应研究[J]. 岩土工程学报, 2018, 40(8): 1433-1443. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201808010.htm CUI Chun-yi, MENG Kun, WU Ya-jun, et al. Dynamic response of vertical vibration of pipe piles in soils with radial inhomogeneousity and viscous damping considering vertical wave effect[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1433-1443. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201808010.htm
[2] 杨林青, 韩泽军, 林皋, 等. 横观各向同性层状地基上任意形状刚性基础动力响应求解与分析[J]. 岩土工程学报, 2020, 42(7): 1257-1267. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202007013.htm YANG Lin-qing, HAN Ze-jun, LIN Gao, et al. Solution and analysis for dynamic response of arbitrarily shaped rigid foundation on transversely isotropic layered soil[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(7): 1257-1267. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202007013.htm
[3] 赵密, 杜修力. 基础频响有理近似的稳定性和识别:离散时间的递归算法[J]. 工程力学, 2010, 27(1): 141-147,153. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201001027.htm ZHAO Mi, DU Xiu-li. Stability and identification for rational approximation of foundation frequency response: discrete-time recursive evaluations[J]. Engineering Mechanics, 2010, 27(1): 141-147, 153. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201001027.htm
[4] 赵密, 杜修力. 基础频响有理近似的稳定性和识别:连续时间的集中参数模型[J]. 工程力学, 2009, 26(12): 76-84, 99. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200912017.htm ZHAO Mi, DU Xiu-li. Stability and identification for rational approximation of foundation frequency response: continuous-time lumped-parameter models[J]. Engineering Mechanics, 2009, 26(12): 76-84, 99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200912017.htm
[5] PARONESSO A, WOLF J P. Recursive evaluation of interaction forces and property matrices from unit-impulse response functions of unbounded medium based on balancing approximation[J]. Earthquake Engineering and Structural Dynamics, 1998, 27: 609-618. doi: 10.1002/(SICI)1096-9845(199806)27:6<609::AID-EQE745>3.0.CO;2-M
[6] WOLF JP, MOTOSAKA M. Recursive evaluation of interaction forces of unbounded soil in the time domain from dynamic-stiffness coefficients in the frequency domain[J]. Earthquake Engineering and Structural Dynamics, 1989, 18: 365-376. doi: 10.1002/eqe.4290180305
[7] SAFAK E. Time-domain representation of frequency- dependent foundation impedance functions[J]. Soil Dynamics and Earthquake Engineering, 2006, 26(1): 65-70. doi: 10.1016/j.soildyn.2005.08.004
[8] 杜修力, 赵建锋, 韩强. 精度可控地基阻抗力的一种时域差分计算方法[J]. 力学学报, 2008, 40(1): 59-66. doi: 10.3321/j.issn:0459-1879.2008.01.008 DU Xiu-li, ZHAO Jian-feng, HAN Qiang. Accuracy controllable time-domain difference approach to calculate foundation resisting force[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(1): 59-66. (in Chinese) doi: 10.3321/j.issn:0459-1879.2008.01.008
[9] LAUDON A D, KWON O S, GHAEMMAGHAMI A R. Stability of the time-domain analysis method including a frequency-dependent soil-foundation system[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(15): 2737-2754. doi: 10.1002/eqe.2606
[10] GASH R, SEVLABI E E, TACIROGLU E. Implementation and stability analysis of discrete-time filters for approximating frequency-dependent impedance functions in the time domain[J]. Soil Dynamics and Earthquake Engineering, 2017, 94: 223-233. doi: 10.1016/j.soildyn.2017.01.021
[11] SUNG Y C, CHEN C C. Z-transferred discerte-time infinite impulse response filter as foundation-soil impedance function for SDOF dynamic structural response considering soil-structure interaction[J]. Earthquake Spectra, 2019, 35(2): 1003-1022.
[12] 赵建锋, 杜修力. 地基阻抗力时域递归参数的计算方法及程序实现[J]. 岩土工程学报, 2008, 30(1): 34-40. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200801007.htm ZHAO Jian-feng, DU Xiu-li. Computation method and realization procedure for time-domain recursive parameters of ground resistance[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(1): 34-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200801007.htm
[13] OPPENHEIM A V, WILLSKY A S, NAWBA S H. Signals & Systems[M]. 2nd ed. New Jersey: Prentice-Hall Inc, 1997.
[14] HAN Y C, SABIN G C W. Impedances for radially inhomogeneous viscoelastic soil media[J]. Journal of Engineering Mechanics, 1995, 121(9): 939-947.
[15] 黄茂松, 吴志明, 任青. 层状地基中群桩的水平振动特性[J]. 岩土工程学报, 2007, 29(1): 32-38. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200701004.htm HUANG Mao-song, WU Zhi-ming, REN Qing. Lateral vibration of pile groups in layered soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 32-38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200701004.htm
[16] WANG C, YAN C Q, WANG J J, et al. Parametric optimization of steam cycle in PWR nuclear power plant using improved genetic-simplex algorithm[J]. Applied Thermal Engineering, 2017, 125: 830-845.
[17] 文学章, 尚守平. 层状地基中桩筏基础的动力阻抗研究[J]. 工程力学, 2009, 26(8): 95-99. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200908019.htm WEN Xue-zhang, SHANG Shou-ping. Research on dynamic impedance functions of pile-raft foundation in layered soil[J]. Engineering Mechanics, 2009, 26(8): 95-99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200908019.htm
-
期刊类型引用(3)
1. 王涛,孙婷婷,占鑫杰,吕冲,陈浩. 氯离子在典型黏土地基中的迁移特性研究. 河南科学. 2023(08): 1134-1141 .  百度学术
百度学术
2. 尹康,刘霖,白瑞刚. 隔离材料对复合污染物的运移阻滞效应研究. 内蒙古工业大学学报(自然科学版). 2023(06): 561-565 .  百度学术
百度学术
3. 杨婷,杨成艳,郑举功,查文化,梁海安,冯岩岩. Ca~(2+)盐溶液在高庙子膨润土中的扩散研究. 辐射防护. 2022(02): 146-154 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: