复杂地基条件下土–结构动力相互作用分析

林皋; 李志远; 李建波

doi:10.11779/CJGE202109001

复杂地基条件下土–结构动力相互作用分析 English Version

林皋^{1, 2,},
李志远^{1, 2},
李建波^{1, 2}

1.
海岸与近海工程国家重点实验室（大连理工大学）,辽宁　大连　116024
2.
工程抗震研究所建设工程学部水利工程学院（大连理工大学）,辽宁　大连　116024

基金项目:

国家重点研发计划项目 NMSRP2016YFB0201001

中央高校基本科研业务费项目 DUT20TD209

详细信息

作者简介:
林皋(1929— ),男,教授,中国科学院院士,主要从事大坝和核电结构抗震安全评价。E-mail：gaolin@dlut.edu.cn

中图分类号: TU435
计量
- 文章访问数: 401
- HTML全文浏览量: 79
- PDF下载量: 367
出版历程
- 收稿日期: 2020-12-17
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Dynamic soil-structure interaction under complex soil environment

LIN Gao^{1, 2,},
LI Zhi-yuan^{1, 2},
LI Jian-bo^{1, 2}

1.
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
2.
Institute of Earthquake Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China

摘要

摘要: 结构和地基动力相互作用（SSI）分析对大坝、桥梁、核电、地下结构的抗震安全评价具有重要意义。本文对SSI分析的发展现状和工程设计实践进行了扼要评述。值得指出,2011年日本福岛核电事故后,国际上普遍提高了对核电结构抗震安全性的需求。因此,对重要结构的安全评价发展更为完善的先进SSI计算模型势在必行。为此目的,对处于复杂地基条件下的SSI分析提出一种新的计算模型,可以方便地考虑结构近场各种非均质因素的影响而不增加计算工作量,其中包括地基分层、基础埋深、建基面水平、存在相邻建筑物、附近出现软弱地质体等因素。这使SSI的计算更为准确和高效。论文的数值算例论证了所建议方法的有效性。
- 土–结构相互作用 /
- 复杂地基环境 /
- 基础结构 /
- 抗震安全评价
Abstract: The dynamic soil-structure interaction (SSI) analysis is of great significance to the earthquake safety evaluation of infrastructures, such as dams, bridges, nuclear power structures, etc. The state of the art and the current design practice of SSI analysis are briefly reviewed. It is worth to mention that after the 2011 accident of Fukushima Nuclear Power Plant in Japan, the international demand for the earthquake safety of nuclear power structures has been raised. Hence, it is imperative to develop more advanced appropriate computational models for the safety evaluation of the important structures. For this purpose, a novel SSI analysis model under complex soil environment is proposed so that the influences of the inhomogeneities appearing in the near field of the structure including the layering of the half-space, the embedment of the foundation, the layout level of the foundation base, the existence of adjacent structures, the nearly soft geologic inclusions, the irregular interfaces between the layers can be easily and conveniently taken into consideration without additional effort. As a result, the computation can be more accurate and efficient. Numerical examples are provided to validate the effectiveness of the proposed approach.
- soil-structure interaction /
- complex soil environment /
- infrastructure /
- earthquake safety evaluation

HTML全文

0. 引言

成都市主城八区均下伏中等风化泥岩,埋深一般为-0.5～-35m,层厚十几米到几十米不等^[1-2],工程性质差,承载力估算困难。随着成渝地区双城经济圈建设的深度推进,成都地区已开建或筹建的高层、超高层建筑的基础持力层均涉及中等风化泥岩,研究该类岩体的承载能力具有一定的工程意义。

江苏^[3]、广东^[4]、重庆^[5]等地在实践中逐渐修正了规范^[6]对软岩地基承载力的取值建议,提出了不同岩石单轴抗压强度分区所对应的折减系数及承载力；长沙、兰州等地以岩基载荷试验为主,辅以点荷载试验、旁压试验等,提出了泥岩承载力的界定标准^[7-9]；并通过不同类型试验结果的对比,探讨了影响地基承载力取值的因素^[10-11],指出确定地基承载力时应考虑岩体的物理力学性质、成因、年代、地下水及其变化情况、建筑物对沉降及差异沉降的要求等^[12]。成都地标DB51/T5026—2001^[13]建议中等风化泥岩地基承载力特征值为500～1000 kPa,也可根据室内天然单轴抗压强度折减法确定地基承载力,工程实践表明规范条文存在两点不足。一方面是建议的承载力取值偏低,成都地区中风化泥岩极限承载力值试验值普遍分布在2000～6000 kPa,且主要集中在4000～6000 kPa^[14],按照安全系数3考虑,其承载力特征值亦大于1000 kPa；另一方面,折减法确定承载力合宜性差,折减系数ψ的取值无既定条款可循,往往带有过多的人为因素,即使对同一类型、同一条件、同一环境的地基岩体,不同的设计人员也会取不同的ψ值,有时甚至出入较大,在没有原位试验的情况下,所提出的承载力缺乏依据,带有一定的随意性,对工程的安全性没有切实保障。在成都地区更为合理的取值研究至今鲜有突破,受到不少诟病。

综上,本文通过对24个场地约100余处原位平板载荷试验与同条件岩石单轴抗压强度试验工程案例进行对比分析,讨论了成都地区中等风化泥岩计算公式中ψ值取值及其与承载力特征值的相关关系。进一步,结合成都高新区在建的某超高层建筑项目,采用原位平板载荷试验（9组）联合钻孔旁压试验法（17孔）针对性的探讨了该类岩体承载力特性,并分析了承压板尺寸等因素对承载能力发挥程度的影响。以上研究旨在探寻单轴抗压强度或旁压试验结果作为承载力设计依据的可能。

1. 成都中等风化泥岩特性

成都地区红层属于盆西小区^[15],是最具代表性的近水平红层分布区。区内中等风化泥岩以J_3p侏罗系蓬莱镇组上统和K_2g白垩系中统灌口组为主（见图1）,其中J_3p泥岩大范围的分布在成都天府新区高楼山—秦皇寺中央商务区—倒石桥一带,其他区域均为K_2g泥岩,从城区东南方至西北方埋深为10～30 m,深度逐渐加深。

图 1 成都地区中等风化泥岩分布略图

Figure 1. Distribution of moderately weathered mudstone in Chengdu

下载: 全尺寸图片幻灯片

区内中等风化泥岩呈紫红色,层理清晰,风化裂隙较发育,巨厚层构造,整体结构。锤击易碎、声哑,用镐难挖掘,岩芯钻方可钻进。岩芯采取率达90%以上（图2）。通过对岩芯的X衍射和矿物成份分析,可知区内泥岩及其风化物含有超50%的SiO₂、Al₂O₃、Fe₂O₃,其不同的组合构成了以蒙脱石、伊利石为主的片状黏土矿物。表1为岩体物理力学参数统计表。

图 2 成都地区典型中等风化泥岩岩芯

Figure 2. Typical moderately weathered mudstone core in Chengdu

下载: 全尺寸图片幻灯片

表 1 中等风化泥岩物理力学性质统计表

Table 1. Physical and mechanical properties of rock

统计指标	天然密度/(g·cm^-3)	单轴抗压强度/MPa		黏聚力/MPa		内摩擦角/(°)
统计指标	天然密度/(g·cm^-3)	天然状态	饱和状态	天然状态	饱和状态	天然状态	饱和状态
最大值	2.62	9.67	8.20	1.2	0.85	40.1	38.6
最小值	2.30	2.71	1.56	0.4	0.23	33.7	31.4
平均值	2.48	6.00	3.88	0.8	0.49	37.9	35.5
样本容量	141	51	39	28	17	28	17

下载: 导出CSV

| 显示表格

2. 原位平板载荷试验与岩石单轴抗压强度试验对比

目前成都地区确定岩石地基承载力特征值主要为岩石单轴抗压强度折减法和原位平板岩基载荷试验法：①第一种方法简便但计算结果与实际地基承载力有较大出入；②第二种计算方法得到的结果普遍被认为是真实的,但费时费力。

笔者整理了24个工程实例中约100个中等风化泥岩的原位平板载荷试验点的相关测试数据,开展了2种方法确定地基承载力的对比分析,结果见表2,试验点覆盖了成都主城八区,具有较好的代表性。需要说明的是,文中所示意的原位平板载荷试验点绝大多数未达到明显的极限荷载,因此岩基的承载力特征值确定标准：①极限荷载f_u/3与比例界限荷载的较小值；②未达到极限状态取比例界限荷载。

表 2 岩基载荷试验与单轴抗压强度试验对比

Table 2. Comparison between load tests and uniaxial compressive strength tests

工程名称	工程地点	f_rk/MPa	f_a/kPa	ψ	停载位移/mm	点数
隆鑫	成华区	4.00	2044	0.51	5.420	3
润都科技	成华区	4.00	1981	0.49	6.760	3
蓉华·上林	成华区	3.05	1841	0.60	3.990	8
			1773	0.58	9.730
			1861	0.61	8.680
科创中心	成华区	5.00	2263	0.45	18.370	8
东方荟	锦江区	5.00	2157	0.43	3.640	4
东大街项目	锦江区	3.07	1900	0.62	3.520	3
仁恒置地广场	锦江区	3.43	1990	0.58	—	2
航天科技大厦	锦江区	6.00	2880	0.48	—	3
西部国金	锦江区	1.48	843	0.57	10.410	3
融御大楼	锦江区	7.30	3010	0.41	0.562	3
海桐三期	锦江区	7.90	2959	0.37	8.300	4
滨江30号地块	高新区	6.80	2740	0.40	10.700	3
半岛城邦	高新区	4.50	2021	0.45	6.600	9
龙湖世纪城	高新区	2.79	1800	0.65	33.190	8
川大科技园	双流区	3.92	1894	0.48	5.290	3
水电·云立方	龙泉驿	5.98	2400	0.40	5.500	3
视高天府公园	天府新区	6.48	2400	0.37	7.320	3
学府城	天府新区	4.99	2290	0.46	1.420	4
学府城	天府新区	4.99	2266	0.45	2.720	2
仁中风华一期	天府新区	5.64	2400	0.43	5.980	6
驿都水岸丽园	天府新区	5.58	2524	0.45	17.500	1
驿都水岸丽园	天府新区	5.00	2162	0.43	18.630	2
东方希望天祥	武侯区	4.39	2000	0.50	1.160	3
海洋乐园	武侯区	6.55	2500	0.38	4.260	6
中邮金融中心	武侯区	5.74	2400	0.42	2.200	3
田园晶品	新都区	3.1	1697	0.55	3.720	6
注：f_rk为岩石天然单轴抗压强度标准值；f_a为承载力特征值；ψ为折减系数。

下载: 导出CSV

| 显示表格

表2中,成都主城八区中等风化泥岩地基承载力特征值试验值70%以上集中在1500～2500 kPa,较规范DB51T5026建议最大值普遍大1.5倍以上,统计原位平板载荷试验与同条件岩石单轴抗压强度试验结果得出折减系数分布在0.37～0.70,总体值大于0.5（表3）；综合可见,折减系数呈现出随单轴抗压强度增加而递减的趋势。

表 3 折减系数和承载力特征值建议值

Table 3. Recommended values of reduction coefficient and characteristic value of bearing capacity

f_rk/MPa	ψ	f_a/kPa	说明
<2	0.7	500~1400	符号意义同表2,岩石单轴抗压强度为天然状态
2~4	0.5~0.7	1400~2000
4~6	0.4~0.5	2000~2400
6~8	0.37~0.4	2400~3000
>8	0.37	>3000

下载: 导出CSV

| 显示表格

表3所列的统计结果对于岩石单轴抗压强度小于2 MPa和大于8 MPa的岩体,由于没有试验样本,可分别取统计数据中折减系数最高区段和最低区段的ψ值,即取0.7,0.37,承载力特征值最小值按现行规范^[12]最小值500 kPa考虑。同时,上述统计结果多数是在未加载到岩基破坏的试验条件下得到的,实际的折减系数比该统计值还要大。但是,仍要注意的是,表3中岩石单轴抗压强度为天然状态,若当基岩浸水软化时,需要适当考虑折减系数减小。

3. 承载力的影响因素分析

进一步依托成都高新区在建的某超高层建筑项目,探讨不同承压板直径对研究区中等风化泥岩地基承载力取值的影响。

3.1 场地条件

该超高层建筑位于成都市南部天府新区秦皇寺中央商务区。场地地貌单元属宽缓浅丘,为剥蚀型浅丘陵地貌,建筑基础底板持力层为侏罗系蓬莱镇组（J_3p）中等风化泥岩。泥岩天然密度2.48 g/cm³、自然状态下单轴抗压强度平均值6.00 MPa、饱和状态单轴抗压强度平均值3.88 MPa。三轴天然抗剪强度参数平均值内摩擦角为37.9°,黏聚力为0.8 MPa。同时,根据钻孔波速测得岩体波速为2200～3200 m/s；室内岩块波速平均值为2370 m/s。

3.2 试验方案

承压板载荷试验在场地开挖的3口深井平硐中进行（编号分别为SJ01,SJ02,SJ03）。试验点点位见图3所示。

图 3 试验点位示意图

Figure 3. Schematic diagram of test sites

下载: 全尺寸图片幻灯片

图3中,SJ01深30 m（高程459.06 m）、SJ02深36 m（高程451.15 m）、SJ03深39 m（高程447.57 m）,井底平硐长×宽×高为2 m×2 m×8 m。每一平硐内分别开展承压板直径R为300,500,800 mm的载荷试验各1组,共9组。载荷试验操作过程严格参考规范^[16],开挖至目标层后对试验点进行粗砂找平,放置承压板、千斤顶、百分表等试验设备。检查无误后采用慢速维持加载法加载,加载分8～12级,每级加载后连续三次读数之差均不大于0.01 mm可施加下一级荷载；当某级荷载下24 h变形速率不能达到相对稳定标准或本级荷载的变形量大于前级荷载变形量的5倍或承压板周边的岩土出现明显隆起或径向裂缝持续发展等现象终止加载。试验现场照片见图4。

图 4 岩基平板载荷试验过程照片

Figure 4. Photos of bearing plate tests

下载: 全尺寸图片幻灯片

试验数据绘制p–s曲线,曲线起始直线段终点的前一级荷载为比例界限荷载；终载前一级荷载为极限荷载。将极限荷载除以3的安全系数,所得值与对应于比例界限的荷载相比较,取小值定为承载力特征值。

3.3 试验结果分析

典型p–s曲线见图5所示。

图 5 p–s曲线（以02深井300 mm承压板为例）

Figure 5. p–s curves (deep well No. 2, plate diameter 300 mm)

下载: 全尺寸图片幻灯片

（1）曲线整体上表现出变形随着荷载的增大而逐渐增大。

（2）以SJ02中直径300 mm载荷试验结果为例,试验荷载分12级加载,试验结束荷载为7800 kPa。加载结束时,位移持续增加且不能稳定,累计变形量为4.182 mm。从曲线上均可直接读出比例界限荷载和极限荷载。曲线第一个拐点（2400 kPa）对应的前一级荷载（2100 kPa）为比例界限荷载；极限荷载为曲线第二个拐点（7800 kPa）对应的前一级荷载（6300 kPa）。极限荷载的1/3与比例界限荷载对比取小值为承载力特征值,即为2100 kPa。

承载板直径与承载力特征值之间的关系见图6所示。其他试验点试验结果统计见表4所示。

图 6 承载板直径与承载力特征值的关系

Figure 6. Plate diameter vs. bearing capacity

下载: 全尺寸图片幻灯片

表 4 研究区中等风化泥岩承载力特征值试验值统计表（承压板载荷试验）

Table 4. In-suit test values of bearing capacity of moderately weathered mudstone in study area

试验点号竖井编号	承压板直径D/mm	原位试验				极限值/3对应荷载f_a/kPa	岩体完整性指数K_v
试验点号竖井编号	承压板直径D/mm	最大加载量/kPa	比例界限对应荷载/kPa	终止条件	裂缝情况	极限值/3对应荷载f_a/kPa	岩体完整性指数K_v
SJ01 （459.06 m）	300	9000	3000	趋近试验装置系统极限	无	2400	0.46
	500	9600	2400	位移持续增大,不能稳定	无	2400	0.46
	800	6300	2700	沉降增大,大于前一级沉降量的5倍	有	2300	0.43
SJ02 （451.15 m）	300	7800	2400	变形不能保持稳定	有	2100	0.39
	500	10800	2400	变形不能保持稳定	无	2000	0.39
	800	11700	2700	沉降增大,大于前一级沉降量的2倍	有	2100	0.39
SJ03 （447.54 m）	300	11800	3600	趋近试验装置系统极限	有	2800	0.49
	500	9600	3000	趋近试验装置系统极限	有	3000	0.50
	800	10800	3600	支硐上壁无法提供足够反力	无	2700	0.43

下载: 导出CSV

| 显示表格

对于同一平硐,中等风化泥岩地基承载力特征值差异小于10%。具体来说,SJ01深井泥岩承载力特征值为2300～2400 kPa；SJ02深井泥岩承载力特征值为2000～2100 kPa；SJ03深井泥岩承载力特征值为2700～3000 kPa。说明,相似性状的泥岩,载荷板尺寸对于其地基承载力性能影响程度不大（见图7所示）,可推测基础宽度对于同一性状的中等风化泥岩地基承载力的影响不明显。

图 7 旁压试验过程照片

Figure 7. Photos of pressuremeter tests

下载: 全尺寸图片幻灯片

不同平硐内试验结果略有差异,与岩体个体差异尤其是岩体完整性和矿物组分不无关系,试验表明：三口平硐内泥岩岩体完整性指数分别为0.43～0.46,0.39,0.43～0.50；黏土矿物含量分别为29%～30%,36%～47%,17%～25%。上述差异导致不同平硐内中等风化泥岩地基承载性能出现差异。另外,岩石地基承载性能差异亦是试验环境条件、操作人为误差等因素综合影响所造成,需进一步详细甄别和探讨。

4. 承载力确定方法讨论

4.1 承载力特征值修正折减法

上述超高层建筑项目中,3口深井平硐中进行承压板载荷试验同时亦在300 mm压板试验点位附近各取3个试样进行了室内单轴抗压强度试验（试验参照规范^[16]）,对修正折减系数法进行验证验证。根据（DB51/T5026—2001）^[13]和（GB50007—2011）^[6]中确定承载力特征值 $f_{a}$ 公式为

$f_{a} = ψ f_{rk}$ ,

(1)

式中, $f_{a}$ 为岩石地基承载力特征值（kPa）, $f_{rk}$ 为岩石饱和单轴抗压强度标准值（kPa）,软岩取为天然单轴抗压强度标准值）, $ψ$ 为折减系数,由当地经验确定。

结合前述研究,对式（1）参数进行修正,得

$f_{a} = ψ^{'} f_{rk}$ ,

(2)

式中, $f_{a}$ 为岩石地基承载力特征值（kPa）, $f_{rk}$ 为岩石饱和单轴抗压强度标准值（kPa,软岩取为天然单轴抗压强度标准值）, $ψ^{'}$ 为修正折减系数（按表3选取）。

试验及验证结果见表5所示。

表 5 修正折减系数法验证结果

Table 5. Test results of modified reduction coefficient method

竖井编号	编号	f_a/kPa	f_rk/MPa	平均f_rk/MPa	ψ	计算值	差异/%
SJ01	1	2400	4.9	5.96	0.40	2384	0.6
	2		5.8
	3		7.19
SJ02	1	2100	3.47	4	0.50	2000	4.7
	2		3.78
	3		4.39
SJ03	1	2800	6.89	7.1	0.39	2769	1.1
	2		8.31
	3		8.41

下载: 导出CSV

| 显示表格

从表5中计算结果可见,本文所提出的折减系数修正法所估算的岩基承载力特征值与原位载荷试验结果相近,差异在5%以内,效果较好,可以作为承载力计算的依据。根据单轴抗压强度分区不同其修正系数可按表3选取,取值区间可采用线性内插来确定。

4.2 旁压试验适宜性探讨

旁压试验其实质是横向载荷试验。软岩中旁压临塑荷载既与岩石单轴抗压强度有关又与岩体的裂隙发育程度有关,利用旁压试验能更好地反映工程岩体的实际强度^[10-11]。近年来,在长沙等地得到广泛应用,然而其在成都地区中等风化泥岩中的适宜性仍需进一步探讨。在上述项目场地中14口勘察钻孔+3口对比钻孔中旁压试验（见图5）,测试深度15～30 m不等。其中,3口对比钻孔TL05,JK14,JK12紧邻SJ01,SJ02,SJ03使试验结果具有可对比性。

采用PM-2B型预钻式旁压仪进行试验（见图7）,主机尺寸23 cm×36 cm×90 cm,最大压力6 MPa,试验操作严格参考规范[17,18],根据试验结果绘制P–V曲线,进一步确定初始压力P₀和临塑压力P_f。两个压力差值为承载力特征值f_ak。

旁压试验结果见表6所示。

表 6 旁压试验结果统计表

Table 6. Results of pressuremeter tests

钻孔编号	测试深度/m	P_f/kPa	P₀/kPa	f_a/kPa	钻孔波速/(m·s^-1)	岩体完整性指数K_v
JK04	28.5	3002.4	625.2	2377.2	2465	0.380
JK03	21.0	1399.5	350.0	1049.5	1873	0.231
JK10	20.0	1294.2	310.5	983.7	2023	0.256
JK12	13.0	1495.5	311.2	1184.3	2160	0.292
JK12	20.0	2670.0	698.5	1971.5	2204	0.304
JK14	28.0	3753.0	850.6	2902.4	2912	0.507
TL01	26.5	3790.2	849.6	2940.6	2445	0.414
TL03	18.5	4085.1	1120.3	2964.8	2754	0.530
TL05	28.0	2828.4	475.6	2352.8	2542	0.447
TL11	20.5	3715.9	850.6	2865.3	3013	0.469
TL13	16.5	3342.3	942.3	2400.0	2555	0.452
TL13	23.0	2209.1	487.2	1721.9	2241	0.348
TL14	17.5	2300.5	422.1	1878.4	2613	0.473
TL16	14.5	2489.0	475.6	2013.4	2178	0.296
TL16	20.5	2737.9	475.6	2262.3	2824	0.498
TL18	23.0	2590.6	432.2	2158.4	2523	0.441
TL22	23.0	2856.7	511.2	2345.5	2930	0.415
TL25	24.5	2707.0	530.1	2176.9	2347	0.381
TL25	26.0	4773.5	681.2	4092.3	3094	0.663
TL35	23.0	3032.5	625.2	2407.3	2659	0.490
TL37	18.0	2494.4	550.0	1944.4	2690	0.501

下载: 导出CSV

| 显示表格

从表6中可见,中等风化泥岩地基承载力特征值测试结果最小值为983.7 kPa,最大值为4092.3 kPa,范围较大,这与每一测试孔测试时周围环境、成孔质量、岩体质量、测试深度等有一定关系。因测试时环境和成孔质量属于随机无量化指标的影响因素。进一步对比表4,6中深井及其对比钻孔试验结果,以探究旁压试验适宜性。以深井平硐内的承压板试验结果为基准。对比结果见图8所示。

图 8 试验结果对比图

Figure 8. Comparison between test results

下载: 全尺寸图片幻灯片

对比结果显示,各测点的泥岩均为中等风化泥岩,测试深度、岩体完整性均相似,两种方法测试结果极为相近。尤其是深井SJ01和钻孔TL05,测试深度分别为30 m和28 m,岩体完整性指数均为0.46左右,得到的地基承载力特征值2300 kPa范围,可以认为采用承压板载荷试验、钻孔旁压试验确定的泥岩地基承载力特征值f_a可互为印证。

5. 结论

本文通过对24个场地约100个原位平板载荷试验与同条件岩石单轴抗压强度试验工程案例进行对比分析,讨论了成都地区中等风化泥岩计算公式中折减系数取值。进一步,依托成都高新区在建的某超高层建筑项目,探讨了修正折减系数法和旁压试验结果作为设计依据的建议。

（1）成都主城八区中等风化泥岩地基承载力特征值主要集中在1500～2500 kPa。

（2）统计原位平板载荷试验与同条件岩石单轴抗压强度试验结果得出折减系数分布在0.37～0.70,总体值大于0.5。

（3）本文所提出的折减系数修正法所估算的岩基承载力特征值在实际工程中实用性较强,其估算结果与原位载荷试验结果差异在5%以内,效果较好,可以作为承载力计算的依据。

（4）对于相似性状的泥岩,泥岩地基承载力受承压板直径影响不显著；且承压板载荷试验、钻孔旁压试验确定的地基承载力特征值可互为印证；

（5）上述成果,可用于该地区同类岩石地基参考,但是岩土体物理力学参数间的相关性取决于样本容量,对上述相关内容的细化有待更多的试验对比和检验及完善。

图 1 全域分析法的SSI计算模型

Figure 1. SSI model of direct method

下载: 全尺寸图片幻灯片

图 2 刚性基础的SSI计算模型

Figure 2. SSI model for rigid foundation

下载: 全尺寸图片幻灯片

图 3 柔性基础的SSI计算模型

Figure 3. SSI model for flexible foundation

下载: 全尺寸图片幻灯片

图 4 复杂地基条件下的SSI计算模型

Figure 4. Computational model for SSI analysis under complex soil conditions

下载: 全尺寸图片幻灯片

图 5 近场与远场界面地基阻抗函数的求解

Figure 5. Evaluation of foundation impedance at interface between near-field and far-field

下载: 全尺寸图片幻灯片

图 6 条带状均布荷载作用下的横观各向同性层状半空间

Figure 6. A transversely isotropic layered half-space subjected to uniformly distributed strip load

下载: 全尺寸图片幻灯片

图 7 表面荷载作用下的竖直位移沿z轴的分布

Figure 7. Distribution of vertical displacement along the z-axis under the action of surface load

下载: 全尺寸图片幻灯片

图 8 沉积河谷计算示意图

Figure 8. Schematic diagram of sedimentary valley

下载: 全尺寸图片幻灯片

图 9 层状沉积场地位移响应

Figure 9. Responses of sedimentary valley embedded in layered half-space

下载: 全尺寸图片幻灯片

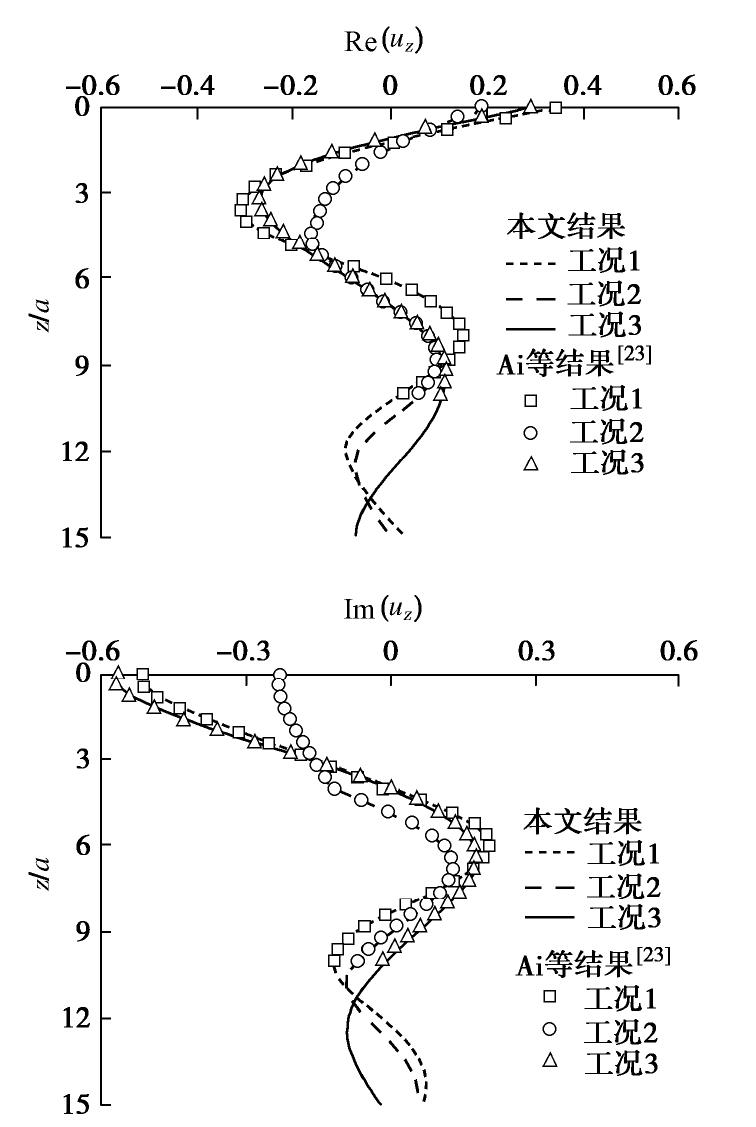
表 1 竖直向杨氏模量和剪切模量

Table 1 Vertical Young’s and shear moduli of three cases

工况	$G_{v}$ / $GPa$	${E^{'}}_{1}$ / $GPa$	${E^{'}}_{2}$ / $GPa$	${E^{'}}_{3}$ / $GPa$
工况1	2	6	3	2
工况2	2	12	3	2
工况3	2	6	6	4

下载: 导出CSV

参考文献(24)

[1]	KAUSEL E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9): 822-832. doi: 10.1016/j.soildyn.2009.11.001
[2]	GAZETAS G. Analysis of machine foundation vibrations: state of the art[J]. International Journal of Soil Dynamics and Earthquake Engineering, 1983, 2(1): 2-42. doi: 10.1016/0261-7277(83)90025-6
[3]	LAMB H. On the Propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society of London, Series A, 1904, 203: 1-42. doi: 10.1098/rsta.1904.0013
[4]	MINDLIN R D. Force at a point in the interior of a semi- infinite solid[J]. Physics, 1936, 7(5): 195-202. doi: 10.1063/1.1745385
[5]	REISSNER E. Stationäre, axialsymmetrische, durch eine schüttelnde Masse erregte Schwingungen eines homogenen elastischen Halbraumes[J]. Ingenieur-Archiv, 1936, 7(6): 381-396. doi: 10.1007/BF02090427
[6]	AS U V, YT U W. Lateral and rocking vibration of footings[J]. ASCE, J Soil Mech Found Div, 1971, 97(SM9): 1227-1248.
[7]	LUCO J E, WESTMANN R A. Dynamic response of circular footings[J]. Journal of Engineering Mechanics, ASCE, 1971, 97: 1381-1395.
[8]	LUCO J E, WESTMANN R A. Dynamic response of a rigid footing bonded to an elastic half space[J]. Journal of Applied Mechanics, 1972, 39(2): 527-534. doi: 10.1115/1.3422711
[9]	HADJIAN A H, TSENG W S, et al. The learning from the large scale Lotung soil-structure interaction experiments[C]//Proc. Second International Conference on Recent Advances in Geothechnial Earthquake Engineering and Soil Dynamics, 1991.
[10]	井口道雄. 大型模型による原子炉建屋と地盤の動的相互作用試験[C]//日本建築学会大会学術講演梗概集,1984-1987, 东京. MICHIO I. Dynamic interaction test between reactor building and ground using a large model[C]//Summary of Academic Lectures at the Architectural Society of Japan Conference, 1984-1987, Tokyo. (in Chinese)
[11]	Seismic Analysis of Safety-Related Nuclear Structures: ASCE Standard/SEI 4-16[S]. 2016.
[12]	Seismic Analysis of Safety-Related Nuclear Structures: ASCE Standard/SEI 4-98[S]. 1998.
[13]	KAUSEL E. Local transmitting boundaries[J]. Journal of Engineering Mechanics, ASCE, 1988, 114(6): 1011-1027. doi: 10.1061/(ASCE)0733-9399(1988)114:6(1011)
[14]	WOLF J P. A comparison of time‐domain transmitting boundaries[J]. Earthquake Engineering & Structural Dynamics, 1986, 14(4): 655-673.
[15]	DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25-42. doi: 10.1061/(ASCE)0733-9399(1994)120:1(25)
[16]	刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域黏弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51. doi: 10.3969/j.issn.1000-4750.2005.06.008 LIU Jing-bo, WANG Zhen-ning, DU Xiu-li, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46-51. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.06.008
[17]	廖振鹏, 黄孔亮, 杨柏坡, 等. 暂态波透射边界[J]. 中国科学(A辑), 1984(6): 556-564. https://www.cnki.com.cn/Article/CJFDTOTAL-JAXK198406007.htm LIAO Zhen-peng, HUANG Kong-liang, YANG Bai-po, et al. Transient wave transmission boundary[J]. Science China (A), 1984(6): 556-564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JAXK198406007.htm
[18]	WOLF J P. Dynamic Soil-Structure Interaction[M]. Englewood Cliffs: Prentice Hall, 1985.
[19]	LIN G, HAN Z J, LU S, et al. Wave motion equation and the dynamic Green’s function for a transverse isotropic multilayered half-space[J]. Soils and Foundations, 2017, 57(3): 397-411. doi: 10.1016/j.sandf.2017.05.007
[20]	李志远. 复杂层状地基中的波动传播和地下结构地震响应的研究[D]. 大连: 大连理工大学, 2019. LI Zhi-yuan. The Research of Wave Propagation and Seismic Response of Underground Structure in Complex Layered Soil[D]. Dalian: Dalian University of Technology, 2019. (in Chinese)
[21]	RADMANOVIC B, KATZ C. A high performance scaled boundary finite element method[C]//IOP Conference Series: Materials Science and Engineering, 2010, IOP Publishing.
[22]	LIN G, LU S, LIU J. Transmitting boundary for transient analysis of wave propagation in layered media formulated based on acceleration unit-impulse response[J]. Soil Dynamics and Earthquake Engineering, 2016, 90: 494-509. doi: 10.1016/j.soildyn.2016.09.021
[23]	AI Z Y, ZHANG Y F. Plane strain dynamic response of a transversely isotropic multilayered half-plane[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 211-219. doi: 10.1016/j.soildyn.2015.04.010
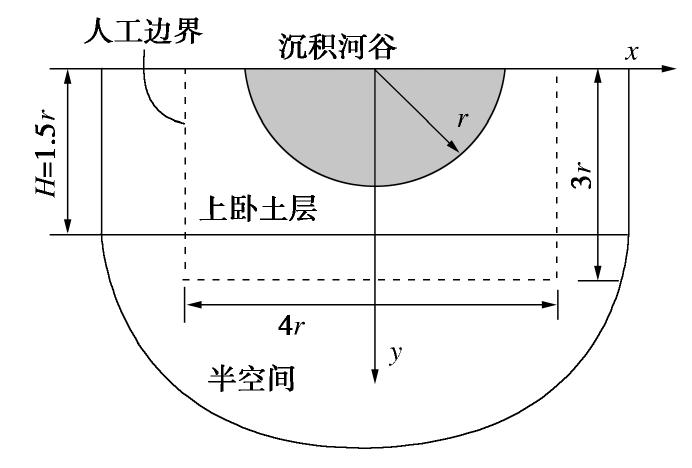
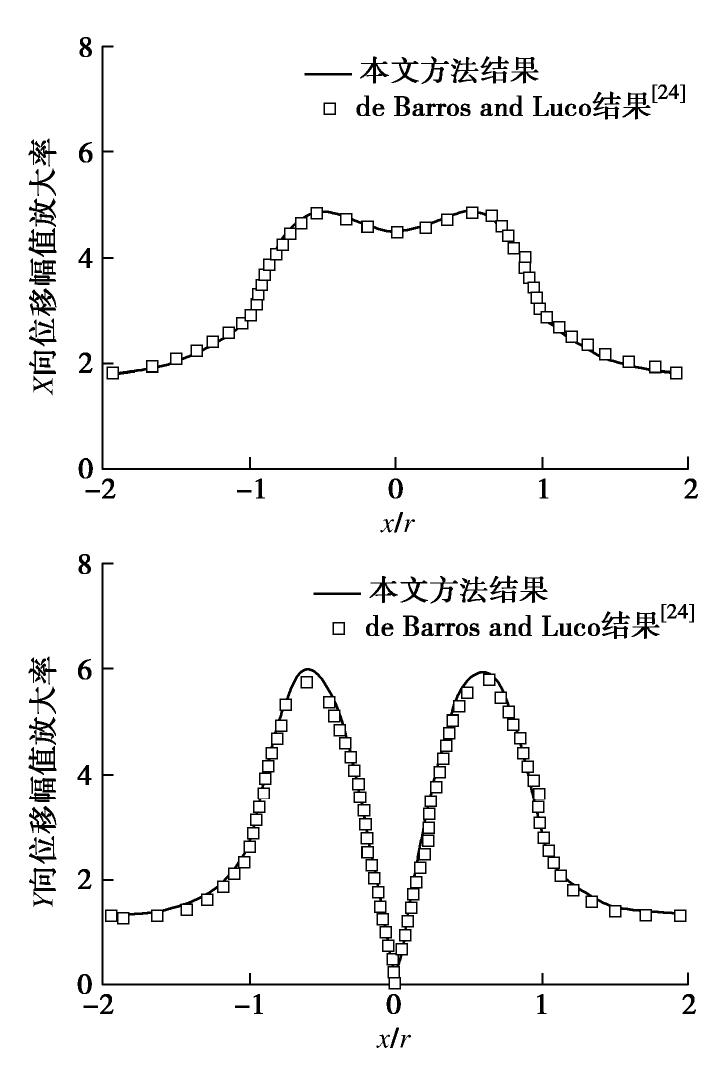
[24]	DE BARROS F C P, ENRIQUE LUCO J. Amplification of obliquely incident waves by a cylindrical valley embedded in a layered half-space[J]. Soil Dynamics and Earthquake Engineering, 1995, 14(3): 163-175. doi: 10.1016/0267-7261(94)00047-K