Measuring method for membrane penetration capacity of coarse-grained soil in triaxial tests
-
摘要: 粗粒土试验的橡皮膜嵌入效应使得试样体积变形测量结果失真,从而影响其强度变形指标测量精度。为此,在同一试验仪器上开展了多组不同直径试样粗粒土的等向固结三轴试验,分析了橡皮膜的嵌入量的变化规律和影响因素,在此基础上提出了一个计算粗粒土橡皮膜嵌入量的经验公式。研究表明,橡皮膜的嵌入量随围压的增大而增大,与其围压大体呈幂函数关系。相同围压下,随着试样直径的增加,橡皮膜的嵌入量占总体变的比例减小;试样直径相同时,围压变化对橡皮膜嵌入量占总体变比例的影响明显小于试样直径变化的影响,且随着试样直径的增大,影响逐渐降低。因此,粗粒土的强度变形试验应尽可能采用较大直径的试样进行,以降低橡皮膜嵌入量对其试验结果的影响。由于粗粒土的母岩性质和级配变化较大,既有橡皮膜嵌入量计算公式将明显低估堆石料试样的橡皮膜嵌入量,建议采用本文提出的方法对粗粒土试样橡皮膜嵌入量进行估算。Abstract: The membrane penetration effects displayed in the coarse-grained soil tests will distort the measurement of volume deformation of samples, thereby affecting the measuring accuracy of strength and deformation index. To this end, by using the same test apparatus, multiple series of isotropic consolidation triaxial tests on the samples of coarse-grained soil with different diameters are implemented. The changing rules of membrane penetration capacity and the related impact factors are analyzed, and an empirical formula is proposed to calculate the membrane penetration capacity of coarse-grained soil. It is shown that the membrane penetration capacity increases with the increase of the confining pressure, and the relationship roughly follows a power function. Under the same confining pressure, with the increase of the sample diameter, the capacity of membrane penetration decreases. The influences of the confining pressure on the membrane penetration capacity are significantly smaller than those of sample size which gradually decreases as the sample diameter increases. Therefore, the strength and deformation tests on coarse-grained soil should be carried out by preparing larger-diameter samples, so that the influences of the membrane penetration effects can be greatly reduced. Due to the great changes in the nature and gradation of coarse-grained parent rock, the existing formulas for the membrane penetration capacity will significantly underestimate the membrane penetration effects of rock-fill samples. It is recommended to use the proposed method to estimate the membrane penetration capacity of coarse-grained soil.
-
Keywords:
- coarse-grained soil /
- membrane /
- penetration capacity /
- measuring method
-
0. 引言
室内三轴试验中,通过在试样周围套入橡皮膜,试样形成不透水的界面,有助于在测试过程中施加边界应力并控制排水条件。根据试验的需要,试验室内橡皮膜形状各异,最常见的是常规三轴试验和真三轴试验所用的圆柱形和长方体型橡皮膜。在进行大型常规固结排水试验时,试样周边的粗粒土不平整,在侧向压力作用下,橡皮膜嵌入到颗粒间的孔隙中,导致测量结果高估试样的体变;而在固结不排水试验中,则导致孔压增大,试样有效应力下降,造成试验结果失真。橡皮膜嵌入量的问题最早是由Newland等[1]提到,并在后来的试验中[2]对测得的试样体变进行修正,橡皮膜的嵌入量为测得的总体积与试样实际体变量之差。
国内外对于橡皮膜嵌入问题的处理主要有3种方法:①通过改变橡皮膜的受力条件,降低橡皮膜嵌入对试验结果的影响,如在橡皮膜与试样之间涂聚氨酯、液体橡胶,或铺细砂、塑料板或铜片[3-8]。但这类方法会对轴向产生较大的阻抗力,需对试样后期偏应力进行校正。铺砂法虽可以保证试样的均匀性,但该方法只限于重塑样[9]。②通过测量系统改进实现膜嵌入量的测量和修正,如Kramer等[10]提出了双层膜法测量橡皮膜嵌入量,以及改进的手动补偿橡皮膜顺变性的方法[11];Ramana等[12]、Tokimatsu等[13]、Nicholson等[14]改进了上述系统,通过计算机控制,不断地将水注入或抽出,实现了不排水条件下橡皮膜顺变性引起的测量结果误差补偿,但是该方法仍然存在膜的厚度会影响压力的均匀传播,以及在不饱和试样在试验过程中量测系统的体积随压力变化而发生变化,与三轴不排水试验试样体积不变的假定相矛盾,而且此方法操作难度较大。在橡皮膜嵌入量计算方面,Roscoe等[15]将不同直径而高度相同的铜棒放置在试样中,通过总体积的变化与铜棒直径的线性关系,确定橡皮膜的嵌入量。但Roscoe的铜棒法存在如下明显不足:a)试样径向应变将大于轴向应变,从而高估橡皮膜的嵌入量;b)高围压下,试样体积变化与铜棒直径不完全呈线性关系;c)粗粒土在静水压力作用下并非各向同性,与其各向同性假设不符[16]。为此,Raju等[17]、Bopp等[18]、吉恩跃等[19]对Roscoe等[15]的铜棒法进行了改进;Frydman等[20]开展了不同粒径玻璃球体的空心圆柱试验,发现在橡皮膜的单位嵌入量与围压的半对数呈线性关系,其斜率与颗粒平均粒径的半对数呈线性关系。Vaid等[21]基于Frydman等[20]的研究结果,通过不同直径的试样提出了两种确定橡皮膜嵌入量的计算方法。③通过弹性力学方法推导膜嵌入量的解析表达式
εm =ηdg (Pdg /Emtm)1/3(P为试样围压,Em,tm分别为橡皮膜的弹性模量和厚度,η为标定参数)并运用实测数据标定相关参数。此类方法大多设定特征粒径dg (通常考虑d10 ,d20 ,d50 )和围压为变量,对不同材料的橡皮膜嵌入量进行估算,并建立围压与单位嵌入量的关系。因此,其在计算宽级配粗粒土试样橡皮膜嵌入量时误差较大。为克服上述方法的不足,本文提出一种利用多组不同直径试样的等向固结三轴试验来推求单位面积橡皮膜嵌入量的方法[22]。
1. 基本原理
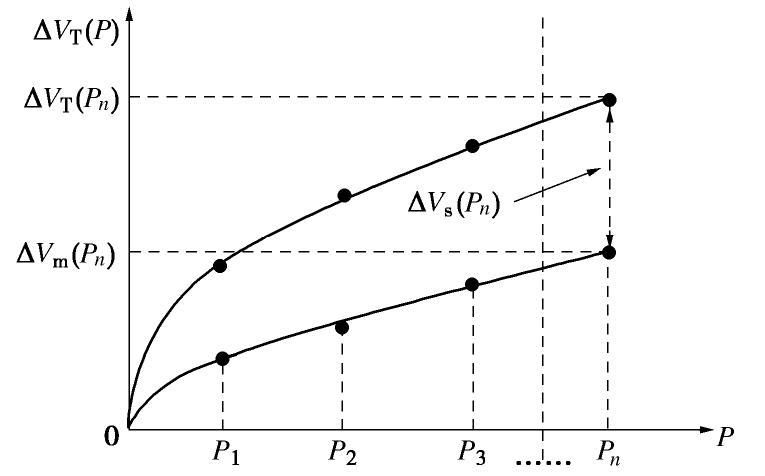
对于固结排水试验,实测粗粒土的体积应变包含两部分:土骨架的体积变化和橡皮膜嵌入引起的体积变化(图1),即
ΔVT(P)=ΔVs(P)+ΔVm(P), (1) 式中,
P 为围压,ΔVT(P) 为特定围压下的总排水量,ΔVs(P) 为特定围压下试样的体变量,ΔVm(P) 为特定围压下橡皮膜的嵌入量。由于试样的体积变化量为
ΔVs(P)=εs(P)V0, (2) 橡皮膜的嵌入量为
ΔVm(P)=εm(P)Am, (3) 式中,
V0 为试样的初始体积,εs(P) ,εm(P) 分别为在特定围压下的土体体积应变和橡皮膜单位面积嵌入量;Am 为试样的侧向表面积。此时,式(1)可表述为
ΔVT(P)=14εs(P)πD2H+εm(P)πDH=14εs(P)AmD+εm(P)Am, (4) 式中,D为试样的直径,H为试样的高度。
将式(4)进行变换后得到
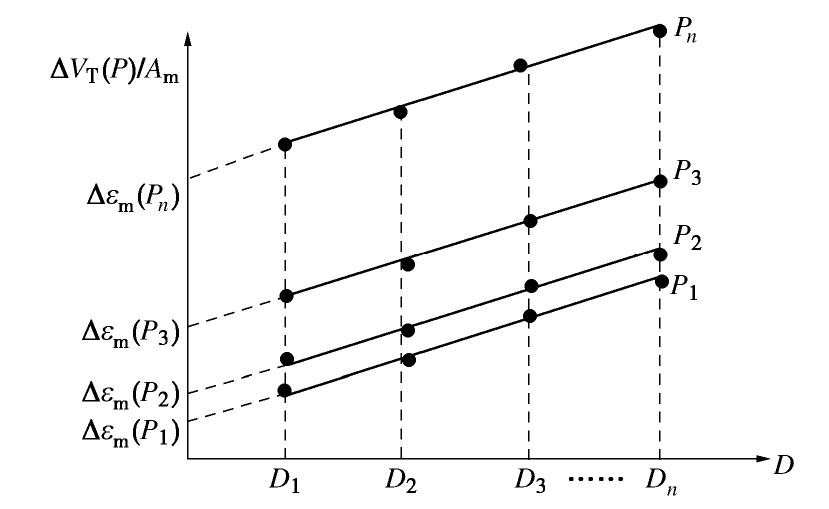
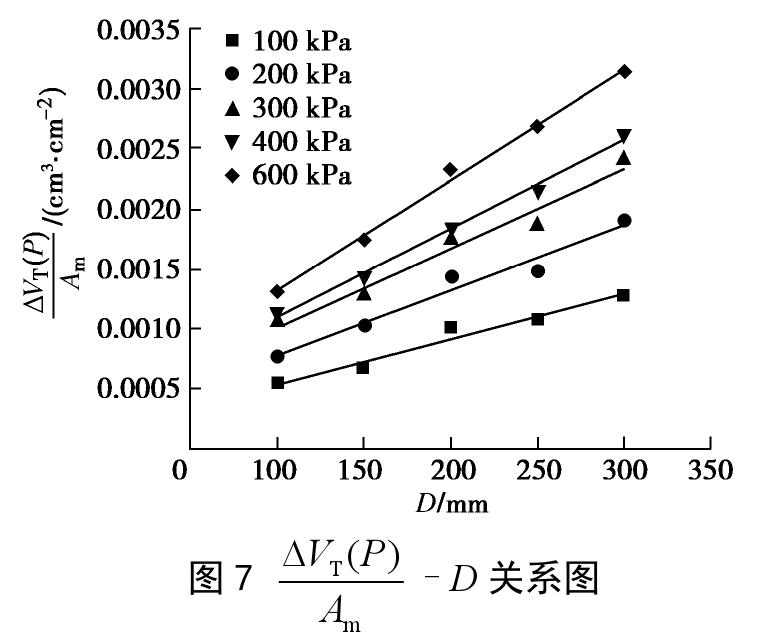
ΔVT(P)/Am=14εs(P)D+εm(P)。 (5) 由式(5),给出了理论推导橡皮膜嵌入量的方法示意图(如图2),以试样排水量与其侧向表面积的比值ΔVT(P)/Am为纵坐标,试样直径D为横坐标,则可得到试样排水量与其直径的关系。显然,图2中纵坐标的截距
εm(P) 即为橡皮膜单位面积嵌入量。2. 试验方案
2.1 试验装置
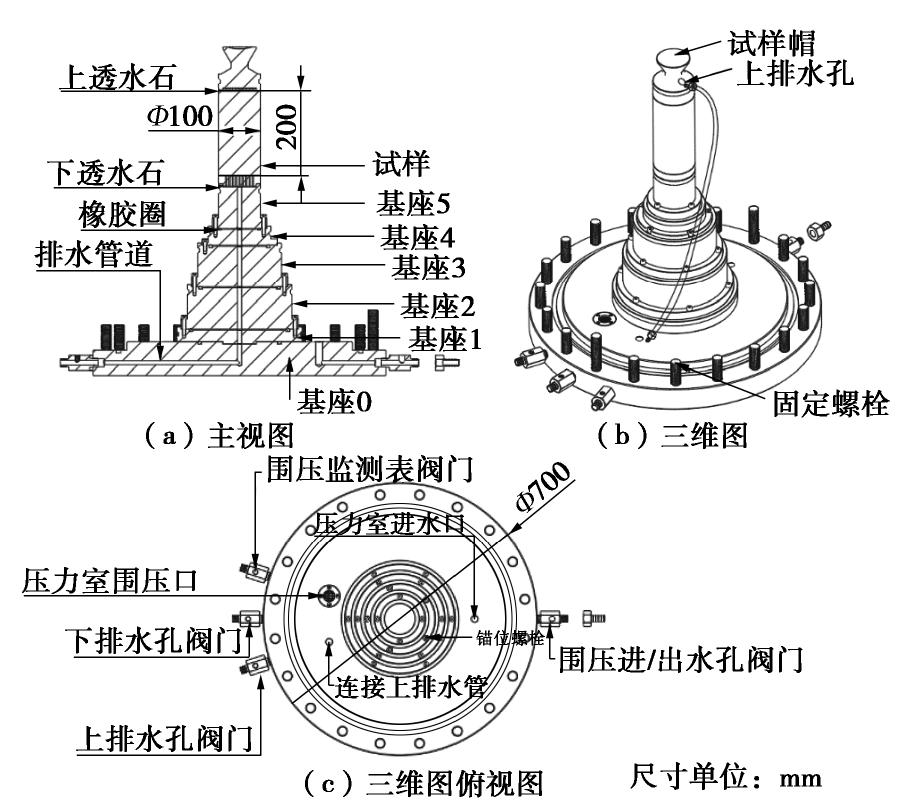
在南京水利科学研究院某大型三轴试验仪上设计并改造了一套多尺度底盘装置(如图3)。该装置以三轴试验仪300 mm直径试样尺寸为基础,考虑上部加压杆的可伸缩长度,根据试验需要加装不同高度的底座(如图3(a)),每层底盘间配有密封圈。不同底座可通过螺栓进行连接,连接螺栓错位分布以解决螺栓孔间的相互影响(如图3(c))。此外,该装置配有不同试样的试样帽,试样帽侧方开有排水孔。上述试验装置可在同一套测量系统上进行100,150,200,250,300 mm直径试样的常规三轴试验,有效消除了因不同试验仪器的系统误差对试验结果的影响。
2.2 试验材料与试验方法
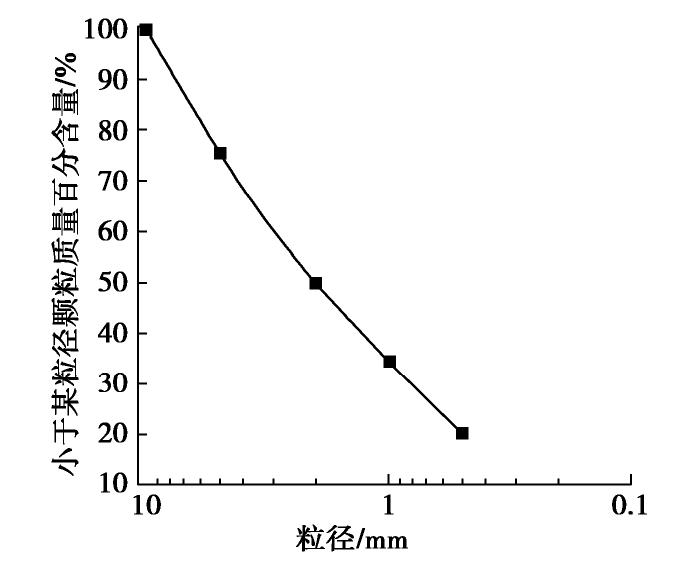
试验所用料为某堆石坝堆石料破碎所得,粒径分为0.5~1,1~2,2~5,5~10 mm五组,级配曲线与材料其它基本参数分别见图4和表1。三轴试验试样直径分别设置为100,150,200,250,300 mm,每组做3个平行试验,共计15组试样。橡皮膜厚度为2 mm,相应的橡皮膜弹性模量Em=1.608 MPa[23]。根据前人研究[24],在初始等向固结条件下,采用分级加载的方法(围压为100,200,400,600 kPa)测量不同围压下试样的排水量。
表 1 材料基本参数Table 1. Basic parameters of materials材料 颗粒相对质量密度G 孔隙比e 试验干密度ρd/(g·cm-3) 平均粒径dg/mm 堆石料 2.70 0.59 1.70 2 2.3 制样及加载过程
如图5所示,每个试样分5层进行装样,装填完成后对试样进行抽真空,使得试样保持直立,抽真空后将试样帽紧密套好。连接好上下排水管,套上压力室,对试样压力室进行充水,待压力室上部出水口有持续水流出一段时间后关闭该出水口阀门,并开始对试样进行饱和,饱和水头2 m,待饱和完成后,对试样加载20 kPa围压以保证橡皮膜贴紧试样壁同时将排水量清零。
制样完成后,对试样进行分级加载并记录不同围压下试样排水量。加载时速率不宜过快,防止加载过快引起孔压上升过快而来不及消散而引起不必要的测量误差。此外考虑加载时间过长带来的流变量影响,确定每加载到预定值稳定且排水量无较大变化后即可进行下一级围压的加载。
3. 试验结果与分析
3.1 橡皮膜嵌入量分析
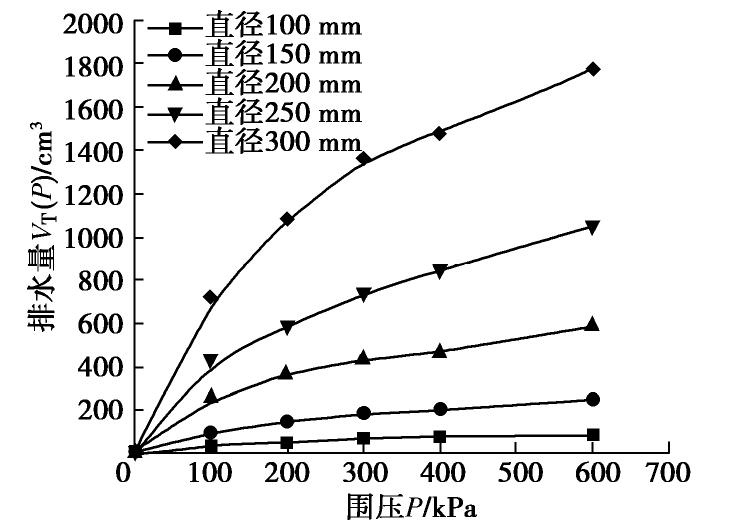
试验得到的不同直径堆石料试样在不同围压下的排水量
ΔVT(P) 见图6。可以看出,随着围压的增加,试样的排水量增大,大体呈幂函数关系,且试样直径越大,其排水量越大。图7为试验得到的试样排水量与其侧向表面积的比值
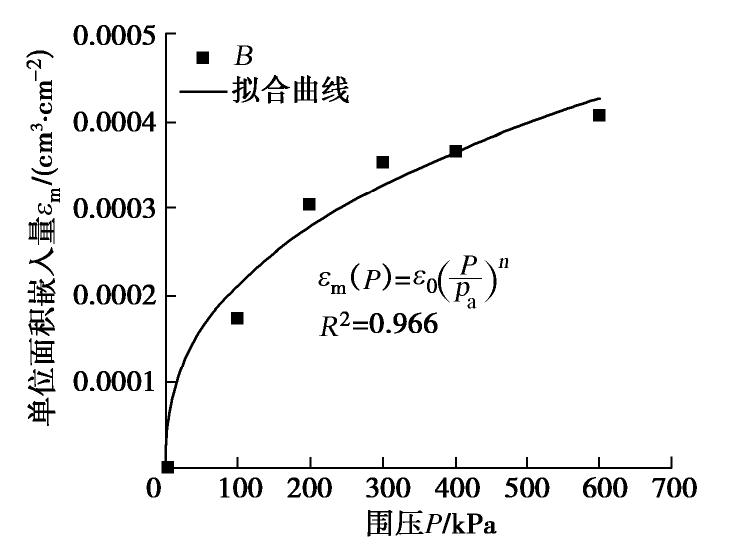
ΔVT(P) /Am与试样直径D的关系。可以看出,随着围压的增加,ΔVT(P) /Am的值增大,且与试样直径D呈现良好的线性关系。由图7推求得到的橡皮膜单位面积嵌入量与围压的关系如图8所示,同样,随着围压的增加,橡皮膜的单位嵌入量逐渐增大,橡皮膜的单位嵌入量与试样围压大体呈幂函数关系。经过拟合橡皮膜的单位嵌入量与围压关系试验结果,可得到一个关于橡皮膜单位嵌入量与围压关系的经验公式:
εm(P)=ε0(Ppa)n, (6) 式中,
pa 为标准大气压力值,ε0 为一个标准大气压力时的橡皮膜嵌入量。利用式(6)可计算得到不同围压下橡皮膜的单位嵌入量。表2给出了根据橡皮膜的单位嵌入量计算得到的不同试样直径在不同围压下,橡皮膜的嵌入体积占总排水体积的百分比。由表2可以看出,试样直径变化对橡皮膜的嵌入体积百分比具有显著影响,相同围压下,随着试样直径的增加,橡皮膜的嵌入量减小;试样直径相同,围压变化对橡皮膜的嵌入体积百分比有一定影响,但明显小于试样直径变化的影响,且随着试样直径的增大,影响逐渐降低,围压变化对直径300 mm试样的嵌入体积百分比的影响最小,在200 kPa时不同直径试样的嵌入量占比出现突变现象,这是因为试样初始围压为100 kPa,试样仍处于疏松状态,在200 kPa时,试样内部颗粒间因挤压产生的变化,此时试样的体变有一个瞬时增大的过程,而产生突变现象,随着围压的增加,试样体积变化逐渐平缓,对总体变化规律影响较小。因此,建议堆石料的强度变形试验,应尽可能采用较大直径的试样进行,以降低橡皮膜嵌入量对其试验结果的影响。
表 2 不同直径与不同围压下橡皮膜嵌入量占比Table 2. Penetration proportions under different diameters and confining pressures(%) 围压/kPa 直径/mm 100 150 200 250 300 100 32.1 25.6 17.2 16.1 13.7 200 39.4 29.4 21.1 20.5 15.9 300 33.5 27.4 20.3 18.8 14.6 400 32.1 25.6 19.8 17.0 14.0 600 30.8 23.3 17.5 15.1 13.0 3.2 与常用橡皮膜嵌入量计算公式的比较
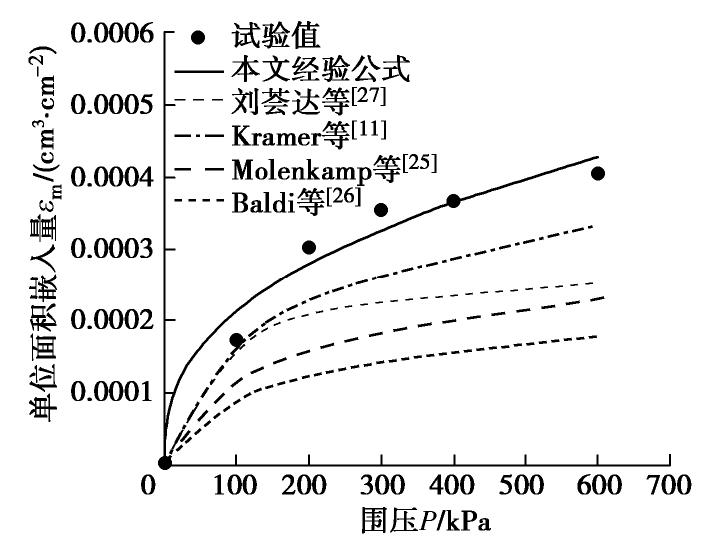
目前常用的粗粒土三轴试验橡皮膜嵌入量计算公式主要为以下两类:①基于弹性力学方法推导的解析表达式εm=ηdg(Pdg/Emtm)1/3(P为围压,Em,tm分别为橡皮膜的弹性模量和厚度,η为标定参数),Kramer等[10]、Molenkamp等[25]、Baldi等[26]根据粗粒土三轴试验,确定η分别为0.23,0.16,0.125;另一类是刘荟达等[27]采用粗粒土的特征粒径
d10 ,d20 ,d50 计算其橡皮膜嵌入量的经验计算公式;S=0.0125d1.2910+0.113d0.7520+0.00382d1.2650 ,Δvm=S⋅lgσ′c 。} (7) 式中
Δvm 为单位嵌入体积单位;σ′c 为试样固结围压。本文基于粗粒土多组不同直径试样的等向固结三轴试验提出的橡皮膜嵌入量公式与上述两类公式计算得出的橡皮膜单位嵌入量结果比较如图9所示。从图9可以看出,各公式计算得出的橡皮膜单位嵌入量均随围压的增大而增大,但本文提出的经验公式计算得出的橡皮膜单位嵌入量明显大于前两类公式。由于粗粒土的母岩性质和级配变化较大,简单采用既有橡皮膜嵌入量计算公式可能导致橡皮膜嵌入量估算值产生较大误差,建议采用本文方法对橡皮膜嵌入量进行估算。
4. 结论
本文在同一试验仪器上开展了多组不同直径试样粗粒土的等向固结三轴试验,研究了橡皮膜的嵌入量的变化规律和影响因素,在此基础上提出了一个计算粗粒土橡皮膜嵌入量的经验公式,得到以下3点结论。
(1)粗粒土三轴试验过程中,橡皮膜会明显嵌入试样中,导致测量出的试样体积变形增大,从而影响粗粒土强度变形指标测量精度。因此粗粒土三轴试验中的橡皮膜嵌入效应不可忽略。
(2)试验结果表明,橡皮膜的嵌入量随围压的增大而增大,与其围压大体呈幂函数关系。相同围压下,随着试样直径的增加,橡皮膜的嵌入量占总体变的比例减小;试样直径相同,围压变化对橡皮膜的嵌入量的影响明显小于试样直径变化的影响,且随着试样直径的增大,影响逐渐降低。建议堆石料的强度变形试验,应尽可能采用较大直径的试样进行,以降低橡皮膜嵌入量对其试验结果的影响。
(3)由于粗粒土的母岩性质和级配变化较大,简单采用既有橡皮膜嵌入量计算公式可能导致橡皮膜嵌入量估算值产生较大误差,建议采用本文方法对橡皮膜嵌入量进行估算。另外,鉴于本文采用的是10 mm粒径的堆石料,为了更好的验证本文提出的经验公式的适用性,后续将开展更大粒径以及更高围压下的堆石料嵌入量试验进行该公式的验证。
-
表 1 材料基本参数
Table 1 Basic parameters of materials
材料 颗粒相对质量密度G 孔隙比e 试验干密度ρd/(g·cm-3) 平均粒径dg/mm 堆石料 2.70 0.59 1.70 2 表 2 不同直径与不同围压下橡皮膜嵌入量占比
Table 2 Penetration proportions under different diameters and confining pressures
(%) 围压/kPa 直径/mm 100 150 200 250 300 100 32.1 25.6 17.2 16.1 13.7 200 39.4 29.4 21.1 20.5 15.9 300 33.5 27.4 20.3 18.8 14.6 400 32.1 25.6 19.8 17.0 14.0 600 30.8 23.3 17.5 15.1 13.0 -
[1] NEWLAND P L, ALLELY B H. Volume changes in drained taixial tests on granular materials[J]. Géotechnique, 1957, 7(1): 17-34. doi: 10.1680/geot.1957.7.1.17
[2] NEWLAND P L, ALLELY B H. Volume changes during undrained triaxial tests on saturated dilatant granular materials[J]. Géotechnique, 1959, 9(4): 174-182. doi: 10.1680/geot.1959.9.4.174
[3] RAJU V S, VENKATARAMANA K. Undrained triaxial tests to assess liquefaction potential of sands: effect of membrane penetration[C]//Proc Int Symp on Soils under Cyclic and Transient Loading Swansea, 1980, Wales.
[4] KIEKBUSCH M, SCHUPPENER B. Membrane penetration and its effects on pore pressures[J]. Journal of the Geotechnical Engineering Division, 1977, 103(11): 1267-1280. doi: 10.1061/AJGEB6.0000519
[5] EVANS M D. Density changes during undrained loading-membrane compliance[J]. Journal of Geotechnical Engineering, 1992, 118(12): 1924-1936 doi: 10.1061/(ASCE)0733-9410(1992)118:12(1924)
[6] SUTTS L D, SHEAHAN T C, TSOI W Y, et al. Membrane penetration remedy for the testing of lightly cemented scrap rubber tire Chips[J]. Geotechnical Testing Journal, 2009, 32(1): 55-63.
[7] KNODEL P C, CHOI J W, ISHIBASHI I. An experimental method for determining membrane penetration[J]. Geotechnical Testing Journal, 1992, 15(4): 413-417. doi: 10.1520/GTJ10258J
[8] LADE P V, HERNANDEZ S B. Membrane penetration effects in undrained tests[J]. Journal of the Geotechnical Engineering Division, 1977, 103(2): 109-125. doi: 10.1061/AJGEB6.0000377
[9] RAGHUNANDAN M E, SHARMA J S, PRADHAN B. A review on the effect of rubber membrane in triaxial tests[J]. Arabian Journal of Geosciences, 2015, 8(5): 3195-3206. doi: 10.1007/s12517-014-1420-0
[10] KRAMER S L, SIVANESWARAN N. Stress-path-dependent correction for membrane penetration[J]. Journal of Geotechnical Engineering, 1989, 115(12): 1787-1804. doi: 10.1061/(ASCE)0733-9410(1989)115:12(1787)
[11] SIVATHAYALAN S, VAID Y P. Truly undrained response of granular soils with no membrane-penetration effects[J]. Canadian Geotechnical Journal, 1998, 35(5): 730-739. doi: 10.1139/t98-048
[12] RAMANA K V, RAJU V S. Constant-volume triaxial tests to study the effects of membrane penetration[J]. Geotechnical Testing Journal, 1981, 4(3): 117-122. doi: 10.1520/GTJ10777J
[13] TOKIMATSU K, NAKAMURA K. A Liquefaction test without membrane penetration effects[J]. Soils and Foundations, 1986, 26(4): 127-138. doi: 10.3208/sandf1972.26.4_127
[14] NICHOLSON P G, SEED R B, ANWAR H A. Elimination of membrane compliance in undrained triaxial testing II. Mitigation by injection compensation[J]. Canadian Geotechnical Journal, 1993, 30(5): 739-746. doi: 10.1139/t93-066
[15] ROSCOE K H, SCHOFIELD A N, THURAIRAJAH A. An evaluation of test data for selecting a yield criterion for soils[M]//Laboratory Shear Testing of Soil, West Conshohocken: ASTM International, 1964: 111-128.
[16] EL-SOHBY M A, ANDRAWES K Z. Deformation characteristics of granular materials under hydrostatic compression[J]. Canadian Geotechnical Journal, 1972, 9(4): 338-350. doi: 10.1139/t72-038
[17] RAJU V S, SADASIVAN S K. Membrane penetration in triaxial tests on sands[J]. Journal of the Geotechnical Engineering Division, 1974, 100(4): 482-489. doi: 10.1061/AJGEB6.0000042
[18] BOPP P A, LADE P V. Membrane penetration in granular materials at high pressures[J]. Geotechnical Testing Journal, 1997, 20(3): 272-278.
[19] 吉恩跃, 朱俊高, 王青龙, 等. 粗颗粒土橡皮膜嵌入试验研究[J]. 岩土工程学报, 2018, 40(2): 346-352. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802021.htm JI En-yue, ZHU Jun-gao, WANG Qing-long, et al. Experiment of membrane penetration on coarse grained soil[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 346-352. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802021.htm
[20] ETRIS S F, LIRB K C, SISCAV K, et al. The membrane effect in triaxial testing of granular soils[J]. Journal of Testing and Evaluation, 1973, 1(1): 37-41. doi: 10.1520/JTE11599J
[21] VAID Y P, NEGUSSEY D. A critical assessment of membrane penetration in the triaxial test[J]. Geotechnical Testing Journal, 1984, 7(2): 70-76. doi: 10.1520/GTJ10595J
[22] 吉恩跃, 陈生水, 傅中志, 等. 直接测量三轴试验橡皮膜嵌入量的装置及其测量方法: CN109060543B[P]. 2018-12-21. JI En-yue, CHEN Sheng-shui, FU Zhong-zhi, et al. Device for Directly Measuring Embedding Amount of Triaxial Rubber Membrance and Measuring Method Thereof: CN109060543B[P]. 2018-12-21. (in Chinese)
[23] 龚选. 粗粒土强度特性及三轴试验橡皮膜影响的研究[D]. 南京: 河海大学, 2014. GONG Xuan. Test Study on Effects of Rubber Membrane Constraint in Triaxial Test and Strength Characteristics of Coarse-Grained Soil[D]. Nanjing: Hohai University, 2014. (in Chinese)
[24] 张丙印, 吕明治, 高莲士. 粗粒料大型三轴试验中橡皮膜嵌入量对体变的影响及校正[J]. 水利水电技术, 2003, 34(2): 30-33. https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ200302010.htm ZHANG Bing-yin, LÜ Ming-zhi, GAO Lian-shi. Correction of membrane penetration in large-scale triaxial tests for granular materials[J]. Water Resources and Hydropower Engineering, 2003, 34(2): 30-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ200302010.htm
[25] MOLENKAMP F, LUGER H J. Modelling and minimization of membrane penetration effects in tests on granular soils[J]. Géotechnique, 1981, 31(4): 471-486. doi: 10.1680/geot.1981.31.4.471
[26] BALDI G, NOVA R. Membrane penetration effects in triaxial testing[J]. Journal of Geotechnical Engineering, 1984, 110(3): 403-420. doi: 10.1061/(ASCE)0733-9410(1984)110:3(403)
[27] 刘荟达, 袁晓铭, 王鸾, 等. 宽级配砾性土橡皮膜嵌入量计算新方法[J]. 岩石力学与工程学报, 2020, 39(4): 804-816. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202004014.htm LIU Hui-da, YUAN Xiao-ming, WANG Luan, et al. A new calculation method for membrane penetration in wide-graded gravelly soils[J]. Chinese Journal of Rock Mechanics Engineering, 2020, 39(4): 804-816. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202004014.htm
-
期刊类型引用(2)
1. 吴杨,吴毅航,马林建,崔杰,刘建坤,戴北冰. 南海岛礁珊瑚砂砾混合料动力特性试验研究. 岩土工程学报. 2024(01): 63-71 .  本站查看
本站查看
2. 吴国立,李东升,刘晓光,冯思超. 粗粒土三轴试验力学与长期变形特性研究综述. 科技创新与应用. 2023(08): 88-91 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: