Influences of temperature change on axial force and deformation of inner support in deep foundation pits
-
摘要: 温度变化对深基坑内支撑轴力和变形的影响明显,当支撑长度和断面尺寸较大时,温差引起的内支撑轴力和变形增量不容忽视。基于内支撑–支护桩–土相互作用且变形协调的前提,提出了采用弹性抗力法对单道支撑和多道支撑的温度应力简化计算方法。结合多道内支撑的深基坑工程案例,采用自主研发的地质灾害与工程结构安全自动化监测预警平台(简称监测平台),实现了深基坑内支撑系统温度变化影响的实时、连续、在线的自动化监测。监测结果验证了本文提出的多道水平支撑温度应力简化计算方法的可行性和可靠性;证明了监测平台是深基坑支撑轴力和变形实时、连续、在线最有效的监测方法。Abstract: The effects of temperature change on axial force and deformation of inner support in deep foundation pits are obvious, and the axial force and deformation increment of inner support caused by the temperature difference cannot be ignored when the support length and section size are large. Based on the premise of inner support-retaining pile-soil interaction and deformation coordination, a simplified method for temperature stress with one-layer support and multi-layer supports is proposed by using the elastic resistance method. Based on the case of deep foundation pit with multi-level supports, the integration platform is used to realize the real-time, continuous and online automatic monitoring of the effects of temperature change in the support system in deep foundation pits. The feasibility and reliability of the proposed simplified method for temperature stress of multi-level horizontal supports is verified by the monitoring results, and it is proved that the integration platform is the most effective monitoring method for the axial force and deformation of inner support in deep foundation pits.
-
Keywords:
- deep foundation pit /
- inner support /
- temperature /
- axial force /
- deformation
-
0. 引言
室内三轴试验中,通过在试样周围套入橡皮膜,试样形成不透水的界面,有助于在测试过程中施加边界应力并控制排水条件。根据试验的需要,试验室内橡皮膜形状各异,最常见的是常规三轴试验和真三轴试验所用的圆柱形和长方体型橡皮膜。在进行大型常规固结排水试验时,试样周边的粗粒土不平整,在侧向压力作用下,橡皮膜嵌入到颗粒间的孔隙中,导致测量结果高估试样的体变;而在固结不排水试验中,则导致孔压增大,试样有效应力下降,造成试验结果失真。橡皮膜嵌入量的问题最早是由Newland等[1]提到,并在后来的试验中[2]对测得的试样体变进行修正,橡皮膜的嵌入量为测得的总体积与试样实际体变量之差。
国内外对于橡皮膜嵌入问题的处理主要有3种方法:①通过改变橡皮膜的受力条件,降低橡皮膜嵌入对试验结果的影响,如在橡皮膜与试样之间涂聚氨酯、液体橡胶,或铺细砂、塑料板或铜片[3-8]。但这类方法会对轴向产生较大的阻抗力,需对试样后期偏应力进行校正。铺砂法虽可以保证试样的均匀性,但该方法只限于重塑样[9]。②通过测量系统改进实现膜嵌入量的测量和修正,如Kramer等[10]提出了双层膜法测量橡皮膜嵌入量,以及改进的手动补偿橡皮膜顺变性的方法[11];Ramana等[12]、Tokimatsu等[13]、Nicholson等[14]改进了上述系统,通过计算机控制,不断地将水注入或抽出,实现了不排水条件下橡皮膜顺变性引起的测量结果误差补偿,但是该方法仍然存在膜的厚度会影响压力的均匀传播,以及在不饱和试样在试验过程中量测系统的体积随压力变化而发生变化,与三轴不排水试验试样体积不变的假定相矛盾,而且此方法操作难度较大。在橡皮膜嵌入量计算方面,Roscoe等[15]将不同直径而高度相同的铜棒放置在试样中,通过总体积的变化与铜棒直径的线性关系,确定橡皮膜的嵌入量。但Roscoe的铜棒法存在如下明显不足:a)试样径向应变将大于轴向应变,从而高估橡皮膜的嵌入量;b)高围压下,试样体积变化与铜棒直径不完全呈线性关系;c)粗粒土在静水压力作用下并非各向同性,与其各向同性假设不符[16]。为此,Raju等[17]、Bopp等[18]、吉恩跃等[19]对Roscoe等[15]的铜棒法进行了改进;Frydman等[20]开展了不同粒径玻璃球体的空心圆柱试验,发现在橡皮膜的单位嵌入量与围压的半对数呈线性关系,其斜率与颗粒平均粒径的半对数呈线性关系。Vaid等[21]基于Frydman等[20]的研究结果,通过不同直径的试样提出了两种确定橡皮膜嵌入量的计算方法。③通过弹性力学方法推导膜嵌入量的解析表达式
εm =ηdg (Pdg /Emtm)1/3(P为试样围压,Em,tm分别为橡皮膜的弹性模量和厚度,η为标定参数)并运用实测数据标定相关参数。此类方法大多设定特征粒径dg (通常考虑d10 ,d20 ,d50 )和围压为变量,对不同材料的橡皮膜嵌入量进行估算,并建立围压与单位嵌入量的关系。因此,其在计算宽级配粗粒土试样橡皮膜嵌入量时误差较大。为克服上述方法的不足,本文提出一种利用多组不同直径试样的等向固结三轴试验来推求单位面积橡皮膜嵌入量的方法[22]。
1. 基本原理
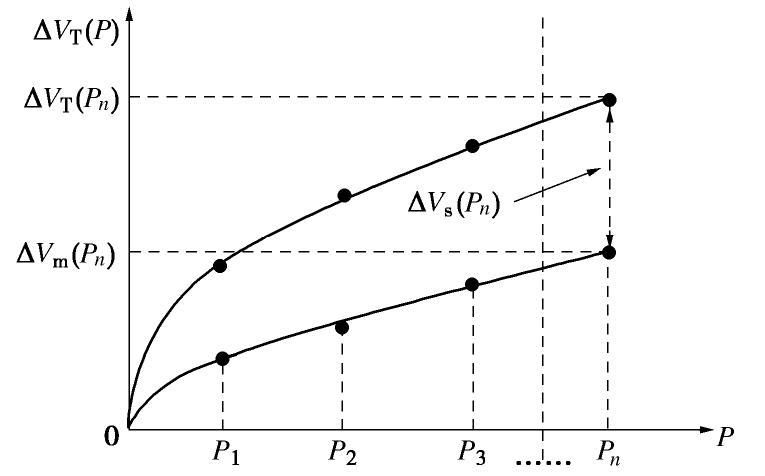
对于固结排水试验,实测粗粒土的体积应变包含两部分:土骨架的体积变化和橡皮膜嵌入引起的体积变化(图1),即
ΔVT(P)=ΔVs(P)+ΔVm(P), (1) 式中,
P 为围压,ΔVT(P) 为特定围压下的总排水量,ΔVs(P) 为特定围压下试样的体变量,ΔVm(P) 为特定围压下橡皮膜的嵌入量。由于试样的体积变化量为
ΔVs(P)=εs(P)V0, (2) 橡皮膜的嵌入量为
ΔVm(P)=εm(P)Am, (3) 式中,
V0 为试样的初始体积,εs(P) ,εm(P) 分别为在特定围压下的土体体积应变和橡皮膜单位面积嵌入量;Am 为试样的侧向表面积。此时,式(1)可表述为
ΔVT(P)=14εs(P)πD2H+εm(P)πDH=14εs(P)AmD+εm(P)Am, (4) 式中,D为试样的直径,H为试样的高度。
将式(4)进行变换后得到
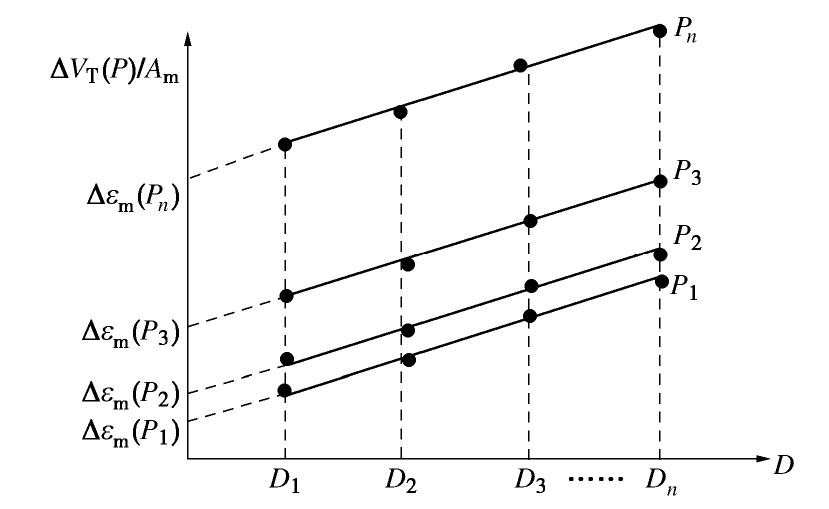
ΔVT(P)/Am=14εs(P)D+εm(P)。 (5) 由式(5),给出了理论推导橡皮膜嵌入量的方法示意图(如图2),以试样排水量与其侧向表面积的比值ΔVT(P)/Am为纵坐标,试样直径D为横坐标,则可得到试样排水量与其直径的关系。显然,图2中纵坐标的截距
εm(P) 即为橡皮膜单位面积嵌入量。2. 试验方案
2.1 试验装置
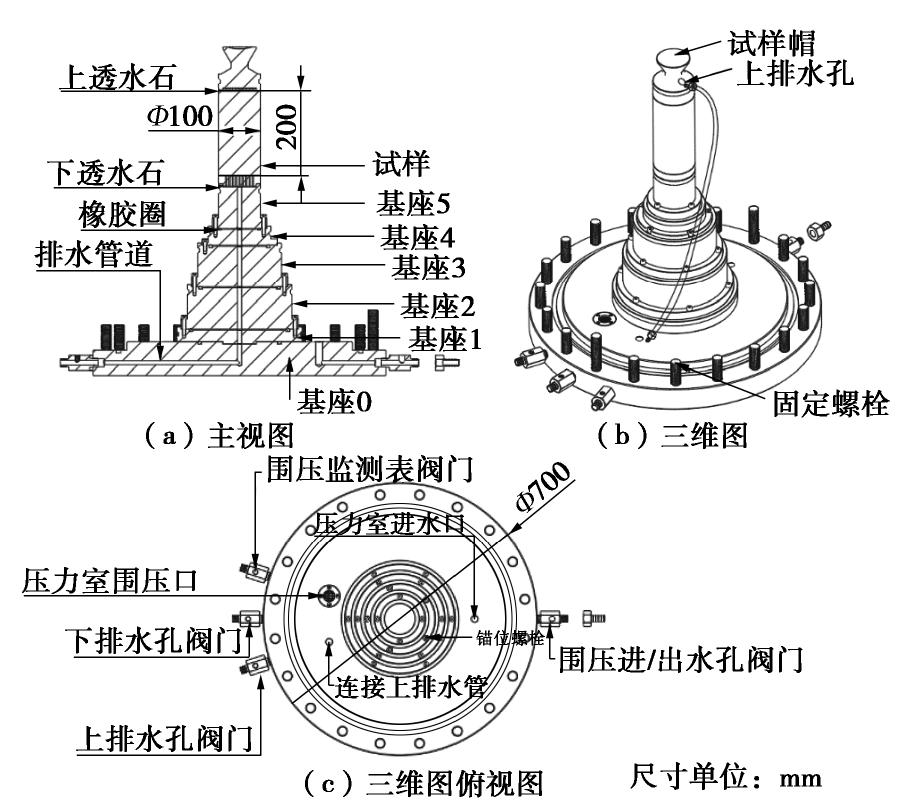
在南京水利科学研究院某大型三轴试验仪上设计并改造了一套多尺度底盘装置(如图3)。该装置以三轴试验仪300 mm直径试样尺寸为基础,考虑上部加压杆的可伸缩长度,根据试验需要加装不同高度的底座(如图3(a)),每层底盘间配有密封圈。不同底座可通过螺栓进行连接,连接螺栓错位分布以解决螺栓孔间的相互影响(如图3(c))。此外,该装置配有不同试样的试样帽,试样帽侧方开有排水孔。上述试验装置可在同一套测量系统上进行100,150,200,250,300 mm直径试样的常规三轴试验,有效消除了因不同试验仪器的系统误差对试验结果的影响。
2.2 试验材料与试验方法
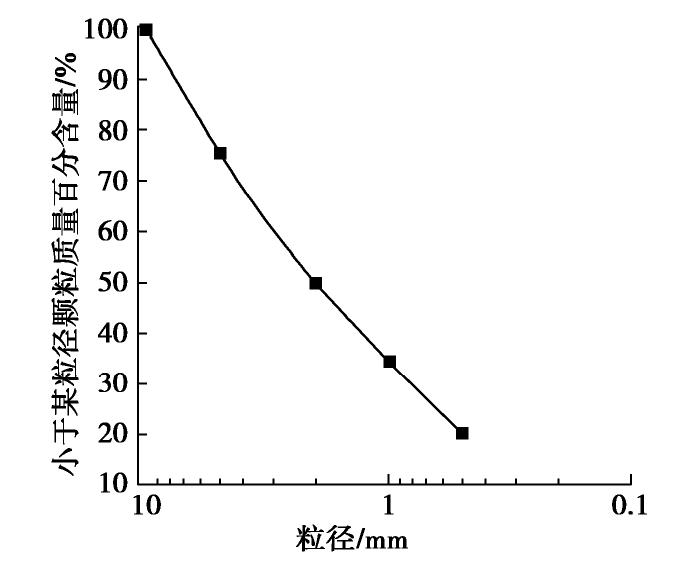
试验所用料为某堆石坝堆石料破碎所得,粒径分为0.5~1,1~2,2~5,5~10 mm五组,级配曲线与材料其它基本参数分别见图4和表1。三轴试验试样直径分别设置为100,150,200,250,300 mm,每组做3个平行试验,共计15组试样。橡皮膜厚度为2 mm,相应的橡皮膜弹性模量Em=1.608 MPa[23]。根据前人研究[24],在初始等向固结条件下,采用分级加载的方法(围压为100,200,400,600 kPa)测量不同围压下试样的排水量。
表 1 材料基本参数Table 1. Basic parameters of materials材料 颗粒相对质量密度G 孔隙比e 试验干密度ρd/(g·cm-3) 平均粒径dg/mm 堆石料 2.70 0.59 1.70 2 2.3 制样及加载过程
如图5所示,每个试样分5层进行装样,装填完成后对试样进行抽真空,使得试样保持直立,抽真空后将试样帽紧密套好。连接好上下排水管,套上压力室,对试样压力室进行充水,待压力室上部出水口有持续水流出一段时间后关闭该出水口阀门,并开始对试样进行饱和,饱和水头2 m,待饱和完成后,对试样加载20 kPa围压以保证橡皮膜贴紧试样壁同时将排水量清零。
制样完成后,对试样进行分级加载并记录不同围压下试样排水量。加载时速率不宜过快,防止加载过快引起孔压上升过快而来不及消散而引起不必要的测量误差。此外考虑加载时间过长带来的流变量影响,确定每加载到预定值稳定且排水量无较大变化后即可进行下一级围压的加载。
3. 试验结果与分析
3.1 橡皮膜嵌入量分析
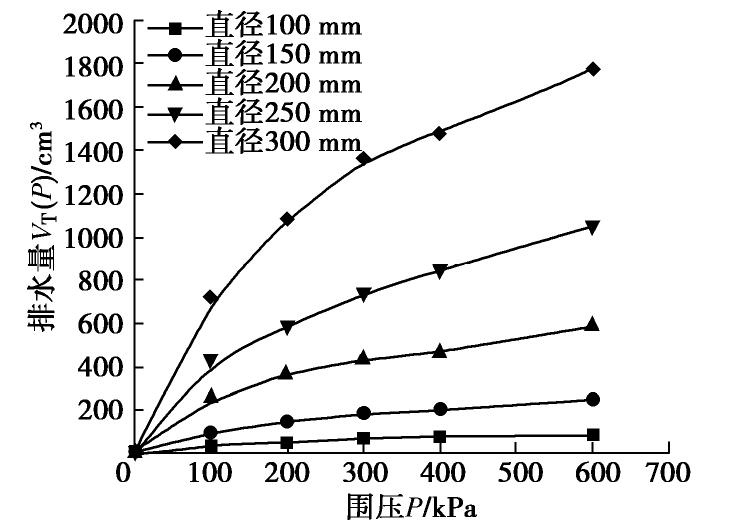
试验得到的不同直径堆石料试样在不同围压下的排水量
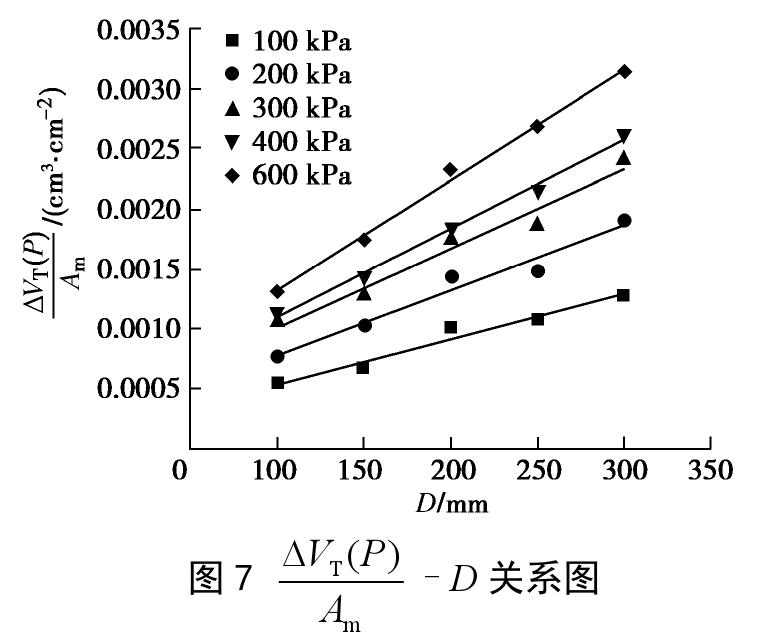
ΔVT(P) 见图6。可以看出,随着围压的增加,试样的排水量增大,大体呈幂函数关系,且试样直径越大,其排水量越大。图7为试验得到的试样排水量与其侧向表面积的比值
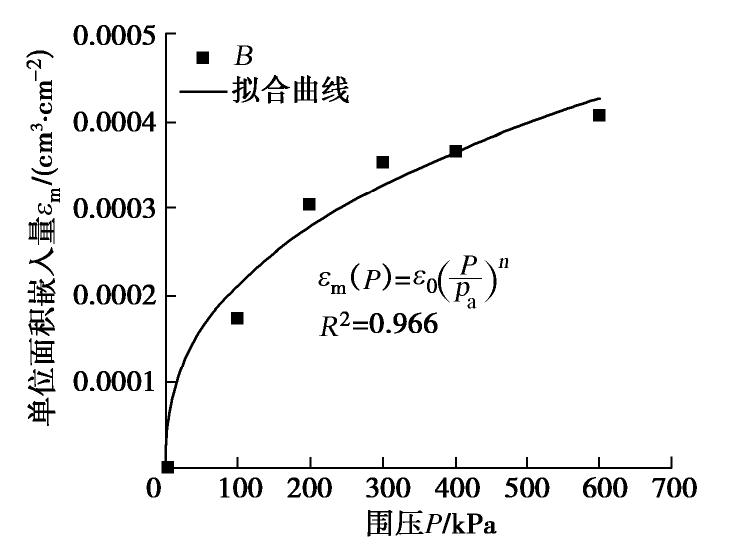
ΔVT(P) /Am与试样直径D的关系。可以看出,随着围压的增加,ΔVT(P) /Am的值增大,且与试样直径D呈现良好的线性关系。由图7推求得到的橡皮膜单位面积嵌入量与围压的关系如图8所示,同样,随着围压的增加,橡皮膜的单位嵌入量逐渐增大,橡皮膜的单位嵌入量与试样围压大体呈幂函数关系。经过拟合橡皮膜的单位嵌入量与围压关系试验结果,可得到一个关于橡皮膜单位嵌入量与围压关系的经验公式:
εm(P)=ε0(Ppa)n, (6) 式中,
pa 为标准大气压力值,ε0 为一个标准大气压力时的橡皮膜嵌入量。利用式(6)可计算得到不同围压下橡皮膜的单位嵌入量。表2给出了根据橡皮膜的单位嵌入量计算得到的不同试样直径在不同围压下,橡皮膜的嵌入体积占总排水体积的百分比。由表2可以看出,试样直径变化对橡皮膜的嵌入体积百分比具有显著影响,相同围压下,随着试样直径的增加,橡皮膜的嵌入量减小;试样直径相同,围压变化对橡皮膜的嵌入体积百分比有一定影响,但明显小于试样直径变化的影响,且随着试样直径的增大,影响逐渐降低,围压变化对直径300 mm试样的嵌入体积百分比的影响最小,在200 kPa时不同直径试样的嵌入量占比出现突变现象,这是因为试样初始围压为100 kPa,试样仍处于疏松状态,在200 kPa时,试样内部颗粒间因挤压产生的变化,此时试样的体变有一个瞬时增大的过程,而产生突变现象,随着围压的增加,试样体积变化逐渐平缓,对总体变化规律影响较小。因此,建议堆石料的强度变形试验,应尽可能采用较大直径的试样进行,以降低橡皮膜嵌入量对其试验结果的影响。
表 2 不同直径与不同围压下橡皮膜嵌入量占比Table 2. Penetration proportions under different diameters and confining pressures(%) 围压/kPa 直径/mm 100 150 200 250 300 100 32.1 25.6 17.2 16.1 13.7 200 39.4 29.4 21.1 20.5 15.9 300 33.5 27.4 20.3 18.8 14.6 400 32.1 25.6 19.8 17.0 14.0 600 30.8 23.3 17.5 15.1 13.0 3.2 与常用橡皮膜嵌入量计算公式的比较
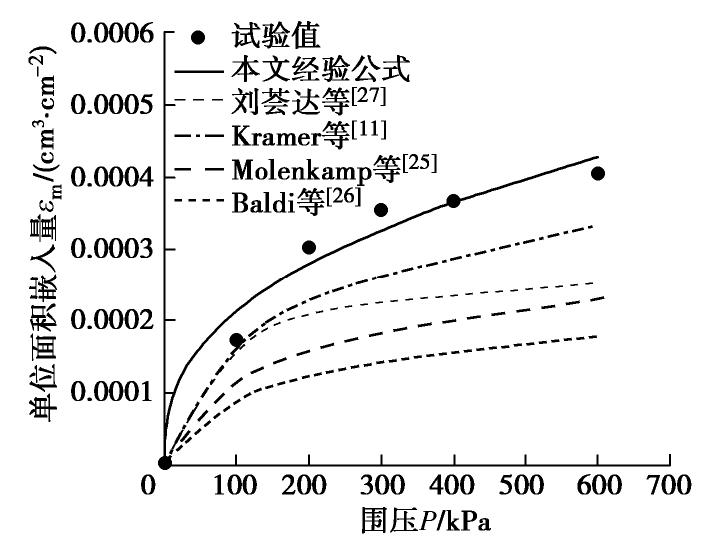
目前常用的粗粒土三轴试验橡皮膜嵌入量计算公式主要为以下两类:①基于弹性力学方法推导的解析表达式εm=ηdg(Pdg/Emtm)1/3(P为围压,Em,tm分别为橡皮膜的弹性模量和厚度,η为标定参数),Kramer等[10]、Molenkamp等[25]、Baldi等[26]根据粗粒土三轴试验,确定η分别为0.23,0.16,0.125;另一类是刘荟达等[27]采用粗粒土的特征粒径
d10 ,d20 ,d50 计算其橡皮膜嵌入量的经验计算公式;S=0.0125d1.2910+0.113d0.7520+0.00382d1.2650 ,Δvm=S⋅lgσ′c 。} (7) 式中
Δvm 为单位嵌入体积单位;σ′c 为试样固结围压。本文基于粗粒土多组不同直径试样的等向固结三轴试验提出的橡皮膜嵌入量公式与上述两类公式计算得出的橡皮膜单位嵌入量结果比较如图9所示。从图9可以看出,各公式计算得出的橡皮膜单位嵌入量均随围压的增大而增大,但本文提出的经验公式计算得出的橡皮膜单位嵌入量明显大于前两类公式。由于粗粒土的母岩性质和级配变化较大,简单采用既有橡皮膜嵌入量计算公式可能导致橡皮膜嵌入量估算值产生较大误差,建议采用本文方法对橡皮膜嵌入量进行估算。
4. 结论
本文在同一试验仪器上开展了多组不同直径试样粗粒土的等向固结三轴试验,研究了橡皮膜的嵌入量的变化规律和影响因素,在此基础上提出了一个计算粗粒土橡皮膜嵌入量的经验公式,得到以下3点结论。
(1)粗粒土三轴试验过程中,橡皮膜会明显嵌入试样中,导致测量出的试样体积变形增大,从而影响粗粒土强度变形指标测量精度。因此粗粒土三轴试验中的橡皮膜嵌入效应不可忽略。
(2)试验结果表明,橡皮膜的嵌入量随围压的增大而增大,与其围压大体呈幂函数关系。相同围压下,随着试样直径的增加,橡皮膜的嵌入量占总体变的比例减小;试样直径相同,围压变化对橡皮膜的嵌入量的影响明显小于试样直径变化的影响,且随着试样直径的增大,影响逐渐降低。建议堆石料的强度变形试验,应尽可能采用较大直径的试样进行,以降低橡皮膜嵌入量对其试验结果的影响。
(3)由于粗粒土的母岩性质和级配变化较大,简单采用既有橡皮膜嵌入量计算公式可能导致橡皮膜嵌入量估算值产生较大误差,建议采用本文方法对橡皮膜嵌入量进行估算。另外,鉴于本文采用的是10 mm粒径的堆石料,为了更好的验证本文提出的经验公式的适用性,后续将开展更大粒径以及更高围压下的堆石料嵌入量试验进行该公式的验证。
-
表 1 实测数据与理论计算结果对比表
Table 1 Comparison between measured data and calculated results
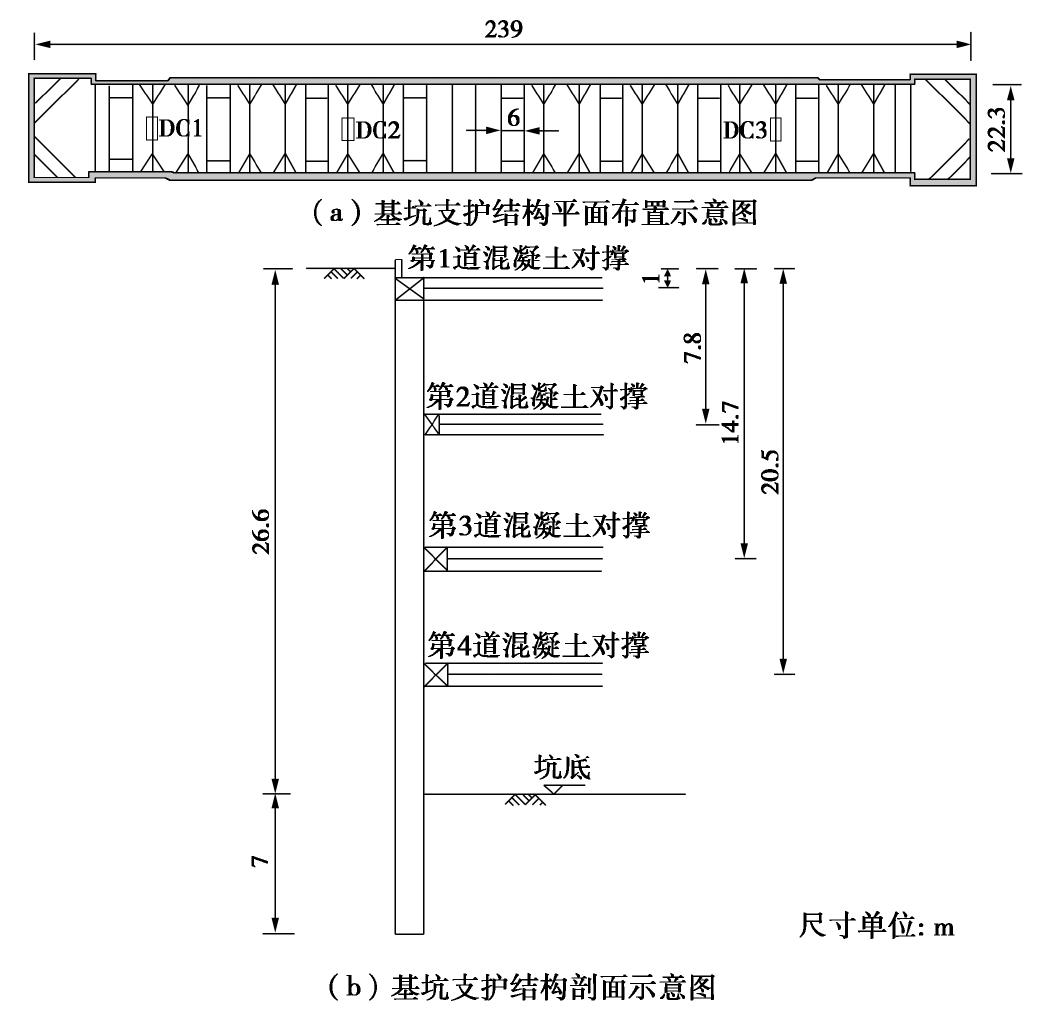
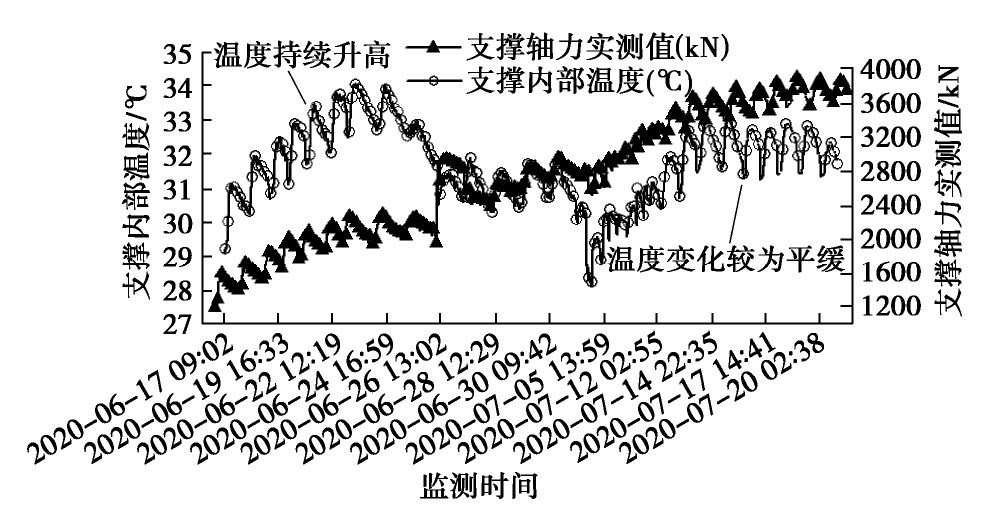
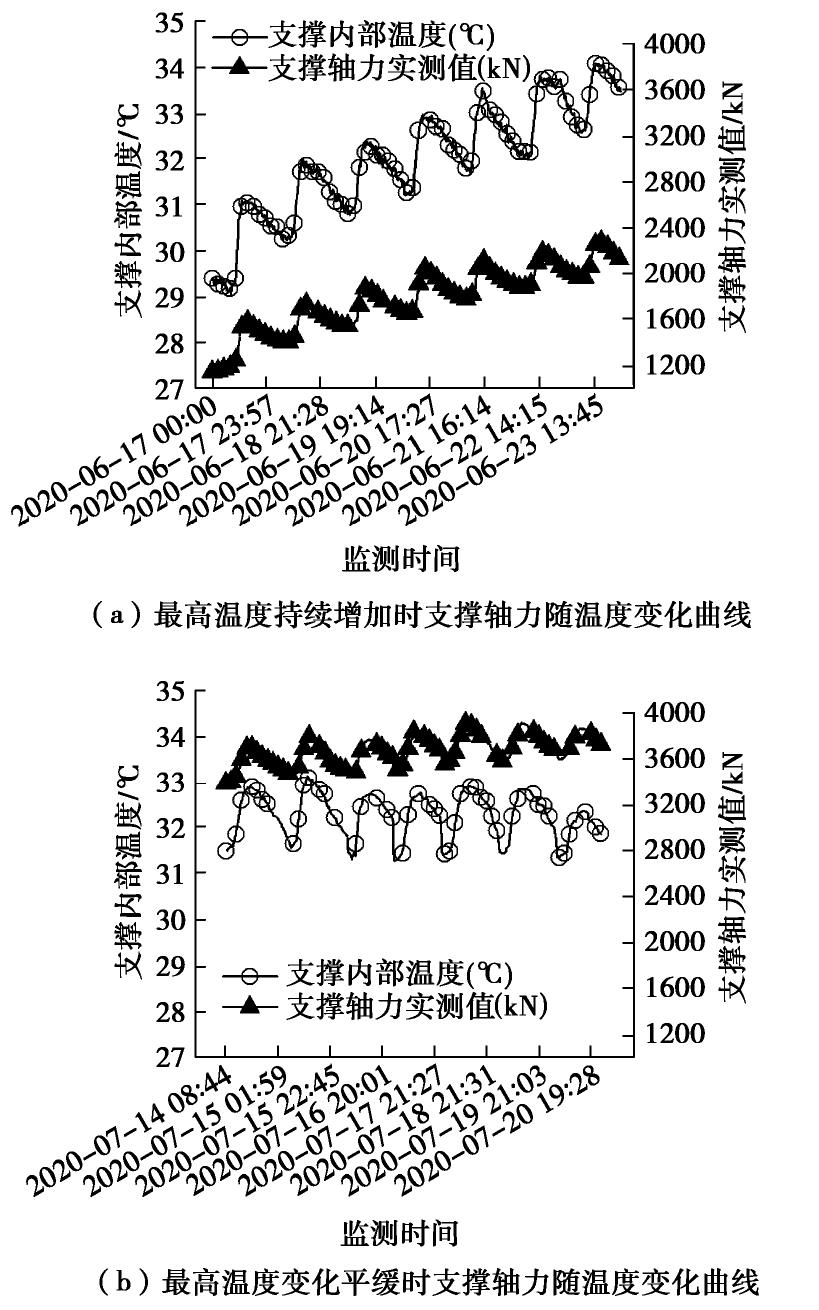
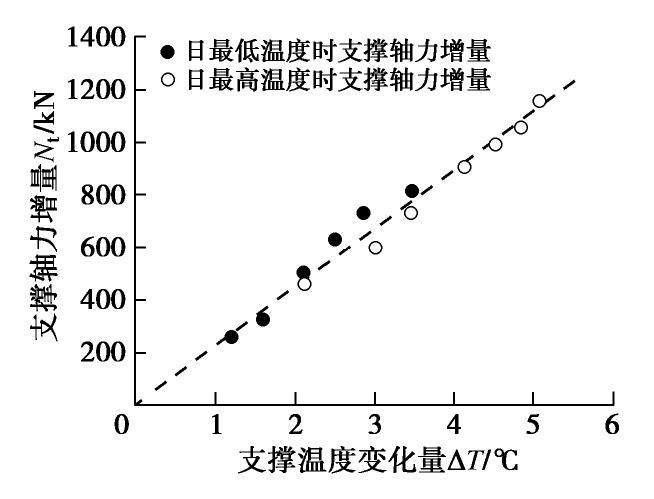
时间 实测轴力最大值Nmax/kN 实测轴力最小值Nmin/kN 支撑内温差 ΔT /℃单位温度支撑轴力增量Nt/(kN·℃-1) 6月17日 1600.29 1133.58 2.12 220.15 6月18日 1731.89 1394.08 1.80 187.67 6月19日 1866.71 1463.55 1.86 216.75 6月20日 2042.26 1635.76 2.02 201.24 6月21日 2125.76 1767.57 2.03 176.45 6月22日 2189.91 1867.32 1.84 162.92 6月23日 2293.05 1952.82 1.60 212.64 理论计算 1.00 232.14 表 2 实测数据与理论计算结果对比表
Table 2 Comparison between measured data and calculated results
时间 实测轴力最大值Nmax/kN 实测轴力最小值Nmin/kN 支撑内温差 ΔT /℃单位温度支撑轴力增量Nt/(kN·℃-1) 7月14日 3699.57 3383.70 1.51 209.19 7月15日 3804.06 3435.85 1.65 223.16 7月16日 3766.85 3449.24 1.66 191.33 7月17日 3836.41 3490.91 1.65 209.39 7月18日 3906.81 3546.86 1.67 215.54 7月19日 3910.63 3563.41 1.51 229.95 7月20日 3862.64 3585.43 1.06 261.52 理论计算 1.00 232.14 表 3 DC2-4支撑内部温度与大气温度实测值
Table 3 Measured values of internal temperature of support DC2-4 and air temperature
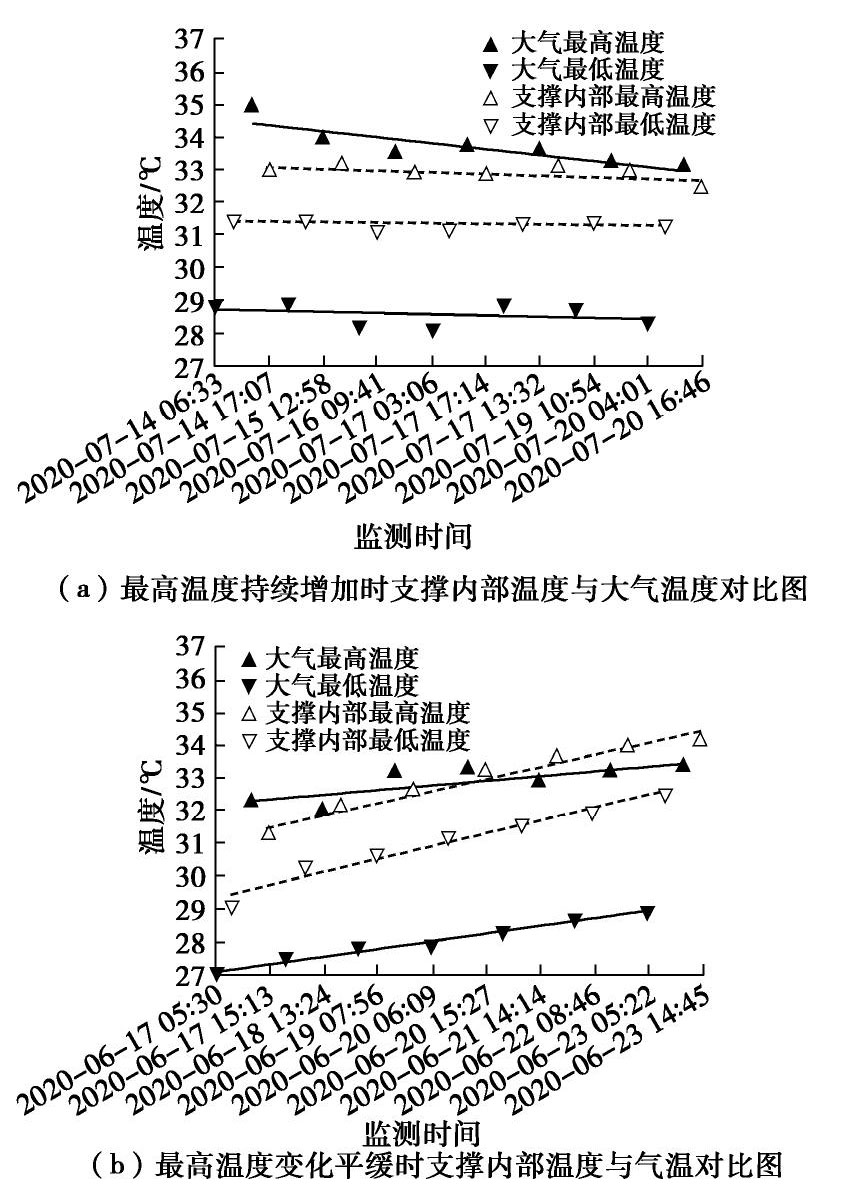
时间 支撑内部最低温度/℃ 测量时间 支撑内部最高温度/℃ 测量时间 6月17日 29.01(26.90) 09:12(05:30) 31.13(32.20) 15:13(14:16) 6月18日 30.21(27.40) 09:11(03:45) 32.01(31.90) 14:26(13:24) 6月19日 30.61(27.70) 07:56(05:30) 32.47(33.10) 17:24(16:43) 6月20日 31.12(27.80) 08:29(06:09) 33.14(33.20) 15:27(15:06) 6月21日 31.51(28.20) 08:18(03:35) 33.54(32.80) 15:24(14:14) 6月22日 31.87(28.60) 08:46(06:04) 33.85(33.10) 14:50(14:05) 6月23日 32.48(28.80) 09:10(05:22) 34.08(33.20) 14:45(13:19) 7月14日 31.44(28.80) 10:14(06:33) 32.95(34.90) 17:07(13:32) 7月15日 31.49(28.90) 08:22(05:01) 33.14(33.90) 16:18(12:58) 7月16日 31.17(28.20) 09:41(05:17) 32.83(33.50) 16:49(15:19) 7月17日 31.15(28.10) 09:30(03:06) 32.80(33.70) 17:14(15:11) 7月18日 31.35(28.90) 09:13(05:46) 33.02(33.60) 15:27(13:32) 7月19日 31.40(28.70) 10:54(03:22) 32.91(33.20) 16:33(14:58) 7月20日 31.30(28.30) 10:11(04:01) 32.36(33.10) 16:46(13:55) 注: 表中括号内数据为大气测站G1166实测大气温度值和测量时间。 -
[1] 建筑基坑支护技术规程:JGJ120—2012[S]. 2012. Technical Specification for Retaining and Protection of Building Foundation Excavations: JGJ 120-2012[S]. 2012. (in Chinese)
[2] 混凝土结构设计规范:GB50010—2010[S]. 2010. Code for Design of Concrete Structures: GB50010—2010[S]. 2010. (in Chinese)
[3] 钢结构设计规范:GB50017—2017[S]. 2017. Code for Design of Steel Structures: GB50017—2012[S]. 2017. (in Chinese)
[4] 张中普, 姚笑青. 某深基坑事故分析及技术处理[J]. 施工技术, 2005, 34(12): 72-73. doi: 10.3969/j.issn.1002-8498.2005.12.027 ZHANG Zhong-pu, YAO Xiao-qing. Accident analysis and technology dispose of certain deep foundation pit[J]. Construction Technology, 2005, 34(12): 72-73. (in Chinese) doi: 10.3969/j.issn.1002-8498.2005.12.027
[5] 郑刚, 顾晓鲁. 考虑支撑-围护桩-土相互作用的基坑支护水平支撑温度应力的简化分析法[J]. 土木工程学报, 2002, 35(3): 87-89, 108. doi: 10.3321/j.issn:1000-131X.2002.03.017 ZHENG Gang, GU Xiao-lu. Simple method for calculating temperature stress in horizontal strut of foundation pit considering strut-pile-soil interaction[J]. China Civil Engineering Journal, 2002, 35(3): 87-89, 108. (in Chinese) doi: 10.3321/j.issn:1000-131X.2002.03.017
[6] 林跃忠, 王铁成, 王来. 钢支撑温度应力对深基坑支护结构的影响研究[J]. 工业建筑, 2004(增刊): 1069-1074. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-QXJX200407001181.htm LIN Yue-zhong, WANG Tie-cheng, WANG Lai. Study on the influence of temperature stress of steel support on the supporting structure of deep foundation pit[J]. Industrial Building, 2004(S0): 1069-1074. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-QXJX200407001181.htm
[7] 陆培毅, 韩丽君, 于勇. 基坑支护支撑温度应力的有限元分析[J]. 岩土力学, 2008, 29(5): 1290-1294. doi: 10.3969/j.issn.1000-7598.2008.05.027 LU Pei-yi, HAN Li-jun, YU Yong. Finite element analysis of temperature stress in strut of foundation pit[J]. Rock and Soil Mechanics, 2008, 29(5): 1290-1294. (in Chinese) doi: 10.3969/j.issn.1000-7598.2008.05.027
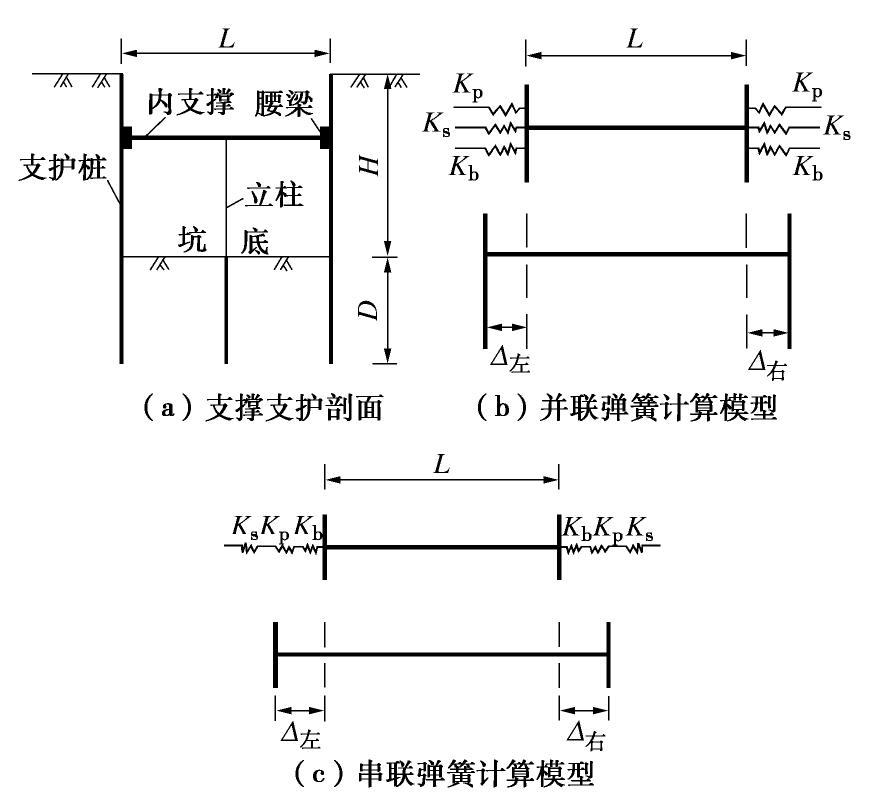
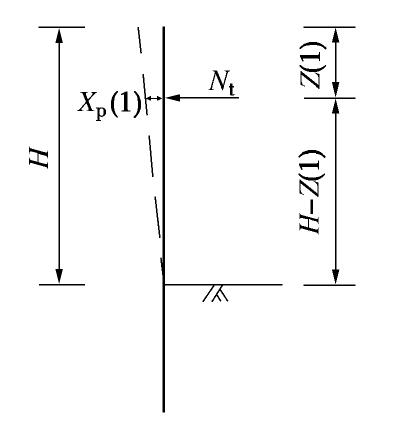
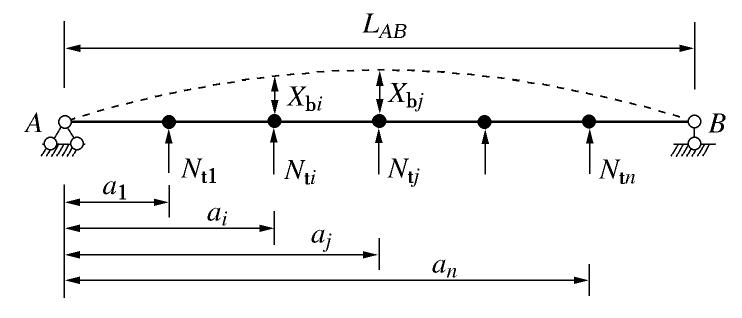
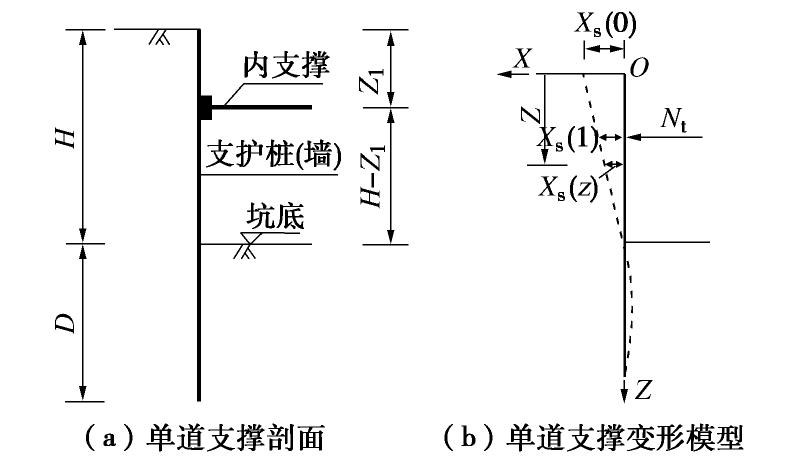
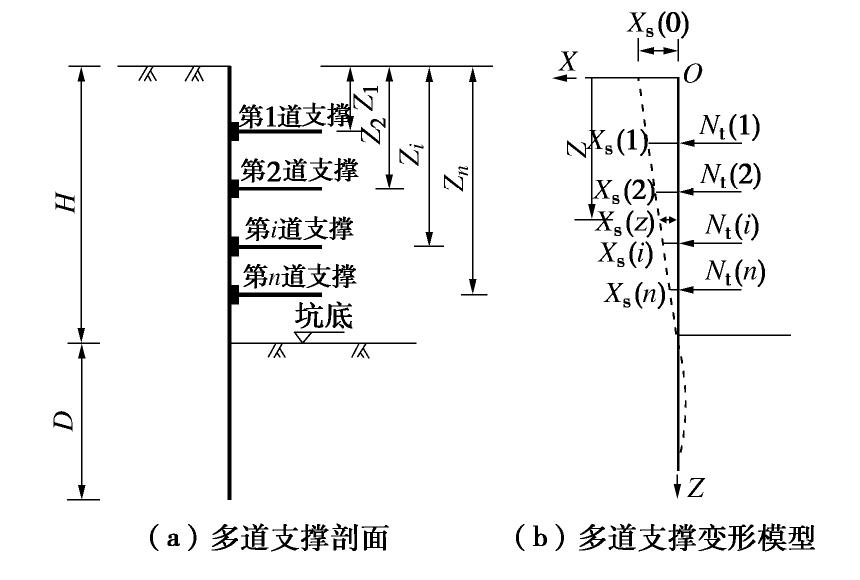
[8] 吴明, 孙鸣宇, 夏唐代, 等. 多层支撑深基坑中考虑支撑-围护桩-土相互作用的水平支撑温度应力简化计算方法[J]. 土木工程学报, 2009, 42(1): 91-94. doi: 10.3321/j.issn:1000-131X.2009.01.014 WU Ming, SUN Ming-yu, XIA Tang-dai, et al. Simplified method of calculating temperature stress in multi-layer struts for deep excavations considering strut-pile-soil interactions[J]. China Civil Engineering Journal, 2009, 42(1): 91-94. (in Chinese) doi: 10.3321/j.issn:1000-131X.2009.01.014
[9] 吴明, 彭建兵, 邓亚虹, 等. 改进的深基坑多层支撑温度应力计算方法[J]. 现代隧道技术, 2013, 50(1): 123-128. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201301022.htm WU Ming, PENG Jian-bing, DENG Ya-hong, et al. Modified method for calculating temperature stress in multi-layer struts of a deep foundation pit[J]. Modern Tunnelling Technology, 2013, 50(1): 123-128.(in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201301022.htm
[10] 艾智勇, 苏辉. 深基坑多层水平支撑温度应力的简化计算方法[J]. 同济大学学报(自然科学版), 2011, 39(2): 199-203. doi: 10.3969/j.issn.0253-374x.2011.02.008 AI Zhi-yong, SU Hui. A simplified method of calculating thermal Stress for multi-layered horizontal struts in deep excavations[J]. Journal of Tongji University(Natural Science), 2011, 39(2): 199-203. (in Chinese) doi: 10.3969/j.issn.0253-374x.2011.02.008
[11] 惠渊峰. 某地铁车站深基坑钢支撑温度应力计算与分析[J]. 建筑科学, 2012, 28(9): 101-103, 111. https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX201209023.htm HUI Yuan-feng. The deep foundation pit steel brace temperature stresses analysis and calculation of subway station[J]. Building Science, 2012, 28(9): 101-103, 111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX201209023.htm
[12] CHAPMAN K R, CORDING E J, SCHNABEL H. Performance of a braced excavation in granular and cohesive soils[C]//ASCE Specially Conference on Performance of Earth and Earth-Supported Structures. Purdue University, 1972: 271-293.
[13] 陈锋, 艾英钵. 基坑钢支撑温度应力的弹性热力学解答[J]. 科学技术与工程, 2013, 13(1): 108-111. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201301023.htm CHEN Feng, AI Ying-bo. Calculation of temperature stress of steel support in foundation pit using thermodynamics of elasticity[J]. Science Technology and Engineering, 2013, 13(1): 108-111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201301023.htm
[14] 范君宇. 深大基坑中水平支撑的温度内力与变形计算[J]. 山西建筑, 2014, 40(18): 59-62. https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201418033.htm FAN Jun-yu. In deep big hole excavated for building foundation level support temperature endogenic force and distortion computational method[J]. Shanxi Architecture, 2014, 40(18): 59-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201418033.htm
[15] 向艳. 温度应力对深基坑支护结构内力与变形的影响研究[J]. 岩土工程学报, 2014, 37(增刊2): 64-69. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2014S2013.htm XIANG Yan. Influence of temperature stress on internal force and deformation of retaining structures for deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2014, 37(S2): 64-69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2014S2013.htm
[16] 刘畅, 张亚龙, 郑刚, 等. 改进的基坑支护水平支撑温度应力及水平位移的计算方法[J]. 岩土工程学报, 2015, 37(增刊1): 61-64. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1014.htm LIU Chang, ZHANG Ya-long, ZHENG Gang, et al. Modified method for calculating temperature stress and displacement in horizontal strut of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 61-64. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1014.htm
[17] 冉岸绿, 孙旻, 王浩, 等. 温度变化对新型钢支撑轴力的影响分析[C]//第十届全国基坑工程研讨会学术论文集. 兰州: 兰州理工大学, 2018: 675-678. RAN An-lu, SUN Min, WANG Hao, et al. Analysis of the influence of temperature change on the axial force of new steel support[C]//Academic Papers of the Tenth Nationwide Foundation Pit Engineering Seminar. Lanzhou: Lanzhou University of Technology, 2018: 675-678. (in Chinese)
-
期刊类型引用(2)
1. 吴杨,吴毅航,马林建,崔杰,刘建坤,戴北冰. 南海岛礁珊瑚砂砾混合料动力特性试验研究. 岩土工程学报. 2024(01): 63-71 .  本站查看
本站查看
2. 吴国立,李东升,刘晓光,冯思超. 粗粒土三轴试验力学与长期变形特性研究综述. 科技创新与应用. 2023(08): 88-91 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: