Mechanism of residual liquefaction of silty seabed under standing waves
-
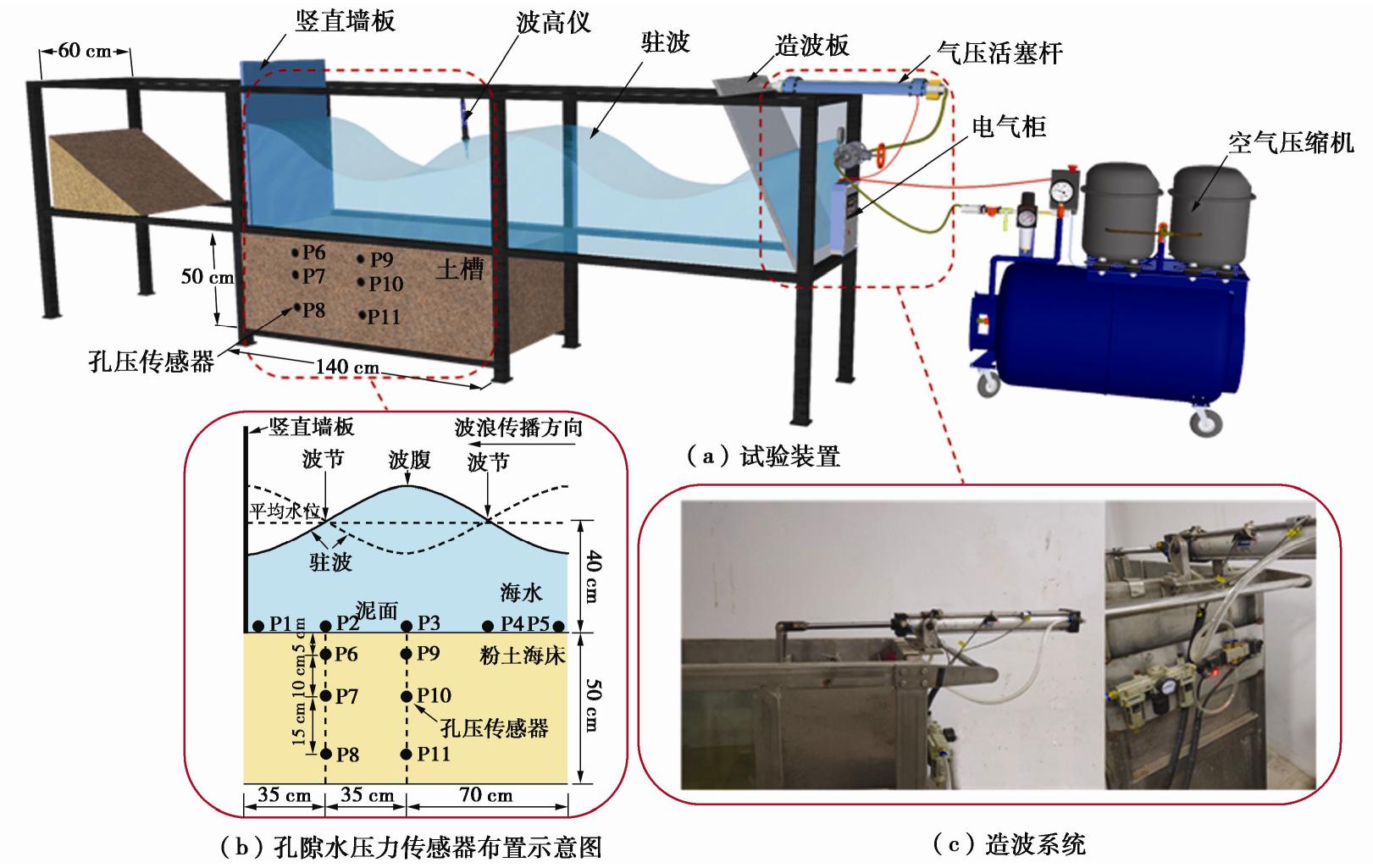
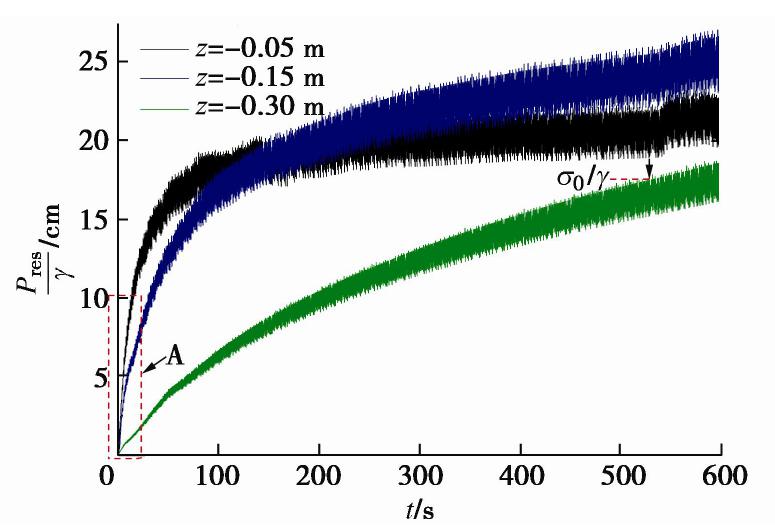
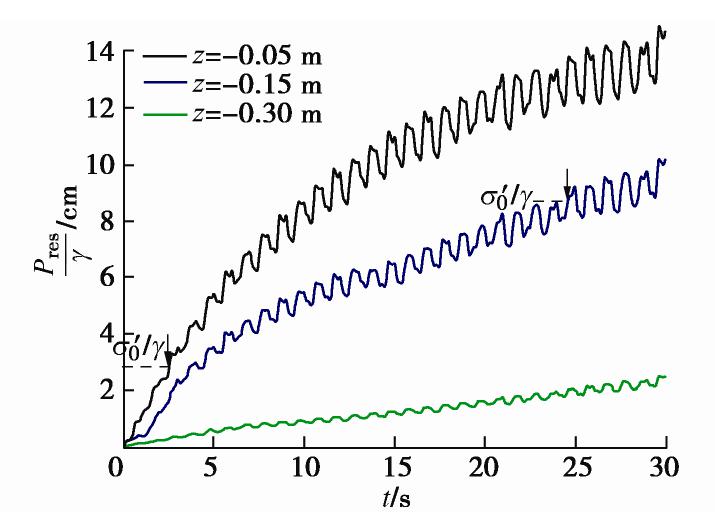
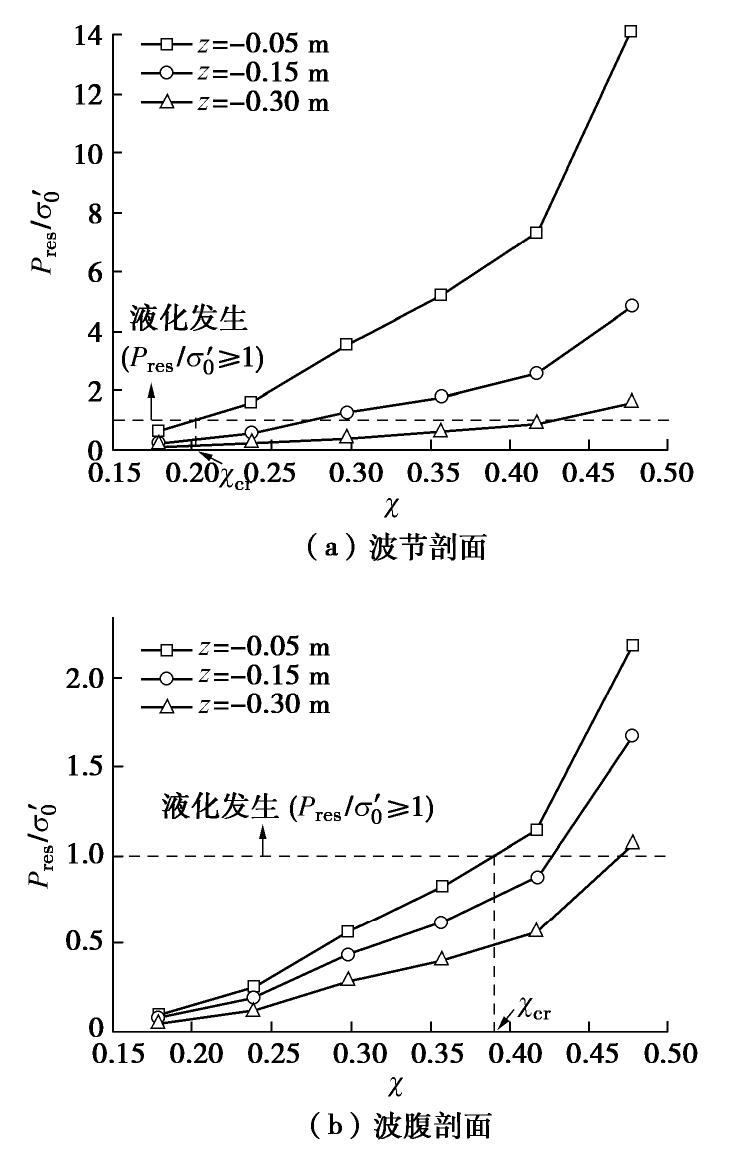
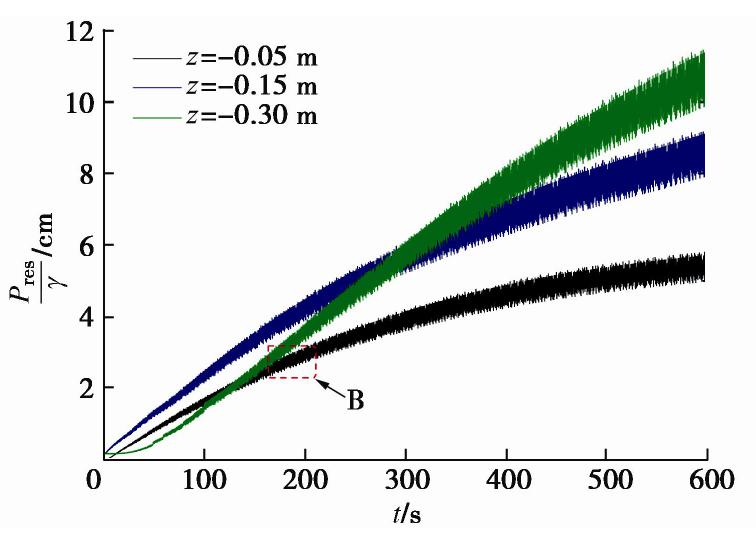
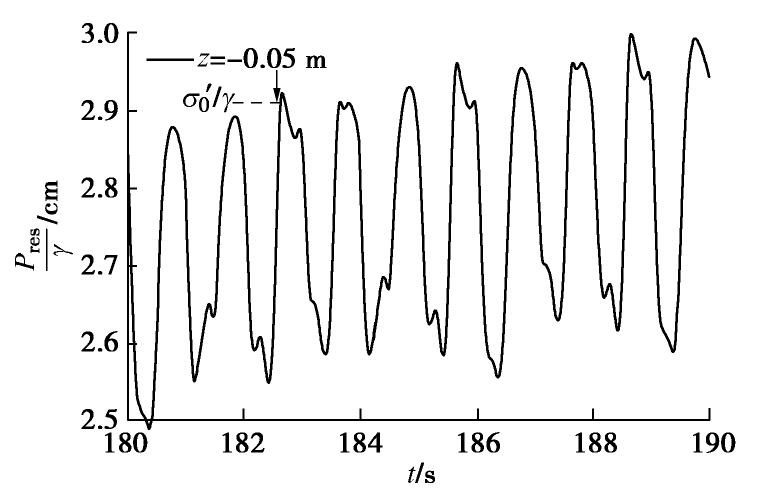
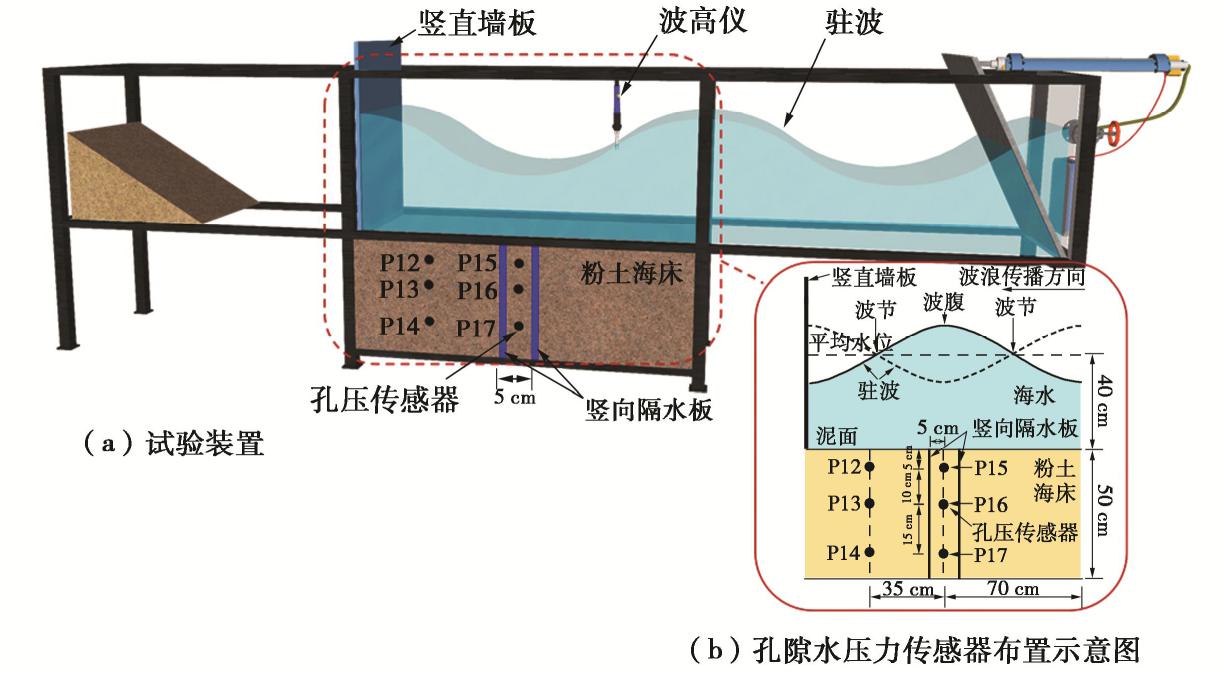
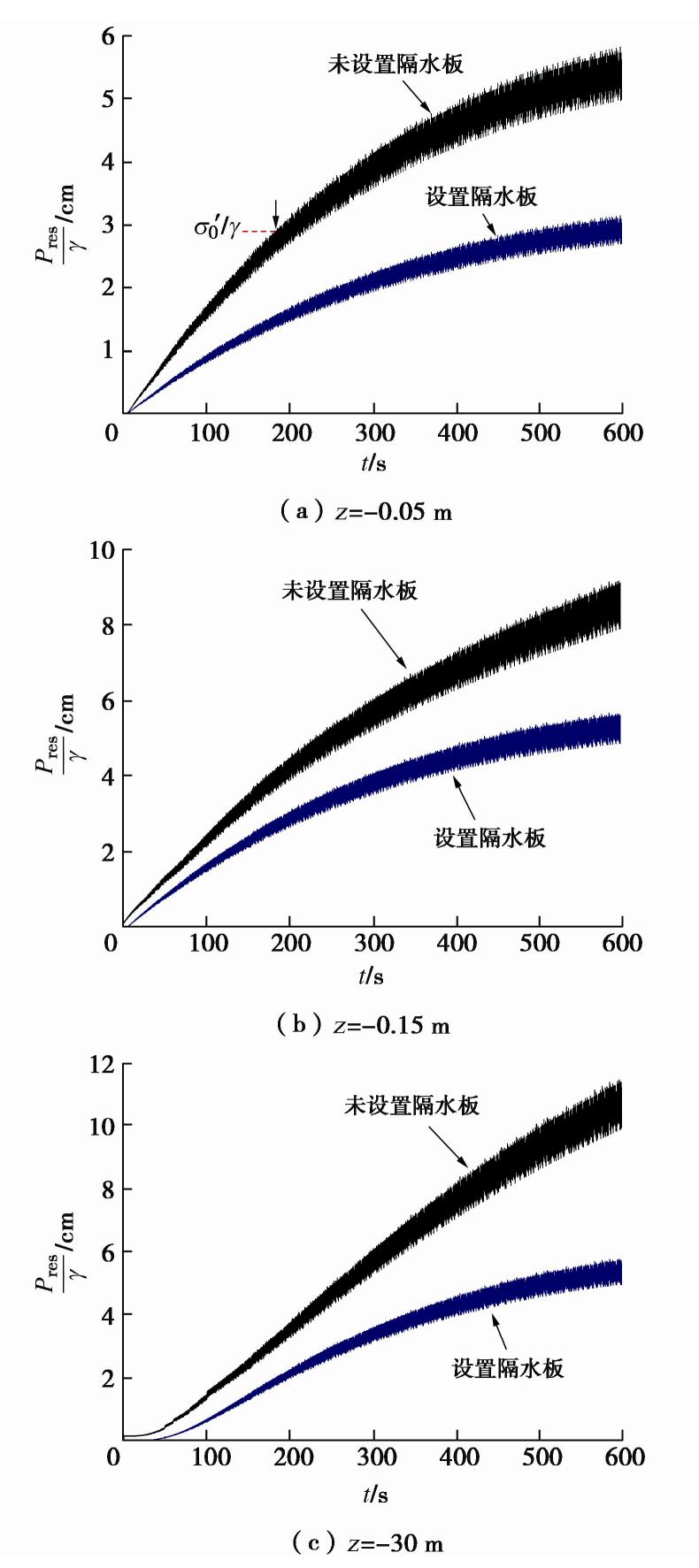
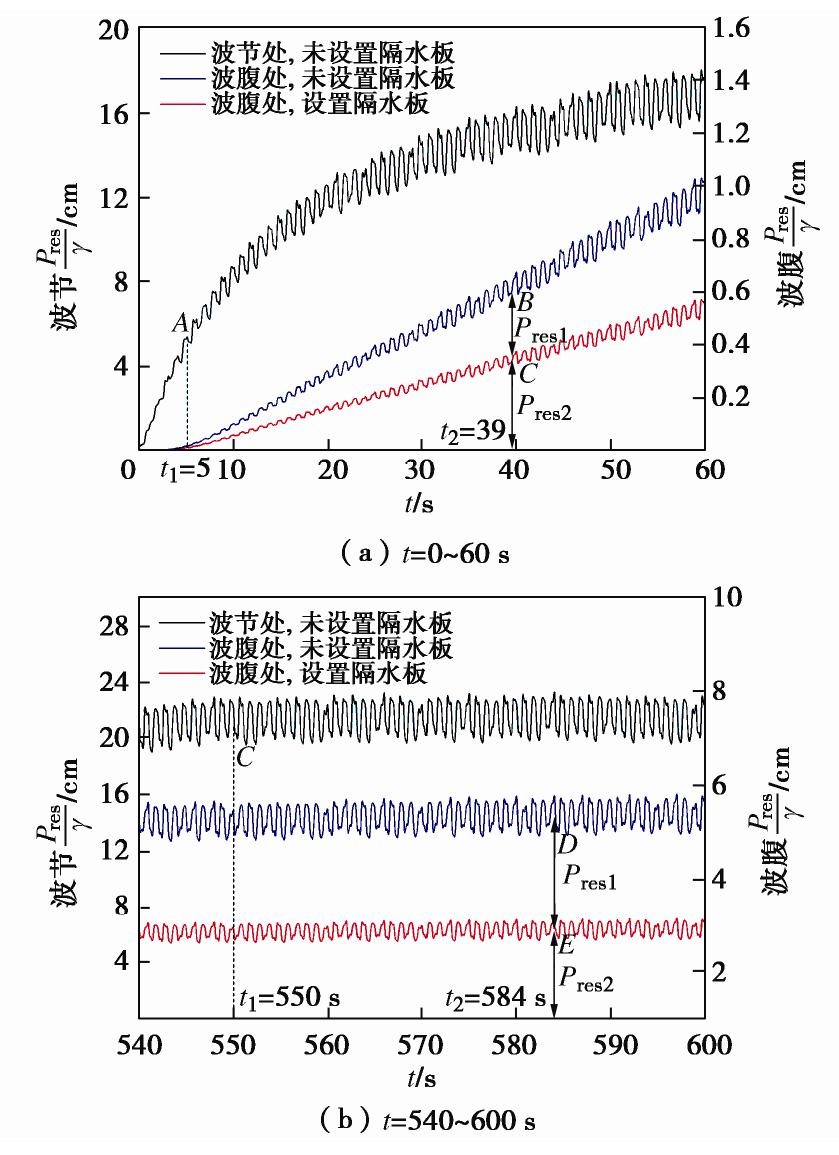
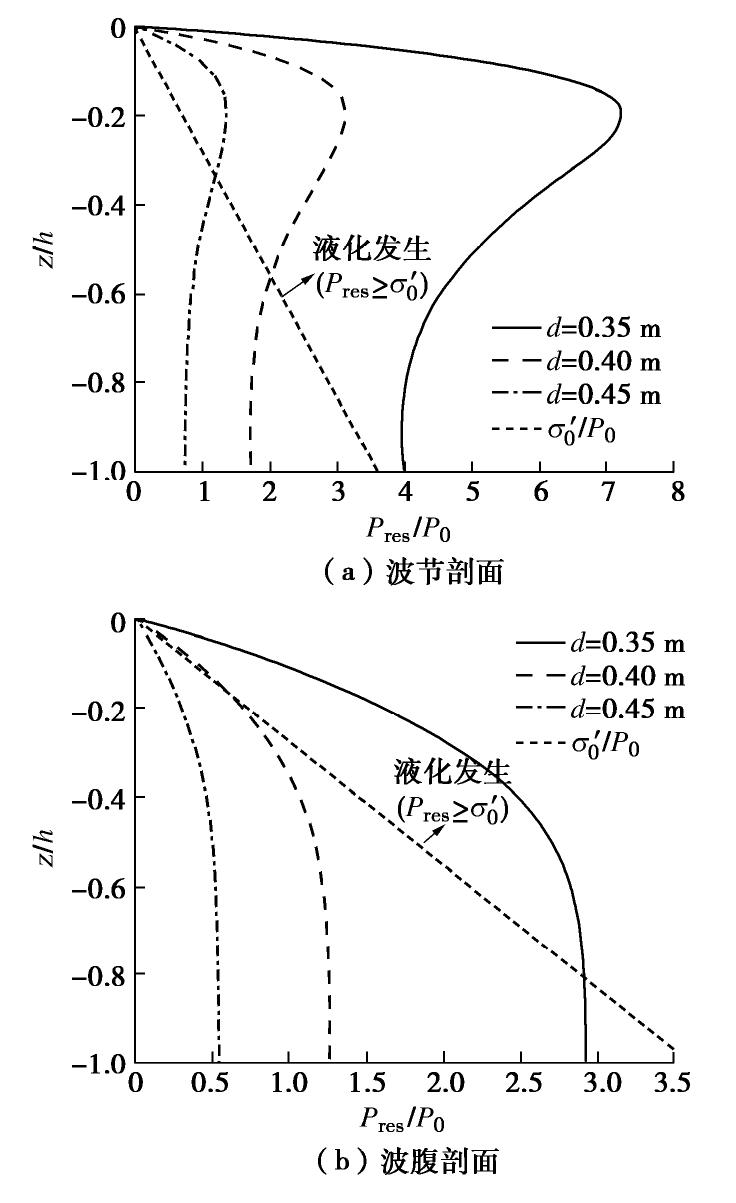
摘要: 波浪被防波堤或岸壁反射时形成驻波,使其前面的水域发生强烈振荡,海床发生液化,可能导致结构物失稳破坏。以黄河三角洲粉土海床为研究对象,进行一系列驻波水槽试验,研究驻波作用下波腹剖面土体累积液化机制,在此基础上,采用数值模型进一步研究驻波作用下波浪参数(水深、波陡)和土体参数(饱和度)对海床累积液化的影响规律。结果表明:驻波作用下海床累积液化的发生与循环应力水平有关,当循环应力比χ达到累积液化所需的临界值χcr时,发生累积液化,深层土体累积液化所需的χcr大于浅层土体。波腹剖面土体液化所需的χcr远大于波节剖面,发生初始液化所需的时间大于波节剖面,液化深度小于波节剖面。波腹剖面土体累积液化是由波节及相邻位置向波腹剖面传递的超孔隙水压力Pres1,和波腹剖面土体受循环正应力影响发生静压屈服引起的超孔隙水压力Pres2两部分共同作用所致。本试验中,在深度z=-0.05 m,波浪作用时间t≈600 s时,前者贡献比α1≈54.3%,后者α2≈45.7%。波节和波腹剖面土体累积孔隙水压力沿深度分布模式有差异,随水深减小,波陡增加,饱和度减小,海床液化深度在波节和波腹剖面均增大。Abstract: The standing waves exist when the progressive waves are reflected by the breakwater or the bank wall, which leads to the water surface oscillating where it is and the waveform doesn’t advance. Seabed soil will undergo liquefaction under standing waves, resulting in the instability of seabed foundation of marine structures. Based on the silt seabed in the Yellow River Delta of China, a series of wave flume experiments are conducted under standing waves so as to investigate the liquefaction mechanism at the antinodal section. Then, a parametric study is conducted with the proposed model to investigate the effects of the soil and wave characteristics on residual liquefaction. The results indicate that the onset of residual liquefaction is linked with cyclic stress ratio. The residual liquefaction occurs when the cyclic stress ratio χ equals the critical value χcr, and the required χcr in deeper layer is larger that of the shallow layer. The required χcr at the antinodal section is far more than that at the nodal section, and the required wave loading time is longer and the liquefaction is smaller than that at the nodal section. The horizontal transporting of pore pressure and the accumulating of plastic volumetric strain induced by cyclic normal stress contribute to the liquefaction at the antinodal section simultaneously, and the experimental results revealthat the former and the latter contribute to 54.3% and 45.7% respectively at the depth of 0.05 m. The discrepancy of the distribution pattern of the excess pore water pressure exists between the nodal section and the antinodal section. The shallower the water depth, the higher the wave steepness, and the smaller the saturability results in a deeper liquefaction depth.
-
0. 引言
近年来,城市轨道交通以其便捷快速的优点在许多城市得到快速的发展。然而随着城市化进程的不断推进,许多已建成的地铁隧道附近不可避免地受到外部工程活动扰动影响,其中突发地表堆载引发的隧道变形事故日益突出[1],如为便于上海嘉闵高架的施工将河道作为堆放材料场地引起地铁9号线产生较大的不均匀沉降[2]以及违规弃土引起的地铁正上方堆载导致隧道的横向变形[3-4]等。地表堆土荷载作用引起的附加应力,会破坏盾构结构原有的平衡状态,引起隧道应力重分布,产生一定的纵向和横向变形,一旦结构内力超过混凝土和螺栓容许应力,会引发管片压损或开裂等[5],对地铁安全造成严重影响。因此研究地表堆载对临近运营地铁盾构隧道的影响具有重要意义。
目前,已有学者对地表堆载荷载作用下盾构隧道的纵向变形进行了研究。戴宏伟等[6]利用Boussinesq解和分层总和法计算自由场的位移,基于Euler-Bernoulli梁模型研究了地表施工荷载对临近地铁隧道的影响,但未考虑土体成层特性和隧道自身的结构特性;魏新江等[7]、魏纲等[8]基于变分法研究了堆载对下卧隧道错台变形的影响,康成等[9]采用Timoshenko梁模型研究了不同堆载形式对隧道纵向变形的影响,高继锦等[10]研究了堆载对下卧交叉隧道竖向位移的影响,但是他们的研究忽略了土体的成层特性;李俊昱等[11]根据层状弹性半空间理论计算了高填方堆载对地埋管线受力和变形的影响,研究成果虽然涉及到土体的成层特性但没有考虑管线接头的影响。综上,这些研究成果或考虑的土层单一,不能分析土层特性对隧道变形的影响;或忽略了隧道接头引起的隧道整体刚度的弱化,无法准确反映分层地基中堆载对隧道纵向变形的影响。黄大维等[3]、张明告等[12]、Zhang等[13]、张治国等[14]研究表明当土层性质差别比较大时,不能简单地将分层地基等效为均值地基,关于这一点,康成等[9]也明确指出。
在实际工程中,由于土是长期自然沉积形成的,因此天然地基并非是均质的弹性体,而是层状分布。基于层状弹性半空间理论[15-16],本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法。利用Fourier变换,首先推导了直角坐标系下非均质土体中堆载引起的附加应力;基于两阶段法[17],采用Timoshenko梁模型和Winkker地基模型,计算地表堆载下隧道的响应;进一步分析上覆土层和下卧土层对隧道内力和变形的影响。与已有的研究成果相比,本文的计算模型可以同时考虑土体的分层特性及隧道的结构特性,通用性更强。
1. 计算模型
1.1 直角坐标系下弹性层状半空间体系基本解
地表堆载作用下将在地层中产生附加应力,从而引起已有地铁隧道产生沉降变形,甚至影响隧道的正常运营。为简化计算,得到堆载下分层地基中的基本解,本文计算模型做如下假定:①地基由多个具有有限厚度的水平层以及半无限空间体组成,每层都是均匀、连续、各向同性的弹性体(如图1所示);②各层之间弹性接触,且不发生相对滑动;③不考虑土体固结和蠕变以及地表堆载随时间的变化,且堆载前隧道变形已经稳定。
从弹性力学中不计体力的平衡微分方程、几何方程和物理方程构造如下控制方程[18]:

(1) 式中,
σz ,τzx ,τyz 分别为竖向应力和剪应力,ux ,uy ,uz 分别为3个方向的位移。为推导方便,采用如下变换:
χ1=∂τxz∂x+∂τyz∂y, Γ1=∂ux∂x+∂uy∂y, χ2=∂τxz∂y−∂τyz∂x,Γ2=∂ux∂y−∂uy∂x。 (2) 双重Fourier变换与逆变换采用如下形式进行:
(˜χ1,˜Γ1,˜σz,˜uz,˜χ2,˜Γ2)=14π2∞∫−∞∞∫−∞(χ1,Γ1,σz,uz,χ2,Γ2)⋅e−i(fxx+fyy)dxdy, (3a) (χ1,Γ1,σz,uz,χ2,Γ2)=∞∫−∞∞∫−∞(˜χ1,˜Γ1,˜σz,˜uz,˜χ2,˜Γ2)⋅ei(fxx+fyy)dfxdfy。 (3b) fx 和fy 分别对应于时域中的x和y坐标。结合式(2),对控制方程(1)进行双重Fourier变换,并写成矩阵形式,有d˜UI1dz=AI1˜UI1, (4a) d˜UI2dz=AI2˜UI2, (4b) 式中,
f=√f2x+f2y ,˜UI1=[˜Γ1˜uz˜χ1˜σz]T ,˜UI2=[˜Γ2˜χ2]TAI1=[0f22(1+μ)E0−μ1−μ00(1+μ)(1−2μ)(1−μ)EE1−μ2f20011−μ2f200−10],AI2=[02(1+μ)EE2(1+μ)f2]。 依据Cayley-Hamilton定理,对矩阵方程式(4a),(4b)进行求解可以得到单层地基中应力和位移的传递函数,传递函数的具体表达形式参见文献[18],由于篇幅限制,本文不再赘述。采用与文献[16]相似的处理方式,就可以得到堆载作用下层状土体的应力位移关系:

(5) 基于文献[19]的方法,对式(5)进行双重Fourier逆变换,可以得到真实空间域中地表堆载引起的附加应力数值解。
对于如图2所示的地面偏心堆载,采用如式(6)的坐标变换,并代入式(5)中,即可以得到偏心荷载下分层地基中应力和位移的响应。
x=x′cosθ−y′sinθ+x0 ,y=x′sinθ+y′cosθ+y0 ,z=z0 。} (6) 1.2 地表荷载作用下盾构隧道变形计算
通过1.1节可以得到地表堆载下分层地基中任一深度处附加应力的计算结果,接下来采用两阶段法[17],计算地铁隧道与土体的相互作用,分析地表堆载下隧道的纵向变形响应。
(1)土体模型
在结构与土体的相互作用计算中,通常采用Winkler地基模型[17, 20]、Pasternak地基模型[21]、连续弹性体模型来模拟软土[13]。Liang等[21-22]分析了基坑开挖对下卧地铁的影响,土体分别采用Winkler地基模型和Pasternak地基模型进行模拟,研究表明两种地基模型下得到的隧道隆起量差别不大,但Winkler地基模型更方便于工程应用。因此,本文土体模型采用Winkler地基模型。关于地基反力系数,Vesic基于地表弹性地基梁,给出了确定地基反力系数的经验公式。由于没有考虑土层埋深对土层刚度的影响,Vesic经验公式会高估了隧道的变形。为了更好地反映埋深对土层刚度的影响,Liang等[21]提出了基于埋深修正的Vesic地基反力系数经验公式:
k=1.3EsηB(1−μ2)12√EsB4EI, (7) 式中,
η=1+11.7z0/B [20],Es ,μ 分别为隧道周围土体变形模量和泊松比,B为隧道外径,EI 取隧道等效抗弯刚度EIeq 。(2)隧道模型
城市地铁隧道通常由预制管片组成,管片与管片之间通过高强螺栓连成一个整体。毫无疑问,管片接头的存在会削弱盾构隧道的整体刚度。大量监测数据表明,隧道沿轴线方向的变形可以分解为两部分:①弯曲引发管片的弯曲变形,造成管片的张开;②不均匀沉降诱发的剪切应力引发管片之间的错台变形[23-24]。戴宏伟等[6]、李俊昱等[11]采用Euler-Bernoulli梁分别计算了隧道和管线的纵向变形,但Euler-Bernoulli梁只能考虑弯曲变形,无法得到管片之间的错台量大小,因此本文采用Timoshenko梁来模拟盾构隧道。
为了考虑管片之间接头的存在引起隧道纵向刚度的衰减,大量学者进行了研究[25-26],其中日本学者Shiba提出的刚度等效方法在工程中得到了大量应用,本文同样也采用该方法。图3为隧道变形示意图,通过变形协调条件,可以得到隧道等效抗弯刚度、等效抗剪刚度、张开量和错台量。
a)等效抗弯刚度和张开量
ϕ+cotϕ=π(0.5+NkblsEcAc) ,φ=lsEcIccosϕ+(ϕ+π/2)sinϕcos3ϕM ,EIeq=cos3ϕcosϕ+(ϕ+π/2)sinϕEcIc 。} (8) 式中,N为纵向螺栓的数量,
kb 为螺栓的刚度:kb= EbAb/lb ,ls 和lb 分别为管片和螺栓的长度,Ec 和Ic 分别为管片的弹性模量和隧道的惯性矩。由弯矩引起管片之间最大张开量可以表示为
Δ=φ(r+m)=MEIeq(r+rsinϕ)lb。 (9) b)等效剪切刚度和错台量
基于Timoshenko梁理论和变形协调条件,隧道的等效剪切刚度可以表示为
Geq=ζlslbNκbGbAb+lsκcGcAc, (10) 式中
ζ 为考虑影响隧道刚度相关因素的修正参数,一般取1;κb 和κc 为Timoshenko梁和管片的剪切刚度修正系数,分别取0.9和0.5;Gb 和Gc 分别为螺栓和隧道的剪切模量;Ab 和Ac 分别为螺栓和隧道的横截面积。由剪切引起管片之间的错台量可以表示为
δ=lsQGeq。 (11) (3)隧道变形计算模型
为简化计算,假设地表荷载作用前隧道变形已经稳定、隧道与周围土体始终保持接触,并且不考虑土体固结、蠕变以及荷载随时间的变化。取隧道微元体单元进行受力分析(如图4所示),可以得到如下两个平衡方程:
Q+pDtdx=qDtdx+Q+dQ/dx (力平衡方程), (12a) −M−Qdx−pDtdxdx/2+qDtdxdx/2+M+dM/dx=0(力矩平衡方程)。 (12b) 式中
Q 和M 分别为作用在隧道上的剪力和弯矩;q 为堆载引起的附加应力;Dt 为隧道外径;p 为地基反力,根据Winkler地基模型,p=kw(x) ,k 为地基反力系数,由式(7)确定,w(x) 为堆载引起的隧道沉降。根据Timoshenko梁理论,内力与变形之间的关系为
M=−EIeqdθdx, Q=Geq(dwdx−θ), (13) 式中,
θ 为梁截面中性面的转动角度。联立式(12a),(12b),(13),可以得到地表竖向荷载下盾构隧道竖向位移w(x)的微分控制方程:
d4w(x)dx4+αd2w(x)dx2+βw(x)=α1d2q(x)dx2+β1q(x), (14) 式中,
α=−kDtGeq ,β=kDtEIeq ,α1=−DtGeq ,β1=DtEIeq 。式(14)为4阶常微分方程,很难直接得到其显式解析解,故采用有限差分法将微分方程转换为代数形式的差分方程,通过编程求其数值解。先将隧道离散成n+5个微单元体,每个单元体的长度为l,如图5所示,-2,-1,n+1和n+2均为虚节点。假设隧道两端均自由,即无弯矩和剪力作用。因此,对于0节点和n节点,分别满足边界条件:
Q0=Qn=0 ,M0= Mn=0 。根据差分原理,结合边界条件,式(14)可以改写为以挠度w(x)为未知数的矩阵表达式:KW=DS, (15) 式中,
W=[w0 w1 ⋯ wn−1 wn]T ,S= [q0 q1 ⋯ qn−1 qn]T ,可以通过式(5)求得,K和D的表示形式见附录。求解式(15)就可以得到地表荷载作用下隧道的纵向变形,然后联立式(9)~(13),进一步可以得到隧道承受的弯矩、剪力、张开量和错台量。1.3 算例验证
(1)与Boussinesq解比较
基于式(5),采用双重Fourier逆变换和高斯积分法,可以得到分层地基中地表堆载引起的附加应力,通过与经典的Boussinesq解进行对比,来验证分层地基应力计算模型以及数值变换的正确性。假设地表作用100 kN的荷载,荷载作用范围为4×10 m,地基土为弹性半空间无限体,弹性模量为10 MPa,泊松比为0.33。分别采用Boussinesq解和本文解(其中土体分层数取为2层和4层)计算10 m处的附加应力,计算结果如图6所示,对比结果表明,本文计算结果与Boussinesq解基本一致,从而验证了本文分层土体附加应力计算模型的可靠性。
(2)与已有文献比较
文献[9]以上海典型隧道为研究背景,分析了均质土体中地表堆载对隧道纵向变形的影响。采用本文的计算结果与文献的结果如图7所示,进一步验证了本文计算模型的正确性。
2. 影响参数分析
假定在隧道轴线正上方地表进行工程堆土,堆土重度为18 kN/m3,堆土高度为4 m,地表附加荷载作用范围为2a×2b=20 m×40 m,隧道轴线埋深为15 m。隧道为上海典型地铁隧道,管片内外径分别为5.5 m和6.2 m,环宽为1.2 m,弹性模量为3.45×107 kPa。螺栓为17个,直径为0.03 m,长度为0.4 m,弹性模量为2.06×108 kPa。在下面分析中,若无特别说明,隧道所取参数不变。
2.1 上覆土体模量
为了便于分析,假设第一层层厚10 m,弹性模量变化范围为5~40 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量为10 MPa,泊松比为0.35。
隧道正上方堆载情况下,上覆土体模量对隧道纵向变形影响如图8(a)所示。隧道竖向沉降最大值出现在荷载作用中心处,随着上覆土体模量越大隧道纵向变形越小;当上覆土体模量从5 MPa增大到40 MPa时,隧道最大沉降从16 mm减小为12 mm,最大沉降幅度减小了25%。这主要是因为上覆土体模量越大,土体强度越高,应力扩散效应越明显,作用在隧道上的附加应力也就越小,从而引起隧道的沉降量也就越小。距堆载中心40 m附近,隧道沉降几乎为零,因此隧道沉降槽宽度约为80 m,是荷载作用宽度(沿隧道轴线方向)的4倍,且沉降槽宽度几乎不受上覆土体模量的影响。
图8(b),(c)分别为隧道所受弯矩和张开量随上覆土层模量的变化情况。由图可知,堆载作用下隧道弯矩和张开量沿隧道纵向的分布一致,最大值均出现在荷载作用中心点处,此处即为隧道最危险截面,隧道管片可能因为过大的压应力或拉应力导致破损或产生裂缝,从而引发隧道渗水,影响隧道安全运营。地表堆载下,隧道受到的最大剪力和错台量出现在荷载作用边缘处,如图8(d),(e)所示,这表明在这些隧道截面处,螺栓承受的剪应力最大,因而最容易发生破坏。
综上,在堆载中心处和边缘处,隧道会因承受较大的弯矩和剪力而出现较大的张开量和错台量,情况严重时甚至导致隧道出现道床脱落管片混凝土挤碎、螺栓剪断、渗漏水以及纵缝张开等[1]病害,影响隧道的安全运营。所以,一旦隧道正上方出现堆载,需要加强这些隧道截面的监测工作或提前采取保护措施,预防隧道病害的产生。
2.2 下卧土体模量
为了便于分析,假设第一层层厚20 m,弹性模量为10 MPa,泊松比为0.35,第二层为半无限空间体,弹性模量变化范围为5~40 MPa,泊松比为0.35。
隧道正上方地表堆载作用下,隧道下卧土体模量对隧道内力和变形的影响如图9所示。由图9(a)可知,下卧土体模量越大,地表荷载作用下隧道沉降越小;当下卧土体模量从5 MPa增大到40 MPa时,隧道最大沉降从22 mm减小为7 mm,最大沉降幅度减小了68%。这主要是因为下卧土体模量越大,土体刚度也就越大,对上覆土体的约束作用也随之增加;当下卧土体的模量趋于无穷大时,下卧土层可以等效为刚性边界,即上覆土体底部的竖向位移完全被约束,此种情况下隧道的纵向变形完全取决于上层土体的性质。此外,与图9(a)比较,隧道沉降范围随着下卧土体模量的增大明显缩小,从5倍加载宽度减小为3倍。
下卧土体模量对隧道承受的弯矩、张开量、剪力以及错台量的影响分别如图9(b)~(e)所示,随着下卧土体模量的增加,隧道内力和变形随之减小,变化趋势与上层土体一致,此处不再赘述。
两层土体情况下,隧道最大沉降随土体模量比变化的计算结果如图10所示。由图10可知,在地表堆载作用下,无论是上覆土体模量增加,还是下卧土体模量增加,隧道竖向最大沉降均会降低,相比而言下卧土层的影响更为明显,说明下卧土层控制隧道沉降的效果要优于硬表层地基的情况。另一方面,当下卧土层模量小于隧道所处土层的模量时(即下卧软土层),隧道沉降急剧增大。因此,若隧道下卧软土层,需要引起重视,不宜进行堆土工程,避免隧道因堆载出现过大的变形。
3. 结论
地表堆载会改变隧道原有的平衡状态,引起隧道结构产生过大变形,诱发一系列的隧道病害。基于层状弹性半空间理论,本文建立了层状地基中地表堆载对既有隧道影响的弹性分析方法,分析了土体分层特性对隧道结构响应的影响,得到以下3点结论。
(1)本文采用弹性层状半空间地基模型,建立了能够考虑非均质土体条件的地表大面积荷载对临近既有隧道影响的弹性分析方法,并编写了层状地基中隧道性状的分析程序,方便求解出地表堆载作用下土体特性对既有盾构隧道的内力和变形响应。通过与已有文献数据的对比,验证了本文模型的合理性。
(2)本文方法具有较强的通用性,不仅可以解答均质地基的情况,还可以解答非均质地基的情况,继而可以反映土体分层特性对隧道的影响。对上海典型地铁隧道性状进行参数分析,结果表明上覆土层和下卧土层的弹性模量对隧道沉降和受力具有较为明显的影响,其中增大下卧层土体弹性模量可以显著减小隧道沉降。
(3)当隧道下卧软土层时,地表堆载作用下隧道更容易发生变形,为了保证隧道的安全运营,应该严格评估隧道地表堆载的影响。
此外,限于篇幅,本文仅考虑了隧道正上方大面积堆载引发的隧道纵向变形响应,未涉及到隧道堆载(尤其是偏载)对隧道侧向变形的影响,因此在后续的研究中也可以进行具体分析。
附录

-
表 1 试验参数及液化情况
Table 1 Parameters of tests and liquefaction results
试验组次 波高/cm 循环应力比χ 波节剖面不同深度处液化情况 波腹剖面不同深度处液化情况 0.05 m 0.15 m 0.3 m 0.05 m 0.15 m 0.3 m 1 12 0.179 × × × × × × 2 16 0.238 √ × × × × × 3 20 0.298 √ √ × × × × 4 24 0.357 √ √ × × × × 5 28 0.417 √ √ × √ × × 6 32 0.477 √ √ √ √ √ √ 注: “√”表示波浪作用期间(0~600 s)该位置发生液化,“×”表示未发生液化。表 2 数值模型的参数取值
Table 2 Input parameters for numerical study
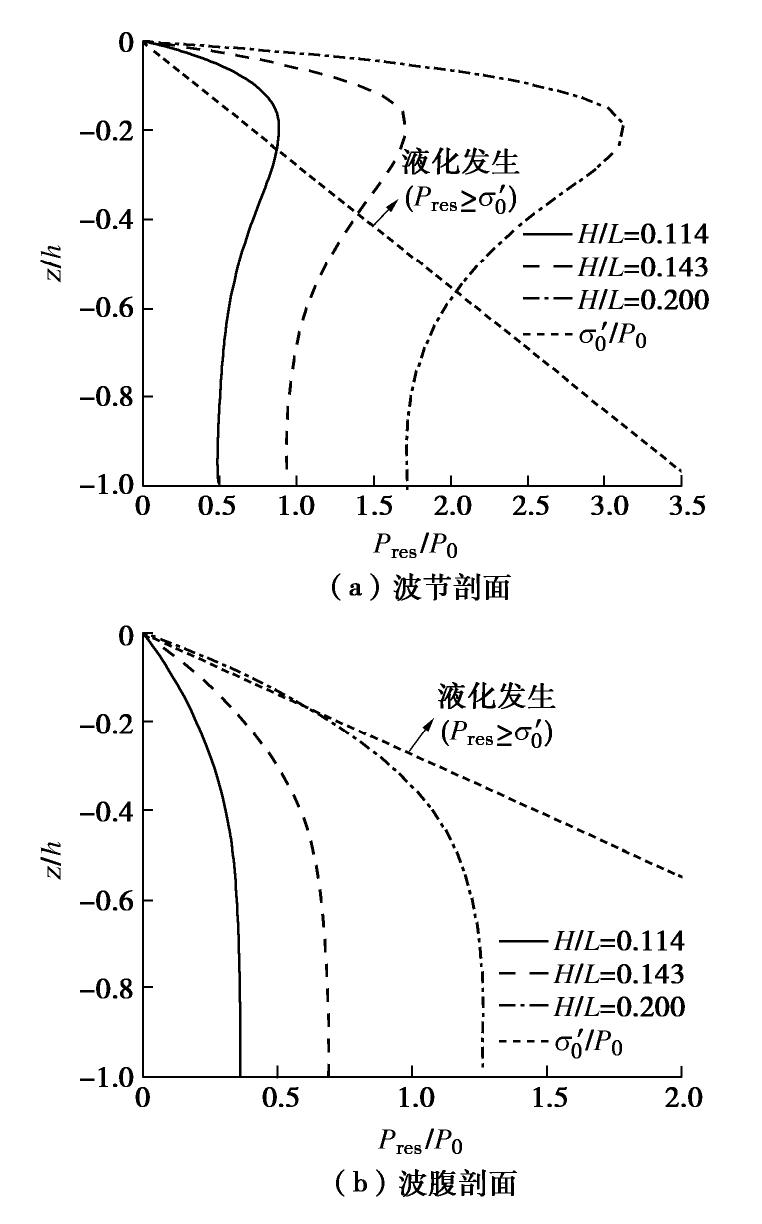
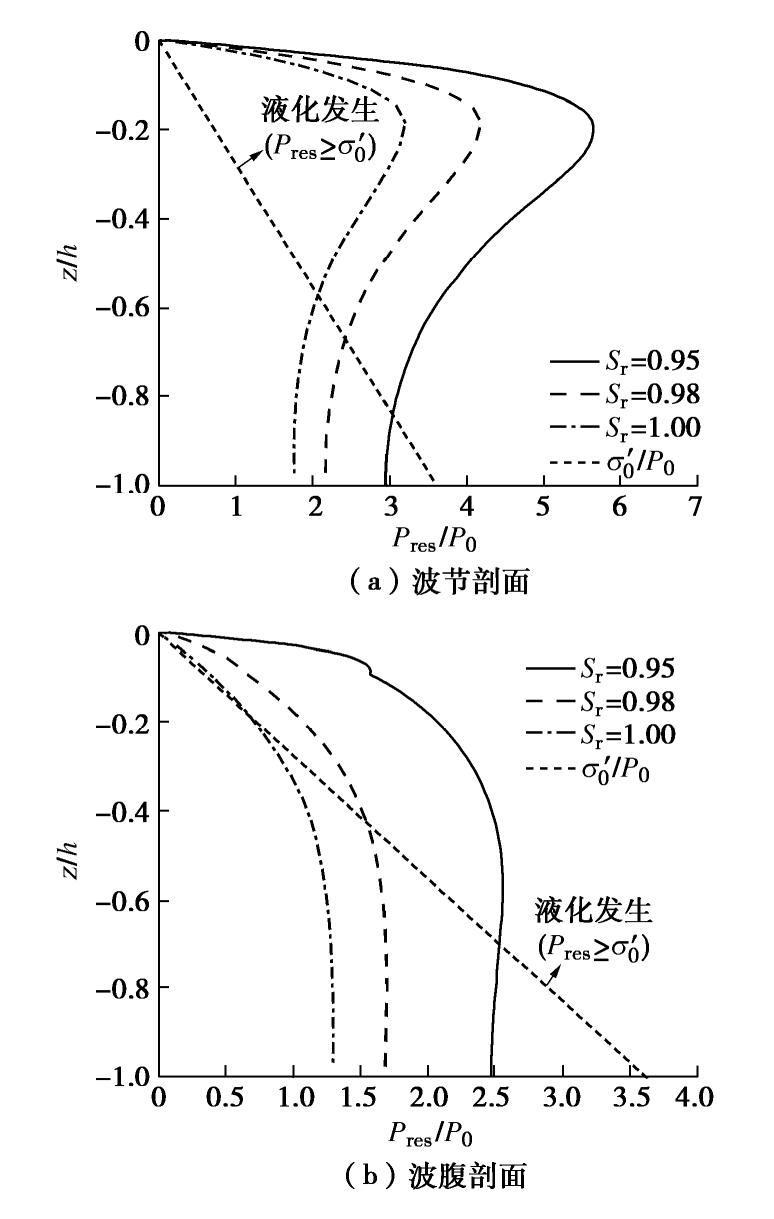
土体浮重度/(N·m-3) 土体饱和度Sr 孔隙度n 泊松比 ν 剪切模量G/Pa 渗透系数ks/(m·s-1) 波长L/m 水深d/m 波周期T/s 波陡H/L 9.2 0.95,0.98,1 0.48 0.3 5.0×105 1×10-6 1.4 0.35,0.40,0.45 1.02 0.114,0.143,0.200 -
[1] 王小雯. 波浪作用下饱和砂质海床液化机理研究[D]. 北京: 清华大学, 2017. WANG Xiao-wen. Research on Mechanics of Wave-Induced Liquefaction in Saturated Sandy Seabed[D]. Beijing: Tsinghua University, 2017. (in Chinese)
[2] 王虎. 波浪作用下黄河三角洲粉质土海床不稳定机制研究[D]. 青岛: 中国海洋大学, 2012. WANG Hu. Mechanism of Wave-Induced Instability of the Silty Seabed in the Yellow River Delta[D]. Qingdao: Ocean University of China, 2012. (in Chinese)
[3] TSAI C P. Wave-induced liquefaction potential in a porous seabed in front of a breakwater[J]. Ocean Engineering, 1995, 22(1): 1-18. doi: 10.1016/0029-8018(94)00042-5
[4] SEKIGUCHI H, KITA K, OKAMOTO O, et al. Response of poro-elastoplastic beds to standing waves[J]. Soils and Foundations, 1995, 35(3): 31-42. doi: 10.3208/sandf.35.31
[5] SASSA S, SEKIGUCHI H. Wave-induced liquefaction of beds of sand in a centrifuge[J]. Géotechnique, 1999, 49(5): 621-638. doi: 10.1680/geot.1999.49.5.621
[6] JENG D S, LIN Y S. Poroelastic analysis of the wave-seabed interaction problem[J]. Computers and Geotechnics, 2000, 26(1): 43-64. doi: 10.1016/S0266-352X(99)00032-4
[7] 周晓智, 陈育民, 刘汉龙. 驻波作用下有限厚度海床动应力路径特性研究[J]. 岩土工程学报, 2018, 40(5): 890-899. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805017.htm ZHOU Xiao-zhi, CHEN Yu-min, LIU Han-long. Study on characteristics of dynamic stress path of finite-thickness seabed under standing waves[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 890-899. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805017.htm
[8] ZHAO H Y, JENG D S, LIAO C C, et al. Three-dimensional modeling of wave-induced residual seabed response around a mono-pile foundation[J]. Coastal Engineering, 2017, 128: 1-21. doi: 10.1016/j.coastaleng.2017.07.002
[9] JENG D S, ZHAO H Y. Two-Dimensional model for accumulation of pore pressure in marine sediments[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2015, 141(3): 04014042. doi: 10.1061/(ASCE)WW.1943-5460.0000282
[10] KIRCA V S O, SUMER B M, FREDSOE J. Residual liquefaction of seabed under standing waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2013, 139(6): 489-501. doi: 10.1061/(ASCE)WW.1943-5460.0000208
[11] WANG H, LIU H J, ZHANG M S. Pore pressure response of seabed in standing waves and its mechanism[J]. Coastal Engineering, 2014, 91: 213-219. doi: 10.1016/j.coastaleng.2014.06.005
[12] YANG G X, YE J H. Nonlinear standing wave-induced liquefaction in loosely deposited seabed[J]. Bulletin of Engineering Geology and the Environment, 2018, 77(1): 205-223. doi: 10.1007/s10064-017-1038-z
[13] SASSA S, SEKIGUCHI H. Analysis of wave-induced liquefaction of sand beds[J]. Géotechnique, 2001, 51(2): 115-126. doi: 10.1680/geot.2001.51.2.115
[14] 蔡正银, 吴诗阳, 武颖利, 等. 高地震烈度区深厚覆盖砂层液化研究[J]. 岩土工程学报, 2020, 42(3): 405-412. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003003.htm CAI Zheng-yin, WU Shi-yang, WU Ying-li, et al. Liquefaction of deep overburden layers in zones with high earthquake intensity[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 405-412. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003003.htm
[15] SASSA S, SEKIGUCHI H. Analysis of wave-induced liquefaction of sand beds[J]. Géotechnique, 2001, 51(5): 115-126.
[16] JENG D S. Soil response in cross-anisotropic seabed due to standing waves[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(1): 9-19. doi: 10.1061/(ASCE)1090-0241(1997)123:1(9)
[17] ZEN K, YAMAZAKI H. Mechanism of wave-induced liquefaction and densification in seabed[J]. Soils and Foundations, 1990, 30(4): 90-104. doi: 10.3208/sandf1972.30.4_90
[18] MUTLU SUMER B, HATIPOGLU F, FREDSOE J, et al. The sequence of sediment behaviour during wave-induced liquefaction[J]. Sedimentology, 2006, 53(3): 611-629. doi: 10.1111/j.1365-3091.2006.00763.x
[19] MADSEN O S. Wave-induced pore pressures and effective stresses in a porous bed[J]. Géotechnique, 1978, 28(4): 377-393. doi: 10.1680/geot.1978.28.4.377
[20] 刘红军, 王小花, 贾永刚, 等. 黄河三角洲饱和粉土液化特性及孔压模型试验研究[J]. 岩土力学, 2005, 26(增刊2): 83-87. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2005S2021.htm LIU Hong-jun, WANG Xiao-hua, JIA Yong-gang, et al. Experimental study on liquefaction properties and pore-water pressure model of saturated silt in Yellow River Delta[J]. Rock and Soil Mechanics, 2005, 26(S2): 83-87. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2005S2021.htm
-
期刊类型引用(19)
1. 彭俊皓,魏玉峰,李常虎,王群,李征征. 基于DBO-GRNN神经网络的冰水堆积物渗透系数预测. 人民长江. 2025(02): 167-174 .  百度学术
百度学术
2. 张杰,黄勇. 长江漫滩区软土渗透系数计算方法对比分析. 中国煤炭地质. 2024(02): 37-42 .  百度学术
百度学术
3. 王宇虓,杜广印,刘松玉,杨泳,周同和,徐金涛. 振杆密实法加固粗粒混合土模型试验. 工程科学与技术. 2024(03): 99-108 .  百度学术
百度学术
4. 樊书抗,杨正权,朱凯斌,赵艺颖,刘小生,赵剑明. 土的级配特征与连续级配方程研究. 水利学报. 2024(05): 597-606 .  百度学术
百度学术
5. 郭海,张安银. 基于PCA的长江漫滩软弱黏性土渗透特性研究. 江苏建筑. 2024(04): 102-105 .  百度学术
百度学术
6. 赵桂锋,蒋明杰,张振,王天成,梅国雄. 粗粒土缩尺级配的渗透系数规律试验. 工程科学与技术. 2024(05): 240-246 .  百度学术
百度学术
7. 李诗琪,杨忠平,刘浩宇,高宇豪,刘新荣. 考虑间断级配影响的土石混合体水力侵蚀分异机理. 土木工程学报. 2024(10): 125-134 .  百度学术
百度学术
8. 付宏渊,杨海涛,吴二鲁,曾铃,钟涛,姜懿芸. 考虑炭质泥岩颗粒破碎的级配演化预测模型. 水利学报. 2024(09): 1058-1070 .  百度学术
百度学术
9. 杨锴,杨奇,徐方,徐俏东,韩学良. 考虑细粒含量的单参数连续级配方程研究. 铁道科学与工程学报. 2024(12): 5094-5103 .  百度学术
百度学术
10. 曲诗章,刘晓明,黎莉,陈仁朋. 基于双分形级配模型参数的粗粒土渗透系数计算公式. 岩土工程学报. 2023(01): 144-152 .  本站查看
本站查看
11. 侯龙清,袁晓铭,陈龙伟,李明东. 一种新型南55渗透仪研制及工程应用. 岩土工程学报. 2023(02): 419-425 .  本站查看
本站查看
12. 李浩,李春艳,张嵩,谢英美. 建筑工程中地质特征及岩土工程支护研究. 能源与环保. 2023(01): 181-186 .  百度学术
百度学术
13. 赵贵章,孔令莹,徐远志,王淑丽,王展. 银川平原典型介质的颗粒级配对渗透系数的影响研究. 中国农村水利水电. 2023(04): 203-207 .  百度学术
百度学术
14. 张福海,徐嘉成,薛浩宇,刘峥嵘. 级配分布对杂填土地基互嵌沉降影响的试验分析. 河南科学. 2023(05): 730-737 .  百度学术
百度学术
15. 林玉祥,林浩东,莫品强,褚锋,庄培芝. 基于XGBoost的堆场软土渗透系数反演研究. 西安理工大学学报. 2023(01): 133-140 .  百度学术
百度学术
16. 袁仕方,曹志翔,韩志洋,张玲洁. 藏东南粗粒土降雨入渗影响因素试验分析. 高原农业. 2022(02): 189-196 .  百度学术
百度学术
17. 丁林楠,李国英,魏匡民. 描述土体级配分布的级配方程及其适用性. 岩土力学. 2022(S1): 173-183 .  百度学术
百度学术
18. 段钊,袁林,毕银丽,王凯,吴延斌,张庆. 紫花苜蓿根系-黄土复合体剪切特性与库仑修正模型. 煤田地质与勘探. 2022(12): 85-95 .  百度学术
百度学术
19. 骆莉莎,周昕,林军. 颗粒形态对粗粒土渗透系数影响的数值模拟研究. 湖南工业职业技术学院学报. 2021(01): 93-96 .  百度学术
百度学术
其他类型引用(16)




 下载:
下载: