基于LBM-IMB-DEM分析岩土多孔介质的渗透淤堵特性

金磊; 曾亚武; 程涛; 李晶晶

doi:10.11779/CJGE202105015

基于LBM-IMB-DEM分析岩土多孔介质的渗透淤堵特性 English Version

1.
湖北理工学院土木建筑工程学院,湖北　黄石　435003
2.
武汉大学土木建筑工程学院,湖北　武汉　430072

基金项目:

湖北省自然科学基金项目 2019CFB199

国家自然科学基金项目 41272342

国家自然科学基金项目 12002121

湖北省高等学校优秀中青年科技创新团队计划项目 T201823

详细信息

作者简介:
金磊(1989—),男,博士,副教授,主要从事岩土流-固耦合数值模拟等方面的研究工作。E-mail: whujinlei@whu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 364
- HTML全文浏览量: 32
- PDF下载量: 312
出版历程
- 收稿日期: 2020-09-06
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-04-30

Seepage clogging characteristics of rock and soil porous media using LBM-IMB-DEM simulation method

1.
School of Civil Engineering and Architecture, Hubei Polytechnic University, Huangshi 435003, China
2.
School of Civil Engineering, Wuhan University, Wuhan 430072, China

摘要

摘要: 岩土多孔介质中发生的渗透淤堵本质上是渗流与颗粒耦合作用的结果。开发了适用于岩土渗流-颗粒耦合模拟的格子Boltzmann方法-浸入运动边界-离散元法（LBM-IMB-DEM）数值计算平台并对岩土多孔介质的渗透淤堵过程开展了孔隙尺度的模拟,分析了多孔介质骨架颗粒分布、骨架颗粒粒径、孔隙率、骨架颗粒定向性及水压力等因素对其渗透淤堵特性的影响。结果表明：多孔介质中骨架颗粒的空间分布不同,其渗透淤堵特性也有所区别；多孔介质的骨架颗粒粒径或孔隙率越小,淤堵后的滞留颗粒越多,淤堵越严重；骨架颗粒定向性对淤堵特性有一定影响,当骨架颗粒为条形且其长轴与流动方向垂直时淤堵最为严重；随水压力增大,淤堵后滞留颗粒在多孔介质中的分布更趋于分散,淤堵更为严重；岩土多孔介质渗透淤堵的程度与其淤堵前的渗透性密切相关,透水性强的多孔介质相对不易发生淤堵。
- 渗透淤堵 /
- 渗流-颗粒耦合 /
- 格子Boltzmann方法（LBM） /
- 离散单元法（DEM） /
- 岩土多孔介质
Abstract: Seepage clogging in rock and soil porous media is essentially the result of the coupling action of seepage and solid particles. A numerical computing platform based on the coupled lattice Boltzmann method-immersed moving boundary-discrete element method (LBM-IMB-DEM) is developed and used to simulate the seepage clogging process in rock and soil porous media. Based on the simulated results, the influences of distribution of skeleton particles, size of skeleton particles, porosity, orientation of skeleton particles and water pressure on the seepage clogging characteristics are analyzed. The results show that different spatial distributions of skeleton particles in the porous media result in different clogging characteristics. The smaller the skeleton particle size or the porosity of porous media is, the more the retained particles are after clogging and the more severe the clogging is. The orientation of skeleton particles in the porous media has a certain influence on clogging, and the clogging is the worst when the skeleton particles are strip-shaped and their long axes are all perpendicular to the flow direction. With the increase of water pressure, the retained particles tend to disperse in the porous media and the clogging is more serious. The clogging in the porous media is closely related to their permeability before clogging, and the porous media with high permeability are relatively less prone to clogging.
- seepage clogging /
- seepage-particle coupling /
- lattice Boltzmann method /
- discrete element method /
- rock and soil porous medium

HTML全文

0. 引言

淤堵按其产生的原因可分为机械淤堵、化学淤堵和生物淤堵等3种类型。岩土工程中,机械淤堵多被称为“渗透淤堵”,它指的是细小土颗粒在渗流作用下进入岩土多孔介质中滞留下来进而降低其渗透性的现象^[1]。渗透淤堵在某些工况下具有积极的作用,如坝基淤堵能减少水库的渗漏量、基坑止水帷幕淤堵能提高其截水效果等^[2-3]。但另一方面,渗透淤堵也常有不利影响甚至造成严重灾害,如减压井等工程排渗系统因淤堵而失效、斜坡体内淤堵引发滑坡、堰塞坝淤堵诱发漫顶溃决等^[4-6]。因此,研究岩土多孔介质的渗透淤堵特性对于工程实践中“趋其利、避其害”具有重要意义。

截至目前,国内外学者大多通过物理模拟试验研究岩土体或土工织物的渗透淤堵作用,如径向渗透模型试验、梯度比试验、砂槽模型试验等^[3-4,7-8]。物理模拟试验可获得试样淤堵过程中的流量、水力梯度和淤堵后的渗透系数等宏观水力参数,但无法洞悉淤堵后滞留颗粒在多孔介质中的空间分布特征及其与孔-喉结构的关系,从而也难以明晰渗透淤堵的内在机制。

岩土多孔介质中的渗透淤堵过程本质上是渗流-颗粒的相互作用即流-固耦合,数值模拟技术是研究此类问题的重要手段。Dabir等^[9]基于孔隙网络模拟了多孔介质中颗粒运移和滞留造成的淤堵。但孔隙网络模拟技术将多孔介质复杂的孔-喉结构简化为规则的球体-圆柱网络,与实际情况差别较大。李识博等^[10]基于商业离散元软件PFC中的流体动力学-离散单元法耦合（CFD-DEM）模块模拟了坝基粗粒土中的渗透淤堵作用。CFD-DEM中的流体计算基于宏观连续介质假设并采用经验或半经验的渗流模型（如达西定律）进行求解,且采用的是粗糙网格和局部平均的方案,难以进行更为精细的孔隙尺度的模拟^[11-12]。

将基于介观的格子Boltzmann方法（LBM）与离散单元法耦合形成的LBM-DEM能有效克服上述CFD-DEM的不足,更适合从孔隙尺度模拟复杂的流体-颗粒系统^[13-15]。近年来,Wang等^[16-17]采用LBM-DEM耦合算法成功地模拟了接触侵蚀和水力劈裂等复杂的岩土流-固耦合问题。为此,本文拟采用LBM模拟岩土多孔介质中的渗流,采用DEM模拟土颗粒在多孔介质中的相互作用与运动,并采用浸入运动边界法（IMB）处理移动的固体颗粒与流体之间的相互作用,基于LBM-IMB-DEM对岩土多孔介质的渗透淤堵过程开展孔隙尺度的模拟,探究多孔介质骨架颗粒分布、骨架颗粒粒径、骨架颗粒定向性、孔隙率及水压力等因素对其渗透淤堵特性的影响。

1. 数值算法

1.1 LBM基本原理

本文基于介观的LBM^[18-19]模拟岩土多孔介质中的渗流。在LBM中,流体的计算域由边长为h（格子步长）的立方体格子所划分,在每个节点上定义一个粒子分布函数 $f_{α} (r, t)$ 表示在 $r$ 位置处 $t$ 时刻以 $e_{α}$ 速度运动的流体粒子的数目。在离散的每个时间步 $Δ t$ 内,流体粒子以离散的速度 $e_{α}$ 运动到相邻的节点上,紧接着在该节点处与其它的粒子发生碰撞,碰撞后粒子的分布函数将更新,该过程称为迁移与碰撞,可用公式分别表示为

$f_{α} (r + e_{α} Δ t, t + Δ t) = f_{α} (r, t)$ ,

(1)

$f_{α} (r, t) = Ω (f_{α} (r, t))$ ,

(2)

式中, $Ω$ 为碰撞算子,它规定了流体粒子的碰撞行为。通过迁移与碰撞的不断循环,流体粒子逐步趋向平衡态分布 $f_{α}^{eq}$ 。

本文采用最为常用的碰撞算子即单松弛时间BGK碰撞模型^[20]：

$Ω (f_{α} (r, t)) = f_{α} (r, t) - \frac{Δ t}{τ} (f_{α} (r, t) - f_{α}^{eq} (r, t))$ ,

(3)

式中, $f_{α}^{eq} (r, t)$ 为局部平衡态分布函数,τ为无量纲弛豫时间。

本文LBM采用的离散速度模型为常用的D2Q9模型^[21],其离散速度、平衡态分布函数及相关计算参数为

$e_{α} = {\begin{array}{l} (0,0) (α = 0) \\ c {\cos [(α - 1) \frac{π}{2}], \sin [(α - 1) \frac{π}{2}]} (α = 1,2,3,4) \\ \sqrt{2} c {\cos [(2 α - 1) \frac{π}{4}], \sin [(2 α - 1) \frac{π}{4}]} (α = 5,6,7,8) \end{array},$

(4)

$f_{α}^{eq} = ρ ω_{α} [1 + \frac{e_{α} u}{c_{s}^{2}} + \frac{{(e_{α} u)}^{2}}{2 c_{s}^{4}} - \frac{u^{2}}{2 c_{s}^{2}}]$ ,

(5)

$c = h / Δ t$ ,

(6)

$c_{s}^{2} = c^{2} / 3$ ,

(7)

$ω_{α} = {\begin{cases} 4 / 9 (α =0) \\ 1 / 9 (α =1,2,3,4) \\ 1 / 36 (α =5,6,7,8) \end{cases}$ ,

(8)

式中,c为格子速度, $c_{s}^{}$ 为格子声速,ω_α为权系数,ρ为流体密度,u为宏观速度。

根据质量和动量守恒定律,模型的宏观密度ρ,速度u和压力p分别定义为

$ρ = \sum_{α = 0}^{8} f_{α}$ ,

(9)

$u = \frac{1}{ρ} \sum_{α = 0}^{8} f_{α} e_{α}$ ,

(10)

$p = ρ c_{s}^{2}$ 。

(11)

此外,流体的运动黏滞系数υ与无量纲弛豫时间τ及格子参数间关系为

$υ = c_{s}^{2} (τ - \frac{1}{2}) Δ t$ 。

(12)

在LBM中,还需要处理好流体的边界,如压力边界和速度边界等。另外,为计算方便一般将物理量做无量纲处理,即采用格子单位。关于边界处理及单位转换可参考文献[13,18,19]。

采用LBM计算低黏度的流体如空气和水时常出现数值不稳定,将工程中常用的大涡模拟（LES）引入LBM中可有效解决该问题,具体可参见文献[13]。

1.2 IMB方法

本文采用IMB方法^[22]处理流体流动与移动的固体颗粒之间的相互作用。在IMB中,需要先将移动的固体颗粒用流体节点进行离散并分别标记出固体内部节点、固体边界节点和流体边界节点,具体标记方法可参考文献[13]。针对这些节点,在LBM的碰撞算子 $Ω$ 中要引入1个附加碰撞项 $Ω_{α}^{S}$ 来表征固体颗粒对流体的作用,其公式为：

$Ω = - \frac{Δ t}{τ} (1 - B) [f_{α} (r, t) - f_{α}^{eq} (r, t)] + B Ω_{α}^{S}$ ,

(13)

$Ω_{α}^{S} = [f_{- α} (r, t) - f_{- α}^{eq} (ρ, u)] - [f_{α} (r, t) - f_{α}^{eq} (ρ, u_{P})]$ ,

(14)

式中,B为附加碰撞项的权函数, $- α$ 为方向 $α$ 的反方向, $u$ , $u_{P}$ 分别为节点 $r$ 处流体和固体的速度。B值由节点的固体占比 $ε$ （节点处控制单元被固体覆盖的体积分数）计算得到,

$B = \frac{ε (τ / Δ t - 0.5)}{(1 - ε) + (τ / Δ t - 0.5)}$ 。

(15)

另一方面,流体对移动的固体颗粒的作用由流体流动施加在颗粒上的力和力矩表征,

$F_{f} = c h \sum_{k = 1}^{n} (B_{k} \sum_{α = 0}^{8} Ω_{α}^{S} e_{α})$ ,

(16)

$T_{f} = c h \sum_{k = 1}^{n} [(r_{k} - r_{P}) \times (B_{k} \sum_{α = 0}^{8} Ω_{α}^{S} e_{α})]$ ,

(17)

式中,n为该固体颗粒所标记节点的数量, $(r_{k} - r_{P})$ 为从颗粒中心指向第k个节点的位置向量。

1.3 DEM基本理论

本文采用基于软球模型的DEM^[23]模拟固体颗粒之间的相互作用,即允许相接触的两个颗粒间有少量重叠。采用线性接触刚度模型和摩擦滑移模型模拟相接触的两颗粒间的本构行为（力-位移法则）,

$F_{c} = F_{c}^{n} + F_{c}^{t} = F_{n} n + F_{t} t$ ,

(18)

$F_{n} = k_{n} δ_{n}$ ,

(19)

$F_{t} = k_{t} δ_{t} \leq μ F_{n}$ ,

(20)

$T_{c} = R \times F_{c}^{t}$ ,

(21)

式中, $F_{c}$ 为颗粒间接触力, $n$ , $t$ 为接触的法向和切向单位向量, $F_{c}^{n}$ , $F_{n}$ 为法向接触力矢量及其大小, $F_{c}^{t}$ , $F_{t}$ 为切向接触力矢量及其大小, $k_{n}$ , $k_{t}$ 分别为接触法向刚度和切向刚度, $δ_{n}$ , $δ_{t}$ 分别为接触法向重叠量和切向相对位移, $μ$ 为颗粒间摩擦系数, $T_{c}$ 为接触力产生的力矩, $R$ 为从颗粒中心指向接触点的位置向量。

固体颗粒可能受到的力包括颗粒间的接触力、颗粒与固体边界墙的接触力、流体的作用力以及重力等,在这些力的作用下颗粒的运动遵循牛顿定律（运动法则）,

$m a = F_{f} + \sum_{i} F_{c i} + F_{b}$ ,

(22)

$I \ddot{θ} = \sum_{i} T_{c i} + T_{f}$ ,

(23)

式中, $m$ , $I$ 分别为颗粒的质量和惯性矩, $a$ , $\ddot{θ}$ 分别为颗粒的线加速度和角加速度, $F_{c i}$ , $T_{c i}$ 分别为第i个接触产生的接触力和力矩, $F_{b}$ 表示其它作用力如重力等。颗粒的运动方程采用显式中心有限差分法求解,以获得每个时刻颗粒的速度和位置。

1.4 LBM-IMB-DEM数值计算平台及其验证

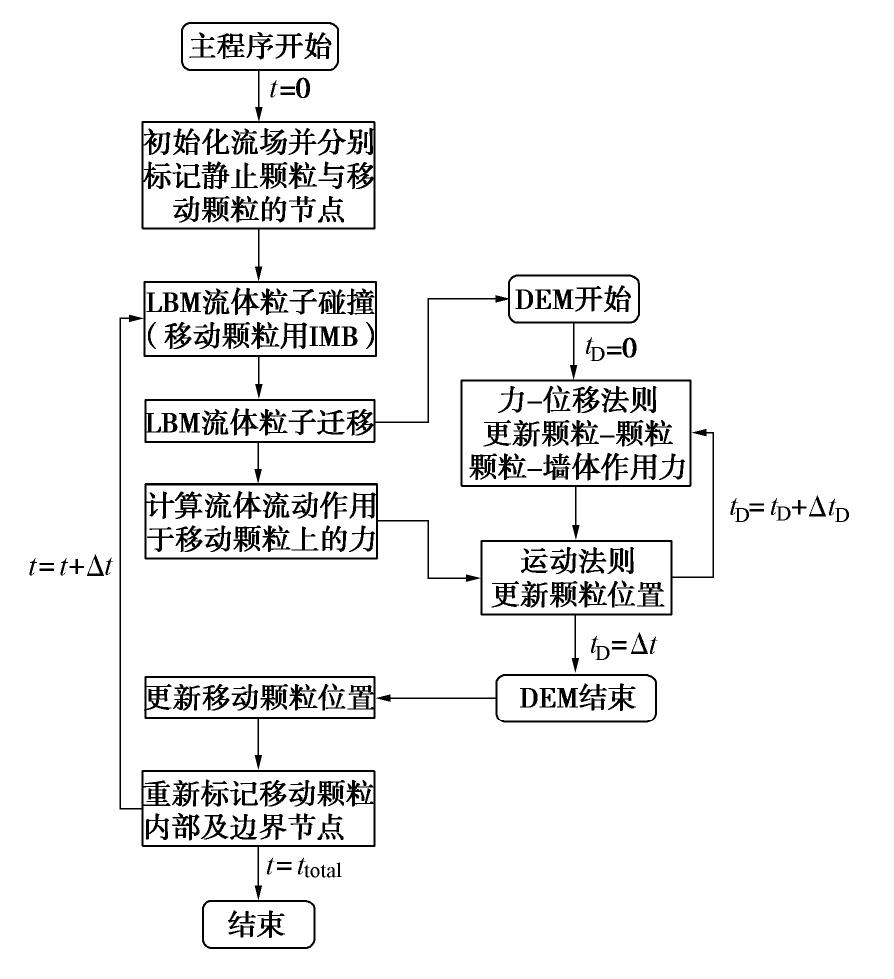
基于1.1—1.3节所述算法的基本理论,运用Fortran语言开发了LBM-IMB-DEM耦合数值计算平台,其中LBM模拟流体流动、DEM模拟固体颗粒间的相互作用与运动、IMB模拟移动的固体颗粒与流体之间的相互作用,耦合程序的计算流程如图1所示。

图 1 LBM-IMB-DEM耦合程序计算流程

Figure 1. Flow chart of coupled LBM-IMB-DEM

下载: 全尺寸图片幻灯片

需要说明的是,LBM与DEM均采用显式时步循环算法且有各自的时间步长,一般来说DEM的时间步长 $Δ t_{D}$ 比LBM的时间步长 $Δ t$ 要小,因此可将DEM的时间步长适当缩短使得 $Δ t / Δ t_{D}$ 为整数,进而可将DEM循环作为LBM的子循环（如图1所示）以达到耦合计算时间的统一。

本文通过一系列经典算例对LBM-IMB-DEM数值计算平台进行了多方面的验证,主要包括：模拟二维Poiseuille流和圆柱绕流验证了LBM的准确性；模拟砂堆和双轴试验并与PFC模拟的结果对比验证了DEM的准确性；模拟单颗粒沉降和两个颗粒沉降DKT的过程验证了IMB的准确性。限于篇幅,这里只给出单颗粒下沉模拟的参数和结果。

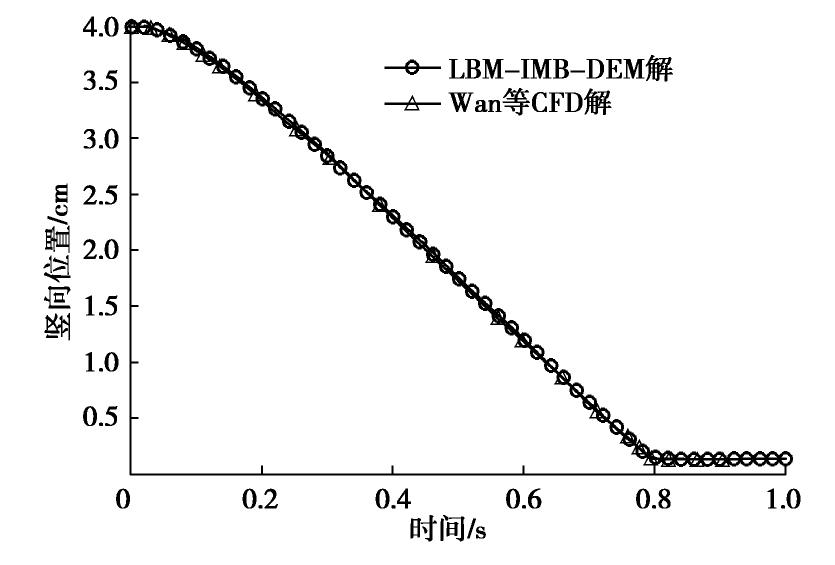
单颗粒下沉算例常被用来验证颗粒-流体耦合算法的准确性。本文建立的单颗粒下沉模型中流体计算域为宽2 cm、高6 cm的长方形区域,将1个直径为0.25 cm的圆形固体颗粒放置于坐标为（1 cm,4 cm）的位置（原点位于计算域的左下角点）。固体颗粒的密度和法向刚度分别为1.25 g/cm³和1.0×10⁷ N/m,计算域四周为固体边界墙且其刚度为1.0×10⁸ N/m,不考虑颗粒与边界墙接触时的切向作用。流体的密度与运动黏度分别为1.0 g/cm³和1.0×10^-5 m²/s,流体计算域的格子步长取为0.01 cm,弛豫时间为0.65,区域四周为不透水边界并由标准反弹准则^[18]进行处理。LBM-IMB-DEM计算过程中,固体颗粒在重力作用下开始向下运动并受到向上的流体力作用,随后颗粒一直下落直到底边界并逐渐稳定下来,将该过程中颗粒竖向位置随时间的变化与Wan等^[24]基于CFD模拟的结果进行对比,如图2所示。可以看到,两者吻合较好,这说明LBM-IMB-DEM耦合算法能较准确地模拟颗粒-流体耦合问题。

图 2 单颗粒下沉模拟结果对比

Figure 2. Comparison of simulated results of single particle sedimentation

下载: 全尺寸图片幻灯片

2. 渗透淤堵的LBM-IMB-DEM模拟

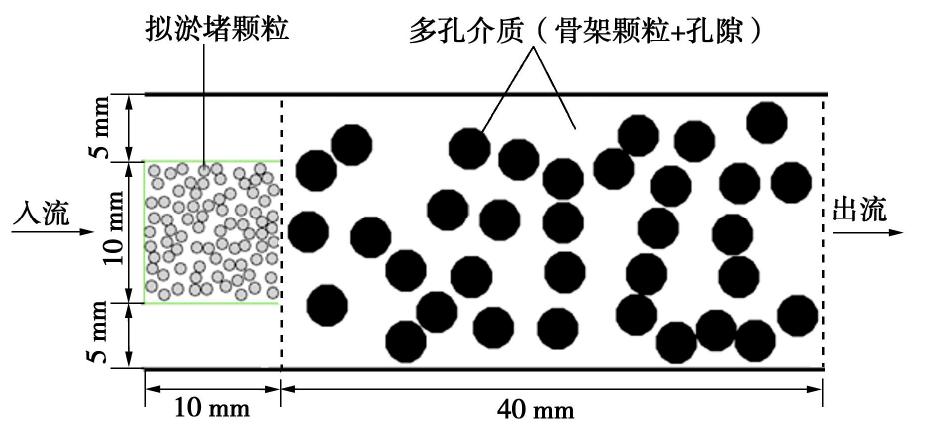
实际的岩土体中颗粒粒径、颗粒形态、颗粒定向性与孔隙等内部结构异常复杂,为了便于系统地研究其淤堵特性,本文建立了简化的岩土多孔介质渗透淤堵二维模型,如图3所示。模型总长50 mm、宽20 mm,其中多孔介质区域长为40 mm（图3中2条虚线之间）,它由一定尺寸的骨架颗粒按一定孔隙率随机分布所构成,这些骨架颗粒在后续的数值计算过程中保持固定。图3中左侧绿色线框内的灰色圆盘为添加的拟淤堵颗粒,其直径为0.8 mm。模型的上、下边界不透水且为固体颗粒的墙边界,水流从左侧进入、右侧流出,左、右边界为压力边界并由非平衡态反弹法^[18]处理,上、下不透水边界及固定的骨架颗粒由标准反弹法^[18]处理。基于LBM-IMB-DEM数值计算平台对模型进行计算以模拟水流作用下拟淤堵颗粒在多孔介质中的迁移和沉积过程,主要计算参数列入表1。

图 3 岩土多孔介质渗透淤堵二维模型

Figure 3. Two-dimensional model for seepage clogging in rock and soil porous media

下载: 全尺寸图片幻灯片

表 1 渗透淤堵LBM-IMB-DEM模拟参数

Table 1. LBM-IMB-DEM simulation parameters for seepage clogging

固体参数	参数值	流体参数	参数值
颗粒密度/(kg·m^-3)	2650	流体密度/(kg·m^-3)	1000
法向刚度/(N·m^-1)	1×10⁷	运动黏度/(m²·s^-1)	1×10^-6
切向刚度/(N·m^-1)	5×10⁶	弛豫时间	0.51
摩擦系数	0.3	格子步长/m	8×10^-5
DEM子循环步数	4	LBM时间步长/s	2.13×10^-5

下载: 导出CSV

| 显示表格

本文定义“淤堵渗透系数比”来表征多孔介质渗透淤堵的严重程度,其定义为多孔介质淤堵后渗透系数与淤堵前渗透系数的比值,该值越小表示淤堵越严重。另外,还定义了“滞留体积百分比”来表征淤堵后多孔介质中滞留颗粒数量的多少,其定义为多孔介质中滞留颗粒的总体积与孔隙体积之比（百分数）。

待颗粒运动与流场都稳定后停止淤堵过程的模拟。随后,针对淤堵前、后的多孔介质模型（图3中2条红色线之间区域）,在保持其中颗粒（包括淤堵颗粒）位置不变的条件下,将其入口与出口密度分别设为1000.1和1000.0（雷诺数较小,基本为层流）并进行迭代计算,当流场收敛到稳态后停止迭代并由达西定律计算其渗透系数,据此可进一步得到该模型的淤堵渗透系数比。需要指出的是下文中所涉及的流场图也均是在此条件下获得的。

3. 模拟结果分析

本文主要模拟了不同骨架颗粒分布、骨架颗粒粒径、多孔介质孔隙率、骨架颗粒定向性及水流入口压力（水流入口密度）等条件下多孔介质的渗透淤堵,下面就这些条件下的模拟结果进行分析。需要说明的是,格子单位与物理单位的比值为一个固定的参考量,也就是说格子单位的变化规律与物理单位的变化规律是完全一致的,一般为了计算方便在计算过程中统一取格子单位。为方便起见,在下文的分析中也直接采用了格子单位（l.u.）下得到的模拟结果。

3.1 骨架颗粒分布的影响

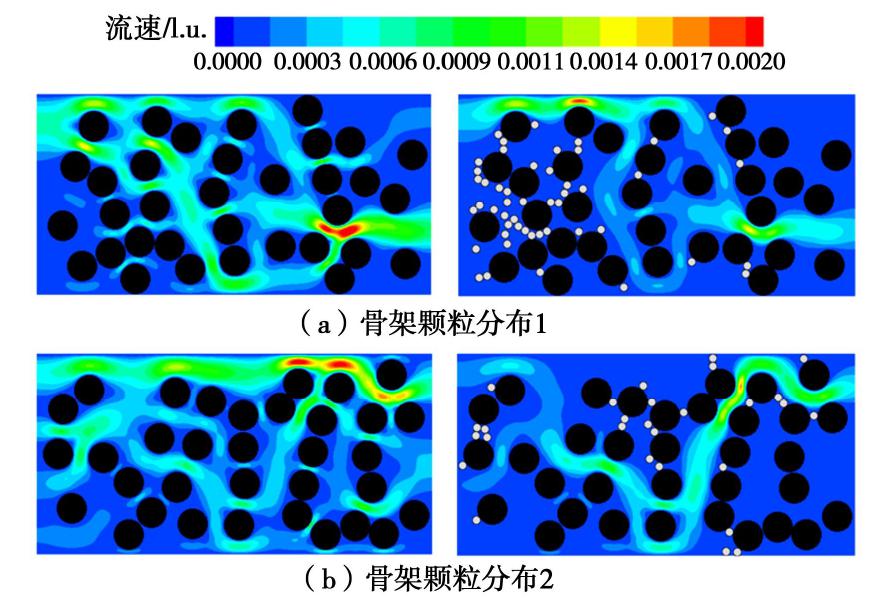
在骨架颗粒是粒径（直径）为37.5（3 mm）的圆形,孔隙率为0.7,水流入口与出口密度分别为1001.0和1000.0的条件下,通过改变随机数种子生成了5种不同骨架颗粒随机分布的多孔介质模型并进行渗透淤堵过程的LBM-IMB-DEM数值模拟。模拟结果如下：5个模型的淤堵渗透系数比分别为0.41,0.36,0.43,0.37和0.43,平均值为0.40；5个模型的滞留体积百分比分别为3.82%,2.53%,2.51%,2.82%和2.55%,平均值为2.85%。其中第1,2种骨架颗粒分布的模型淤堵前后的流场与滞留颗粒分布情况如图4所示。

图 4 不同骨架颗粒分布时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 4. Distribution of retained particles and rate of fluid flow in porous media versus distribution of skeleton particles

下载: 全尺寸图片幻灯片

由模拟结果及图4可知：渗透淤堵发生后,尽管多孔介质中滞留颗粒体积只占总孔隙体积很小一部分（小于5.0%）,但这些颗粒多驻留在孔喉处,致使流动通道数显著减少,因而淤堵后的渗透系数仅为淤堵前的40%；骨架颗粒分布1的模型中滞留颗粒相对于分布2时的较多,但部分滞留颗粒位于离入口较近的骨架颗粒表面和非流动区域,而分布2的滞留颗粒基本都位于孔喉处,所以分布2的淤堵渗透系数比反而较小,即淤堵更为严重。

由上述分析可得,多孔介质中骨架颗粒的空间分布不同,其孔隙结构也不同,渗透淤堵特性也有所区别。为此,在下文分析不同骨架颗粒粒径等条件下（除不同水流入口压力的情形）多孔介质渗透淤堵时,淤堵前渗透系数、淤堵渗透系数比和滞留体积百分比均采用5个随机分布模型的平均值。

3.2 骨架颗粒粒径的影响

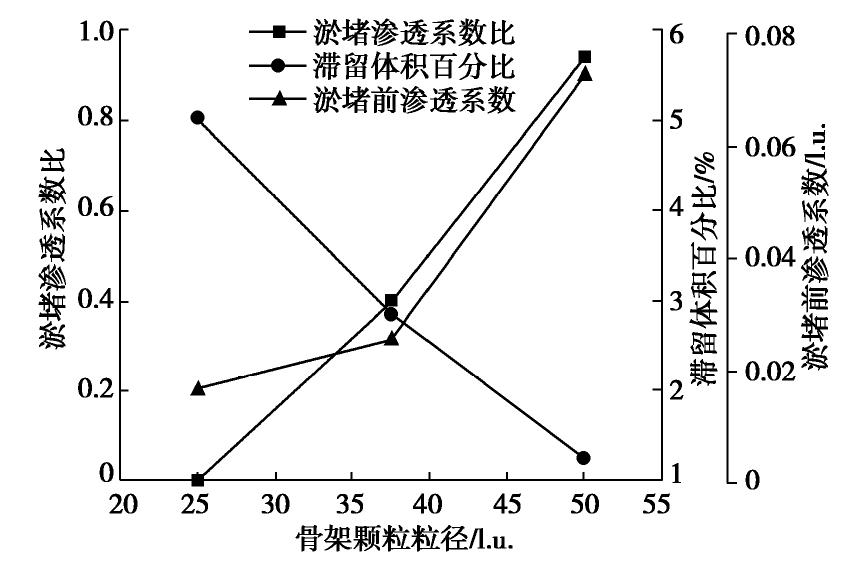
在孔隙率为0.7,骨架颗粒是圆形,水流入口与出口密度分别为1001.0和1000.0的条件下,分别生成骨架颗粒粒径为25,37.5和50的多孔介质模型并进行渗透淤堵过程的LBM-IMB-DEM数值模拟。各模型淤堵后的淤堵渗透系数比、滞留体积百分比及淤堵前的渗透系数如图5所示,淤堵前、后的流场和滞留颗粒分布情况如图6所示。

图 5 不同骨架颗粒粒径时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 5. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with size of skeleton particles

下载: 全尺寸图片幻灯片

图 6 不同骨架颗粒粒径时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 6. Distribution of retained particles and rate of fluid flow in porous media versus size of skeleton particles

下载: 全尺寸图片幻灯片

由图5,6可知,随着骨架颗粒粒径的增大,淤堵前多孔介质中的流动通道数虽然减少,但其宽度显著增加,透水性也随之增大,细颗粒在水流携带下也更容易通过,故淤堵后滞留体积百分比逐渐减小,淤堵渗透系数比不断增大。因此,骨架颗粒粒径越小,多孔介质越容易发生淤堵,淤堵的程度也更严重,如图6（a）中细颗粒很快就堵塞了入口附近的孔喉,后续颗粒继续堆积在入口处,最终所有流动通道都被完全堵塞。

3.3 多孔介质孔隙率的影响

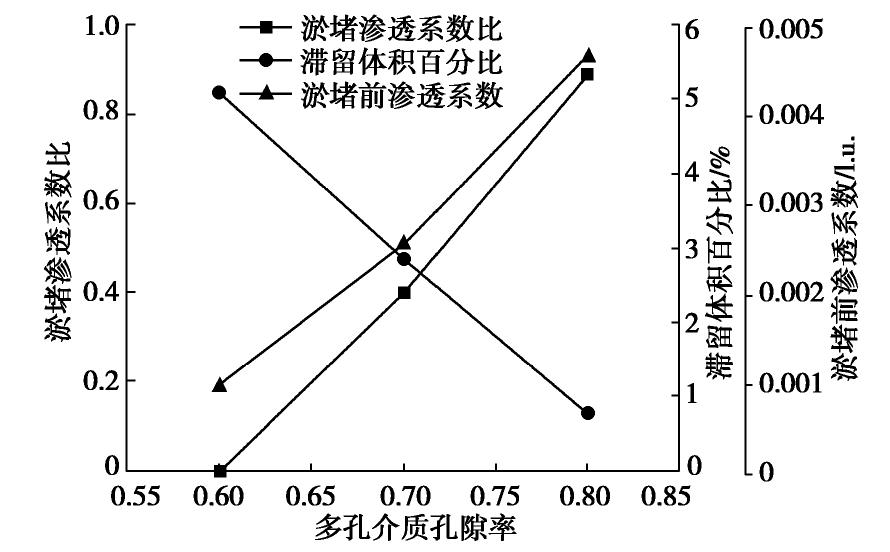
在骨架颗粒是37.5的圆形、水流入口与出口密度分别为1001.0和1000.0的条件下,分别生成孔隙率为0.6,0.7和0.8的多孔介质模型并进行渗透淤堵过程的LBM-IMB-DEM数值模拟。各孔隙率的模型淤堵前渗透系数及淤堵后的淤堵渗透系数比和滞留体积百分比如图7所示,淤堵前、后的流场和滞留颗粒分布情况如图8所示。

图 7 不同孔隙率时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 7. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with porosity of porous media

下载: 全尺寸图片幻灯片

图 8 不同孔隙率时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 8. Distribution of retained particles and rate of fluid flow in porous media versus porosity

下载: 全尺寸图片幻灯片

由图7,8可见,随着孔隙率的增加,多孔介质中孔隙变大,连通性也更好,故其透水性增强,细颗粒在水流携带下也更容易通过,滞留体积百分比随之减小,淤堵渗透系数比逐渐增大。因此,孔隙率越小,多孔介质越容易发生淤堵。

3.4 骨架颗粒定向性的影响

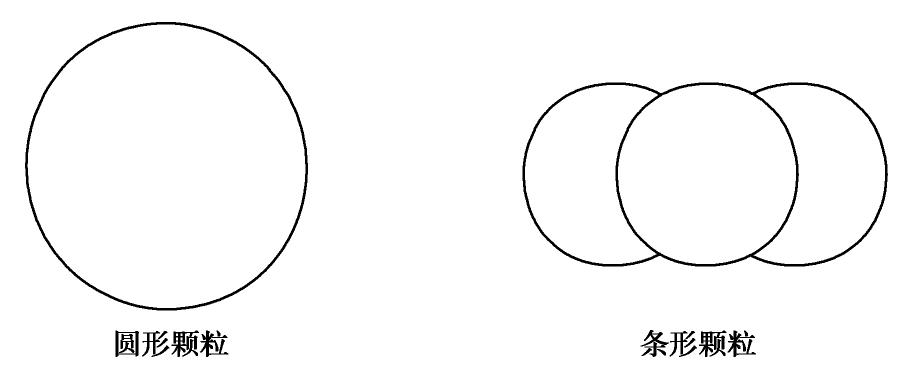
为了探究多孔介质中骨架颗粒定向性对其渗透淤堵特性的影响,本文建立了如图9所示的条形颗粒,其由3个同面积的圆组合而成且颗粒面积等于直径为37.5的圆形颗粒的面积。在骨架颗粒为条形、多孔介质孔隙率为0.7、水流入口与出口密度分别为1001.0和1000.0的条件下,分别生成颗粒长轴方向平行于流动方向、垂直于流动方向和随机的3种多孔介质模型。

图 9 颗粒形状示意图

Figure 9. Schematic diagram of particle shapes

下载: 全尺寸图片幻灯片

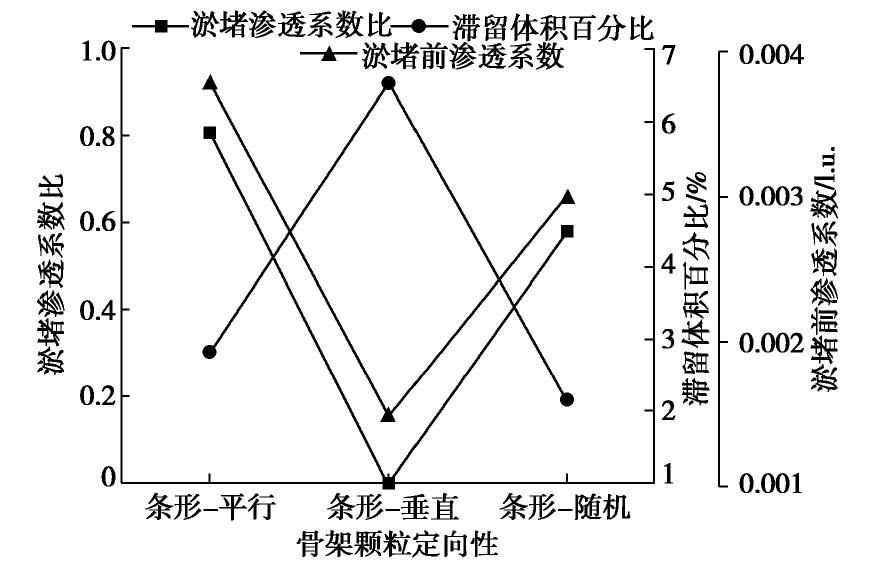
通过渗透淤堵过程的LBM-IMB-DEM数值模拟得到这3种模型淤堵后的淤堵渗透系数比和滞留体积百分比以及淤堵前渗透系数,如图10所示,淤堵前、后的流场和滞留颗粒分布情况如图11所示。

图 10 不同骨架颗粒定向性时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 10. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with orientation of skeleton particles

下载: 全尺寸图片幻灯片

图 11 不同骨架颗粒定向性时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 11. Distribution of retained particles and rate of fluid flow in porous media versus orientation of skeleton particles

下载: 全尺寸图片幻灯片

由图10,11可见：骨架颗粒长轴平行于流动方向时,多孔介质中流动通道较宽、连通性较好且迂曲度较小,故其透水性最强,细颗粒在水流携带下也最容易通过,淤堵渗透系数比最大；骨架颗粒长轴垂直于流动方向时,多孔介质中流动方向的孔喉直径较小且渗流通道的迂曲度较大,故其淤堵前透水性最弱,最后被细颗粒完全堵塞；骨架颗粒长轴方向随机时多孔介质的淤堵渗透系数比居于前两者之间。

从图5,7,10可以看出,表征多孔介质渗透淤堵程度的淤堵渗透系数比的变化规律与淤堵前渗透系数的变化是一致的,这也表明透水性强的多孔介质更不容易发生淤堵。然而,淤堵渗透系数比和滞留体积百分比的变化规律并不完全一致,如前所述的图4中两种情形,图10中也出现了局部的不一致情况,这表明多孔介质中滞留颗粒越多并不一定代表其淤堵越严重。

3.5 水压力的影响

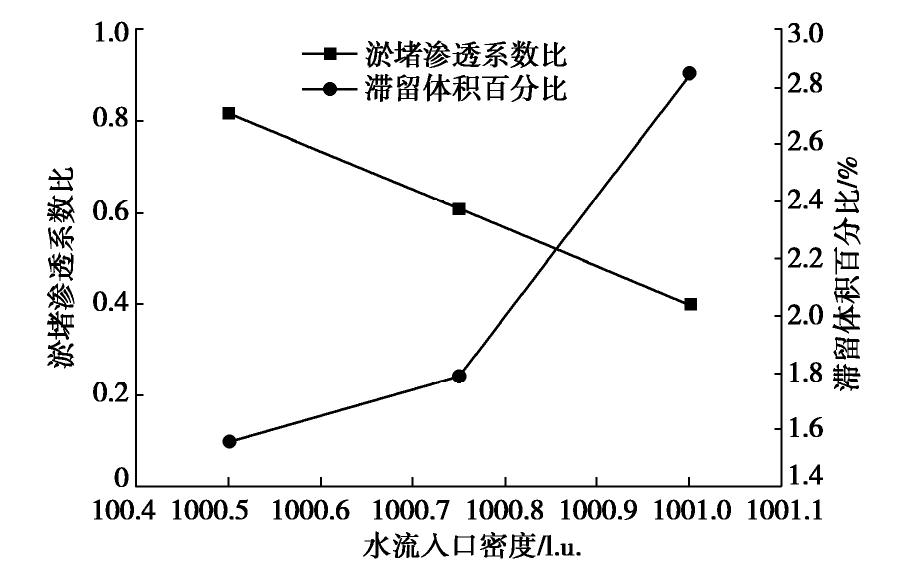
为了探究水压力对多孔介质渗透淤堵特性的影响,将图4（b）中所示多孔介质模型分别在水流入口密度为1000.5,1000.75和1001.0（出口密度均为1000.0）的条件下进行渗透淤堵过程的LBM-IMB-DEM模拟。这3种条件下多孔介质淤堵后的淤堵渗透系数比和滞留体积百分比如图12所示。

图 12 不同水流入口密度时多孔介质的淤堵渗透系数比、滞留体积百分比

Figure 12. Variation of permeability ratio of clogging and percentage of retention volume with inlet density

下载: 全尺寸图片幻灯片

由图12可见,当水流出口密度保持不变,随着水流入口密度的增加,多孔介质淤堵后的滞留体积百分比逐渐增加,淤堵渗透系数比逐渐减小。究其原因,水流入口的密度越大即水压力越大（式（11））,流速也就越大,在较大的流速下入口处的细颗粒运动速度较快并趋于在多孔介质中分散开来,这样其驻留在孔喉处的概率更大,最终滞留的颗粒更多,淤堵也更为严重。如图13所示,入口密度为1001.0时细颗粒堵塞了多孔介质上下边界附近的流动通道,但入口密度为1000.5时这些部位并未发生堵塞。

图 13 不同水流入口密度时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 13. Distribution of retained particles and rate of fluid flow in porous media versus inlet density

下载: 全尺寸图片幻灯片

4. 结论

本文基于LBM-IMB-DEM耦合算法从孔隙尺度模拟了岩土多孔介质渗透淤堵的过程,分析了多孔介质骨架颗粒分布、骨架颗粒粒径、孔隙率、骨架颗粒定向性以及水压力等因素对多孔介质淤堵后滞留体积百分比和淤堵渗透系数比的影响,并通过滞留颗粒在多孔介质中的分布及相应流场的变化情况探究了各因素影响的内在机制。

（1）LBM-IMB-DEM耦合算法能较准确地模拟颗粒-流体动力耦合问题,在岩土流-固耦合精细模拟等研究领域具有广阔的应用前景。

（2）岩土多孔介质中骨架颗粒的空间分布不同,其孔隙结构特征也不同,渗透淤堵特性也有所区别。

（3）岩土多孔介质的骨架颗粒粒径或孔隙率越小,渗透淤堵后的滞留颗粒越多,淤堵也更为严重。

（4）岩土多孔介质中骨架颗粒的定向性对其渗透淤堵特性有一定的影响,当骨架颗粒为条形且其长轴与流动方向垂直时淤堵最为严重。

（5）随水压力增大,渗透淤堵后滞留颗粒在多孔介质中更趋于分散,淤堵更为严重。

（6）岩土多孔介质渗透淤堵的程度与其淤堵前的渗透性密切相关,表现为透水性强的多孔介质相对不易发生淤堵。

后续研究还应进一步考虑其他因素如拟淤堵颗粒的粒径与形状、骨架颗粒的粒径分布,骨架颗粒的形状、流体的黏度等对多孔介质渗透淤堵特性的影响,并应进一步开发三维的LBM-DEM耦合计算程序以便开展渗透淤堵过程的三维模拟。

本文在LBM-IMB-DEM耦合计算程序的开发和测试过程中得到了美国Los Alamos国家实验室王敏博士的悉心指导,在此致以衷心的感谢！

图 1 LBM-IMB-DEM耦合程序计算流程

Figure 1. Flow chart of coupled LBM-IMB-DEM

下载: 全尺寸图片幻灯片

图 2 单颗粒下沉模拟结果对比

Figure 2. Comparison of simulated results of single particle sedimentation

下载: 全尺寸图片幻灯片

图 3 岩土多孔介质渗透淤堵二维模型

Figure 3. Two-dimensional model for seepage clogging in rock and soil porous media

下载: 全尺寸图片幻灯片

图 4 不同骨架颗粒分布时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 4. Distribution of retained particles and rate of fluid flow in porous media versus distribution of skeleton particles

下载: 全尺寸图片幻灯片

图 5 不同骨架颗粒粒径时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 5. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with size of skeleton particles

下载: 全尺寸图片幻灯片

图 6 不同骨架颗粒粒径时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 6. Distribution of retained particles and rate of fluid flow in porous media versus size of skeleton particles

下载: 全尺寸图片幻灯片

图 7 不同孔隙率时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 7. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with porosity of porous media

下载: 全尺寸图片幻灯片

图 8 不同孔隙率时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 8. Distribution of retained particles and rate of fluid flow in porous media versus porosity

下载: 全尺寸图片幻灯片

图 9 颗粒形状示意图

Figure 9. Schematic diagram of particle shapes

下载: 全尺寸图片幻灯片

图 10 不同骨架颗粒定向性时多孔介质的淤堵渗透系数比、滞留体积百分比和淤堵前渗透系数

Figure 10. Variation of permeability ratio of clogging, percentage of retention volume and permeability coefficient before clogging with orientation of skeleton particles

下载: 全尺寸图片幻灯片

图 11 不同骨架颗粒定向性时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 11. Distribution of retained particles and rate of fluid flow in porous media versus orientation of skeleton particles

下载: 全尺寸图片幻灯片

图 12 不同水流入口密度时多孔介质的淤堵渗透系数比、滞留体积百分比

Figure 12. Variation of permeability ratio of clogging and percentage of retention volume with inlet density

下载: 全尺寸图片幻灯片

图 13 不同水流入口密度时多孔介质淤堵前、后的流场与滞留颗粒分布

Figure 13. Distribution of retained particles and rate of fluid flow in porous media versus inlet density

下载: 全尺寸图片幻灯片

表 1 渗透淤堵LBM-IMB-DEM模拟参数

Table 1 LBM-IMB-DEM simulation parameters for seepage clogging

固体参数	参数值	流体参数	参数值
颗粒密度/(kg·m^-3)	2650	流体密度/(kg·m^-3)	1000
法向刚度/(N·m^-1)	1×10⁷	运动黏度/(m²·s^-1)	1×10^-6
切向刚度/(N·m^-1)	5×10⁶	弛豫时间	0.51
摩擦系数	0.3	格子步长/m	8×10^-5
DEM子循环步数	4	LBM时间步长/s	2.13×10^-5

下载: 导出CSV

参考文献(24)

[1]	翟超, 郭伟锋, 严驰. 黏性土渗透淤堵室内模拟试验及分析[J]. 岩土工程学报, 2016, 38(增刊1): 147-151. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S1029.htm ZHAI Chao, GUO Wei-feng, YAN Chi. Laboratory model tests and mechanism of infiltration clogging effect of clayey soil[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(S1): 147-151. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S1029.htm
[2]	李识博, 王常明, 王钢城, 等. 粗粒土淤堵模式判别及最优淤堵粒径区间确定[J]. 水利学报, 2013, 44(10): 1217-1224. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201310013.htm LI Shi-bo, WANG Chang-ming, WANG Gang-cheng, et al. Clogging types distinguishing of coarse-grained soil and determination of optimal range of clogging grain size[J]. Journal of Hydraulic Engineering, 2013, 44(10): 1217-1224. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201310013.htm
[3]	曹洪, 朱东风, 范泽, 等. 止水帷幕缝隙渗漏变化过程试验研究[J]. 水利学报, 2019, 50(6): 699-709. doi: 10.13243/j.cnki.slxb.20181117 CAO Hong, ZHU Dong-feng, FAN Ze, et al. Laboratory study of leakage process for cut-off wall with crack[J]. Journal of Hydraulic Engineering, 2019, 50(6): 699-709. (in Chinese) doi: 10.13243/j.cnki.slxb.20181117
[4]	吴昌瑜, 张伟, 李思慎, 等. 减压井机械淤堵机制与防治方法试验研究[J]. 岩土力学, 2009, 30(10): 3181-3187. doi: 10.3969/j.issn.1000-7598.2009.10.050 WU Chang-yu, ZHANG Wei, LI Si-shen, et al. Research on mechanical clogging mechanism of releaf well and its control method[J]. Rock and Soil Mechanics, 2009, 30(10): 3181-3187. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.10.050
[5]	尚岳全, 孙红月, 侯利国, 等. 管网渗流系统对含碎石黏性土边坡的稳定作用[J]. 岩石力学与工程学报, 2005, 24(8): 1371-1375. doi: 10.3321/j.issn:1000-6915.2005.08.015 SHANG Yue-quan, SUN Hong-yue, HOU Li-guo, et al. Study of the stability of pebbly clay slopes with pipe drainage system[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1371-1375. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.08.015
[6]	年廷凯, 吴昊, 陈光齐, 等. 堰塞坝稳定性评价方法及灾害链效应研究进展[J]. 岩石力学与工程学报, 2018, 37(8): 1796-1812. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201808003.htm NIAN Ting-kai, WU Hao, CHEN Guang-qi, et al. Research progress on stability evaluation method and disaster chain effect of landslide dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(8): 1796-1812. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201808003.htm
[7]	乐超, 徐超, 吴雪峰, 等. 两种塑料排水板滤膜淤堵特性试验研究[J]. 岩土力学, 2014, 35(9): 2529-2534. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201409014.htm LE Chao, XU Chao, WU Xue-feng, et al. Experimental research on clogging characteristic of two types of PVD filters[J]. Rock and Soil Mechanics, 2014, 35(9): 2529-2534. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201409014.htm
[8]	刘胜, 王媛, 冯迪. 尾矿库中新型复合排渗管排渗特征试验研究[J]. 岩土工程学报, 2019, 41(12): 2360-2366. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912031.htm LIU Sheng, WANG Yuan, FENG Di. Experimental study on drainage characteristics of new composite drainage pipes in tailings pond[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2360-2366. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912031.htm
[9]	DABIR S, DABIR B, MOGHANLOO R G. A new approach to study deposition of heavy organic compounds in porous media[J]. Fuel, 2016, 185: 273-280.
[10]	李识博, 王常明, 王钢城, 等. 松散堆积物坝基渗透淤堵试验及颗粒流模拟[J]. 水利学报, 2012, 43(10): 1163-1170. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201210007.htm LI Shi-bo, WANG Chang-ming, WANG Gang-cheng, et al. Infiltration clogging test and simulation by PFC3D for loose dam foundation[J]. Journal of Hydraulic Engineering, 2012, 43(10): 1163-1170. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201210007.htm
[11]	ZHAO J D, SHAN T. Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics[J]. Powder Technology, 2013, 239(17): 248-258.
[12]	蒋明镜, 张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报, 2014, 36(5): 793-801. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm JIANG Ming-jing, ZHANG Wang-cheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 793-801. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm
[13]	FENG Y T, HAN K, OWEN D R J. Coupled lattice Boltzmann method and discrete element modelling of particle transport in turbulent fluid flows: computational issues[J]. International Journal for Numerical Methods in Engineering, 2010, 72(9): 1111-1134.
[14]	DAVID F B, BENJAMIN K C, BRIAN J O L, et al. Direct simulation of fluid-solid mechanics in porous media using the discrete element and lattice-Boltzmann methods[J]. Journal of Geophysical Research, 2007, 112: B10209.
[15]	WANG M, FENG Y T, OWEN D R J, et al. A novel algorithm of immersed moving boundary scheme for fluid-particle interactions in DEM-LBM[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 346: 109-125.
[16]	WANG M, FENG Y T, PANDE G N, et al. A coupled 3-dimensional bonded discrete element and lattice Boltzmann method for fluid-solid coupling in cohesive geomaterials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42: 1405-1424.
[17]	WANG M, FENG Y T, WANG C. Numerical investigation of initiation and propagation of hydraulic fracture using the coupled bonded particle-lattice Boltzmann method[J]. Computers & Structures, 2017, 181: 32-40.
[18]	何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2008. HE Ya-ling, WANG Yong, LI Qing. Lattice Boltzmann Method: Theory and Applications[M]. Beijing: Science Press, 2008. (in Chinese)
[19]	郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2008. GUO Zhao-li, ZHENG Chu-guang. Theory and Applications of Lattice Boltzmann Method[M]. Beijing: Science Press, 2008. (in Chinese)
[20]	BHATNAGAR P L, GROSS E P, KROOK M K. A model for collision processes in gases: I small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511-525.
[21]	QIAN Y H, D’HUMIÈRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters, 1992, 17(6): 479-484.
[22]	NOBLE D R, TORCZYNSKI J R. A lattice-Boltzmann method for partially saturated computational cells[J]. International Journal of Modern Physics C, 1998, 9(8): 1189-1201.
[23]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65.
[24]	WAN D, TUREK S. Direct numerical simulation of particulate flow via multigrid FEM techniques and the fictitious boundary method[J]. International Journal for Numerical Methods in Fluids, 2006, 51(5): 531-566.

施引文献(12)

期刊类型引用(4)

1.	罗仁宇，李奇志，祖公博，黄云进，杨耿超，姚清河. 基于卷积神经网络的超分辨率格子Boltzmann方法研究. 力学学报. 2024(12): 3612-3624 . 百度学术
2.	侯娟，滕宇阳，李昊，刘磊. 多孔介质曲折度对膨润土衬垫渗透性能的影响. 湖南大学学报(自然科学版). 2022(01): 155-164 . 百度学术
3.	陈经明，周泽超，陈茜茜，李寻，罗跃. 酸法地浸采铀多井系统中渗透系数时空演化模拟. 有色金属科学与工程. 2022(03): 106-116 . 百度学术
4.	吴志平，刘波平，王康，李石滨，胡毕炜，胡必伟，游杰. 基于高性能计算的离散介质冲击过程. 计算机与现代化. 2022(10): 41-46 . 百度学术