单薄山体岩质高边坡爆破振动响应分析及安全控制

孙鹏昌; 卢文波; 雷振; 陈明; 李瑞泽; 李福千

doi:10.11779/CJGE202105011

单薄山体岩质高边坡爆破振动响应分析及安全控制 English Version

孙鹏昌^{1, 2,},
卢文波^{1, 2, ,},
雷振³,
陈明^{1, 2},
李瑞泽^{1, 2},
李福千³

1.
武汉大学水资源与水电工程科学国家重点实验室,湖北　武汉　430072
2.
武汉大学水工岩石力学教育部重点实验室,湖北　武汉430072
3.
中国水利水电第八局工程局有限公司,湖南　长沙　410004

基金项目:

国家自然科学基金面上项目 51779190

国家自然科学基金面上项目 51779193

湖北省技术创新专项重大项目 2017ACA102

详细信息

作者简介:
孙鹏昌(1994—),男,博士研究生,主要从事岩石动力学和工程爆破方面的研究工作。E-mail: sunpch@whu.edu.cn

通讯作者:
卢文波, E-mail: wblu@whu.edu.cn

中图分类号: TU45
计量
- 文章访问数: 310
- HTML全文浏览量: 34
- PDF下载量: 247
出版历程
- 收稿日期: 2020-06-30
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-04-30

Blasting vibration response and control of high rock slopes of thin mountain

SUN Peng-chang^{1, 2,},
LU Wen-bo^{1, 2, ,},
LEI Zhen³,
CHEN Ming^{1, 2},
LI Rui-ze^{1, 2},
LI Fu-qian³

1.
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
2.
Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China
3.
Sinohydro Bureau 8 Co., Ltd., Changsha 410004, China

摘要

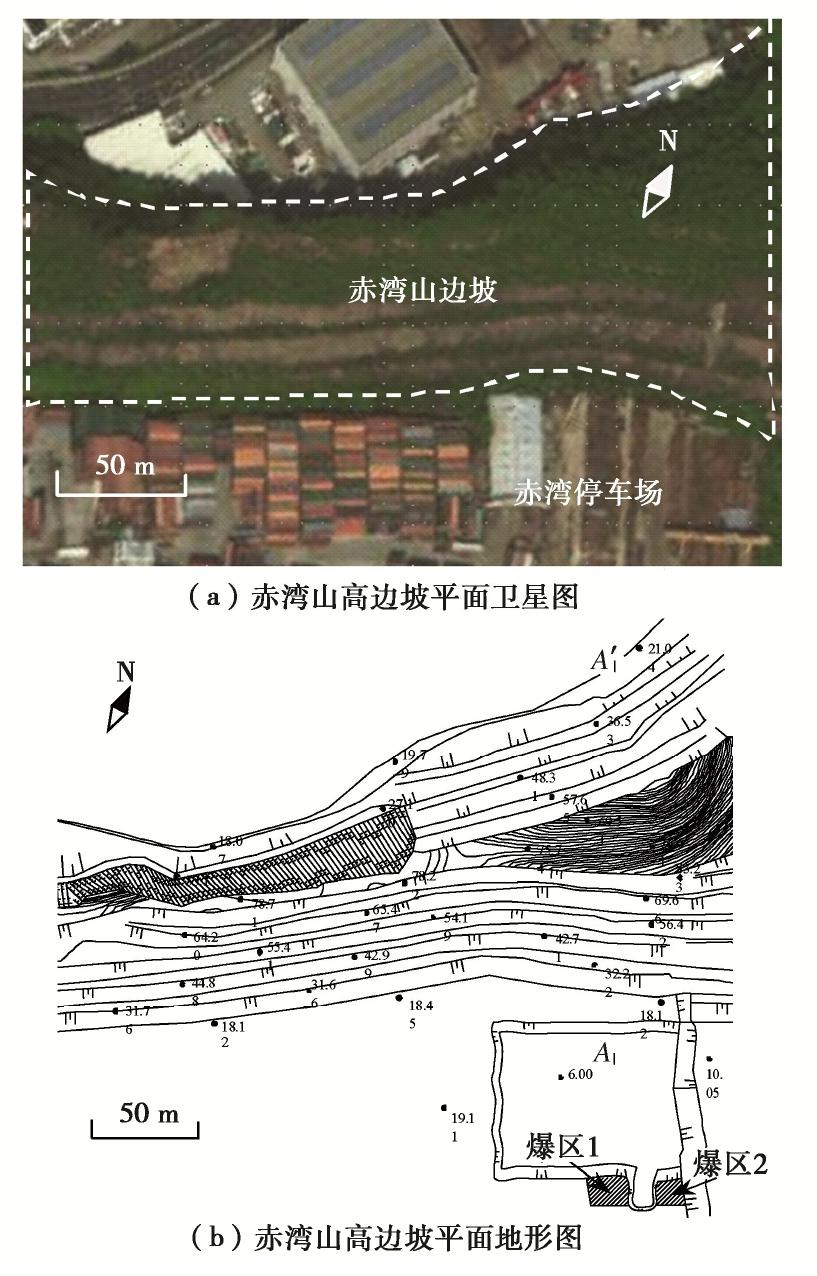
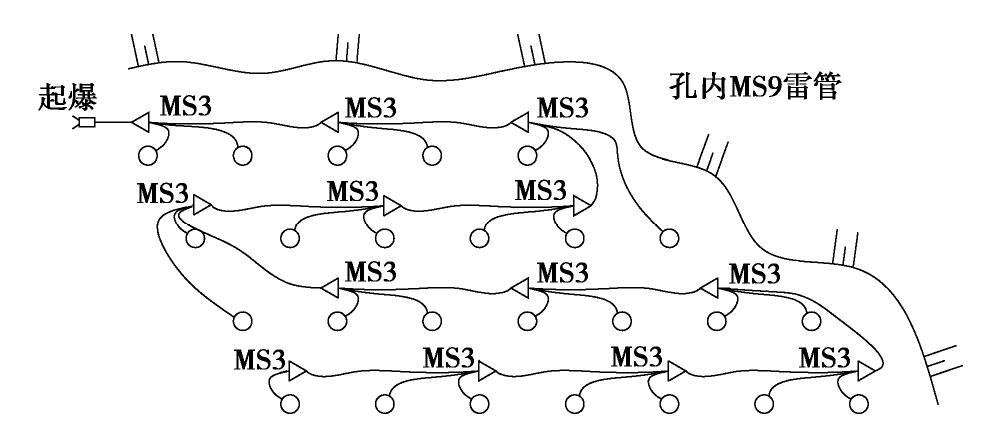
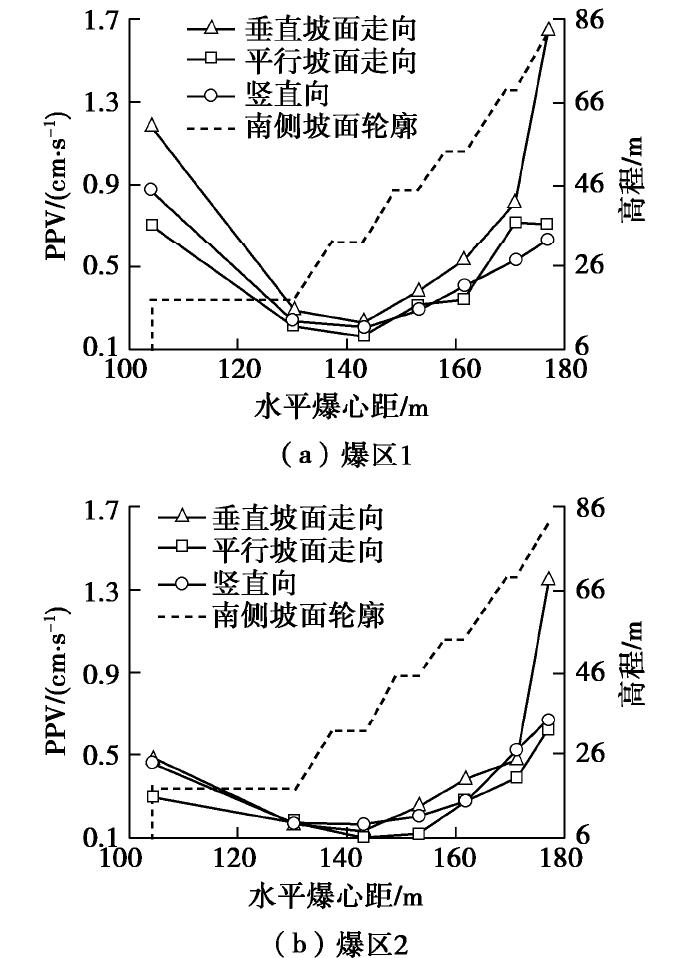
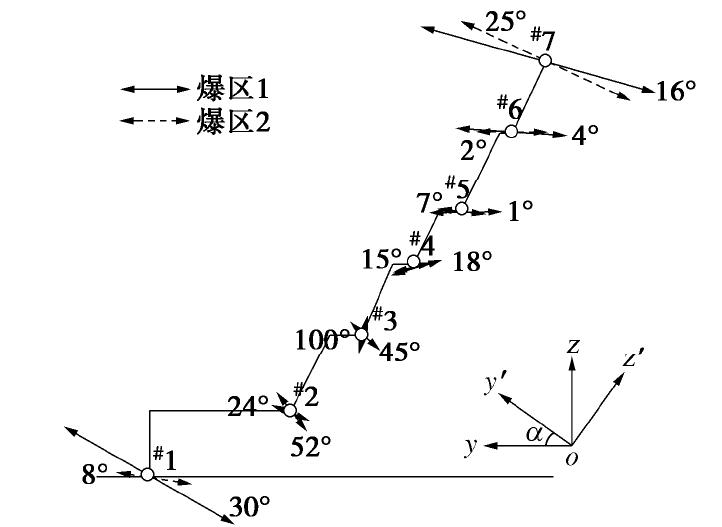
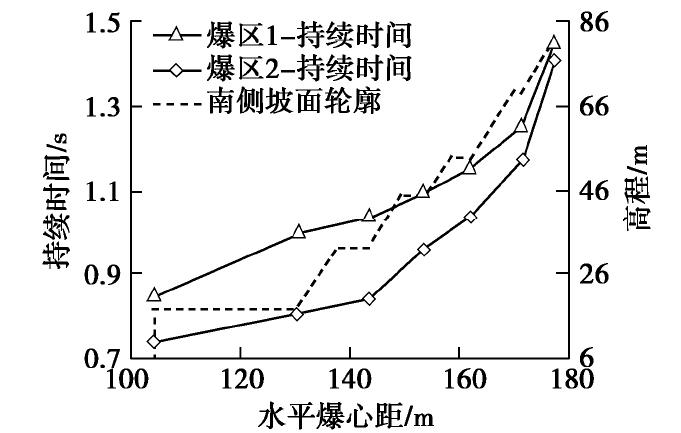
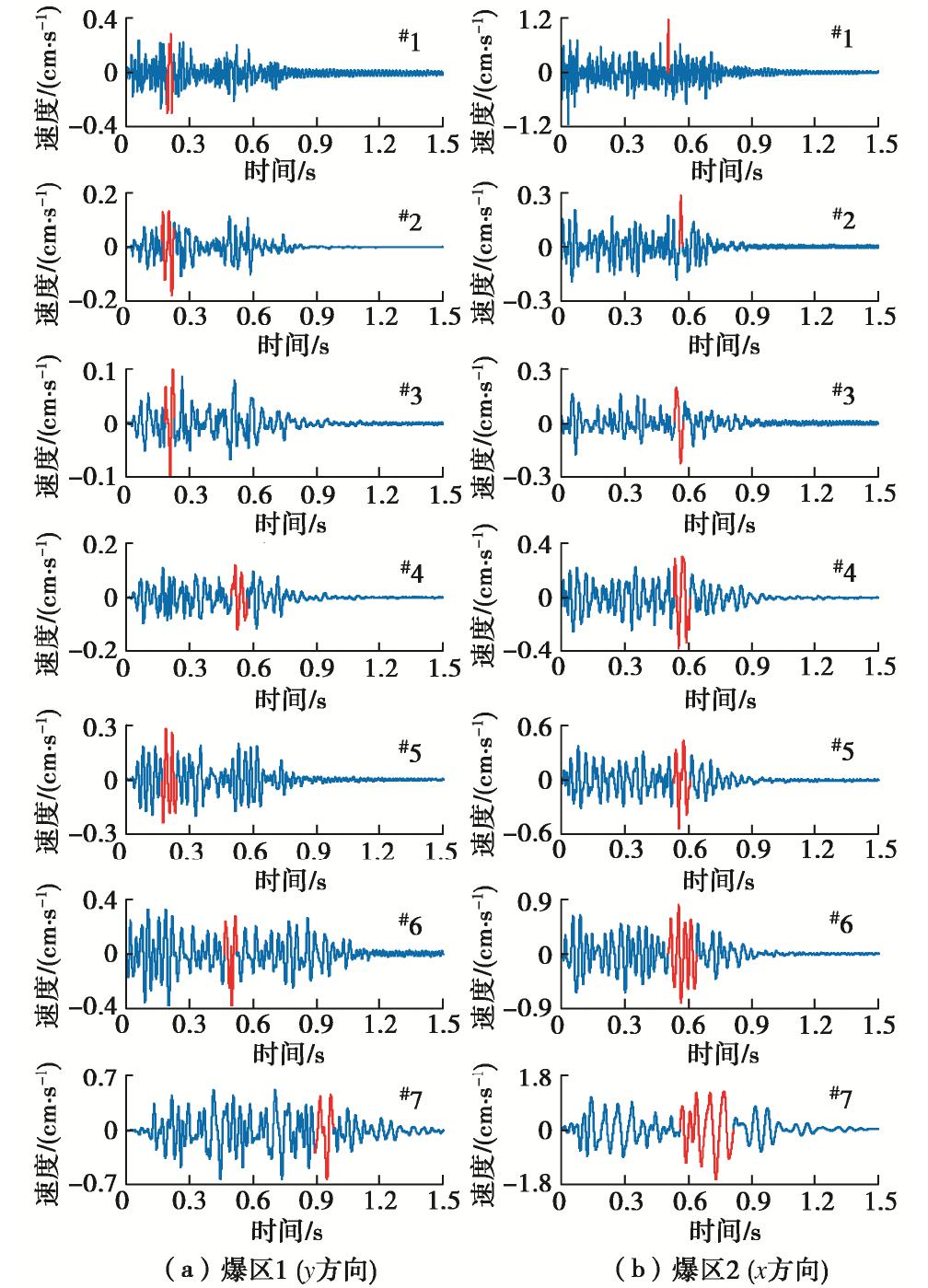
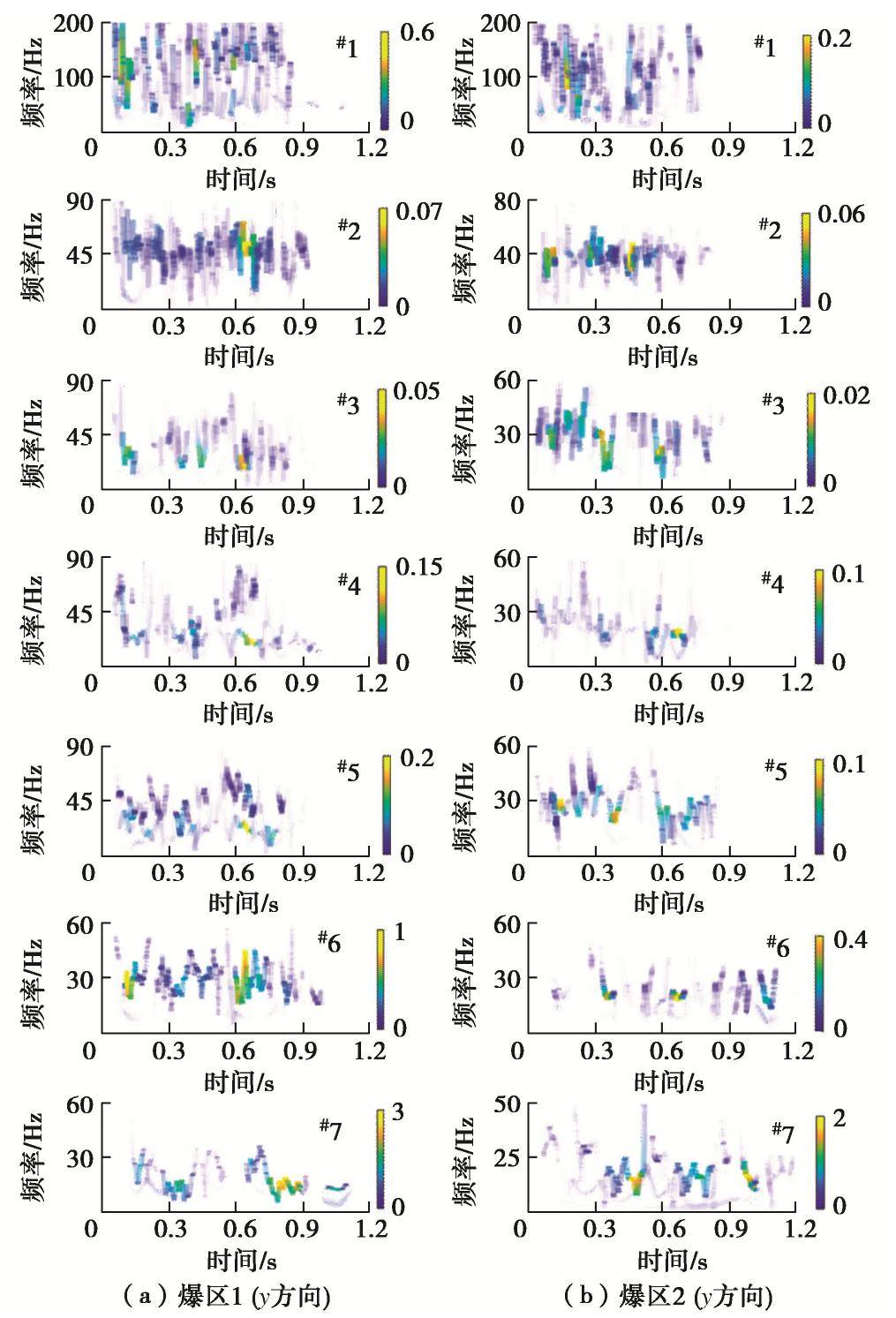
摘要: 针对赤湾山高边坡爆破振动响应问题,开展了爆破振动实测数据分析和动力有限元数值模拟,分析了单薄山体岩质高边坡的爆破振动响应特征。结果表明：幅值方面,迎爆侧坡面存在明显的爆破振动高程放大效应,高程放大效应测点的主振方向偏于垂直坡面走向；背爆侧坡面爆破振动随爆心距增加整体呈衰减趋势。持续时间方面,迎爆侧坡面爆破振动完整波形持续时间和优势振动持续时间均随水平爆心距和高程增加而显著延长；坡顶附近,测点起振时刻越晚,其爆破振动峰值反而越大。频率方面,赤湾山边坡自振频率远大于常见单面边坡的自振频率；随水平爆心距和高程增加,迎爆侧坡面爆破振动视主频整体呈衰减趋势,优势频带由100 Hz左右衰减至15 Hz左右,且落在边坡固有频率内。结合赤湾山高边坡爆破振动响应特征和工程实际,采取电子雷管起爆网路、优化开挖程序和抵抗线方向、边坡支护防护等措施控制爆破振动。
- 岩质高边坡 /
- 爆破振动 /
- 单薄山体 /
- 放大效应 /
- 时频分析 /
- 振动控制
Abstract: The blasting vibration response characteristics of high rock slopes of a thin mountain are studied by analyzing the monitoring data and numerical results of blasting vibration of Chiwan Mountain high rock slope. The results in vibration amplitude show that the elevation amplification effect of blasting vibration exits on the south slope, and main vibration directions of the monitoring points showing elevation amplification effect are across the slope. However, the blasting vibration decays versus distance on the north slope. In terms of vibration duration, durations of complete blasting vibration and dominant vibration waveforms on the south slope are significantly prolonged with the increase in distance from the blasting source to the monitoring points. Near the top of the slope, the later the starting point of blasting vibration is, the larger the particle peak velocity of the blasting vibration is. In terms of frequency characteristics, the natural frequency of Chiwan Mountain high rock slope is much higher than that of the common single-sided rock slope. With the increase of the distance from the blasting source to the monitoring points, apparent frequency of blasting vibration on the south slope decreases, and the dominant frequency band of blasting vibration is reduced from high frequency band around 100 Hz to the low one around 15 Hz that falls within the natural frequency range of the slope. Finally, three measures, including electronic detonator initiation network, excavation procedure and resistance line direction optimization, and support and protection, are proposed for controlling the blasting vibration of Chiwan Mountain high rock slope.
- high rock slope /
- blasting vibration /
- thin mountain /
- amplification effect /
- time-frequency analysis /
- vibration control

HTML全文

0. 引言

水利水电、矿山、交通和市政等工程都涉及到岩质高边坡爆破振动响应问题,高边坡爆破振动响应是影响高边坡岩体稳定性和爆破生产安全的重要因素。准确分析岩质高边坡爆破振动幅值、持续时间和频率等振动响应特征可为高边坡爆破振动控制提供依据,对爆破生产安全顺利进行具有重要意义。

国内外学者主要采用现场实测数据分析和数值模拟方法分析岩质高边坡爆破振动响应,且主要集中于爆破振动幅值分析。在现场实测数据分析方面,郭学彬等^[1]、谭文辉等^[2]、Kahriman等^[3]、Ak等^[4]、Choi等^[5-6]通过爆破振动实测数据分析了边坡爆破振动速度衰减规律和高程放大效应等问题；在数值模拟方面,陈明等^[7]、杨风威等^[8]、Jiang等^[9-10]、武旭等^[11]采用数值模拟方法分析了爆破振动速度的高程效应。此外,钟冬望等^[12]采用模型试验并结合动力有限元分析了岩质边坡爆破振动响应。已有研究结果表明,忽略边坡台阶突出部分,边坡坡面爆破振动随水平爆心距和高程增加整体呈衰减趋势,仅在坡形骤变、坡度较大等特殊情况下存在局部放大效应。

前述研究仅针对雄厚山体单面岩质边坡,而边坡爆破振动响应与山体厚薄有关系,单薄山体岩质高边坡的爆破振动响应可参考与其形态类似的凸形地形振动的响应特征。李新平等^[13]、Hu等^[14]研究了船闸中隔墩的爆破振动响应,洪悯萱^[15]、Fuyuki等^[16]、Dally等^[17]、Sklavounos等^[18]采用不同方法分析了波与凸形地形的相互作用,唐海等^[19]、Zhang等^[20]通过现场试验分析了凸形地形的爆破振动响应。凸形地形与单面边坡的爆破振动响应特征不同,凸形地形爆破振动普遍存在高程放大效应,顶部靠近两侧自由面附近尤为明显。可见,单薄山体岩质高边坡由于形态差异与单面边坡爆破振动响应特征不同可能更不利于边坡岩体稳定和爆破振动控制。

目前,单薄山体岩质高边坡爆破振动响应的相关研究较少、已有岩质边坡及凸形地形振动响应研究集中于爆破振动幅值特征,关于持续时间和频率特征的研究较少。针对以上问题,以赤湾山高边坡这一典型的单薄山体岩质高边坡为例,开展爆破振动现场监测和动力有限元数值模拟,分析单薄山体岩质高边坡爆破振动幅值、持续时间和频率等振动响应特征,研究中未考虑台阶突出部分的影响,研究结果可完善对岩质高边坡爆破振动响应的认识,为类似单薄山体岩质高边坡爆破振动影响评价和控制提供参考。

1. 工程背景

1.1 赤湾山高边坡概况

赤湾山高边坡为城区复杂环境下的单薄山体双面岩质高边坡。如图1所示,赤湾山高边坡位于深圳地铁12号线赤湾停车场北侧,为人工开山取石填海等工程建设时放坡形成的台阶状边坡。边坡平面呈直线型,长约200.0 m,总体走向为N65°E,坡顶高程76.0～83.0 m,坡脚高程17.0～21.0 m,坡高约60.0 m。山体两侧人工开挖仅遗留山脊部分作为防风墙,坡顶仅宽1.5 m左右,坡脚宽72.0～150.0 m,山体单薄。南侧边坡倾向南东,坡度约61°,呈五级阶状,台阶宽度约2.0～4.0 m；北侧边坡倾向北西,被削坡为二～四级台阶。赤湾山高边坡典型横断面如图2所示。

图 1 赤湾山高边坡平面图

Figure 1. Plan view of Chiwan Mountain high rock slope

下载: 全尺寸图片幻灯片

图 2 赤湾山高边坡横断面图(A—

A^{'}

)

Figure 2. Cross section of Chiwan Mountain high rock slope (A-

A^{'}

)

下载: 全尺寸图片幻灯片

赤湾山高边坡岩体性状较好,局部发育有大倾角节理。赤湾山高边坡坡面岩体裸露,主要由中等风化和微风化花岗岩等组成,粗粒结构,块状构造,岩石属硬岩—坚硬岩,岩体基本质量等级为Ⅱ～Ⅲ类,属Ⅵ级坚石,局部强风化岩分布于坡顶薄层,根据详细勘察阶段试验结果得出的岩体参数值见表1。据地质调查结果,赤湾山高边坡内未发现断层。边坡坡顶或南侧边坡台阶肩部发育有倾向南东、倾角大于坡角的节理（即顺坡大倾角节理）和与边坡反倾大倾角节理,对边坡的局部稳定可能产生不利影响。

表 1 赤湾山高边坡岩体参数表

Table 1. Parameters of rock mass of Chiwan Mountain high slope

岩体类别	天然重度/(kN·m^-3)	黏聚力/kPa	内摩擦角/(°)	弹性模量/MPa	泊松比
强风化岩	22.5	200	38.0	400	0.28
中风化岩	25.0	500	40.5	2000	0.26
微风化岩	26.1	2000	42.5	15000	0.24

下载: 导出CSV

| 显示表格

1.2 爆破振动监测

针对邻近赤湾山高边坡的场平石方爆破,开展了赤湾山高边坡爆破振动监测,多次监测结果显示出的赤湾山高边坡爆破振动响应特征基本一致,以如图1（b）所示的两次邻近赤湾山高边坡场平石方爆破为例阐述赤湾山高边坡爆破振动响应特征。两次爆破的主要爆破参数见表2,炮孔装药采用径向不耦合、轴向连续的装药结构,每个炮孔内均设置两发MS9导爆管雷管,1～2孔一段,段间采用MS3导爆管雷管延时,典型起爆网路示意图如图3所示。

表 2 场平石方爆破参数表

Table 2. Blasting parameters for site formation

爆区	孔径/mm	药径/mm	孔深/m	间排距/(m×m)	堵塞长度/m	单耗/(kg·m^-3)
1	115	90	11.0~13.5	4.0×3.5	3.5~4.0	0.36
2	115	90	10.2~12.6	4.0×3.5	3.0~4.0	0.35

下载: 导出CSV

| 显示表格

图 3 起爆网路示意图（爆区1）

Figure 3. Schematic diagram of initiation network (blasting area 1)

下载: 全尺寸图片幻灯片

爆破振动监测点布置于南侧（迎爆侧）边坡不同高程马道内侧。爆破振动监测点沿着图1（b）中边坡A— $A^{'}$ 剖线布置,位于边坡各级马道内侧,图2给出了^#1—^#7爆破振动监测点的位置示意。爆破振动监测采用如图4所示的Blast-UM型爆破测振仪,仪器采样频率为10000 Hz,测量范围为0.001～35 cm/s。传感器为三向速度传感器,x向平行坡面走向,y向垂直坡面走向,z向为竖直向。典型爆破振动波形如图5所示。

图 4 爆破振动监测系统

Figure 4. Monitoring system for blast vibration

下载: 全尺寸图片幻灯片

图 5 爆破振动实测波形图(爆区1—^#1)

Figure 5. Waveforms of blasting vibration (blasting area 1-^#1)

下载: 全尺寸图片幻灯片

2. 爆破振动响应分析

2.1 爆破振动幅值

（1）爆破振动高程效应

赤湾山高边坡爆破振动存在明显的高程放大效应。边坡各测点质点峰值振动速度（PPV）分布情况如图6所示,随水平爆心距和高程增加,垂直、平行坡面走向和竖直向PPV的变化趋势一致,均是先衰减后放大。32.0 m高程处的^#3测点的PPV最小,从45.0m高程处的^#4测点起,PPV随高程增加明显增大,坡顶PPV至少是^#3测点PPV的3倍多。垂直、平行坡面走向和竖直向PPV中,垂直坡面走向PPV最大。

图 6 爆破振动速度分布

Figure 6. Distribution of blasting vibration on slope

下载: 全尺寸图片幻灯片

（2）爆破主振方向

爆破振动可以分解为任意3个正交方向分量,对于边坡横断面内的爆破振动,实测垂直坡面走向、竖直向爆破振动分量分别记为 $v_{y}$ , $v_{z}$ ,坐标系顺时针旋转角度α后的爆破振动分量分别记为 $v_{y^{'}}$ , $v_{z^{'}}$ ,则

\begin{array}{l} v_{y^{'}} = v_{z} \sin α + v_{y} \cos α, \\ v_{z^{'}} = v_{z} \cos α - v_{y} \sin α 。 \end{array}}

(1)

若 $α = α_{0}$ , ${PPV}_{y^{'}}$ 或 ${PPV}_{z^{'}}$ 在所有可能PPV中最大,则此时 $v_{y^{'}}$ 或 $v_{z^{'}}$ 的振动方向为主振方向。

赤湾山高边坡爆破主振方向分布情况如图7所示,图中双箭头方向表示主振方向,长度表示主振方向PPV的相对大小。^#1—^#3测点主振方向均顺时针偏离y方向较大,^#4—^#7测点主振方向偏离角度在25°以内,其中^#5—^#6测点主振方向偏离角度在4°以内。各测点主振方向PPV见表3。

图 7 爆破主振方向分布

Figure 7. Distribution of main vibration direction on slope

下载: 全尺寸图片幻灯片

表 3 爆破主振方向PPV

Table 3. PPV in main vibration direction

测点编号	爆区1			爆区2
测点编号	y向PPV/(cm·s^-1)	主振PPV/(cm·s^-1)	偏差/%	y向PPV/(cm·s^-1)	主振PPV/(cm·s^-1)	偏差/%
^#1	1.19	1.37	14.9	0.48	0.48	0.1
^#2	0.29	0.37	26.3	0.17	0.19	11.8
^#3	0.23	0.26	14.0	0.13	0.16	23.1
^#4	0.38	0.40	4.9	0.25	0.26	4.0
^#5	0.53	0.53	0.9	0.39	0.40	2.6
^#6	0.82	0.82	0.4	0.48	0.48	0.1
^#7	1.65	1.71	3.8	1.35	1.48	9.6

下载: 导出CSV

| 显示表格

爆破主振方向分布与爆破振动高程效应表现出明显的相关性。对于^#1—^#3爆破振动衰减测点,竖直向振动占比较大,主振方向趋于垂直坡面走向和竖直向之间,主振方向PPV超过垂直坡面走向PPV 11%以上；对于^#4—^#7爆破振动高程放大测点,垂直坡面走向振动主导,主振方向偏于垂直坡面走向,主振方向PPV与垂直坡面走向PPV差别较小。

2.2 爆破振动持续时间

（1）完整波形持续时间

各测点爆破振动完整波形持续时间如图8所示,随水平爆心距和高程增加,完整波形的持续时间延长,坡顶测点完整波形的持续时间为1.4 s左右,较^#1测点完整波形的持续时间延长70%以上,延长程度远高于药量和爆心距相同条件下平地或单面边坡完整波形持续时间的延长程度^[21]。

图 8 爆破振动完整波形持续时间

Figure 8. Durations of complete blasting vibration waveform

下载: 全尺寸图片幻灯片

（2）优势振动持续时间

完整波形中振幅较大波形段的持续时间对边坡稳定有重要影响,将波幅超过60% PPV的连续波形段作为优势振动波形。图9中的红色波形段为各测点优势振动波形,^#1测点优势振动持续时间不到0.05 s,随水平爆心距和高程增加,优势振动持续时间延长,坡顶测点优势振动持续时间为0.25 s（爆区1）、0.09 s（爆区2）,较^#1测点优势振动持续时间延长2倍多。

图 9 优势振动持续时间

Figure 9. Durations of dominant blasting vibration

下载: 全尺寸图片幻灯片

2.3 爆破振动频率

分析边坡爆破振动频率特征前,先对爆破振动实测数据进行零基线校正和通带滤波处理,滤波通带设置为5～200 Hz。

（1）爆破振动视主频

爆破振动峰值对应的半波频率称为视主频,视主频能较好地反映爆破振动频率特征^[22],赤湾山高边坡各测点爆破振动视主频如图10所示,处于20～100 Hz之间,随水平爆心距和高程增加,垂直、平行坡面走向和竖直向视主频的变化趋势一致,整体呈衰减趋势。^#1—^#3测点视主频陡降,从约60 Hz以上降至40 Hz以下；^#4—^#7测点视主频波动降低,坡顶测点视主频为20 Hz左右。赤湾山高边坡爆破振动视主频陡降和波动降低分界点与爆破振动衰减和放大的分界点一致。

图 10 边坡爆破振动视主频

Figure 10. Apparent frequencies of blasting vibration

下载: 全尺寸图片幻灯片

（2）爆破振动时频特性

视主频无法反映爆破振动不同时刻的频率特征,而Huang等^[23]提出的Hilbert-Huang变换（HHT）则是一种自适应性强、高效的时频分析方法,被证明是一种优越的分析处理爆破振动信号的时频方法^[24]。HHT主要由经验模态分解（empirical mode decomposition,EMD）法和Hilbert变换两部分组成。EMD方法通过信号上、下包络线的平均值求“瞬态平衡位置”,再提取固有模态函数（intrinsic mode function,IMF）。爆破振动信号经分解后得到多个IMF分量,对每个IMF分量进行Hilbert变换,再综合所有IMF分量的频谱就可获得爆破振动信号的Hilbert谱,从而分析爆破振动的时频特性。赤湾山高边坡各测点爆破振动Hilbert谱如图11所示。

图 11 爆破振动Hilbert时频谱(y向)

Figure 11. Hilbert spectra of blasting vibration in y direction

下载: 全尺寸图片幻灯片

赤湾山高边坡爆破振动Hilbert谱线随水平爆心距和高程增加由繁到简,各时刻频率成分由丰富趋向单一,优势频带整体衰减。^#1—^#7测点,爆破振动频率成分从0～200 Hz收窄至0～30 Hz,优势频带由^#1测点的100 Hz左右逐渐衰减至^#7测点的15 Hz左右。同一测点爆破振动频率随时间波动变化。

3. 爆破振动响应数值模拟

赤湾山高边坡爆破振动测点布置条件有限,未能获取北侧（背爆侧）边坡坡面的爆破振动实测数据,而背爆侧边坡坡脚分布有工业建筑物,需评估爆破振动对背爆侧边坡的影响,为此采用数值模拟方法研究背爆侧边坡的爆破振动特性。

3.1 数值模型和参数

采用动力有限元软件LS-DYNA对赤湾山高边坡爆破振动进行数值模拟。考虑到^#1,^#2测点间节理发育且存在排水沟,边坡数值模型以A— $A^{'}$ 剖面为基础,水平方向取^#2测点与背爆侧边坡21.0 m马道内侧以北10.0 m之间的边坡部分,竖直方向取赤湾停车场场平标高6.0 m至坡顶之间的边坡部分。边坡数值模型如图12所示,共有11979个单元和24496个节点。

图 12 高边坡数值模型

Figure 12. Numerical model for high rock slope

下载: 全尺寸图片幻灯片

实测爆破振动PPV均小于1.7 cm/s,爆区到坡脚的距离超过100 m,边坡爆破振动近似为弹性振动,数值模型中的岩体采用线弹性材料模拟,材料参数按照表1中微风化花岗岩的参数进行设置。根据现场实际情况,模型底部和北侧边界设置为无反射边界以减小边界应力波反射对数值模拟结果的影响。模型南侧边界为荷载施加边界,以^#2测点垂直坡面走向和竖直向爆破振动速度作为荷载。数值模拟时考虑了边坡的自重应力,动力计算前对边坡数值模型进行自重应力初始化。迎爆侧坡面^#2—^#7监测点与实际测点位置一致,背爆侧坡面N-1—N-6监测点的位置如图12所示。

3.2 数值模拟结果分析

（1）数值模型验证

迎爆侧坡面^#2—^#7监测点的爆破振动数值模拟结果列于表4中,将其与实测结果进行对比。各测点PPV数值模拟结果与实测结果相差均较小,基本在20%以内。随水平爆心距和高程增加,水平和竖直向PPV数值模拟结果均先衰减后放大,与实测结果表现出的规律一致。上述结果表明,数值模型一定程度上能够有效地模拟赤湾山高边坡的爆破振动响应。

表 4 迎爆侧坡面爆破振动数值模拟结果

Table 4. Numerical results of blasting vibration on south slope

测点编号	水平向PPV/(cm·s^-1)		水平向偏差/%	竖直向PPV/(cm·s^-1)		竖直向偏差/%
测点编号	实测	数值	水平向偏差/%	实测	数值	竖直向偏差/%
^#2	0.29	0.34	17.2	0.23	0.26	13.0
^#3	0.23	0.27	17.4	0.20	0.24	20.0
^#4	0.38	0.42	10.5	0.29	0.33	13.8
^#5	0.53	0.57	7.5	0.41	0.45	9.8
^#6	0.82	0.71	13.4	0.53	0.58	9.4
^#7	1.65	1.34	18.8	0.63	0.65	3.2

下载: 导出CSV

| 显示表格

（2）背爆侧坡面爆破振动

背爆侧坡面N-1—N-6监测点爆破振动数值模拟结果如图13所示,随爆心距增加,水平向和竖直向PPV的变化趋势一致,整体呈现衰减趋势。坡顶PPV最大,其中水平向PPV超过1.20 cm/s,坡脚PPV小于0.30 cm/s。爆破振动持续时间和频率与边坡岩体的黏性性质、节理裂隙分布特征和应力状态等爆破振动传播介质特征相关,图12所示的边坡数值模型未考虑岩体的黏性性质和节理裂隙分布特征,应力状态模拟也并不完全,因此,背爆侧坡面爆破振动持续时间和频率的数值模拟结果不作为分析对象。

图 13 背爆侧坡面爆破振动速度数值模拟结果

Figure 13. Numerical results of blasting vibration on north slope

下载: 全尺寸图片幻灯片

（3）爆破振动起振时序

爆破振动监测仪时间系统精度为1 s,赤湾山高边坡爆破振动完整波形持续时间最长约1.5 s,由爆破振动实测数据难以分辨不同测点起振时刻的先后,而数值模拟能便捷地对不同测点起振时刻排序。赤湾山迎爆和背爆侧坡面所有监测点起振时刻的先后顺序如图14所示,迎爆侧^#2—^#7测点和背爆侧N-1—N-6测点随爆心距增大依次起振。起振时刻越晚,爆破振动传播时间越长,能量耗散越多,爆破振动幅值一般越小,但迎爆侧^#3—^#7测点依次起振,PPV反而增大,背爆侧N-5和N-6测点情况类似,在爆源和岩体介质条件相同时,山体形态对爆破振动产生了一定影响。

图 14 边坡测点爆破振动起振时序

Figure 14. Time sequence for starting point of blasting vibration

下载: 全尺寸图片幻灯片

（4）高边坡动力特性

边坡爆破振动特征不仅包括爆破振动幅值、持续时间和频率三要素,还与边坡动力特性相关。赤湾山高边坡数值模型进行模态分析得到如图15所示边坡前9阶固有频率和振型,前3阶固有频率小于15 Hz,第4—第9阶固有频率在17～26 Hz,均远大于常见单面边坡的自振频率^[25]。

图 15 赤湾山高边坡前9阶模态参数

Figure 15. First 9 modal parameters of Chiwan Mountain high slope

下载: 全尺寸图片幻灯片

图10,11的边坡爆破振动频率特征显示,^#3—^#7测点部分优势频带落在第4—第9阶固有频率区间,而第4—第9阶振型均以坡顶附近振动幅度大,可能引发坡顶附近区域出现共振^[26]。

4. 爆破振动安全控制措施

爆破振动控制措施主要包括在爆源处控制爆破振动、在爆破地震波传播途径上削弱振动强度以及对保护对象进行加固防护等3个方面。结合赤湾山高边坡爆破振动响应特征和工程实际,提出如下3条措施。

（1）采用电子雷管起爆网路

由于导爆管雷管延时精度低,图3所示的导爆管起爆网路在实际爆破过程中可能存在重段现象,导致单段起爆炮孔数超过两个,单段起爆药量大于设计的单段起爆药量。另外,图3所示的起爆网路段间采用MS3导爆管雷管延时,延时时间为50 ms,YANG^[27]发现起爆时差 $Δ τ$ 将爆破振动的傅里叶主频（傅里叶幅值谱峰值对应的频率）移到潜在偏移频率 $f = 1 / Δ τ$ 附近,即50 ms的段间延时将使爆破振动的傅里叶主频移到20 Hz附近,而20 Hz左右的傅里叶主频处于边坡固有频率区间,可能引发共振。

电子雷管延时精度高,误差可控制在1 ms以内,采用电子雷管起爆网路可以较好解决上述问题。一方面,电子雷管起爆网路可实现逐孔起爆,从而降低单段起爆药量；另一方面,通过设置合理的延时参数可使爆破振动的傅里叶主频避开边坡的固有频率区间。延时参数合理的起爆网路均可以代替如图3所示的起爆网路。图16所示的电子雷管起爆网路孔间延时时间为20 ms对应的潜在偏移频率为50 Hz附近,避开了对边坡振动起主要贡献作用的固有频率。此外,该电子雷管起爆网路的持续时间较图3所示起爆网路的持续时间短约60%～70%。

图 16 电子雷管起爆网路示意图

Figure 16. Electronic detonator initiation network

下载: 全尺寸图片幻灯片

（2）优化开挖程序和抵抗线方向

根据图1,2可知,爆破区域距离边坡大于100 m,坡顶爆破振动最大,达到1.65 cm/s,远小于规范中边坡爆破振动安全控制标准的最小值5.0 cm/s^[28]。但是紧邻边坡坡脚仍有大方量岩体需要开挖,邻近坡脚岩体爆破开挖时,爆区紧邻边坡,边坡尤其是坡顶的爆破振动可能超过规范中边坡爆破振动安全控制标准。

针对上述问题,通过优化开挖程序和抵抗线方向,避免边坡位于爆破振动较大的爆区后冲向,使边坡位于爆区的侧冲向或前方,从而降低爆破振动对边坡的影响。在已有的爆破开挖条件下,采用分区分块的爆破开挖方案,待开挖区域按照如图17（a）所示的Ⅰ→Ⅱ→Ⅲ→...分区顺序依次进行爆破开挖。对于每个分区,参照如图17（b）所示的Ⅰ区分块顺序Ⅰ-1→Ⅰ-2→Ⅰ-3→Ⅰ-4→Ⅰ-5→Ⅰ-6依次进行爆破开挖。Ⅰ-1、Ⅰ-2、Ⅰ-3三个爆区的抵抗线方向偏东,边坡位于爆区的侧冲向；Ⅰ-4、Ⅰ-5、Ⅰ-6三个爆区的抵抗线方向偏北,边坡位于爆区前方,且边坡与爆区间有Ⅰ-1、Ⅰ-2、Ⅰ-3三个爆区开挖形成的宽沟,可起到减震作用。

图 17 爆破开挖分区分块示意图

Figure 17. Procedures of blasting excavation

下载: 全尺寸图片幻灯片

（3）不稳定块体支护和坡面防护

爆破振动实测数据分析结果显示,迎爆侧坡面存在明显的爆破振动高程放大效应,坡顶PPV较大；坡顶测点完整波形持续时间和优势振动持续时间较坡脚测点持续时间显著延长。数值模拟结果显示,背爆侧坡面坡顶测点PPV远大于其它测点PPV。坡顶附近爆破振动幅值放大、持续时间延长均对坡顶爆破振动控制不利,可见边坡坡顶附近区域是边坡爆破振动控制的重点部位。且边坡坡顶、迎爆侧台阶肩部发育的大倾角节理对边坡的局部稳定有不利影响。

对于上述坡顶和坡面可能产生的局部失稳情况,考虑从目标保护对象角度采取措施,对边坡施加支护防护措施。如图18（a）所示,对坡顶附近不稳定块体施加锚杆支护,可增强坡顶附近区域抵抗爆破振动影响的能力；如图18（b）所示,在坡面安设柔性防护网,可限制坡面岩体的风化剥落或岩体崩落,将落石控制于一定范围内运动,避免爆破振动引起边坡落石对施工人员和机械造成损害。

图 18 边坡支护和防护措施

Figure 18. Support and protection measures

下载: 全尺寸图片幻灯片

5. 结论

基于赤湾山高边坡这一典型单薄山体岩质高边坡的爆破振动实测数据,结合动力有限元数值模型分析,研究了单薄山体岩质高边坡的爆破振动特性,主要得到4点结论。

（1）赤湾山高边坡迎爆侧坡面爆破振动随水平爆心距和高程增加先衰减后放大,^#3测点起爆破振动存在明显的高程放大效应,坡顶PPV至少是振动衰减放大拐点PPV的3倍多,爆破振动高程放大测点主振方向偏于垂直坡面走向；赤湾山高边坡背爆侧坡面爆破振动随爆心距增加整体呈现衰减趋势。

（2）赤湾山高边坡迎爆侧坡面爆破振动完整波形持续时间和优势振动持续时间随水平爆心距和高程增加而延长,坡顶测点完整波形持续时间较坡脚测点延长至少约70%,坡顶测点优势振动持续时间较坡脚测点延长至少约2倍；迎爆侧坡面高程放大测点依次起振,PPV反而增大,背爆侧坡面N-5先于N-6起振,PPV反而较小。

（3）赤湾山高边坡固有频率大于常见单面边坡固有频率；随水平爆心距和高程增加,迎爆侧坡面爆破振动视主频整体呈衰减趋势,优势频带由100 Hz左右衰减至15 Hz左右,落在边坡第4—第9阶固有频率内。

（4）针对赤湾山高边坡爆破振动响应特征和工程实际,可采取电子雷管起爆网路、优化开挖程序和抵抗线方向、不稳定块体支护和坡面防护等措施控制爆破振动对边坡的影响。

图 1 赤湾山高边坡平面图

Figure 1. Plan view of Chiwan Mountain high rock slope

下载: 全尺寸图片幻灯片

图 2 赤湾山高边坡横断面图(A— $A^{'}$ )

Figure 2. Cross section of Chiwan Mountain high rock slope (A- $A^{'}$ )

下载: 全尺寸图片幻灯片

图 3 起爆网路示意图（爆区1）

Figure 3. Schematic diagram of initiation network (blasting area 1)

下载: 全尺寸图片幻灯片

图 4 爆破振动监测系统

Figure 4. Monitoring system for blast vibration

下载: 全尺寸图片幻灯片

图 5 爆破振动实测波形图(爆区1—^#1)

Figure 5. Waveforms of blasting vibration (blasting area 1-^#1)

下载: 全尺寸图片幻灯片

图 6 爆破振动速度分布

Figure 6. Distribution of blasting vibration on slope

下载: 全尺寸图片幻灯片

图 7 爆破主振方向分布

Figure 7. Distribution of main vibration direction on slope

下载: 全尺寸图片幻灯片

图 8 爆破振动完整波形持续时间

Figure 8. Durations of complete blasting vibration waveform

下载: 全尺寸图片幻灯片

图 9 优势振动持续时间

Figure 9. Durations of dominant blasting vibration

下载: 全尺寸图片幻灯片

图 10 边坡爆破振动视主频

Figure 10. Apparent frequencies of blasting vibration

下载: 全尺寸图片幻灯片

图 11 爆破振动Hilbert时频谱(y向)

Figure 11. Hilbert spectra of blasting vibration in y direction

下载: 全尺寸图片幻灯片

图 12 高边坡数值模型

Figure 12. Numerical model for high rock slope

下载: 全尺寸图片幻灯片

图 13 背爆侧坡面爆破振动速度数值模拟结果

Figure 13. Numerical results of blasting vibration on north slope

下载: 全尺寸图片幻灯片

图 14 边坡测点爆破振动起振时序

Figure 14. Time sequence for starting point of blasting vibration

下载: 全尺寸图片幻灯片

图 15 赤湾山高边坡前9阶模态参数

Figure 15. First 9 modal parameters of Chiwan Mountain high slope

下载: 全尺寸图片幻灯片

图 16 电子雷管起爆网路示意图

Figure 16. Electronic detonator initiation network

下载: 全尺寸图片幻灯片

图 17 爆破开挖分区分块示意图

Figure 17. Procedures of blasting excavation

下载: 全尺寸图片幻灯片

图 18 边坡支护和防护措施

Figure 18. Support and protection measures

下载: 全尺寸图片幻灯片

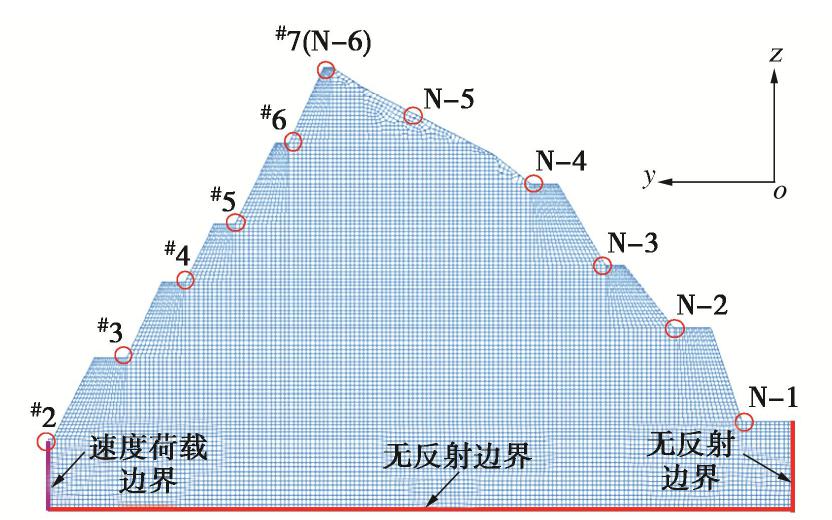
表 1 赤湾山高边坡岩体参数表

Table 1 Parameters of rock mass of Chiwan Mountain high slope

岩体类别	天然重度/(kN·m^-3)	黏聚力/kPa	内摩擦角/(°)	弹性模量/MPa	泊松比
强风化岩	22.5	200	38.0	400	0.28
中风化岩	25.0	500	40.5	2000	0.26
微风化岩	26.1	2000	42.5	15000	0.24

下载: 导出CSV

表 2 场平石方爆破参数表

Table 2 Blasting parameters for site formation

爆区	孔径/mm	药径/mm	孔深/m	间排距/(m×m)	堵塞长度/m	单耗/(kg·m^-3)
1	115	90	11.0~13.5	4.0×3.5	3.5~4.0	0.36
2	115	90	10.2~12.6	4.0×3.5	3.0~4.0	0.35

下载: 导出CSV

表 3 爆破主振方向PPV

Table 3 PPV in main vibration direction

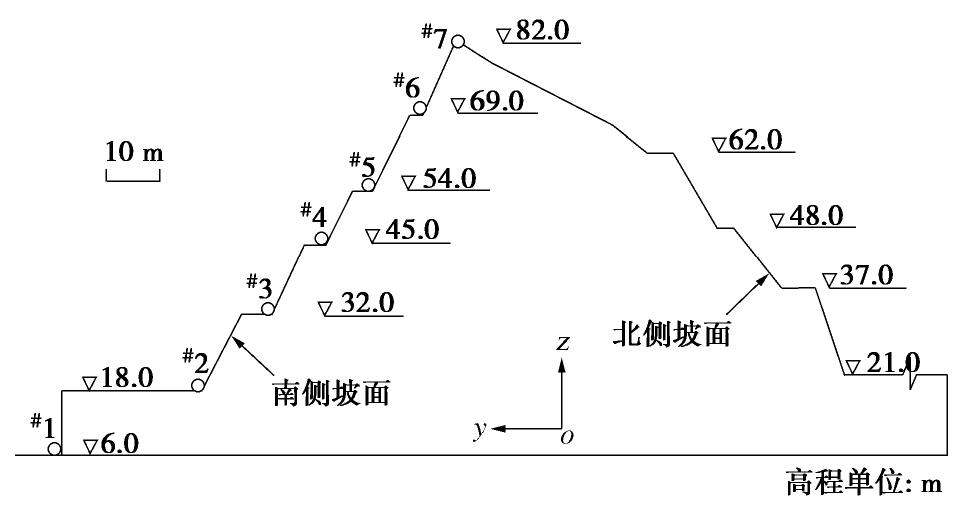
测点编号	爆区1			爆区2
测点编号	y向PPV/(cm·s^-1)	主振PPV/(cm·s^-1)	偏差/%	y向PPV/(cm·s^-1)	主振PPV/(cm·s^-1)	偏差/%
^#1	1.19	1.37	14.9	0.48	0.48	0.1
^#2	0.29	0.37	26.3	0.17	0.19	11.8
^#3	0.23	0.26	14.0	0.13	0.16	23.1
^#4	0.38	0.40	4.9	0.25	0.26	4.0
^#5	0.53	0.53	0.9	0.39	0.40	2.6
^#6	0.82	0.82	0.4	0.48	0.48	0.1
^#7	1.65	1.71	3.8	1.35	1.48	9.6

下载: 导出CSV

表 4 迎爆侧坡面爆破振动数值模拟结果

Table 4 Numerical results of blasting vibration on south slope

测点编号	水平向PPV/(cm·s^-1)		水平向偏差/%	竖直向PPV/(cm·s^-1)		竖直向偏差/%
测点编号	实测	数值	水平向偏差/%	实测	数值	竖直向偏差/%
^#2	0.29	0.34	17.2	0.23	0.26	13.0
^#3	0.23	0.27	17.4	0.20	0.24	20.0
^#4	0.38	0.42	10.5	0.29	0.33	13.8
^#5	0.53	0.57	7.5	0.41	0.45	9.8
^#6	0.82	0.71	13.4	0.53	0.58	9.4
^#7	1.65	1.34	18.8	0.63	0.65	3.2

下载: 导出CSV

参考文献(28)

[1]	郭学彬, 肖正学, 张志呈. 爆破振动作用的坡面效应[J]. 岩石力学与工程学报, 2001, 20(1): 83-87. doi: 10.3321/j.issn:1000-6915.2001.01.019 GUO Xue-bin, XIAO Zheng-xue, ZHANG Zhi-cheng. Slope effect of blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(1): 83-87. (in Chinese) doi: 10.3321/j.issn:1000-6915.2001.01.019
[2]	谭文辉, 璩世杰, 毛市龙, 等. 边坡爆破振动高程效应分析[J]. 岩土工程学报, 2010, 32(4): 619-623. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201004024.htm TAN Wen-hui, QU Shi-jie, MAO Shi-long, et al. Altitude effect of blasting vibration in slopes[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 619-623. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201004024.htm
[3]	KAHRIMAN A. Analysis of parameters of ground vibration produced from bench blasting at a limestone quarry[J]. Soil Dynamics & Earthquake Engineering, 2004, 24(11): 887-892.
[4]	AK H, IPHAR M, YAVUZ M, et al. Evaluation of ground vibration effect of blasting operations in a magnesite mine[J]. Soil Dynamics & Earthquake Engineering, 2009, 29(4): 669-676.
[5]	CHOI B H, RYU C H, DEB D, et al. Case study of establishing a safe blasting criterion for the pit slopes of an open-pit coal mine[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 57: 1-10. doi: 10.1016/j.ijrmms.2012.07.014
[6]	DEB D, KAUSHIK K N R, CHOI B H, et al. Stability assessment of a pit slope under blast loading: a case study of Pasir Coal Mine[J]. Geotechnical and Geological Engineering, 2011, 29: 419-429. doi: 10.1007/s10706-010-9387-4
[7]	陈明, 卢文波, 李鹏, 等. 岩质边坡爆破振动速度的高程放大效应研究[J]. 岩石力学与工程学报, 2011, 30(11): 2189-2195. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201111005.htm CHEN Ming, LU Wen-bo, LI Peng, et al. Elevation amplification effect of blasting vibration velocity in rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2189-2195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201111005.htm
[8]	杨风威, 李海波, 刘亚群, 等. 台山核电站边坡爆破振动监测及数值模拟研究[J]. 岩土力学, 2011, 32(增刊2): 628-633. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2104.htm YANG Feng-wei, LI Hai-bo, LIU Ya-qun, et al. Monitoring of blasting vibration and numerical simulation of slope in Taishan nuclear power station[J]. Rock and Soil Mechanics, 2011, 32(S2): 628-633. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2104.htm
[9]	JIANG N, ZHOU C B, LU S W, et al. Propagation and prediction of blasting vibration on slope in an open pit during underground mining[J]. Tunnelling and Underground Space Technology, 2017, 70: 409-421. doi: 10.1016/j.tust.2017.09.005
[10]	蒋楠, 周传波, 平雯, 等. 岩质边坡爆破振动速度高程效应[J]. 中南大学学报(自然科学版), 2014, 45(1): 238-243. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201401033.htm JIANG Nan, ZHOU Chuan-bo, PING Wen, et al. Altitude effect of blasting vibration velocity in rock slopes[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 238-243. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201401033.htm
[11]	武旭, 张云鹏, 郭奇峰. 台阶地形爆破振动放大与衰减效应研究[J]. 爆炸与冲击, 2017, 37(6): 128-133. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201706017.htm WU Xu, ZAHNG Yun-peng, GUO Qi-feng. Amplification and attenuation effect of blasting vibration on step topography[J]. Explosion and Shock Waves, 2017, 37(6): 128-133. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201706017.htm
[12]	钟冬望, 吴亮, 陈浩. 爆炸荷载下岩质边坡动力特性试验及数值分析研究[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2964-2971. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1056.htm ZHONG Dong-wang, WU Liang, CHEN Hao. Model test and numerical simulation study of dynamic characteristics of rock slope under blast loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2964-2971. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1056.htm
[13]	李新平, 胡元育, 祝文化, 等. 复杂环境下爆破减振保护层的现场试验研究[J]. 岩石力学与工程学报, 1997, 16(6): 584-589. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX199706012.htm LI Xin-ping, HU Yuan-yu, ZHU Wen-hua, et al. In-situ testing study of protective layer for blasting vibration reduction under complex environment[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(6): 584-589. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX199706012.htm
[14]	HU Y G, LU W B, ZHANG L, et al. Dynamic response and control of middle rock sidewall under impact of blast loading[J]. Journal of Vibration and Control, 2019. doi: 10.1177/1077546319829566.
[15]	洪悯萱. 波的传播及其与介质间断相互作用的数值模拟研究[J]. 岩土力学, 1987, 8(3): 23-31. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX198703005.htm HONG Min-xuan. Numerical modelling of wave propagation and interaction[J]. Rock and Soil Mechanics, 1987, 8(3): 23-31. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX198703005.htm
[16]	FUYUKI M, NAKANO M. Finite difference analysis of Rayleigh wave transmission past an upward step change[J]. Bulletin of the Seismological Society of America, 1984, 74(3): 893-911.
[17]	DALLY J W, LEWIS D. A photoelastic analysis of propagation of Rayleigh waves past a step change in elevation[J]. Bulletin of the Seismological Society of America, 1968, 58(2): 539-563.
[18]	SKLAVOUNOS S, RIGAS F. Computer simulation of shock waves transmission in obstructed terrains[J]. Journal of Loss Prevention in the Process Industries, 2004, 17(6): 407-417.
[19]	唐海, 李海波, 蒋鹏灿, 等. 地形地貌对爆破振动波传播的影响实验研究[J]. 岩石力学与工程学报, 2007, 26(9): 1817-1823. TANG Hai, LI Hai-bo, JIANG Peng-can, et al. Experimental study on the effect of topography on the propagation of blasting wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1817-1823. (in Chinese)
[20]	ZHANG Q, BAI C H, LIU Q M, et al. Experimental research on amplitude change of blasting seismic wave with topography[J]. Journal of Beijing Institute of Technology, 2000, 9(3): 237-242.
[21]	钟冬望, 何理, 操鹏, 等. 爆破振动持时分析及微差爆破延期时间优选[J]. 爆炸与冲击, 2016, 36(5): 703-709. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201605018.htm ZHONG Dong-wang, HE Li, CAO Peng, et al. Analysis of blasting vibration duration and optimizing of delayed time interval for millisecond blasting[J]. Explosion and Shock Waves, 2016, 36(5): 703-709. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201605018.htm
[22]	刘达, 卢文波, 陈明, 等. 隧洞钻爆开挖爆破振动主频衰减公式研究[J]. 岩石力学与工程学报, 2018, 37(9): 2015-2026. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201809002.htm LIU Da, LU Wen-bo, CHEN Ming, et al. Attenuation formula of the dominant frequency of blasting vibration during tunnel excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 2015-2026. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201809002.htm
[23]	HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of The Royal Society A: Mathematical Physical and Engineering, 1998, 454: 903-995.
[24]	张义平, 李夕兵, 赵国彦, 等. 爆破震动信号的时频分析[J]. 岩土工程学报, 2005, 27(12): 1472-1477. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200512019.htm ZAHNG Yi-ping, LI Xi-bing, ZHAO Guo-yan, et al. Time-frequency analysis of blasting vibration signals[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(12): 1472-1477. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200512019.htm
[25]	许名标, 彭德红. 某水电站边坡开挖爆破震动动力响应有限元分析[J]. 岩土工程学报, 2006, 28(6): 770-775. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200606018.htm XU Ming-biao, PENG De-hong. Finite element analysis of dynamic response on blasting vibration in slope excavation of a hydroelectric power station[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 770-775. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200606018.htm
[26]	DOWDING C H. Construction Vibrations[M]. N J: Prentice Hall, 1996.
[27]	YANG R. PPV Management and Frequency Shifting in Soft Ground Near Highwalls to Reduce Blast Damage[C]//Asian-Pacific Symposium on Blasting Techniques, 2009, Dalian.
[28]	爆破安全规程：GB6722—2014[S]. 2014. Safety Regulations for Blasting: GB6722—2014[S]. 2014. (in Chinese)

施引文献(48)

期刊类型引用(28)

1.	刘送永，崔松，顾聪聪. 高压泡沫涨裂破岩特性试验研究. 岩土工程学报. 2025(01): 125-134 . 本站查看
2.	肖云涛，崔正荣，鲍伟伟，王恒. 罗恩盆地露天采场爆破减振控噪技术研究与应用. 金属矿山. 2025(03): 121-127 . 百度学术
3.	孙鹏昌. 城区单薄山体岩石高边坡爆破振动高程效应研究. 工程爆破. 2024(03): 152-159 . 百度学术
4.	杨勇，王世林，黄绞龙，林宇亮，黄贤忠. 场平工程开挖爆破的动力传播规律研究. 公路工程. 2024(04): 155-161 . 百度学术
5.	杨仁树，赵勇，方士正，赵杰，王渝，刘朕. 起爆方式对间隔装药应力场分布及裂纹扩展的影响. 工程科学学报. 2023(05): 714-727 . 百度学术
6.	孙中博，赵毅鑫，王海亮，任建东. 临近地铁车站爆破振动效应对高层建筑的影响. 矿业科学学报. 2023(01): 83-92 . 百度学术
7.	冷振东，范勇，涂书芳，周桂松，郭一鸣. 电子雷管起爆技术研究进展与发展建议. 中国工程科学. 2023(01): 142-154 . 百度学术
8.	王晨光，杜新国，王可用，孙永，胡忠经，王令玉，孙迪. 数码电子雷管在泄洪排沙洞爆破中的减振特性研究. 爆破. 2023(01): 205-212 . 百度学术
9.	徐振洋，莫宏毅，包松，赵建宇，王雪松，刘鑫，陈占扬. 基于VMD-Teager的露天边坡爆破振动信号能量特征研究. 振动与冲击. 2023(07): 77-88+105 . 百度学术
10.	张薇薇. 坝肩边坡桩锚结构参数优化与经济性分析. 东北水利水电. 2023(05): 4-6 . 百度学术
11.	乔雄，刘文高，骆维斌，倪伟淋，杨鑫，黄锦聪，刘锦龙. 交通荷载对双井子堡古城墙振动影响的现场实测与数值分析. 振动工程学报. 2023(03): 776-788 . 百度学术
12.	郎旭，张智宇. 某露天采场填方松散体边坡爆破振动动力响应分析. 中国矿山工程. 2023(03): 7-12 . 百度学术
13.	宿利平，王宁，杜连杰，高玉龙，张小军，高文学. 爆炸荷载下路堑岩质边坡振动效应研究. 施工技术(中英文). 2023(12): 32-36 . 百度学术
14.	李涛，王林峰，李松，张继旭，唐宁. 单孔爆破作用下隧道围岩损伤范围计算及影响因素分析研究. 现代隧道技术. 2023(04): 23-32+66 . 百度学术
15.	李贺龙，王浩，诸洲，张建经，郭建婷，牛家永. 基于量纲分析的戈壁地区爆破振动衰减模型. 科学技术与工程. 2023(28): 11947-11953 . 百度学术
16.	何丽平，汪晓俊，郭剑雄，潘剑，张继奎，蒋楠. 砂泥岩互层岩质边坡爆破振动衰减规律现场试验研究. 高压物理学报. 2023(05): 174-183 . 百度学术
17.	孙苗，杨钧凯，吴立. 改进希尔伯特-黄变换含噪振动信号时频分析. 上海交通大学学报. 2023(12): 1648-1656 . 百度学术
18.	李祥龙，杨长辉，王建国，侯猛，程明. 基于数值模拟和频谱分析的孔间精确延时探究. 有色金属工程. 2022(02): 99-105 . 百度学术
19.	杨琳，付天杰，郭华杰. 浅孔台阶爆破的合理性研究. 爆破. 2022(01): 87-94 . 百度学术
20.	宋宏坤. 基于爆破振速衰减规律的爆破振动控制技术. 中外公路. 2022(02): 188-193 . 百度学术
21.	王进忠，年鑫喆. 深孔台阶爆破振动衰减及信号能量频域分布特征. 现代矿业. 2022(04): 86-90 . 百度学术
22.	杨琳，付天杰，郭华杰. 大规模深孔控制爆破起爆网路技术. 工程爆破. 2022(02): 62-69 . 百度学术
23.	邹烽，席田，胡业红，谢文，何梦，高凤琴，诸洲，张建经. 爆破振动综合减震措施的减震效应研究. 中国安全生产科学技术. 2022(06): 119-126 . 百度学术
24.	包松，郭连军，莫宏毅，任碧琦，徐振洋. 高程影响下爆破振动速度衰减模型优选研究. 有色金属工程. 2022(09): 115-121 . 百度学术
25.	包松，郭连军，莫宏毅，徐振洋. 考虑高程与能量的爆破振动持时分析. 金属矿山. 2021(08): 67-70 . 百度学术
26.	朱玉宝，方晓剑，黄天元. 温州绕西南仰义枢纽拼宽段静态爆破边坡工程支护设计研究. 低碳世界. 2021(09): 92-94 . 百度学术
27.	杨琳，付天杰，郭华杰. 紧靠电厂高危边坡的深孔控制爆破技术研究. 爆破. 2021(04): 68-74 . 百度学术
28.	刘翔宇，吴昊骏，吴晓东，王思杰. 考虑电子雷管延期误差的隧道爆破叠加振动研究. 爆破. 2021(04): 143-148 . 百度学术