移动荷载作用下横观各向同性层状地基–薄板结构动力响应半解析研究

冯多; 徐林荣; 蔡雨; 苏娜

doi:10.11779/CJGE202105009

移动荷载作用下横观各向同性层状地基–薄板结构动力响应半解析研究 English Version

冯多^1,,
徐林荣^{1, 2, ,},
蔡雨¹,
苏娜¹

1.
中南大学土木工程学院,湖南　长沙　410075
2.
中南大学高速铁路建造技术国家工程实验室,湖南　长沙　410075

基金项目:

国家自然科学基金面上项目 51778634

浙江省交通运输厅科研计划项目 2019001

详细信息

作者简介:
冯多(1996—),男,硕士研究生,主要从事于高速公路、高速铁路路基动力响应等方面的研究工作。E-mail: 870366824@qq.com

通讯作者:
徐林荣, E-mail: lrxu@csu.edu.cn

中图分类号: TU435
计量
- 文章访问数: 240
- HTML全文浏览量: 14
- PDF下载量: 138
出版历程
- 收稿日期: 2020-03-26
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-04-30

Semi-analytical solution to dynamic response of transversely isotropic layered foundation-thin plate structure under moving loads

FENG Duo^1,,
XU Lin-rong^{1, 2, ,},
CAI Yu¹,
SU Na¹

1.
School of Civil Engineering, Central South University, Changsha 410075, China
2.
National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410075, China

摘要

摘要: 为研究各向异性和动载参数对层状地基–薄板结构动力响应的影响规律,在已有各向异性弹性动力学理论的基础上,利用积分变换及矩阵分析理论,获得移动矩形简谐荷载作用下横观各向同性层状地基–薄板（无限大）结构的稳态动力响应半解析解答。通过对比既有算例所得结果,验证半解析解的准确性,进而对板体位移动力响应进行参数分析。结果表明：各向同性、横观各向同性假设下的计算结果存在较大差异。移动荷载较静载使板体位移幅值不对称分布,且存在临界速度使荷载作用区域幅值最大。荷载激振频率增大会减小板体竖向位移的响应范围。第一层地基的各向异性水平相较其余层对板体位移影响较大,增大其n值（水平、竖直弹性模量比）可改善板体在动力作用下的位移响应分布特征。
- 移动荷载 /
- 横观各向同性 /
- 层状地基 /
- 弹性薄板 /
- 半解析解
Abstract: To study the influences of anisotropy and dynamic parameters on the response of a layered foundation-thin plate structure, from the basis of the anisotropic elastodynamics, a semi-analytical solution to the dynamic response of TI layered foundation-thin plate (infinite) model under moving rectangular harmonic loads is established by using the integral transformation and the matrix theory. The accuracy of the semi-analytical solution is verified by comparing the results of the existing examples, and then the parametric analysis of the displacement dynamic response of the plate is carried out. The results show that there is a large difference between the calculated results under the assumption of isotropy and transverse isotropy. Compared with that of the static loads, the displacement amplitude of the moving loads is asymmetric, and there is a critical velocity which makes the maximum amplitude of the loading area. The affected range of the displacement reduces with the increase of the frequency. The anisotropy of the first layer has a greater impact on the displacement than other layers. Adjusting its n value can optimize the displacement characteristics of the plate under dynamic loads.
- moving load /
- transverse isotropy /
- layered foundation /
- elastic thin plate /
- semi-analytical solution

HTML全文

0. 引言

层状地基–薄板结构是一种工程上广泛应用的力学模型^[1]。随着高速公路、铁路、大运量航运的快速发展,其附属基础土建设施在高速荷载作用下的响应规律已与传统静力分析结论明显不符,因此移动荷载作用下该模型的动力响应已成为领域研究热点之一^[2]。早期受限于数学理论和电算水平,学者多在平面应变、各向同性、半无限空间地基的假设下研究该问题。但岩土体作为一种天然沉积的层状各向异性材料,其横观各向同性（transversely isotropic简称TI）及三维空间特性会对动力响应造成一定影响^[3-5]。近年来,数值计算水平的提升使得相应半解析研究逐渐成为可能,部分学者已在求解方法以及相关工程应用上获得了一定的启发性结论^[6-8]。

TI半无限体的Green函数最早由Rajapakse等^[9]通过引入3个势函数给出,其求解了内部荷载作用下的柱系响应结果,研究表明位移响应受激励频率、材料参数影响大,而应力则不受具体参数影响。对于层状地基,Barros等^[10]利用TRM得到层状弹性体作用移动线载后的稳态解答。薛松涛等^[11]通过研究斜SH波入射成层TI地基的传播特征建立直角坐标下的动力刚度矩阵,并指出横观各向同性可显著改变空间波动特性。艾智勇等^[12]从弹性动力学方程解法入手导出解析层元,进而获得直角坐标下的层状TI地基空间动力刚度矩阵。韩泽军等^[13]通过引入对偶变量获得精细积分形式的层状TI地基刚度矩阵,但存在数值计算程序复杂等具体问题。

Eskandari-Ghadi等^[14]证明可用2个位移势函数来完备表达TI弹性体不解耦的位移变量,当实际位移场旋度与材料对称轴垂直时,仅用一个势函数即可。在此基础上,Rahimain等^[15]研究了轴对称波动规律。Khojasteh等^[16]导出半无限空间、轴对称双层地基的Green函数。巴振宁等^[17]利用Ghadi解推导了TI层状地基的Green函数。但上述势函数需利用无穷级数构成的方程组确定多项式系数,求解过程繁琐且物理含义不强。

为简化分析,一般考虑简单荷载、层间完全连接下的结构响应规律。Achenbach^[18]研究了移动点载作用下半平面–薄板结构动力响应,指出振动水平受板、地基相对刚度、接触面粗糙性影响大。房营光^[19]解析了半平面–无限大板响应规律,计算表明板体接触应力随速度增加向地基转移。王博等^[20]的数值分析表明地基不同向弹性模量对板体变形影响较大。此外,王春玲等^[21]和Muho^[22]利用无穷级数逼近分别获得TI半空间上有限、无限大板的响应结果,但级数形式复杂且与荷载类型有关。

综上可见,现有研究多集中于半无限空间–薄板结构,而层状地基–薄板结构对应研究则较少,并且理论基于势函数分解等数学方法,程序复杂、物理含义弱。本文研究TI层状地基–薄板结构在典型移动荷载下的动力响应,意在寻求一种推导简洁、求解方便的算法,并在此基础上分析具体参数改变对动力响应的影响规律,为相关工程结构设计、施工提供参考。

1. 直角坐标系下的振动方程

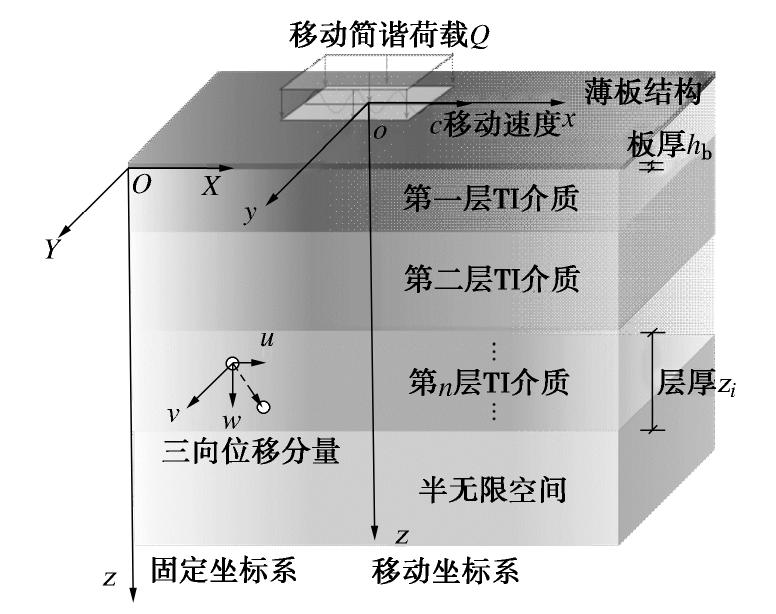
简化抽象的层状地基–薄板体系如图1所示分为板体、层状体、半无限空间三部分。板体满足薄板假定,层状体及半无限空间为TI均质材料。层状体水平叠放,层间相互连接且几何、材料特性不同,顶面作用匀速移动矩形简谐荷载。

图 1 TI层状地基-薄板体系示意图

Figure 1. Transversely isotropic layered foundation-plate system

下载: 全尺寸图片幻灯片

为简化求解过程,在移动坐标系下建立力学模型,其建立原则、与固定坐标系间变换关系及模型参数在1.1节、1.2节、2.1节中详细说明。

1.1 坐标系统变换

参考坐标系建立在层状地基顶面,竖向坐标正向朝下且满足右手法则。当体系受到高速移动荷载作用时,基于X-Y-Z-O固定直角坐标系分析将使后续求解产生较大计算成本。在稳态振动的前提下,基于以速度 $c (\to)$ 运动的x-y-z-o移动直角坐标系分析将简化计算流程。

根据时间t内荷载移动位移,两坐标系间坐标变换关系为 $\vec{R} - \vec{c} t = \vec{r}$ ,若荷载仅沿x轴正向运动（略去 $c (\to)$ 箭头）,由位移场F_i变化规律与坐标系选择无关易得： $F_{X} (X, Y, Z, t) =$ $F_{x} (x, y, z, t) =$ $F_{x} (X - c t, y, z, t)$ 。则两系下位移分量的微分关系为

$\begin{array}{l} \frac{\partial^{n} F_{R}}{\partial R^{n}} = \frac{\partial^{n} F_{r}}{\partial r^{n}}, \\ \frac{\partial^{n} F_{X}}{\partial t^{n}} = {(\frac{\partial F_{x}}{\partial x} - c \frac{\partial F_{x}}{\partial t})}^{(n)}, \end{array}}$

(1)

式中,F_i为位移场以下标区分对应坐标系,R为固定坐标系中任意点坐标分量如X,r为移动坐标系中任意点坐标分量如x。

因稳态响应变量可用荷载圆频率 $ω$ 表示,故各函数有其分离时间变量形式即F(x,y,z,t)= F(x,y,z)e^iωt,则式（1）中时间导数项变为

$\begin{array}{l} \frac{\partial F_{X}}{\partial t} = [i ω F_{x} (x, y, z) - c \frac{\partial F_{x} (x, y, z)}{\partial x}] e^{i ω t}, \\ \frac{\partial^{2} F_{X}}{\partial t^{2}} = [c^{2} \frac{\partial^{2} F_{x} (x, y, z)}{\partial x^{2}} - 2 c ω \frac{\partial F_{x} (x, y, z)}{\partial x} i - \\ ω^{2} F_{x} (x, y, z) \begin{array}{l} \end{array}] e^{i ω t} 。 \end{array}}$

(2)

移动坐标系下求解结果可通过 $\vec{R} = \vec{r} + c t$ 映射到常用固定坐标系对应坐标点处。

1.2 模型基本方程及变量解耦

固定坐标系下各位移变量表示的横观各向同性体物理方程组为

$(\begin{matrix} σ_{11} \\ σ_{22} \\ σ_{33} \\ σ_{13} \\ σ_{23} \\ σ_{12} \end{matrix}) = (\begin{matrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{11} & C_{13} & 0 & 0 & 0 \\ C_{33} & 0 & 0 & 0 \\ C_{44} & 0 & 0 \\ Sym . & C_{44} & 0 \\ C_{66} \end{matrix}) (\begin{matrix} \frac{\partial u}{\partial X} \\ \frac{\partial v}{\partial Y} \\ \frac{\partial w}{\partial Z} \\ \frac{\partial w}{\partial X} + \frac{\partial u}{\partial Z} \\ \frac{\partial w}{\partial Y} + \frac{\partial v}{\partial Z} \\ \frac{\partial u}{\partial Y} + \frac{\partial v}{\partial X} \end{matrix})$ 。

(3)

式中 $u, v, w$ 为任意点在固定坐标系下的位移分量（省略下标R）；X,Y,Z为固定系坐标； $σ_{11}$ - $σ_{12}$ 等表示应力分量；中部方阵代表弹性矩阵,各弹性常数需满足正定性要求^[23]：

$\begin{array}{l} C_{11}, C_{33}, C_{44}, C_{12} > 0, \\ C_{11} C_{33} - C_{13}^{2} - C_{33} C_{66} > 0 。 \end{array}}$

(4)

为引入质量密度ρ及时间变量t,将式（3）代入平衡方程得到忽略体力的Lame-Navier运动方程组：

(5)

薄板结构采用Kirchhoff薄板模型,其在固定坐标系下的动力控制方程为

$D_{q} \nabla^{4} γ (X, Y, t) + ρ_{b} h_{b} \frac{\partial^{2} γ (X, Y, t)}{\partial t^{2}} = Q (X, Y, t) - P (X, Y, t),$

(6)

式中, $D_{q} = E_{p} h_{b}^{3} / [12 (1 - μ_{p}^{2})]$ 为薄板抗弯刚度,E_p,μ_p,ρ_b,h_b分别为薄板弹性模量、泊松比、质量密度、板厚, $γ$ 为待求板体挠度,Q为外部竖向荷载,P为待求板间竖向接触力。

为便于求解,式（5）各方程需解耦,解耦原理与波的传播特性有关,引入下列变换^[24]：

$\begin{array}{l} [\begin{matrix} u^{'} \\ v^{'} \end{matrix}] = T [\begin{matrix} u \\ v \end{matrix}], \\ [\begin{matrix} σ_{c} \\ σ_{d} \end{matrix}] = T [\begin{matrix} σ_{13} \\ σ_{23} \end{matrix}], \\ T = [\begin{matrix} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \\ \frac{\partial}{\partial y} & \frac{- \partial}{\partial x} \end{matrix}], \end{array}}$

(7)

式中,T为变换矩阵, $u^{'}, v^{'}, σ_{c}, σ_{d}$ 分别为变换后的位移及应力分量。

联立式（1）,（3）,（7）可得解耦后的部分物理方程：

$\begin{array}{l} σ_{c} = C_{44} \nabla^{2} w + C_{44} \frac{\partial u^{'}}{\partial z}, \\ σ_{d} = C_{44} \frac{\partial v^{'}}{\partial z}, \\ σ_{z} = σ_{33} = C_{13} u^{'} + C_{33} \frac{\partial w}{\partial z} 。 \end{array}}$

(8)

联立式（1）,（2）,（5）,（7）得到解耦后的运动方程：

(9)

实际应用中,多采用工程常数描述模型材料特性,其与弹性常数转换按下式计算：

$\begin{array}{l} E_{h} = - \frac{8 C_{13}^{2} (C_{11} - C_{12}) (C_{11} C_{33} - C_{13}^{2})}{{(2 C_{13}^{2} - C_{11} C_{33} + C_{12} C_{33})}^{2}}, \\ E_{v} = \frac{2 (C_{11} C_{33} - C_{13}^{2})}{C_{11} + C_{12}}, \\ μ_{vh} = \frac{2 C_{13}^{2} - C_{11} C_{33} + C_{12} C_{33}}{2 C_{11} C_{13} + 2 C_{12} C_{13}}, \\ μ_{h} = \frac{2 C_{13}^{2} + C_{11} C_{33} - C_{12} C_{33}}{2 C_{13}^{2} - C_{11} C_{13} + C_{12} C_{13}}, \\ G_{v} = C_{44}, \end{array}}$

(10)

式中, $E_{v}$ , $E_{h}$ 为竖、水平向弹性模量, $μ_{h}$ , $μ_{vh}$ 为平行、垂直材料TI面的泊松比, $G_{v}$ 为垂直TI面的剪切模量。

对板体动力方程式（6）按移动系简谐变量化简得

$\begin{matrix} ρ_{b} h_{b} (\frac{\partial^{2} γ (x, y)}{\partial x^{2}} - 2 c ω \frac{\partial γ (x, y)}{\partial x} i - ω^{2} γ (x, y)) \\ = Q (x, y) - P (x, y) - D_{q} \nabla^{4} γ (x, y) \end{matrix}$ 。

(11)

1.3 控制方程求解

上述控制方程较复杂,本文通过双重傅里叶变换将偏微分方程组转化为常微分方程组,从而获得频率域下的位移解答。若有三元函数f(x,y,z),其双重傅里叶正逆变换规定如下：

$\bar{\bar{f}} (k_{x}, k_{y}, z) = \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} f (x, y, z) e^{- i (k_{x} x + k_{y} y)} d x d y$ ,

(12)

$f (x, y, z) = \frac{1}{4 π^{2}} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \bar{\bar{f}} (k_{x}, k_{y}, z) e^{i (k_{x} x + k_{y} y)} d k_{x} d k_{y}$ 。

(13)

式中,f为变换域下与f对应的函数变量,k_x,k_y为变换域下的坐标变量即波数,定义 $k^{2} = k_{x}^{2} + k_{y}^{2}$ 。

联立式（8）,（9）,（12）得常微分形式对应方程：

$\begin{array}{l} {\bar{\bar{σ}}}_{c} = - C_{44} k^{2} \bar{\bar{w}} + C_{44} \frac{d \bar{\bar{u'}}}{d z}, \\ {\bar{\bar{σ}}}_{d} = C_{44} \frac{d \bar{\bar{v'}}}{d z}, \\ {\bar{\bar{σ}}}_{z} = C_{13} \bar{\bar{u}}' + C_{33} \frac{d \bar{\bar{w}}}{d z}, \end{array}}$

(14)

$\begin{array}{l} - C_{11} k^{2} \bar{\bar{u}}' - (C_{13} + C_{44}) k^{2} \frac{d \bar{\bar{w}}}{d z} + C_{44} \frac{d^{2} \bar{\bar{u'}}}{d z^{2}} + \\ ρ {(ω - c k_{x})}^{2} \bar{\bar{u}}' = 0, \\ - C_{44} k^{2} \bar{\bar{w}} + C_{33} \frac{d^{2} \bar{\bar{w}}}{d z^{2}} + (C_{13} + C_{44}) \frac{d \bar{\bar{u'}}}{d z} + \\ ρ {(ω - c k_{x})}^{2} \bar{\bar{w}} = 0, \\ - (\frac{C_{11} - C_{12}}{2}) k^{2} \bar{\bar{v}}' + C_{44} \frac{d^{2} \bar{\bar{v}}'}{d z^{2}} + ρ {(ω - c k_{x})}^{2} \bar{\bar{v}}' = 0 。 \end{array}}$

(15)

为便求解,引入广义位移变量 $\bar{\bar{U}}', \bar{\bar{V}}'$ 及其组成的状态变量 ${\bar{\bar{W}}}_{i}$ 将位移变量统一：

$\begin{array}{l} \bar{\bar{U}}' (k_{x}, k_{y}, z) = {(\bar{\bar{u}}', k^{2} \bar{\bar{w}})}^{T}, \\ \bar{\bar{V}}' (k_{x}, k_{y}, z) = \bar{\bar{v}}', \end{array}}$

(16)

$\begin{array}{l} {\bar{\bar{W}}}_{1} (k_{x}, k_{y}, z) = {(\bar{\bar{U}}', \frac{d \bar{\bar{U}}'}{d z})}^{T}, \\ {\bar{\bar{W}}}_{2} (k_{x}, k_{y}, z) = {(\bar{\bar{V}}', \frac{d \bar{\bar{V}}'}{d z})}^{T} 。 \end{array}}$

(17)

联立式（15）,（17）可得两组矩阵微分方程（A,B系数矩阵中元素的具体形式见附录）：

$\begin{array}{l} {\frac{d {\bar{\bar{W}}}_{1} (k_{x}, k_{y}, z)}{d z}}_{4 \times 1} = A {(k_{x}, k_{y})}_{4 \times 4} {\bar{\bar{W}}}_{1} {(k_{x}, k_{y}, z)}_{4 \times 1}, \\ {\frac{d {\bar{\bar{W}}}_{2} (k_{x}, k_{y}, z)}{d z}}_{2 \times 1} = B {(k_{x}, k_{y})}_{2 \times 2} {\bar{\bar{W}}}_{2} {(k_{x}, k_{y}, z)}_{2 \times 1} 。 \end{array}}$

(18)

根据矩阵分析理论,上述两组矩阵方程存在exp(A(k_x,k_y)z)C(k_x,k_y)形式的一般解满足要求,令 $\bar{\bar{W_{1}}} (k_{x}, k_{y}, z) = \exp (A z) \bar{\bar{W_{1}}} (k_{x}, k_{y}, 0)$ ,根据汉密尔顿-凯莱定理, ${\bar{\bar{W}}}_{1} (k_{x}, k_{y}, z)$ 可以传递矩阵T₁的形式表达：

$\begin{matrix} \bar{\bar{W_{1}}} {(k_{x}, k_{y}, z)}_{4 \times 1} = \sum_{i = 0}^{3} b_{i} (z) A^{i}_{4 \times 4} {\bar{\bar{W}}}_{1} {(k, 0)}_{4 \times 1} \\ = T_{1} {(k, z)}_{4 \times 4} \bar{\bar{W_{1}}} {(k, 0)}_{4 \times 1} \end{matrix}$ 。

(19)

具体先计算矩阵A的特征多项式：

$\det (λ I - A) = \prod_{i = 1}^{4} (λ - λ_{i}) = 0$ 。

(20)

其解经计算：

$\begin{array}{l} λ_{1, 2}^{2} = a + b, \\ λ_{3, 4}^{2} = a - b 。 \end{array}}$

(21)

式中,a,b见附录。以4个特征值互异为例,可列得其含参多项式 $r (λ_{i}, z)$ ：

$r (λ_{i}, z) = \exp (λ_{i} z) = \sum_{j = 1}^{4} b_{j} (z) λ_{i}^{j}$ 。

(22)

联立含参多项式解得b_j,进而由A得T₁表达式：

$r (A, z) = \exp (A z) = \sum_{i = 1}^{4} b_{i} (z) A^{i} = T_{1} {(k, z)}_{4 \times 4}$ 。

(23)

则可求得状态变量 ${\bar{\bar{W}}}_{1}$ 并分割传递矩阵T₁：

$\bar{\bar{W_{1}}} {(k, z)}_{4 \times 1} = T_{1} (k, z) \bar{\bar{W_{1}}} (k, 0) = [\begin{matrix} T_{11} & T_{12} \\ T_{13} & T_{14} \end{matrix}] \bar{\bar{W_{1}}} {(k, 0)}_{4 \times 1}$ 。

(24)

进而得到 $\bar{\bar{U}}' (k, z)$ 与顶面状态变量 ${\bar{\bar{W}}}_{1} (k, 0)$ 关系：

$\bar{\bar{U}}' (k, z) = (\begin{matrix} T_{11} & T_{12} \end{matrix}) {\bar{\bar{W}}}_{1} (k, 0)$ 。

(25)

同理可推得

$\bar{\bar{V}}' (k, z) = (\begin{matrix} T_{11} & T_{12} \end{matrix}) {\bar{\bar{W}}}_{2} (k, 0)$ 。

(26)

为推导刚度矩阵,定义广义应力变量 ${\bar{\bar{V}}}_{1} 、 {\bar{\bar{V}}}_{2}$ 如下。联立式（14）,（16）求取广义应力与状态变量间关系：

${\bar{\bar{V}}}_{1} (k, z) = {[\bar{\bar{σ_{c}}}, \bar{\bar{σ_{z}}}]}^{T}, {\bar{\bar{V}}}_{2} (k, z) = [\bar{\bar{σ_{d}}}]$ ,

(27)

$\begin{array}{l} {\bar{\bar{V}}}_{1} {(k, z)}_{2 \times 1} = L_{1}_{2 \times 4} {\bar{\bar{W}}}_{1} {(k, z)}_{4 \times 1}, \\ {\bar{\bar{V}}}_{2} {(k, z)}_{1 \times 1} = L_{2}_{1 \times 2} {\bar{\bar{W}}}_{2} {(k, z)}_{2 \times 1}, \end{array}}$

(28)

式中,矩阵L₁,L₂具体形式见附录。联立式（25）,（28）并代入z=z_i可推得单层结构的刚度矩阵K₁：

$\begin{array}{l} {(\begin{matrix} - {\bar{\bar{V}}}_{1} (k, 0) \\ {\bar{\bar{V}}}_{1} (k, z_{i}) \end{matrix})}_{4 \times 1} = K_{14 \times 4} {(\begin{array}{l} \bar{\bar{U}}' (k, 0) \\ \bar{\bar{U}}' (k, z_{i}) \end{array})}_{4 \times 1} \\ = (\begin{array}{l} - L_{1} I (k) \\ L_{1} T_{1} (k, z_{i}) \end{array}) {(\begin{matrix} I & 0 \\ T_{11} (k, z_{i}) & T_{12} (k, z_{i}) \end{matrix})}^{- 1} (\begin{array}{l} \bar{\bar{U}}' (k, 0) \\ \bar{\bar{U}}' (k, z_{i}) \end{array}) \end{array}$ 。

(29)

同理可以推得v′位移变量对应的刚度矩阵：

${(\begin{matrix} - {\bar{\bar{V}}}_{2} (k, 0) \\ {\bar{\bar{V}}}_{2} (k, z) \end{matrix})}_{2 \times 1} = K_{22 \times 2} {(\begin{array}{l} \bar{\bar{V}}' (k, 0) \\ \bar{\bar{V}}' (k, z) \end{array})}_{2 \times 1}$ 。

(30)

上述刚度矩阵与层厚、材料属性及波数有关。对于下覆半无限体,此法存在伪逆不满足边界条件的困难,对此笔者参考Gao等^[25]所用方法推导对应刚度矩阵。以 $\bar{\bar{U}}'$ 为例,联立式（14）～（16）并整理得

$\begin{matrix} K_{22} \frac{d^{2} \bar{\bar{U'}}}{d z^{2}} + (K_{21} + K_{12}) \frac{d \bar{\bar{U'}}}{d z} - \\ (K_{11} - ρ {(ω - c k_{x})}^{2} I) \bar{\bar{U'}} = 0 \end{matrix}$ ,

(31)

$V_{1} = K_{22} \frac{d^{2} \bar{\bar{U'}}}{d z^{2}} + K_{21} \bar{\bar{U'}}$ ,

(32)

式中,K_ij为系数矩阵。

整理式（31）,（32）得

$\frac{d}{d z} {(\begin{matrix} \bar{\bar{U'}} & \bar{\bar{V_{1}}} \end{matrix})}^{T} = H_{4 \times 4} {(\begin{matrix} \bar{\bar{U'}} & \bar{\bar{V_{1}}} \end{matrix})}^{T}$ ,

(33)

式中,H系数矩阵有如下形式：

$\begin{array}{l} H = [\begin{matrix} - K_{22}^{- 1} K_{21} & K_{22}^{- 1} \\ K_{11} - ρ {(ω - c k_{x})}^{2} I' + K_{12} K_{22}^{- 1} K_{21} & - K_{12} K_{22}^{- 1} \end{matrix}], \\ I' = [\begin{matrix} 1 & 0 \\ 0 & k^{- 2} \end{matrix}] 。 \end{array}}$

(34)

求H矩阵的右特征向量：

$H Θ = Θ Λ$ ,

(35)

式中,Θ,Λ由特征向量及特征值组成：

$\begin{array}{l} Θ_{4 \times 4} = [\begin{matrix} Θ_{11} & Θ_{12} \\ Θ_{21} & Θ_{22} \end{matrix}], \\ Λ_{4 \times 4} = d i a g (λ_{i}, \dots, - λ_{i}, \dots) 。 \end{array}}$

(36)

易推得

$(\begin{matrix} \bar{\bar{U'}} \\ \bar{\bar{V_{1}}} \end{matrix}) = [\begin{matrix} Θ_{11} & Θ_{12} \\ Θ_{21} & Θ_{22} \end{matrix}] {[c_{i} \exp (λ_{i} z), \dots, c_{i} \exp (- λ_{i} z)]}^{T}$ 。

(37)

因半空间体在边界无穷处广义位移存在极限,故取 $c_{i} \exp (- λ_{i})$ 所对应Θ矩阵列元素计算：

$\bar{\bar{V_{1}}} = (Θ_{22} Θ_{12}^{- 1}) \bar{\bar{U'}} = K_{3} \bar{\bar{U'}}$ 。

(38)

同理可以推得 $\bar{\bar{V'}}, \bar{\bar{V_{2}}}$ 对应刚度矩阵 $K_{4}$ 。

对薄板动力控制方程式（6）同样进行傅里叶变换：

$D_{q} k^{4} \bar{\bar{γ}} - \bar{\bar{Q}} (x, y) + \bar{\bar{P}} (x, y) = ρ_{b} h_{b} {(ω - c k_{x})}^{2} \bar{\bar{γ}} (x, y)$ 。

(39)

2. 体系控制方程

综上利用数学技巧推得层状体和半空间体对应刚度矩阵。以下根据边界条件推导下覆半空间的层状横观各向同性体总体刚度方程。

2.1 边界条件

对本问题,各层间相接面完全连接,其广义应力、位移间协调关系为

$\begin{array}{l} \bar{\bar{V_{1}}} (k, H_{i}^{1}) = \bar{\bar{V_{1}}} (k, H_{i + 1}^{0}), \\ \bar{\bar{V_{2}}} (k, H_{i}^{1}) = \bar{\bar{V_{2}}} (k, H_{i + 1}^{0}), \\ \bar{\bar{U'}} (k, H_{i}^{1}) = \bar{\bar{U'}} (k, H_{i + 1}^{0}), \\ \bar{\bar{V'}} (k, H_{i}^{1}) = \bar{\bar{V'}} (k, H_{i + 1}^{0}), \end{array}}$

(40)

式中,H_i上标0/1分别代表上/下层界面。

层状结构与板体接触条件为

$\begin{array}{l} {\bar{\bar{V}}}_{1} (k, H_{1}^{0}) = {(0 \bar{\bar{P}} (k, 0))}^{T}, \\ {\bar{\bar{V}}}_{2} (k, H_{1}^{0}) = 0, \end{array}}$

(41)

$\begin{array}{l} \bar{\bar{U'}} (k, H_{1}^{0}) = {(\begin{matrix} \bar{\bar{u'}} (k, 0) & k^{2} \bar{\bar{γ}} (k, 0) \end{matrix})}^{T}, \\ \bar{\bar{V'}} (k, H_{1}^{0}) = \bar{\bar{v'}} (k, 0), \end{array}}$

(42)

式中, $\bar{\bar{P}} (k, 0)$ 为二重正变换下的层间接触应力, $\bar{\bar{γ}} (k, 0)$ 为板体挠度变换值。

板上作用有移动简谐矩阵荷载,其表达式如下：

$\begin{matrix} Q (x, y, t) = \frac{q e^{i ω t}}{4 l_{1} l_{2}} [(H (x + l_{1}) - H (x - l_{1})) \cdot \\ (H (y + l_{2}) - H (y - l_{2}))] \end{matrix}$ ,

(43)

式中,q为矩形荷载作用区域合力,l₁,l₂为矩形区域尺寸,H为单位阶跃函数。

2.2 整体方程建立

依据上述关系,联立式（29）,（30）,（38）,（40）～（42）即得TI层状地基–薄板结构的整体动力刚度方程式（44）,（45）,当广义应力取单位值时即可求得动力Green函数。位移分量为复数,其模值可作振动幅值,幅角则表示相位情况。

此外当层数n较大时,刚度矩阵求逆成本剧增,高效算法的编制难度会大于模型求解本身。卢正等^[26]及杨广庆^[27]对路基的动力学研究表明,力学参数差异不大的层状体可用Odemark当量理论换算成等效层结构,且理论计算结果可满足工程设计需求。

综上建立由薄板、第一层TI地基、第二层等效TI地基、半无限TI空间组成的典型力学模型,进而分析其动力响应规律。

$\begin{matrix} {(\begin{matrix} 0 \\ ⋮ \\ 0 \end{matrix})}_{2 n + 2} = {(\begin{matrix} K_{21}^{1} & K_{22}^{1} & \dots & 0 \\ K_{23}^{1} & K_{24}^{1} + K_{21}^{2} & ⋮ \\ ⋮ & ⋱ & K_{24}^{n - 1} + K_{21}^{n} & K_{22}^{n} \\ 0 & \dots & K_{23}^{n} & K_{24}^{n} + K_{21}^{n + 1} \end{matrix})}_{{(2 n + 2)}^{2}} \cdot \\ {(\begin{matrix} \bar{\bar{v'}} (k, 0) \\ ⋮ \\ \bar{\bar{V}}' (k, H_{n}^{1}) \end{matrix})}_{2 n + 2} \end{matrix}$ ,

(44)

$\begin{matrix} {(\begin{matrix} 0 \\ \bar{\bar{P}} (k, 0) \\ \begin{array}{l} ⋮ \\ 0 \end{array} \end{matrix})}_{2 n + 2} \\ = {(\begin{matrix} K_{11}^{1} & K_{12}^{1} & \dots & 0 \\ K_{13}^{1} & K_{14}^{1} + K_{11}^{2} & \dots & ⋮ \\ ⋮ & \dots & K_{14}^{n - 1} + K_{11}^{n} & K_{12}^{n} \\ 0 & \dots & K_{13}^{n} & K_{14}^{n} + K_{11}^{n + 1} \end{matrix})}_{{(2 n + 2)}^{2}} \cdot \\ {(\begin{array}{l} \bar{\bar{u'}} (k, 0) \\ k^{2} \bar{\bar{γ}} (k, 0) \\ ⋮ \\ \bar{\bar{U}}' (k, H_{n}^{1}) \end{array})}_{2 n + 2} \end{matrix}$ 。

(45)

3. 数值计算及参数分析

联立式（7）,（39）,（43）先后解得 $\bar{\bar{P}}$ 、变换位移,经式（13）逆变换最终得位移振幅值。为避免积分奇异性并考虑土体黏弹性,对材料参数引入阻尼系数 $ξ$ ,形如 $E^{'}$ =E(1+ξi)。表面位移w可通过式（45）单独求解,工程应用中常将该值作为基本控制指标,下文以竖向位移为主讨论。

利用符号计算求解上述方程较为繁琐,拟采用数值计算求解空间域位移。具体对波数域位移变量作离散快速傅里叶逆变换,经试算在|k_x|,|k_y|<10、2048×2048积分域下所得结果可满足精度要求。本文使用Mathematica进行公式推导,数值计算程序则采用MATLAB编制。

3.1 验证

因TI层状地基-薄板结构动力响应研究相对较少,令各层参数一致（板厚h_b≈0）将模型退化为半空间体,重复已有算例参数计算说明上述方法准确性。

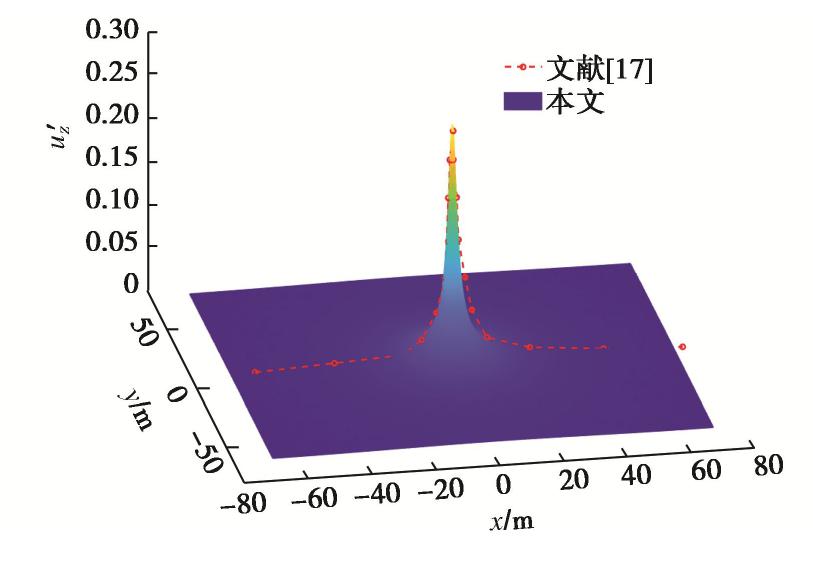
算例一研究移动点载下半空间体响应规律,BA等^[17]所建模型参数为 $μ_{h}$ = $μ_{vh}$ =0.25,E_h=5×10⁹ N/m²,E_v=2E_h,G_v=0.6E_h,ρ=2000 kg/m³, $c = 0.5 \sqrt{G_{v} / ρ}$ ,其解出（0,0,10）处无量纲竖向位移u′_z=G_vzu_z /q分布规律如图2所示（已将时间坐标转化为移动系下x坐标）。

图 2 移动恒点载作用TI半空间顶面竖向位移计算结果

Figure 2. Calculated results of top vertical displacement of TI half space under moving dead point loads

下载: 全尺寸图片幻灯片

从图2可见,上文算法所得结果与原结果吻合度较高,说明导出模型具备一定的合理性。

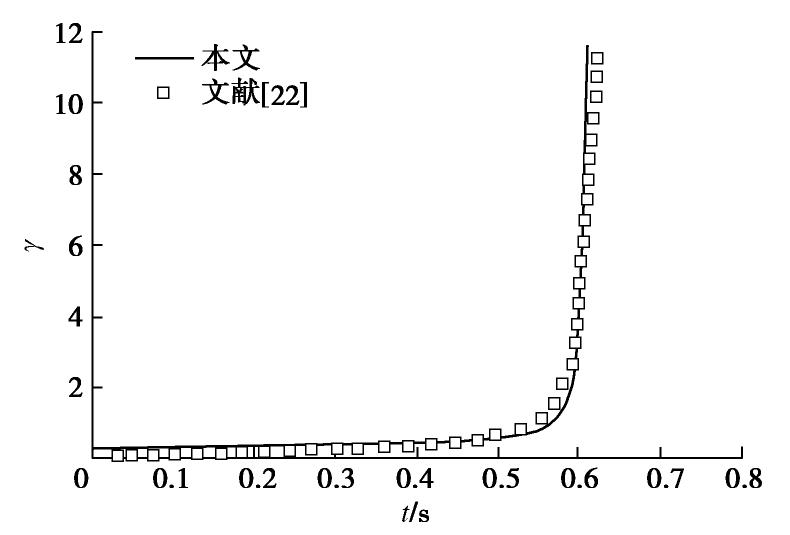
算例二研究移动矩形荷载下半空间-薄板结构响应规律,Muho^[22]所建模型参数为 $μ_{h}$ = $μ_{vh}$ =0.35,E_h=0.2×10⁹ N/m²,E_v=10E_h,G_v=3E_h,ρ=2100 kg/m³,E_p=30×10⁹ N/m²,μ_p=0.2,ρ_b=2300 kg/m³,h_b=0.2 m,l₁=l₂=0.15 m,q=80 kN,c=40 m/s,其解出板上中心点无量纲挠度γ′=γE_p/(qh_b)时程曲线如图3所示。

图 3 移动矩形荷载作用下TI半空间-薄板结构板体位移时程曲线计算结果

Figure 3. Calculated results of time-history curve of displacement of TI half-space-thin plate structure under moving rectangular loads

下载: 全尺寸图片幻灯片

由图3可见,本文模型结果与既有结果基本一致。两算例对比表明本文推导模型及数值算法具备一定的准确性,可用于移动荷载作用下TI层状地基-薄板结构的动力响应研究。

3.2 地基各向异性的影响

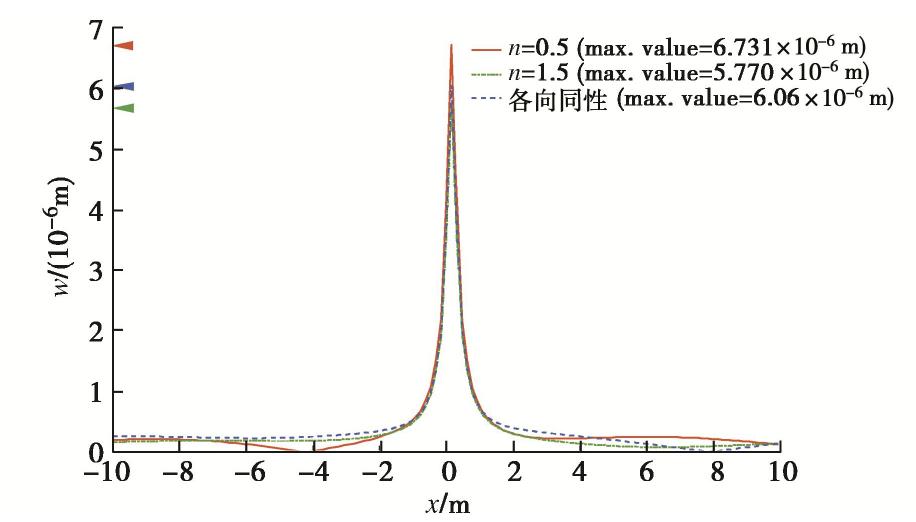
利用材料水平、竖直弹性模量比n表示各向异性程度,n取值一般在0.5～3.0,则对比n为0.5,1.0（各向同性处理）,1.5时单层地基的顶面竖向位移。板体及荷载参数：E_p=30×10⁹ Pa,μ_p=0.15,h_b=0.25 m,ρ_b=2400 kg/m³,c=200 m/s,ω=40 rad/s,l₁=0.25 m,l₂=0.25 m,q=100000 Pa。

n=0.5时模型各部分力学参数如表1所示,其余工况通过固定E_v,改变E_h调整n值,如n=1.5时,第一层弹模E_v=10×10⁹ Pa、E_h=15×10⁹ Pa,下文同。

表 1 层状地基各部分基本材料参数

Table 1. Basic material parameters of each part of layered foundation

参数/位置	第一层	半无限空间
E_v/(10⁹ Pa)	10	20
E_h/(10⁹ Pa)	5	10
G_v/(10⁹ Pa)	3	3
μ_h	0.25	0.25
μ_vh	0.25	0.25
z/m	10	∞
ρ/(kg·m^-3)	2000	2000

下载: 导出CSV

| 显示表格

各工况x方向板体位移幅值波形如图4所示,为便于比较曲线最值,图例及图左侧附有文字、楔形标记说明最值大小及位置,下文同。由图可知板体中心位移幅值在n=0.5时最大、n=1.5时最小。板体水平面波形受到地基各向异性影响,n为1.0,1.5时波形曲线呈对称分布,n=0.5时波形曲线向荷载移动方向偏移,虽出现零振幅点,但荷载影响范围显著增大。可见此类计算工况下,地基各向异性水平影响顶部面波传递规律,荷载作用中心板体位移幅值变化最大,相比各向同性情形出现一定幅度增减。

图 4 不同地基水平、竖直弹性模量比n下板体位移幅值在x方向的波形（y=0）

Figure 4. Waveshapes of position displacement amplitude of plate under different foundation levels and vertical elastic modulus ratios in x direction (y=0)

下载: 全尺寸图片幻灯片

3.3 荷载移动速率的影响

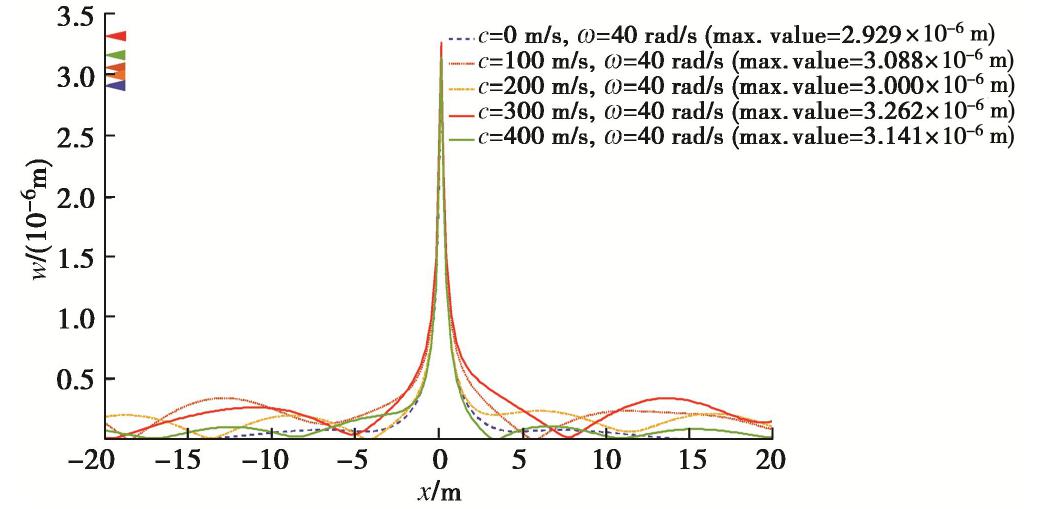
为研究荷载移动速率对动力响应的影响,取c为0,100,200,300,400 m/s 5种情况对比说明荷载移动速度对顶面竖向位移幅值的影响规律。模型取为单层地基-薄板结构,其余参数均与3.2节一致。

各工况x方向板体位移幅值波形如图5所示,可见移动速度对顶面竖向位移影响较大。当c从0逐渐增长至400 m/s时,波形出现不对称,零振幅点向移动方向偏移。增至300 m/s时,正向波形呈放大趋势,增至400 m/s时,正向波形迅速缩小。此外中心幅值随移动速率变化先增大后减小,300 m/s时幅值最大。可见此类计算工况下,临界荷载移动速率在300～400 m/s,其变化直接影响荷载作用区域面波具体分布形式。

图 5 不同荷载移动速率下板体位移幅值在x方向的波形（y=0）

Figure 5. Waveshapes of plate position displacement amplitude in x direction at different load movement rates (y=0)

下载: 全尺寸图片幻灯片

3.4 荷载加载频率的影响

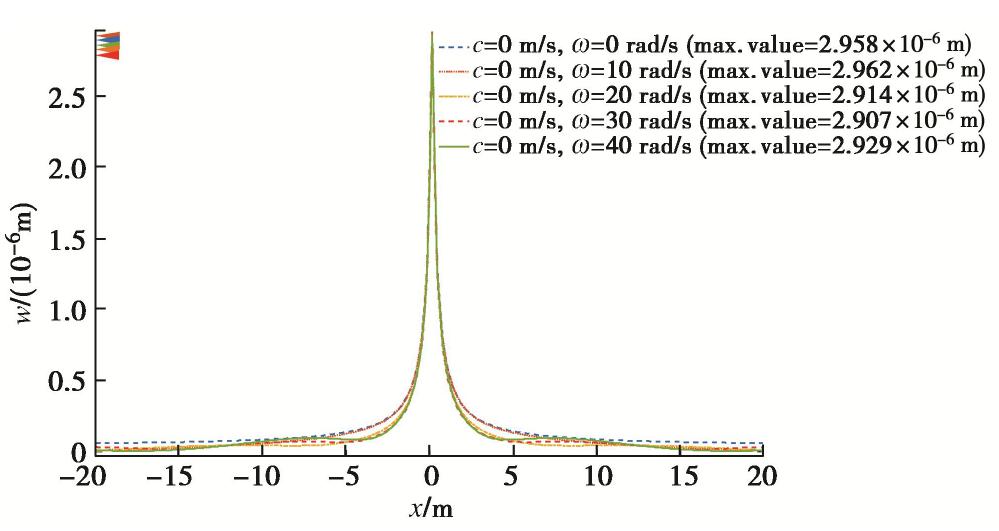
荷载移动会影响水平向波形分布,为单独分析荷载加载频率对动力响应的影响,取c=0 m/s,ω为0,10,20,30,40 rad/s对比计算。模型取为单层地基-薄板结构,其余参数均与3.2节一致。

各工况x方向板体位移幅值波形如图6所示。由图可知：板体中心位移幅值受加载频率影响较小,不同频率主要影响水平面位移波形分布。当ω=0 rad/s时,位移沿水平轴的分布范围最广,荷载作用范围（拐点）延伸到了半径20 m之外。增大加载频率,荷载作用范围缩小,ω=40 rad/s时,波形集中分布在10 m之内。可见荷载加载频率主要影响顶面板体位移波形的集中程度或动荷载作用范围大小。

图 6 不同荷载加载频率下板体位移幅值在x方向的波形（y=0）

Figure 6. Waveshapes of plate position displacement amplitude in x direction under different loading frequencies (y=0)

下载: 全尺寸图片幻灯片

3.5 层状结构的影响

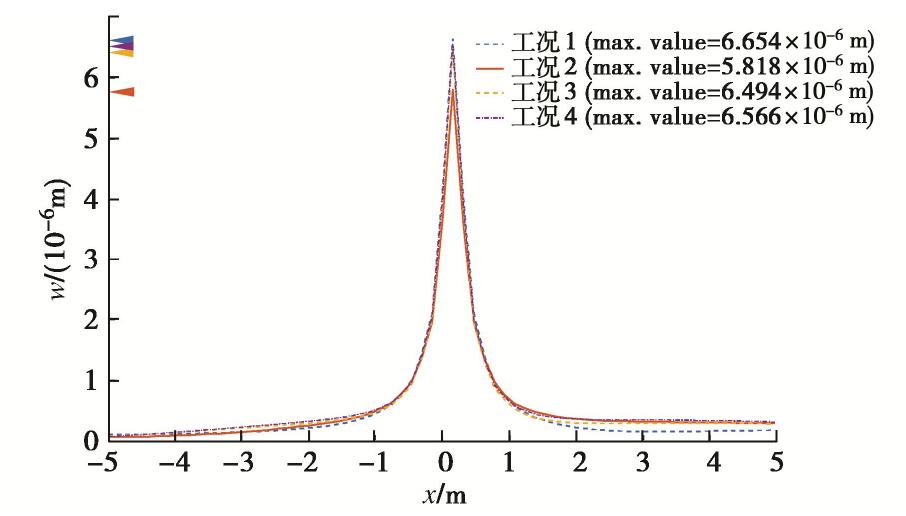
为研究地基各层结构参数改变对板体位移幅值的影响,对双层地基-板体结构按表2调整形成4种工况,由此分析各层地基对动力响应的影响。各工况材料、荷载参数在前基础上调整。

表 2 各计算工况下单层地基弹性模量比

Table 2. Elastic modulus ratios of single-layer foundation under various calculation conditions

层数/工况参数	水平、竖直弹性模量之比n				层厚/m
层数/工况参数	情形一	情形二	情形三	情形四	层厚/m
第一层	0.5	0.75	0.5	0.5	5
第二层	0.5	0.5	0.75	0.5	5
半无限空间	0.5	0.5	0.5	0.75	∞

下载: 导出CSV

| 显示表格

各工况计算结果如图7所示,由图可知：不同层n值改变或提升某层力学性能对顶面竖向位移影响不同。增大第二层或半空间n值对中心位移影响较小,而增加第一层将使位移大幅减小。此外单独增加各层n值会使荷载作用范围相比一般情形增加,且移动方向增长幅度更大。可见第一层各向异性水平变化将对顶面竖向位移产生较大影响。

图 7 某层地基水平、竖向弹性模量比改变时板体位移幅值在x方向的波形（y=0）

Figure 7. Waveshapes of plate position displacement amplitude in x direction when the horizontal and vertical elastic modulus ratio of a certain layer of foundation is changed (y=0)

下载: 全尺寸图片幻灯片

4. 结论

本文在已有各向异性体弹性动力学理论基础上,针对横观各向同性层状地基–薄板（无限大）这一典型力学模型,推导出二重积分形式的稳态响应解,并通过数值计算得到移动简谐荷载作用下的半解析解答。进而研究材料、荷载参数对板体位移的影响规律。

（1）对比横观各向同性、各向同性地基下计算结果,板体位移响应最值出现一定幅度增减。现有框架下的计算、设计结果可能与实际情况存在一定偏差。

（2）移动荷载相较静载使板体位移幅值的水平分布出现左右不对称,不对称程度与具体移动速率大小有关。存在临界速度使得荷载作用区域幅值最大。

（3）荷载加载频率对板体位移响应影响不如移动速率大,其主要影响荷载作用下的响应范围。

（4）分层各向异性水平改变对顶面竖向位移的影响程度不同,第一层地基相比其余层对降低竖向位移响应有较大作用,可利用此特性改善层状体系结构在动力作用下的响应特征。

附录：

（1）A矩阵元素形式

$\begin{array}{l} A_{13} = 1, A_{24} = 1, A_{31} = [C_{11} k^{2} - ρ {(ω - c k_{x})}^{2}] / C_{44}, \\ A_{34} = (C_{13} + C_{44}) / C_{44}, \\ A_{42} = [C_{44} k^{2} - ρ {(ω - c k_{x})}^{2}] / C_{44}, \\ A_{43} = - k^{2} (C_{13} + C_{44}) / C_{33}, \\ A_{11} = A_{12} = A_{14} = A_{21} = A_{22} = 0, \\ A_{23} = A_{32} = A_{33} = A_{41} = A_{44} = 0 。 \end{array}$

（2）B矩阵的元素形式

$\begin{array}{l} B_{11} = B_{22} = 0, B_{12} = 1, \\ B_{21} = [k^{2} (C_{11} - C_{12}) / 2 - ρ {(ω - c k_{x})}^{2}] / C_{44} 。 \end{array}$

（3）L₁,L₂矩阵的元素形式

$L_{1} = [\begin{matrix} 0 & - C_{44} & C_{44} & 0 \\ C_{13} & 0 & 0 & C_{33} / k^{2} \end{matrix}], L_{2} = [\begin{matrix} 0 & C_{44} \end{matrix}]$ 。

（4）a,b变量形式

图 1 TI层状地基-薄板体系示意图

Figure 1. Transversely isotropic layered foundation-plate system

下载: 全尺寸图片幻灯片

图 2 移动恒点载作用TI半空间顶面竖向位移计算结果

Figure 2. Calculated results of top vertical displacement of TI half space under moving dead point loads

下载: 全尺寸图片幻灯片

图 3 移动矩形荷载作用下TI半空间-薄板结构板体位移时程曲线计算结果

Figure 3. Calculated results of time-history curve of displacement of TI half-space-thin plate structure under moving rectangular loads

下载: 全尺寸图片幻灯片

图 4 不同地基水平、竖直弹性模量比n下板体位移幅值在x方向的波形（y=0）

Figure 4. Waveshapes of position displacement amplitude of plate under different foundation levels and vertical elastic modulus ratios in x direction (y=0)

下载: 全尺寸图片幻灯片

图 5 不同荷载移动速率下板体位移幅值在x方向的波形（y=0）

Figure 5. Waveshapes of plate position displacement amplitude in x direction at different load movement rates (y=0)

下载: 全尺寸图片幻灯片

图 6 不同荷载加载频率下板体位移幅值在x方向的波形（y=0）

Figure 6. Waveshapes of plate position displacement amplitude in x direction under different loading frequencies (y=0)

下载: 全尺寸图片幻灯片

图 7 某层地基水平、竖向弹性模量比改变时板体位移幅值在x方向的波形（y=0）

Figure 7. Waveshapes of plate position displacement amplitude in x direction when the horizontal and vertical elastic modulus ratio of a certain layer of foundation is changed (y=0)

下载: 全尺寸图片幻灯片

表 1 层状地基各部分基本材料参数

Table 1 Basic material parameters of each part of layered foundation

参数/位置第一层半无限空间

E_v/(10⁹ Pa) 10 20
E_h/(10⁹ Pa) 5 10
G_v/(10⁹ Pa) 3 3
μ_h 0.25 0.25
μ_vh 0.25 0.25
z/m 10 ∞
ρ/(kg·m^-3) 2000 2000

下载: 导出CSV

表 2 各计算工况下单层地基弹性模量比

Table 2 Elastic modulus ratios of single-layer foundation under various calculation conditions

层数/工况参数水平、竖直弹性模量之比n 层厚/m
情形一情形二情形三情形四

第一层 0.5 0.75 0.5 0.5 5
第二层 0.5 0.5 0.75 0.5 5
半无限空间 0.5 0.5 0.5 0.75 ∞

下载: 导出CSV

参考文献(27)

[1]	郭大智, 冯德成. 层状弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001. GUO Da-zhi, FENG De-cheng. Mechanics of Layered Elastic System[M]. Harbin: Harbin University of Technology Press, 2001. (in Chinese)
[2]	凌道盛, 王云龙, 赵云, 等. 飞机主起落架移动荷载作用下道基动力响应分析[J]. 岩土工程学报, 2018, 40(1): 64-73. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801006.htm LING Dao-sheng, WANG Yun-long, ZHAO Yun, et al. Dynamic response of Subgrade under moving loads of main landing gears[J]. Journal of Geotechnical Engineering, 2018, 40(1): 64-73. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801006.htm
[3]	SYNGE L. Elastic waves in anisotropic media[J]. Studies in Applied Mathematics, 1956, 35(1/2/3/4): 323-334.
[4]	BUCHWALD V T. Rayleigh waves in transversely isotropic media[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1961(@@@3): 293-318.
[5]	MUKHOPADHYAY A. Stresses produced by a normal load moving over a transversely isotropic layer of ice lying on a rigid foundation[J]. Pure and Applied Geophysics, 1965, 60(1): 29-41. doi: 10.1007/BF00874804
[6]	BA Z, LIANG J, LEE V W, et al. A semi-analytical method for vibrations of a layered transversely isotropic ground-track system due to moving train loads[J]. Soil Dynamics & Earthquake Engineering, 2019, 121(6): 25-39.
[7]	Keawsawasvong SURAPARB, Senjuntichai TEERAPONG. Dynamic interaction between multiple rigid strips and transversely isotropic poroelastic layer[J]. Computers and Geotechnics, 2019, 114: 103-144.
[8]	BA Z, AN D. Seismic response of a 3-D canyon in a multi-layered TI half-space modeled by an indirect boundary integral equation method[J]. Geophysical Journal International, 2019, 217(3): 1949-1973. doi: 10.1093/gji/ggz122
[9]	RAJAPAKSE Nimal, WANG Y. Green's functions for transversely isotropic elastic half space[J]. Journal of Engineering Mechanics, 1993, 119(9): 1724-1736. doi: 10.1061/(ASCE)0733-9399(1993)119:9(1724)
[10]	BARROS F C P D, LUCO J E. Response of a layered viscoelastic half-space to a moving point load[J]. Wave Motion, 1994, 19(2): 189-210. doi: 10.1016/0165-2125(94)90066-3
[11]	薛松涛, 谢丽宇. 有阻尼横观各向同性层状场地对入射SH波的响应分析[J]. 工程力学, 2001(@@@A02): 576-580. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU200110002119.htm XUE Song-tao, XIE Li-yu. Response analysis of damped transversely isotropic layered ground to incident SH wave[J]. Engineering Mechanics, 2001(@@@A02): 576-580. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU200110002119.htm
[12]	艾智勇, 胡亚东. 3D 横观各向同性地基非耦合解析层元[J]. 岩土工程学报, 2013, 35(增刊2): 717-720. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2131.htm AI Zhi-yong, HU Ya-dong. 3D transverse isotropic foundation uncoupled analytical layer element[J]. Journal of geotechnical engineering, 2013, 35(S2): 717-720. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2131.htm
[13]	韩泽军, 林皋, 周小文, 等. 横观各向同性层状地基上埋置刚性条带基础动力刚度矩阵求解[J]. 岩土工程学报, 2016, 38(6): 1117-1124. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201606019.htm HAN Ze-jun, LIN Gao, ZHOU Xiao-wen, et al. Solution of dynamic stiffness matrix of embedded rigid strip foundation on transversely isotropic layered foundation[J]. Journal of Geotechnical Engineering, 2016, 38(6): 1117-1124. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201606019.htm
[14]	ESKANDARI-GHADI M. A Complete solution of the wave equations for transversely isotropic media[J]. Journal of Elasticity, 2005, 81(1): 1-19. doi: 10.1007/s10659-005-9000-x
[15]	RAHIMIAN M, Eskandari-Ghadi M, PAK R Y, et al. Elastodynamic potential method for transversely isotropic solid[J]. J Eng Mech, 2007, 133(10): 1134-1145.
[16]	KHOJASTEH A, RAHIMIAN M, ESKANDARI M, et al. Asymmetric wave propagation in a transversely isotropic half-space in displacement potentials[J]. International Journal of Engineering Science, 2008, 46(7): 690-710. doi: 10.1016/j.ijengsci.2008.01.007
[17]	BA Zhen-ning, LIANG J, LEE V W, et al. 3D dynamic response of a multi-layered transversely isotropic half-space subjected to a moving point load along a horizontal straight line with constant speed[J]. International Journal of Solids and Structures, 2016, 100: 427-445.
[18]	ACHENBACH J D, KESHAVA S P, HERRMANN G. Moving load on a plate resting on an elastic half space[J]. Journal of Applied Mechanics, 1967, 34(4): 910-914. doi: 10.1115/1.3607855
[19]	房营光. 移动载荷作用下横观各向同性地基上无限板的动力响应[J]. 广东工学院学报, 1992(@@@2): 33-39. https://www.cnki.com.cn/Article/CJFDTOTAL-GDGX199202006.htm FANG Ying-guang. Dynamic response of infinite plate on transversely isotropic foundation under moving load[J]. Journal of Guangdong Institute of Technology, 1992(@@@2): 33-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDGX199202006.htm
[20]	王博, 张春丽, 祝彦知. 正交各向异性路基路面在移动荷载作用下的空间动力响应[J]. 郑州大学学报(工学版), 2019, 40(1): 54-58, 65. https://www.cnki.com.cn/Article/CJFDTOTAL-ZZGY201901009.htm WANG Bo, ZHANG Chun-li, ZHU Yan-zhi. Spatial dynamic response of orthotropic subgrade and pavement under moving load[J]. Journal of Zhengzhou University (Engineering Edition), 2019, 40(1): 54-58, 65. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZZGY201901009.htm
[21]	王春玲, 高典, 刘俊卿. 横观各向同性弹性半空间地基上四边自由各向异性矩形薄板弯曲解析解[J]. 力学季刊, 2015(@@@1): 99-108. https://www.cnki.com.cn/Article/CJFDTOTAL-SHLX201501011.htm WANG Chun-ling, GAO Dian, LIU Jun-qing. Analytical solution of bending of anisotropic rectangular thin plates on transversely isotropic elastic half space foundation[J]. Quarterly of Mechanics, 2015(@@@1): 99-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SHLX201501011.htm
[22]	MUHO E V. Dynamic response of an elastic plate on a transversely isotropic viscoelastic half-space with variable with depth moduli to a rectangular moving load[J]. Soil Dynamics and Earthquake Engineering. 2020, 139: 106330.
[23]	EUBANKS RA, STERNBERG E. On the axisymmetric problem of elasticity theory for a medium with transverse isotropy[J]. Journal of Rational Mechanics and Analysis, 1954, 3: 89-101.
[24]	Michel BOUCHON. Discrete wave number representation of elastic wave fields in three-space dimensions[J]. Journal of Geophysical Research, 1979, 84(B7): 3609-3614.
[25]	GAU Qiang, Z Wanxie, HOWSON W P. A precise method for solving wave propagation problems in layered anisotropic media[J]. Wave Motion, 2004, 40(3): 191-207.
[26]	卢正, 王长柏, 付建军, 等. 交通荷载作用下公路路基工作区深度研究[J]. 岩土力学, 2013, 34(2): 316-321. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201302004.htm LU Zheng, WANG Chang-bo, FU Jian-jun, et al. Research on influence depth of road subgrade induced by vehicle loads[J]. Rock and Soil Mechanics, 2013, 34(2): 316-321. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201302004.htm
[27]	杨广庆. 水泥改良土的动力特性试验研究[J]. 岩石力学与工程学报, 2003, 22(7): 1156-1156. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200307021.htm YANG Guang-qing. Study of dynamic performance of cement-improved soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(7): 1156-1156. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200307021.htm

施引文献(9)

期刊类型引用(2)

1.	马强，黄业禹，周凤玺，曹小林. 基于TRM法的移动荷载作用下层状非饱和土地基动力响应研究. 工程力学. 2025(02): 153-163 . 百度学术
2.	朱兆斌. 交通荷载下Kelvin地基上混凝土路面厚板动力响应研究. 粉煤灰综合利用. 2024(06): 124-130+142 . 百度学术