黏土片与球状颗粒间范德华作用的简便计算方法

申志福; 高峰; 蒋明镜; 王志华; 刘璐; 高洪梅

doi:10.11779/CJGE202104021

黏土片与球状颗粒间范德华作用的简便计算方法 English Version

1.
南京工业大学交通运输工程学院,江苏　南京　210000
2.
天津大学建筑工程学院土木工程系,天津　300350

基金项目:

国家自然科学基金青年基金项目 51908284

江苏省科技厅自然科学基金青年基金项目 BK20190667

江苏省高等学校自然科学研究面上项目 19KJB560015

国家自然科学基金重大项目 51890911

江苏高校“青蓝工程”资助项目

详细信息

作者简介:
申志福(1988—),男,四川绵阳人,工学博士,副教授,主要从事宏微观土力学方面研究。E-mail: zhifu.shen@njtech.edu.cn

通讯作者:
高洪梅, E-mail: hongmei54@163.com

中图分类号: TU431;TU47
计量
- 文章访问数: 395
- HTML全文浏览量: 22
- PDF下载量: 221
出版历程
- 收稿日期: 2020-04-12
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-03-31

An easy method to calculate van der Waals interaction between clay plate and spherical particle

1.
School of Transportation Engineering, Nanjing Tech University, Nanjing 210000, China
2.
Department of Civil Engineering, School of Civil Engineering, Tianjin University, Tianjin 300350, China

摘要

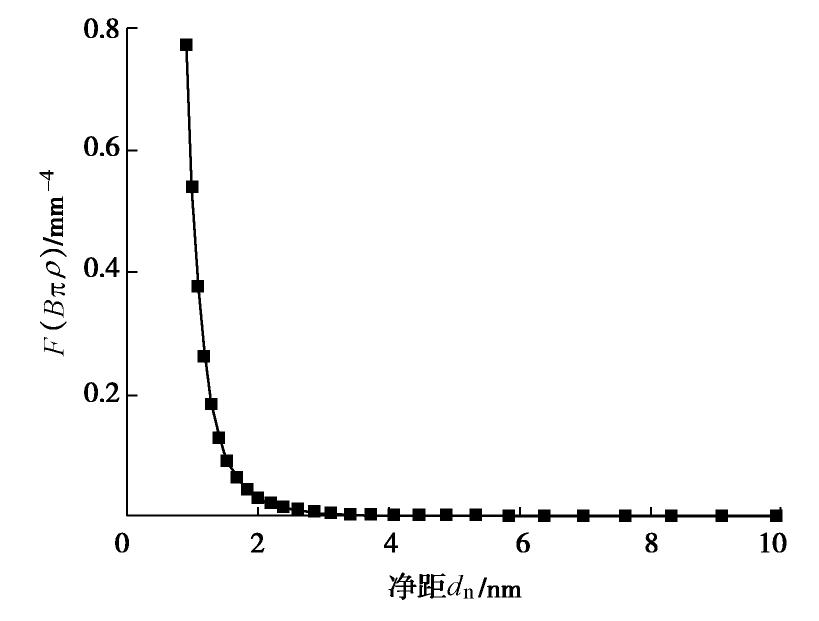
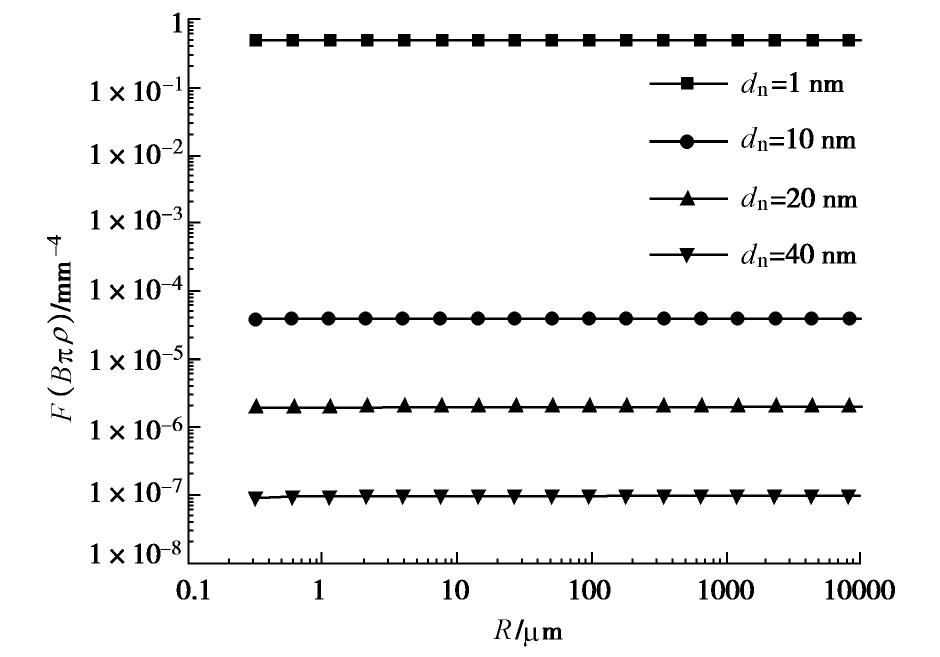
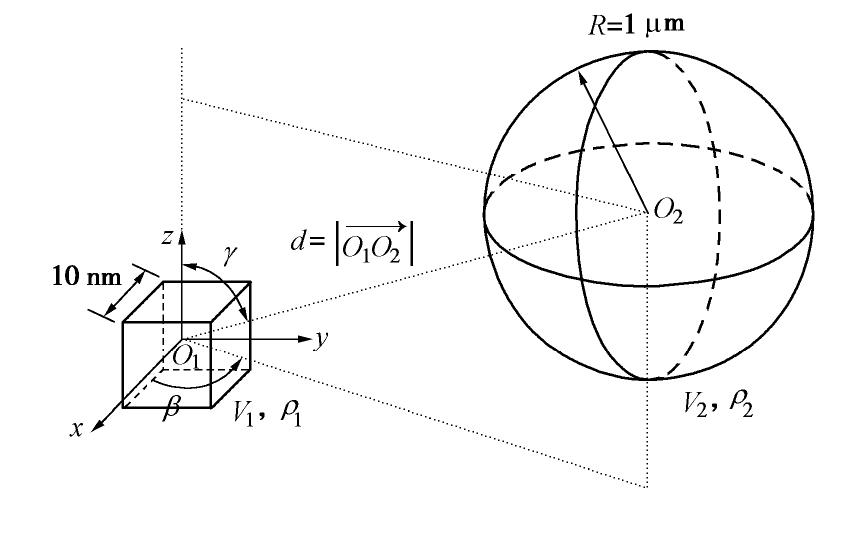
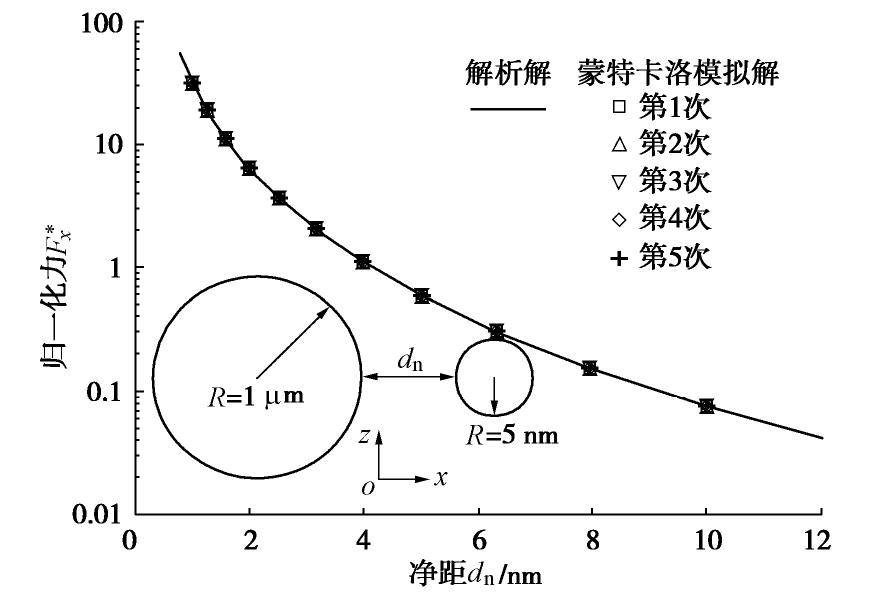
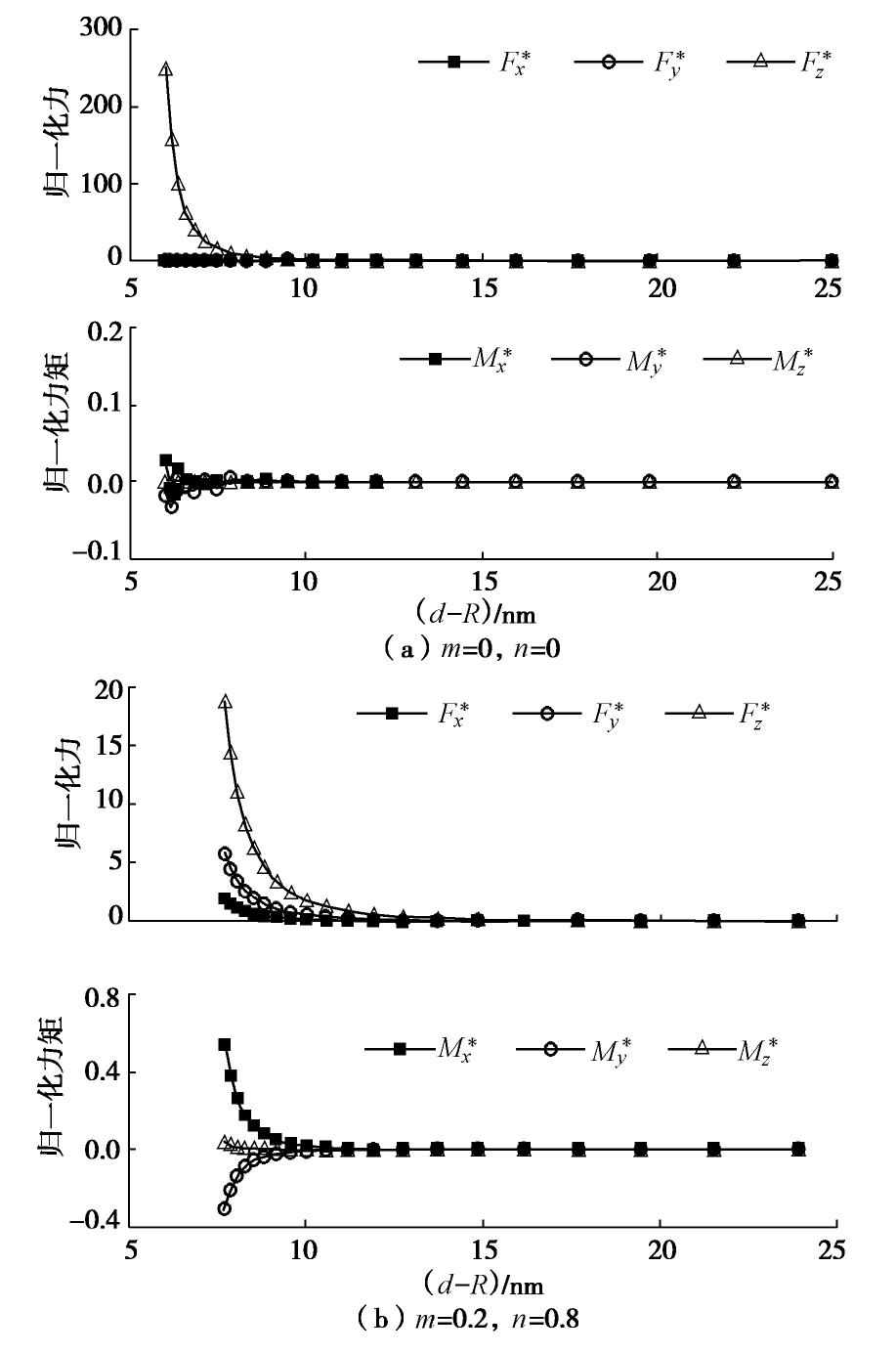
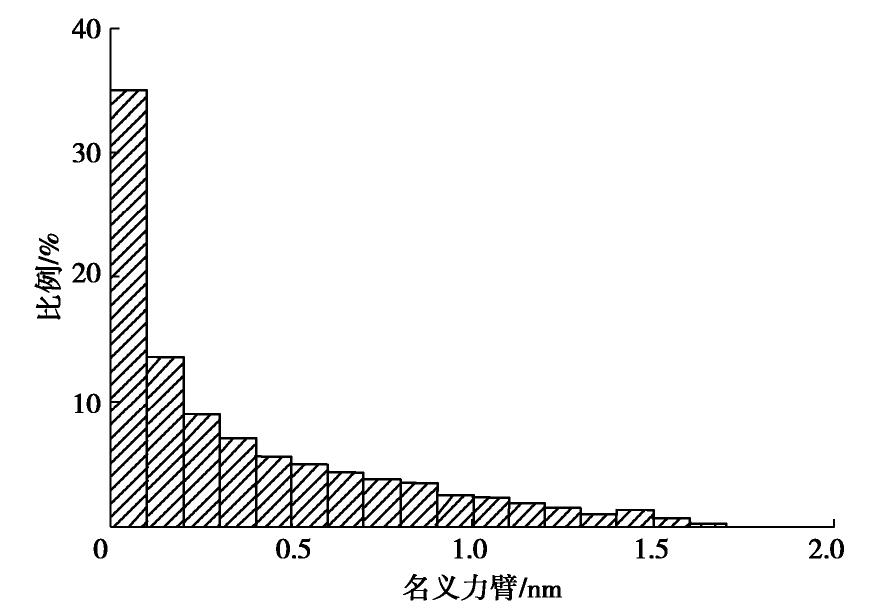
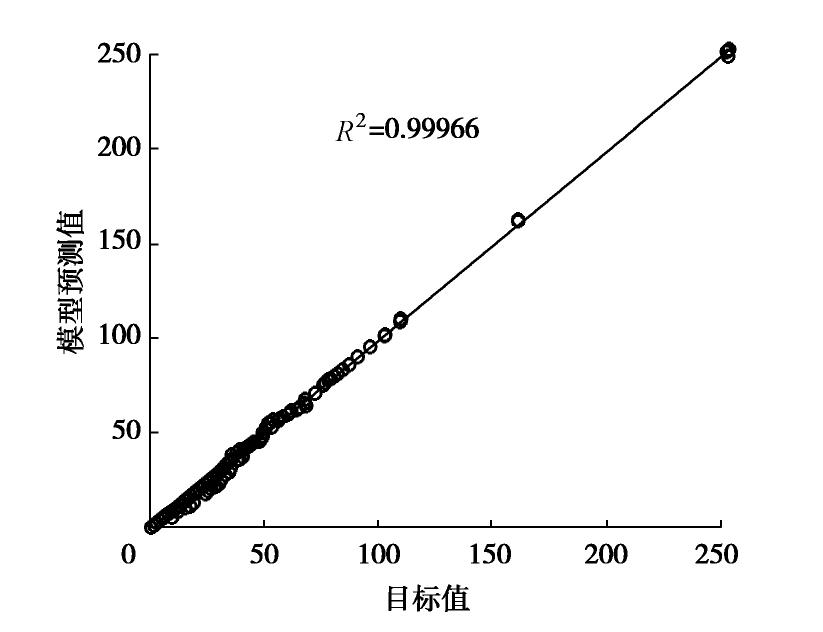
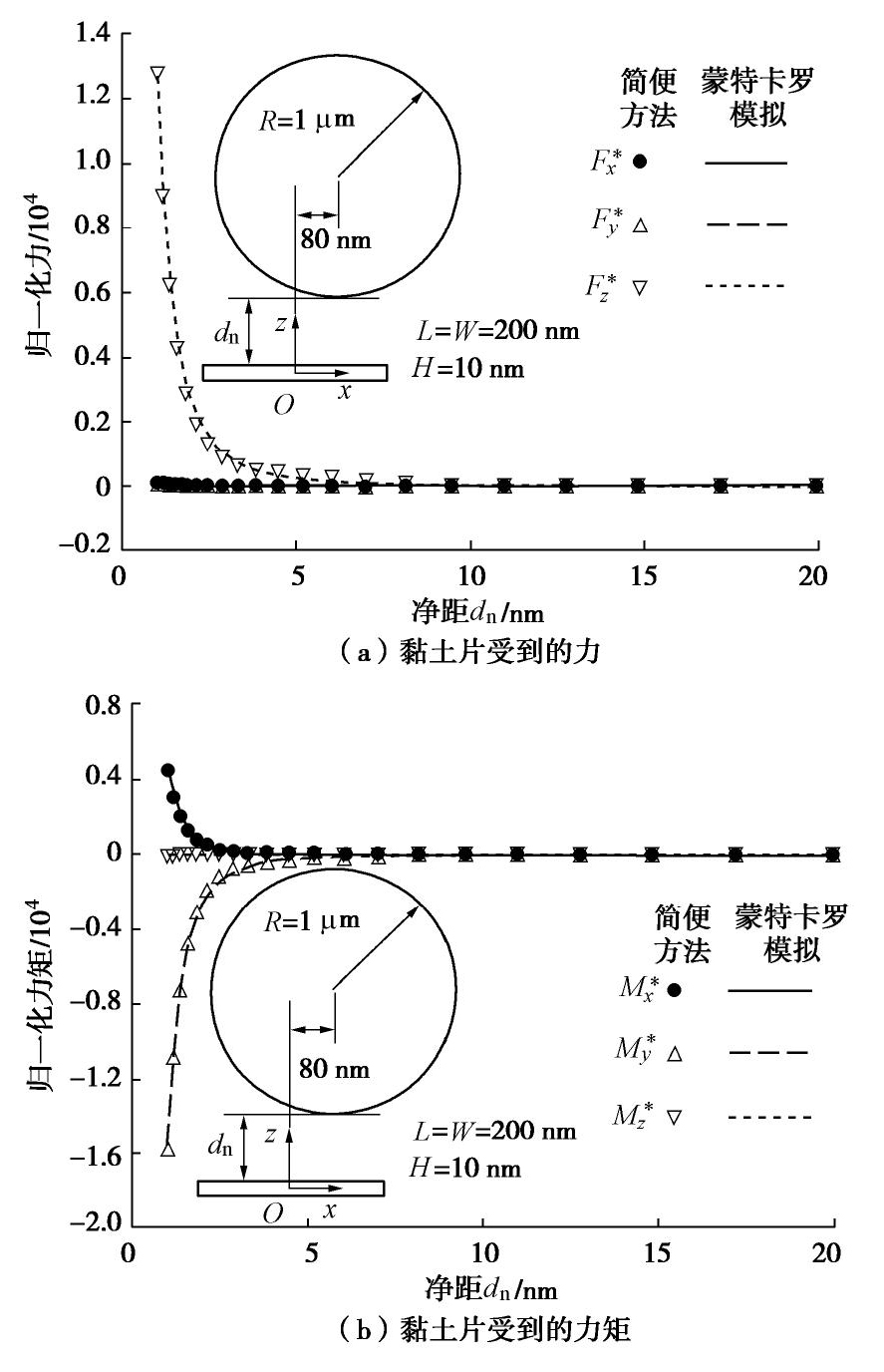
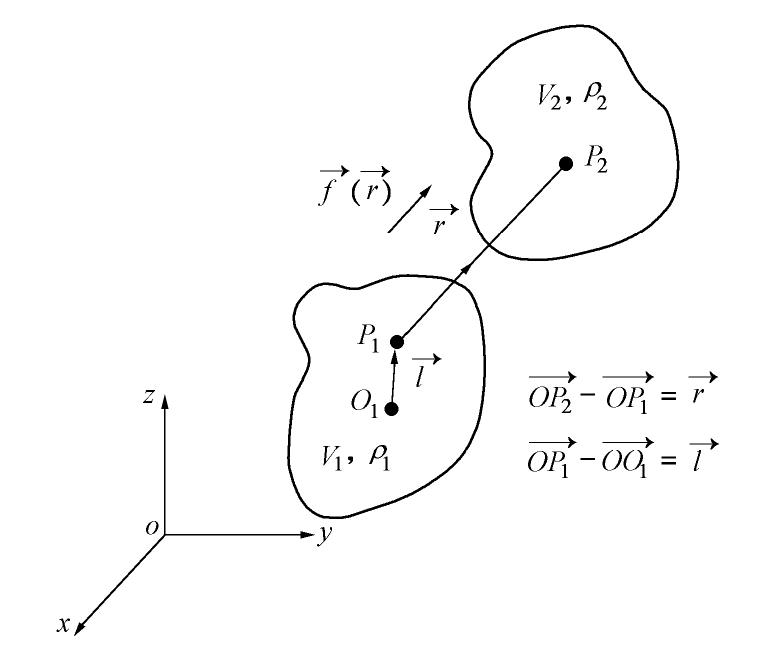
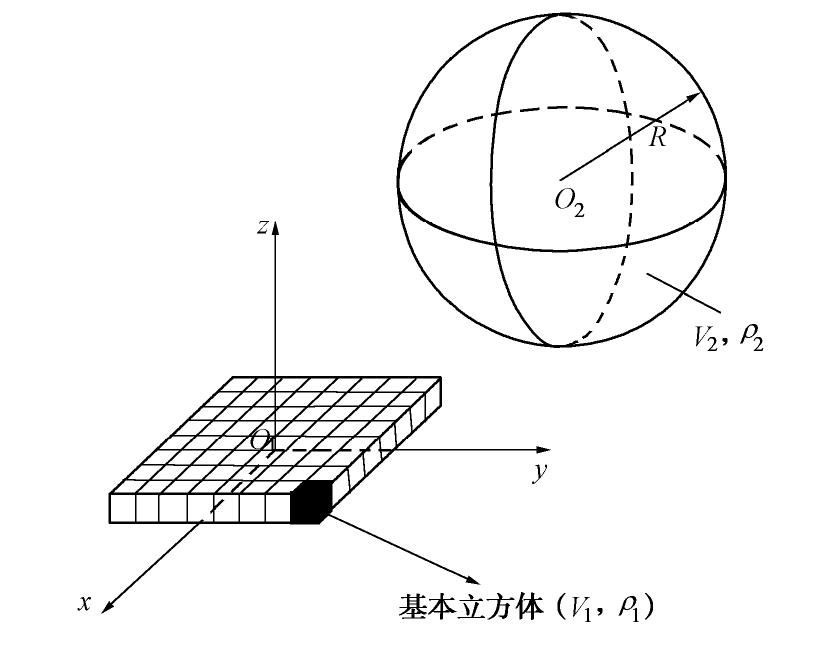
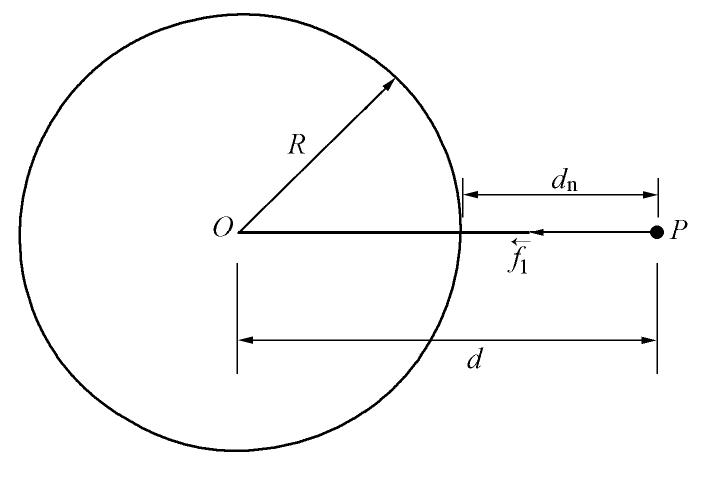
摘要: 黏粒（黏土片）与非塑性粉粒间相互作用是控制粉质黏土/黏质粉土这一大类土体力学特性的关键因素之一,范德华力是两种颗粒间最主要的相互作用形式,也是饱和土真黏聚力的来源。然而,在土体宏微观关联理论分析、离散元模拟等研究中尚难以得到该力的解析解。为此,提出一种简便计算方法,其基本思想是将粉粒视为球体,将黏土片视为由规则排列的基本立方体构成,将问题转变为可实现的基本立方体与球状颗粒间的范德华作用求解。首先采用蒙特卡罗模拟,计算得到不同空间排列方式下基本立方体与球状颗粒间范德华作用力；随后,训练一个三层人工神经网络模型用于高精度拟合范德华力与两种颗粒空间关系参数的函数关系；最后采用叠加法即可简便求得黏土片与球状颗粒间范德华作用的合力与合力矩。结果表明,提出的简便计算方法准确性高、计算速度快,且拟合的模型参数适用于黏土片与土体中大于1 $μm$ 的球状颗粒间范德华作用计算。
- 范德华力 /
- 黏土片 /
- 球状颗粒 /
- 蒙特卡罗模拟 /
- 人工神经网络
Abstract: The interaction between clay plate and non-plastic silty particle is one of the key factors determining the mechanical behavior of silty clay and clayey silt, which form a major category of soil in geotechnical engineering. The van der Waals force is the most important interaction between clay plate and non-plastic silty particle, which is also the origin of true cohesion in saturated clay. However, it is extremely difficult to obtain the analytical solution for this force to be applied in micro-macro cross-scale correlation and discrete element method simulation of soil. An easy method is proposed in this study for this purpose. The basic idea is to view the non-plastic silty particle as the spherical particle and to divide the cubic clay plate into basic cubes. Then, the problem is simplified to obtain the van der Waals interaction between the basic cube and the spherical particle, which can be solved in the following way. First, the Monte Carlo simulation is used to collect the data of van der Waals interaction of the basic cube and the sphere with a wide range of relative position. Then, an artificial neuro network was trained to fit the function between the van der Waals force and the relative position of the two objects with high accuracy. Finally, the total force and torque applied on the clay plate are summed up over all the basic cubes constituting the clay plate. It is found that the proposed easy method has strength in both accuracy and efficiency. The model-fitting parameters can be used to calculate the van der Waals interaction between the clay plate and the spherical particle with a diameter greater than 1 m.
- van der Waals force /
- clay plate /
- spherical particle /
- Monte Carlo simulation /
- artificial neuro network

HTML全文

0. 引言

正确认识和定量描述岩体性质是任何岩土工程安全、合理和高效施工的基础。室内岩石力学试验结果往往不能反映节理岩体的宏观特征和工程分类^[1],因此,现场地质钻探通常作为岩土工程的常规勘测手段^[2-3]。通过对钻孔和岩芯重新排列后,岩土工程人员观察结构面分布和判断填充物的性质^[4],在此基础上,经过大量繁琐编纂和地质描绘,形成描述岩体结构特征的图表^[5]。事实上,钻孔过程中钻具与岩体直接接触,钻具响应信息综合反映了岩体性质^[6]。因此,钻孔过程本身就是一种定量测定岩体性质的原位试验。

钻孔过程中蕴藏着大量地质信息,岩土工程界希望利用监测仪器记录钻孔过程的数据,用于分析岩体性质。最初,Teale^[7]、Hughes^[8]、Detournay等^[9]和Yagiz^[10]的研究重点是建立钻孔数据与完整岩石力学参数的关系。然而,岩体是由完整岩石和结构面共同组成,工程实践表明,大多数情况下岩体结构特征比完整岩石的性质对工程更重要^[11]。岩体完整性是地质力学分类中的主要评分项目,如Q系统^[12]、RMR^[13]和GSI^[14]。此后的研究^[15-17]尝试通过钻探资料获得岩体空间结构特征,特别是钻孔过程在围岩分类^[18-19]、地层界面辨识^[20-21]等方面的应用,对实际工程有较大的参考价值。一般认为,使用同一钻机和同一钻头钻取完整岩石时,钻进速度应为常数^{[6, 22-23]}。基于这一假设,岳中琦^[24]通过试验数据拟合建立了钻孔速度与岩石质量指标（RQD）之间的关系；Ru等^[25]基于最小二乘支持向量机和蒙特卡罗理论建立了钻速指数的概率评估方法。

然而,受钻进压力、钻进扭矩和钻头转速影响,钻进速度并不是常数。这一现象普遍反映在岩石可钻性评估中^[26-27]。将钻进速度作为评价岩体完整性特征的唯一标准显然是不可靠的。只有消除各种因素对钻进速度影响,才能建立合理的岩体完整性评价指标。

为滤除钻进压力、钻进扭矩和钻头转速对钻进速度的影响,本研究在完整和裂隙岩体中开展了各种因素下的现场数字钻探试验。然后,对钻孔速度修正和归一化,提出了一种新的描述岩体完整性的指标：钻进过程指数（DPI）。钻进过程指数在完整岩块中是一个常数,可以通过数字变化反映裂隙岩体的结构特征。

1. 数字钻进过程试验

1.1 试验设备

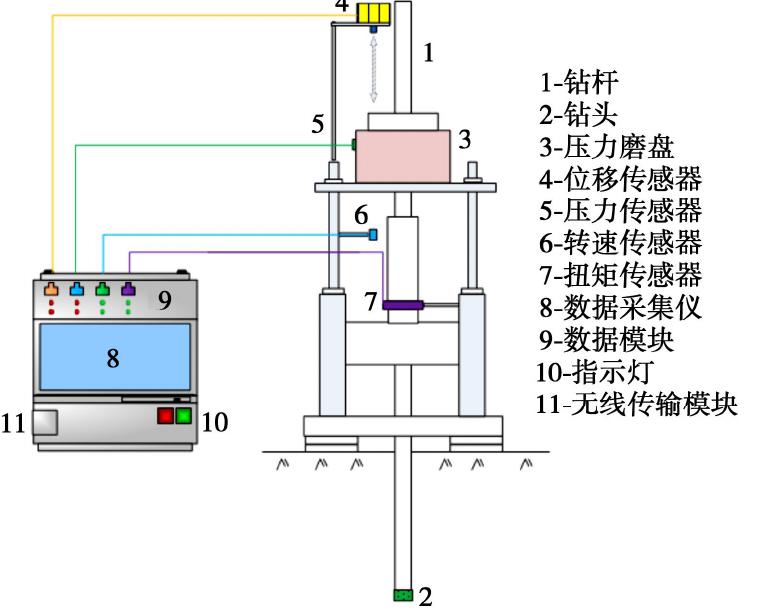
为了建立钻具响应参数和岩体完整性的关系,将一种新研发的地质钻机数字钻进监测系统（图1）运用于钻孔原位测试过程。如图2所示,这个系统由高精度数字传感器、自动采集仪以及数据分析软件组成。

图 1 地质钻机数字钻进监测系统的原理图

Figure 1. Schematic diagram of digital drilling monitoring system

下载: 全尺寸图片幻灯片

图 2 数字钻进监测系统及原位测试

Figure 2. Digital drilling system and in-situ tests

下载: 全尺寸图片幻灯片

液压传感器（图2（b））安装于钻机推进装置的输油管道,用于监测钻进压力（F,kN）。在钻机钻杆上设立特殊的标志点,转速传感器（图2（g））安装在距离标志点10～12 mm处,用于监测钻头转速（N,rev/s）,并通过非接触式空气耦合装置传输数据信号。盘式扭矩传感器（图2（f））安装于钻杆上,内部转子随钻杆转动时测量受力,由外部定子解译信号并传输到数据采集仪,用于监测钻进扭矩（M,N·m）。通过激光传感器（图2（e））监测钻进位移（S,mm）,激光传感器的标靶放置在随钻杆移动的钻机磨盘上,监测精度可达0.1 mm。F,N,M以及S会被同步和实时采集,数据采样时间间隔为1 s,并传输给数据自动采集仪（图2（c））和网络云端（图2（d））。

此外,钻进装置可根据工程对钻孔的实际需要进行调整。试验中采用了地质钻探用金刚石取芯钻头,其内直径为75 mm,钻头长250 mm,与岩土工程规定的获取RQD用钻头规格相一致^[28]。

1.2 均质材料钻进试验

为厘清影响钻进速度的关键因素,开展了一系列均质材料的钻进正交试验。首先,用直径200 mm取芯钻头钻孔；然后,在此钻孔中由深到浅回灌C20等级砂浆,并养护至标准强度,形成均质材料的钻孔；最后,采用数字钻进系统开展原位钻进测试。

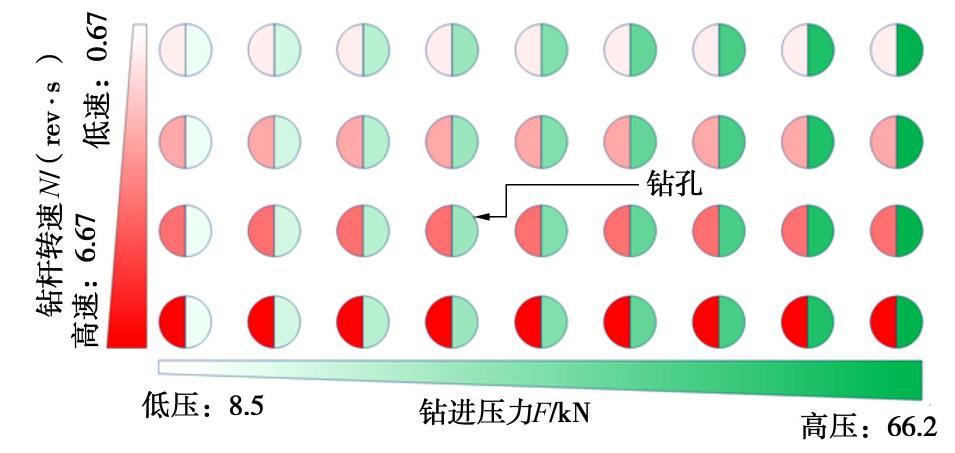
试验用地质钻机型具有4个可调节挡位,各个挡位对应的转速分别是0.67,1.92,3.67和6.67 rev/s,见图3。钻机钻进压力由油压泵控制,当油压为零时,钻具和夹持装置受重力作用使钻头产生最小压力值,约为8.5 kN,钻机钻进压力最大值可以达到80.0 kN。需要说明的是,在特定钻杆钻头转速下施加过大的钻进压力,会导致转速异常,即卡钻,所以试验中最终能够实现的钻进压力变化范围为8.5～66.2 kN（见图3）。钻头钻进扭矩作为一种破岩过程中的岩体所给予的反作用力,将受制于钻进压力和岩体特征参数。综上所述,在正常工作状态下的数字钻进时,地质钻机的主要特征参数（F,N和M）被全部监测和数据化。

图 3 均质材料钻进试验

Figure 3. Drilling tests on homogeneous materials

下载: 全尺寸图片幻灯片

1.3 裂隙岩体钻进试验

裂隙岩体现场试验依托云南省德厚水库,该工程库区广泛分布石灰岩,岩溶普遍发育。处理岩溶渗漏及防渗是工程建设的首要任务,受区域地质条件的限制,探明岩体裂隙的分布状况用于指导工程灌浆尤为重要。为能精细获取钻孔附近岩体结构特征分布,同步开展数字钻进原位试验（见图2）和传统钻孔取芯。

2. 影响钻进速度的关键因素分析

2.1 均质材料钻进试验结果

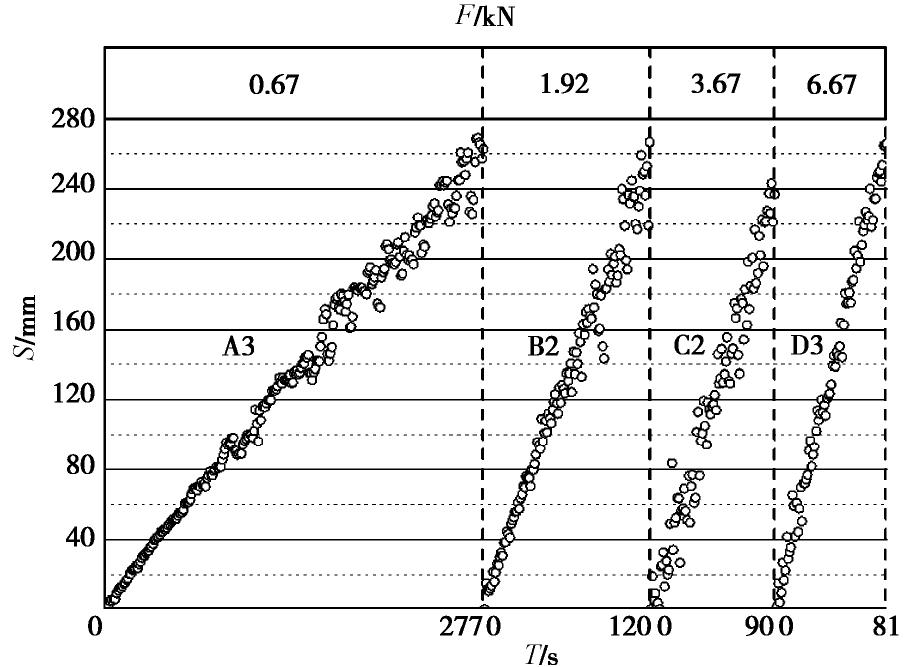
针对均质材料数字钻进试验,一共开展了37组测试,相应的的统计分析见表1。当钻头转速（N）分别为0.67,1.92,3.67和6.67 rev/s时,随着钻进压力（F）增加,试验方案编号依次为A1～A10、B1～B10、C1～C8和D1～D9。试验设计的F值是10～60 kN,增加梯度是10 kN,但由于实际的F还要取决于钻具和材料之间相互作用,所以它是波动值。钻进位移（S）主要在200～250 mm,随着钻进时间（T）减小,钻进速度（V）会逐渐增加,变化范围是0.71～5.46 mm/s。

表 1 均质材料钻进试验结果

Table 1. Drilling test results of homogeneous materials

编号	N/(rev·s^-1)	F/kN	M/(N·m^-1)	S/mm	T/s	V/(mm·s^-1)
A1	0.67	9.3	75.87	251.34	354	0.71
A2	0.67	11.5	92.59	252.75	337	0.75
A3	0.67	19.3	100.21	265.92	277	0.96
A4	0.67	28.8	119.40	260.91	223	1.17
A5	0.67	35.7	135.62	248.92	196	1.27
A6	0.67	41.3	153.17	239.94	186	1.29
A7	0.67	45.5	194.11	265.22	149	1.78
A8	0.67	51.6	184.27	258.44	142	1.82
A9	0.67	60.4	198.10	259.86	122	2.13
A10	0.67	66.2	224.30	170.04	78	2.18
B1	1.92	8.5	68.62	245.96	143	1.72
B2	1.92	19.3	96.66	266.40	120	2.22
B3	1.92	23.5	115.26	271.20	120	2.26
B4	1.92	29.3	119.63	226.54	94	2.41
B5	1.92	35.8	140.94	263.68	103	2.56
B6	1.92	42	165.21	252.01	79	3.19
B7	1.92	46.5	166.01	264.60	70	3.78
B8	1.92	53.1	186.22	252.72	72	3.51
B9	1.92	58.2	193.7	237.25	65	3.65
B10	1.92	60.5	211.73	199.92	68	2.94
C1	3.67	9.7	73.66	235.47	141	1.67
C2	3.67	18.3	99.04	236.71	90	2.63
C3	3.67	29.0	120.11	284.00	80	3.55
C4	3.67	34.9	138.58	241.68	57	4.24
C5	3.67	40.2	142.66	264.24	72	3.67
C6	3.67	46.7	172.63	246.62	59	4.18
C7	3.67	51.5	192.12	211.19	49	4.31
C8	3.67	57.5	200.30	178.02	43	4.14
D1	6.67	8.5	69.01	255.06	117	2.18
D2	6.67	11.5	79.32	263.61	101	2.61
D3	6.67	18.8	99.36	265.68	81	3.28
D4	6.67	25.1	110.88	236.28	66	3.58
D5	6.67	30.4	126.78	247.04	64	3.86
D6	6.67	35.5	143.69	240.30	54	4.45
D7	6.67	42.5	157.99	261.66	42	6.23
D8	6.67	48.8	175.45	231.65	41	5.65
D9	6.67	53.6	195.36	202.02	37	5.46

下载: 导出CSV

| 显示表格

2.2 钻进压力

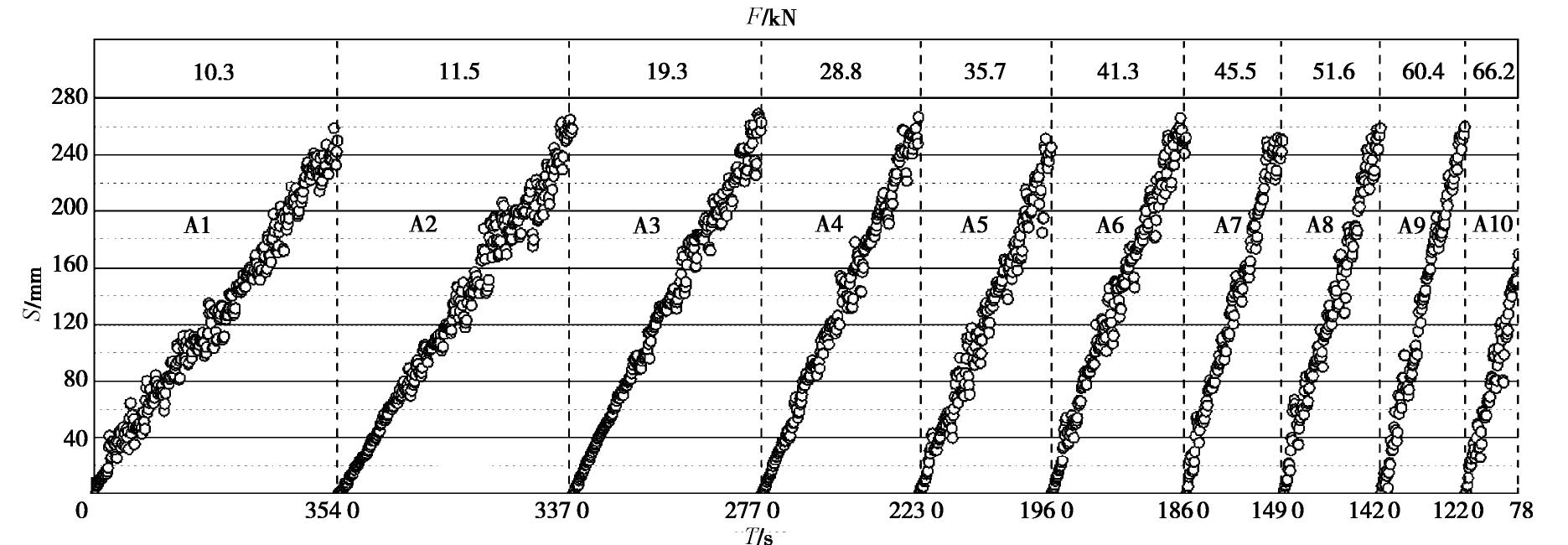
不同钻进压力时钻进位移和钻进时间的监测值见图4。S和T的散点值会聚集成直线,直线斜率为钻进速度（V,mm/s）。在相同钻进压力时,钻进速度基本为固定值,这与Yue等^[6,24]和Yarali等^[22]的研究结论一致。但是,随着钻进压力增加,直线斜率明显不同,这表明钻进速度会随着钻进压力增大而改变,并非为固定值。钻进位移约250 mm,当钻进压力位9.3 kN时,用时为354 s；当钻进压力位60.4 kN时,用时仅为122 s。这个钻进压力变化前后,钻进速度由0.71 mm/s增加至2.13 mm/s,增加了将近200 %。由此可见,钻进压力对钻进速度的影响是显著的。

图 4 各种钻进压力下钻进位移和钻进时间监测值

Figure 4. Monitoring values of drilling displacement and drilling time under various thrusts

下载: 全尺寸图片幻灯片

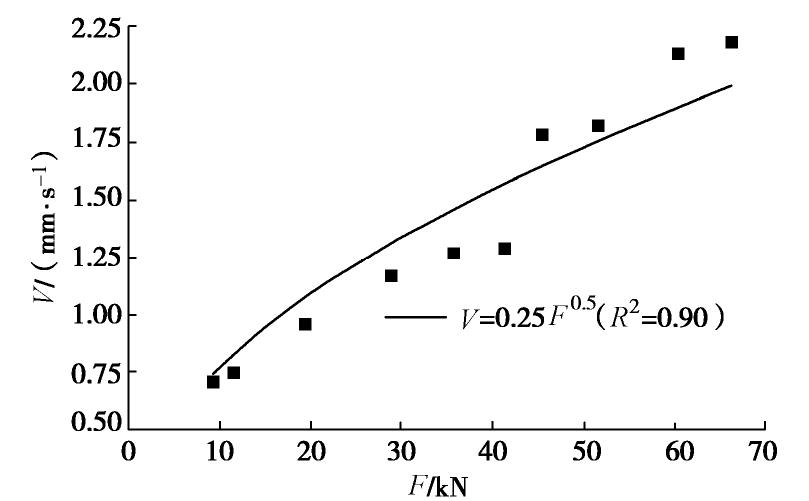
图4中的10种钻进压力和其对应钻进速度整理成图5的散点图。通过曲线拟合得到了钻进压力和钻进速度的关系,两者呈现良好的指数函数关系,相关指数（R²）达到了0.90,关系式如下所示：

图 5 钻进压力和钻进速度的函数关系

Figure 5. Relationship between thrust and drilling rate

下载: 全尺寸图片幻灯片

$V = 0.25 F^{0.5} (R^{2} = 0.90)$ 。

(1)

2.3 钻进扭矩

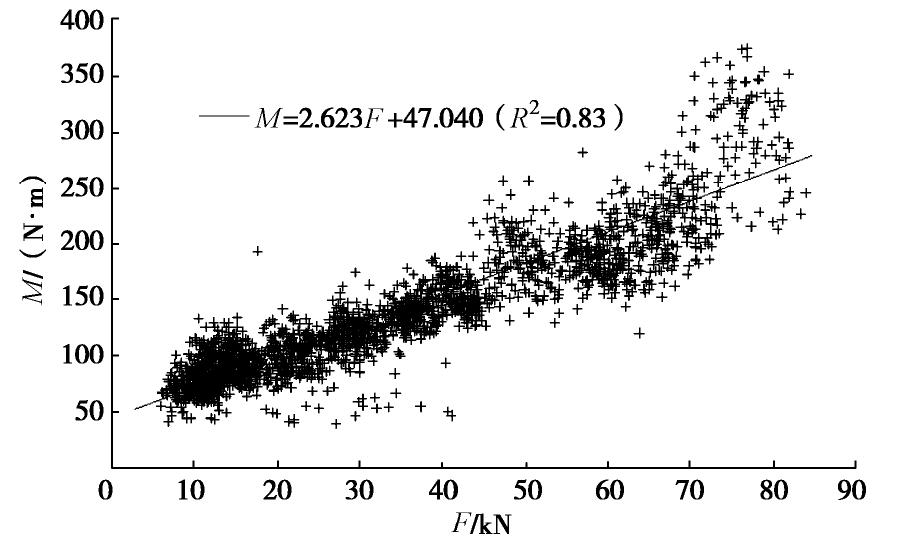
钻进扭矩（M）并非是钻机的直接输出参数,而是钻进过程中岩体对钻机的反作用效果。钻机在运行中实际钻进压力和钻进扭矩都是持续波动的,从图6可以看出,M和F呈现出典型的正相关,二者关系可表达为

图 6 钻进扭矩与钻进压力的相关性

Figure 6. Correlation between rotational torque and thrust

下载: 全尺寸图片幻灯片

$M = 2.623 F + 47.040 (R^{2} = 0.83)$ 。

(2)

尤其在F<70 kN时,M和F的相关性会更好,实际钻进过程中,钻进压力普遍小于70 kN,这种现象对解释钻进压力和钻进扭矩关系是有利的。对于一般地质钻机采用钻进压力表达钻进扭矩是可靠的,可以将两种因素合并为一个独立因素考虑。同时,数字钻进时监测钻进压力是非常容易实现的,而采用扭矩传感器监测钻进扭矩异常困难（见图2）。所以,采用钻进压力表达钻进扭矩,将降低了数字钻机技术的硬件应用难度,有利于这种新技术在工程中的广泛应用。

2.4 钻头转速

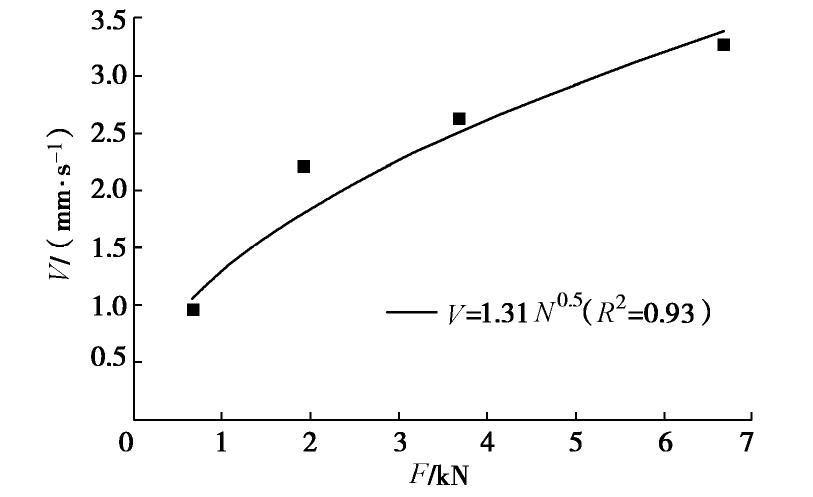
在钻进压力接近20 kN时,不同钻头转速下钻进位移（S）和钻进时间（T）的监测值见图7。钻头转速由0.67 rev/s增加至6.67 rev/s,钻进速度由0.96 mm/s增加至3.28 mm/s,增加了3.42倍。钻头转速N和钻进速度V之间同样存在很好的指数函数关系（图8）,表达为

图 7 各种钻头转速下钻头位移和钻进时间监测值

Figure 7. Monitoring values of bit displacement and drilling time at various bit rotational speeds

下载: 全尺寸图片幻灯片

图 8 钻头转速和钻进速度的函数关系

Figure 8. Functional relationship between rotational speed and drilling rate

下载: 全尺寸图片幻灯片

$V = 1 .31 N^{0.5} (R^{2} = 0.9 3)$ 。

(3)

2.5 多重因素组合

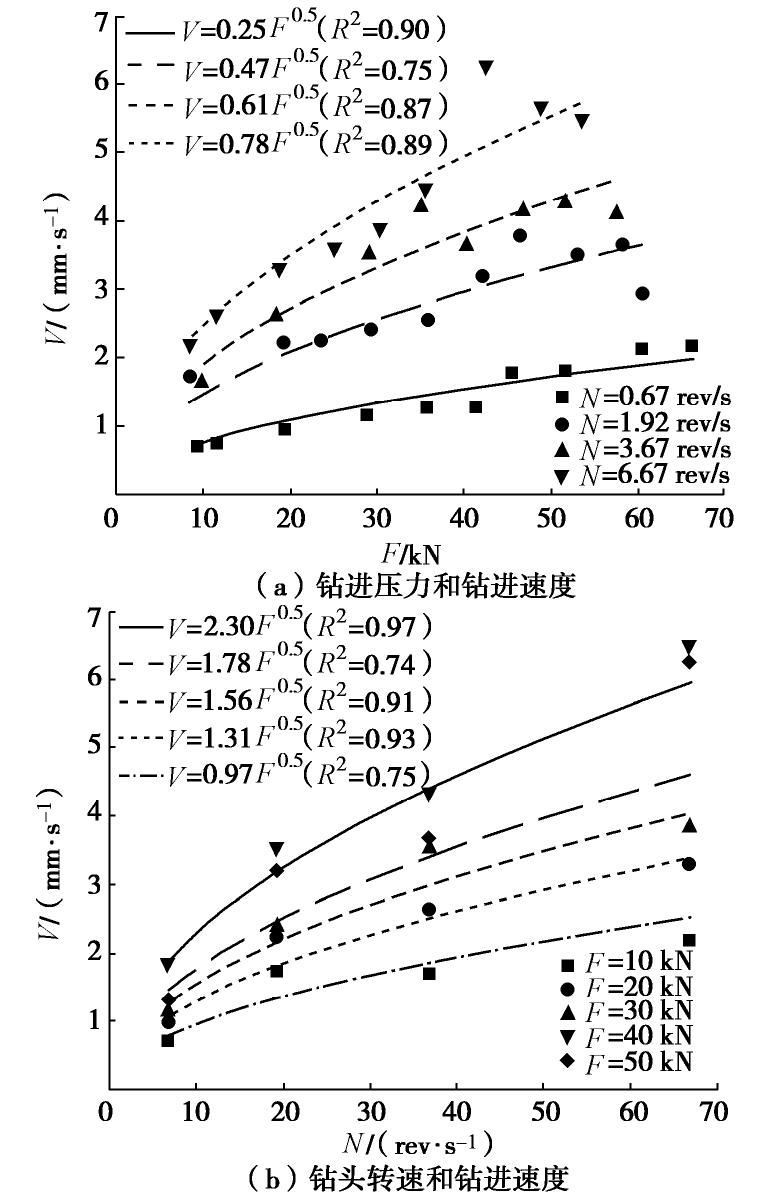
将正交试验的所有结果进行统计分析,得到了图9所示的钻进速度变化曲线。需要指出,在数据统计分析中,考虑到式（2）的转换关系,将钻进扭矩的作用融入钻进压力加以考虑。从图9中可以看出,各个线条形成辐射状的曲线簇,钻进速度与钻进压力和钻头转速呈现较好的指数函数关系,相关系数（R²）均在0.74以上,最高达0.97。

图 9 钻进速度的变化规律

Figure 9. Variation patterns of drilling rate

下载: 全尺寸图片幻灯片

3. 钻进过程指数

3.1 均质材料钻进过程指数

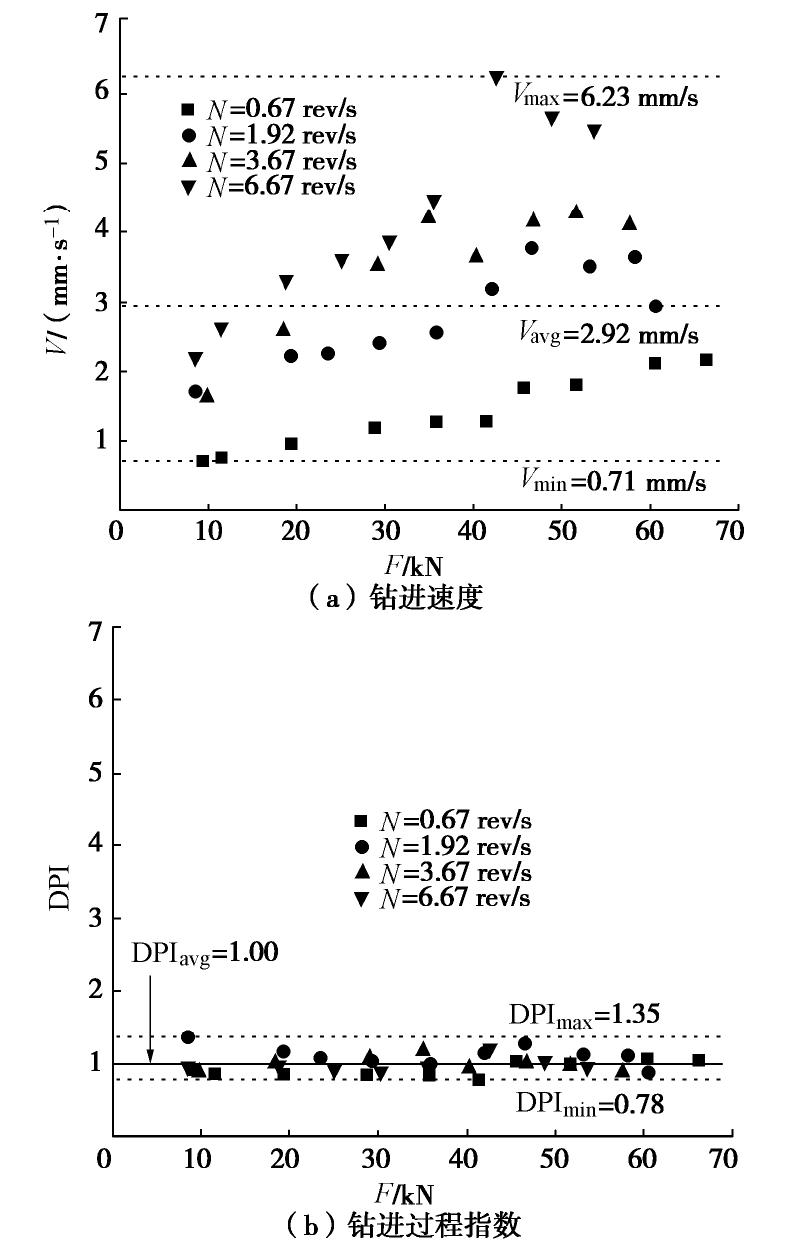
如图10（a）所示,在钻进压力和钻头转速发生变化时,钻进速度的离散性非常大,最小钻进速度（V_min）为0.71 mm/s,而最大钻进速度（V_max）达到了6.23 mm/s。所以,试验数据表明,即使在均质材料中机械参数对钻进速度的影响是显著的,仅采用钻进速度作为评价岩体参数的唯一标准是不合理的。为此,在钻进速度指标的基础上,滤除F,N和M对V的影响,提出了钻进速度的归一化参数：钻进过程指数（drilling process index,DPI）。这个新指标在均质材料中应具有唯一性,基于图9的曲线规律,采用多元函数回归,将DPI定义为

图 10 钻进速度的变化规律

Figure 10. Discreteness of drilling rate and DPI

下载: 全尺寸图片幻灯片

$DPI = α \cdot V \cdot F^{-0 .5} \cdot N^{-0 .5}$ ,

(4)

式中, $α$ 为常量,是一个与岩石强度有关的参数,根据表1和图9的试验数据,本试验中 $α$ =3.19。

钻进过程指数变化规律见图10（b）,无论钻进压力和钻头转速怎么变化,DPI均处于0.78和1.35之间,在均质材料中它是非常稳定的数值,平均值（DPI_avg）为1。因此,利用钻进过程指数表达岩体完整性明显比传统的钻进速度更为合理。

3.2 裂隙岩体钻进过程指数

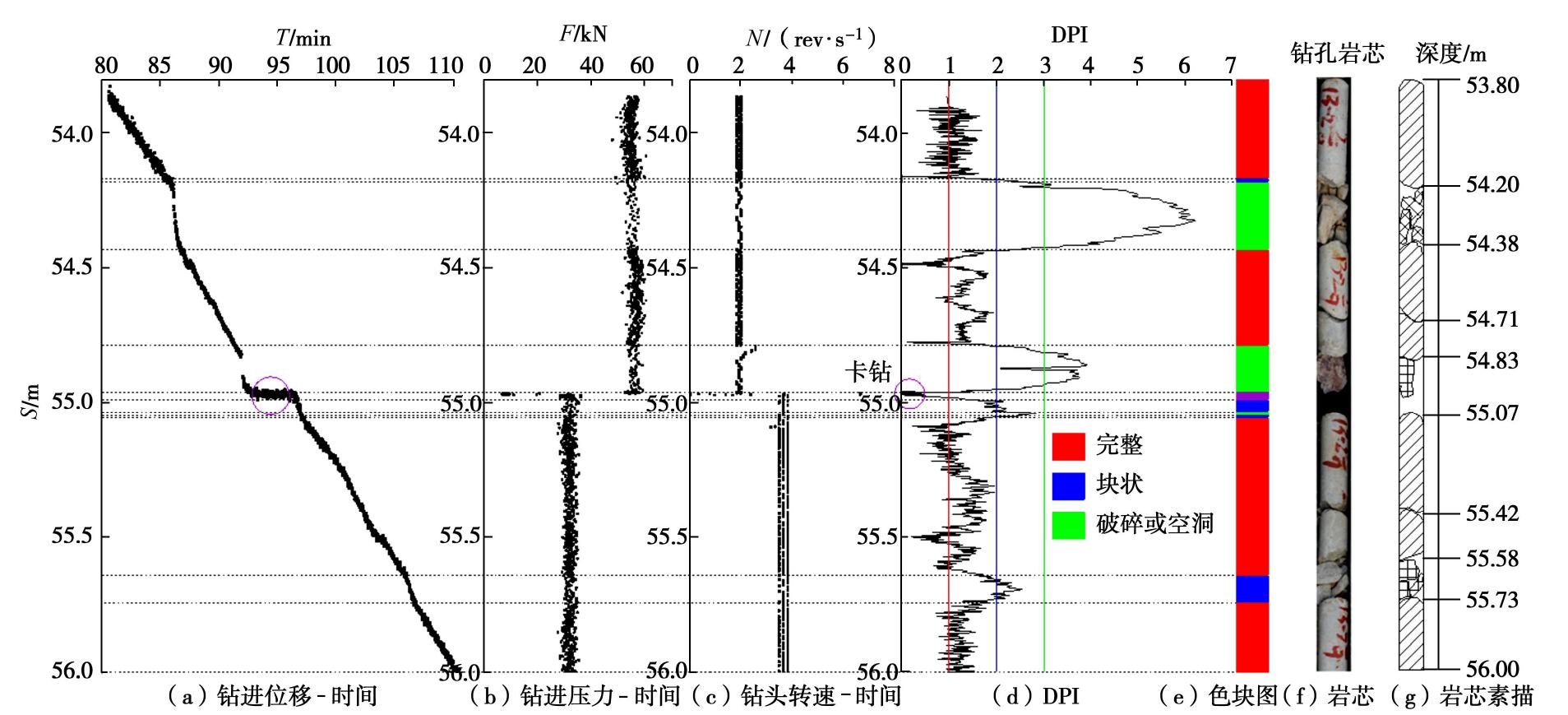
为了获取裂隙岩体的DPI分布特征,在德厚水库开展了工程岩体的数字钻进试验,同时钻孔取芯观测以实现对比验证。图11（a）描绘了库区的覆盖范围和大坝的位置,探测区域主要分布石灰岩,岩溶特别发育,岩体存在破碎层和空洞（见图11（b））,获取的岩芯按照深度排列（见图11（c））。

图 11 现场试验场地资料

Figure 11. Basic information of in-situ tests

下载: 全尺寸图片幻灯片

在裂隙岩体中数字钻进位移–时间曲线是波动的（见图12（a））,对应钻进压力和钻头转速见图12（b）和图12（c）,进一步数据处理得到裂隙岩体的DPI（见图12（d））。均质岩体中的DPI的理想值为1,而在裂隙岩体中的DPI是一个变量,主要特征可归纳如下：

图 12 裂隙岩体的DPI和完整性

Figure 12. DPI and integrity of fractured rock mass

下载: 全尺寸图片幻灯片

（1）当岩体完整时,DPI的变化范围是0～2,平均DPI接近1,例如钻进深度为53.8～54.2 m、54.4～54.8 m、55.1～55.6 m以及55.7～56.0 m,在图12（e）中用红色区域填充。

（2）当岩体为块状或小裂隙时,DPI会增大,处于2～3之间,分布在钻进深度54.2,55.1和55.6 m处,在图12（e）中用蓝色区域填充。

（3）岩体非常破碎或出现空洞时,钻进深度54.2～54.4 m和54.8～55.0 m,DPI会超过3,在图12（e）中用绿色区域填充。DPI峰值甚至可以达到6以上,此时DPI的具体数值意义不大,可以统一认为是岩体不完整。

（4）在深度54.9 m处,DPI值突变为0,主因是钻进速度瞬间降低至零,出现了卡钻现象。

按照表2中DPI和岩体完整性的关系,绘制了图12（e）的岩体完整性的色彩柱状图,和传统的岩芯柱状图（图12（f））及素描图（图12（g））相比,它能定量的表述钻孔内岩体完整性,具有重要应用价值。

表 2 DPI和岩体完整性的关系

Table 2. Relationship between DPI and rock mass integrity

岩体完整性	完整	块体状	破碎或空洞
DPI	0<DPI≤2	2<DPI≤3	3<DPI

下载: 导出CSV

| 显示表格

3.3 钻进过程指数的本质

以往研究常采用钻进速度描述岩体参数,本项试验结果（表1和图9）证实钻进速度会受到钻进压力F和钻头转速N的影响。因此,必须根据不同钻进状态下的变化规律,再消除各种因素的影响,才能解译真实的数字钻进指标和岩体参数之间的映射关系。

由图9可以看出,均质材料中“钻进速度V和钻进压力F”以及“钻进速度V和钻头转速N”均呈现良好的指数关系（V与F^0.5和N^0.5）。因此,可将钻进速度V与钻进压力F和钻头转速N的负指数（ $F_{}^{- 0 .5}$ 和N^-0.5）相乘,来消除F和N对V的影响。也就是说钻进过程中的真实常量并非钻进速度^{[6, 22-23]},而是V·F^0.5·N^0.5。为使数字钻进数据（V·F^0.5·N^0.5）能表达裂隙岩体的完整性,定义了钻进过程指数（DPI）。在完整岩石中,平均钻进过程指数（DPI_avg）固定为1,满足下式：

${DPI}_{avg} = \frac{\sum_{i}^{n} V \cdot F^{- 0 .5} \cdot N^{- 0 .5}}{n \cdot V_{avg} \cdot F_{avg}^{- 0 .5} \cdot N_{avg}^{- 0 .5}} = 1$ ,

(5)

式中,V_avg,F_avg和N_avg分别为完整岩石的钻进速度、钻进压力和钻头转速的平均值。

对于一段完整岩体,根据式（5）,可以得出式（4）中拟合参数 $α$ 为

$α = \frac{1}{V_{avg} \cdot F_{avg}^{- 0 .5} \cdot N_{avg}^{- 0 .5}}$ 。

(6)

若F和N不发生变化,在软质岩钻进中,V_avg相对较大,对应 $α$ 值相对较小,那么在硬质岩中 $α$ 值相对较大,所以 $α$ 是一个与岩体强度参数有关的参数。另外,需要指出,在完整岩石中, $α$ 可直接按式（6）计算取值,在裂隙岩体中, $α$ 应在完整岩体段取值。例如,在图12（d）中, $α$ 可采用53.8～54.2 m、54.4～54.8 m、55.1～55.6 m或55.7～56.0 m段对应的V_avg· $F_{avg}^{- 0 .5}$ · $N_{avg}^{- 0 .5}$ 的倒数。

对于裂隙岩体,完整段岩体DPI均值仍接近1；破碎段岩体材料均一性发生变化,本质是在 $α$ ,F和N不变时V会增大,也即常量V·F^0.5·N^0.5的增加,表现为DPI升高。

3.4 DPI和RQD的关系

岩土工程中常用RQD表达岩体的完整性,并广泛应用到岩体质量评价和岩体分类^[13]。根据RQD实际意义和DPI的特点,RQD和DPI的关系可定义为

$\begin{array}{l} RQD = \frac{\sum L_{i} (0 ＜ DPI \leq 2)}{L} \times 100 %, \\ L_{i} (0 ＜ DPI \leq 2) \geq 10 cm, \end{array}}$

(7)

式中, $L_{i} (0 ＜ DPI \leq 2)$ 指DPI处于0～2之间时对应的岩芯长度。

对于图12的裂隙岩体,根据式（7）得到的RQD值为74,采用图12（f）的岩芯传统量测方法得到的RQD为72,二者是非常吻合。数字钻进过程指数为获取RQD提供了一种简易的、定量的新方法。通过自动化和信息化的数据运算得到DPI以获取岩体完整性,减少了人工统计RQD和编纂岩芯柱状素描图等繁杂的工序,还降低了人为主观因素在评价岩体完整性中的不利影响。

4. 结论

通过开展均质材料和裂隙岩体中的数字钻进试验,重点探讨了钻进压力、钻头转速和钻进扭矩等机械参数对钻进速度的影响,并提出了一种用于定量评价岩体完整性的新指标。研究结果表明：

（1）钻进压力和钻进扭矩具有良好的线性相关性,两个因素可简化为单因素：钻进压力。数字钻进过程中钻进速度是变量,与钻进压力和钻头转速呈现较好的指数函数关系。

（2）通过对钻进速度进行归一化处理,滤除了钻机机械参数对钻进速度的影响,得到了用于表达岩体完整性的新指标：DPI。完整岩体DPI为0～2、块状岩体DPI为2～3,非常破碎与空洞岩体DPI大于3。

（3）DPI和RQD具有很好的相关性,通过这种数字技术获取DPI评价岩体完整性,减少了人工繁琐地质编纂工作和人为主观因素。

图 1 宏观体之间的范德华相互作用

Figure 1. Van der Waals interaction between macroscopic bodies

下载: 全尺寸图片幻灯片

图 2 黏土片与球体间相对几何关系

Figure 2. Geometric relationship between clay plate and sphere

下载: 全尺寸图片幻灯片

图 3 点与球体间范德华力

Figure 3. Van der Waals force between point and sphere

下载: 全尺寸图片幻灯片

图 4 点与球体间范德华力与净距的关系

Figure 4. Relationship between van der Waals force and net distance between point and sphere

下载: 全尺寸图片幻灯片

图 5 球体半径对点与球体间范德华力的影响

Figure 5. Effects of sphere radius on van der Waals force between point and sphere

下载: 全尺寸图片幻灯片

图 6 基本立方体与球体间几何关系示意图

Figure 6. Geometric relationship between basic cube and sphere

下载: 全尺寸图片幻灯片

图 7 蒙特卡罗模拟与解析解对比

Figure 7. Comparison between Monte Carlo simulation and analytical solution

下载: 全尺寸图片幻灯片

图 8 基本立方体与球体间范德华作用计算结果

Figure 8. Van der Waals interactions between basic cube and sphere

下载: 全尺寸图片幻灯片

图 9 名义力臂分布直方图

Figure 9. Histogram of nominal force arm

下载: 全尺寸图片幻灯片

图 10 神经网络预测值精度验证

Figure 10. Accuracy verification of neural network fitting

下载: 全尺寸图片幻灯片

图 11 黏土片受到球体的范德华作用

Figure 11. Van der Waals action of sphere on clay plate

下载: 全尺寸图片幻灯片

图 12 黏土片尺寸对其所受范德华力的影响

Figure 12. Effects of clay plate size on van der Waals force

下载: 全尺寸图片幻灯片

参考文献(11)

[1]	陈芳, 周洋, 苏新, 等. 南海神狐海域含水合物层粒度变化及与水合物饱和度的关系[J]. 海洋地质与第四纪地质, 2011, 31(5): 95-100. https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ201105017.htm CHEN Fang, ZHOU Yang, SU Xin, et al. Gas hydrate saturation and its relation with grain size of the hydrate-bearing sediments in the Shenhu area of Northern South China Sea[J]. Marine Geology & Quaternary Geology, 2011, 31(5): 95-100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ201105017.htm
[2]	蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG M J. New paradigm for modern soil mechanics: geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 104-116. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[3]	JIANG M J, SHEN Z F, THORNTON C. Microscopic contact model of lunar regolith for high efficiency discrete element analyses[J]. Computers and Geotechnics, 2013, 54: 104-116. doi: 10.1016/j.compgeo.2013.07.006
[4]	YAO M, ANANDARAJAH A. Three-Dimensional discrete element method of analysis of clays[J]. Journal of Engineering Mechanics, 2003, 129(6): 585-596. doi: 10.1061/(ASCE)0733-9399(2003)129:6(585)
[5]	LONDON F. On the theory and systematics of molecular forces[J]. Journal of Physics, 1930, 63(3/4): 245-279. (in German)
[6]	CASIMIR H B G, POLDER D. The influence of retardation on the London-van der Waals forces[J]. Physical Review, 1948, 73(4): 360-372. doi: 10.1103/PhysRev.73.360
[7]	LIFSHITZ E M. The theory of molecular attractive forces between solids[J]. Soviet Physics, 1956, 2(1): 73-83.
[8]	ANANDARAJAH A, CHEN J. Single correction function for computing retarded van der Waals attraction[J]. Journal of Colloid and Interface Science, 1995, 176(2): 293-300. doi: 10.1006/jcis.1995.9964
[9]	HAMAKER H C. The London-van der Waals attraction between spherical particles[J]. Physica, 1937, 4(10): 1058-1072. doi: 10.1016/S0031-8914(37)80203-7
[10]	De BOER J H. The influence of van der Waals' forces and primary bonds on binding energy, strength and orientation, with special reference to some artificial resins[J]. Transactions of the Faraday Society, 1936, 32: 10-37. doi: 10.1039/tf9363200010
[11]	ANANDARAJAH A, CHEN J. Van der Waals attractive force between clay particles in water and contaminants[J]. Soils and Foundations, 1997, 37(2): 27-37. doi: 10.3208/sandf.37.2_27

施引文献(31)

期刊类型引用(21)

1.	张琨，王珂，任建喜，冯上鑫，常鹏博，赵玉桃，苗彦平，胡俭. 随钻钻进参数优化下煤体原位应力响应特征解析. 煤田地质与勘探. 2025(02): 213-222 . 百度学术
2.	赵同彬，赵志刚，齐炎山，尹延春，牛旭，李淇凡. 基于大直径钻孔钻进多参量的煤体应力钻测方法. 煤炭科学技术. 2025(01): 122-132 . 百度学术
3.	李杨，王雁冰，岳小磊，岳中文，李为. 冲旋作用下随钻测量系统研发与应用. 采矿与安全工程学报. 2024(01): 114-122 . 百度学术
4.	许振浩，邵瑞琦，林鹏，李术才，向航，韩涛，李珊. 隧道不良地质识别:方法、现状及智能化发展方向. 地球学报. 2024(01): 5-24 . 百度学术
5.	查浩，魏玉峰，李树武，李常虎，赵天丞. 考虑轴向裂隙影响的岩体完整性计算模型. 岩石力学与工程学报. 2024(S2): 3972-3980 . 百度学术
6.	肖浩汉，曹瑞琅，王玉杰，赵宇飞，孙彦鹏. 随钻监测数据预处理方法研究. 水利学报. 2024(11): 1379-1390 . 百度学术
7.	王琦，高红科，冯帆. 岩体力学参数旋切钻进测试方法研究进展. 绿色矿山. 2024(04): 333-343 . 百度学术
8.	徐海寒，秦昊，张辉，陈晓. 机器学习算法在岩性识别上的应用对比研究. 防护工程. 2024(06): 54-61 . 百度学术
9.	岳中文，戴诗清，李杨，岳小磊，李世辉，曹武. 煤巷液压锚杆钻机随钻参数采集系统及其应用. 矿业科学学报. 2023(01): 66-73 . 百度学术
10.	汪小刚. 岩体工程力学参数取值方法研究Ⅰ:原位试验与定量类比. 水利学报. 2023(01): 13-23 . 百度学术
11.	贾连辉，陈帅，贾正文，荆留杰，陈强，牛孔肖. 钻爆法隧道智能建造体系及关键技术研究. 隧道建设(中英文). 2023(03): 392-407 . 百度学术
12.	李明超，李明泽，韩帅，张佳文，赵文超. 耦合多源勘察信息的水工岩体完整性智能评价方法. 岩土工程学报. 2023(08): 1674-1683 . 本站查看
13.	刘华吉，孙红林，张占荣，尤明龙，谭飞，李炜. 基于随钻参数的砂岩与砂质泥岩地层分界面智能识别. 隧道建设(中英文). 2023(S1): 304-312 . 百度学术
14.	曹瑞琅，王玉杰，邢泊，赵宇飞，沈强. 基于冲击耗能指数定量评价岩石硬度试验研究. 岩土力学. 2023(09): 2619-2627 . 百度学术
15.	许振浩，王朝阳，张津源，于东晓，林鹏，张啸，潘东东，李天昊. TBM隧道掘进地质感知与岩-机数字孪生：方法、现状与数智化发展方向. 应用基础与工程科学学报. 2023(06): 1361-1381 . 百度学术
16.	冯上鑫，王善勇. 旋切作用下岩石破碎机理及岩石可钻性的试验研究. 煤炭学报. 2022(03): 1395-1404 . 百度学术
17.	岳中文，岳小磊，杨仁树，王煦，李为，戴诗清，李杨. 随钻岩性识别技术研究进展. 矿业科学学报. 2022(04): 389-402 . 百度学术
18.	杨启贵，张传健，颜天佑，刘琪，李建贺. 长距离调水工程建设与安全运行集成研究及应用. 岩土工程学报. 2022(07): 1188-1210 . 本站查看
19.	徐振洋，吴怡璇，王雪松，刘鑫，郭连军，柴青平. 旋压钻进破岩的应力特征研究. 金属矿山. 2022(10): 24-29 . 百度学术
20.	侯仕军，丁伟捷，田帅康，梁书锋，刘殿书. 随钻测量技术在非油气工程领域的应用现状与展望. 矿业研究与开发. 2022(12): 41-49 . 百度学术
21.	庹晓军，刘强，曹瑞琅，赵宇飞，何瑞良. 基于随钻技术的振冲碎石桩施工质量评价方法研究. 水利水电快报. 2021(12): 59-64 . 百度学术