Optimal duration of endurance time acceleration functions for shallow buried underground structures
-
摘要: 为研究持时对地下结构耐震时程分析结果的影响,选取II类和III类工程场地中典型的两层三跨地铁车站为原型,以基岩场地地震动均值反应谱为目标谱,构造了6种典型持时的耐震加速度时程曲线作为输入。通过将耐震分析结果与增量动力分析基准结果对比表明,耐震加速度时程曲线的持时对分析结果影响显著。根据目标时间点与地震动能量指标阿里亚斯强度值的变化规律,给出了最优目标时间点的确定公式并进行验证。由研究结果可知,对于II和III类工程场地,耐震时程曲线较优持时分别为30 s和45 s；给出的目标时间点的确定公式对上述两类场地中的地下结构抗震性能评价具有一定适用性,当构造的耐震时程曲线在目标时间区段内的能量值与实际地震动的能量值较为接近时,耐震时程分析结果最为精确。Abstract: The effects of duration of the endurance time analysis on the seismic response of the underground structures are investigated. The typical two-story three-span subway station embedded in the sites of classes II and III is used as the prototype. The response spectra at the engineering bedrock is used as the target ones to develop six endurance time acceleration functions as the input motions for the nonlinear soil-structure interaction system. Using the results from the incremental dynamic analysis as the reference, the effects of time duration of the endurance time analysis on the seismic analysis of underground structures are significant. A formula to compute the optimal time duration based on the variations of earthquake ground motion energy measure, Arias intensity, with the target time is proposed and validated. It can be seen from the numerical results that endurance time acceleration functions with durations of 30 and 45 s are more favorable for the underground structures embedded in the sites of classes II and III, respectively. Moreover, the proposed formula for the optimal duration estimation is feasible for the seismic performance evaluation of underground structures in the above two site classes. The results from the endurance time analysis are more accurate when the total energy in the artificial endurance time acceleration function is close to the actual earthquake records.
-
0. 引言
1995年日本阪神地震中,大开地铁车站几乎完全塌毁,是历史上首次记录到的大型地下结构遭受严重震害的实例[1]；2008年汶川特大地震中,成都市在建的地铁车站遭受了不同程度的破坏[2]；2013年中国的庐山地震和2016年日本的熊本地震,均对山岭隧道造成了严重破坏。这些震害清楚地表明,地下结构同样面临着地震灾害的威胁,因此,近年来对地下结构开展抗震性能评价成为土木工程领域和地震工程领域热门的研究课题。基于性能的结构抗震设计（performance- based seismic design,PBSD）要求结构能够在不同的地震危险水准下满足不同的性能要求,进而对结构多目标抗震性能提出需求[3]。目前,对地下结构常用的抗震性能评价方法有拟静力分析方法,如地下结构Pushover法[4-6]和非线性动力时程分析方法,如增量动力分析法[7]（increment dynamic analysis, IDA）、云分析法[8]、多条带分析法[9]等。钟紫蓝等[10]总结了上述两类方法存在的局限性,同时将耐震时程分析法（endurance time analysis, ETA）引入到地下结构抗震性能评价中来,以大开地铁车站为原型,验证了该方法在地下结构抗震性能评价中的适用性与精度,为地下结构抗震性能快速评价提供了新思路。
耐震时程分析法的关键在于根据预先定义的目标反应谱构造一条随着持时增加而地震动强度不断增强的加速度时程曲线（endurance time acceleration function, ETAF）[11],其构造函数[12]如下式所示：
SaT(T,t)= ttTarget× SaC(T), (1) 式中,tTarget为目标时间点,t为任一时间点,SaC(T)为目标反应谱（通常为规范设计谱或者预先定义的地震动反应谱）,T为结构的自振周期,SaT(T,t)为0～t时刻所构造的ETAF反应谱。由式（1）可知,只需确定目标时间点tTarget和目标反应谱SaC(T),所构造的0～t时刻内的ETAF的加速度反应谱便与持时t成线性关系。将式（1）转化为无约束优化问题,便可通过不断迭代求解,构造一条较优的耐震时程曲线[10]。
目标时间点tTarget是耐震时程曲线构造函数中较为关键的参数,它的确定理论上应与结构的自振周期以及代表性地震动持时有关[12]。刘向阳[13]以4种不同层高的钢框架为研究对象,分析了持时长短对钢框架结构耐震响应的影响,结果表明持时过长或较短均会导致ETA结果与IDA基准结果离散度较大,且对于不同层高的钢框架结构,持时为45 s的耐震时程曲线分析结果,均具有较好的准确性与可靠性；Valamanesh等[14]研究了耐震时程曲线的特征参数随目标时间点的变化规律,通过与地震动特性进行差异对比,发现在特定的目标时间段内ETAF与有效的地震动特征参数之间存在较好的一致性。然而,现阶段针对tTarget的确定还未形成统一认识,钟紫蓝等[10]也指出,关于目标时间点的确定有待进一步研究。
本文在文献[10]的研究基础上,选取15条基岩场地地震动记录,并基于基岩场地地震动反应谱生成tTarget分别为5,10,15,20,25,30 s的ETAFs各3条,研究两种典型场地下持时长短对地铁车站耐震时程分析结果的影响,并根据耐震时程的阿里亚斯强度指标与目标时间点的变化规律,给出地下结构耐震时程分析法持时的确定公式并进行验证。
1. 有限元模型建立
1.1 计算模型与参数
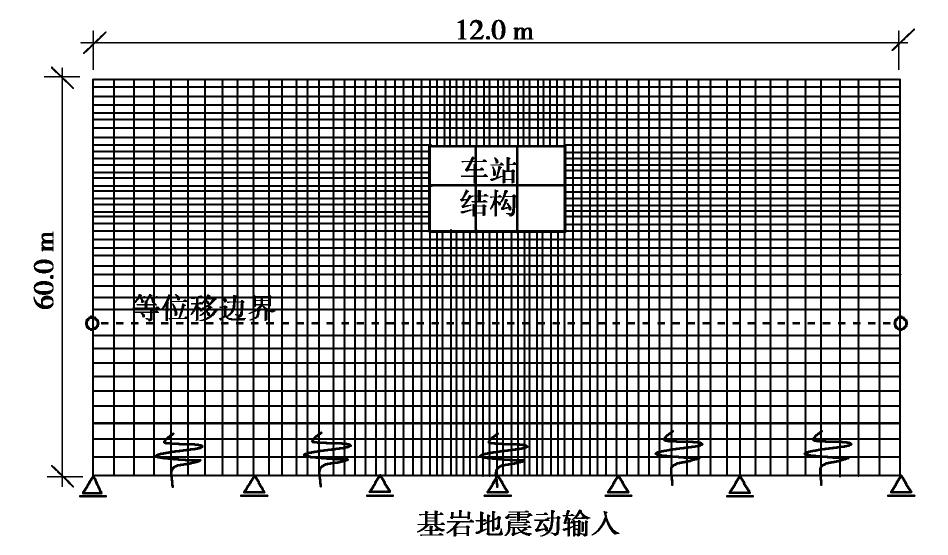
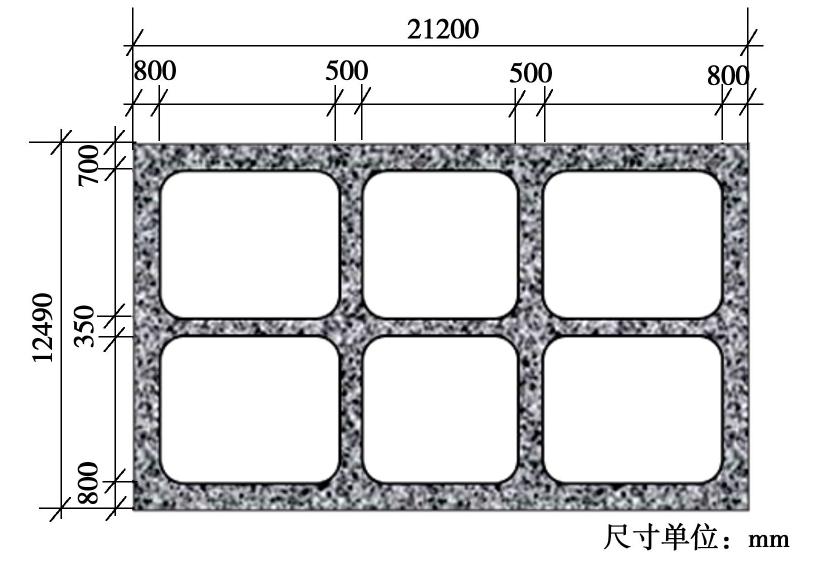
本文以南京某两层三跨地铁车站结构[15]为研究对象,结构的横断面尺寸如图1所示。该地铁车站结构的顶、底板的配筋率为1.10%,中层隔板的配筋率为1.70%,左右侧墙配筋率为0.65%,中柱配筋率为1.0%。
中国城市的地铁结构大多是在沉积土层中建造的,地震动参数和场地条件对基岩地震动都具有不同的放大效应,使得场地表现出不同的地震响应规律,进而影响结构在地震下的反应。针对这一情况,本文选取了两种典型场地条件,土层厚度均为60 m,地下结构埋深为10 m。表1,2分别给出了两类场地的土层划分及物理参数,两类场地均是由砂性土和黏性土组成,按照中国《建筑抗震设计规范》(GB50011—2010)[16]对工程场地的划分标准,所选两类场地的等效剪切波速分别为251,147 m/s,分别属于II类与III类工程场地。
表 1 Ⅱ类场地土层物理参数表Table 1. Physical parameters of site class II soil土层 类别 厚度/m 密度ρ/(t·m-3) 剪切波速Vs/(m·s-1) 黏聚力c/kPa 摩擦角φ/(°) 
1 人工填土 4.0 1.90 180 20.0 12.0 2 粉质黏土 4.0 1.90 230 30.0 20.0 3 细中砂 17.0 2.00 300 1.0 35.0 4 细粉砂 15.0 2.00 320 1.0 35.0 5 粗砂 20.0 2.23 380 1.0 35.0 表 2 Ⅲ类场地土层物理参数表Table 2. Physical parameters of site class III soil土层 类别 厚度/m 密度ρ/(t·m-3) 剪切波速Vs/(m·s-1) 黏聚力c/kPa 摩擦角φ/(°) 
1 淤泥质土 5.5 1.90 120 13.5 12.0 2 淤泥粉质黏土 16.5 1.90 160 15.0 12.0 3 粉细砂 17.0 1.90 205 1.0 35.0 4 黏土 21.0 2.02 263 20.0 20.0 1.2 有限元模型建立
基于文献[10]已验证的建模分析方法,本文在OpenSees有限元软件中建立二维的土-地下结构相互作用分析模型,如图2所示,模型宽度为120 m,场地高度取至距地表为60 m的工程基岩面。地铁车站为典型的钢筋混凝土结构,采用C30等级混凝土,钢筋及混凝土材料参数及本构模型参见文献[10]。周围土场采用四节点平面应变单元模拟,土体材料均采用多屈服面弹塑性材料：砂性土为Pressure depend multi yield材料,其屈服面是Drucker-Prager本构模型[17]；黏性土为Pressure independ multi yield材料,其屈服面是内嵌的Von Mises本构模型[18]。模型在初始地应力平衡后,再进行动力时程分析。
2. 地震动记录的筛选与生成
2.1 基岩场地地震动记录筛选
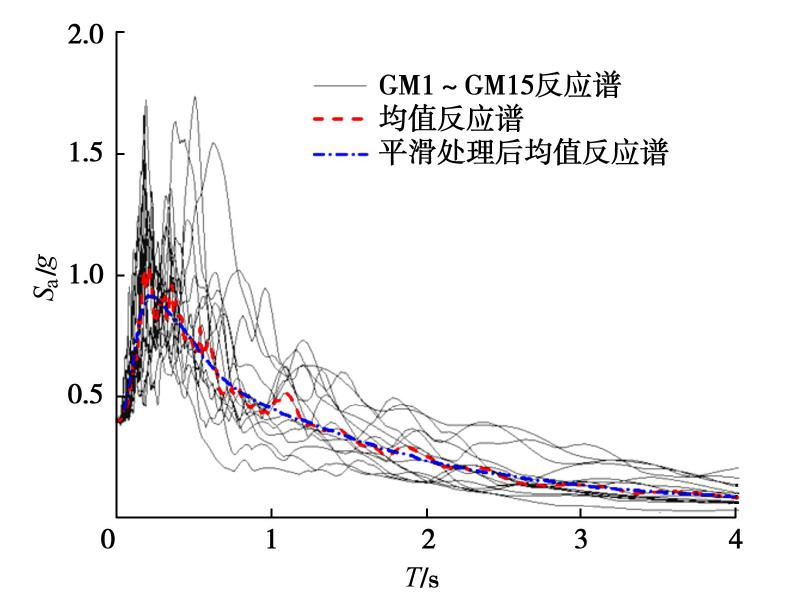
本文基于美国ASCE规范[19]依据剪切波速对场地类型的划分,在美国太平洋强震数据库中筛选了15条露头基岩场地的地震动（ground motion,GM）,根据8度设防规定将所选15条天然地震动调幅至0.4g,计算所选地震动的反应谱及其均值反应谱如图3所示。对所选的露头基岩地震动的PGA先进行幅值折半,后按比例进行调幅以进行IDA分析,调幅范围为0～0.8g,增幅为0.05g,每条地震动共缩放16次,经调幅的地震动由模型底部下卧工程基岩处进行输入,如图2所示。
![]()
图 3 基岩场地地震动加速度反应谱(ξ=5%)Figure 3. Elastic acceleration response spectra of bedrock earthquake records (ξ=5%)2.2 不同持时的ETAFs生成
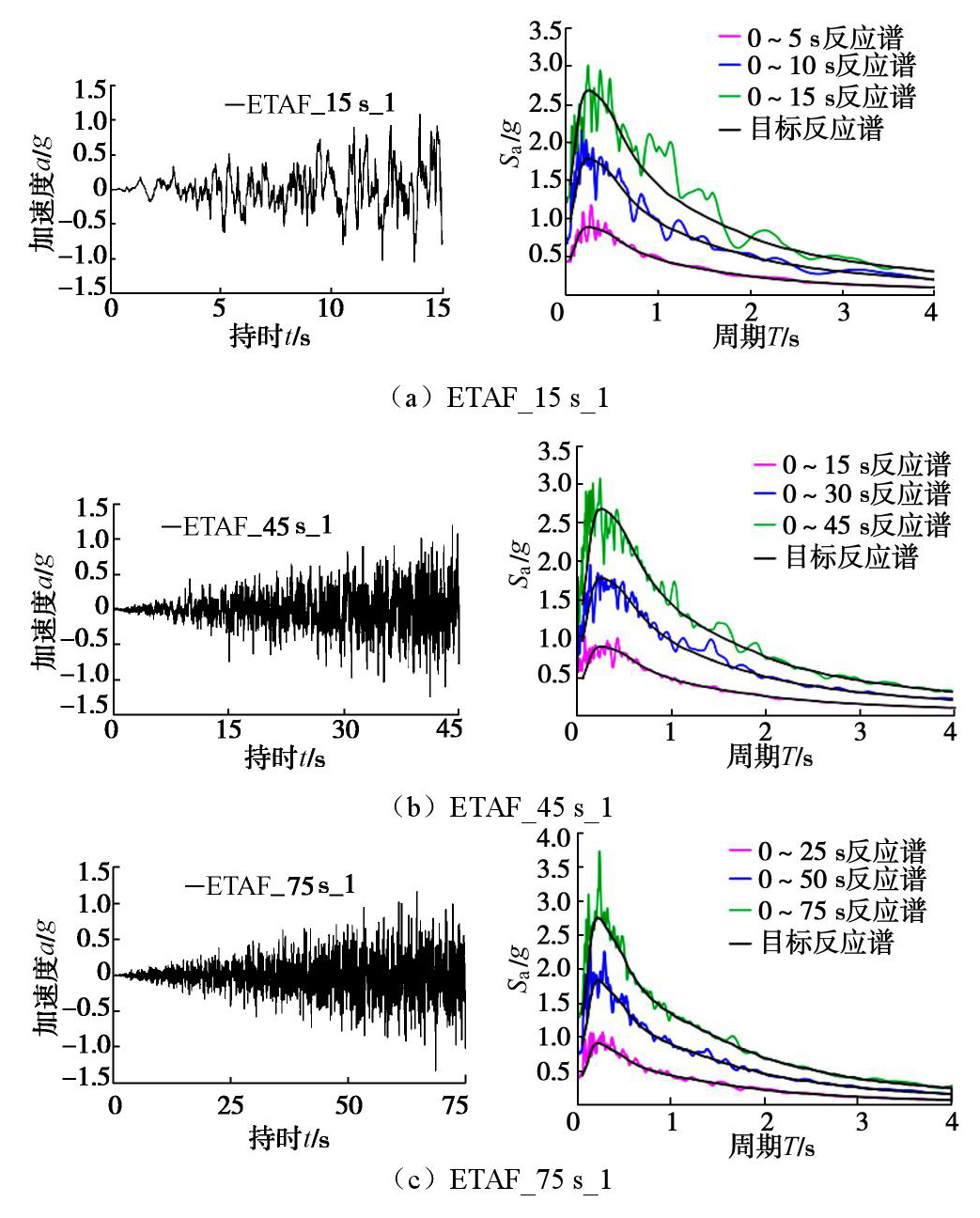
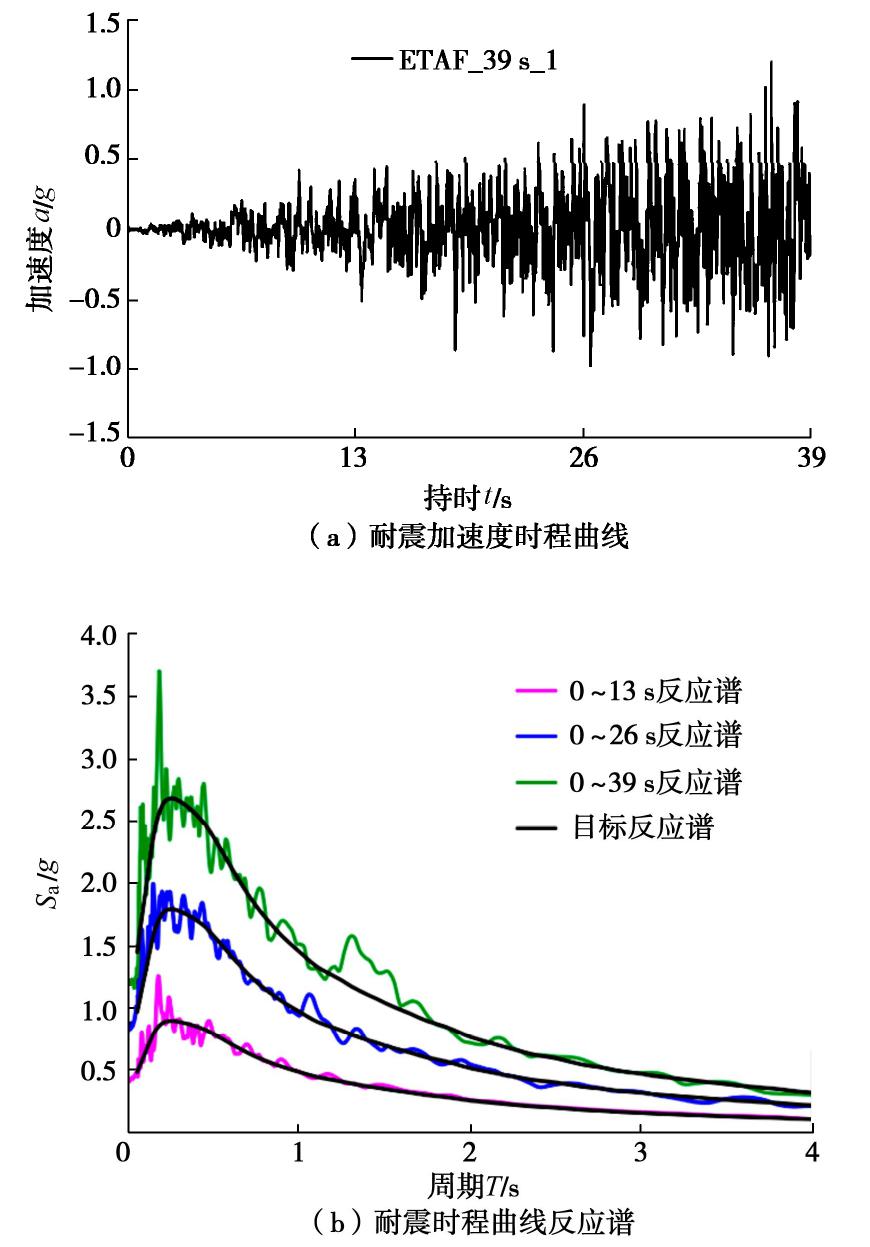
本文基岩场地地震动的均值反应谱作为预先定义的目标反应谱SaC(T),利用地震动信号处理程序EQSignal[20-21]生成持时分别为15,30,45,60,75,90 s的6种ETAFs各3条,tTarget分别为5,10,15,20,25,30 s。由于版面有限,仅取持时为15,45,75 s其中一条作为展示,如图4所示,所生成的ETAFs在各目标时间段内的反应谱与目标谱吻合良好,表明所生成的ETAFs具有足够的精度。
![]()
图 4 基于基岩地震动反应谱的不同持时耐震时程曲线示意图Figure 4. Different durations of ETAFs based on response spectra of bedrock本文为研究持时对地下结构ETA分析结果的影响,选择考虑地震动持时的Arias强度指标IA作为表征物理量[22],其定义为
IA=π2g∫td0a2(t)dt, (2) 式中,td为总持时,IA可以有效反映地震动的滞回能量。对不同持时ETAFs进行参数统计,如表3所示,无论是在全时程内还是在0～1倍目标时间区段内,不同持时的ETAFs的PGA基本处于同一水准,相差较小,但是随着持时的增加,所构造的耐震时程曲线的Arias强度IA值不断增大。
表 3 不同持时耐震加速度时程参数Table 3. Parameters of different durations of ETAFs参数 15 s 30 s 45 s 60 s 75 s 90 s 全时程PGA 1.16 1.24 1.26 1.24 1.25 1.21 0~tTarget间PGA 0.41 0.37 0.42 0.39 0.40 0.39 全时程IA值 2.07 3.32 4.79 5.90 6.61 7.32 0~tTarget间IA值 0.11 0.16 0.21 0.25 0.29 0.32 3. 持时对ETA结果影响
3.1 ETA分析结果
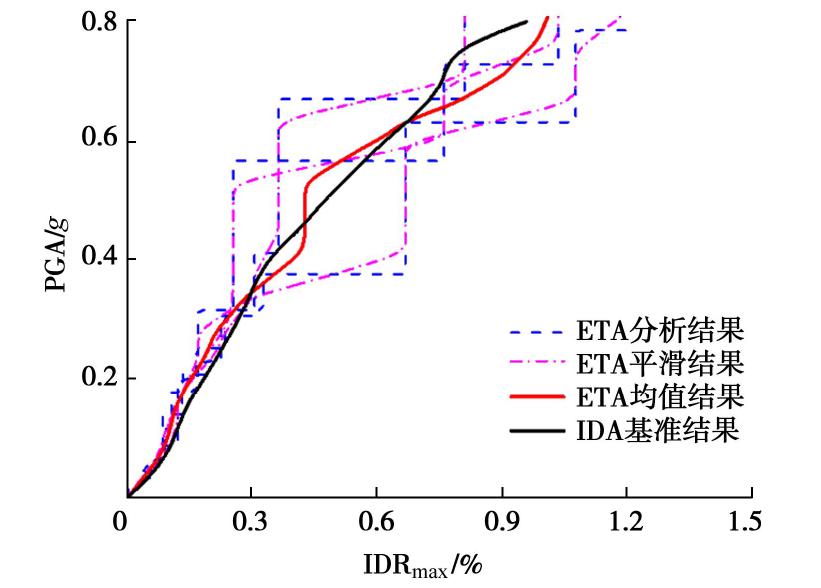
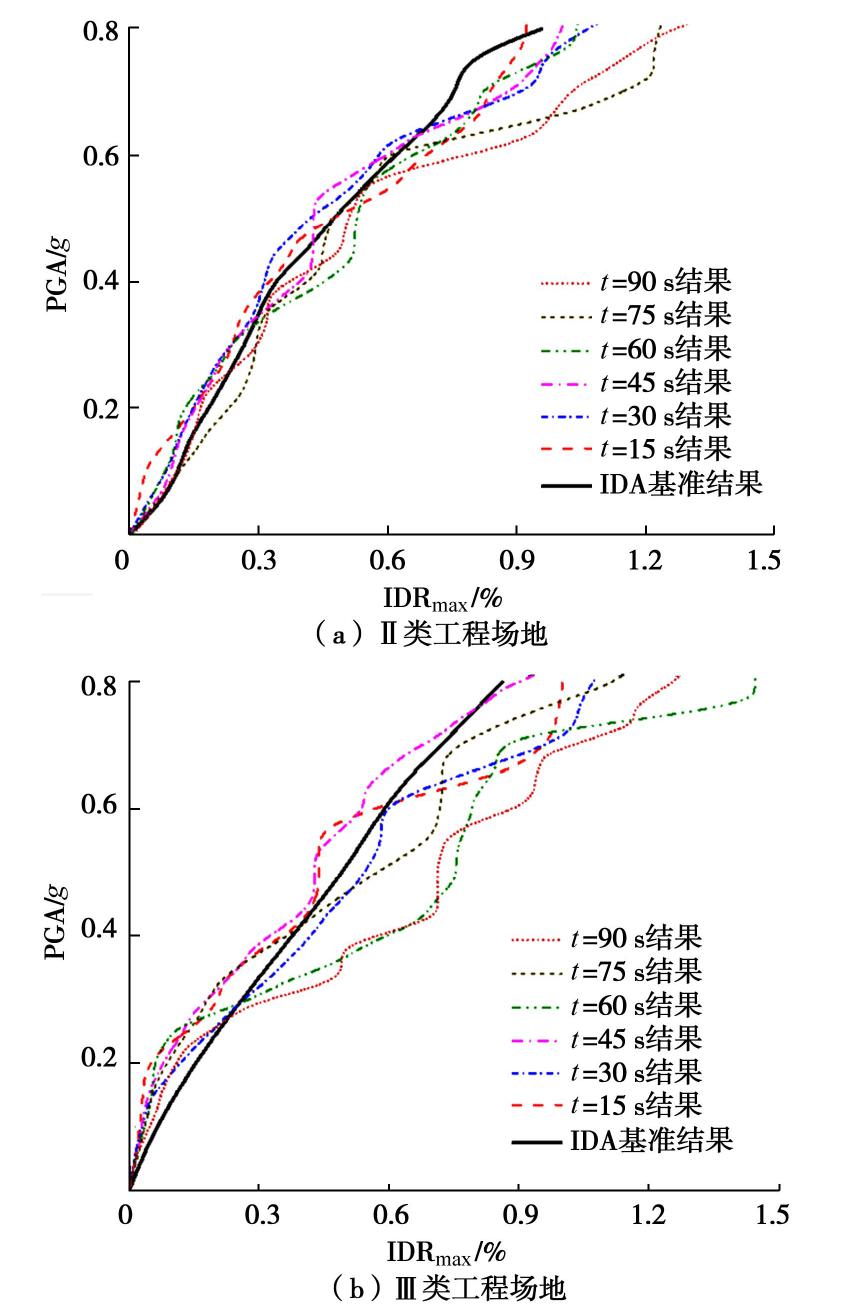
为与IDA结果进行对比,本文根据式（3）提取结构上、下两层地震响应的最大峰值层间位移角（interstory drift ratio, IDR）作为地铁车站结构地震响应指标,选择工程基岩面处输入地震动的峰值加速度PGA作为地震动强度指标（intensity measure, IM）[23]。通过式（4）,（5）分别计算车站结构IDR的耐震响应和耐震时程曲线的加速度的累积最大值,以PGA为纵坐标,以IDRmax为横坐标,得到ETA分析的地下结构性能曲线,如图5所示,随着输入地震动强度的增大,地下结构IDR呈阶梯型增加；为消除这种阶梯特性的影响,对其进行平滑处理,最终ETA分析结果取3次耐震分析的平均值,并与IDA基准结果进行对比,如图中红线与黑线所示。由图5可知,在II类场地中,持时为45 s的ETA结果与IDA基准结果趋势一致,吻合较好。
IDRmax=MAX|(IDRi)| (i=上层、下层), (3) EDP(t)=MAX|EDP(τ)| (τ∈[0,t]), (4) IM(t)=MAX|a(τ)| (τ∈[0,t])。 (5) 将两类场地中不同持时的ETA结果均值与IDA均值进行对比,如图6所示。由图可知,持时不同的ETA分析结果与IDA基准曲线之间差异明显,特别是在III类工程场地中,其中持时为45 s的ETA结果与IDA结果吻合较好,而采用其他持时的ETAF作输入时,分析结果与IDA结果差异较明显。
![]()
图 6 不同持时的ETA结果与IDA结果对比Figure 6. Comparison between ETA results at different durations and IDA results为一进步直观评价不同持时的ETA结果与IDA结果吻合情况,对二者的均值曲线进行插值取点,即提取相同PGA下的ETA数据与IDA数据,以IDA数据作为横坐标,以ETA数据为纵坐标,进行散点绘制和直线拟合,如图7所示。线性拟合系数b可以较直观反应不同地震强度下ETA结果与IDA结果整体吻合度,b值越接近于1.0,表明二者结果相当,ETA可以较好的替代IDA；b值小于1.0,表明ETA低估了结构的地震响应,结果偏于危险；b值大于1.0,表明ETA高估了结构的地震响应,结果偏于安全。引入均方根误差
σ 可以反映ETA数据偏离IDA基准数据的程度,σ 越小,表示二者吻合精度越高,σ 的计算如下式所示：![]()
图 7 不同持时的ETA结果与IDA结果相关性拟合Figure 7. Correlation between ETA at different durations and IDA resultsσ=√N∑i=1(ETAi−IDAi)2N, (6) 式中,N为插值取点次数。
将两类场地中不同持时的评价参数汇总,见表4。为综合考虑斜率b与均方根误差
σ 对评价结果的影响,本文提出效率指标ξ,计算如下式所示：表 4 不同持时ETA结果与IDA结果拟合参数汇总Table 4. Summary of fitting parameters of ETA results at different durations and IDA results参数 场地 15 s 30 s 45 s 60 s 75 s 90 s 斜率b II 0.942 1.0290 0.9730 1.040 1.182 1.234 III 1.085 1.1800 0.9730 1.456 1.166 1.436 均方根σ II 0.109 0.0740 0.0940 0.082 0.170 0.163 III 0.350 0.3730 0.1990 0.947 0.963 0.983 效率ξ II 0.006 0.0021 0.0030 0.003 0.031 0.038 III 0.030 0.0670 0.0054 0.431 0.160 0.428 ξ=σ×(|1−b|), (7) 效率指标
ξ 值越小,一定程度上代表了该持时的ETA结果与IDA结果吻合越好。由统计结果可知,II类场地中较优持时为30 s；III类场地中持时为45 s的ETA结果的效率指标最小,与IDA基准曲线吻合最好。3.2 持时公式拟合
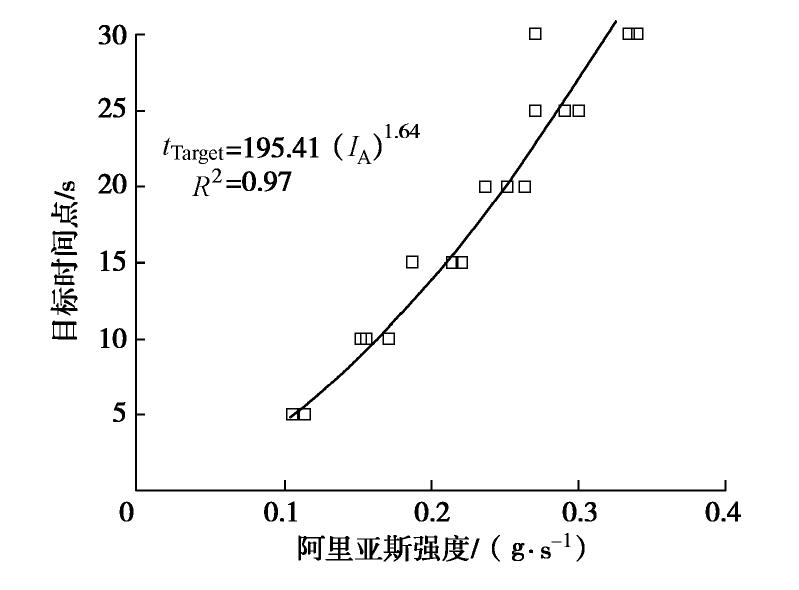
由表3可知,在0到1倍tTarget区间内,不同持时的ETAFs的PGA处于同一水准,约为0.40g,但随着持时的增加,其IA值也逐渐增加,二者存在一定的正相关关系。将不同持时的tTarget与IA值变化规律进行公式拟合,IA值与目标时间点成指数分布,见下式所示：
tTarget=195.41(IA)1.64, (8) 拟合优度R2为0.97,表明拟合的公式与数据点之间具有较好的相关性,如图8所示。
3.3 持时公式验证
统计所选15条天然地震动在峰值0.40g下的平均IA值约为0.195 g·s,位于目标时间点10～15 s,推断在目标时间点10～15 s存在最优目标时间点。基于式（8）可求得对应ETAFs的目标时间点tTarget约为13 s,由此生成3条总持时为39 s的ETAFs,图9展示了其中一条ETAF及其在各目标时间段内的反应谱。
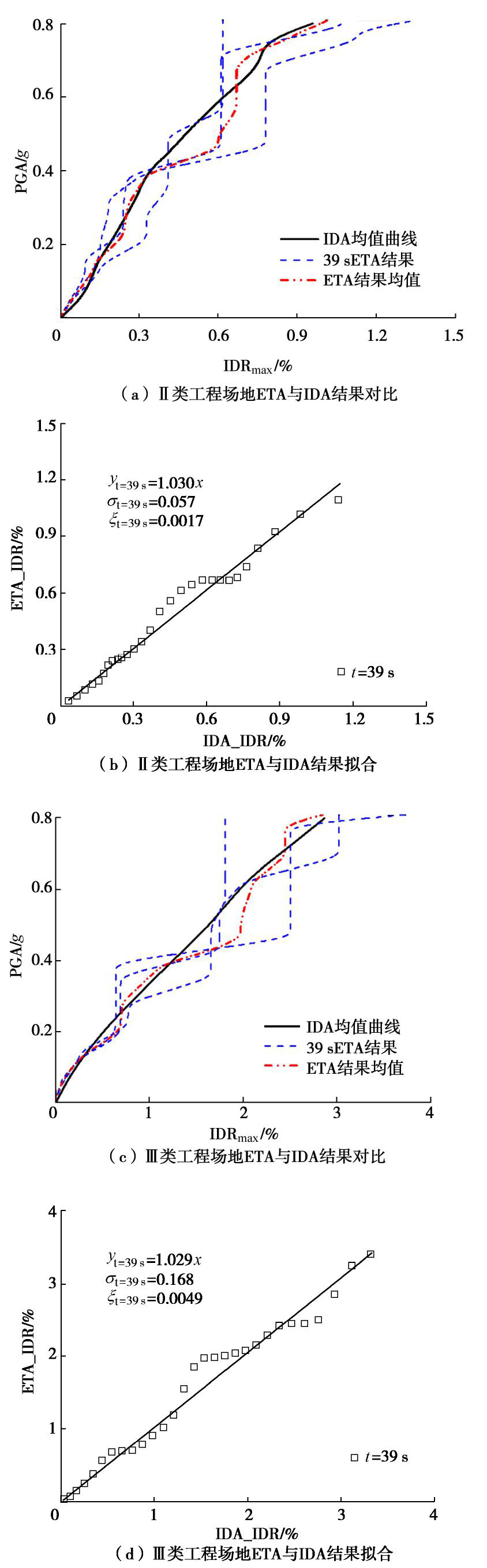
将构造的3条持时为39 s的ETAFs作为工程基岩处地震动进行输入,得到39 s的ETA分析结果与IDA结果如图10所示,并对二者性能曲线进行参数评价,由结果可知,在II类场地中,持时为39 s的ETA结果效率指标ξ为0.0017,比持时为30 s的效率指标缩小了约19%；在III类场地中,该持时的效率指标ξ为0.0049,与持时为45 s的效率指标较为接近,缩小了约9%。由斜率b值（b>1.0）可知,在两类场地中,持时为39 s的ETA评价结果也更加安全。因此,本文所拟合的目标时间点确定公式具有一定的准确性和适用性。
4. 结论
本文在ETA对地下结构抗震性能评价的基础上,针对ETAFs的持时确定展开研究,以两类场地中的两层三跨地铁车站为研究对象,生成不同持时的ETAFs,根据各持时ETAFs的阿里亚斯强度值与目标时间点的变化规律,给出地下结构耐震时程分析法持时的确定公式并进行验证,得到如下结论：
（1）耐震时程分析方法能以较少的非线性分析次数和较小的误差达到评价地下结构峰值地震响应的目的,为地下结构抗震性能分析、预测和评价提供了一种高效率方法。
（2）耐震加速度时程曲线的持时长短对地下结构ETA分析结果存在影响,Ⅱ类场地中较优持时为30 s,Ⅲ类场地中较优持时为45 s。
（3）依据阿里亚斯强度IA值随目标时间点变化的分布规律,给出的目标时间点的确定公式对于Ⅱ类和Ⅲ类场地中地下结构抗震性能评价具有一定的准确性和适用性；当耐震时程曲线在目标时间点处的能量值与天然地震动的能量值接近时,ETA分析结果较为准确。
-
![]()
图 3 基岩场地地震动加速度反应谱(ξ=5%)
Figure 3. Elastic acceleration response spectra of bedrock earthquake records (ξ=5%)
![]()
图 4 基于基岩地震动反应谱的不同持时耐震时程曲线示意图
Figure 4. Different durations of ETAFs based on response spectra of bedrock
![]()
图 6 不同持时的ETA结果与IDA结果对比
Figure 6. Comparison between ETA results at different durations and IDA results
![]()
图 7 不同持时的ETA结果与IDA结果相关性拟合
Figure 7. Correlation between ETA at different durations and IDA results
表 1 Ⅱ类场地土层物理参数表
Table 1 Physical parameters of site class II soil
土层 类别 厚度/m 密度ρ/(t·m-3) 剪切波速Vs/(m·s-1) 黏聚力c/kPa 摩擦角φ/(°) 1 人工填土 4.0 1.90 180 20.0 12.0 2 粉质黏土 4.0 1.90 230 30.0 20.0 3 细中砂 17.0 2.00 300 1.0 35.0 4 细粉砂 15.0 2.00 320 1.0 35.0 5 粗砂 20.0 2.23 380 1.0 35.0 
下载: 导出CSV
表 2 Ⅲ类场地土层物理参数表
Table 2 Physical parameters of site class III soil
土层 类别 厚度/m 密度ρ/(t·m-3) 剪切波速Vs/(m·s-1) 黏聚力c/kPa 摩擦角φ/(°) 1 淤泥质土 5.5 1.90 120 13.5 12.0 2 淤泥粉质黏土 16.5 1.90 160 15.0 12.0 3 粉细砂 17.0 1.90 205 1.0 35.0 4 黏土 21.0 2.02 263 20.0 20.0
下载: 导出CSV
表 3 不同持时耐震加速度时程参数
Table 3 Parameters of different durations of ETAFs
参数 15 s 30 s 45 s 60 s 75 s 90 s 全时程PGA 1.16 1.24 1.26 1.24 1.25 1.21 0~tTarget间PGA 0.41 0.37 0.42 0.39 0.40 0.39 全时程IA值 2.07 3.32 4.79 5.90 6.61 7.32 0~tTarget间IA值 0.11 0.16 0.21 0.25 0.29 0.32
下载: 导出CSV
表 4 不同持时ETA结果与IDA结果拟合参数汇总
Table 4 Summary of fitting parameters of ETA results at different durations and IDA results
参数 场地 15 s 30 s 45 s 60 s 75 s 90 s 斜率b II 0.942 1.0290 0.9730 1.040 1.182 1.234 III 1.085 1.1800 0.9730 1.456 1.166 1.436 均方根σ II 0.109 0.0740 0.0940 0.082 0.170 0.163 III 0.350 0.3730 0.1990 0.947 0.963 0.983 效率ξ II 0.006 0.0021 0.0030 0.003 0.031 0.038 III 0.030 0.0670 0.0054 0.431 0.160 0.428
下载: 导出CSV
-
[1] 杜修力, 马超, 路德春, 等. 大开地铁车站地震破坏模拟与机理分析[J]. 土木工程学报, 2017, 50(1): 53-62. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201701007.htm DU Xiu-li, MA Chao, LU De-chun, et al. Collapse simulation and failure mechanism analysis of the Daikai subway station under seismic loads[J]. China Civil Engineering Journal, 2017, 50(1): 53-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201701007.htm
[2] 李田彬. 汶川特大地震中山岭隧道变形破坏特征及影响因素分析[J]. 工程地质学报, 2008, 16(6): 742-750. doi: 10.3969/j.issn.1004-9665.2008.06.003 LI Tian-bin. Failure characteristics and influence factor analysis of mountain tunnels at epicenter zones of great Wenchuan earthquake[J]. Journal of Engineering Geology, 2008, 16(6): 742-750. (in Chinese) doi: 10.3969/j.issn.1004-9665.2008.06.003
[3] SEAOC. Performance Based Seismic Engineering of buildings[R]. Version 2000 Committee. Sacramento: Structural Engineers Association of California, 1995.
[4] 刘晶波, 刘祥庆, 李彬. 地下结构抗震分析与设计的Pushover分析方法[J]. 土木工程学报, 2008, 41(4): 73-80. doi: 10.3321/j.issn:1000-131X.2008.04.011 LIU Jing-bo, LIU Xiang-qing, LI Bin. A pushover analysis method for seismic analysis and design of underground structures[J]. China Civil Engineering Journal, 2008, 41(4): 73-80. (in Chinese) doi: 10.3321/j.issn:1000-131X.2008.04.011
[5] 刘晶波, 刘祥庆, 薛颖亮. 地下结构抗震分析与设计的Pushover方法适用性研究[J]. 工程力学, 2009, 26(1): 49-57. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200901018.htm LIU Jing-bo, LIU Xiang-qing, XUE Ying-liang. Study on applicability of a pushover analysis method for seismic analysis and design of underground structures[J]. Engineering Mechanics, 2009, 26(1): 49-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200901018.htm
[6] 刘晶波, 王文晖, 赵冬冬, 等. 循环往复加载的地下结构Pushover分析方法及其在地震损伤分析中的应用[J]. 地震工程学报, 2013, 35(1): 21-28. doi: 10.3969/j.issn.1000-0844.2013.01.0021 LIU Jing-bo, WANG Wen-hui, ZHAO Dong-dong, et al. Pushover analysis method of underground structures under reversal load and its application in seismic damage analysis[J]. China Earthquake Engineering Journal, 2013, 35(1): 21-28. (in Chinese) doi: 10.3969/j.issn.1000-0844.2013.01.0021
[7] VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514. doi: 10.1002/eqe.141
[8] HARIRI-ARDEBILI M, SAOUMA V. Probabilistic seismic demand model and optimal intensity measure for concrete dams[J]. Structure Safety, 2016, 59: 67-85. doi: 10.1016/j.strusafe.2015.12.001
[9] JALAVER F, CORNELL C. Alternative non-linear demand estimation methods for probability-based seismic assessments[J]. Earthquake Engineering and Structural Dynamics, 2009, 38(8): 951-972. doi: 10.1002/eqe.876
[10] 钟紫蓝, 甄立斌, 申轶尧, 等. 基于耐震时程分析法的地下结构抗震性能评价[J]. 岩土工程学报, 2020, 42(8): 1482-1490. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008019.htm ZHONG Zi-lan, ZHEN Li-bin, SHEN Yi-yao, et al. Seismic performance evaluation of underground structures using endurance time analysis[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1482-1490. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008019.htm
[11] ESTEKANCHI H E, VAFAI A, SADEGHAZAR M. Endurance time method for seismic analysis and design of structures[J]. Scientia Iranica, 2004, 11(4): 361-370.
[12] ESTEKANCHI H E, VALAMANESH V, VAFAI A. Application of endurance time method in linear seismic analysis[J]. Engineering Structure, 2007, 29(10): 2551-2562. doi: 10.1016/j.engstruct.2007.01.009
[13] 刘向阳. 增量地震激励分析法的研究与应用[D]. 哈尔滨: 哈尔滨工业大学, 2017. LIU Xiang-yang. Research and Application on Structural Dynamic Analysis Using Incremental Earthquake Excitation[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese)
[14] VALAMANESH V, ESTEKANCHI H E, VAFAI A. Characteristics of second generation endurance time acceleration functions[J]. Scientia Iranica, 2010, 17(1): 53-61.
[15] 陈国兴, 庄海洋, 杜修力, 等. 土-地铁车站结构动力相互作用大型振动台模型试验研究[J]. 地震工程与工程振动, 2007, 27(2): 171-176. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200702026.htm CHEN Guo-xing, ZHUANG Hai-yang, DU Xiu-li, et al. Analysis of large shaking table test of dynamic soil-subway station interaction[J]. Earthquake Engineering and Engineering Dynamics, 2007, 27(2): 171-176. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200702026.htm
[16] 建筑抗震设计规范：B50011—2010[S]. 2010. Code for Seismic Design of Buildings: B50011—2010[S]. 2010. (in Chinese)
[17] YANG Z, ELGAMAL A, PARRA E. Computational model for cyclic mobility and associated shear deformation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1119-1127.
[18] PARRA-COLMENARES E J. Numerical Modeling of Liquefaction and Lateral Ground Deformation Including Cyclic Mobility and Dilation Response in Soil Systems[D]. Corvallis: Oregon State University, 1996.
[19] Minimum Design Loads for Buildings and Other Structures: ASCE/SEI 7-10[S]. 2011.
[20] 潘超, 张瑞甫. EQSignal：地震波处理与生成工具[CP/OL]. PAN Chao, ZHANG Rui-fu. A useful tool to process and generate earthquake signals[CP/OL]. (in Chinese)
[21] PAN C, ZHANG R, LUO H, et al. Target-based algorithm for baseline correction of inconsistent vibration signals[J]. Journal of Vibration and Control, 2017, 24(12): 2562-2575.
[22] ARIAS A. A Measure of Earthquake Intensity. Seismic Design of Nuclear Power Plants[M]. Cambridge MA: MIT Press, 1970.
[23] 钟紫蓝, 申轶尧, 甄立斌, 等. 地震动强度参数与地铁车站结构动力响应指标分析[J]. 岩土工程学报, 2019, 42(3): 486-494. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003014.htm ZHONG Zi-lan, SHEN Yi-yao, ZHEN Li-bin, et al. Ground motion intensity measures and dynamic response indexes of metro station structures[J]. Chinese Journal of Geotechnical Engineering, 2019, 42(3): 486-494. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003014.htm
-
期刊类型引用(6)
1. 李子奇，王宇瀚，王力. 基于ETM的中小连续梁桥纵桥向地震碰撞响应分析. 公路交通科技. 2025(02): 137-145 . 
百度学术
2. 王国波，王鸿杰，王建宁，金立国，赵丁凤. 基于耐震时程法的地下结构序列地震作用抗震性能研究. 振动与冲击. 2024(15): 261-268+276 . 百度学术
3. 甄立斌，史跃波，钟紫蓝，杜修力，罗文林. 基于耐震时程分析法的高效地下结构地震易损性分析. 岩土工程学报. 2023(04): 777-784 . 本站查看
4. 崔溦，刘贵锋，张社荣，王超，王枭华. 考虑斜入射的重力坝耐震时程法抗震性能评估. 水力发电学报. 2023(12): 132-145 . 百度学术
5. 禹海涛，李心熙，袁勇，马超. 沉管隧道纵向地震易损性分析方法. 中国公路学报. 2022(10): 13-22 . 百度学术
6. 陈瑜，张小艳，许汉华，刘文连，李泽. 岩质边坡稳定性时程分析下限法研究. 水资源与水工程学报. 2021(02): 217-224 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 290
- HTML全文浏览量: 49
- PDF下载量: 141
- 被引次数: 8
