金东大桥隧道锚现场模型试验及承载能力分析

余美万; 张奇华; 高利萍; 罗荣; 李玉婕; 王帅; 边智华

doi:10.11779/CJGE202102014

金东大桥隧道锚现场模型试验及承载能力分析 English Version

1.
长江科学院水利部岩土力学与工程重点实验室,湖北　武汉　430010
2.
中国地质大学（武汉）教育部长江三峡库区地质灾害研究中心,湖北　武汉　430074
3.
云南省昆明市东川区交通运输局,云南　昆明　654100

基金项目:

国家自然科学基金青年基金项目 51409013

国家自然科学基金青年基金项目 42002276

湖北省自然科学基金项目 2019CFB258

详细信息

作者简介:
余美万（1970— ）,男,高级工程师,主要从事工程岩体力学试验及测试工作。E-mail：yumw027@163.com

中图分类号: TU43
计量
- 文章访问数: 239
- HTML全文浏览量: 22
- PDF下载量: 127
出版历程
- 收稿日期: 2018-05-22
- 修回日期: 2020-05-28
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

Field model tests and bearing capacity analysis of tunnel anchorage of Jindong Bridge

1.
Key Laboratory of Geotechnical Mechanics and Engineering of Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan 430010, China
2.
Three Gorges Research Center for Geohazards, Ministry of Education, China University of Geosciences, Wuhan 430074, China
3.
Dongchuan District Transportation Bureau of Kunming City, Kunming 654100, China

摘要

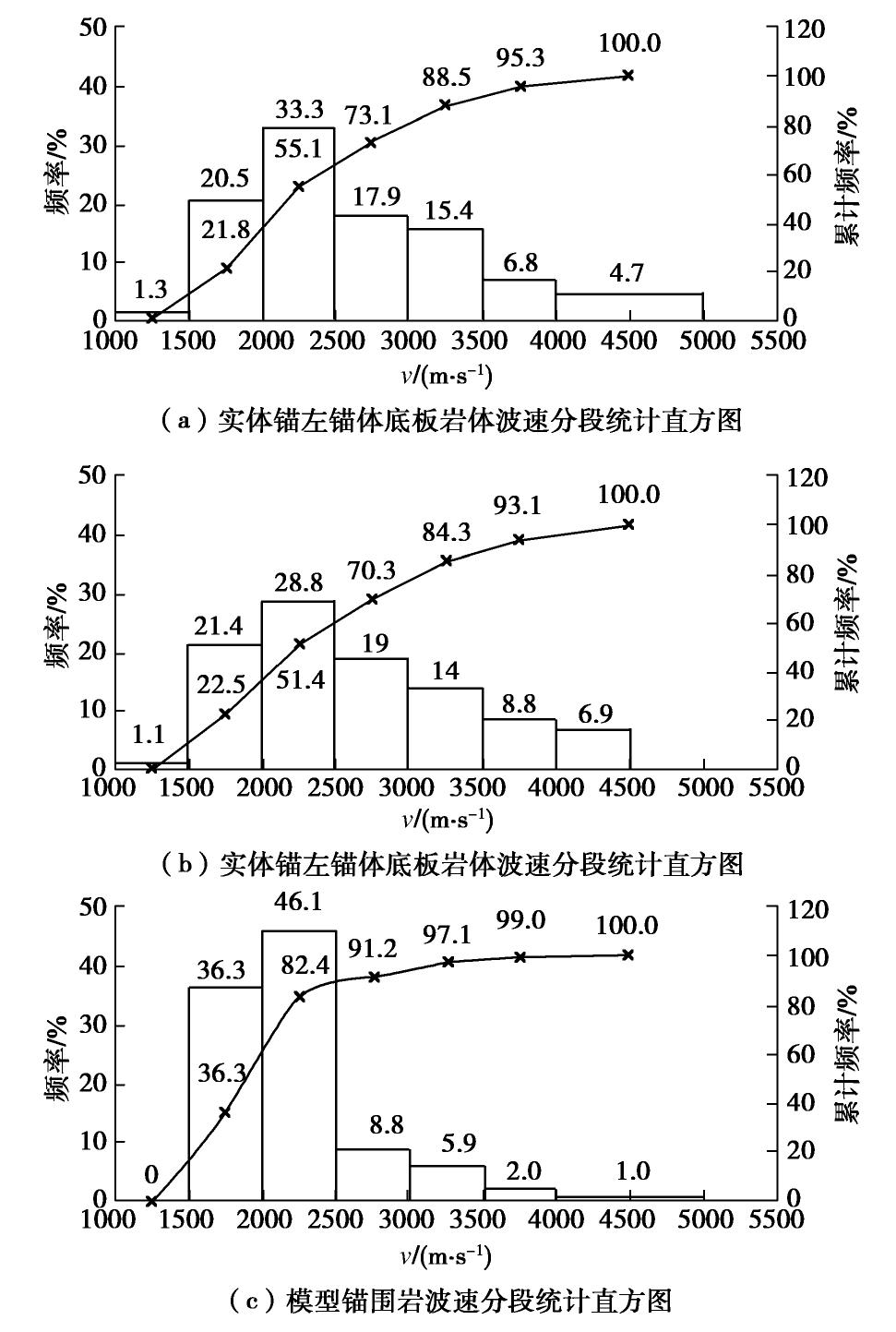
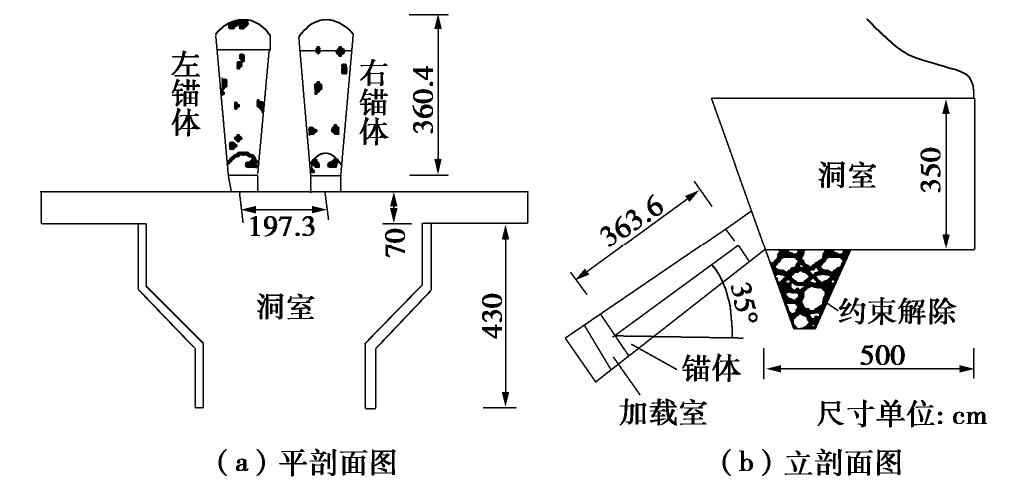
摘要: 金东大桥隧道锚建在复杂岩体地层中,尚无类似的工程经验借鉴,为分析该桥隧道锚承载能力,在实体锚上游侧山体边坡开挖模型试验洞,制作相似比1∶11的隧道锚模型,采用后推法进行模型试验,包括弹塑性阶段试验、蠕变试验和满负荷的超载试验,配套进行了岩体（石）物理力学性质试验、岩体声波测试。分析结果表明：模型锚岩体性状与实体锚基本接近,模型锚围岩声波低于实体锚,模型锚地层具有较好的地质代表性；模型锚至少在8倍设计荷载作用下变形处于近似弹性阶段,在6倍设计荷载长期作用下未出现蠕变现象,推断实体锚围岩的超载稳定系数>8,长期安全稳定系数>6,成果可为类似复杂围岩的工程设计提供参考。
- 金东大桥 /
- 隧道锚 /
- 现场模型试验 /
- 承载能力
Abstract: Tunnel anchorage of Jindong Bridge is built in the complicated rock stratum, but there is no similar engineering experience for reference. In order to analyze the bearing capacity of tunnel anchorage of Jindong Bridge, a model test tunnel is excavated on the side slope of the mountain at the upstream side of the real anchorage to make a tunnel anchorage model of 1∶11; then, the backstepping method is adopted to conduct the model tests, including elastic-plastic stage tests, creep tests and full-load overload tests, as well as the supporting tests such as physical mechanical property tests on rock mass (rock block) and acoustic wave tests on rock mass. The test results show that the character of the model anchorage rock mass is basically the same as that of the real anchorage, the acoustic wave of the surrounding rock of the model anchorage is lower than that of the real anchorage, and the stratum of the model anchorage has a better geological representation. The model anchorage exhibits the approximate elastic deformation under the action of 8 times the design load, and there is no creep under the long-term action of 6 times the design load. It is deduced that the surrounding rock of the real tunnel anchorage has the overload stability coefficient of more than 8 and the long-term safety stability coefficient of more than 6. The results can be used as the reference for the engineering design of similar complicated surrounding rock.
- Jindong Bridge /
- tunnel anchorage /
- field model test /
- bearing capacity

HTML全文

0. 引言

深层地质处置被认为是处置高放废物最合理的方法。膨润土具有低渗透性、较好的吸附性和较大的膨胀性等特点,被广泛认为是深层地质处置库理想的缓冲/回填材料^[1-3]。由压实膨润土构成的屏障的一个重要功能是填充建造或运行过程中可能产生的裂缝,形成封闭的环境,防止核素迁移。在过去几十年中,膨润土基缓冲/回填材料的膨胀特性得到了广泛的研究^[4-7]。研究结果表明,膨润土的膨胀受干密度、孔隙流体化学物质和温度等多种因素的影响^[8-10]。

相关研究表明,温度对不同膨润土膨胀的影响是不同的,即使在不同的试验条件下对同一膨润土的影响也不相同^[11-13]。Pusch等^[14]指出温度对膨润土膨胀力的影响与其主要的阳离子有一定关系,温度升高可提高高密实钠膨润土的膨胀力,但会降低二价膨润土膨胀力。蒙脱石类黏土的膨胀过程大致可分为晶层膨胀和渗透膨胀^[15]。在水分进入膨润土的初始阶段,膨胀是由存在于蒙脱石单元层之间的可交换阳离子的水化作用引起的（阳离子与水发生化合反应,在其周围形成一定的水分子层）,称之为晶层膨胀。随着水分进一步渗入并充填蒙脱石集合体内的孔隙,集合体膨胀并裂开成薄层叠体,甚至为单层晶层,形成渗透膨胀也称为双电层膨胀^[16]。扩散双电层（DDL）模型适用于渗透膨胀。根据DDL模型,DDL的厚度随温度的升高而增大。因此,如果DDL在粒间孔隙中发育良好,温度会促进黏土的膨胀。通常,扩散双电层在钠基膨润土中容易发展,但其间距随着阳离子价的增加而减小,导致二价膨润土中DDL的形成相对困难。因此,温度往往会促进钠基膨润土的膨胀,例如GMZ膨润土^[17-18]。此外,DDL的发展还取决于荷载或试样的干密度,在小荷载或低密度的试样中,扩散双电层可以得到很好的发展。在这种情况下,渗透膨胀仍是主要的膨胀形式。Romero等^[19]报告了FEBEX Ca/Mg-膨润土的自由膨胀率随温度升高而增加。Cho等^[4]发现加热可以促进干密度较低的Korea钙基膨润土的膨胀力。Bag等^[12]也发现温度升高使Bikane钙基膨润土的膨胀力有轻微的增加。然而,对于高压实膨润土,无论是钠基膨润土^[13,20]还是二价膨润土^[21],膨胀性能均随温度的增加而降低。这主要是因为晶层膨胀是高压下高压实膨润土主要的膨胀形式^[13]。在这种情况下,晶层间水分子的动能受到热量的促进,导致水分子不稳定,蒙脱石吸水能力降低^[13]。因此,根据目前的研究可以推断,在渗透膨胀为主的情况下,膨润土的膨胀特性随着温度的升高而增强,而在晶层膨胀的情况下则相反。

高庙子（GMZ）膨润土被认为是中国深层地质处置首选的缓冲/回填材料。不同条件下GMZ膨润土膨胀性能的研究已取得较丰富的成果^{[16-17, 22]}。但温度对GMZ膨润土膨胀性能的影响还不够明确。另外,目前比较缺乏膨胀性能随温度变化的定量评价模型。DDL模型是适用于压实膨润土渗透膨胀的计算方法^[23]。但目前也发现了DDL模型的一些局限性,如DDL模型不适用于晶层膨胀或浓盐溶液中的膨胀计算。此外,该模型所需参数较多且较难确定,不方便应用。Xu等^[24]发现蒙脱石孔隙率e_m与竖向压力p之间存在分形关系,可表示为e_m=Kp^D-3。这是一种定量评价膨润土膨胀性能的简便有效方法,模型得到了室温下不同膨胀性黏土试验数据的验证^{[3, 25]}。但该模型并没有考虑到温度变化对膨胀性能的影响。

本文开展不同温度下GMZ膨润土膨胀性能试验,分析了温度对膨胀性能的影响机理,基于DDL模型和分形模型,建立了一种温度作用下GMZ膨润土膨胀性能的简便计算方法。

1. 材料与试验方法

1.1 GMZ膨润土

GMZ膨润土来源于内蒙古自治区高庙子矿床。该膨润土被选用作为中国高放废物处置库的缓冲/回填主料。对GMZ膨润土进行研究可为处置库的设计提供科学依据。GMZ膨润土的物理化学指标见表1。

表 1 GMZ膨润土的物理化学指标^[22]

Table 1. Physicochemical indices of GMZ bentonite

土粒相对质量密度	液限w_L/%	塑限w_P/%	塑性指数I_P	蒙脱石含量C_m/%	阳离子交换量/(cmol·kg^-1)	主要交换性阳离子/(cmol·kg^-1)
土粒相对质量密度	液限w_L/%	塑限w_P/%	塑性指数I_P	蒙脱石含量C_m/%	阳离子交换量/(cmol·kg^-1)	Na⁺	Ca²⁺	Mg²⁺	K⁺
2.66	276	37	239	75	75.1	36.2	24.7	11.9	3.62

下载: 导出CSV

| 显示表格

1.2 试验装置

所用不同温度下膨胀试验的试验装置如图1所示,该装置其主要包括自制的固结室和电加热套,温度可以用温度控制器调节。电加热套和固结室可以安装于普通的三联中压固结仪。

图 1 温度作用下膨胀性能试验装置

Figure 1. Experimental apparatus for swelling tests under different temperatures

下载: 全尺寸图片幻灯片

1.3 膨胀试验

将GMZ膨润土配制成含水率约18.0 %的湿土,并在环刀中静压制成高度1.0 cm,直径6.18 cm的饼状试样。将压实试样放入自制的固结室中,连同外部加热套安装于三联固结仪中。设置目标温度,一次性施加所需荷载,加蒸馏水进行渗流饱和,外部容器中水面高度保持高于试样顶面的1.0 cm左右。采用百分表记录膨润土的膨胀率随时间的增加过程,膨胀率为高度变化量与原试样高度之比,当在24 h内百分表指针保持不动,认为试样膨胀饱和完成,此时的最终膨胀率称为最大膨胀率。

在膨胀力试验中,将压实试样安装在固结仪中并对其施加恒定温度后,记录指针的初始读数,向试样中注入蒸馏水。当样品开始膨胀时,迅速施加竖向荷载到样品上,让指针回到原来的位置,在试验过程中保持指针变化量小于0.01 mm。当百分表读数在某压力下保持24 h不变时,认为达到最大膨胀压力p_s,试验完成。

Pastina等^[26]发现高放废物储存库中的最高温度可接近于90℃,且距离核废料储藏罐距离越远温度越低。据此本文将膨胀变形和膨胀力试验的温度设定为25℃,40℃,60℃和90℃。膨胀变形试验中各试样的初始状态和试验条件见表2。

表 2 膨胀变形试验中试样的初始状态和试验条件

Table 2. Initial and experimental conditions of samples in swelling deformation tests

初始干密度/(g·cm^-3)	初始含水率/%	温度/℃	竖向荷载/kPa
1.70 ± 0.03	17.7~18.1	25,40,60,90	6.25,12.5,25,50,100,200,400,800
1.50 ± 0.03	17.5~17.9	25,40,60,90	100,400
1.60 ± 0.03	17.6~18.2	25,40,60,90	100,400

下载: 导出CSV

| 显示表格

1.4 氮吸附试验

在蒸馏水中膨胀后,卸载膨润土试样,在105℃的烘箱中干燥12 h,然后磨成粉末状,过200目筛。对原GMZ膨润土粉末和40℃,90℃水中膨胀后的试样进行了N₂吸附试验,分析了温度对GMZ膨润土表面性质的影响。

2. 膨胀试验结果

图2为不同温度下初始干密度为1.7 g/cm³的GMZ膨润土的最大膨胀率ε_max。可以发现,ε_max随竖向荷载的增大而减小,随温度的升高而增大。这是由于在本次试验条件下,渗透膨胀为主要膨胀形式,这种状况下,蒙脱石颗粒间扩散双电层厚度随温度的增加而增大,进而增强了膨胀变形。从图中也可发现,温度升高引起的膨胀率的增加随竖向压力的增大而减小。当竖向荷载较小时,试样的膨胀率随着温度的升高明显增大,而竖向荷载较大时,试样的膨胀率随温度升高轻微增加。

图 2 不同温度下的GMZ膨润土的最大膨胀率

Figure 2. ε_max of GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

图3为初始干密度为1.7 g/cm³试样的最大膨胀率与温度之间的关系。可以看出在给定的压力下,试样的ε_max随温度增加线性增加,而随着竖向荷载的增加,线性ε_max-T_c关系的斜率逐渐减小。

图 3 不同荷载作用下GMZ膨润土的ε_max-T_c关系

Figure 3. Relationship between ε_max and T_c of GMZ bentonite under different stresses

下载: 全尺寸图片幻灯片

如图4所示,在相同的荷载和温度条件下,GMZ膨润土试样的ε_max随初始干密度ρ_d的增大线性增加,这与室温下不同膨润土的试验结果一致^{[1, 27]}。

图 4 25℃和60℃时GMZ膨润土的ε_max-ρ_d关系

Figure 4. Relationship between ε_max and ρ_d for GMZ bentonite at 25℃ and 60℃

下载: 全尺寸图片幻灯片

在膨胀力试验中,膨润土试样的干密度相对较低（ρ_d=1.35～1.55 g/cm³）。从图5中可以发现,在给定温度下,膨胀力随初始干密度呈指数增长,对于相同密度的样品,膨胀力随温度升高而增大。此外,相较于膨胀变形随温度增加轻微增加,温度对GMZ膨润土膨胀力的影响较大,且随初始干密度的增大而显著增大。这种差异主要是由于GMZ膨润土具有较高的膨胀性,需要较高的应力来防止膨胀变形；此外,根据Zhang等^[28]GMZ膨润土压缩曲线发现压实膨润土的压缩模量可达到30 MPa^-1。微小的变形变化需要较大的荷载维持,所以膨胀变形随温度略有增加,而膨胀力显著增加。

图 5 不同温度下GMZ膨润土的p_s-ρ_d关系

Figure 5. Relationship between p_s and ρ_d for GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

3. 膨胀性能计算

3.1 e_m-p分形关系

GMZ膨润土的膨胀性能主要是由其中蒙脱石矿物所引起的^[29]。膨润土的膨胀性能可采用膨胀饱和时的蒙脱石孔隙比e_m表示^[29]：

$e_{m} = \frac{e}{α} = \frac{V_{w}}{V_{m}}$ 。

(1)

式中 e为膨润土试样膨胀饱和的孔隙比； $α$ 为膨润土中蒙脱石的含量；V_w为饱和试样中的水体积； $V_{m}$ 为蒙脱石的体积。

基于N₂等温吸附方程^[30],Xu等^[25]给出了蒙脱石吸附水的相应表达式：

$e_{m} = η {(\ln h_{r})}^{D - 3}$ ,

(2)

式中,η为吸水系数,h_r为相对湿度。

当含水率高于10%时,Kahr等给出膨润土的膨胀力计算公式为^[31]

$p = \frac{R T}{M υ} \ln h_{r}$ ,

(3)

式中,R为气体常数,T为热力学温度,M和 $υ$ 分别为水的分子质量和部分比体积。因此,将式（2）和（3）相结合,可以得出膨胀性能的e_m-p分形关系^[24]：

$e_{m} = {Kp}^{D - 3}$ ,

(4)

式中,D为膨润土表面分维,K为反映膨润土中蒙脱石矿物膨胀性能的系数,简称为蒙脱石膨胀系数,K越大蒙脱石的膨胀性能越大,在温度一定时只与蒙脱石交换性阳离子有关^[32]。

膨润土的分形维数可通过N₂吸附得到。图6绘制了不同蒸气压p/p₀下原始GMZ膨润土粉末和40℃和90℃下试样的N₂吸附量V_ads。可以发现3个试样的等温吸附线基本相同。采用Frenkel-Halsey-Hill方程计算了试样的表面分维^[33],各试样的D值约为2.75。表明膨润土的分形维数基本不受试验温度的影响,这主要是因为GMZ膨润土的矿物组成在25℃到90℃范围的蒸馏水中没有发生改变^[18],膨润土的表面结构在膨胀过程中没有受到化学反应的作用。

图 6 GMZ膨润土的N₂等温吸附线

Figure 6. N₂ adsorption isotherms of GMZ bentonite samples

下载: 全尺寸图片幻灯片

3.2 K-T_c关系

如上所述,当荷载一定时,膨润土的膨胀随温度的升高而增大,而分形维数为常数,所以可以认为温度对GMZ膨润土膨胀的影响主要表现在蒙脱石膨胀系数K的变化,该系数随温度的升高而增大。膨润土的膨胀性能随温度的升高而提高,也说明此时渗透膨胀为主,而DDL模型在这种情况下有很好的应用。因此,利用DDL模型可以计算GMZ膨润土在不同温度下的膨胀系数K。

Gouy-Chapman的DDL理论是基于两个蒙脱石层间的排斥力和吸引力提出的^[34]。完全饱和时的e_m表示为^[34]

$e_{m} = \frac{d - R_{ion}}{t + R_{ion}}$ 。

(5)

式中,t为蒙脱石层的厚度（0.96 nm）,d为两蒙脱石层之间距离的一半,R_ion为未水化的交换性阳离子的平均半径。

DDL模型表明膨胀力可以表示为^[34]

$p = f_{r} - f_{a}$ ,

(6)

式中,f_a为范德华力,表达式为^[34]

（ ） （ ）

$f_{a} = \frac{A_{h}}{24 π} [\frac{1}{d^{3}} + \frac{2}{（ d + t ）^{3}} - \frac{2}{（ d + t / 2 ）^{3}}]$ 。

(7)

式中,A_h为Hamaker常数（2.2×10^-20 J）。

蒙脱石间排斥力f_r计算式为^[34]

$f_{r} = 2 n b T (\cosh u - 1)$ ,

(8)

$u = 8 artanh [e^{- κ d} \tanh (Z / 4)]$ ,

(9)

$κ = \sqrt{\frac{2 n ν^{2} {e^{'}}^{2}}{ε k T}}$ ,

(10)

$Z = 2 arsinh (96.5 \times \frac{CEC}{S} \sqrt{\frac{1}{8 n ε k T}})$ 。

(11)

式中 u为平行蒙脱石层间中平面的静电势；1/κ为Debye长度（m）；b为Boltzmann常数（1.38×10^-23J/k）；ε为孔隙水的静态介电常数（6.95×10^-10C²/J/m）；n₀为孔隙水离子浓度（10×6.023×10²³个/m³）；CEC为阳离子交换量（75.1 cmol/kg）； $e^{'}$ 为电子电荷（1.602×10^-19C）；S为GMZ膨润土的总比表面积（0.75×810 m²/g）。

通常认为当膨润土在一定荷载作用下饱和时,渗透膨胀是在晶层膨胀完成之后才开始的^[15]。因此,半间距d应满足^[22]

$d > \frac{t + R_{i o n}}{t} d_{m} + R_{i o n}$ ,

(12)

其中,

$d_{m} = \frac{1}{CEC} \sum_{i}^{} {EXC}_{i} d_{i}$ ,

(13)

$R_{ion} = \frac{1}{CEC} \sum_{i}^{} {EXC}_{i} R_{i}$ 。

(14)

式中 EXC_i和R_i分别为第i个交换性阳离子的交换量和离子半径；Na⁺、K⁺、Mg²⁺和Ca²⁺的半径分别为0.098,0.133,0.082,0.1115 nm^[15]；d_i为仅存在第i个交换性阳离子蒙脱石晶层膨胀最大距离,对于K⁺、Ca²⁺、Mg²⁺和Na⁺,d_i分别为0.6,0.9,0.9,1.2 nm^[15]。因此,根据式（12）,常温时GMZ膨润土发生渗透膨胀d值应大于1.25 nm^[22]。将该值作为GMZ膨润土发生渗透膨胀和晶层膨胀的临界值,代入式（5）可以算出临界蒙脱石孔隙比约为1.086,并可估算出相应的荷载值为1820 kPa。所以对于GMZ膨润土而言,当荷载小于1820 kPa时,渗透膨胀为主要膨胀形态,反之,则以晶层膨胀为主。

由于渗透膨胀时蒙脱石层间间距随温度的升高而略有增加,在DDL模型的计算中,令GMZ膨润土在每个温度下的d等于1.3 nm,此时相应的蒙脱石孔隙比为1.13,对应于不同温度下保持体积不变的膨胀力试验。通过计算可以发现（表3）,DDL理论计算的膨胀力p随温度的增加而增大,得出的膨胀系数K随温度呈线性增加（图7）,K与温度T_c的关系式为

表 3 不同温度下膨胀系数K计算

Table 3. Calculated values of swelling coefficient K under different temperatures

T_c/℃	Z	κ/m^-1	u	p/kPa	K
25	19.172	691409134	3.456	1393.12	6.904
30	19.156	685683554	3.485	1465.08	6.992
40	19.123	674646562	3.542	1615.84	7.165
50	19.092	664125934	3.598	1775.94	7.336
60	19.061	654082622	3.652	1945.66	7.506
70	19.032	644481593	3.705	2125.26	7.673
80	19.003	635291309	3.756	2315.02	7.839
90	18.975	626483295	3.806	2515.22	8.003

下载: 导出CSV

| 显示表格

图 7 计算的GMZ膨润土K-T_c关系

Figure 7. Calculated relationship between K and T_c for GMZ bentonite

下载: 全尺寸图片幻灯片

$K = 0.017 T_{c} + 6.486$ ,

(15)

式中,T_c为摄氏温度（℃）。

3.3 验证与计算

结合K-T_c关系可得到不同温度下GMZ膨润土的e_m-p关系：

$e_{m} = (0.017 T_{c} + 6.486) p^{D - 3}$ 。

(16)

从式（16）可以看出,当荷载相同时,孔隙比与温度之间存在线性关系。采用式（16）估算了不同温度下GMZ膨润土e_m（图8）。室温条件下,Sun等^[35]GMZ膨润土试验数据也用于比较。结果表明,不同温度下GMZ膨润土的蒙脱石孔隙比的估算值与试验值吻合较好。

图 8 不同温度下GMZ膨润土的蒙脱石孔隙比估算值

Figure 8. Estimation of montmorillonite void ratio of GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

根据Bag等^[12]对Bikaner膨润土开展的膨胀试验结果,发现相同荷载下,Bikaner膨润土试样的孔隙比也随温度呈线性增加,不同温度下的e-p关系式可表示为 $e = (0.033 T_{c} + 6.58) p^{D - 3}$ ,其中D= 2.785。Bikaner膨润土膨胀预测值与试验数据的比较如图9所示,孔隙比预测值与试验数据之间吻合较好。

图 9 不同温度下GMZ膨润土的蒙脱石孔隙比估算值^[13]

Figure 9. Estimation of void ratio for Bikaner bentonite under different temperatures

下载: 全尺寸图片幻灯片

根据土力学公式,饱和后试样的最大膨胀率与试样孔隙比之间的关系为

$ε_{max} = \frac{e - e_{0}}{1 + e_{0}} \times 100 %$ 。

(17)

式中,e为饱和后膨润土试样的孔隙比,e₀为初始孔隙比,可以表达为

$e_{0} = \frac{d_{s} ρ_{w}}{ρ_{d}} - 1$ 。

(18)

式中,d_s为GMZ膨润土土粒相对质量密度,ρ_w为水的密度,ρ_d为试样的干密度。

结合式（1）,（17）和（18）,膨润土的最大膨胀率 $ε_{\max}$ 与孔隙比e_m之间关系为

$ε_{\max} = (\frac{{αe}_{m} + 1}{d_{s} ρ_{w}} ρ_{d} - 1) × 100 %$ 。

(19)

将式（16）代入式（19）中,可以得出不同温度下GMZ膨润土的最大膨胀率。从式（19）也可以看出,当荷载和温度条件相同时, $ε_{\max}$ 随试样的初始干密度线性增加,这与试验数据一致（图4）。同样,如图10所示,在相同的荷载和密度条件下, $ε_{\max}$ 随温度线性增加。 $ε_{\max}$ -T_c关系的斜率随竖向荷载减小,但随初始干密度增大而增大,表明温度对膨胀变形的影响随压力的增大而减弱,随干密度的增大而增强。

图 10 不同温度下GMZ膨润土最大膨胀率的预测值

Figure 10. Prediction of maximum swelling strain of GMZ bentonite at different temperatures

下载: 全尺寸图片幻灯片

当式（19）中的膨胀率等于零时,可得出不同温度下GMZ膨润土的膨胀力：

$p_{s} = {[\frac{1}{K α} (\frac{G_{s}}{ρ_{d}} - 1)]}^{\frac{1}{D- 3}}$ 。

(20)

由式（20）可知,膨胀力应随温度或初始干密度呈指数增长。初始干密度显著促进了温度对膨胀力的影响。如图11所示,不同温度下膨胀压力的预测值与试验数据之间也具有较好的一致性。

图 11 不同干密度不同温度时GMZ膨润土的膨胀力

Figure 11. Prediction of swelling pressure of GMZ bentonite with different densities under different temperatures

下载: 全尺寸图片幻灯片

4. 结论

（1）由于在本次试验条件下,渗透膨胀占主导地位,温度增加了黏土颗粒间扩散双电层的厚度,进而提高了GMZ膨润土的膨胀性能。使得膨胀率和膨胀力均随温度的升高而增大。

（2）当其他条件相同时,GMZ膨润土的最大膨胀率随温度呈线性增加,膨胀力随温度和干密度呈指数增长。温度对膨胀性能的影响还与试样干密度有关,干密度越大,温度升高对膨胀性能的促进作用越明显。

（3）压实膨润土的膨胀性能可采用分形模型表达成e_m=Kp^D-3。试验结果表明,GMZ膨润土在在25℃～90℃范围内蒸馏水中膨胀时,其分形维数D不变。同时,采用DDL模型计算得出蒙脱石的膨胀系数K随温度呈线性增加,GMZ膨润土的K-T_c关系可表示为 $K = 0.017 T_{c} + 6.486$ 。利用e_m-p与温度的关系,可以估算出GMZ膨润土在不同温度下的膨胀变形和膨胀压力。

（4）本文中计算模型是建立在膨润土矿物在100 ℃以内基本不发生改变的基础上的。当温度更高时,膨润土中某些矿物可能会发生化学反应并对膨胀性能产生影响,这种条件下膨胀性能的变化仍有待进一步的研究。

图 1 岩体波速分段统计直方图

Figure 1. Statistical histogram for subsection of wave velocity of rock mass

下载: 全尺寸图片幻灯片

图 2 模型锚布置图

Figure 2. Arrangement of model anchorage

下载: 全尺寸图片幻灯片

图 3 模型锚洞照片

Figure 3. Photos of model anchorage holes

下载: 全尺寸图片幻灯片

图 4 锚体与围岩前表面测点布置图

Figure 4. Arrangement of measuring points on front surface of anchorage and surrounding rock

下载: 全尺寸图片幻灯片

图 5 锚体与围岩内外测点布置图

Figure 5. Arrangement of internal and external measuring points of anchorage and surrounding rock

下载: 全尺寸图片幻灯片

图 6 1p荷载试验锚体应变-时间曲线

Figure 6. Anchorage strain-time curves of loading tests under 1p

下载: 全尺寸图片幻灯片

图 7 8p荷载试验锚体应变-时间曲线

Figure 7. Anchorage strain-time curves of loading tests under 8p

下载: 全尺寸图片幻灯片

图 8 1p~24.59p荷载试验锚体应变曲线

Figure 8. Anchorage load-strain curves of loading tests under 1p~24.59p

下载: 全尺寸图片幻灯片

图 9 1p~8p荷载试验测线变形曲线

Figure 9. Deformation curves at measuring points of loading tests under 1p~8p

下载: 全尺寸图片幻灯片

图 10 1p和3p荷载试验典型测点荷载-变形曲线

Figure 10. Load-strain curves at typical measuring points of loading tests under 1p and 3p

下载: 全尺寸图片幻灯片

图 11 5p和8p荷载试验典型测点荷载-变形曲线

Figure 11. Load-strain curves at typical measuring points of loading tests under 5p and 8p

下载: 全尺寸图片幻灯片

图 12 锚体与围岩前表面及内部测点变形-时间曲线

Figure 12. Strain-time curves at measuring points of anchorage and surrounding rock

下载: 全尺寸图片幻灯片

图 13 锚体内部测点应变-时间曲线

Figure 13. Strain-time curves at internal measuring points of anchorage

下载: 全尺寸图片幻灯片

表 1 锚碇围岩岩性及主要物理力学参数

Table 1 Lithology and primary physical and mechanical parameters of surrounding rock of anchorage

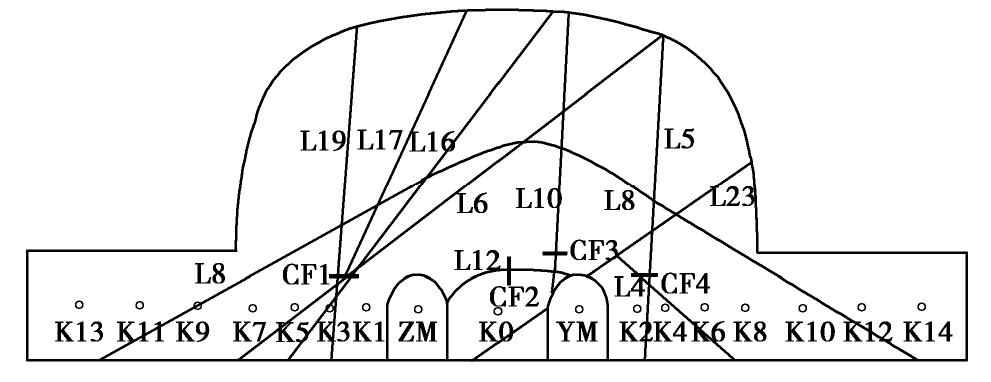
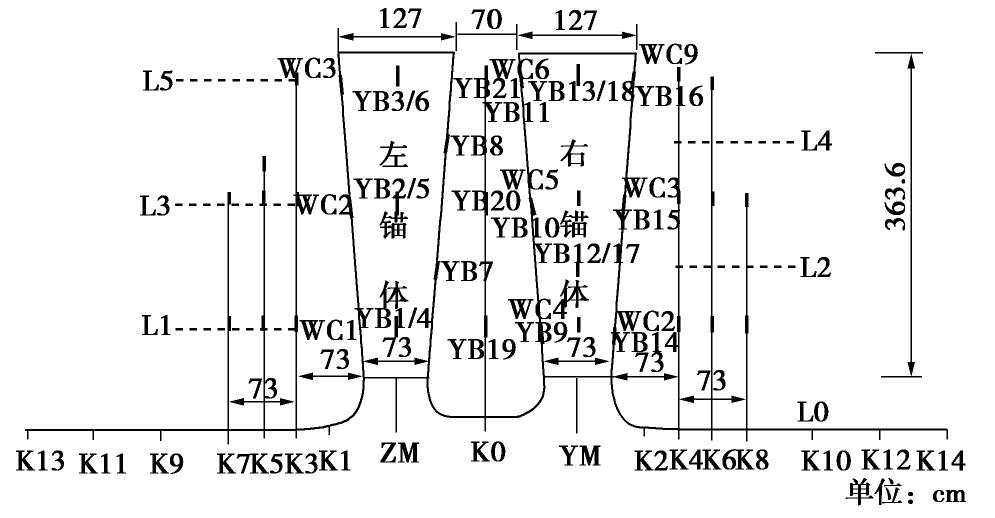
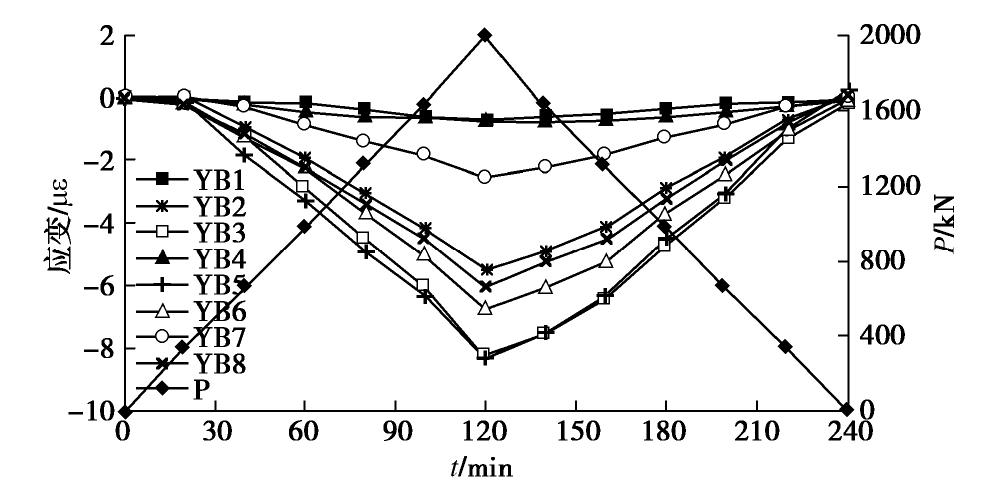
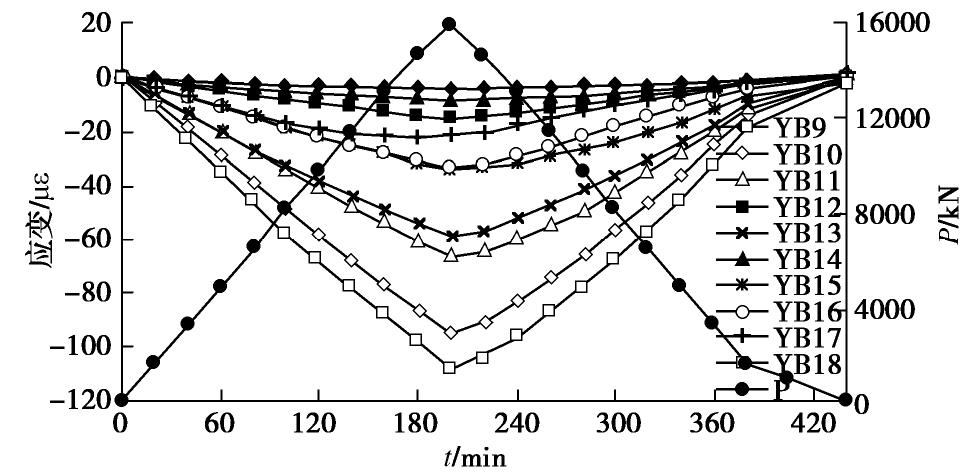
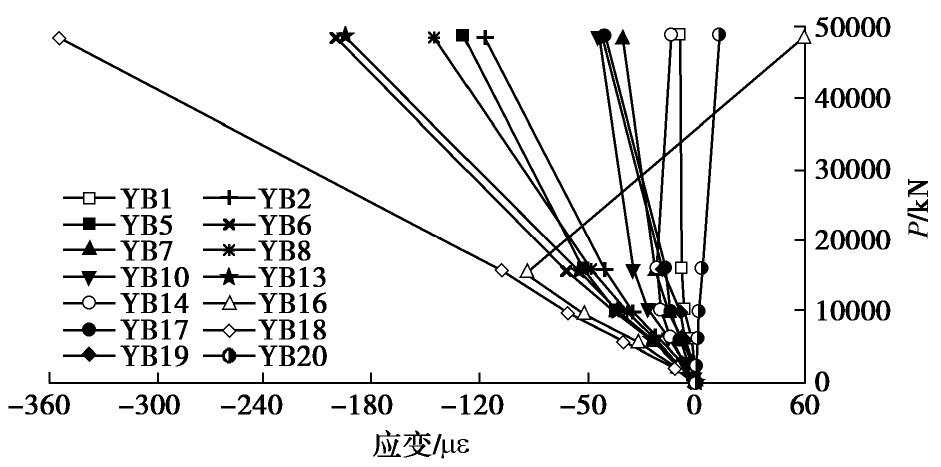
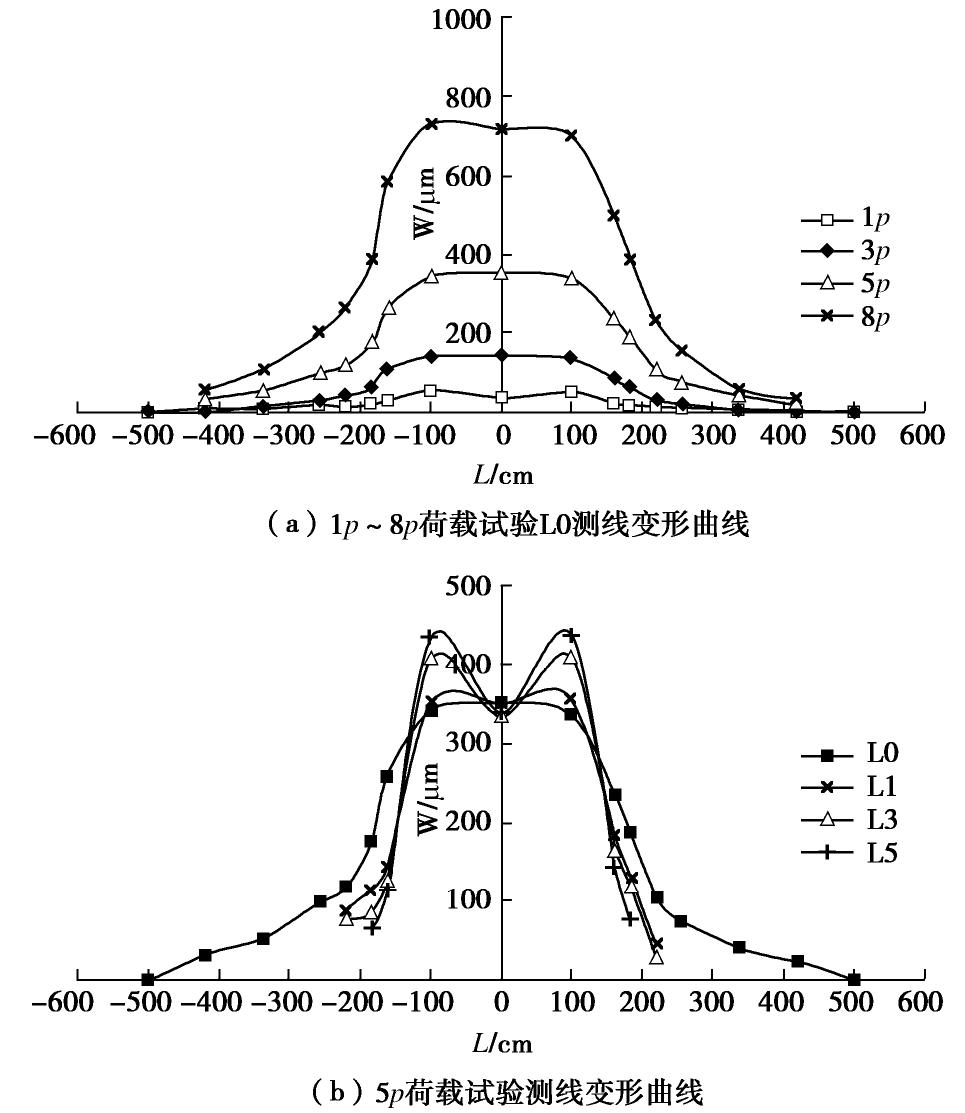
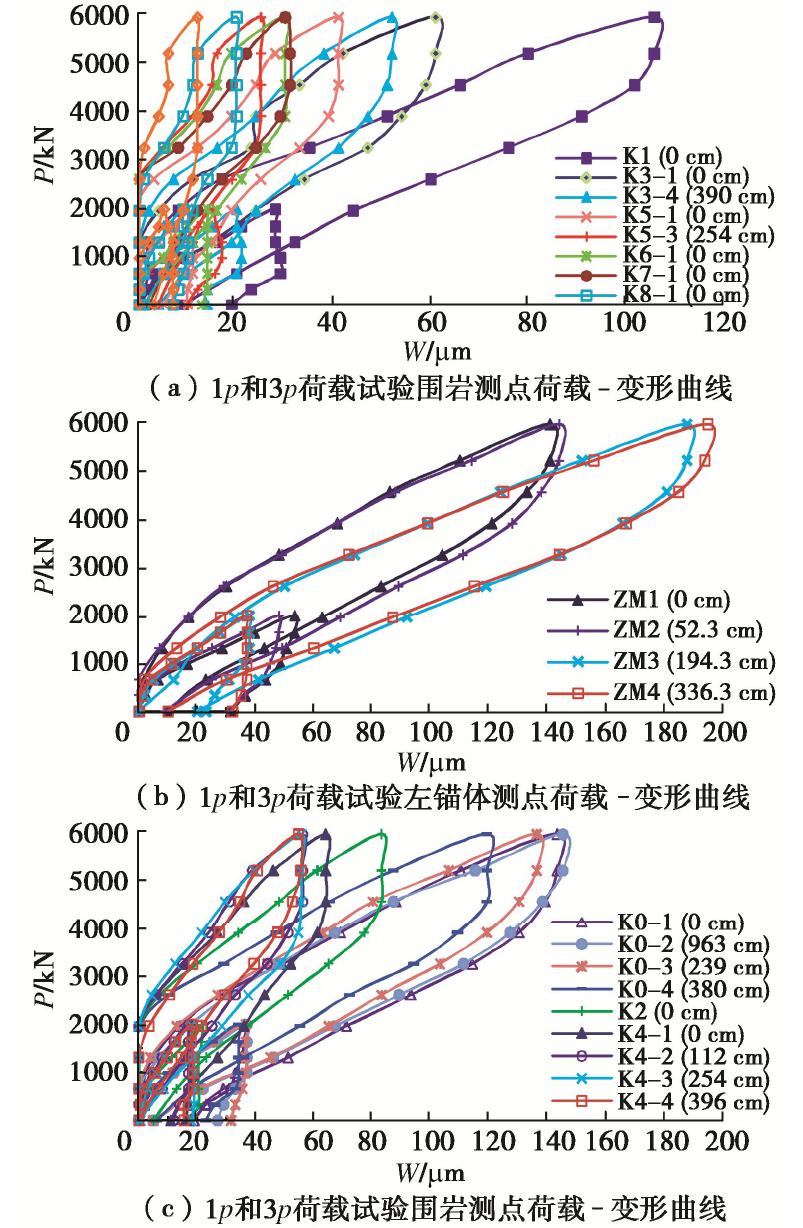
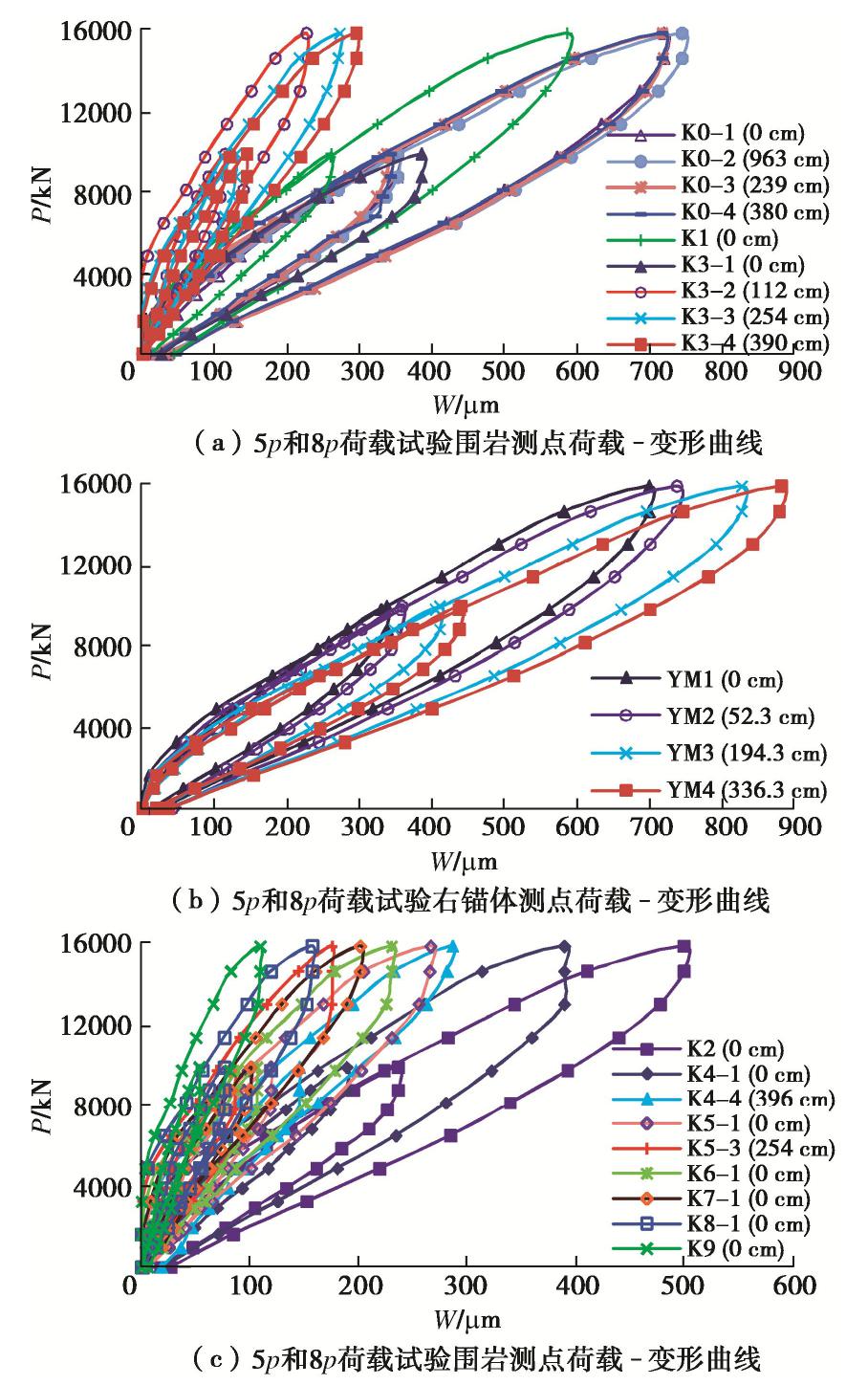
洞别	岩性名称	天然块体密度/(g·cm^-3)	含水率/%	孔隙率/%	饱和单轴抗压强度/MPa	软化系数	泊松比	抗拉强度/MPa	岩体变形模量/ GPa	混凝土与岩体抗剪强度f, C/MPa
洞别	岩性名称	天然块体密度/(g·cm^-3)	含水率/%	孔隙率/%	饱和单轴抗压强度/MPa	软化系数	泊松比	抗拉强度/MPa	岩体变形模量/ GPa	抗剪断	抗剪(摩擦)
实体锚左锚洞	粉砂质白云岩夹黑云母石英片岩	2.64~2.93	0.10~0.30	0.69~3.86	19.9~81.0	0.35~0.90	0.26~0.29	2.79~5.01	2.13~2.51	1.50, 1.28	1.15, 0.62
实体锚左锚洞	粉砂质白云岩夹黑云母石英片岩	2.74	0.17	1.90	56.1	0.68	0.25	4.10	2.35	1.50, 1.28	1.15, 0.62
实体锚右锚洞	石英白云母片岩、含碳白云母石英片岩	2.73~2.82	0.70~0.85	3.98~4.11	16.8~21.0	0.73~0.83	0.20~0.25	1.49~2.11	—	0.49, 0.91	0.47, 0.47
	石英白云母片岩、含碳白云母石英片岩	2.77	0.77	4.04	18.7	0.76	0.23	1.81	—	0.49, 0.91	0.47, 0.47
	方解石黑云母变质细砂岩	2.72~2.77	0.14~0.19	1.14~1.71	52.2~53.3	0.64~0.81	0.22~0.26	3.44~4.60	0.74~159	1.20, 1.36	1.08, 0.58
	方解石黑云母变质细砂岩	2.73	0.16	1.43	52.9	0.71	0.24	3.99	1.16	1.20, 1.36	1.08, 0.58
模型洞	含榴黑云角闪斜长片麻岩	2.63~2.76	0.09~0.78	0.91~6.11	29.8~58.5	0.44~0.87	0.21~0.26	3.55~4.83	—	—	—
模型洞	含榴黑云角闪斜长片麻岩	2.71	0.44	3.06	42.1	0.73	0.25	4.15	—	—	—
注：表中横线上数值为范围值,横线下数值为平均值。

下载: 导出CSV

表 2 1p~24.59p荷载试验模型锚与围岩测点变形最大值

Table 2 Maximum deformations of anchorage and surrounding rock at measuring points of loading tests under 1p~8p

荷载级别	测线	左侧测孔（测点）						左锚	中隔墙	右锚	右侧测孔（测点）
荷载级别	测线	K11	K9	K7	K5	K3	K1	ZM	K0	YM	K2	K4	K6	K8	K10	K12
1p	L0	7	7	18	11	20.5	29	53.5	36	49	21.5	18	14	10	8	6
	L1			14.5	17.5	21		48	37	48		19	16.5	9
	L3				17	18		38	36.5	38		17	12
	L5				13	17		37	34	30		18.5	9
3p	L0	1	12	30	41	61	106	141	143	136	83	64	30	20	6	0
	L1			22	36	52		144	145	142.5		55.5	43	8
	L3				25	48		188	136	173		56	37
	L5				14.5	33		195	119	191		54.5	24
5p	L0	33	53	100	119	177	260	342.5	352	337	236	188.5	106	76	42	24
	L1			89	115	144		352	352	358		185	131	48
	L3			80	86	129		408	336.5	410		168	121	29
	L5				65	116		436	342	439		145	79
8p	L0	56	109	201	265	385	585	730	719	699	499	389	230	157	59	33
	L1			159	228	295		750	744	737		392	263	91
	L3			157	175	272		831	718	826		352	264	20
	L5				121	228		871	717	881		286	159
24.59 p	L0~ L5	845	1303	1980		4030	4770	5209	4940	5230	3790	3790		1860	830	442

下载: 导出CSV

表 3 1p~8p荷载试验锚体与围岩测点变形残余量

Table 3 Residual deformations point of anchorage and surrounding rock at measuring points of loading tests under 1p~8p (μm)

荷载	K3-1	K3-2	K3-3	K3-4	K1	ZM1	ZM2	ZM3	ZM4	K0-1	K0-2	K0-3	K0-4	YM1	YM2	YM3	YM4	K2	K4-1	K4-2	K4-3	K4-4
1p	20.5	13	14	14	19	31.5	31	23	32	19	27	31.5	23	39	34	32	23	17.5	16	18	12	15.5
3p	5	9	2	4	9	10	9	20	10	16	5	5	6	10	5.5	8	6	5	11	0.5	0	5
5p	9	5	2	2	10	12.5	22	21	20	19	13	17	19	15	21	21	19	17	0.5	12	2	18
8p	26	1	0	0	44	33	40	41	35	34	30	36	46	28	42	35	36	27	20	1	0	1

下载: 导出CSV

表 4 1p~8p荷载试验位错计及测缝计测点最大值及残余量

Table 4 Maximum values and residual volumes at measuring points by dislocation meter and jointmeter of loading tests undr 1p~8p (μm)

荷载级别测点编号	1p				3p				5p				8p
荷载级别测点编号	WC3	WC7	CF2	CF3	WC3	WC7	CF2	CF3	WC3	WC7	CF2	CF3	WC3	WC7	CF2	CF3
最大值	3.95	0	0	5.6	17.25	3.45	1.68	2.8	14.22	4.62	2.25	11.25	18.96	2.31	1.68	14
残余量	1.58	0	0	5.6	5.75	0	1.68	1.12	0	2.31	2.25	7.25	6.3	2.31	1.68	0

下载: 导出CSV

参考文献(13)

[1]	夏才初, 程鸿鑫, 李荣强. 广东虎门大桥东锚碇现场结构模型试验研究[J]. 岩石力学与工程学报, 1997, 16(6): 571-576. doi: 10.3321/j.issn:1000-6915.1997.06.010 XIA Cai-chu, CHENG Hong-xin, LI Rong-qiang. Testing study on field structure model of the east anchorage of Guangdong Humen Bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(6): 571-576. (in Chinese) doi: 10.3321/j.issn:1000-6915.1997.06.010
[2]	肖本职, 吴相超, 彭朝全. 重庆鹅公岩大桥隧道锚围岩稳定性[J]. 岩石力学与工程学报, 2005, 24(增刊2): 5591-5597. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2005S2057.htm XIAO Ben-zhi, WU Xiang-chao, PENG Chao-quan. Stability of the anchorage wall rock of tunnel for Chongqing Egongyan bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S2): 5591-5597. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2005S2057.htm
[3]	邬爱清, 彭元诚, 黄正加, 等. 超大跨度悬索桥隧道锚承载特性的岩石力学综合研究[J]. 岩石力学与工程学报, 2010, 29(3): 433-441. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201003003.htm WU Ai-qing, PENG Yuan-cheng, HUANG Zheng-jia, et al. Rock mechanics comprehensive study of bearing capacity characteristics of tunnel anchorage for super-large span suspension bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 433-441. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201003003.htm
[4]	胡波, 曾钱帮, 饶旦, 等. 锚碇－围岩系统在拉剪复合应力条件下的变形规律及破坏机制研究－以坝陵河特大岩锚悬索桥为例[J]. 岩石力学与工程学报, 2007, 26(4): 712-719. doi: 10.3321/j.issn:1000-6915.2007.04.008 HU Bo, ZENG Qian-bang, RAO Dan, et al. Study of deformation law and failure mechanism of anchorage-surrounding rock system under tensile-shear complex stresses -taking super-large suspension bridge on Baling river for example[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 712-719. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.04.008
[5]	张奇华, 余美万, 喻正富, 等. 普立特大桥隧道锚现场模型试验研究－抗拔能力试验[J]. 岩石力学与工程学报, 2015, 34(1): 93-103. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501010.htm ZHANG Qi-hua, YU Mei-wan, YU Zheng-fu, et al. Field model tests on pullout capacity of tunnel-type anchorages of Puli bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 93-103. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501010.htm
[6]	蒋昱州, 王瑞红, 朱杰兵, 等. 伍家岗大桥隧道锚三维地质力学模型试验研究[J]. 岩石力学与工程学报, 2016, 35(增刊2): 4103-4113. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S2071.htm JIANG Yu-zhou, WANG Rui-hong, ZHU Jie-bing. Geomechanical model test on global stability for Wujiagang bridge tunnel-type anchorages[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 4103-4113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S2071.htm
[7]	张宜虎, 邬爱清, 周火明, 等. 悬索桥隧道锚承载能力和变形特征研究综述[J]. 岩土力学, 2019, 40(9): 3576-3584. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909031.htm ZHANG Yi-hu, WU Ai-qing, ZHOU Huo-ming, et al. Review of bearing capacity and deformation characteristics of tunneltype anchorage for suspension bridge[J]. Rockand Soil Mechanics, 2019, 40(9): 3576-3584. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909031.htm
[8]	江南, 冯君. 铁路悬索桥隧道锚受载破裂力学行为研究[J]. 岩石力学与工程学报, 2018, 37(7): 1665-1670. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201807010.htm JIANG Nan, FENG Jun. Damage behavior of tunnel-type anchorages of railway suspension bridges under loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(7): 1659-1670. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201807010.htm
[9]	李栋梁, 刘新荣, 吴相超, 等. 浅埋软岩隧道式锚碇稳定性原位模试验研究[J]. 岩土工程学报, 2017, 39(11): 2078-2087. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201711018.htm LI Dong-liang, LIU Xin-rong, WU Xiang-chao, et al. Stability of shallow buried soft rock tunnel anchorage by in-situ model test[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2078-2087. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201711018.htm
[10]	公路悬索桥设计规范：JTG/T D65-05--2015[S]. 北京: 人民交通出版社, 2015. Specification of design for highway suspension bridge: JTG/TD65-05--2015[S]. Beijing: China Communications Press, 2015. (in Chinese)
[11]	廖明进, 王全才, 袁从华, 等. 基于楔形效应的隧道锚抗拔承载能力研究[J]. 岩土力学, 2016, 37(1): 185-192, 202. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601023.htm LIAO Ming-jin, WANG Quan-cai, YUAN Cong-hua, et al. Research on the pull-out capacity of the tunnel-type anchorage basedon wedge-effect[J]. Rock and Soil Mechanics, 2016, 37(1): 186-192, 202. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601023.htm
[12]	江南, 黄林, 冯君, 等. 铁路悬索桥隧道式锚碇设计计算方法研究[J]. 岩土力学, 2020, 41(3): 999-1009, 1047. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003031.htm JIANG Nan, HUANG Ling, FENG Jun, et al. Research on design and calculation method of tunnel-type anchorage of railway suspension bridge[J]. Rockand Soil Mechanics, 2020, 41(3): 999-1009, 1047. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003031.htm
[13]	张奇华, 李玉婕, 余美万, 等. 隧道锚围岩抗拔机制及抗拔力计算模式初步研究[J]. 岩土力学, 2017, 38(3): 810-820. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201703025.htm ZHANG Qi-hua, LI Yu-jie, YU Mei-wan, et al. Preliminary study on pullout mechanisms and computational mode of pullout force for rocks surrounding tunnel-type anchorage[J]. Rockand Soil Mechanics, 2017, 38(3): 810-820. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201703025.htm

施引文献(15)

期刊类型引用(9)

1.	陈梦豪，付海，曹珊珊，林铭宇，陈良宇. 温度对MX-80膨润土物理性能的影响. 金陵科技学院学报. 2024(01): 46-53 . 百度学术
2.	李裕诚，陈永贵，刘丽，叶为民，王琼. 高压实膨润土多尺度膨胀力特性研究进展. 岩土工程学报. 2024(11): 2457-2464 . 本站查看
3.	薄纯悦，刘春红，冷佳欣，陈聪. 含水率和干密度对三峡库区紫色土膨胀特性的影响. 土壤. 2024(06): 1381-1389 . 百度学术
4.	项国圣，卞云飞，付文青，周殷康. 热-碱作用对压实膨润土抗剪性能的影响. 安徽建筑大学学报. 2024(06): 8-14 . 百度学术
5.	李彩霞，李俊，徐猛，刘敏，刘桂祺. 氯盐溶液对钠基膨润土垫层膨胀性能的影响. 土木与环境工程学报(中英文). 2023(01): 97-104 . 百度学术
6.	王琼，张佳南，高岑，苏薇，刘樟荣，叶为民. 基于梯度提升决策树算法的膨润土膨胀力预测. 世界核地质科学. 2023(03): 775-786 . 百度学术
7.	曾召田，张瀚彬，邵捷昇，车东泽，吕海波，梁珍. MX-80膨润土高温老化时间效应的细微观分析. 岩土力学. 2023(S1): 145-153 . 百度学术
8.	胡志杰，项国圣，付文青，王浩，李华健. 荷载-溶液作用下膨润土压缩渗透性能研究. 地下空间与工程学报. 2023(06): 1851-1858 . 百度学术
9.	项国圣，胡志杰，葛磊，王浩. 含盐水溶液作用下膨润土膨胀性能衰减机理. 华北水利水电大学学报(自然科学版). 2022(05): 85-91 . 百度学术