Stochastic back analysis of material parameters of tailings dams using Bayesian updating approach
-
摘要: 为准确获得有限数据条件下的尾矿坝材料参数取值,在贝叶斯更新理论和有限元分析框架下,提出了考虑不确定性的尾矿坝材料参数随机反演方法。为提高参数随机反演分析的计算效率,利用随机多项式展开建立尾矿坝代表性监测点位移与输入参数之间的隐式函数关系。以某实际尾矿坝为例,基于有限的位移监测数据进行多层尾矿材料参数随机反演分析,说明了提出方法的有效性。结果表明,提出方法可以有效缩减尾矿坝材料参数的不确定性,准确推断尾矿坝材料参数的概率分布,并识别不同材料参数(弹性模量和泊松比等)对尾矿坝变形的影响程度。Abstract: To obtain accurate values of the material parameters of tailings dams based on the limited data, a stochastic back analysis approach considering the uncertainties of the material parameters of tailings dams is proposed under the framework of Bayesian updating and finite element analysis. To improve the computational efficiency of back analysis, a polynomial chaos expansion is adopted to replace the implicit function between the displacements of tailing dams at the representative monitoring points and uncertain input parameters. A real tailings dam is taken as an example to demonstrate the effectiveness of the proposed approach for stochastic back analysis of parameters of multi-layered tailings materials based on the monitoring data of displacements. The results indicate that the proposed approach can effectively reduce the estimation in the uncertainties of the material parameters of tailings dams, accurately infer the probability distributions of the material parameters, and identify the influence degree of different material parameters (e.g., elastic modulus, Poisson’s ratio) on the deformation of the tailings dams.
-
0. 引言
海底管道是海洋油气能源运输的生命线,其安全运营是保障海洋油气资源开发的关键之一。深海管道在安装过程中通常直接铺设在海床表面,在管道自重、波浪、洋流等荷载和施工船舶扰动等动态铺设效应的共同作用下贯入海床至一定深度。管道动态运动一方面引起土体不排水抗剪强度降低,造成土体重塑,另一方面使得海床表面形成沟壕,两者共同作用造成管道贯入深度大于准静态计算值。管道埋置深度的准确评估对深海管道的设计至关重要,特别是在管道的在位稳定性、疲劳寿命[1]、热胀屈曲和轴向移动[2-3]等几个方面。
对于管道在不排水黏土中的静态竖向贯入过程的模型试验[4]已有大量相关研究。受土体参数限制,对于更为一般的问题,往往采用经典塑性理论[5-7]或小应变有限元分析理论[8-9]进行分析。近年来,随着数值模拟技术的高速发展,大变形分析开始得到广泛运用。当前,最常见的大变形模拟方法包括基于有限元分析的任意欧拉-拉格朗日法(ALE法)[10]、耦合欧拉-拉格朗日法(CEL法)[11-12]和小应变下网格重划分与差值方法(RITSS法)[2],但采用上述方法的研究对管道贯入深度多局限于一倍管径内。Hawlader等[13]建立了计算流体动力学模型和CEL模型对单调贯入至5倍直径的管道运动过程进行模拟,真实反映了由管道贯入引起的极端土体变形,但由于网格重划分涉及到复杂的应力映射,该模型未模拟土体的坍塌回流问题。在管道贯入海床的过程中,管周土体将发生严重重塑并坍塌至管道上部。这一过程中土体自由界面表面演变复杂,对数值模拟带来了极大的挑战。因此,开发一种稳定高效的数值模拟方法是解决此类问题的关键。
本文基于连续极限分析法(SLA)对管道在竖向循环运动过程中的土体大变形问题进行了研究。首先分析了单调和循环位移下管土相互作用特性,并与已有的模型试验结果进行了对比验证。之后模拟了不同复杂加载路径下管道与土体的循环竖向作用,探索了土体抗力和破坏机构演变规律。该工作以期为复杂荷载条件下管-土相互作用简化模型的建立提供探索性依据,同时推广SLA方法在极端大变形岩土工程问题中的应用。
1. 数值模型
1.1 SLA法介绍
该方法在早期通常用于解决结构工程领域的一些简单问题,例如框架和平板等,此后被Kong等[14-15]进一步拓展使其适用于土结相互作用的分析。SLA方法以牛津大学开发的有限元极限分析软件OxLim为核心,使用极限上限分析求解塑性变形区域的速度场,并将其在单个时间步内进行积分从而更新模型的瞬时位移场。通过重复这一小应变极限分析步骤,最终获得大变形问题的求解。
在SLA数值分析中,土体本构模型通常采用改进后的Tresca模型。Einav等[16]在大量研究基础上提出通过如下经验公式考虑应变软化和应变率效应对土体不排水抗剪强度的影响:
su=su0×[δrem+(1−δrem)e-3ξ/ξ95]×[(1+μlgmax(γmax,γref)γref], (1) 式中,su0为土体的初始不排水抗剪强度,一般情况下由su0 = sum + kz确定,sum为泥面强度,k为强度沿深度变化梯度,z为泥面以下深度;第二项应变软化参数用于考虑由塑性应变
ξ 累积造成的土体强度衰减,第三项率效应参数则用于说明应变速率对土体强度的影响。残余强度系数δrem 对应为灵敏度St 的倒数,表示土体完全重塑后强度与初始强度的比值,延展参数ξ95 则与土样强度降低到其峰值强度5%时的累积剪应变相对应。其中,海洋软土的δrem 变化范围一般为0.2~0.5,ξ95 为10~50。黏度系数μ 用于分析土体强度随应变率增大而增强的关系,˙γmax 为土体最大剪应变速率,˙γref 为土体参考剪应变速率,对于海洋软土而言,μ取值范围通常为0.05~0.2,˙γref 一般取3×10−6/s[16]。1.2 管土模型及参数选取
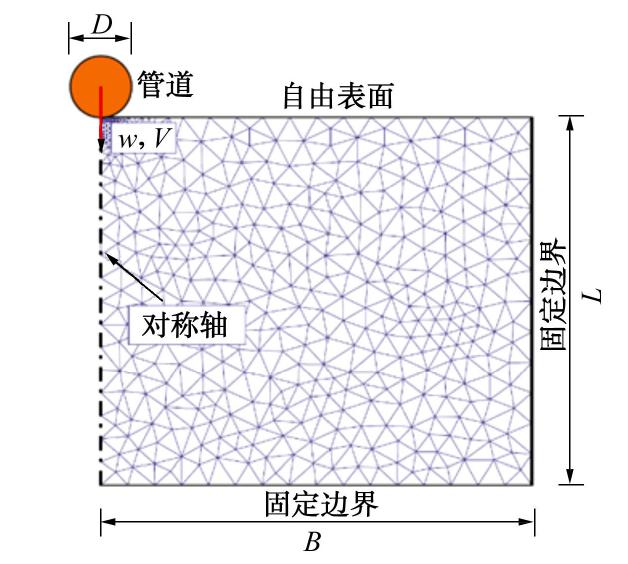
本文基于平面应变假定进行分析,图1为管道-土体相互作用模型及初始网格划分,管道直径为D,其属性设置为平面应变刚体,整个圆周划由60条直线段连接而成;管道在竖直方向上可自由移动,仅对其旋转自由度进行约束。土体的半宽、半深分别用B和L表示,底边和右侧边界设置为固定约束,表面设置为自由边界。由于该计算模型具有对称性,本文对其右半部分进行考虑,并对对称轴上的节点的横向移动进行约束。模型的最小单元尺寸为0.0005D2,每次分析的管道增量位移δd设置为0.005D。
土体浮重度为
γ′ ,管土界面切向最大容许剪应力为τint =αsu ,其中α 表示界面黏聚力系数(α =0为完全光滑,α =1为完全粗糙),su为土体不排水抗剪强度。管土法向最大拉应力为T,在贯入过程中假定管土界面不能承受拉应力(T=0),而上拔过程中管道底侧承受无穷拉应力(T=∞)。2. 单调加载
本节采用SLA方法对较深埋深管道的竖向贯入过程进行数值模拟,Lee[17]在常重力下针对高岭土地基进行了此类问题的小比尺物理模型试验,从中观察到土体由整体破坏到局部破坏的破坏机构演变。本节将模型管道视作刚体,由海床表面贯入至4D处,假定管土界面完全光滑,故本算例中
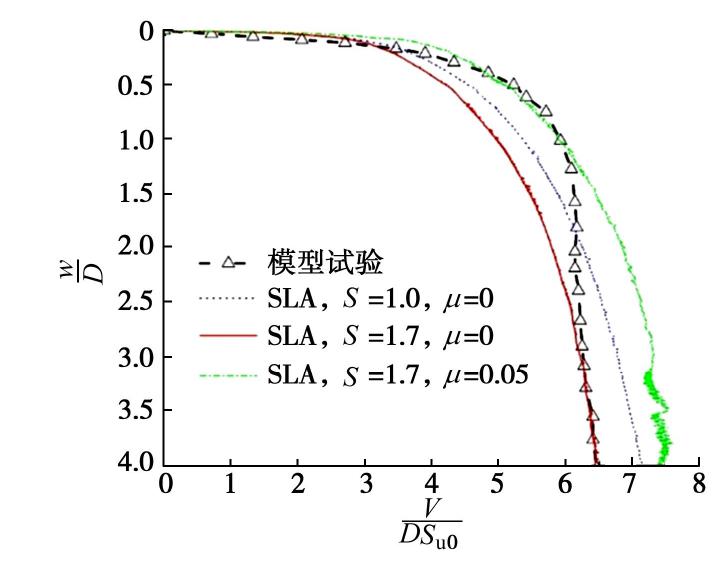
α =0,具体土体参数见表1所示。图2为管道从海床表面贯入至4D过程的荷载-位移关系曲线。结果表明:不考虑应变软化和率效应的理想土(St = 1,
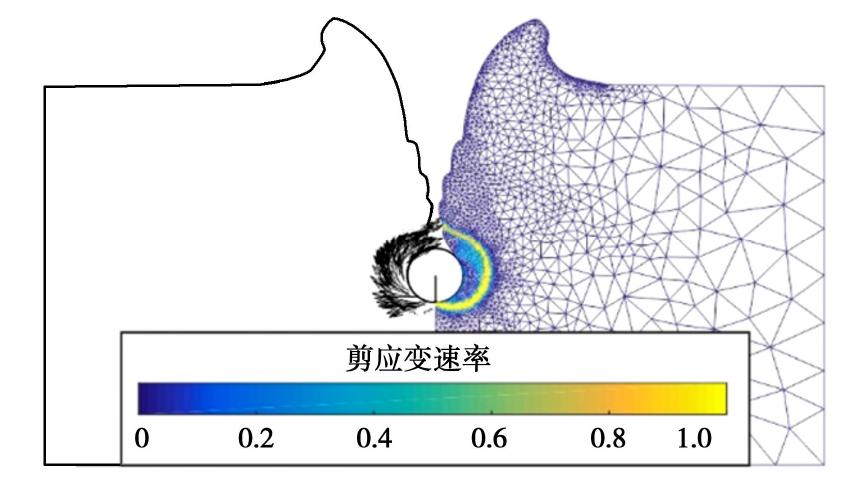
μ = 0)在整个加载过程中与模型试验结果存在明显差异,考虑土体的软化而不考虑率效应的算例(St = 1.7,μ = 0)可以更合理地预测了深埋处的阻力,但在深度小于3D时仍存在计算结果偏小的情况;当考虑率效应(μ = 0)时土体抗力计算结果出现明显的增大,在埋深小于1D时与模型试验结果高度吻合。图3为管道贯入至一定深度后土体速度场和无量纲化剪切应变率分布情况。随着管道贯入深度逐渐增大,最终剪切破坏带集中分布在管道周围,土体破坏机构转变为局部破坏模式。由于该模型试验是在常重力下以较小比例进行,土体重量的影响远小于现场,因此在模型试验和数值模拟中均未发现管道上方土体的回填现象。
3. 循环加载
本节对复杂加载路径下管道与土体的循环竖向作用进行分析。首先对循环位移下管土相互作用特性进行模拟,并将模拟结果与Hu等[18]提供的离心试验结果进行了比较,验证了SLA模型的有效性;之后针对几个关键参数开展参数分析,对复杂加载路径下土体抗力和破坏机构演变规律进行探究。
3.1 验证
采用SLA方法对Hu等[18]离心机试验的最初几个加载循环进行模拟。该试验中,管道从泥面处贯入至初始埋深3D,之后进行一次振幅为3D的上拔/再贯入循环。管-土界面张拉力在上拔过程中设为无穷大,贯入过程中为零,其他具体土体参数见表1所示。注意,由于Hu等[18]给出的初始土体强度在泥面处大小为0,为保证模拟过程数值稳定性,将土体初始强度设置为su0=1+4.8z,这一处理使SLA模型中3D深度处的初始土体强度与离心试验保持一致。离心机试验中未提供的参数St和
ξ95 分别取3.3和10,土体有效重度γ′ 取6 kN/m3,与实际深海海床土体重度一致。图4(a)将数值模拟结果(
μ =0.05)与离心机试验得到的土体抗力进行比较。在初始贯入阶段两种方法的计算结果吻合程度较好,在下行到达3D深度、阻力到达最大值前贯入阻力与埋深基本成线性增加关系;稍有不同的是,在开始贯入前离心试验中的管道所受的土体抗力为非零值,该抗力是否源于浮力尚不明确。在上拔阶段,由于假设土体为刚塑性材料且管-土界面张拉力在上拔过程中为无穷大,管道在向上运动初始阶段土体抗力会立刻达到峰值,而在离心试验结果中则需要大约0.3D的距离以达到峰值阻力,但在管道上行至2.4D深度后重新逼近离心试验结果。在再贯入阶段,数值模拟结果与试验曲线吻合较好,土体抗力较初次贯入时有明显减小,表明土体内部发生了严重的重塑现象。图4(b)显示了率效应对土体抗力的影响,此处仅给出初始贯入过程和上拔阶段的结果。在初始贯入阶段,μ =0.05和0.1的数值模拟结果均与离心机试验结果高度吻合;而在上拔过程中土体抗力随μ 的增大而显著增加,特别是在埋置深度大于1D时,与离心机试验结果存在较大差距。图5展示了竖向循环加载试验中不同阶段的土体变形以及应变软化系数和率效应系数分布情况。此处,率效应系数与最大剪切应变率
˙γmax 相关,也间接反映土体剪切变形程度。管道上拔后管周剪切带附近土体强度接近于完全重塑土强度,远离剪切带上方的土体则经历不同程度应变软化,因此,在再贯入过程中的竖向土体抗力远小于初始贯入过程中的竖向土体抗力(图4(a))。3.2 参数研究
本节对管道与土体的循环竖向作用中循环振幅wult和加载路径的影响进行探究。土体初始强度设置为su0=1+2z,土体重度为3 kN/m3。考虑土体的软化而不考虑率效应,残余强度系数
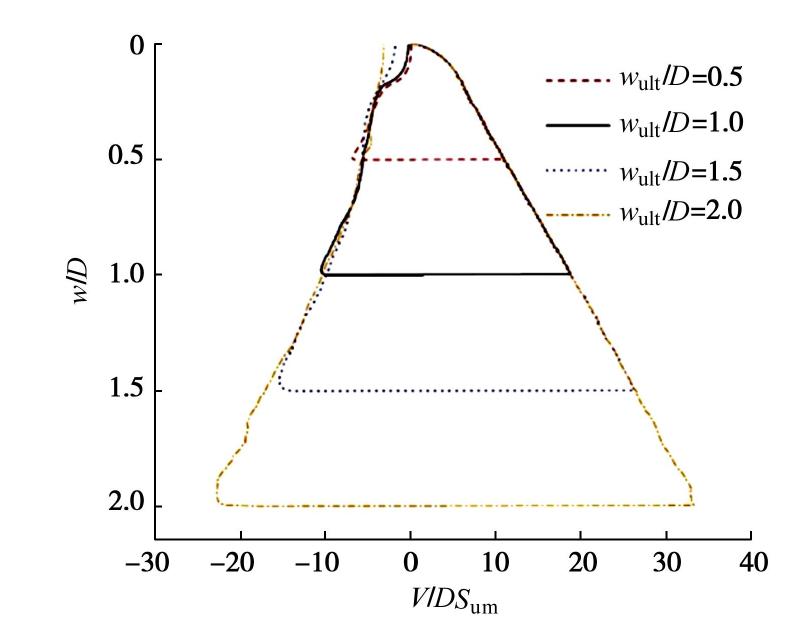
δrem 和延性参数ξ95分别取0.3和20,其他参数与3.1节中一致。图6为管道竖向贯入至一定深度(wult)后上拔至海床表面过程中土体抗力的变化规律。对4组不同深度进行分析:wult/D=0.5,1.0,1.5,2.0。在加载过程中4种工况下土体抗力变化具有相似的规律。值得注意的是,wult/D=0.5和1两种工况下管道上拔至泥面处时土体抗力接近于0,这与海洋立管的典型管土相互作用模型吻合,而其它两种工况则表现出大于0的土体抗力。
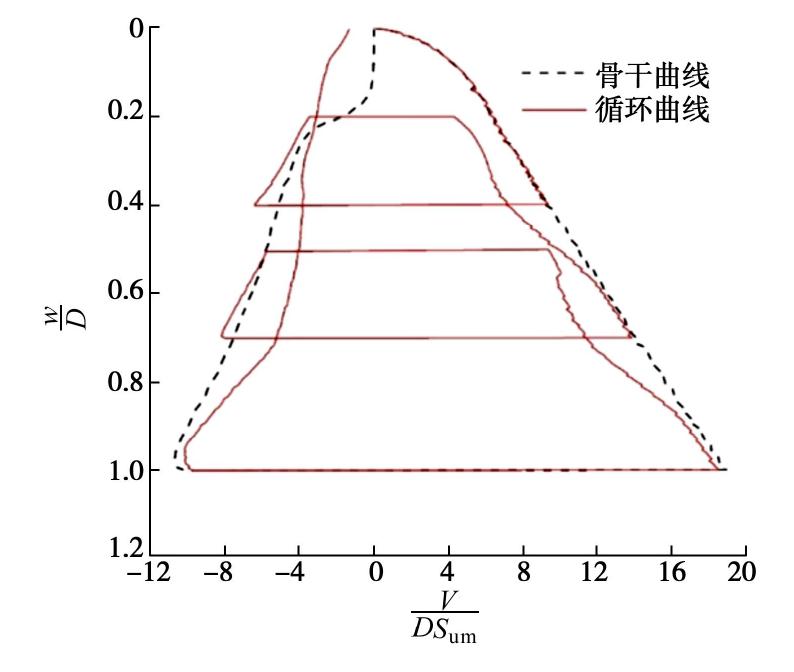
图7为非横幅循环加载路径下的土体抗力-埋深关系曲线,上述wult/D=1的算例在图中作为参照,将该曲线定义为骨干曲线。在管道每一次再贯入过程的初始阶段,受先期管道运动的影响,土体抗力最初与骨干曲线值相比较小,当管道继续向下贯入,超过历史最大埋深后,土体抗力与骨干曲线逐渐逼近,这种现象与Randolph等[19]的研究结论一致。此外,图7中前2次循环的管道上拔承载力与骨干曲线值相比偏大,直到第3次循环(0.2≤w/D≤1.0)其值低于骨干曲线,表明管道移动距离越大,土体应变软化越严重,对管道的上拔承载力的削弱作用越明显。值得注意的是,在第三次上拔过程的最后阶段(w/D≤0.2),循环贯入工况下管道承受的土体抗力明显大于直接贯入的情况,且当管道上升至泥面处时土体抗力为非零值,该现象与图8中两种工况下软化系数相吻合。观察图8可以发现,在循环贯入—上拔试验中管道底部存在土体黏结的情况,而在单次贯入—上拔的工况下管道几乎完全脱离土体。
图9(a)为管道小振幅(0.1D)竖向循环加载路径下的土体抗力-埋深关系曲线。管道在初始状态贯入至0.5D后在0.4D和0.5D之间进行十次垂直振动循环,然后再贯入至1D深度,最后上拔至海床表面。此外,图中同样给出管道直接贯入到1D然后上拔至泥面的骨干曲线以作对比。图9(a)表明,在循环运动过程中土体竖向抗力随循环次数增加而逐渐下降,尽管这一弱化速率随振次逐渐降低,当管道结束循环再次向下贯入时,土体抗力在初始阶段远小于骨干曲线值,随着深度增加逐渐逼近骨干曲线。图9(b)为管道在较大振幅(0.5D)竖向循环加载路径下的土体抗力-埋深关系曲线。在此工况下管道首先被直接贯入至2D,处于完全掩埋状态,然后在1.5D~2D进行5次垂直振动循环,管道在结束循环后最终贯入至3D处,其现象与图9(a)相似。图9(a)和9(b)涵盖了全埋管道和部分埋入管道的贯入/上拔荷载特性,展示了SLA在复杂加载路径下模拟循环管土相互作用的能力。
4. 结论
本文采用连续极限分析(SLA)方法对深海管道的竖向管土大变形相互作用进行了研究,针对不同复杂位移路径和土体变形的工况进行了详细分析,得到以下3点结论。
(1)SLA法通过求解一系列连续小变形问题实现对极端大变形问题的模拟,该过程中通过网格重划分与场变量映射避免了网格失真问题。本文中SLA法对管道位移过程中涉及的破坏机构演变、土体沟槽、土坡坍塌回流和上拔破土行为均能进行有效模拟,且所得管土抗力与模型试验结果高度吻合。
(2)SLA因无需构建应力应变关系从而可采用较长的时间步长分析大变形问题,因此具有较高的数值稳定性和计算效率。例如,本文中竖向循环贯入涉及9倍直径(图4(a))的管道位移和土体极端大变形,利用SLA法在常用计算机上可在2 h内完成模拟。
(3)管道在竖向循环运动过程中土体发生应变软化使得管道竖向抗力峰值随循环次数增加而逐渐减小,但埋深突破历史最大埋深时逐渐逼近骨干曲线,表现出典型的迟滞现象,与以往模型试验结果高度吻合。采用SLA法可标定Randolph等[19]所提出的管-土相互作用非线性弹簧模型,以进行简化三维模拟分析管道疲劳问题。
本文首次针对管道自泥面贯入后的竖向循环管土相互作用展开了研究,介绍了连续极限分析SLA法并得到了模型试验的验证,同时开展典型复杂工况下的模拟展示了SLA在模拟极端土体大变形问题方面的特点和优势。由于文章篇幅限制,未进一步开展更细致的参数分析以建立简化的管-土竖向作用弹簧模型。此外,本文因采用总应力法,未考虑管道贯入过程中所产生的超静孔压,也是本文的局限性之一。
-
表 1 尾矿材料物理力学参数
Table 1 Physicomechanical parameters of tailings materials
土层 弹性模量/MPa 泊松比 黏聚力/kPa 内摩擦角/(°) 重度/(kN·m-³) 堆石 120 0.22 42.0 35 21.5 粗砂 50 0.30 7.9 32 22.3 细砂 40 0.30 8.1 28 21.5 粉砂 40 0.30 9.0 25 21.8 粉土 30 0.35 9.7 29 20.2 基岩 7700 0.28 30000 51 24.0 表 2 不同尾矿材料参数先验和后验统计特征的比较
Table 2 Comparison of prior and posterior statistics of parameters of tailings materials
土层 弹性模量先验信息 弹性模量后验信息 泊松比先验信息 泊松比后验信息 均值/MPa 变异系数 均值/MPa 变异系数 均值 变异系数 均值 变异系数 堆石 120 0.15 124.40 0.144 0.22 0.1 0.221 0.100 粗砂 50 0.15 51.779 0.069 0.30 0.1 0.299 0.087 细砂 40 0.15 37.330 0.129 0.30 0.1 0.285 0.091 粉砂 40 0.15 39.871 0.150 0.30 0.1 0.302 0.099 粉土 30 0.15 30.221 0.149 0.35 0.1 0.350 0.100 -
[1] 李康宏, 邓祥辉, 何萌, 等. 基于钻孔资料的某尾矿坝渗透系数反演分析有限元模型建立[J]. 岩石力学与工程学报, 2004, 23(增刊1): 4329-4332. LI Kang-hong, DEGN Xiang-hui, HE Meng. et al. The finite element model of permeability inversion analysis for a tailings dam based on borehole data is established[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S1): 4329-4332. (in Chinese)
[2] 林旭, 茆福文, 张巍, 等. 尾矿坝初始地应力反演研究[J]. 水利技术监督, 2020(1): 198-201. LING Xu, MAO Fu-wen, ZHANG Wei. Inversion study on initial geostress of tailings dam[J]. Technical Supervision in Water Resources, 2020(1): 198-201. (in Chinese)
[3] 徐维生, 柴军瑞, 李娟娟, 等. 尾矿库坝体加高方案排水分析[J]. 水土保持通报, 2010, 30(5): 226-228. XU Wei-sheng, CAI Jun-rui, LI Juan-juan, et al. Drainage analysis of dam body elevation scheme for tailings pond[J]. Bulletin of Soil and Water Conservation, 2010, 30(5): 226-228. (in Chinese)
[4] 任赞松. 尾矿库坝体稳定性与溃坝危险性评价[D]. 成都: 成都理工大学, 2018. REN Zan-song. Assessment of the Stability of Tailings Dam and the Risk of Dam Failure[D]. Chengdu: Chengdu University of Technology, 2018. (in Chinese)
[5] 李彪. 尹庄新水尾矿库加高扩容坝体三维渗流及控制技术研究[D]. 北京: 北方工业大学, 2019. LI Biao. Study on Three-dimensional Seepage and Control Technology of Heightened and Expanded Dam Body of Yinzhuang Xinshui Tailings Reservoir[D]. Beijing: North China University of Technology, 2019. (in Chinese)
[6] BHARAT T V, SHARMA J. Prediction of compression and permeability characteristics of mine tailings using natural computation and large-strain consolidation framework[C]//Geo-Frontiers 2011: Advances in Geotechnical Engineering, 2011.
[7] 金佳旭. 地震荷载作用下上游式尾矿库动力特性研究[D]. 沈阳: 东北大学, 2013. JIN Jia-xu. Research on Dynamic Characteristics of Upstream Tailings Under Earthquake Load[D]. Shenyang: Northeastern University, 2013. (in Chinese)
[8] EL-RAMLY H, MORGENSTERN N R, CRUDEN D M. Probabilistic stability analysis of a tailings dyke on presheared clay shale[J]. Canadian Geotechnical Journal, 2003, 40(1): 192-208. doi: 10.1139/t02-095
[9] DAS T, HEGDE A. A comparative deterministic and probabilistic stability analysis of rock-fill tailing dam[C]//Advances in Computer Methods and Geomechanics. Lecture Notes in Civil Engineering, Vol 55, 2020, Singapore.
[10] STRAUB D, PAPAIOANNOU I. Bayesian updating with structural reliability methods[J]. Journal of Engineering Mechanics, 2015, 141(3): 04014134. doi: 10.1061/(ASCE)EM.1943-7889.0000839
[11] 蒋水华, 李典庆. 边坡可靠度更新的贝叶斯方法[M]. 北京: 科学出版社, 2019. JIANG Shui-hua, LI Dian-qing. Bayesian Approach for Updating of Slope Reliability[M]. Beijing: Science Press, 2019. (in Chinese)
[12] AU S K, BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263-277. doi: 10.1016/S0266-8920(01)00019-4
[13] DIAZDELAO F A, GARBUNO-Inigo A, AU S K, et al. Bayesian updating and model class selection with Subset Simulation[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 317: 1102-1121. doi: 10.1016/j.cma.2017.01.006
[14] PAPAIOANNOU I, STRAUB D. Reliability updating in geotechnical engineering including spatial variability of soil[J]. Computers and Geotechnics, 2012, 42: 44-51. doi: 10.1016/j.compgeo.2011.12.004
[15] 曹荣国. 大黑山尾矿坝渗流与稳定性分析研究[D]. 长春: 吉林大学, 2017. CAO Guo-rong. The Study and Analysis of Seepage and Stability About Tailings Dam in Daheishan[D]. Changchun: Jilin University, 2017. (in Chinese)
[16] 中仿科技公司. 岩土应力变形分析软件SIGMA/W用户指南[M]. 北京: 冶金工业出版社, 2011. CnTech. SIGMA/W User Guide for Geotechnical Stress and Deformation Analysis Software[M]. Beijing: Science Press, 2019. (in Chinese)
[17] 李典庆, 蒋水华. 边坡可靠度非侵入式随机分析方法[M]. 北京: 科学出版社, 2016. LI Dian-qing, JIANG Shui-hua. Non-Invasive Stochastic Analysis Method for Slope Reliability[M]. Beijing: Science Press, 2019. (in Chinese)
[18] MIRO S, KÖNIG M, HARTMANN D, et al. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study[J]. Computers and Geotechnics, 2015, 68: 38-53. doi: 10.1016/j.compgeo.2015.03.012
-
期刊类型引用(2)
1. 张鑫,郭广礼,李怀展,张连贵,刘峰建,蒋乾,陈延康. 煤矿开采影响下浅埋输油管线变形及力学响应特性. 科学技术与工程. 2023(35): 15052-15059 .  百度学术
百度学术
2. 郑晓明,张春会,李雪婷,田英辉,李永靖. 砂土海床海底管道贯入的数值模拟. 河北科技大学学报. 2022(04): 440-448 .  百度学术
百度学术
其他类型引用(2)



 下载:
下载: