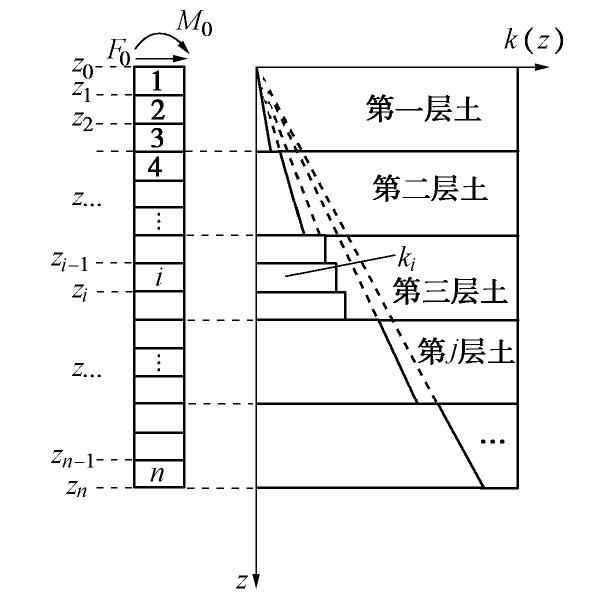
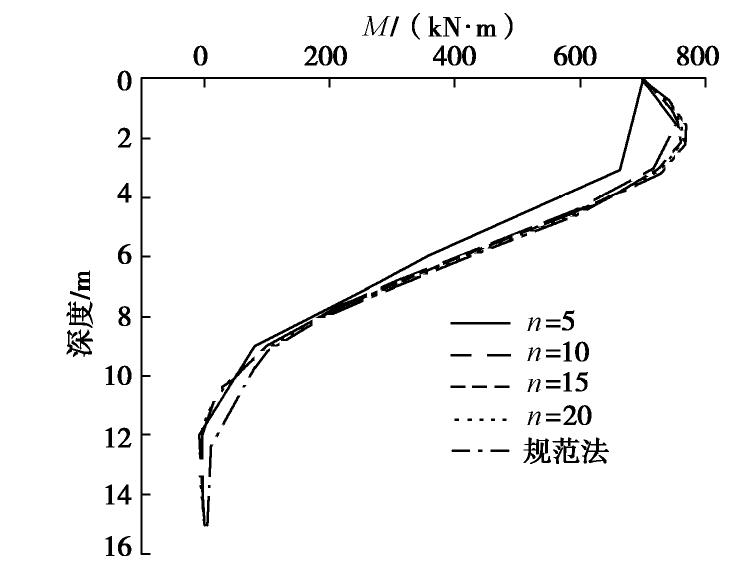
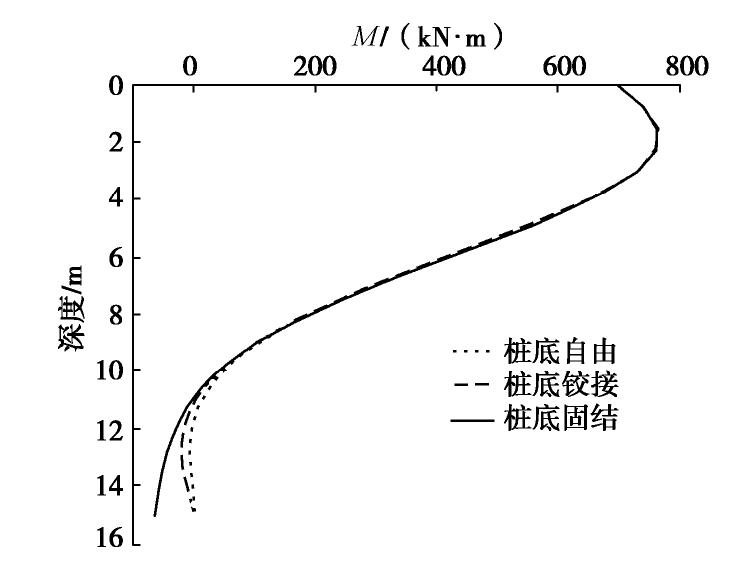
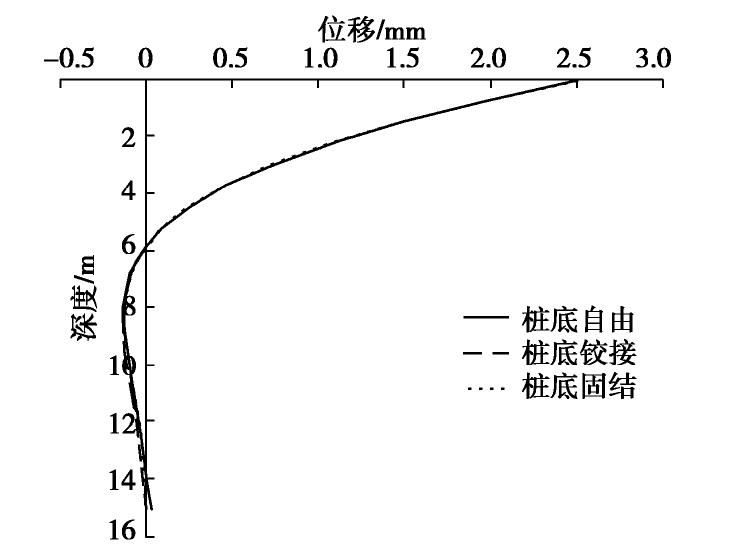
Linear equation solution of horizontally loaded piles and its application
-
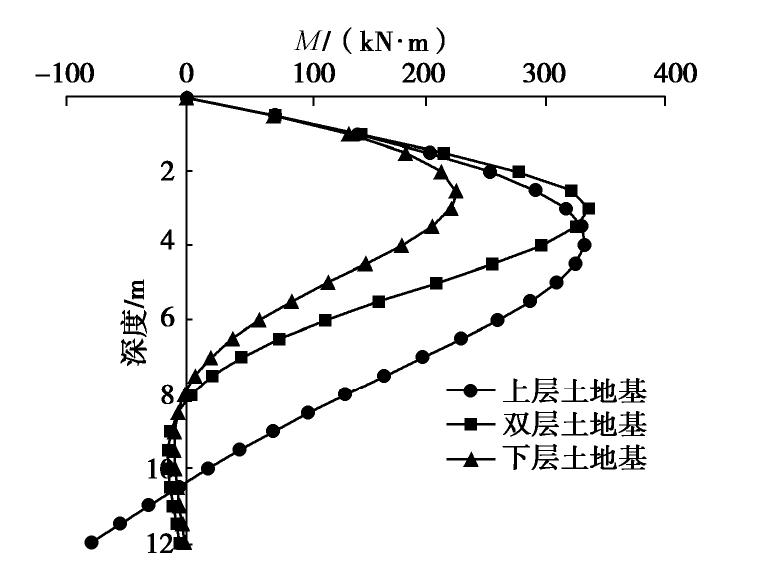
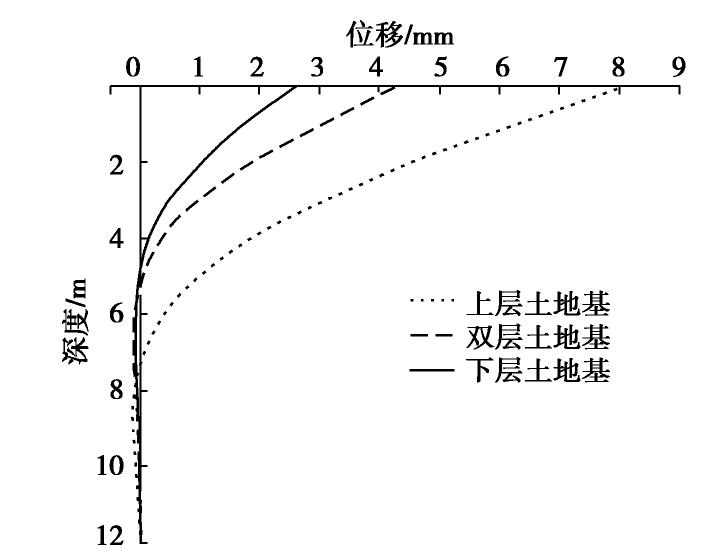
摘要: 根据Winkler地基梁理论,将地基系数沿着深度方向的任意函数以积分中值定理为原则进行微段常数化,引入四阶微分方程的张氏解析解,通过结点内力与位移连续的条件对全桩全结点构建线性方程组,避免矩阵多次传递即可一次性解得所有结点的内力与位移,相比幂级数法与有限元法更加简单,将此过程用matlab编制程序进行实现,通过两个算例验证了线性方程解法在单层地基与多层地基情况下水平受荷桩桩身响应计算的正确性。最后分别在算例基础上更改多组参数,表明在桩顶水平荷载的作用下,桩身弯矩最大值、弯矩零点值与位移零点值出现的位置分别受桩顶附近土层抗力、桩中部土层的抗力与整个桩周土层抗力大小控制,且对于同一种情况下的桩身水平响应而言,其弯矩零点所出现的位置将比位移零点所出现的位置滞后（2～3）d。
-
关键词:
- 水平受荷桩 /
- Winkler地基梁 /
- m法 /
- 矩阵传递法 /
- 线性方程
Abstract: According to the Winkler foundation beam theory, the foundation function is constantized by the integral median theorem, and a linear equation system is constructed for the entire pile and all nodes through the condition that the internal forces and displacements of the nodes are continuous. This process is implemented by matlab programming, and two examples are used to verify the correctness of the calculation of the response of the horizontally loaded pile body in the case of single-layer foundation and multi-layer foundation. In the calculation example, multiple sets of parameters are changed, which shows that the location of the maximum value of the bending moment of the pile body, the zero point value of the bending moment and the zero point value of displacement are affected by the resistance of the soil layer near the pile top and the soil layer in the middle of the pile under the horizontal load of the pile top. The resistance is controlled by the resistance of the entire soil layer around the pile, and for the horizontal response of the pile body under the same situation, the position where the bending moment zero appears will lag behind the position where the displacement zero appears by about (2~3)d.-
Keywords:
- pile foundation /
- Winkler foundation beam /
- m method /
- matrix transfer method /
- linear equation
-
0. 引言
黄土节理在气候相对干燥的黄土高原地区普遍发育,是黄土地区工程建设中的不利因素。为了更好的满足工程建设所需土体的强度和渗透性,有必要开展黄土节理灌浆加固方面的研究。节理本身作为一条天然的灌浆通道,结合微生物溶液低黏滞性和高流动性的特点[1],微生物溶液用于黄土节理的灌浆加固成为潜在的可能。
微生物诱导碳酸钙固化土体的过程是微生物溶液进行生化反应生成碳酸钙填充土体孔隙,胶结土体颗粒,以此改善土体强度和渗透性的过程[2]。由于微生物溶液本身需要生物酶(巴氏芽孢杆菌)催化尿素水解来进行酶促反应,相比于传统的水泥或化学注浆,MICP灌浆加固岩土体有其独特的灌浆参数和灌浆影响因素[3],具体体现在影响生物化学反应的因素方面,主要包括脲酶活性、胶结液浓度、灌浆速率、温度、pH和土体的颗粒级配等。尹黎阳等[4]系统分析了上述灌浆因素对岩土固化效果的影响,给出了微生物灌浆所需的适宜环境条件。李捷等[5]研究了不同脲酶活性对珊瑚砂矿化效果的影响,找到了最佳的脲酶活性。赵志峰等[6]在常规的温度、pH影响因素中考虑了土体中胶结阳离子含量和氯化盐含量,通过试验证明土中胶结阳离子含量可以忽略不计,氯化盐对脲酶活性有抑制作用。彭劼等[7-8]研究了不同温度下MICP固化砂土的效果,通过试验表明温度能够影响碳酸钙的生成速率。Wijngaarden等[9]通过数值模拟的方法探究不同灌浆速率下的饱和砂柱灌浆效果,旨在解决微生物灌浆的均匀性问题。
综上所述,微生物灌浆的生化反应过程比较复杂,涉及的灌浆因素较多,一般通过试验方法很难做到综合分析。现有的灌浆因素分析主要集中在完整的岩土体,对包含节理裂隙岩土体的情况研究较少。本文在自行建立含节理黄土微生物灌浆模型的基础上,利用COMSOL软件通过数值模拟的方法,重点考虑初始脲酶活性、胶结液浓度、节理开度等因素,动态模拟出微生物溶液在节理-黄土体中的扩散过程,以此分析各灌浆因素对节理开度变化和黄土体有效加固范围的影响。
1. 运移扩散方程的建立
1.1 渗流方程
节理黄土体渗流方程的建立依据裂隙岩土体双重介质模型[10],黄土体非饱和渗流的Richards方程为
(1) 式中
节理假定为竖直,且节理面光滑,节理介质的非饱和渗流通常称为水流连续性的“立方定律”,
(2) 式中b为节理开度,b=b(x, y, t);
式(1), (2)的求解都需要用到土水特征曲线,通常采用的是V-G模型[11]:
(3) 式中,θr为节理或黄土的残余体积含水率,θs为节理或黄土的饱和体积含水率,hp为节理或黄土的吸力水头,α, a, η为试验拟合参数,且η=1-1/a。
节理介质的饱和渗透系数采用立方定律,再乘以相应的折减系数值,
(4) 式中,bf为折减系数值,ρ, μ分别为溶液的密度和溶液动力黏度系数,取水的参数,忽略微生物溶液组分浓度的变化导致其参数的改变,g为重力加速度。
裂隙性土体中裂隙的饱和渗透系数值大约比土体饱和渗透系数值高2~6个数量级,土体中节理(裂隙)的渗透系数目前尚未给出具体表达式,有待进一步研究。根据课题组前期开展的天然黄土节理水流入渗试验[12],典型节理开度下,节理的饱和渗透比黄土体高大约2个数量级；按照立方定律求解出节理饱和渗透系数以后,乘以折减系数bf,使得与已有试验结果保持同一数量级,以此保证数值计算时参数的合理性。
节理的相对渗透系数采用Van Genuchten给出的相应表达式：
(5) 式(5)的参数同式(3)。
1.2 溶质运移方程
黄土体微生物溶液运移扩散方程采用的是对流-扩散-反应方程,反应项包含孔隙率变化[9]:
(6) 式中n为孔隙率；Ci为微生物溶液中反应物离子的浓度；∇为哈密尔顿算子；Dm为水动力弥散系数,Dm=βvm+D0, β为弥散度,vm为渗流速度,D0为分子扩散系数；mi为化学计量数,murea=mCa+=-1反应物中尿素和钙离子：生成物铵根离子
r的表达式是由米氏方程演化而来：
(7) 式中,vmax为初始脲酶活性,Km米氏常数,tmax为灌浆时长。
节理介质中的反应性溶质运移扩散方程与黄土类似,此时反应项包含节理开度变化：
(8) 式中,Df为节理中水动力弥散系数,vf为节理中溶液的流速,其余参数同式(6)。
1.3 介质变化方程
碳酸钙沉淀填充黄土孔隙导致孔隙率减小：
(9) 式中,
节理开度变化方程借助节理孔隙率[13],参照黄土孔隙率的变化方程来推导,节理中碳酸钙沉淀的控制方程：
(10) 式中,γ为土体单位长度的节理数,假定为1 m-1。
碳酸钙沉淀填充节理导致节理开度减小：
(11) 联立式(6), (8), (9), (11),结合相应的物理场参数和边界条件,可对此偏微分方程组进行求解。
1.4 模型求解与定解条件
本文计算模型为宽度120 cm,高度为100 cm的矩形区域,节理位于中间深度贯穿模型；假定节理竖直,且表面光滑。物理场中非饱和渗流场参数参考文献[14],溶质运移参数参考文献[15]。黄土的干密度取1.43 g/cm3,质量含水率为20.4%,暂不考虑黄土渗透系数的各向异性问题。模型上部边界：溶液沿节理灌浆口饱和下渗,孔隙水压力水头为0；给定具体浓度值,采取细菌菌液和胶结液混合注入的方式。模型左右两侧为不透水边界且无溶质流出。模型底部边界：溶液可以自由流出,非饱和渗流场设为“流出”边界,浓度场设为“通量”边界。
物理方程的求解采用有限元仿真软件COMSOL,对耦合的物理场进行求解。
2. 灌浆因素分析
微生物灌浆模型最重要的求解因变量是溶液中离子的浓度。本节重点对初始脲酶活性、胶结液浓度、节理开度3个影响因素进行数值模拟分析,模拟时,依据单一变量原则,只改变要分析的某一因素的取值,其余因素取值不变。灌浆因素研究方案见表1,初始脲酶活性(水解速率)r与vmax的关系式参考文献[16]。
表 1 灌浆因素研究方案Table 1. Research program of grouting factorsvmax/r/(kmol·m-3·s-1) Cin/(kmol·m-3)·M-1 b0/mm 9×10-5 1 0.5 通过求解不同影响因素下的各离子浓度扩散情况及碳酸钙生成的扩散范围,可以对不同工艺下的灌浆效果进行评价,优化灌浆工艺,进一步了解节理黄土体微生物灌浆机制。
2.1 初始脲酶活性
细菌溶液中的脲酶活性对于微生物灌浆起决定作用,因为微生物灌浆的实质就是在脲酶的催化下,尿素与氯化钙的混合溶液反应产生碳酸钙沉淀的过程。如果细菌溶液中的脲酶活性很低或者细菌死亡导致无脲酶活性,即电导率为0,尿素无法水解,混合溶液的生物化学反应就不会发生,无法对节理黄土体进行加固。学者们对于脲酶活性的分析大致分为两类：①直接分析不同脲酶活性的值对加固效果的影响[3];②通过脲酶分解尿素产生的铵根离子来间接反映脲酶的活性[16]。
考虑初始脲酶活性分别为1.5倍,2.0倍,2.5倍,其余参数保持不变。模拟计算得到的灌浆口碳酸钙生成情况如图1所示。
![]()
图 1 碳酸钙随时间的变化曲线Figure 1. Variation curves of joint aperture and calcium carbonate with time从图1可以看出,碳酸钙的生成量随着尿素活性的增大而逐渐增大。说明在有限的注浆加固时间内,适当的提高酶促反应速率,加快尿素溶液的分解,加大碳酸钙的生成,可以更加有效地减小节理开度值。
铵根离子浓度间接反映了微生物灌浆过程中尿素水解速率的大小。图2给出了节理沿伸方向上不同脲酶活性所对应的浓度锋前端铵根离子浓度的变化曲线。
曲线分为两种变化趋势：在距灌浆口18 cm范围内,铵根离子浓度的变化曲线呈现上升趋势,反映出该部分尿素水解速率较快,是节理的主要封堵加固区域；后部分由于尿素水解速率的降低,反应生成的铵根离子浓度逐渐变小,也间接的说明脲酶的活性逐渐在节理加固区域被消耗掉。铵根离子浓度整体上随着脲酶活性的增大逐渐增大,曲线斜率表示尿素的水解速率[3]。
2.2 胶结液浓度
采用3种微生物胶结液浓度,分别为0.5, 0.7, 1 mol/L。为了探究相同胶结液用量下的含节理黄土微生物灌浆效果,3组模拟计算的时间分别为6, 4, 3 h。不同胶结液浓度下不同节理位置处铵根离子变化曲线如图3所示。
![]()
图 3 不同胶结液浓度的铵根离子浓度变化曲线Figure 3. Variation curves of ammonium ion concentration with different cement solution concentrations由图3可知,在距离节理灌浆口25 cm范围内,胶结液浓度越高对应的产生铵根离子的浓度越高,表明该尿素水解速率越高；在25 cm范围之外,出现了相反的情况：胶结液浓度越高尿素的水解速率降低,可能原因在于在持续灌浆过程中,胶结液中高浓度的钙离子可能会抑制尿酸的水解；但对于节理裂隙中的尿素水解速率影响不大。高浓度的胶结液尿素水解速率高,导致瞬间产生更多的碳酸钙,近而堵塞了后续微生物溶液沿节理的下渗。但由于胶结液浓度低,注入的微生物溶液需要更长的时间,意味着注入的总微生物溶液的体积在增加,相应的化学反应产生的废液量也再增加,废液沿节理流向两侧土体的总流量增多,会加大对土体强度的损伤。
2.3 节理开度
根据目前已有的含节理黄土的渗流研究结论可知,节理开度是影响节理渗流的主要因素。由立方定律表示的节理饱和渗透系数值可知,节理开度影响饱和渗透系数的大小,进而影响微生物溶液沿节理的下渗,最终影响节理-黄土体的加固效果。因此有必要分析节理开度对节理-黄土体微生物灌浆效果的影响。考虑节理开度分别为0.5, 1, 1.5 mm, bf=5×10-5,其余各物理参数见表1。
图4给出了不同节理开度下孔隙率等值线的变化范围和生化反应生成碳酸钙的等值线的范围。由此可得到不同节理开度的有效加固范围如表2所示。
![]()
图 4 不同节理开度的孔隙率等值线图Figure 4. Contour diagram of porosity with different joint apertures表 2 不同节理开度的有效加固范围Table 2. Effective reinforcement areas with different joint apertures(cm) 节理开度 孔隙率 碳酸钙 减小深度 减小宽度 加固深度 加固宽度 0 22.16 8.59 30.67 11.17 10 44.40 9.68 57.51 12.44 15 60.34 10.43 74.00 13.37 由表1可知,随着节理开度的逐渐增大,黄土体的加固范围在逐渐增大。由于节理的开度较大,单位时间内流经节理的微生物溶液增多,导致微生物溶液沿节理向两侧土体扩散的范围增大,进而在更大的范围反应产生碳酸钙沉淀,相应的土体孔隙率减小的范围会逐渐增加。
3. 结论
本文在建立的含节理黄土微生物灌浆模型的基础上,利用有限元仿真软件COMSOL软件,通过考虑初始脲酶活性、胶结液浓度、节理开度等因素,动态模拟出微生物溶液在节理-黄土体中的扩散过程,以此分析各灌浆因素对节理开度变化和黄土体有效加固范围的影响,得到3点结论。
(1)初始脲酶活性对于含节理黄土体的微生物灌浆起决定性作用,初始脲酶活性越高,单位时间内反应转化生成的碳酸钙越多,使得节理填充率越高。
(2)在胶结液总量不变的情况下,不同胶结液浓度对黄土体有效加固区范围影响较小。但较高浓度的胶结液所产生的废液量较少。实际应用中,为兼顾加固效果和减少废液量,应选用适宜的胶结液浓度。
(3)节理开度对于含节理黄土体在深度方向的加固效果要明显好于宽度方向,这与节理渗流规律接近。从不同灌浆因素的效果综合来看,靠近节理灌浆口位置处的加固效果优于其他位置,自由入渗加固含节理黄土体的深度有限。
-
![]()
图 4 不同桩端约束的桩身位移
Figure 4. Displacements of pile body with different pile end constraints
-
[1] ROWE R K. Pile foundation analysis and design: Book review[J]. Canadian Geotechnical Journal, 1981, 18(3): 472-473. doi: 10.1139/t81-056
[2] 龚晓南. 桩基工程手册[M]. 北京: 中国建筑工业出版社, 2016. GONG Xiao-nan, Handbook of Pile Foundation of Engineering[M]. Beijing: China Architecture and Building Press, 2016. (in Chinese)
[3] 吴恒立. 计算弹性地基中推力桩的双参数法(推力桩计算理论研究报告之一)[J]. 重庆交通大学学报(自然科学版, 1983(1): 11-24. https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT198301001.htm WU Heng-li. Double-parameter method used in calculating the laterally loaded pile in the elastic foundation[J]. Journal of Chongqing Jiaotong University, 1983(1): 11-24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT198301001.htm
[4] 竹下淳. 横向重な受けゐ有限长クィの数值解法[J]. 土木技术, 1966, 24(5): 32-46. TAKESHITA Jun. Numerical solution of finite-length piles under lateral and vertical loads[J]. Civil Engineering Technology, 1966, 24(5): 32-46. (in Japanese)
[5] PISE P J. Laterally loaded piles in a two-layer soil system[J]. J Geotech Engng Div, ASCE, 1982, 108: 1177-1181. doi: 10.1061/AJGEB6.0001342
[6] 中国建筑科学研究院. 建筑桩基技术规范：JGJ 94—2008[S]. 北京: 中国建筑工业出版社, 2008. China Academy of Building Sciences. Technical Code for Building Pile Foundation: JGJ 94—2008[S]. Beijing: China Architecture and Building Press, 2008. (in Chinese)
[7] 公路桥涵地基与基础设计规范：JTG D63—2007[S]. 北京: 人民交通出版社, 2007. Code for Design of Ground Base and Foundation of Highway Bridges and Culverts: JTG D63—2007[S]. Beijing: China Communications Press, 2007. (in Chinese)
[8] 赵明华. 多层地基及横向荷载下桩的分析[J]. 中南公路工程, 1986(4): 54-60. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGL198604007.htm ZHAO Ming-hua. Analysis of pile under multi-layer foundation and transverse load[J]. Central South Highway Engineering, 1986(4): 54-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGL198604007.htm
[9] 赵明华, 王贻荪, 肖鹤松. 多层地基横向受荷桩的分析[J]. 建筑结构, 1994(2): 6-10. https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG199402001.htm ZHAO Ming-hua, WANG Yi-sun, XIAO Sun-he. Analysis of laterally loaded pile in multi-layer foundation[J]. Building Structure, 1994(2): 6-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG199402001.htm
[10] 彭文祥, 赵明华. 成层地基中倾斜荷载作用下桩的受力研究[J]. 中南公路工程, 1999(1): 27-30. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGL199901009.htm PENG Wen-xiang, ZHAO Ming-hua. Study on the force of pile under inclined load in layered foundation[J]. Central South Highway Engineering, 1999(1): 27-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGL199901009.htm
[11] 戴自航, 陈林靖. 多层地基中水平荷载桩计算m法的两种数值解[J]. 岩土工程学报, 2007, 29(5): 690-696. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200705010.htm DAI Zi-hang, CHEN Lin-qing. Two numerical solutions of laterally loaded piles installed in multi-layered soils by m method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 690-696. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200705010.htm
[12] 竺明星, 龚维明, 何小元. 成层地基土中水平受荷桩桩身响应的矩阵传递解[J]. 岩土工程学报, 2015, 37(增刊2): 46-50. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S2011.htm ZHU Ming-xing, GONG Wei-ming, HE Xiao-yuan. Transfer matrix solutions for responses of laterally loaded piles in multilayered soil deposits[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 46-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S2011.htm
[13] 詹红志, 王亮清, 王昌硕, 等. 考虑滑床不同地基系数的抗滑桩受力特征研究[J]. 岩土力学, 2014, 35(增刊2): 250-256. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2035.htm ZHAN Hong-zhi, WANG Liang-qing, WANG Chang-shuo, et al. Study of mechanical characters of anti-sliding piles considering different foundation coefficients of sliding bed[J]. Rock and Soil Mechanics, 2014, 35(S2): 250-256. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2035.htm
[14] 竺明星, 龚维明, 何小元, 等. 纵横向受荷基桩变形内力的矩阵传递解[J]. 岩土力学, 2014, 35(11): 3281-3288. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201411037.htm ZHU Ming-xing, GONG Wei-ming, HE Xiao-yuan, et al. Matrix transfer solutions to deformation and internal forces of piles under combined vertical and lateral loads[J]. Rock and Soil Mechanics, 2014, 35(11): 3281-3288. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201411037.htm
[15] 赵明华, 邹新军, 罗松南, 等. 横向受荷桩桩侧土体位移应力分布弹性解[J]. 岩土工程学报, 2004, 26(6): 767-771. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200406007.htm ZHAO Ming-hua, ZHOU Xin-jun, LUO Song-nan, et al. Elastic analytic solution to the displacement and stress distribution in the soil around laterally loaded piles[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 767-771. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200406007.htm
[16] 杨明辉. 岩质陡坡桥梁桩基承载机理及其分析方法研究[D]. 长沙: 湖南大学, 2006. YANG Ming-hui. Study on bearing mechanism and analysis method of pile foundation of rock steep slope bridge[D]. Changsha: Hunan University,2006. (in Chinese)
[17] 冯忠居, 赵明华. 特殊地区基础工程[M]. 北京: 人民交通出版社, 2008. FENG Zhong-ju, ZHAO Ming-hua. Basic Engineering in Special Area[M]. Beijing: China Communications Press, 2008. (in Chinese)
[18] 赵明华. 桥梁桩基计算与检测[M]. 北京: 人民交通出版社, 2000. ZHAO Ming-hua. Calculation and Test of Bridge Pile Foundation[M]. Beijing: China Communications Press, 2000. (in Chinese)
下载:
计量
- 文章访问数: 254
- HTML全文浏览量: 37
- PDF下载量: 143
