饱和软黏土的蛋形单面边界面模型

徐日庆; 鞠露莹; 俞建霖; 蒋佳琪; 丁盼

doi:10.11779/CJGE202012002

饱和软黏土的蛋形单面边界面模型 English Version

徐日庆^{1, 2, 3,},
鞠露莹^{1, 2},
俞建霖^{1, 2, ,},
蒋佳琪^{1, 2},
丁盼^{1, 2}

1.
浙江大学滨海和城市岩土工程研究中心,浙江　杭州　310058
2.
浙江省城市地下空间开发工程技术研究中心,浙江　杭州　310058
3.
浙江加州国际纳米技术研究院台州分院,浙江　台州　318000

基金项目:

国家自然科学基金项目 41672264

浙江省重点研发计划 2019C03103

详细信息

作者简介:
徐日庆(1962—),男,博士,教授,博士生导师,主要从事土的工程性质以及土本构模型等方面的教学与研究工作。E-mail：xurq@zju.edu.cn

通讯作者:
俞建霖, E-mail：yujianlin72@126.com

中图分类号: TU43
计量
- 文章访问数: 269
- HTML全文浏览量: 28
- PDF下载量: 151
出版历程
- 收稿日期: 2020-02-19
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-11-30

Egg-shaped bounding surface model for saturated soft clay

XU Ri-qing^{1, 2, 3,},
JU Lu-ying^{1, 2},
YU Jian-lin^{1, 2, ,},
JIANG Jia-qi^{1, 2},
DING Pan^{1, 2}

1.
Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
2.
Engineering Research Center of Urban Underground Space Development of Zhejiang Province, Hangzhou 310058, China
3.
Zhejiang-California International Nano Systems Institute Taizhou Branch, Taizhou 318000, China

摘要

摘要: 为描述饱和软黏土在循环荷载作用下的动力特性,建立了一个蛋形单面边界面模型。首先,模型通过引入蛋形边界面,克服了剑桥形式的边界面在角点处塑性应变增量方向不明确的缺陷,并将蛋形边界面退化为包含剑桥形式与椭圆形式等在内的不同形式的函数,体现了模型的普适性。其次,模型采用适用于饱和软黏土的相关联流动法则,以塑性体应变作为等向硬化过程中的内变量,利用广义各向同性硬化法则与移动映射中心的映射法则,准确描述了土体应力诱发各向异性与卸载过程中的塑性。然后,明确提出了模型参数确定方法,并通过参数分析阐述了模型各循环参数对饱和软黏土动力特性的影响。最后,利用高岭土在不排水条件下的单向循环三轴试验及Itsukaichi海洋黏土在不排水条件下的等向固结静三轴试验将模型模拟值与实测值进行对比,结果表明：模型计算结果与试验结果吻合良好,模型可合理描述饱和软黏土在不排水单向循环荷载及不排水剪切静荷载作用下的特性。
- 饱和软黏土 /
- 蛋形边界面模型 /
- 动力特性 /
- 广义各向同性硬化准则 /
- 循环三轴试验 /
- 静三轴试验
Abstract: In order to describe the dynamic characteristics of saturated soft clay under cyclic loading, an egg-shaped one-sided bounding surface model is established. First, by introducing the egg-shaped bounding surface, the model overcomes the defect that the direction of the plastic strain increment at the corner of the Cambridge-type bounding surface is not clear, and degrades the egg-shaped bounding surface into different types including the Cambridge form and the elliptical form, which reflects the universality of the model. Next, the model adopts the associated flow rule applicable to saturated soft clay, uses plastic volumetric strain as the internal variable in the isotropic hardening process, and uses the general isotropic hardening rule and the mapping rule of the moving mapping center to accurately describe the soil stress induced anisotropy and plasticity during unloading. Then, the method for determining the model parameters is clarified, and the influence of each model parameter on the dynamic characteristics of saturated soft clay is explained through parameter analysis. Finally, using the one-way cyclic triaxial tests on kaolin clay under undrained condition and the isotropic consolidated tests on Itsukaichi marine clay under undrained condition, the simulated values are compared with the measured ones. The results show that the simulated results agree well with the test ones, and the proposed model can reasonably describe the characteristics of saturated soft clay under undrained cyclic loading and static shearing loading.
- saturated soft clay /
- egg-shaped bounding surface /
- dynamic characteristic /
- generalized isotropic hardening criterion /
- cyclic triaxial test /
- static triaxial test

HTML全文

0. 引言

中国东南沿海地区相当一部分地铁隧道建设在饱和软黏土地基中,为研究隧道列车循环荷载作用下饱和软黏土的滞回性、非线性和应变累积性等动力特性,需建立土的动本构关系。为此,国内外学者提出了形式多样的土动本构模型,这些模型大致可分为黏弹性模型和动力弹塑性模型两大类^[1]。在众多动力弹塑性模型中,边界面模型以其形式简单、概念明确,备受众多学者青睐,被广泛研究与应用。

为研究土的动力特性,许多学者相继提出并发展了双面边界面模型^[2-6],由于涉及到边界面和屈服面两个面的运动,这类模型计算过程较为繁琐。为解决这一问题,Dafalias等^[7]将屈服面简化为一点,提出了单面边界面模型,但此模型采用固定的映射中心,仅可考虑弹性卸载,不能模拟土体卸载时的塑性。为弥补这一缺陷,黄茂松等^[8]采用可移动映射中心的概念,建立了能够模拟土体塑性卸载的单面边界面模型。胡存等^[9-10]提出了分段形式的塑性模量插值函数,并将可移动的映射中心与广义各向同性硬化准则相结合,使模型可通过运动硬化过程反映土体应力诱发各向异性。此外,关于饱和软黏土边界面的形式,一直以来是国内外的研究热点。Dafalias^[11]最先提出的单面边界面模型由两段椭圆和一段双曲线组合而成,形式复杂,为模型的推导及运算带来很大困难。为简化边界面的形式,Dafalias^[11]结合土体旋转硬化过程,提出了一种椭圆形式的边界面模型。李兴照等^[12]建立了考虑软土流变性的边界面模型,在修正剑桥形式的边界面中引入了形状控制参数,使模型更为灵活。秦立科^[13]采用Zienkiewice-Pande^[14]修正的剑桥形式屈服面作为边界面,研究了非饱和黄土的动力特性。骆俊晖等^[15]同时考虑土体循环动力特性与时间效应,以Manzari等^[16]修正的剑桥形屈服面形式作为边界面建立了边界面模型。姚仰平等^[17]采取变换应力方法,将原真实应力空间中变化的屈服面转化为变换应力空间中的椭圆屈服面,并利用椭圆形参考屈服面与当前屈服面间的演化规律描述土体动力特性。由此可见,多数学者仍在临界状态理论的框架中,沿用椭圆形式或不同种类的剑桥模型拓展形式作为边界面。椭圆形式的边界面在偏平面中关于短轴对称,反映了土体软化和硬化对半均分的性质,适用土体范围较小。由Roscoe线和临界状态线组合而成的剑桥或修正剑桥形式的边界面形式简洁,参数较少且容易测得,对预测土体性质做出了重大贡献,但Roscoe线与临界状态线相交的角点导数不连续,塑性应变增量方向不明确,应力修正较复杂,给数值计算带来了很大困难。为克服修正剑桥模型的角点问题,Abbo等^[18]提出了光滑的双曲线形式屈服面,有利于数值计算,但此屈服面参数较多且缺乏明确物理意义。为减少模型参数,任放等^[19]提出了封闭光滑的蛋形屈服面,但并未将其应用到边界面模型中。徐日庆等^[20]结合强度发挥度,提出了蛋形边界面的概念,并通过剪切波速测试建立了蛋形边界面各参数与土体剪切波速和土体内摩擦角间的关系^[21],为边界面的形式提供了新的发展思路,但并未对循环荷载作用下土的动力特性进行深入研究。

鉴于已有边界面模型无法同时克服角点缺陷并较好地反映土体动力特性,本文详细分析了蛋形边界面的特点,建立了蛋形单面边界面模型,深入研究了饱和软黏土的循环动力特性。模型采用封闭光滑蛋形边界面的形式,避免剑桥形式边界面的角点缺陷；使用移动映射中心的映射法则,反映土体卸载过程中的塑性；利用新型的广义各向同性硬化准则模拟土体运动硬化过程,表征土体应力诱发各向异性。然后,提出模型参数确定方式并详细分析各参数对饱和软黏土动力特性的影响。最后,利用Fortran语言编制隐式积分算法有限元程序获得数值解,并将其与高岭土循环三轴试验结果及Itsukaichi海洋黏土静三轴试验结果进行对比,验证本文模型的合理性。

1. 边界面模型的建立

各边界面模型的不同之处主要在于边界面形式的选取、映射法则和硬化法则的设定以及塑性模量插值函数的选择。本文主要针对蛋形边界面的形式展开讨论,并建立蛋形单面边界面模型。

1.1 边界面方程

蛋形边界面在p-q平面中的形式如图1所示。

图 1 p-q平面中的蛋形边界面

Figure 1. Egg-shaped bounding surface inp-q plane

下载: 全尺寸图片幻灯片

图1中蛋形边界面的表达式为

f = {(\frac{p - d p_{0}}{a p_{0}})}^{2} + {(\frac{1 - β^{2}}{1 + β (p - d p_{0}) {(a p_{0})}^{- 1}})}^{2} {(\frac{q}{b p_{0}})}^{2} = 1,

(1)

式中, $a p_{0}$ , $b p_{0}$ 分别为蛋形长半轴和短半轴, $e p_{0}$ 为蛋形中心点横坐标, $β$ 为蛋形形状控制参数,与土体内摩擦角有关, $p_{0}$ 为土体先期固结压力,p为有效平均正应力,q为有效剪应力。

为研究土体运动硬化过程,反映土体应力诱发各向异性,本文采用运动的蛋形边界面,并将其改写为

F = {(\frac{\bar{p} - α_{p}^{(m)}}{a_{F}^{(m)}})}^{2} + {(\frac{1 - β^{2}}{1 + β (\bar{p} - α_{p}^{(m)}) {(a_{F}^{(m)})}^{- 1}})}^{2} {(\frac{\bar{q} - α_{q}^{(m)}}{\frac{b}{a} a_{F}^{(m)}})}^{2} = 1,

(2)

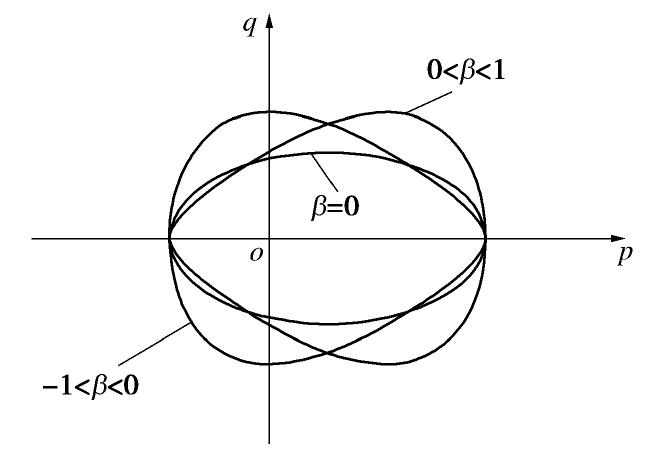
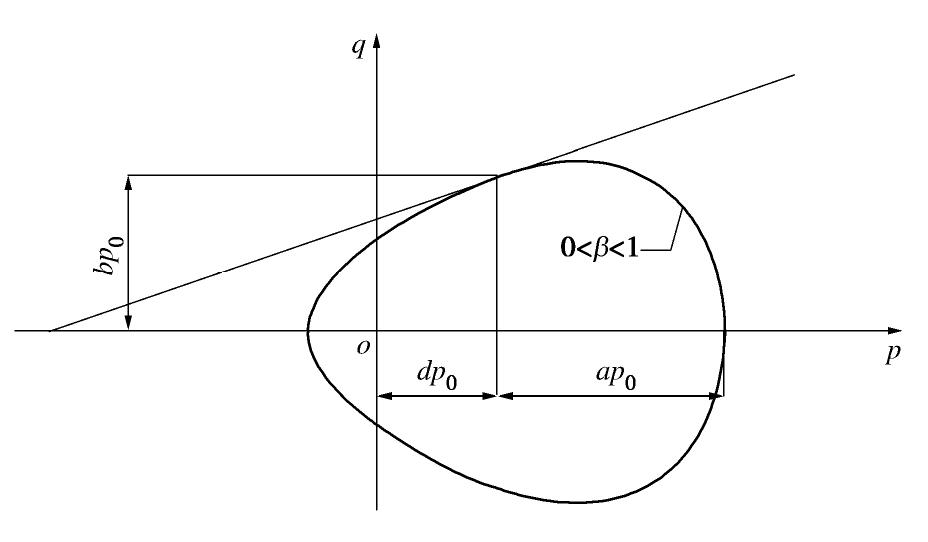
式中,( $\bar{p}$ , $\bar{q}$ ),(p,q)分别为虚应力点坐标和真实应力点坐标,( $α_{p}$ , $α_{q}$ )为蛋形边界面中心点坐标,m为加卸载次数, $a_{F}^{(m)}$ 为第m次加载时的蛋形半长轴。

式（2）中,边界面形状控制参数β取值不同时,边界面可退化为不同的函数形式,如图2所示。

图 2 蛋形边界面的退化形式

Figure 2. Degenerated form of egg-shaped bounding surface

下载: 全尺寸图片幻灯片

由图2可见：当-1<β<0时,边界面退化为剑桥模型子弹头形式；β=0时,边界面退化成椭圆形式；0<β<1时,边界面退化为蛋形；β趋近于1时,边界面逐渐退化成光滑的三角形。

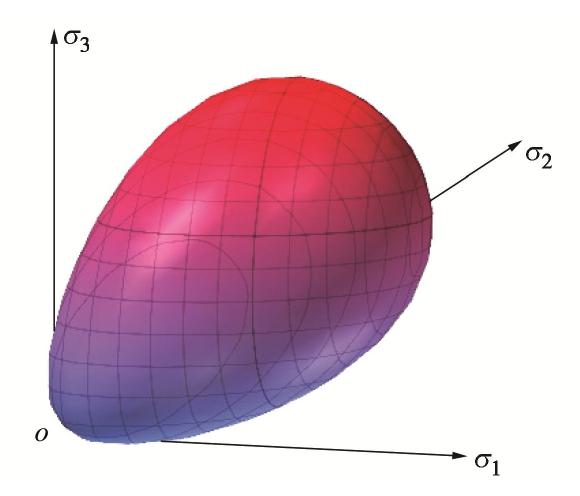
蛋形边界面在主应力空间中的形式如图3所示。

图 3 主应力空间下的蛋形边界面

Figure 3. Egg-shaped bounding surface in principal stress space

下载: 全尺寸图片幻灯片

由图3可见,光滑的蛋形边界面可将剑桥模型的盖帽部分与直线部分以简洁的形式统一起来,使得边界面上的点处处连续可导,塑性应变增量方向明确。由于边界面闭合,土体的屈服极限不会随静水压力增长而无限增大,相较于Mises,Mohr-coulomb等开口屈服面形式的边界面^[22-23],采用蛋形边界面可更加真实地反映土体强度特性。另外,由图2可看出,取特定范围的参数时,蛋形边界面可退化为包含剑桥子弹头形式、椭圆形式等在内的边界面形式,由此说明此边界面是一种更加广义的边界面形式,能够更为合理地反应土体性质。故本文采用蛋形形式的边界面,建立反映饱和软黏土循环加载特性的边界面模型。

此外,研究表明,对于饱和软黏土,采用相关联流动法则可以较好地反应土体性质^[24-25],故本文沿用相关联流动法则,即边界面F与塑性势面Q形式相同：

Q = F

。

(3)

模型塑性应变率表达式如下：

d ε_{i j} = 〈 L 〉 \frac{\partial F}{\partial σ_{i j}}

(4)

式中,L为加载因子,<>为Macauley符号,当L>0时,<L>=L,当L<0时,<L>=0。本文模型中卸载过程相当于反向加载,故在加卸载过程中,L都为正值。

1.2 映射法则

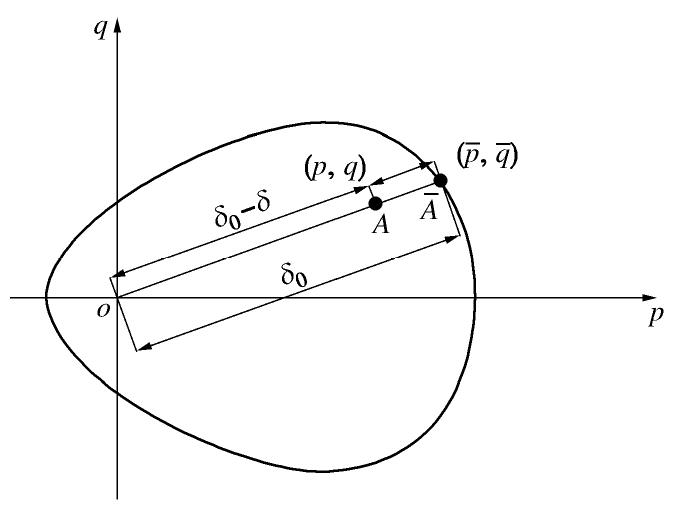
Dafalias提出的经典径向映射法则如下：采用零弹性域的概念,将屈服面简化为坐标原点,并将其作为固定的映射中心,只保留边界面,将映射中心与真实应力点的连线交于边界面上的点,称为虚应力点。图4给出了映射中心o点、真实应力点A点及虚应力点 $\bar{A}$ 点间的对应关系。利用这种映射法则可通过建立真实应力点与虚应力点间塑性模量关系,反映土体循环特性,但固定的映射中心无法反映土体卸载过程中的塑性。为弥补这一缺陷,本文在Dafalias映射准则的基础上,采用移动的映射中心,即在初始等向固结过程中,以应力空间坐标原点作为映射中心；后续剪切加卸载过程中,以每个加载步的应力反向点作为映射中心,以反映土体滞回性与卸载时的塑性。

图 4 映射中心与映射法则

Figure 4. Mapping center and rule

下载: 全尺寸图片幻灯片

{\bar{σ}}_{i j} = h (σ_{i j} - o_{i j}) + o_{i j}

(5)

h = \frac{δ_{0}}{δ_{0} - δ}

(6)

式中, ${\bar{σ}}_{i j}$ 为虚应力点坐标, $σ_{i j}$ 为真实应力点坐标,o_ij为映射中心坐标, $δ_{0}$ 为映射中心与虚应力点间的距离,δ为映射中心与真实应力点间的距离,h为映射中心与虚应力点间距离和映射中心与真实应力点间距离的比值。

1.3 硬化准则

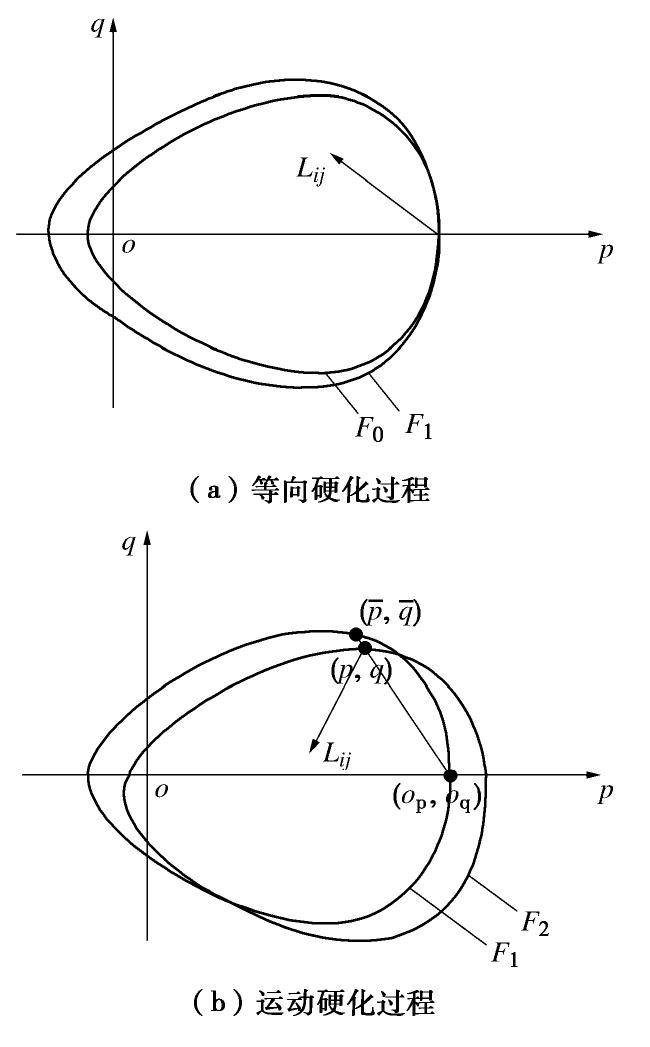
本文采用广义各向同性硬化法则,描述土体等向硬化过程与运动硬化过程,以表征其各向同性与应力诱发各向异性。整个过程如下：土体正常固结后进行剪切加载,此时边界面以映射中心（o_p,o_q）为基点不断膨胀,从初始边界面F₀膨胀为F₁,此单一加载过程即为土体的等向硬化过程；当加载至真实应力点到达预设峰值或真实应力点与虚应力点重合时,将边界面上的虚应力点移动至真实应力点处,边界面也随之从F₁位置移动到F₂位置,而后将真实应力点作为映射中心,沿塑性流动方向L_ij进行下一阶段加载或卸载,在此过程中边界面大小不变,只发生位置移动,即为土体运动硬化过程。两个过程如图5所示。

图 5 边界面的硬化准则

Figure 5. Hardening criteria for bounding surfaces

下载: 全尺寸图片幻灯片

在土体等向硬化过程中,本文选取塑性体应变为内变量,与先期固结压力有关的边界面半长轴 $a_{F}^{(m)}$ 为硬化参数,二者关系如下：

a_{F}^{(m)} = a_{F}^{(0)} \exp {\frac{1 + e_{0}}{λ - κ} [{(ε_{v}^{p})}_{m} - {(ε_{v}^{p})}_{0}]}

(7)

a_{F}^{(0)} = a p_{0}

(8)

式中,e₀为软黏土初始孔隙比, $λ$ 为压缩曲线的斜率；κ为固结回弹曲线的斜率, $a_{F}^{(0)}$ 为初始加载时蛋形边界面的半长轴。

本文以蛋形边界面中心点位置的变化反映蛋形边界面在循环荷载作用下的胀缩和移动,以此模拟土体等向硬化过程和运动硬化过程。

在等向硬化过程中,蛋形边界面以映射中心为硬化中心,通过蛋形半长轴的伸缩,反映中心点位置的移动。蛋形中心点坐标可表示为

\begin{matrix} α_{p (m + 1)}^{(i + 1)} = o_{p}^{(m + 1)} + (α_{p (m + 1)}^{(i)} - o_{p}^{(m + 1)}) \frac{a_{F (m + 1)}^{(i + 1)}}{a_{F (m + 1)}^{(i)}}, \\ α_{q (m + 1)}^{(i + 1)} = o_{q}^{(m + 1)} + (α_{q (m + 1)}^{(i)} - o_{q}^{(m + 1)}) \frac{a_{F (m + 1)}^{(i + 1)}}{a_{F (m + 1)}^{(i)}}, \end{matrix}}

(9)

式中,i为等向硬化过程中的增量步数,( $α_{p (m + 1)}^{(i + 1)}$ , $α_{q (m + 1)}^{(i + 1)}$ )为在第m+1次加载的第i+1个增量步中蛋形边界面中心点坐标, $a_{F (m + 1)}^{(i + 1)}$ 和 $a_{F (m + 1)}^{(i)}$ 分别为在m+1次加载的第i+1个增量步和第i个增量步中蛋形边界面半长轴的取值,( $o_{p}^{(m + 1)}$ , $o_{q}^{(m + 1)}$ )为第m+1次加载中映射中心的坐标。

在运动硬化过程中,边界面中心点位置移动可由虚应力点位置的移动表示：

\begin{matrix} α_{p}^{(m + 1)} = α_{p}^{(m)} + (p - \bar{p}), \\ α_{q}^{(m + 1)} = α_{q}^{(m)} + (q - \bar{q}) 。 \end{matrix}}

(10)

1.4 一致性方程与插值函数

蛋形边界面的一致性方程如下：

\frac{\partial F}{\partial \bar{p}} d \bar{p} + \frac{\partial F}{\partial \bar{q}} d \bar{q} + \frac{\partial F}{\partial ε_{v}^{p}} d ε_{v}^{p} = 0

。

(11)

将式（2）代入式（11）,结合式（4）可得到边界面上虚应力点塑性模量大小：

\begin{array}{l} {\bar{K}}_{p} = - \frac{1 + e_{0}}{λ - κ} (\frac{2 (\bar{p} - α_{p})}{{(a_{F}^{(m)})}^{2}} - \frac{2 α {(1 - α^{2})}^{2}}{{[a_{F}^{(m)} + α (\bar{p} - α_{p})]}^{3}} \frac{a^{2}}{b^{2}} {(\bar{q} - α_{q})}^{2}) \cdot \\ (- \frac{2 {(\bar{p} - α_{p})}^{2}}{{(a_{F}^{(m)})}^{3}} - \frac{2 {(1 - α^{2})}^{2}}{{[a_{F}^{(m)} + α (\bar{p} - α_{p})]}^{3}} \frac{a^{2}}{b^{2}} {(\bar{q} - α_{q})}^{2}) \cdot a_{F}^{(m)} 。 \end{array}

(12)

为得到真实应力点处塑性模量大小,本文采用文献[8]中提出的形式统一的插值函数,建立真实应力点与虚应力点间塑性模量的关系,

K_{p} = {\bar{K}}_{p} + p_{at} ς [{(\frac{\partial F}{\partial \bar{p}})}^{2} + {(\frac{\partial F}{\partial \bar{q}})}^{2}] [{(\frac{δ_{0}}{δ_{0} - δ})}^{φ} - 1]

(13)

φ = φ_{0} e^{- ξ ε_{s}^{p}}

(14)

ε_{s}^{p} = \int | d ε_{q}^{p} |

(15)

式中,φ₀,ς,ξ为拟合的模型参数, $p_{at}$ 为大气压力, $ε_{s}^{p}$ 为累积塑性偏应变,K_p, ${\bar{K}}_{p}$ 为真实应力点和虚应力点的塑性模量。

由式（13）可看出,在单一加载或卸载过程中,K_p从无穷大不断减小至 ${\bar{K}}_{p}$ ,此现象对应真实应力点从映射中心逐渐移动至边界面上虚应力点位置的过程。

1.5 应力应变增量关系

按照增量弹塑性理论,土中任意一点总应变增量可表示为弹性和塑性两部分。弹性应变增量分为弹性体应变增量 $d ε_{v}^{e}$ 和弹性剪应变增量 $d ε_{q}^{e}$ ,可由广义胡克定律求解：

d ε_{v}^{e} = \frac{1}{K} d p

(16)

d ε_{q}^{e} = \frac{1}{3 G} d q

。

(17)

式中,弹性体积模量K和弹性剪切模量G可用下式表示：

K = \frac{1 + e_{0}}{κ} \frac{1}{p}

(18)

G = \frac{3 (1 - 2 ν)}{2(1 + ν)} K

(19)

其中, $ν$ 为土体泊松比。

塑性应变增量可分为塑性体应变增量 $d ε_{v}^{p}$ 和塑性剪应变增量 $d ε_{q}^{p}$ ：

d ε_{v}^{p} = 〈 L 〉 \frac{\partial F}{\partial \bar{p}}

(20)

d ε_{q}^{p} = 〈 L 〉 \frac{\partial F}{\partial \bar{q}}

。

(21)

结合一致性方程与应变增量关系,可得应力应变增量关系：

{\begin{matrix} d ε_{v} \\ d ε_{q} \end{matrix}} = [\begin{matrix} \frac{1}{K} + \frac{1}{K_{p}} \frac{\partial F}{\partial \bar{p}} \frac{\partial F}{\partial \bar{p}} & \frac{1}{K_{p}} \frac{\partial F}{\partial \bar{p}} \frac{\partial F}{\partial \bar{q}} \\ \frac{1}{K_{p}} \frac{\partial F}{\partial \bar{p}} \frac{\partial F}{\partial \bar{q}} & \frac{1}{3 G} + \frac{1}{K_{p}} \frac{\partial F}{\partial \bar{q}} \frac{\partial F}{\partial \bar{q}} \end{matrix}] {\begin{matrix} d p \\ d q \end{matrix}}

。

(22)

土体在不排水剪切状态下的体应变增量为零：

d ε_{v} = d ε_{v}^{p} + d ε_{v}^{e} = 0

。

(23)

将一致性方程和常规三轴试验条件下土体应力增量表达式代入式（22）可得土中孔隙水压力增量表达式：

d u = \frac{1}{3} d q + K 〈 \frac{1}{K_{p}} (\frac{\partial F}{\partial \bar{p}} d \bar{p} + \frac{\partial F}{\partial \bar{q}} d \bar{q}) 〉 \frac{\partial F}{\partial \bar{p}} + d σ_{3}^{t}

(24)

式中,du为孔隙水压力增量,t为总应力形式。

2. 模型参数确定及参数分析

2.1 模型参数确定

本文采用的模型参数共计10个,主要分为以下3类：①第一类是边界面形状参数a,b,β；②第二类是塑性模量插值函数中的参数ς,φ₀, $ξ$ ；③第三类是与土体性质直接相关的参数e₀, $λ$ ,κ, $ν$ 。

第一类边界面形状参数a,b,β,可用于调整蛋形边界面的形状,使其更好地反映真实土体特性。它们可根据土体剪切波速和内摩擦角确定^[21],也可采用正常固结土样的常规三轴试验确定。

第二类循环参数ς,φ₀, $ξ$ 反映前期应变历史对循环加载的影响。它们的值可通过对试样循环加卸载得出的应力应变关系曲线和孔压—循环加载次数关系曲线以及p-q空间内有效应力路径的预测来确定^[26]。

第三类参数e₀, $λ$ , $κ$ 和 $ν$ 都是反映土体基本性质的参数。其中,e₀是土体初始孔隙比,可由土的物理性质指标计算, $λ$ , $κ$ 可分别由等压固结试验和固结回弹试验计算,土体泊松比 $ν$ 可根据经验取值,软黏土取值范围一般为0.2～0.4。

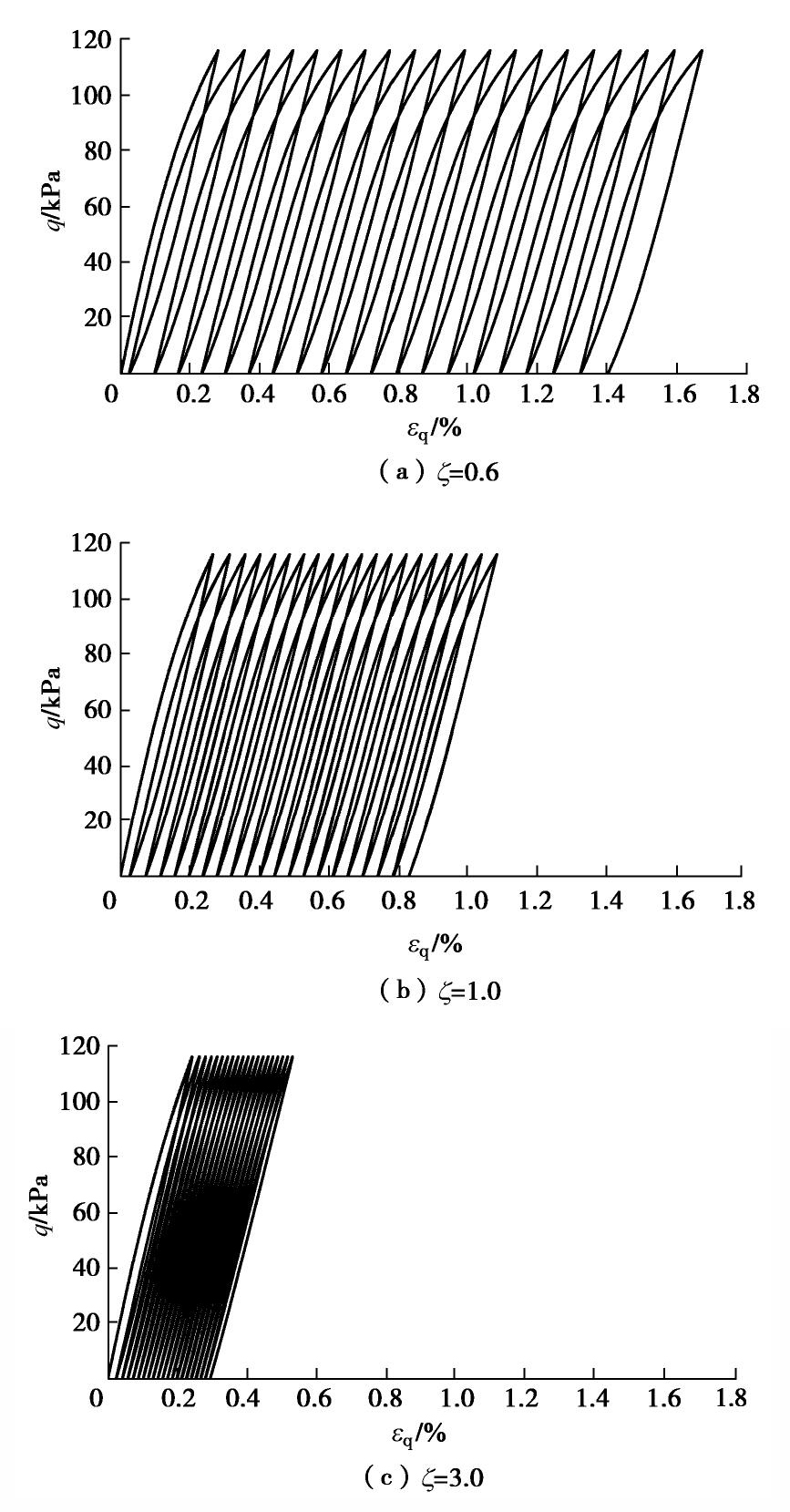
为进一步研究塑性模量插值函数中3个参数φ₀, $ς$ 和 $ξ$ 对模型模拟结果的影响,本文在固结压力为450 kPa,荷载循环幅值为116 kPa,荷载循环周次约为20次的情况下,利用Fortran语言编程求解土体在3个参数取值不同时的应力应变关系,并绘制应力应变曲线,以分析3个参数对土本构关系的影响。分析其中一个参数的影响时,其余参数同表1中高岭土取值。

表 1 土体参数表

Table 1. Soil parameters

试验土类	e₀	λ	κ	$ν$	a	b	β	ς	ξ	φ₀
高岭土	1.021	0.173	0.034	0.2	0.60	0.4	0.35	0.6	2.0	3.95
Itsukaichi海洋黏土	2.422	0.348	0.057	0.3	0.85	0.3	0.70	—	—	—

下载: 导出CSV

| 显示表格

2.2 参数 $ς$ 对本构关系的影响

图6给出了 $ς$ 对土体应变累积性的影响。从图6中可看出：在其余参数取值相同的情况下, $ς$ 越大,模型累积应变越小,导致应力应变曲线越密集。此现象可根据塑性模量插值函数分析解释： $ς$ 越大,真实应力点塑性模量越大,模型的塑性越不明显,而表现为近似弹性,故其累积的塑性应变越小,应力应变曲线更为密集。所以 $ς$ 越大,土体的应变累积性越不明显。

图 6 参数

ς

对模型的影响

Figure 6. Effects of parameterς on model

下载: 全尺寸图片幻灯片

2.3 参数ξ对本构关系的影响

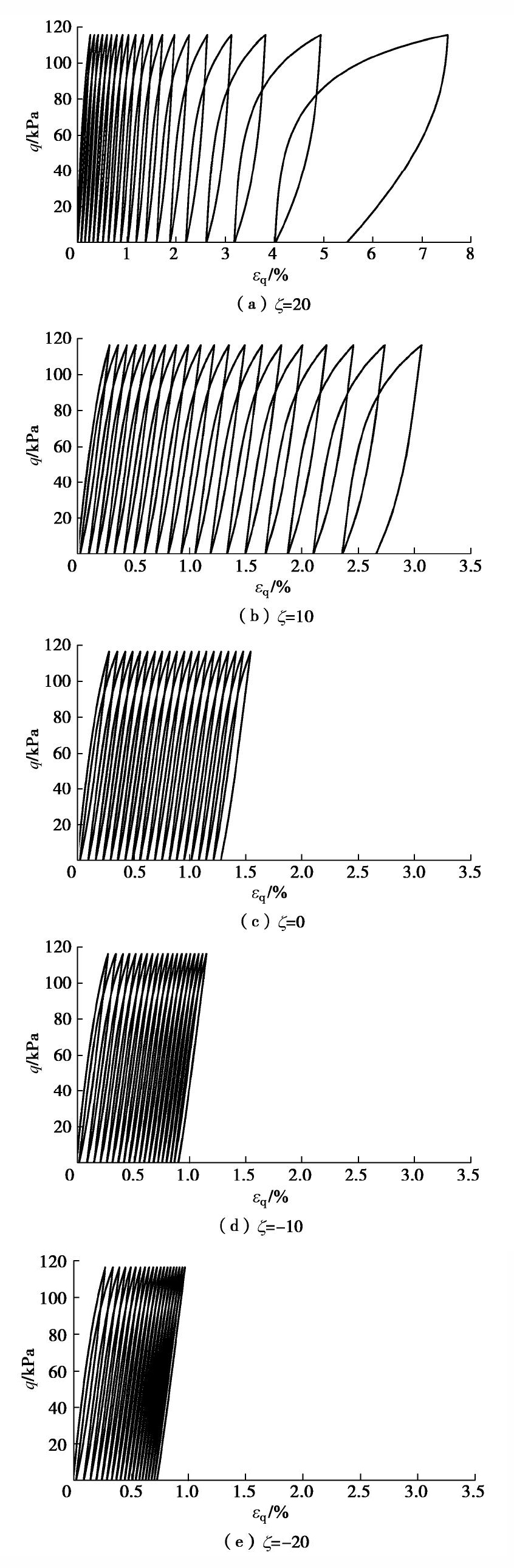
图7给出了 $ξ$ 值对应力应变关系发散性的影响。从图7中可看出：当 $ξ$ >0,应力应变曲线随循环周次的增加逐渐发散, $ξ$ 越大,曲线的分散程度越高；当 $ξ$ <0,应力应变曲线随循环周次的增加逐渐趋于密集,且随 $ξ$ 绝对值的增大,曲线愈加密集。故参数ξ影响应力应变曲线的发散性, $ξ$ 值越大,应力应变曲线越发散,表现出循环振散的特点。

图 7 参数

ξ

对模型的影响

Figure 7. Effects of parameterξ on model

下载: 全尺寸图片幻灯片

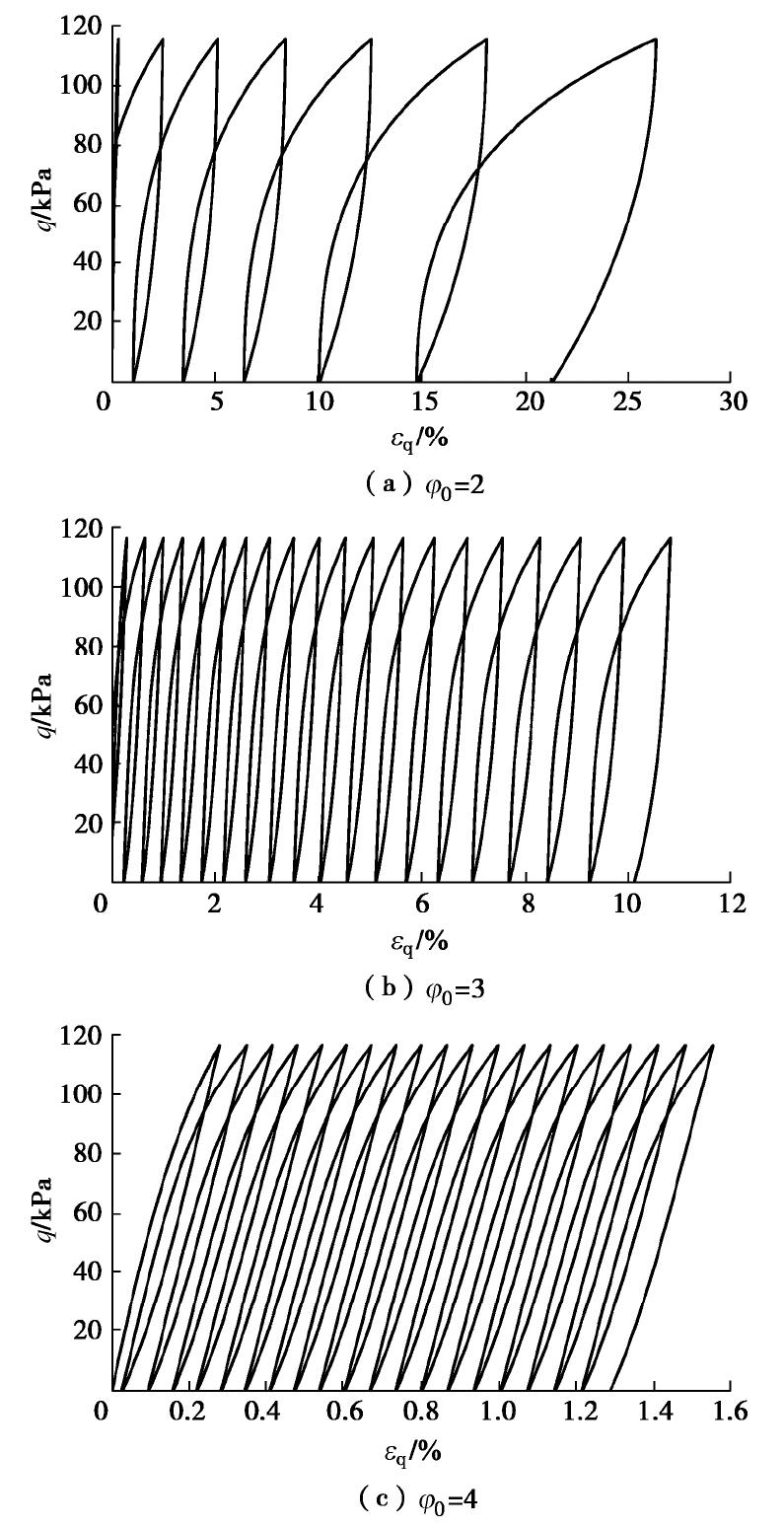
2.4 参数 $φ_{0}$ 对本构关系的影响

图8给出了参数 $φ_{0}$ 对应力应变曲线发散性和土体累积应变性的影响。从图中可看出： $φ_{0}$ 越小,应力应变曲线越发散,土体累积应变值越大。出现这一现象的原因是：在塑性模量插值函数中, $φ_{0}$ 以指数形式存在,对真实应力点塑性模量影响较大,故 $φ_{0}$ 可通过影响塑性模量使模型表现出弹性或塑性,进而影响应力应变曲线的发散性和累积应变大小。

图 8 参数

φ_{0}

对模型的影响

Figure 8. Effects of parameter

φ_{0}

on model

下载: 全尺寸图片幻灯片

上述参数分析结果表明塑性模量插值函数中的3个参数对应力应变曲线影响不尽相同。其中,参数 $ς$ 主要影响土体应变累积特性,参数 $ξ$ 主要影响应力应变曲线的发散性,而参数φ₀则同时影响土体应变累积特性与曲线发散性。

3. 模型验证

3.1 饱和高岭土循环三轴试验模拟

本节针对文献[4]中正常固结饱和高岭土的常规三轴试验结果及其在不排水条件下的循环三轴试验结果,利用本文推导的弹塑性柔度矩阵,编写Fortran程序,对饱和软黏土在不排水条件下受单向循环荷载作用的应力应变关系、孔压发展特性和应力路径进行了模拟及预测。

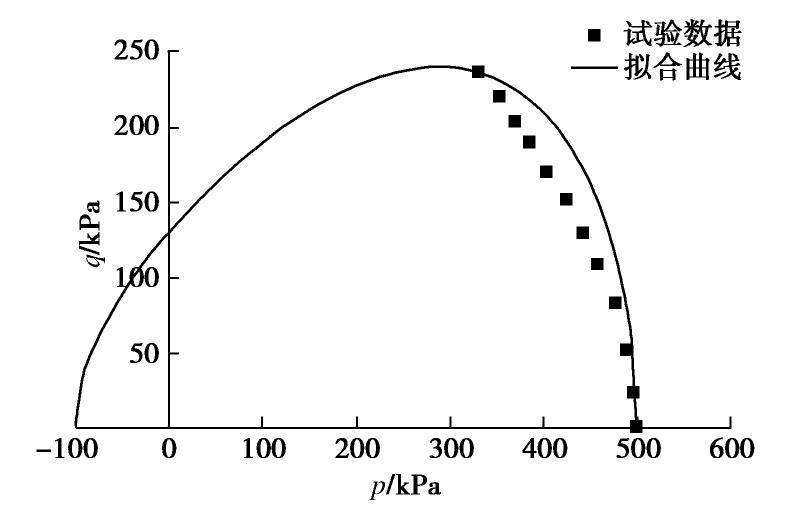
文献[4]将高岭土在常规三轴试验中等向固结至100,300,500 kPa,之后在不排水条件下剪切加载至土体破坏,并据此描绘出不同围压下的p-q数据点。试验土样的土粒相对密度G_s=2.63,塑限 $w_{P}$ =25%,液限 $w_{L}$ =45%,塑性指数 $I_{P}$ =20。本文根据围压为500 kPa时剪切加载得到的p-q数据点,拟合得出蛋形边界面形状控制参数a,b,β。试验数据点与本文拟合的蛋形边界面曲线如图9所示。

图 9 等向固结不排水软黏土的p-q曲线

Figure 9. p-q curve of isotropically consolidated undrained clay

下载: 全尺寸图片幻灯片

根据试验数据拟合结果可得3个边界面形状参数取值：a=0.6,b=0.4,β=0.35。模型的第二类参数通过数值模拟确定最佳值。第三类参数按照文献[4]中的参数取值,各参数取值如表1所示。

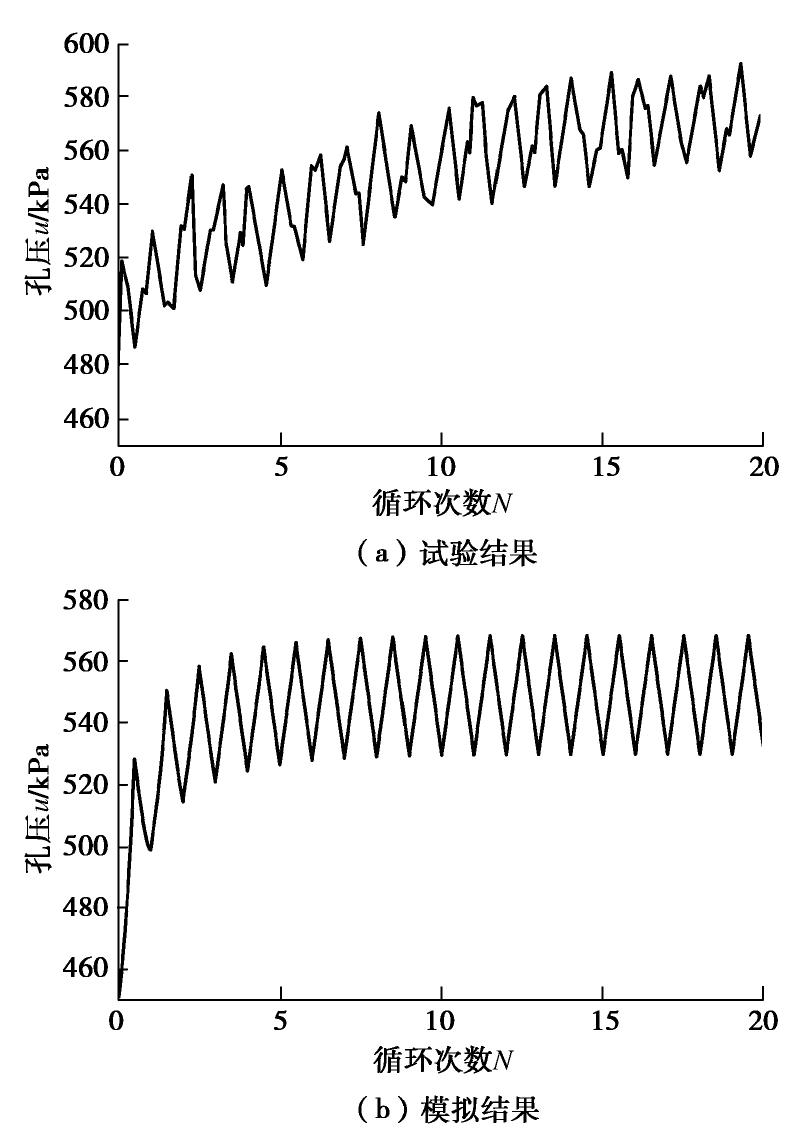
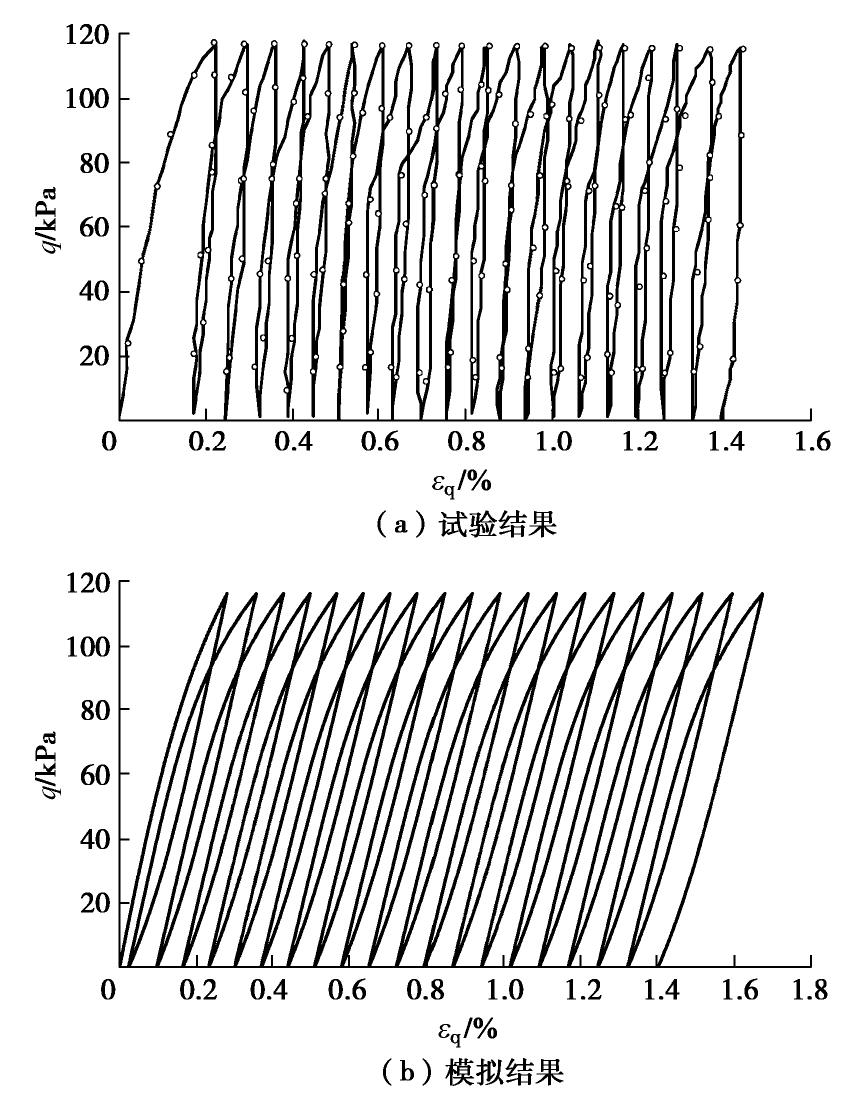
在正常固结不排水单向循环三轴试验中,土体等向固结至围压p_c0 =450 kPa,在动应力幅值q_d =116 kPa的条件下对高岭土进行循环加卸载。根据此试验条件,采用表1中的模型参数,可利用本文模型模拟土样在循环加卸载过程中的应力应变曲线和孔压-循环加载次数关系曲线,并预测应力路径。模型模拟结果与文献[4]中的试验结果对比如图10,11所示。

图 10 孔压-循环加载次数曲线图

Figure 10. Curves of pore pressure-cycle loading times

下载: 全尺寸图片幻灯片

图 11 应力-应变曲线图

Figure 11. Stress-strain curves

下载: 全尺寸图片幻灯片

图10中采用本文模型模拟的孔压随循环周次变化结果表现出了较好的稳定性,饱和软黏土的孔压随循环周次的增加先逐渐增大,之后趋于稳定,变化趋势与试验结果一致。但模型预测的稳定孔压值比实际情况偏小,原因在于：在本文模型模拟的结果中,荷载作用大约5个循环周次后,孔压便处于稳定循环状态,而在试验结果中,直至荷载循环15个周次后,孔压才逐渐趋于稳定,因此导致二者最终的稳定孔压值产生差异。

由图11可看出,荷载循环20个周次后,由本文模型计算得出的应变累积值与试验结果较为接近,说明模型能较好地模拟软黏土的应变累积性。此外,由图11（b）可见,本文建立的模型可模拟出土体在循环荷载作用下的滞回圈,能够合理地描述饱和软黏土的滞回性与卸荷时的非线性。在初始加卸载过程中,模型累积应变较小,导致塑性模量值在加卸载过程中相差不大,因此未表现出较强的塑性。随着循环周次增加,应力应变曲线的滞回圈越来越明显,土体逐渐表现出较明显的塑性,与试验结果一致。

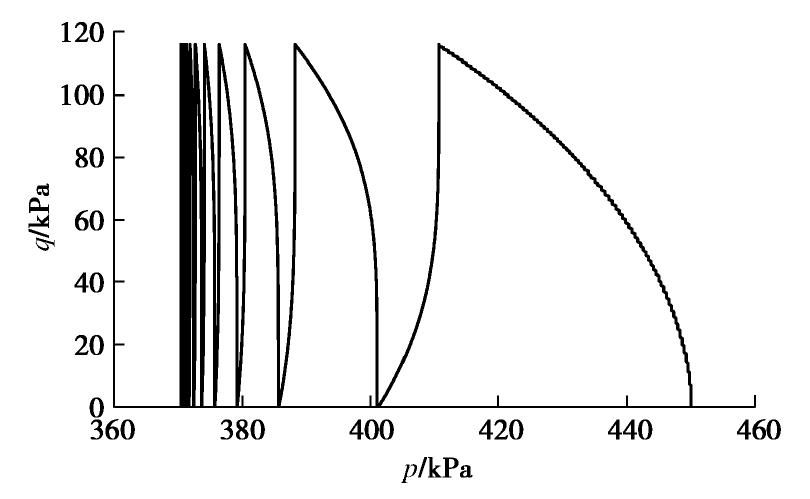
图12为本文模型预测的应力路径图,从图中可看出,本文建立的模型能够较合理地反映饱和软黏土的不排水应力路径在剪切过程中的移动及稳定状态。

图 12 应力路径预测图

Figure 12. Prediction of stress path

下载: 全尺寸图片幻灯片

综上,本文模型模拟结果与试验数据基本吻合,说明模型可较好描述饱和软黏土在不排水单向循环荷载作用下的动力特性。

3.2 Itsukaichi海洋黏土不排水静三轴试验模拟

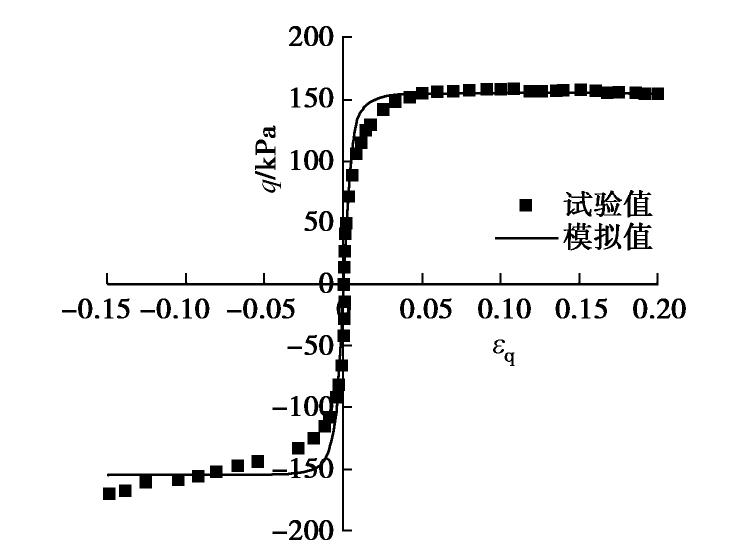
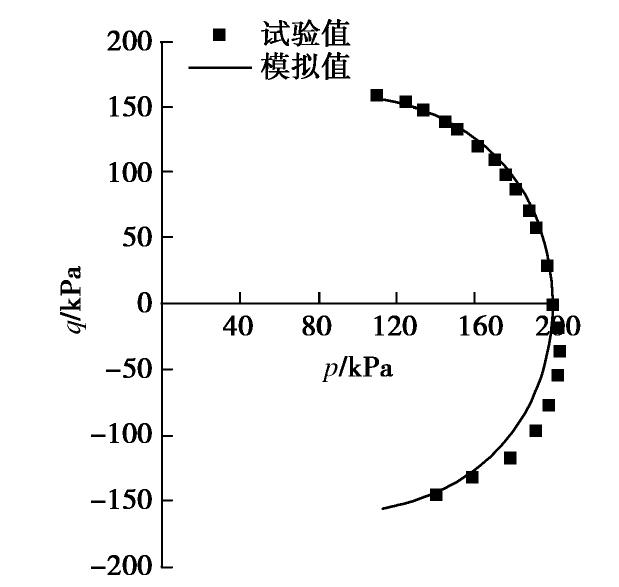
本节采用正常固结的饱和Itsukaichi海洋黏土^[27]验证模型预测土体各向异性的能力。试验土样的土粒相对密度G_s=2.532,含水率w=97.2%,塑限 $w_{P}$ =51.4%,液限 $w_{L}$ =124.2%,塑性指数 $I_{P}$ =72.8,其余模型参数如表1所示。首先将Itsukaichi海洋黏土等向固结至围压为200 kPa的状态,然后对其进行常规三轴剪切加载试验,以获得饱和软黏土在不排水剪切条件下的应力应变关系和不排水应力路径。最后将试验结果与本文模型模拟结果进行对比,如图13,14所示。

图 13 应力应变关系实测数据与模拟值

Figure 13. Stress-strain relationship of test data and model simulations

下载: 全尺寸图片幻灯片

图 14 应力路径实测数据与模拟值

Figure 14. Stress paths of test data and simulations

下载: 全尺寸图片幻灯片

对比图13中静三轴试验的应力应变关系实测值与模拟值,可以发现,在压缩剪切阶段,Itsukaichi海洋黏土的试验结果与模型模拟结果基本吻合；而在拉伸剪切阶段,由于土体拉伸强度远小于压缩强度,故提前进入破坏状态,而模型所预测的则为土体屈服强度,因此试验值与模拟值有少许出入。这表明该模型对饱和软黏土的应力应变关系具有较好的模拟能力。

对比图14中不排水应力路径的试验值与模拟值,可以发现,Itsukaichi海洋黏土的静三轴不排水剪应力路径与模型模拟结果基本吻合,这说明该模型对饱和软黏土的应力路径具有较好的模拟能力。

上述海洋黏土在不排水剪切条件下的静三轴试验验证说明该模型可用于饱和软黏土静三轴试验的模拟,进一步说明本文模型对不同土体的静三轴试验及循环三轴试验的适用性。

4. 结论

为准确反映饱和软黏土的循环动力特性与应力诱发各向异性,本文建立了蛋形单面边界面模型,提出了模型参数确定方法及详细的参数分析过程,并采用Fortran编程求得模型数值解,将数值解与高岭土的不排水单向循环三轴试验结果及Itsukaichi海洋黏土的等向固结不排水静三轴试验结果进行了对比,得到以下4点结论。

（1）本文采用的蛋形边界面封闭光滑,处处连续可导,塑性增量方向明确,克服了剑桥形式边界面角点处导数不连续与椭圆形边界面灵活性差、不能真实反映土体性质的缺陷。该蛋形边界面可退化为包含剑桥形式和椭圆形式在内等不同形式的边界面,形式更为广泛,故基于蛋形边界面建立的模型具备较强的普适性,可灵活反映土体强度及变形特性。

（2）本文模型改进了蛋形边界面,基于广义各向同性硬化法则及移动的映射中心,采用了适合饱和软黏土性质的相关联流动法则,以塑性体应变为内变量,最终建立了能够反映饱和软黏土动力特性及应力诱发各向异性的蛋形单面边界面模型。

（3）利用Fortran语言编制隐式积分算法程序,在塑性模型插值函数中的3个参数取值不同的情况下,计算得出了不排水单向循环三轴试验的应力应变曲线,分析了各参数对土体性质的影响,结果表明：3个参数对土体的动力特性起不同的控制作用,土体的应变累积性和应力应变曲线发散性都会随参数取值变化而受到明显影响。

（4）在不排水条件下,利用本文模型分别模拟了饱和高岭土循环三轴试验和饱和Itsukaichi海洋黏土静三轴试验,并与试验结果进行对比验证,结果表明模型模拟值与试验值较为吻合,说明本文提出的蛋形单面边界面模型可较好地模拟饱和软黏土的不排水剪切静荷载试验及不排水单向循环荷载作用下的应力诱发各向异性和动力特性。

图 1 p-q平面中的蛋形边界面

Figure 1. Egg-shaped bounding surface inp-q plane

下载: 全尺寸图片幻灯片

图 2 蛋形边界面的退化形式

Figure 2. Degenerated form of egg-shaped bounding surface

下载: 全尺寸图片幻灯片

图 3 主应力空间下的蛋形边界面

Figure 3. Egg-shaped bounding surface in principal stress space

下载: 全尺寸图片幻灯片

图 4 映射中心与映射法则

Figure 4. Mapping center and rule

下载: 全尺寸图片幻灯片

图 5 边界面的硬化准则

Figure 5. Hardening criteria for bounding surfaces

下载: 全尺寸图片幻灯片

图 6 参数 $ς$ 对模型的影响

Figure 6. Effects of parameterς on model

下载: 全尺寸图片幻灯片

图 7 参数 $ξ$ 对模型的影响

Figure 7. Effects of parameterξ on model

下载: 全尺寸图片幻灯片

图 8 参数 $φ_{0}$ 对模型的影响

Figure 8. Effects of parameter $φ_{0}$ on model

下载: 全尺寸图片幻灯片

图 9 等向固结不排水软黏土的p-q曲线

Figure 9. p-q curve of isotropically consolidated undrained clay

下载: 全尺寸图片幻灯片

图 10 孔压-循环加载次数曲线图

Figure 10. Curves of pore pressure-cycle loading times

下载: 全尺寸图片幻灯片

图 11 应力-应变曲线图

Figure 11. Stress-strain curves

下载: 全尺寸图片幻灯片

图 12 应力路径预测图

Figure 12. Prediction of stress path

下载: 全尺寸图片幻灯片

图 13 应力应变关系实测数据与模拟值

Figure 13. Stress-strain relationship of test data and model simulations

下载: 全尺寸图片幻灯片

图 14 应力路径实测数据与模拟值

Figure 14. Stress paths of test data and simulations

下载: 全尺寸图片幻灯片

表 1 土体参数表

Table 1 Soil parameters

试验土类	e₀	λ	κ	$ν$	a	b	β	ς	ξ	φ₀
高岭土	1.021	0.173	0.034	0.2	0.60	0.4	0.35	0.6	2.0	3.95
Itsukaichi海洋黏土	2.422	0.348	0.057	0.3	0.85	0.3	0.70	—	—	—

下载: 导出CSV

参考文献(27)

[1]	孔亮, 郑颖人, 王燕昌. 土体动本构模型研究评述[J]. 宁夏大学学报(自然版), 2001, 22(1): 17-22. https://www.cnki.com.cn/Article/CJFDTOTAL-NXDZ200101005.htm KONG Liang, ZHENG Ying-ren, WANG Yan-chang. Review of research on soil constitutive models[J]. Journal of Ningxia University (Natural Edition), 2001, 22(1): 17-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NXDZ200101005.htm
[2]	DAFALIAS Y F, POPOV E P. A model of non-linearly hardening materials for complex loading[J]. ActaMechanica, 1975, 21(3): 173-192.
[3]	KRIEG R D. A practical two surface plasticity theory[J]. Journal of Applied Mechanics, ASME, 1975, 42(3): 641-646. doi: 10.1115/1.3423656
[4]	LI T, MEISSNER H. Two-surface plasticity model for cyclic undrained behavior of clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(7): 613-626. doi: 10.1061/(ASCE)1090-0241(2002)128:7(613)
[5]	李涛, MEISSNER H. 循环荷载作用下饱和黏性土的弹塑性双面模型[J]. 土木工程学报, 2006, 39(1): 92-97. doi: 10.3321/j.issn:1000-131X.2006.01.019 LI Tao, MEISSNER H. Elastoplastic double-sided model of saturated clay under cyclic loading[J]. Journal of Civil Engineering, 2006, 39(1): 92-97. (in Chinese) doi: 10.3321/j.issn:1000-131X.2006.01.019
[6]	李潇旋, 李涛, 李舰, 等. 循环荷载下非饱和结构性黏土的弹塑性双面模型[J]. 岩土力学, 2020, 41(4): 2-9. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202004005.htm LI Xiao-xuan, LI Tao, LI Jian, et al. Elastoplastic double-sided model of unsaturated structured clay under cyclic loading[J]. Rock and Soil Mechanics, 2020, 41(4): 2-9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202004005.htm
[7]	DAFALIAS Y F, HEMNANN L R. Bounding surface formulation of soil plasticity[C]//Soil Mechanics-Transient and Cyclic Loads, 1980, New York.
[8]	黄茂松, 刘明, 柳艳华. 循环荷载下软黏土的各向异性边界面模型[J]. 水利学报, 2009, 40(2): 188-193. doi: 10.3321/j.issn:0559-9350.2009.02.009 HUANG Mao-song, LIU Ming, LIU Yan-hua. Anisotropic boundary surface model of soft clay under cyclic loading[J]. Journal of Hydraulic Engineering, 2009, 40(2): 188-193. (in Chinese) doi: 10.3321/j.issn:0559-9350.2009.02.009
[9]	HU C, LIU H X. A new bounding-surface plasticity model for cyclic behaviors of saturated clay[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1/2/3): 101-119.
[10]	HU C, LIU H X. Implicit and explicit integration schemes in the anisotropic bounding surface plasticity model for cyclic behaviours of saturated clay[J]. Computers and Geotechnics, 2014, 55: 27-41. doi: 10.1016/j.compgeo.2013.07.012
[11]	DAFALIAS, Y F. An anisotropic critical state soil plasticity model[J]. Mechanics Research Communications, 1986, 13(6): 341-347. doi: 10.1016/0093-6413(86)90047-9
[12]	李兴照, 黄茂松. 循环荷载作用下流变性软黏土的边界面模型[J]. 岩土工程学报, 2007, 29(2): 249-254. doi: 10.3321/j.issn:1000-4548.2007.02.016 LI Xing-zhao, HUANG Mao-song. Boundary surface model of rheologically soft clay under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 249-254. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.02.016
[13]	秦立科. 非饱和黄土动力本构模型及其在地铁车站地震反应分析中的应用[D]. 西安: 长安大学, 2010. QIN Li-ke. Dynamic Constitutive Model of Unsaturated Loess and its Application in Seismic Response Analysis of Subway Stations[D]. Xi'an: Chang'an University, 2010. (in Chinese)
[14]	ZIENKIEWICZ-PANDE O C. The finite element method in engineering science[M]. 2nd ed. New York: McGraw-Hill, 1971.
[15]	骆俊晖, 缪林昌, 李仞玨. 考虑时间效应边界面模型在地铁工程中的应用[J]. 岩石力学与工程学报, 2017, 36(6): 236-246. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201706025.htm LUO Jun-hui, MIAO Lin-chang, LI Yi. Application of boundary surface model considering time effect in metro engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 236-246. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201706025.htm
[16]	MANZARI M T, NOUR M A. On implicit integration of bounding surface plasticity models[J]. Computers and Structures, 1997, 63(3): 385-395.
[17]	姚仰平, 万征, 陈生水. 考虑颗粒破碎的动力UH模型[J]. 岩土工程学报, 2011, 33(7): 1036-1044. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201107007.htm YAO Yang-ping, WAN Zheng, CHEN Sheng-shui. Dynamic UH model considering particle crushing[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(7): 1036-1044. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201107007.htm
[18]	ABBO A J, SLOAN S W. A smooth hyperbolic approximation to the Mohr-Coulomb Yield Criterion[J]. Computers and Structures, 1995, 54(3): 427-441.
[19]	任放, 盛谦, 常燕庭. 岩土类工程材料的蛋形屈服函数[J]. 岩土工程学报, 1993, 15(4): 33-39. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC199304004.htm REN Fang, SHENG Qian, CHANG Yan-ting. Egg-shaped yield function of geotechnical engineering materials[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(4): 33-39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC199304004.htm
[20]	徐日庆, 杨林德, 龚晓南. 土的边界面应力应变本构关系[J]. 同济大学学报, 1997, 25(1): 29-33. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ199701005.htm XU Ri-qing, YANG Lin-de, GONG Xiao-nan. Stress strain constitutive relationship of boundary surface of soils[J]. Journal of Tongji University, 1997, 25(1): 29-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ199701005.htm
[21]	XU R Q, WANG X C, RONG X N. Macro- and meso-scale parametric analysis of egg-shaped yield surface of structural soil[J]. International Journal of Offshore and Polar Engineering, 2014, 24(4): 301-308.
[22]	CHENG X L, WANG J H, WANG Z X. Incremental elastoplastic FEM for simulating the deformation process of suction caissons subjected to cyclic loads in soft clays[J]. Applied Ocean Research, 2016, 59: 274-285.
[23]	徐干成, 谢定义, 郑颖人. 饱和砂土循环动应力应变特性的弹塑性模拟研究[J]. 岩土工程学报, 1995, 17(2): 1-12. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC502.000.htm XU Qian-cheng, XIE Ding-yi, ZHENG Ying-ren. Elastoplastic simulation of cyclic dynamic stress and strain characteristics of saturated sand[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(2): 1-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC502.000.htm
[24]	沈恺伦, 王立忠. 天然软黏土屈服面及流动法则试验研究[J]. 土木工程学报, 2009, 42(4): 119-127. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200904019.htm SHEN Kai-lun, WANG Li-zhong. Experimental study on yield surface and flow law of natural soft clay[J]. Journal of Civil Engineering, 2009, 42(4): 119-127. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200904019.htm
[25]	沈扬, 周建, 龚晓南, 等. 考虑主应力方向变化的原状软黏土应力应变性状试验研究[J]. 岩土力学, 2009, 30(12): 3720-3726. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200912030.htm SHEN Yang, ZHOU Jian, GONG Xiao-nan, et al. Experimental study on stress-strain behavior of intact soft clay considering changes in principal stress direction[J]. Rock and Soil Mechanics, 2009, 30(12): 3720-3726. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200912030.htm
[26]	钟辉虹, 黄茂松, 吴世明, 等. 循环荷载作用下软黏土变形特性研究[J]. 岩土工程学报, 2002, 24(5): 629-632. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200205020.htm ZHONG Hui-hong, HUANG Mao-song, WU Shi-ming, et al. Research on deformation characteristics of soft clay under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 629-632. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200205020.htm
[27]	HYODO M, YAMAMOTO Y, SUGIYAMA M. Undrained cyclic shear behaviour of normally consolidated clay subjected to initial static shear stress[J]. Japanese Society of Soil Mechanics and Foundation Engineering, 1994, 34(4): 1-11.