深部圆形巷道围岩能量的调整机制及平衡关系

陈昊祥; 王明洋; 戚承志; 李杰

doi:10.11779/CJGE202010010

深部圆形巷道围岩能量的调整机制及平衡关系 English Version

陈昊祥^{1, 2,},
王明洋^2, ,,
戚承志¹,
李杰²

1.
北京建筑大学北京交通基础设施建设国际合作基地,北京　100044
2.
陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏　南京　210007

基金项目:

国家自然科学基金重大科研仪器研制项目 51527810

国家自然科学基金项目 51679249

国家重点基础研究发展计划（973计划）项目 2013CB036005

详细信息

作者简介:
陈昊祥(1992—),男,博士后,主要从事深部岩体力学与工程等方面的研究。E-mail：chx@stu.bucea.edu.cn

通讯作者:
王明洋, E-mail：wmyrf@163.com

中图分类号: TU431
计量
- 文章访问数: 296
- HTML全文浏览量: 26
- PDF下载量: 126
出版历程
- 收稿日期: 2019-11-27
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-09-30

Mechanism of energy adjustment and balance of rock masses near a deep circular tunnel

1.
Beijing International Cooperation Base for Municipal Transportation Infrastructures, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
2.
State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact, Army Engineering University of PLA, Nanjing 210007, China

摘要

摘要: 巷道开挖过程中,能量的调整与再平衡会深刻地影响围岩的力学行为,理解围岩中能量的变化规律有助于工程灾变的防控及支护方案的优化。从应力状态与变形协调角度出发,分析了深部圆形巷道围岩的变形破坏模式,研究了准静态、弹塑性卸载条件下围岩中能量的调整机制以及传递、转换规律。在数学上严格证明了围岩内部能量的平衡关系,并详细分析了各组份能量的物理意义。结果表明：能量由外部围岩输入并以径向压力做功的形式向内部围岩传递,此时输入的能量部分以弹性应变能形式储存于围岩内,部分通过塑性变形耗散,剩余部分则通过围岩压力做功的形式释放并用于抵抗支护压力（无支护时,此部分能量将转化为围岩动能）,此过程严格满足能量守恒定律。
- 深部围岩 /
- 准静态卸载 /
- 弹塑性 /
- 能量调整与平衡
Abstract: During the excavation of deep tunnels, the adjustment and balance of energy have a significant influence on the mechanical behavior of the surrounding rock masses. Understanding the energy changes in the surrounding rocks will facilitate the prevention of geotechnical disasters and the optimization of supporting schemes. The deformation and failure modes of the surrounding rock masses around a deep-level circular tunnel are analyzed by considering the stress conditions and deformation compatibility. The mechanism of energy adjustment and laws of energy transmission and transformation in the surrounding rock masses under quasi-static unloading condition are investigated. The energy balance in the surrounding rock masses is proved rigorously from the mathematical viewpoint, and the physical interpretations for each energy component are given. The results indicate that the input external energy from far region is transferred to near region in the form of work done by radial stress. The input external energy can be divided into three parts: the potential energy stored in the rock masses, the energy dissipated by plastic deformation and the work done by pressure of rock masses that will transfer into potential energy in supporting (or kinetic energy of the surrounding rock). The adjustment process of the whole energy accords with conservation of energy.
- deep rock mass /
- quasi-static unloading /
- elasto-plasticity /
- adjustment and balance of energy

HTML全文

0. 引言

能量的聚集和释放在岩石的变形破坏过程中起着重要作用,研究表明岩爆、微震、围岩的塑性变形或破碎、分区破裂化以及大变形失稳等工程灾变现象都与围岩中的能量释放有关^[1-5]。尤明庆等^[2]对岩石试样变形与破坏过程中能量的变化进行了分析,发现岩石试样破坏过程中必须持续从外界接受能量,且吸收的能量主要由岩样剪切变形消耗,而围岩储存的弹性应变能将释放并转换为岩块的动能。Cook等^[6-9]发现巷道开挖过程中伴随着巨大的能量变化,认为“岩爆”是由围岩中势能过量聚集引起,阐明了微震和岩爆现象与围岩空间能量释放率之间的关系。虽然Cook等人提出的能量原理得到了广泛的应用,但是能量各组份的计算却并不严格。之后,Walsh^[10]在弹性理论框架下系统地推导了巷道围岩能量变化过程中各组份的表达式。Salamon^[11]分析了分格开挖过程中围岩能量的变化情况,研究表明开挖步的大小严重影响能量的转移和平衡。Brady等^[12-13]讨论了球形硐室准静态和动力卸载条件下弹性能量的变化情况,得到了球形硐室动静开挖过程中能量的平衡关系。华安增^[3]分析了隧道开挖前后围岩弹性应变能的释放与集聚情况,发现围岩能量到达储能极限时,将释放多余的能量,此时围岩将进入塑性或破碎状态。潘岳等^[14-16]由能量守恒原理导出了围岩动力失稳突变模型的平衡方程,证明了做功和能量平衡关系也适用于弹性体系几何失稳问题；求解了弹性、非线性软化模型巷道围岩应力分布表达式,用重积分计算了围岩塑性区中的偏应变能,证明了巷道围岩释放的能量等于围岩压力p_a与开挖边界位移u_a的积分乘内壁周长。潘岳等的研究仅给出了能量之间的数学关系,未能对其物理意义作出解释。Kramarenko等^[17]、Revuzhenkor等^[18]提出了能量流线及能量流矢量的观点,认为能量类似于可压缩流体,可以在固体介质中按一定的规律进行流动。之后研究了不同加载条件下含椭圆形切口弹性平板的应力-应变关系,分析了可变形体中能量转移问题,揭示了变形材料实际上是能量传递的介质。Lu等^[19]、范勇等^[20-21]研究了巷道围岩弹性动力卸载作用下的能量变化规律,优化了局部能量释放效率指标,分析了瞬态卸荷条件下能量的释放过程,确定了能量释放与围岩损伤之间的关系,并基于能量条件估算了围岩破坏区的范围。

上述研究为分析巷道开挖过程中围岩能量的变化规律提供了良好的理论基础,但不足的是,研究大都仅考虑了弹性卸载条件,很少涉及塑性卸载条件下围岩能量的平衡关系和调节机制。本文主要针对深部圆形巷道围岩准静态、弹塑性开挖问题,理论上严格推导了能量的平衡关系,详细地分析了围岩能量的调整机制以及传递和转换规律。

1. 围岩能量的调整与聚集

假设地下硐室在开挖前,岩石处于静水压力状态^[3],即

$σ_{1} = σ_{2} = σ_{3} = σ_{0}$ ,

(1)

式中, $σ_{1}$ , $σ_{2}$ , $σ_{3}$ 分别为第一、二、三主应力, $σ_{0}$ 为初始地应力（远场应力）。

围岩的弹性应变能密度U为

$U = [σ_{1}^{2} + σ_{2}^{2} + σ_{3}^{2} - 2 ν (σ_{1} σ_{2} + σ_{2} σ_{3} + σ_{3} σ_{1})] / (2 E)$ 。

(2)

式中,ν为泊松比,E为弹性模量。因此开挖前围岩的弹性应变能（体积应变能）密度U₀为

$U_{0} = 3 σ_{0}^{2} (1 - 2 ν) / (2 E)$ 。

(3)

开挖过程中,围岩经历径向卸载,且卸载过程初期,围岩处于弹性阶段。如果初始应力σ₀较大,卸载发生一段时间后,巷道内壁开始屈服。随着卸载过程的进行,塑性区范围将逐渐向外扩展。因此可将卸载过程分为弹性卸载和塑性卸载两个阶段分别进行研究。

1.1 弹性卸载过程中能量的调节机制

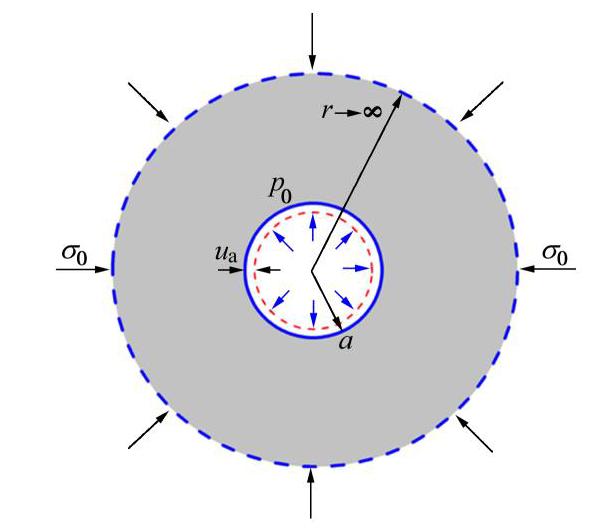
如果在岩体中开挖一个半径为a的圆形巷道,且巷道周围岩体处于弹性状态。此时,巷道可简化为平面应变问题,力学模型如图1所示,开挖边界径向位移u_a,内压力（支护压力）p₀,远场应力σ₀。

图 1 圆形硐室弹性卸载力学示意图

Figure 1. Configuration for excavation of circular tunnel under elastic unloading

下载: 全尺寸图片幻灯片

对于平面轴对称问题,选用柱坐标系（r,θ,z）,由经典的弹性理论可知巷道周围岩体中的应力场：

$\begin{array}{l} σ_{r} = σ_{0} - (σ_{0} - p_{0}) a^{2} / r^{2}, \\ σ_{θ} = σ_{0} + (σ_{0} - p_{0}) a^{2} / r^{2}, \\ σ_{z} = σ_{0}, \\ τ_{r θ} = τ_{θ z} = τ_{z r} = 0, \end{array}}$

(4)

以及位移场：

$\begin{array}{l} u_{r} = \frac{(σ_{0} - p_{0})}{2 μ} \frac{a^{2}}{r}, \\ u_{θ} = u_{z} = 0 。 \end{array}}$

(5)

式中 $σ_{r}, σ_{θ}, σ_{z}$ 为半径r处围岩的径向、环向和轴向应力； $τ_{r θ}, τ_{θ z}, τ_{z r}$ 为半径r处围岩的剪应力； $u_{r}, u_{θ}, u_{z}$ 为半径r处围岩的径向、环向和轴向位移；μ为岩石的剪切模量,且E = 2(1+ν)μ,ν为泊松比。

将式（4）代入式（2）可得开挖后半径r处围岩的弹性应变能密度为

$U_{1} = 3 (1 - 2 ν) σ_{0}^{2} / (2 E) + \frac{{(σ_{0} - p_{0})}^{2}}{2 μ} \frac{a^{4}}{r^{4}}$ 。

(6)

圆形巷道开挖前后半径r处围岩的弹性应变能密度增量 $Δ U$ 为

$Δ U = U_{1} - U_{0} = \frac{{(σ_{0} - p_{0})}^{2}}{2 μ} \frac{a^{4}}{r^{4}}$ 。

(7)

在外力作用下,物体的变形通常可以分为体积变形和剪切变形,而对应的弹性应变能分别为体积应变能和剪切应变能。因此弹性应变能密度U的表达式还可以写作体积应变能 $U_{V}$ 和剪切应变能 $U_{d}$ 之和：

$U = U_{V} + U_{d} = σ_{m}^{2} / 2 K + J_{2} / 2 μ$ 。

(8)

式中,体积应变能密度 $U_{V} = σ_{m}^{2} / 2 K$ 和畸变能密度 $U_{d} = J_{2} / 2 μ$ , $σ_{m} = (σ_{1} + σ_{2} + σ_{3}) / 3$ 为静水压力,K为材料的体积模量,J₂为偏应力张量第二不变量。

巷道开挖前后,围岩所受的静水压力 $σ_{m}$ 并未发生改变,故储存的体积应变能密度亦未改变。

$U_{V} = σ_{m}^{2} / 2 K = 3 σ_{0}^{2} (1 - 2 ν) / (2 E)$ 。

(9)

巷道开挖后,由于剪应力的存在,围岩将发生剪切变形,并产生与之对应的剪切应变能（畸应变能）,此时半径r处围岩的畸应变能密度 $U_{d}$ 为

$U_{d} = e_{i j} s_{i j} / 2 = J_{2} / 2 μ = \frac{{(σ_{0} - p_{0})}^{2}}{2 μ} \frac{a^{4}}{r^{4}}$ ,

(10)

式中,s_ij为偏应力张量,e_ij为偏应变张量。此时岩体中增加的弹性应变能密度均以畸变能形式储存于围岩之中,即

$Δ U = U_{d} = \frac{{(σ_{0} - p_{0})}^{2}}{2 μ} \frac{a^{4}}{r^{4}}$ 。

(11)

对应变能密度增量 $Δ U$ 在整个平面内积分,可得围岩中增加的总弹性应变能 $Δ E_{0}$ 为

$Δ E_{0} = \int_{0}^{2 π} d θ \int_{a}^{\infty} r Δ U d r = \frac{π a^{2} {(σ_{0} - p_{0})}^{2}}{2 μ}$ 。

(12)

由式（4）,（5）可知,当r = a时

$σ_{r} |_{r = a} = p_{0} = σ_{0} - 2 μ \frac{u_{a}}{a}$ 。

(13)

式中, $σ_{r} |_{r = a}$ 为围岩压力。此时,围岩压力为初始地应力 $σ_{0}$ 与围岩自承应力R(u_a)=2μ u_a/a之差。

对式（13）在位移u_a上积分可得开挖过程中围岩压力做功的释放能量,即

$W_{c} = 2 π a \int_{0}^{u_{a}} σ_{r} |_{r = a} d u_{a} = \frac{π a^{2} (σ_{0}^{2} - p_{0}^{2})}{2 μ}$ 。

(14)

此部分能量将用于抵抗支护压力做功或转换为围岩动能（无支护时）。

由式（4）,（5）可知,半径r = R处径向应力与径向位移分别为

$\begin{array}{l} σ_{R} = σ_{0} - (σ_{0} - p_{0}) \frac{a^{2}}{R^{2}}, \\ u_{R} = \frac{(σ_{0} - p_{0})}{2 μ} \frac{a^{2}}{R}, \end{array}}$

(15)

此时,径向应力 $σ_{R}$ 做功（平均压力乘以位移）

$\begin{matrix} W_{0} = 2 π R \times \frac{1}{2} [σ_{0} + σ_{0} - (σ_{0} - p_{0}) \frac{a^{2}}{R^{2}}] \frac{(σ_{0} - p_{0})}{2 μ} \frac{a^{2}}{R} \\ = \frac{π a^{2} (σ_{0} - p_{0})}{μ} [σ_{0} - \frac{(σ_{0} - p_{0}) a^{2}}{2 R^{2}}] \end{matrix}$ 。

(16)

当 $R \to \infty$ 时,即可得远处围岩做功

$W_{0} = \frac{π a^{2} σ_{0} (σ_{0} - p_{0})}{μ}$ 。

(17)

由式（12）,（14）和（17）可知,

$W_{0} = Δ E_{0} + W_{c}$ ,

(18)

围岩储存的弹性应变能增量 $Δ E_{0}$ 与围岩压力做功释放的能量 $W_{c}$ 完全由远处围岩输入的能量 $W_{0}$ 提供,严格满足能量守恒定律。

1.2 围岩本构关系及破坏准则的选取

（1）围岩本构关系的选取

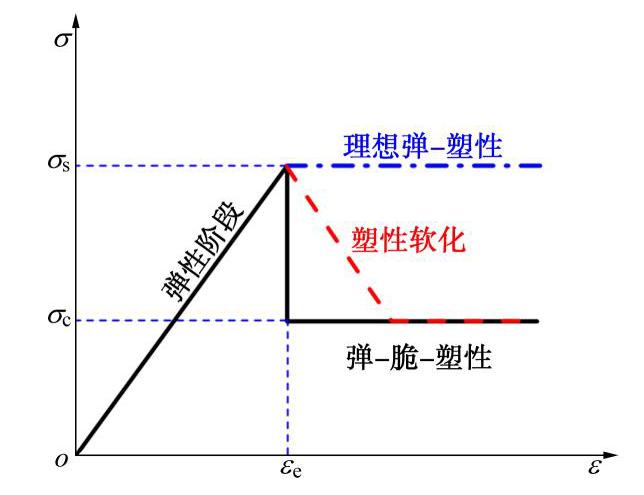
岩石常见的本构关系主要有理想弹-塑性、塑性软化和理想弹-脆-塑性3种,如图2所示。其中, $σ_{s}$ 为岩石的峰值强度, $σ_{c}$ 为岩石的残余强度, $ε_{e}$ 为岩石的弹性极限应变。

图 2 岩石常见的应力-应变关系曲线

Figure 2. Stress-strain curves for rock materials

下载: 全尺寸图片幻灯片

观察图2可以发现,理想弹-塑性本构关系只是理想弹-脆-塑性本构关系的一种特殊情况,即残余强度 $σ_{c}$ 等于峰值强度 $σ_{s}$ 。而应变软化本构关系则处于理想弹-塑性和理想弹-脆-塑性之间,此时理想弹-塑性和理想弹-脆-塑性可作为应变软化本构关系的上、下限。在实际工程中岩石的软化模量通常是未知的,而且岩石软化阶段的力学性质较为复杂。如能确定岩石软化阶段力学性质的上下极限,即可对岩石的塑性力学性质进行估计并可有效地降低计算难度。基于上述原因,本节将假设围岩满足理想弹-脆-塑性本构关系。

（2）岩石破坏准则的选取

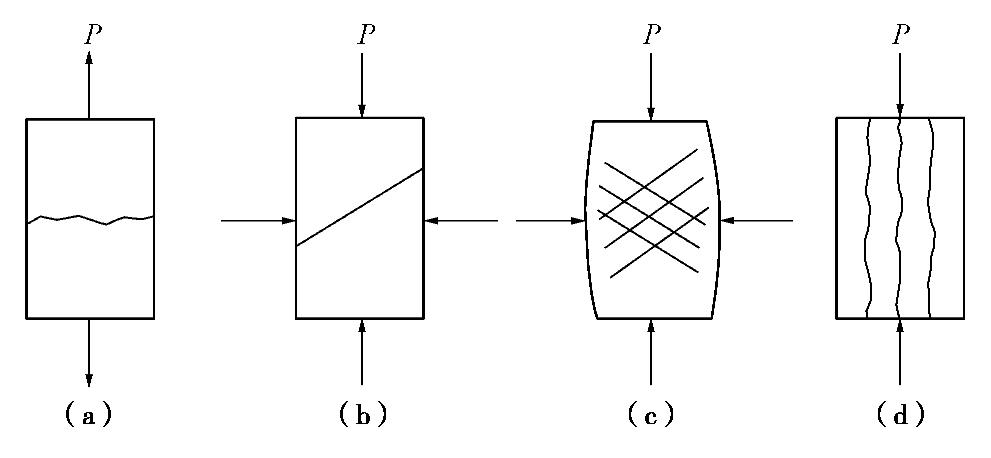
破坏准则是指材料在弹性极限状态下,应力状态与材料物理力学参数之间的关系,是材料由弹性阶段向塑性阶段过渡的判别标准。岩石等准脆性材料破坏准则的选取不仅与其自身物理力学性质有关,还依赖于岩石应力状态和变形破坏模式。岩石在不同的外力作用下,表现出的破坏模式差别很大,因此破坏准则的选取亦不尽相同。如图3所示为岩石受力破坏的典型模式：拉伸破坏、剪切破坏、多重剪切破坏和劈裂破坏。

图 3 岩石常见的破坏形式

Figure 3. Facture patterns of rock materials

下载: 全尺寸图片幻灯片

在选取适当的破坏准则之前,首先需要对围岩的受力状态和变形模式进行分析研究。在径向卸载和环向加载的作用下,圆形巷道开挖边界上岩石的受力状态接近于单轴或低侧限受压。此时硐室壁上围岩的剪应力达到最大值,但是由于泊松效应,围岩的径向拉应变也达到最大。由图3可知,此时围岩可能发生的破坏形式为剪切破坏和劈裂破坏。上述的两种破坏形式都得到了大量现场观测结果的证实,因此围岩到底发生何种破坏仍存在很大争议。作者将从应力状态和变形模式两个方面对围岩可能发生的破坏形式进行研究和分析,旨在为围岩破坏形式的确定以及破坏准则的选取提供一定的理论支撑。

首先对围岩的应力状态进行分析,可通过Lode参数表征,即

$μ_{σ} =2 \frac{σ_{2} - σ_{3}}{σ_{1} - σ_{3}} - 1$ 。

(19)

Lode参数 $μ_{σ}$ 主要用于表征第二主应力 $σ_{2}$ 的位置,某种意义上Lode参数还可以被看作是物质点偏应力张量的简化形式,或是材料的偏应力状态。对于相同的 $μ_{σ}$ 值,3个主应力之间的关系是相似的。因此当Lode参数确定时,材料的偏应力状态即被确定。通常,Lode参数的取值范围为 $- 1 \leq μ_{σ} \leq 1$ ：对于纯压缩状态（ $σ_{1} > 0, σ_{2} = σ_{3} = 0$ ） $, μ_{σ} = - 1$ ；对于纯拉伸状态（ $σ_{1} = σ_{2} = 0, σ_{3} < 0$ ） $, μ_{σ} = 1$ ；对于纯剪切状态（ $σ_{1} > 0, σ_{2} = 0, σ_{3} = - σ_{1}$ ） $, μ_{σ} = 0$ 。

由式（4）通过简单的计算可知,圆形硐室开挖面上围岩的应力Lode参数为 $μ_{σ} = 0$ ,此时围岩的偏应力状态更接近于纯剪状态,故圆形巷道围岩最可能发生剪切破坏。

从变形方面考虑,深部硐室围岩在高地应力作用下如果发生劈裂破坏,由于空隙的产生围岩将发生显著的径向位移并伴随体积膨胀。但是由于环向变形受到限制,围岩并不能自由地沿径向发生移动,因此劈裂破坏很难发生。最有可能的是,围岩先发生剪切破坏被剪切面切割成多个块体,然后块体沿剪切面向巷道内部发生滑动。如此才能产生足够的位移使得内部围岩进行变形与应力调整。

需要指出的是,实际工程中施工人员通常以围岩是否产生肉眼可见的裂纹来判断岩石是否发生劈裂破坏,但是仅通过观察裂纹并不能判断围岩是否已经发生塑性剪切变形。而且研究表明^[22],已经进入塑性阶段的岩体更容易发生劈裂破坏。根据上述分析,作者认为圆形巷道边界围岩在发生劈裂破坏之前,很可能已产生了塑性剪切变形,而岩石劈裂则属于二次破坏现象,文献[22]的作者也持相似观点。

通过应力状态与变形分析,作者认为深部圆形巷道围岩在高地应力作用下应先发生剪切破坏,故破坏准则也应选取相应的剪应力破坏准则。岩石作为大颗粒摩擦型介质,其强度来源主要为黏聚力和摩擦力。通常可采用莫尔-库仑破坏准则来描述岩土材料破坏时的应力状态,但莫尔-库仑破坏准则的物理解释却存不足。莫尔-库仑准则认为材料的黏聚力与摩擦力同时发挥作用,但大量的单轴压缩与直剪实验结果表明：黏聚力与摩擦力并非同时发挥作用,岩石的强度也并非两部分的简单叠加。在剪切力作用下,岩石的黏聚力率先发挥作用。当剪切力升高到一定程度后岩石内部开始出现剪切面,此时黏聚力逐渐丧失,摩擦力开始逐步发挥；当剪切面贯通后,内聚力减小为零,此时岩石的强度完全由摩擦力提供。Treasca准则作为莫尔-库仑准则的特殊情况,其物理意义明确且不失一般性,还可以简化后续问题的计算量。

本文旨在研究围岩卸载过程中的变形破坏模式以及能量的调节与平衡关系,而破坏准则的选取仅对围岩塑性区半径r_p有显著影响。需要指出的是,在文章后续的推导过程中塑性区半径r_p一直保留着变量形式,并未对其进行赋值,因此Treasca准则的选取对文章的主要研究内容影响不大。

1.3 塑性卸载过程中能量的调节机制

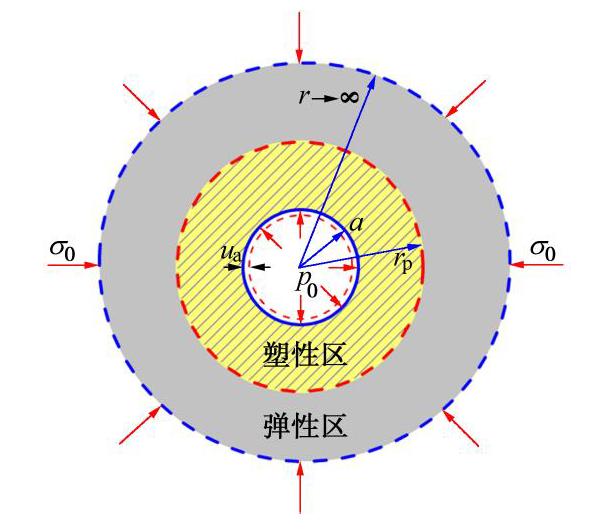
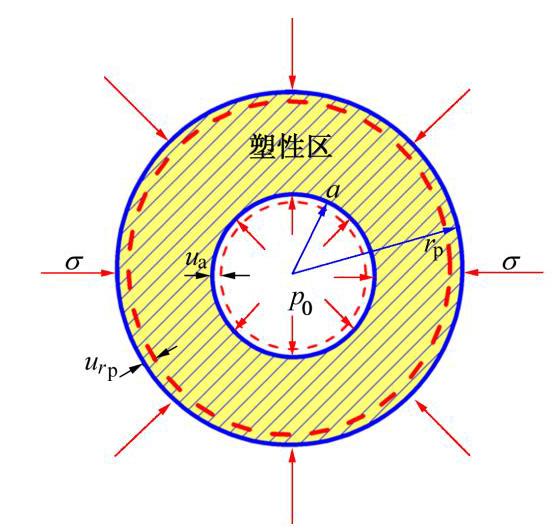
如图4所示为圆形巷道塑性卸载条件下的力学模型图,圆形巷道半径为a,塑性区半径为r_p,开挖边界径向位移u_a,内压力p₀,远场应力σ₀。

图 4 圆形硐室弹塑性卸载力学示意图

Figure 4. Configuration for excavation of circular tunnel under elasto-plastic unloading

下载: 全尺寸图片幻灯片

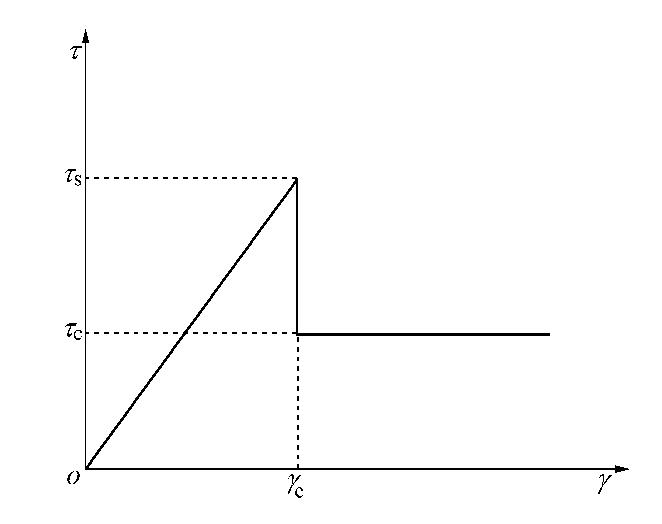
为了简洁表征围岩破坏的物理机制,围岩的本构关系采用图5所示的弹-脆-塑性模型,围岩塑性不可压缩且服从Treasca破坏准则。图中 $τ$ 为剪应力, $τ_{s}$ 为岩石的峰值剪切强度, $τ_{c}$ 为岩石的残余剪切强度, $γ$ 为剪应变, $γ_{e}$ 为弹性剪应变极限。

图 5 理想弹-脆-塑性本构模型

Figure 5. Elastic-brittle-plastic constitutive model for rock masses

下载: 全尺寸图片幻灯片

由经典的弹塑性理论可知,围岩塑性区半径

$r_{p} = a \cdot e^{(σ_{0} - p_{0} - τ_{s}) / 2 τ_{c}}$ ,

(20)

塑性区（即 $a \leq r \leq r_{p}$ 范围）内围岩的应力场与位移场分别为

$\begin{array}{l} σ_{r} = 2 τ_{c} \ln (r / a) + p_{0}, \\ σ_{θ} = 2 τ_{c} [1 + \ln (r / a)] + p_{0}, \\ σ_{z} = σ_{0}, \\ τ_{r θ} = τ_{θ z} = τ_{z r} = 0, \end{array}}$

(21)

$u_{r} = \frac{τ_{s}}{2 μ} \frac{r_{p}^{2}}{r}$ 。

(22)

此时弹性区围岩的受力状态相当于在半径为 $r_{p}^{}$ 处施加了一个支护压力,由式（4）和（5）可知弹性区（即 $r \geq r_{p}$ 范围）围岩的应力场为

$\begin{array}{l} σ_{r} = σ_{0} - τ_{s} \frac{r_{p}^{2}}{r^{2}}, \\ σ_{θ} = σ_{0} + τ_{s} \frac{r_{p}^{2}}{r^{2}}, \\ σ_{z} = σ_{0}, \\ τ_{r θ} = τ_{θ z} = τ_{z r} = 0, \end{array}}$

(23)

位移场为

$u_{r} = \frac{τ_{s}}{2 μ} \frac{r_{p}^{2}}{r}$ 。

(24)

将式（23）代入式（2）可得,弹性区围岩中储存的弹性应变能密度为

$U_{1}^{e} = 3 (1 - 2 ν) σ_{0}^{2} / (2 E) + \frac{τ_{s}^{2}}{2 μ} \frac{r_{p}^{4}}{r^{4}}$ ,

(25)

且围岩的储能极限为

$U_{1} = 3 (1 - 2 ν) σ_{0}^{2} / (2 E) + \frac{τ_{s}^{2}}{2 μ}$ ,

(26)

由式（21）可知塑性区围岩中残存的弹性应变能密度

$\begin{matrix} U_{1}^{p} = \frac{σ_{0}^{2} - 4 τ_{c} (ν σ_{0} - τ_{c})}{2 E} + \\ \frac{4 τ_{c}}{E} [τ_{c} (1 - ν) (1 + \ln \frac{r}{a}) - ν σ_{0}] \ln \frac{r}{a} \end{matrix}$ 。

(27)

残余弹性应变能密度的计算遵从以下两个假设：①岩石线性卸载且卸载模量等于弹性模量；②岩石在完全卸载条件下应力将降低为零,虽存在残余应变,但不存在残余应力。结合式（21）与式（2）可得塑性区内任意位置岩石的残余弹性能密度,具体如式（27）所示。

当r = a处,围岩的残余弹性应变能密度

$U_{1}^{p} |_{r = a} = \frac{σ_{0}^{2} - 4 τ_{c} (ν σ_{0} - τ_{c})}{2 E}$ ,

(28)

当r = r_p处,围岩的残余弹性应变能密度

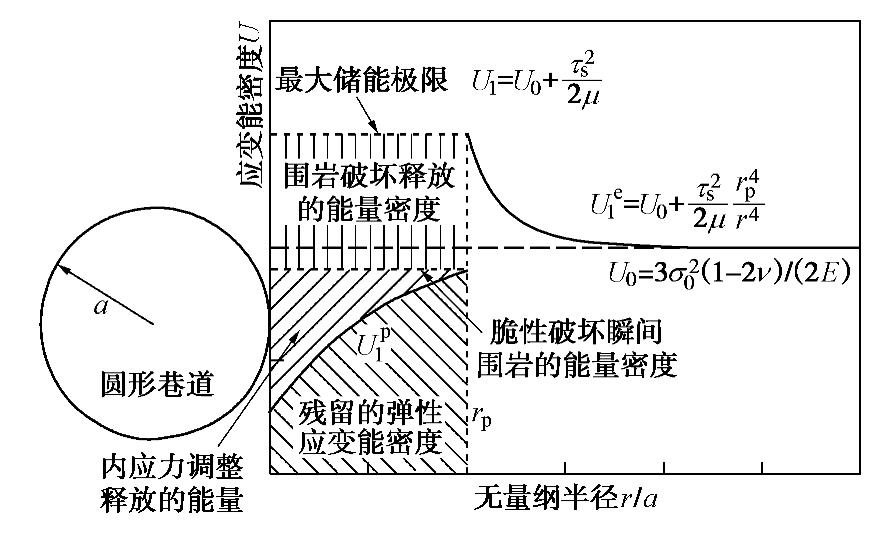
$\begin{matrix} U_{1}^{p} |_{r = r_{p}} = \frac{3 (1 - 2 ν) σ_{0}^{2}}{2 E} + \\ \frac{τ_{c}^{2} - 2 (1 - 2 ν) (τ_{s} - τ_{c}) σ_{0} + (1 - ν) (τ_{s} - 2 τ_{c}) τ_{s}}{E} \end{matrix}$ 。

(29)

如图6所示为圆形巷道开挖前后围岩中弹性应变能密度随无量纲半径r/a的变化规律。在弹性卸载过程中随着巷道开挖面上径向应力的逐步减小,围岩中储存的弹性应变能逐步增加,越靠近硐室边界,围岩集聚的弹性应变能密度越高。此过程中围岩还会通过弹性回弹向外释放能量,而这部分能量并不会造成围岩的破坏。当围岩达到弹性变形极限时,此时储存的弹性应变能密度也达到了围岩的储能极限。随着径向压力的进一步减小,围岩开始进入破坏状态,输入的能量也将超过围岩的储能极限,多余的能量将被释放出去,并会造成围岩产生塑性变形或破坏。对于弹-脆-塑性本构关系,围岩达到储能极限后,储存的能量密度会从极限值直接跌落到破裂瞬间对应的能量密度。随后塑性区围岩继续通过内应力调整释放出多余能量,主要被围岩以摩擦、振动或破裂等形式耗散掉,而剩余的能量则以弹性应变能的形式残留在塑性区岩体内。如果释放的能量大于围岩破坏所能耗散的极限时,多余的能量则将转化为围岩的动能。

图 6 围岩弹性应变能密度U随无量纲半径r/a的变化曲线

Figure 6. Distribution of elastic strain energy U of surrounding rock masses along with dimensionless radius r/a

下载: 全尺寸图片幻灯片

由上述分析可知,塑性区围岩的能量调整过程可分为两个阶段：①弹性卸载—围岩中储存的能量尚未达到储能极限；②塑性卸载—围岩储存能量达到弹性极限后,通过破碎和内应力调整释放多余能量。上述的两个阶段在时空上存在着明显的先后顺序,内层围岩先达到储能极限然后进入塑性状态并向外释放多余能量,塑性区将从内层围岩逐渐向外传递,如此重复。上述过程应满足能量守恒定律,即塑性区围岩破碎释放的弹性能、内应力调整释放的能量以及残余的弹性应变能此三者之和应等于围岩的弹性储能极限。

由式（26）可知,塑性区围岩中的极限储能增量

$Δ U = U_{1} - U_{0} = \frac{τ_{s}^{2}}{2 μ}$ 。

(30)

对应变能密度增量 $Δ U$ 在塑性区平面内积分,得到塑性区围岩弹性能增量的极限值 $Δ E$ 为

$Δ E = \int_{0}^{2 π} d θ \int_{a}^{\infty} r Δ U d r = \frac{π (r_{p}^{2} - a^{2}) τ_{s}^{2}}{2 μ}$ 。

(31)

由式（23）可知,当围岩压力 $σ_{r} |_{r = a} = p_{0} = σ_{0} - τ_{s}$ 时,围岩内壁将进入塑性状态。而此时对应的最大径向弹性位移

$u_{a}^{e} = \frac{τ_{s}}{2 μ} a$ 。

(32)

结合式（20）与（22）可知,塑性卸载阶段围岩的特征曲线为

$σ_{r} |_{r = a} = p_{0} = σ_{0} - τ_{s} [1 + \frac{τ_{c}}{τ_{s}} \ln (\frac{2 μ}{τ_{s}} \frac{u_{a}}{a})]$ 。

(33)

此时,围岩边界位移u_a取值范围为

$\frac{τ_{s}}{2 μ} a \leq u_{a} \leq \frac{τ_{s}}{2 μ} \frac{r_{p}^{2}}{a}$ 。

(34)

结合式（13）与（34）可得：

当 $u_{a} \leq (τ_{s} / 2 μ) a,$

$σ_{r} |_{r = a} = p_{0} = σ_{0} - 2 μ \frac{u_{a}}{a}$ ；

(35a)

当 $(a τ_{s} / 2 μ) < u_{a} < (τ_{s} r_{p}^{2} / 2 μ a),$

$σ_{r} |_{r = a} = p_{0} = σ_{0} - τ_{s} [1 + \frac{τ_{c}}{τ_{s}} \ln (\frac{2 μ}{τ_{s}} \frac{u_{a}}{a})]$ 。

(35b)

由式（35）可知,塑性卸载时围岩压力亦可化为初始地应力 $σ_{0}$ 与岩石自身承担应力R(u_a)之差的形式,即p₀= $σ_{0}$ -R(u_a),此时围岩自身承担的应力R(u_a)为分段函数。如图7所示为围岩弹塑性卸载的特征曲线。

图 7 圆形硐室弹塑性卸载围岩的特征曲线

Figure 7. Convergence curve for surrounding rock masses around circular tunnel under elasto-plastic unloading

下载: 全尺寸图片幻灯片

对特征曲线积分可得围岩压力做功向外释放的能量,即

$W_{c} = 2 π a \int_{0}^{u_{a}} p_{0} d u_{a} = \frac{π a^{2} τ_{s}^{2}}{2 μ} [1 + 2 \frac{τ_{c}}{τ_{s}} (\frac{r_{p}^{2}}{a^{2}} - 1)]$ 。

(36)

塑性卸载条件下围岩可分为弹性区和塑性区,可分别对两个区域内的能量变化情况进行独立分析。关于弹性区内围岩的能量调节机制可参看2.1节,本节只需详细讨论塑性区围岩能量的变化情况即可。

取塑性区围岩作为隔离体进行分析,如图8所示为塑性区围岩的受力示意图,图中σ 为弹性区围岩作用于塑性区围岩边界上的径向应力,u_rp为半径r_p处围岩的位移。

图 8 塑性区围岩受力示意图

Figure 8. Configuration for plastic range

下载: 全尺寸图片幻灯片

由式（23）和（24）可知,作用于塑性区围岩边界r=r_p处的径向应力 $σ_{r}$ 由初始应力 $σ_{0}$ 变为 $σ =$ $σ_{0} - τ_{s}$ ,而对应的径向位移u_rp则由零变为 $τ_{s} r_{p} / 2 μ$ 。因此可知弹性区围岩通过径向应力做功向塑性区围岩输入的能量W₀等于平均压力与位移的乘积,即

$\begin{matrix} W_{0} = 2 π r_{p} \times \frac{1}{2} [σ_{0} + σ_{0} - τ_{s}] \times \frac{τ_{s}}{2 μ} r_{p} \\ = \frac{π r_{p}^{2} τ_{s}^{2}}{2 μ} (\frac{2 σ_{0}}{τ_{s}} - 1) \end{matrix}$ 。

(37)

关于塑性变形所消耗的能量W_p的计算,需要先计算耗散的应变能密度U_d。为了计算耗散的应变能密度 $U_{d}$ ,则需要计算每个物质点中的塑性应变能增量 $Δ U_{d}$ ,

$\begin{matrix} Δ U_{d} = σ_{θ} d ε_{θ} + σ_{r} d ε_{r} + σ_{z} d ε_{z} + \\ τ_{θ r} d γ_{θ r} + τ_{r z} d γ_{r z} + τ_{z θ} d γ_{z θ} \end{matrix}$ 。

(38)

由于 $d ε_{z} = d γ_{θ r} = d γ_{r z} = d γ_{z θ} = 0$ ,式（38）可化为

$Δ U_{d} = σ_{θ} d ε_{θ} + σ_{r} d ε_{r} = (σ_{θ} - σ_{r}) d ε_{θ} + σ_{r} d(ε_{θ} + ε_{r})$ 。

(39)

又因为塑性体积不可压缩,故 $ε_{θ} + ε_{r} = 0$ ,且塑性区围岩中应力满足 $σ_{θ} - σ_{r} = 2 τ_{c}$ ,于是可得

$Δ U_{d} = 2 τ_{c} d ε_{θ} = - 2 τ_{c} d ε_{r}$ 。

(40)

对式（40）积分,可得塑性耗散的应变能密度U_d

$U_{d} = \int_{ε_{θ}^{e}}^{ε_{θ}^{p}} Δ U_{d} d ε_{θ} = \int_{ε_{θ}^{e}}^{ε_{θ}^{p}} (σ_{θ} - σ_{r}) d ε_{θ} = \frac{τ_{c} τ_{s}}{μ} (\frac{r_{p}^{2}}{r^{2}} - 1)$ ,

(41)

式中, $ε_{θ}^{e} = τ_{s} / (2 μ)$ 为围岩的极限弹性环向应变, $ε_{θ}^{p} = τ_{s} r_{p}^{2} / (2 μ r^{2})$ 为围岩塑性环向应变。

对塑性耗散应变能密度U_d在整个塑性区内积分,可得

$\begin{matrix} W_{p} = \int_{0}^{2 π} d θ \int_{a}^{r_{p}} r U_{d} d r \\ = \frac{π a^{2} τ_{s}^{2}}{2 μ} [2 (\frac{σ_{0}}{τ_{s}} - 1) \frac{r_{p}^{2}}{a^{2}} - 2 \frac{τ_{c}}{τ_{s}} (\frac{r_{p}^{2}}{a^{2}} - 1)] \end{matrix}$ ,

(42)

由式（31）,（36）,（37）及式（42）可知

$W_{0} = Δ E + W_{c} + W_{P}$ 。

(43)

围岩塑性卸载过程中严格满足能量守恒。

此时能量 $W_{0}$ 以径向应力做功的形式由弹塑性边界流入,传递过程中部分将能量转化为围岩的弹性势能 $Δ E$ ,并储存在围岩内（需要注意的是, $Δ E$ 为曾经储存在塑性区围岩内的最大弹性势能,当超过储能极限后会释放出部分能量,并造成围岩的破坏,关于能量 $Δ E$ 具体分配情况可参看图6）；部分能量 $W_{P}$ 耗散在不可回复的变形、裂痕和滑移线上；剩余能量 $W_{c}$ 则通过开挖边界流出,最终转化为塑性区围岩的动能。

2. 围岩中能量的传递方式

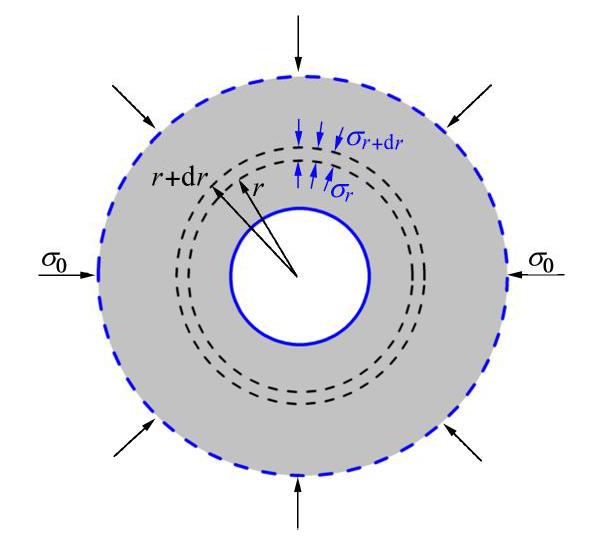
取半径r处一个厚度为dr的薄环作为隔离体（如图9所示）,并对其内部的能量变化进行分析。

图 9 能量的传递过程示意图

Figure 9. Configuration for energy transfer

下载: 全尺寸图片幻灯片

由式（11）得到的围岩应变能密度增量 $Δ U$ 可知,开挖前后半径r处厚度为dr的环型岩体内增加的弹性应变能

$Δ E_{s} = Δ U \times S = \frac{π {(σ_{0} - p_{0})}^{2}}{μ} \frac{a^{4}}{r^{3}} d r$ 。

(44)

巷道开挖过程中,距离圆心r + dr的圆形面上径向应力 $σ_{r + d r}$ 由σ₀减小为 $σ_{0} - a^{2} (σ_{0} - p_{0}) / {(r + d r)}^{2}$ ,径向位移u_r则由零增大到 $a^{2} (σ_{0} - p_{0}) / [2 μ (r + d r)]$ ,此时径向力 $σ_{r + d r}$ 沿位移方向的做功为

$W^{'} = \frac{π a^{2} {(σ_{0} - p_{0})}^{2}}{μ} [\frac{σ_{0}}{σ_{0} - p_{0}} - \frac{a^{2}}{2 {(r + d r)}^{2}}]$ ,

(45)

同理,在半径为r处,径向应力 $σ_{r}$ 的做功为

$W_{0} = \frac{π a^{2} {(σ_{0} - p_{0})}^{2}}{μ} (\frac{σ_{0}}{σ_{0} - p_{0}} - \frac{a^{2}}{2 r^{2}})$ ,

(46)

式（45）减式（46）,忽略dr的高阶项,可得

$Δ W = W^{'} - W_{0} = \frac{π {(σ_{0} - p_{0})}^{2}}{μ} \frac{a^{4}}{r^{3}} d r$ 。

(47)

比较式（44）与（47）可知,围岩增加的弹性应变能等于外部围岩径向力做功输入的能量与岩体以径向应力做功形式向内部围岩释放的能量之差,即 $Δ E_{s} = W^{'} - W_{0}$ ,严格满足能量守恒定律。由此可知,外部围岩输入的能量是通过径向压力做功形式一层一层向内部围岩传递,而且在传递过程中部分能量会以应变能的形式储存在围岩中。

3. 围岩压力做功

由式（35）可知,围岩压力p₀的物理本质为初始地应力 $σ_{0}$ 与围岩自承应力R(u_a)之差。关于围岩压力的物理解释以及严格的数学证明,限于篇幅本文并不作过多讨论。但考虑到围岩压力物理意义以及实际计算方法中概念的不清晰,作者将单独撰文进行说明。

对围岩压力在位移上积分即可得到围岩压力释放的能量。因此,围岩压力做功可表示为如下形式：

$W_{c} = 2 π a \int_{0}^{u_{a}} p_{0} d u_{a} = 2 π a σ_{0} u_{a} - 2 π a \int_{0}^{u_{a}} R (u_{a}) d u_{a}$ 。

(48)

由质量守恒和连续性假设可知,围岩变形满足如下几何关系：

$u_{r} = \frac{a}{r} u_{a}$ 。

(49)

考虑式（16）与式（49）可得, $r = R \to \infty$ 处围岩做功

$W_{0} = 2 π R \times \frac{1}{2} [σ_{0} + σ_{0} - (σ_{0} - p_{0}) \frac{a^{2}}{R^{2}}] \times \frac{a}{R} u_{a} = 2 π a σ_{0} u_{a},$

(50)

而对自承应力R(u_a)积分,可得

$\begin{matrix} W_{R} = 2 π a \int_{0}^{u_{a}} R (u_{a}) d u_{a} \\ = \frac{π a^{2} τ_{s}^{2}}{2 μ} [2 \frac{σ_{0}}{τ_{s}} \frac{r_{p}^{2}}{a^{2}} - 2 \frac{τ_{c}}{τ_{s}} (\frac{r_{p}^{2}}{a^{2}} - 1) - 1] \end{matrix}$ 。

(51)

此时,式（48）可化为

$W_{c} = W_{0} - W_{R}$ ,

(52)

由此可知,围岩压力做功的本质即为外部围岩做功 $W_{0}$ 与围岩自承应力做功 $W_{R}$ 之差。如果卸载过程中对巷道内壁施加衬砌或支护结构,此时围岩压力真实存在,其做功将用于抵抗支护力做功并转换为衬砌或支护结构的弹性势能。对于未施加支护结构的巷道而言,围岩压力则为虚力,根据动能定理可知此时围岩压力做功将转换为围岩的动能。需要特别说明的是,在准静态卸载条件下围岩压力做功转换的动能会以微振动或粘性阻尼等形式耗散掉,通常情况下并不会引起围岩产生显著的运动。

由式（25）可知,此时弹性区围岩储存的弹性能

$Δ E_{1} = \int_{0}^{2 π} d θ \int_{r_{p}}^{\infty} r Δ U d r = \frac{π a^{2} τ_{s}^{2}}{2 μ} \frac{r_{p}^{2}}{a^{2}}$ 。

(53)

由式（31）,（42）和（53）,整个卸载过程中围岩中储存总的应变能为

$\begin{matrix} Δ E^{'} = Δ E + Δ E_{1} + W_{p} \\ = \frac{π a^{2} τ_{s}^{2}}{2 μ} [2 \frac{σ_{0}}{τ_{s}} \frac{r_{p}^{2}}{a^{2}} - 2 \frac{τ_{c}}{τ_{s}} (\frac{r_{p}^{2}}{a^{2}} - 1) - 1] \end{matrix}$ ,

(54)

由式（51）和（54）可知,自承应力R(u_a)做功 $W_{R}$ 等于围岩中储存的应变能 $Δ E^{'}$ ,即自承应力做功的物理本质为围岩通过应力调整所存储的全部应变能。

4. 结论

本文主要研究了准静态、弹塑性卸载条件下深部圆形巷道围岩中能量的调整机制以及传递和转换规律,分析了围岩内部能量的平衡关系。主要结论如下：

（1）弹性卸载过程中,圆形巷道弹性区围岩储存的体积应变能不会改变,而畸变能则显著增加。此时,围岩储存的弹性应变能 $Δ E_{0}$ 与弹性区边界径向压力做功释放的能量 $W_{c}$ 完全由远处围岩输入的能量 $W_{0}$ 提供,严格满足能量守恒定律。

（2）通过应力状态（Lode参数）与变形分析可知,深部圆形巷道的破坏模式应倾向于剪切破坏。劈裂破坏可能发生于剪切破坏之后,属二次破坏。

（3）能量以径向应力做功的形式由弹塑性边界流入塑性区,传递过程中部分能量将转化为围岩的弹性势能 $Δ E$ ；部分能量 $W_{P}$ 耗散在不可回复的变形、裂痕和滑移线上；剩余能量 $W_{c}$ 则通过开挖边界流出,最终转化为衬砌或支护结构的弹性势能或围岩的动能（无支护）,此过程亦满足能量守恒定律。

（4）外部围岩输入的能量是通过径向压力做功形式一层一层向内部围岩传递,而且在传递过程中部分能量会以应变能的形式储存在围岩中。

（5）围岩压力p₀的物理本质为初始地应力 $σ_{0}$ 与围岩自承应力R(u_a)之差；围岩压力做功 $W_{c}$ 的本质即为外部围岩做功 $W_{0}$ 与围岩自承应力做功 $W_{R}$ 之差。

图 1 圆形硐室弹性卸载力学示意图

Figure 1. Configuration for excavation of circular tunnel under elastic unloading

下载: 全尺寸图片幻灯片

图 2 岩石常见的应力-应变关系曲线

Figure 2. Stress-strain curves for rock materials

下载: 全尺寸图片幻灯片

图 3 岩石常见的破坏形式

Figure 3. Facture patterns of rock materials

下载: 全尺寸图片幻灯片

图 4 圆形硐室弹塑性卸载力学示意图

Figure 4. Configuration for excavation of circular tunnel under elasto-plastic unloading

下载: 全尺寸图片幻灯片

图 5 理想弹-脆-塑性本构模型

Figure 5. Elastic-brittle-plastic constitutive model for rock masses

下载: 全尺寸图片幻灯片

图 6 围岩弹性应变能密度U随无量纲半径r/a的变化曲线

Figure 6. Distribution of elastic strain energy U of surrounding rock masses along with dimensionless radius r/a

下载: 全尺寸图片幻灯片

图 7 圆形硐室弹塑性卸载围岩的特征曲线

Figure 7. Convergence curve for surrounding rock masses around circular tunnel under elasto-plastic unloading

下载: 全尺寸图片幻灯片

图 8 塑性区围岩受力示意图

Figure 8. Configuration for plastic range

下载: 全尺寸图片幻灯片

图 9 能量的传递过程示意图

Figure 9. Configuration for energy transfer

下载: 全尺寸图片幻灯片

参考文献(22)

[1]	钱七虎. 深部地下空间开发中的关键科学问题[M]//钱七虎院士论文选集. 北京: 科学出版社, 2007. QIAN Qi-hu. The Critical Issues in the Development of Deep Underground Space[M]//Selections from Academician Qian Qihu's Theses. Beijing: Science Press, 2007. (in Chinese)
[2]	尤明庆, 华安增. 岩石试样破坏过程的能量分析[J]. 岩石力学与工程学报, 2002, 21(6): 778-781. doi: 10.3321/j.issn:1000-6915.2002.06.004 YOU Qing-ming, HUA An-zeng. Energy analysis on failure process of rock specimens[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 778-781. (in Chinese). doi: 10.3321/j.issn:1000-6915.2002.06.004
[3]	华安增. 地下工程周围岩体能量分析[J]. 岩石力学与工程学报, 2003, 22(7): 1054-1059. doi: 10.3321/j.issn:1000-6915.2003.07.002 HUA An-zeng. Energy analysis of surrounding rocks in underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(7): 1054-1059. (in Chinese) doi: 10.3321/j.issn:1000-6915.2003.07.002
[4]	王明洋, 陈昊祥, 李杰, 等. 深部巷道分区破裂化计算理论与实测对比研究[J]. 岩石力学与工程学报, 2018, 37(10): 2209-2218. doi: 10.13722/j.cnki.jrme.2018.0458 WANG Ming-yang, CHEN Hao-xiang, LI Jie, et al. Theoretical research for zonal disintegration of rock mass around deep tunnels and its comparison with in-situ observation[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2209-2218. (in Chinese) doi: 10.13722/j.cnki.jrme.2018.0458
[5]	陈昊祥, 王明洋, 李杰. 深部岩体变形破坏的特征能量因子与应用[J]. 爆炸与冲击, 2019, 39(8): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201908003.htm CHEN Hao-xiang, WANG Ming-yang, LI Jie. Characteristic energy factor of the deep rock masses and its application[J]. Explosion and Shock Wave, 2019, 39(8): 1-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201908003.htm
[6]	COOK N G W. The basic mechanics of rock bursts[J]. Journal of the South African Institute of Mining and Metallurgy, 1963, 64(10): 71-81.
[7]	COOK N G W, HOEK E, PRETORIUS J P G, et al. Rock mechanics applied to the study of rockbursts[J]. Journal of the South African Institute of Mining and Metallurgy, 1966, 66(10): 436-528.
[8]	COOK N G W. Seismicity associated with mining[J]. Engineering Geology, 1976, 10(2/3/4): 99-122.
[9]	COOK N G W. The design of underground excavattons[C]//Proc 8th Symp on Rock Mech, 1967, New York: 167-193.
[10]	WALSH J B. Energy changes due to mining[J]. International Journal of Rock Mechanics and Mining Science, 1977, 14(1): 25-33. doi: 10.1016/0148-9062(77)90559-9
[11]	SALAMONM D G. Energy considerations in rock mechanics: fundamental results[J]. Journal of the South African Institute of Mining and Metallurgy, 1984, 84(8): 233-246.
[12]	BRADY B H G, BROWN E T. Energy changes and stability in underground mining: design applications of boundary element methods[J]. Transactions of the Institution of Mining and Metallurgy, 1981, 90: 61-68.
[13]	BRADY B H G, BROWN E T. Rock Mechanics for Underground Mining[M]. Dordrecht: Springer, 2006: 264-269.
[14]	潘岳, 王志强. 岩体动力失稳的功、能增量—突变理论研究方法[J]. 岩石力学与工程学报, 2004, 23(9): 1433-1438. doi: 10.3321/j.issn:1000-6915.2004.09.005 PAN Yue, WANG Zhi-qiang. Research approach on increment of work and energy: catastrophe theory of rock dynamic destabilization[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(9): 1433-1438. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.09.005
[15]	潘岳, 王志强. 应变非线性软化的硐室围岩荷载-位移关系研究[J]. 岩土力学, 2004, 25(10): 1515-1521. doi: 10.3969/j.issn.1000-7598.2004.10.001 PAN Yue, WANG Zhi-qiang. Research on relationship of load-displacement for cavern surrounding rock with strain nonlinear softening[J]. Rock and Soil Mechanics, 2004, 25(10): 1515-1521. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.10.001
[16]	潘岳, 王志强, 吴敏应. 巷道开挖围岩能量释放与偏应力应变能生成的分析计算[J]. 岩土力学, 2007, 28(4): 663-669. doi: 10.3969/j.issn.1000-7598.2007.04.006 PAN Yue, WANG Zhi-qiang, WU Min-ying. Analysis and calculation of energy release and deviatoric stress energy generation of surrounding rock in tunnel excavation process[J]. Rock and Soil Mechanics, 2007, 28(4): 663-669. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.04.006
[17]	KRAMARENKO V I, REVUZHENKO A F. Flow of energy in a deformed medium[J]. Journal of Mining Science, 1988, 24(6): 536-540. doi: 10.1007/BF02498611
[18]	REVUZHENKOR A F, KLISHIN S V. Energy flux lines in a deformable rock mass with elliptical openings[J]. Journal of Mining Science, 2009, 45(3): 201-206.
[19]	LU W B, YANG J H, YAN P, et al. Dynamic response of rock mass induced by the transient release of in-situ stress[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 53(7): 129-141.
[20]	范勇, 卢文波, 严鹏, 等. 地下洞室开挖过程围岩应变能调整力学机制[J]. 岩土力学, 2013, 34(12): 3580-3586. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312036.htm FAN Yong, LU Wen-bo, YAN Peng, et al. Mechanism of strain energy adjustment of surrounding rock during excavation of underground caverns[J]. Rock and Soil Mechanics, 2013, 34(12): 3580-3586. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312036.htm
[21]	FAN Y, LU W B, YAN P, CHEN M, ZHANG Y Z. Transient characters of energy changes induced by blasting excavation of deep-buried tunnels[J]. Tunneling and Underground Space Technology, 2015, 49: 9-17.
[22]	SHEMYAKIN E I, KURLENYA M V, OPARIN V N, et al. Zonal disintegration of around underground workings: Part Ⅳ practical applications[J]. Journal of Mining Science, 1989, 25(4): 297-302.

施引文献(12)

期刊类型引用(8)

1.	郑可跃，施成华，娄义黎，贾朝军，雷明锋，杨益. 深部高地应力隧道开挖卸荷围岩能量计算方法及演化机制. 岩土力学. 2025(01): 165-177 . 百度学术
2.	孟庆彬，辛学奎，宋子鸣，宋洋，程争民，王昌. 巷道开挖过程中围岩能量耗散特征. 采矿与安全工程学报. 2024(01): 142-150 . 百度学术
3.	李宁. 断层破碎带巷道破坏及支护技术研究. 山东煤炭科技. 2024(04): 6-9+14 . 百度学术
4.	孟庆彬，辛学奎，宋子鸣，程争民，宋洋. 锚杆支护吸能调控效应理论解析与数值模拟. 中南大学学报(自然科学版). 2024(09): 3426-3440 . 百度学术
5.	彭雨杰，王强，曹安业，薛成春，吕国伟，郝琪，刘耀琪，白贤栖，李东. 特厚煤层掘进巷道冲击地压机理及影响因素. 煤田地质与勘探. 2024(12): 25-39 . 百度学术
6.	王猛，李志学，夏恩乐，李振华，邹永德，韦四江，王襄禹，杨达明. 深部巷道围岩能量耗散与支护调控效应. 采矿与安全工程学报. 2022(04): 741-749 . 百度学术
7.	陈昊祥，王明洋，燕发源，戚承志. 深部巷道围岩塑性区演化的理论模型与实测对比研究. 岩土工程学报. 2022(10): 1855-1863 . 本站查看
8.	赵洪宝，程辉，王磊，刘一洪，吉东亮，张一潇. 非静水压力条件下巷道围岩偏应力场分布特征与围岩破坏规律. 煤炭学报. 2021(02): 370-381 . 百度学术