横观各向同性冻胀寒区隧道应力与位移的塑性统一解

张常光; 高本贤; 单冶鹏; 李宗辉

doi:10.11779/CJGE202010007

横观各向同性冻胀寒区隧道应力与位移的塑性统一解 English Version

1.
长安大学建筑工程学院,陕西　西安　710061
2.
成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川　成都　610059

基金项目:

国家自然科学基金项目 41202191

地质灾害防治与地质环境保护国家重点实验室开放基金项目 SKLGP2020K022

长安大学中央高校基本科研业务费专项资金项目 300102280108

详细信息

作者简介:
张常光(1982—),男,山东菏泽人,博士,教授,从事非饱和土与地下工程等研究。E-mail：zcg1016@163.com

中图分类号: TU457
计量
- 文章访问数: 272
- HTML全文浏览量: 34
- PDF下载量: 122
出版历程
- 收稿日期: 2020-01-12
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-09-30

Unified plastic solution for stress and displacement of tunnels in cold regions considering transversely isotropic frost heave

1.
School of Civil Engineering, Chang'an University, Xi'an 710061, China
2.
Stake Key Laboratory of Geohazard Prevetion and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China

摘要

摘要: 以统一强度理论作为寒区隧道冻结围岩塑性状态的判定依据,考虑中间主应力效应和横观各向同性冻胀对围岩强度的综合影响,建立了寒区隧道应力与位移的塑性统一解析解,给出冻结围岩塑性状态的判定方法,并对所得解答进行讨论、验证和参数分析。研究表明：统一解的正确性被有关文献的Mohr-Coulomb准则解答和外接圆Drucker- Prager准则解答所验证,具有广泛的理论意义和良好的工程应用前景；中间主应力对冻结围岩位移的影响显著,应考虑中间主应力效应以充分发挥寒区隧道的承载潜能；围岩不均匀冻胀系数和体积冻胀率的增加均导致冻胀力增大,使得寒区隧道稳定性降低,应采取有效保温措施予以缓解围岩冻胀效应。该结果可为寒区隧道设计提供一定的理论指导。
- 寒区隧道 /
- 统一强度理论 /
- 冻胀力 /
- 中间主应力 /
- 横观各向同性冻胀
Abstract: The unified strength theory is used as a yield criterion to determine the plastic state of frozen surrounding rock of tunnels in cold regions. Taking comprehensive influences of the intermediate principal stress effect and transversely isotropic frost heave on the strength of frozen surrounding rock into account, a unified analytical plastic solution for the stress and displacement of tunnels in cold regions is proposed. A method is then introduced to address the plastic state of frozen surrounding rock. Furthermore, discussions, verifications and parametric studies of the proposed solution are performed. It is found herein that the validity of the unified solution is demonstrated by comparing with the results from Mohr-Coulomb criterion and circumscribed Drucker-Prager criterion available in the reference, thus it is of extensive theoretical significance and good engineering application prospect. The intermediate principal stress has a significant impact on the displacement of frozen surrounding rock, and then more rock strength potentialities are achieved. The frost-heave force increases with the increase of the anisotropic frost-heave coefficient and the volumetric frost-heave strain. It results in that the stability of tunnels in cold regions decreases, and effective insulation measures are taken to reduce the frost-heave effect of the surrounding rock. The result of this study can provide some theoretical suggestions for the design of tunnels in cold regions.
- cold-region tunnel /
- unified strength theory /
- frost-heave force /
- intermediate principal stress /
- transversely isotropic frost heave

HTML全文

0. 引言

高海拔、高纬度寒冷地区常年的低温环境使得隧道内的含水围岩冻结并膨胀,产生的冻胀力严重影响了隧道稳定性,是寒区隧道冻害的主要原因之一。寒区隧道冻胀力是其应力场与位移场计算的重要参数,代表性研究成果有：Lai等^[1]假定围岩均匀冻胀,利用Laplace变换原理推导了冻胀力的黏弹性解析解；Gao等^[2]利用位移连续性条件获得冻胀力的弹性解,并建立了冻结围岩应力和塑性区半径的半解析法；Feng等^[3]提出了冻结围岩应力与位移的Mohr-Coulomb（MC）准则解答,甄田田^[4]得到了冻结围岩应力和位移的外接圆Drucker-Prager（DP）准则解答。上述解答均引入了围岩各向同性冻胀的假设。大量的冻结试验结果表明^[5-6]：岩土类材料在单向冻结条件下为不均匀冻胀。在寒冷地区的隧道中,冷空气沿径向对围岩进行流入式冻结,与冻结方向平行的径向冻胀明显大于垂直的环向冻胀。针对不均匀冻胀围岩,夏才初等^[7]证明了寒区隧道围岩不均匀冻胀属于横观各向同性冻胀,Lü等^[8]建立了横观各向同性冻胀时寒区隧道应力和位移的MC准则解答。

实际上,冻结岩土体真三轴强度随中间主应力的增加显著提高^[9-11],但中间主应力效应低于小主应力围压作用对冻结岩土体强度的影响。而现有寒区隧道冻结围岩的弹塑性解答,绝大部分是基于未考虑中间主应力的MC准则,不能反映中间主应力对冻结围岩强度的提高作用,所得结果相对保守；反之,外接圆DP准则假定中间主应力效应与小主应力的围压作用相等,高估了中间主应力的强度提高作用,所得结果偏于危险。统一强度理论是系列化线性强度准则的集合^[12],可以合理反映岩土类材料强度的中间主应力效应及其影响程度,已在隧道、矿井等地下工程中得到一定的应用^[13-15]。

因此,本文基于统一强度理论以反映中间主应力对冻结围岩的强度提高作用,推导了非均匀冻胀寒区隧道应力与位移的塑性统一解,给出冻结围岩塑性状态的判定方法,并与文献MC准则解答和外接圆DP准则解答进行对比验证,最后探讨中间主应力效应和围岩冻胀特性的影响规律。本文结果可为寒区隧道设计提供一定的理论指导。

1. 基本假设

为得到不均匀冻胀寒区隧道应力与位移的塑性解析解,特做如下基本假设：

（1）隧道长度远大于其横截面尺寸,可简化为平面应变问题。

（2）围岩和支护都是均匀连续的各向同性材料,其中围岩为满足统一强度理论的理想弹塑性材料,支护为线弹性材料且隧道开挖后立即施作。

（3）圆形隧道受静水型地应力作用,忽略塑性区围岩的自重影响。

（4）隧道围岩为横观各向同性冻胀,且隧道纵向冻胀与垂直方向冻胀的线冻胀率相等；不计冻结过程,不均匀冻胀系数k为常数并保持不变^[7-8]。

2. 寒区隧道塑性统一解

2.1 力学模型

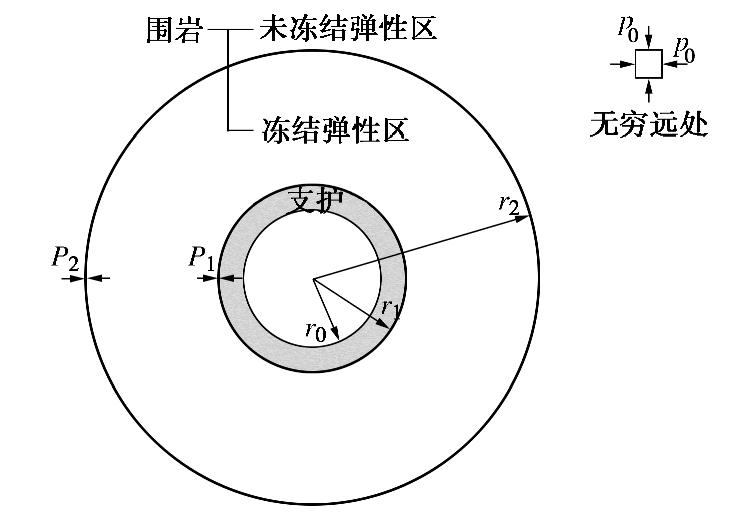
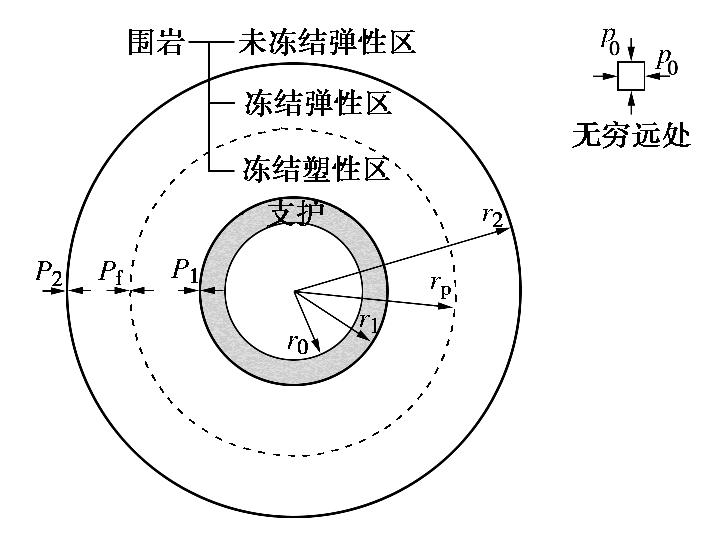
图1为寒区隧道的塑性力学模型,包括4个分区：支护区（Ⅰ,r₀≤r≤r₁）,冻结围岩塑性区（Ⅱ,r₁≤r≤r_p）,冻结围岩弹性区（Ⅲ,r_p≤r≤r₂）和未冻结围岩弹性区（Ⅳ,r≥r₂）。围岩（Ⅱ区、III区)冻结膨胀受到支护（Ⅰ区）和未冻结围岩（Ⅳ区）的约束,冻胀力反作用于支护上。其中, $r_{0}$ 为支护内半径,r₁为支护外半径,r_p为冻结围岩塑性区半径,r₂为冻结围岩弹性区外半径； $p_{0}$ 为初始地应力,P₁为冻结围岩塑性区与支护区交界处的径向应力,P₂为围岩冻结弹性区与未冻结弹性区交界处的径向应力,P_f为围岩冻结塑性区与冻结弹性区交界处的径向应力。

图 1 寒区隧道的塑性力学模型

Figure 1. Plastic mechanical model for a tunnel in cold regions

下载: 全尺寸图片幻灯片

在冻结围岩塑性区内, $σ_{1}$ = $σ_{θ}$ , $σ_{3}$ = $σ_{r}$ ,平面应变状态下的统一强度理论为^[12-15]

$\begin{array}{l} σ_{θ} = M σ_{r} + N, \\ M = \frac{(2 + b) + (2 + 3 b) \sin φ}{(2 + b) (1 - \sin φ)}, \\ N = \frac{4 (1 + b) c \cos φ}{(2 + b) (1 - \sin φ)} 。 \end{array}}$

(1)

式中 $σ_{1}$ 和 $σ_{3}$ 为大主应力、小主应力, $σ_{r}$ 和 $σ_{θ}$ 为径向应力、环向应力,以压应力为正；c和φ为冻结围岩的黏聚力、内摩擦角；M和N为方程参数。统一强度理论参数b反映了中间主应力对围岩强度屈服或破坏的影响程度,取值范围为：0≤b≤1。参数b也是强度准则选择参数,不同的参数b对应不同的强度准则：b=0时式（1）退化为MC准则,b=1时为双剪应力准则,0<b<1时为一系列新强度准则。

冻结围岩的弹性本构方程为^[7-8]

$\begin{matrix} ε_{r}^{e} = \frac{1 - μ_{2}^{2}}{E_{2}} (Δ σ_{r} - \frac{μ_{2}}{1 - μ_{2}} Δ σ_{θ}) - (ε_{r, f} + μ_{2} ε_{θ, f}), \\ ε_{θ}^{e} = \frac{1 - μ_{2}^{2}}{E_{2}} (Δ σ_{θ} - \frac{μ_{2}}{1 - μ_{2}} Δ σ_{r}) - (ε_{θ, f} + μ_{2} ε_{r, f}), \end{matrix}}$

(2)

式中E为弹性模量,μ为泊松比；下标代表区域,1为支护（Ⅰ区）,2为冻结围岩（Ⅱ区、Ⅲ区）,3为未冻结围岩（Ⅳ区）；Δσ_r和Δσ_θ为径向应力增量和环向应力增量；k为不均匀冻胀系数,等于平行冻结方向的径向线冻胀率与垂直方向的环向线冻胀率的比值； $ε_{r, f}$ 和 $ε_{θ, f}$ 为寒区隧道平行、垂直冻胀方向的线冻胀率,且有 $ε_{r, f}$ =k $ε_{v, f}$ /(k+2), $ε_{θ, f}$ = $ε_{v, f}$ /(k+2)； $ε_{z, f}$ 为寒区隧道纵向的线冻胀率, $ε_{z, f}$ = $ε_{θ, f}$ ； $ε_{v, f}$ 为冻结围岩的体积冻胀率,是由冻胀引起单位体积围岩的体积膨胀应变,一般通过试验确定,对于横观各向同性冻胀寒区隧道围岩有 $ε_{v, f} = ε_{r, f} + ε_{θ, f} + ε_{z, f} = ε_{r, f} + 2 ε_{θ, f}$ 。

2.2 未冻结围岩弹性区与支护区

由弹性力学厚壁圆筒理论,可得围岩未冻弹性区与支护区的应力分别为^[3]

$\begin{matrix} σ_{r}^{IV} = p_{0} - (p_{0} - P_{2}) {(r_{2} / r)}^{2}, \\ σ_{θ}^{IV} = p_{0} - (P_{2} - p_{0}) {(r_{2} / r)}^{2}, \end{matrix}}$

(3)

$\begin{array}{l} σ_{r}^{I} = \frac{1 - {(r_{0} / r)}^{2}}{1 - {(r_{0} / r_{1})}^{2}} P_{1}, \\ σ_{θ}^{I} = \frac{1 + {(r_{0} / r)}^{2}}{1 - {(r_{0} / r_{1})}^{2}} P_{1} 。 \end{array}}$

(4)

相应的径向位移分别为

$u^{IV} = \frac{(1 + μ_{3}) (p_{0} - P_{2})}{E_{3}} \frac{r_{2}^{2}}{r}$ ,

(5)

$u^{I} = \frac{(1 + μ_{1}) r [1 - 2 μ_{1} + {(r_{0} / r)}^{2}] P_{1} r_{1}^{2}}{E_{1} (r_{1}^{2} - r_{0}^{2})}$ 。

(6)

2.3 冻结围岩弹性区

由弹性力学厚壁圆筒理论得冻结围岩弹性区的应力为^[3]

$\begin{matrix} σ_{r}^{III} = \frac{{(r_{2} / r)}^{2} - 1}{{(r_{2} / r_{p})}^{2} - 1} P_{f} + \frac{1 - {(r_{p} / r)}^{2}}{1 - {(r_{p} / r_{2})}^{2}} P_{2}, \\ σ_{θ}^{III} = \frac{1 + {(r_{2} / r)}^{2}}{1 - {(r_{2} / r_{p})}^{2}} P_{f} + \frac{1 + {(r_{p} / r)}^{2}}{1 - {(r_{p} / r_{2})}^{2}} P_{2} 。 \end{matrix}}$

(7)

根据式（2）和式（7）并结合几何方程 $ε_{θ}$ =u/r,可得冻结围岩弹性区的径向位移u^III为

$\begin{matrix} u^{III} = \frac{（ 1 + μ_{2}) r}{E_{2}} {\frac{[2 μ_{2} - 1 - {(r_{2} / r)}^{2}] P_{f} r_{p}^{2} + [1 + {(r_{p} / r)}^{2} - 2 μ_{2}] P_{2} r_{2}^{2}}{r_{2}^{2} - r_{p}^{2}} - \\ (1 - 2 μ_{2}) p_{0} \begin{array}{l} \end{array}} - \frac{(μ_{2} k + 1) r}{k + 2} ε_{v, f} \end{matrix}$ 。

(8)

2.4 冻结围岩塑性区

平面轴对称问题的极坐标平衡微分方程为

$\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{θ}}{r} = 0$ 。

(9)

联立式（1）和式（9）与应力边界条件 $σ_{r} |_{r = r_{1}} = P_{1}$ ,求得冻结围岩的塑性区应力为

$\begin{matrix} σ_{r}^{II} = (P_{1} - \frac{N}{1 - M}) {(r / r_{1})}^{M - 1} + \frac{N}{1 - M}, \\ σ_{θ}^{II} = M (P_{1} - \frac{N}{1 - M}) {(r / r_{1})}^{M - 1} + \frac{N}{1 - M} 。 \end{matrix}}$

(10)

冻结围岩塑性区的径向应变 $ε_{r}$ 和环向应变 $ε_{θ}$ 均可分解为塑性应变和弹性应变两部分,采用线性非关联流动法则并结合几何方程 $ε_{r}$ =du/dr和 $ε_{θ}$ =u/r得

$\frac{d u}{d} + β \frac{u}{r} = β ε_{θ}^{e} + ε_{r}^{e}$ ,

(11)

式中, $β$ 为剪胀特征参数。

将式（10）代入式（2）,再将结果代入式（11）,继而对式（11）进行积分,并以冻结围岩弹-塑性交界处弹性区一侧的径向位移式（8）为边界条件,求得冻结围岩塑性区的径向位移u^II为

$\begin{array}{l} u^{II} = \frac{1}{r^{β}} {A_{1} (P_{1} - \frac{N}{1 - M}) (r^{β + M} - r_{p}^{β + m}) - \\ A_{2} (r^{β + 1} - r_{p}^{β + 1})} + {(r_{p} / r)}^{β} u^{III} |_{r - r_{p}} \end{array}$ ,

(12)

式中, $A_{1} = \frac{1 + μ_{2}}{E_{2}} \frac{[1 - (1 + M) μ_{2} - β (μ_{2} - M + M μ_{2})]}{r_{1}^{M - 1} (β + M)}$ , $A_{2} = \frac{1 + μ_{2}}{E_{2}} (1 - 2 μ_{2}) (p_{0} - \frac{N}{1 - M}) + \frac{(1 + μ_{2} β) k + (μ_{2} + β)}{(k + 2) (β + 1)} ε_{v, f} 。$

2.5 隧道冻胀力与洞壁位移

在r=r₁,r=r_p和r=r₂交界处的剩余可用边界条件为

$\begin{matrix} {u^{I} |}_{r = r_{1}} = {u^{II} |}_{r = r_{1}}, \\ {σ_{r}^{II} |}_{r = r_{p}} = {σ_{r}^{III} |}_{r = r_{p}}, \\ {u^{III} |}_{r = r_{2}} = {u^{IV} |}_{r = r_{2}} 。 \end{matrix}}$

(13)

同时,冻结围岩弹-塑性交界处弹性区一侧的应力式（7）满足统一强度理论式（1）,即

$σ_{θ}^{III} |_{r = r_{p}} = M σ_{r}^{III} |_{r = r_{p}} + N$ 。

(14)

联立式（13）和式（14）,可求得P₁,P_f,P₂和r_p。其中,有关冻结围岩塑性区半径r_p的隐式方程和支护处的接触压力P₁如下：

(15)

式中, $A_{3} = \frac{(1 + μ_{1}) [1 - 2 μ_{1} + {(r_{0} / r_{1})}^{2}] r_{1}^{3}}{E_{1} (r_{1}^{2} - r_{2}^{2})}$ , $A_{4} = \frac{N (r_{p}^{2} - r_{2}^{2})}{(1 + M) r_{2}^{2} + (1 - M) r_{p}^{2}}$ 。

$\begin{matrix} P_{1} = {\frac{[\frac{E_{2}}{E_{3}} (1 + μ_{3}) (r_{2}^{2} - r_{p}^{2}) + (1 + μ_{2}) (1 - 2 μ_{2}) (r_{2}^{2} - r_{p}^{2})] 2 p_{0} r_{2}^{2} + 4 (1 - μ_{2}^{2}) r_{2}^{2} r_{p}^{2} A_{4} + 2 E_{2} (r_{2}^{2} - r_{p}^{2}) r_{2}^{2} (\frac{μ_{2} k + 1}{k + 2} ε_{v, f})}{[\frac{E_{2}}{E_{3}} (1 + μ_{3}) (r_{2}^{2} - r_{p}^{2}) + (1 + μ_{2}) (r_{p}^{2} + r_{2}^{2} - 2 μ_{2} r_{2}^{2})] [(1 + M) r_{2}^{2} + (1 - M) r_{p}^{2}] - 4 (1 - μ_{2}^{2}) r_{2}^{2} r_{p}^{2}} + \\ A_{4} - \frac{N}{1 - M}} \cdot {(\frac{r_{1}}{r_{p}})}^{M - 1} + \frac{N}{1 - M} \end{matrix}$ 。

(16)

进而得寒区隧道围岩的冻胀力为

$Δ P_{1} = P_{1} - {P^{'}}_{1}$ ,

(17)

式中,ΔP₁为作用在支护上的冻胀力, ${P^{'}}_{1}$ 为围岩冻结前作用在支护上的初始径向应力,可通过试验确定或按围岩未冻结时理论求解。

将r=r₁代入式（6）并结合式（16）,可得寒区隧道洞壁位移u₀为

$u_{0} = A_{3} P_{1}$ 。

(18)

2.6 冻结围岩塑性状态判定

若围岩在冻结前已满足式（1）进入塑性状态,则冻结后围岩仍将处于塑性状态,可采用本文上述基于图1的塑性统一解。反之,如果冻结前围岩处于弹性状态,则需判定冻结后围岩是否进入塑性状态。可先假设冻结后围岩仍保持弹性状态,此时寒区隧道的弹性力学模型如图2所示。

图 2 寒区隧道的弹性力学模型

Figure 2. Elastic mechanical model of a cold region tunnel

下载: 全尺寸图片幻灯片

图2中不存在冻结围岩塑性区即图1中的Ⅱ区,且支护Ⅰ区和未冻结围岩弹性Ⅳ区的应力与位移仍为式（3）～（6）,但冻结围岩弹性Ⅲ区的应力和位移变为

$\begin{matrix} σ_{r}^{III} = \frac{{(r_{2} / r)}^{2} - 1}{{(r_{2} / r_{1})}^{2} - 1} P_{1} + \frac{1 - {(r_{1} / r)}^{2}}{1 - {(r_{1} / r_{2})}^{2}} P_{2}, \\ σ_{θ}^{III} = \frac{1 + {(r_{2} / r)}^{2}}{1 - {(r_{2} / r_{1})}^{2}} P_{1} + \frac{1 + {(r_{1} / r)}^{2}}{1 - {(r_{1} / r_{2})}^{2}} P_{2} 。 \end{matrix}}$

(19)

$\begin{matrix} u^{III} = \frac{(1 + μ_{2}) r}{E_{2}} {\frac{[2 μ_{2} - 1 - {(r_{2} / r)}^{2}] P_{1} r_{1}^{2} + [1 + {(r_{1} / r)}^{2} - 2 μ_{2}] P_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}} - \\ (1 - 2 μ_{2}) p_{0} \begin{array}{l} \end{array}} - \frac{(μ_{2} k + 1) r}{k + 2} ε_{v, f} \end{matrix}$ 。

(20)

在分区交界r=r₁和r=r₂处的位移连续条件为

${u^{I} |}_{r = r_{1}} = {u^{III} |}_{r = r_{1}}, {u^{III} |}_{r = r_{2}} = {u^{IV} |}_{r = r_{2}}$ 。

(21)

将式（5）,（6）,（20）代入式（21）可求得

$\begin{matrix} P_{1} = \frac{1}{A_{5}} [\frac{2 (1 - μ_{2}^{2}) r_{2}^{2}}{E_{2} (r_{2}^{2} - r_{1}^{2})} P_{2} - \frac{(1 + μ_{2}) (1 - 2 μ_{2})}{E_{2}} p_{0} - \\ (\frac{μ_{2} k + 1}{k + 2} ε_{v, f})] \end{matrix}$ ,

(22)

$P_{2} = \frac{A_{5} B_{1} - \frac{2 (1 - μ_{2}^{2}) r_{1}^{2}}{E_{2} (r_{2}^{2} - r_{1}^{2})} B_{2}}{A_{5} B_{3} - {[\frac{2 (1 - μ_{2}^{2})}{E_{2} (r_{2}^{2} - r_{1}^{2})}]}^{2} r_{1}^{2} r_{2}^{2}}$ 。

(23)

式中

$A_{5} = \frac{(1 + μ_{1}) (r_{0}^{2} + r_{1}^{2} - 2 μ_{1} r_{1}^{2})}{E_{1} (r_{1}^{2} - r_{0}^{2})} - \frac{(1 + μ_{2}) (2 μ_{2} r_{1}^{2} - r_{1}^{2} - r_{2}^{2})}{E_{2} (r_{2}^{2} - r_{1}^{2})} ；$

$B_{1} = \frac{1 + μ_{3}}{E_{3}} p_{0} + \frac{(1 + μ_{2}) (1 - 2 μ_{2})}{E_{2}} p_{0} + \frac{μ_{2} k + 1}{k + 2} ε_{v, f} ；$

$B_{2} = \frac{(1 + μ_{2}) (1 - 2 μ_{2})}{E_{2}} p_{0} + \frac{μ_{2} k + 1}{k + 2} ε_{v, f}$

$B_{3} = \frac{1 + μ_{3}}{E_{3}} + \frac{(1 + μ_{2}) (r_{1}^{2} + r_{2}^{2} - 2 μ_{2} r_{2}^{2})}{E_{2} (r_{2}^{2} - r_{1}^{2})}$

将式（22）和式（23）代入式（19）,可得冻结围岩弹性III区的应力分布,继而把此时III区内边界r=r₁处的应力代入统一强度理论式（1）,则可判定围岩冻结后是否进入塑性状态。如果冻结后围岩已进入塑性状态,则采用本文提出的塑性统一解。反之,若冻结后围岩仍保持弹性状态,式（3）～（6）及式（19）和式（20）即为寒区隧道应力与位移的弹性解,同时将式（22）代入式（17）和式（18）,可得寒区隧道冻胀力ΔP₁和洞壁位移u₀的弹性解。

3. 讨论与验证

3.1 解答讨论

本文基于统一强度理论并考虑围岩不均匀冻胀建立了寒区隧道应力和位移的塑性统一解,即式（3）～（8）,式（10）,式（12）以及式（17）和式（18）,其中式（17）和式（18）分别为隧道冻胀力和洞壁位移的塑性解。所得塑性统一解考虑了冻结围岩强度的中间主应力效应（即统一强度理论参数b）与寒区隧道横观各向同性冻胀（即不均匀冻胀系数k）的综合影响,具有广泛的理论意义和应用前景。根据参数b和系数k的不同取值,本文塑性统一解可退化为众多已有解答。例如,当参数b=0,系数k=1时,本文塑性统一解退化为文献[3]中各向同性冻胀时寒区隧道不考虑中间主应力的MC准则解答；参数b=0时退化为文献[8]中横观各向同性冻胀时寒区隧道的MC准则解答；参数b=1时对应中间主应力效应最大的双剪应力准则解答,0<b<1时则为一系列有序的新准则解答；系数k=1对应各向同性冻胀解答,系数k>1对应横观各向同性冻胀解答。因此,本文所得寒区隧道塑性统一解具有很好的可比性,还包括若干未见发表的新解答,可根据实际情况进行合理调整和选择,具有重要的工程参考价值。

3.2 解答验证

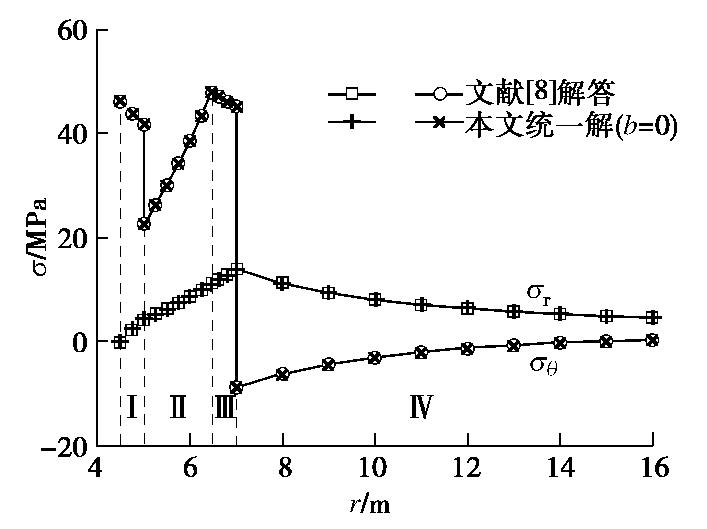
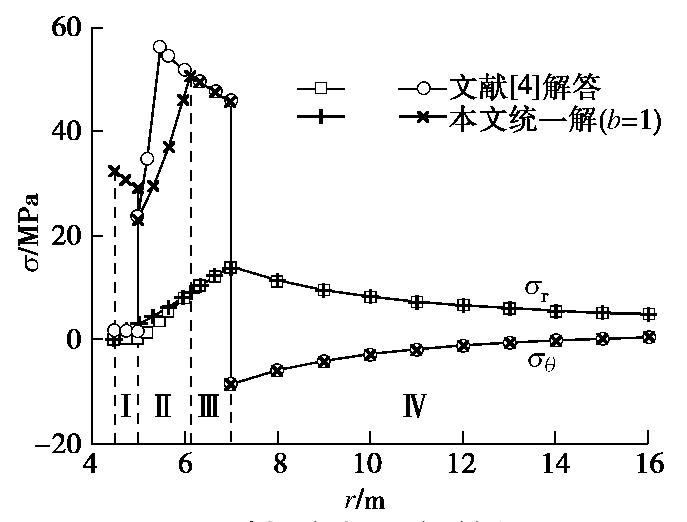
甄田田^[4]推导了各向同性冻胀时寒区隧道应力和位移的外接圆DP准则解答,Lü等^[8]建立了横观各向同性冻胀时寒区隧道应力和位移的MC准则解答。将本文寒区隧道应力的塑性统一解（k取1,参数b取0,1）与文献[4, 8]的应力解答进行对比,如图3,4所示。

图 3 b=0时与文献[8]解答的对比

Figure 3. Comparison between results from this study with b=0 and those in Reference [8]

下载: 全尺寸图片幻灯片

图 4 b=1时与文献[4]解答的对比

Figure 4. Comparison between results from this study with b=1 and those in Reference [4]

下载: 全尺寸图片幻灯片

由图3可以看出,参数b=0时本文应力统一解与文献[8]的MC准则解答完全吻合,验证了本文结果的正确性。另外,由图4知参数b=1时本文冻结围岩的塑性区半径r_p为6.15 m,大于文献[4]由外接圆DP准则求得的5.47 m,使得二者在支护和冻结围岩塑性区的应力分布存在一定差异。这是由于外接圆DP准则假定围岩强度的中间主应力效应与小主应力围压作用一样,高估了中间主应力的实际强度提高作用,使得冻结围岩塑性区半径变小、支护环向应力几乎为零,故选用外接圆DP准则时需特别谨慎。

4. 参数分析

中间主应力和围岩冻胀特性会对寒区隧道应力分布和塑性区位移产生影响,探究这两个因素的影响程度,可为寒区隧道设计提供一定理论参考。①中间主应力效应,不同的b值对应不同的中间主应力效应和强度准则；②围岩不均匀冻胀,不均匀冻胀系数k反映不均匀冻胀的程度,体积冻胀率 $ε_{v, f}$ 体现围岩冻结膨胀的大小。其中,由式（3）～（4）、式（7）和式（10）确定隧道应力分布,由式（12）计算冻结围岩的塑性区位移。寒区隧道的基本参数来自文献[3]。

4.1 中间主应力效应

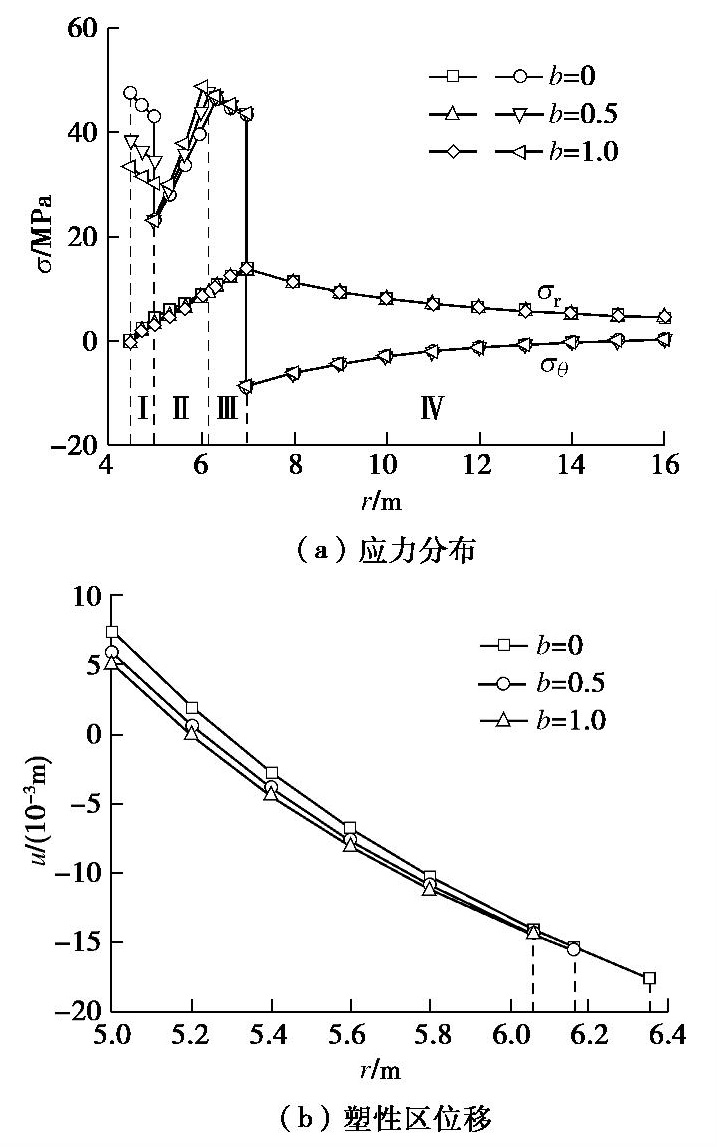
通过统一强度理论参数b来反映中间主应力 $σ_{2}$ 对冻结围岩强度的提高作用,参数b可连续取0～1,参数b越大则中间主应力效应越显著。当k=1.5,b=0,0.5和1时,图5给出了寒区隧道应力分布和塑性区位移的变化规律。

图 5 中间主应力的影响

Figure 5. Influences of intermediate principal stress

下载: 全尺寸图片幻灯片

由图5可以看出,随着参数b的增加,寒区隧道的塑性区位移与支护环向应力都在逐渐减小,而冻结围岩塑性区的环向应力却在增大,其余环向应力的差别不明显、径向应力整体差别较小。当参数b从0增加到1时,洞壁位移相对减小了30.04%,即中间主应力效应使得寒区隧道冻结围岩变形明显减小,表明合理考虑中间主应力效应能更好地发挥冻结围岩的强度潜能,具有可观的经济效益,但高围压时会减弱些。

4.2 围岩冻胀特性

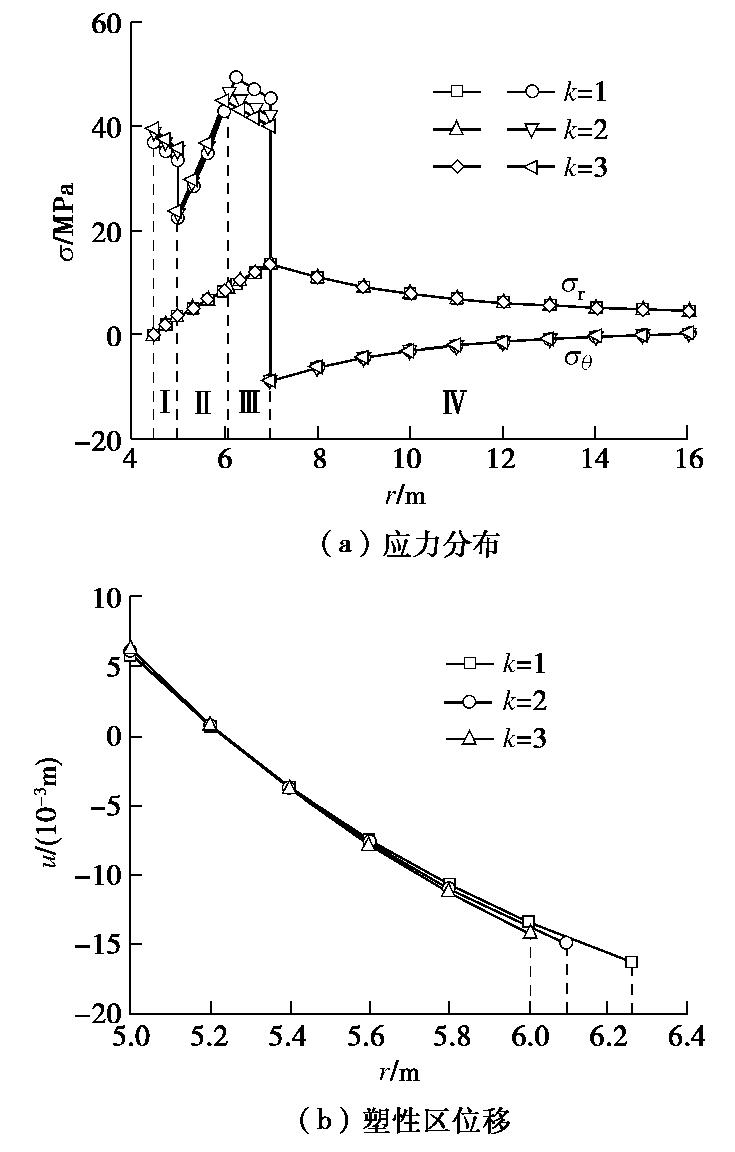
不均匀冻胀系数k反映横观各向同性冻胀时围岩不同方向上的冻胀差异,寒区隧道冻胀试验^[5-6]表明系数k常在1～3之间,图6给出了b=0.5,k=1,2和3时寒区隧道应力分布和塑性区位移的变化规律。

图 6 不均匀冻胀系数的影响

Figure 6. Influences of anisotropic frost-heave coefficient

下载: 全尺寸图片幻灯片

从图6可以看出,塑性区半径随系数k的增加而有所减小,表明不均匀冻胀限制了冻结围岩塑性区的发展,但系数k由1增加到3时作用于支护的冻胀力增大了0.25 MPa,即以冻胀力增大换来了围岩塑性区的减小,这使得按各向同性冻胀假定设计的寒区隧道支护结构偏于危险,因此应慎重采用各向同性冻胀假设。同时,不同系数k时冻结围岩弹性区的环向应力变化较大,其余各区域的应力分布和塑性区位移差异不明显。

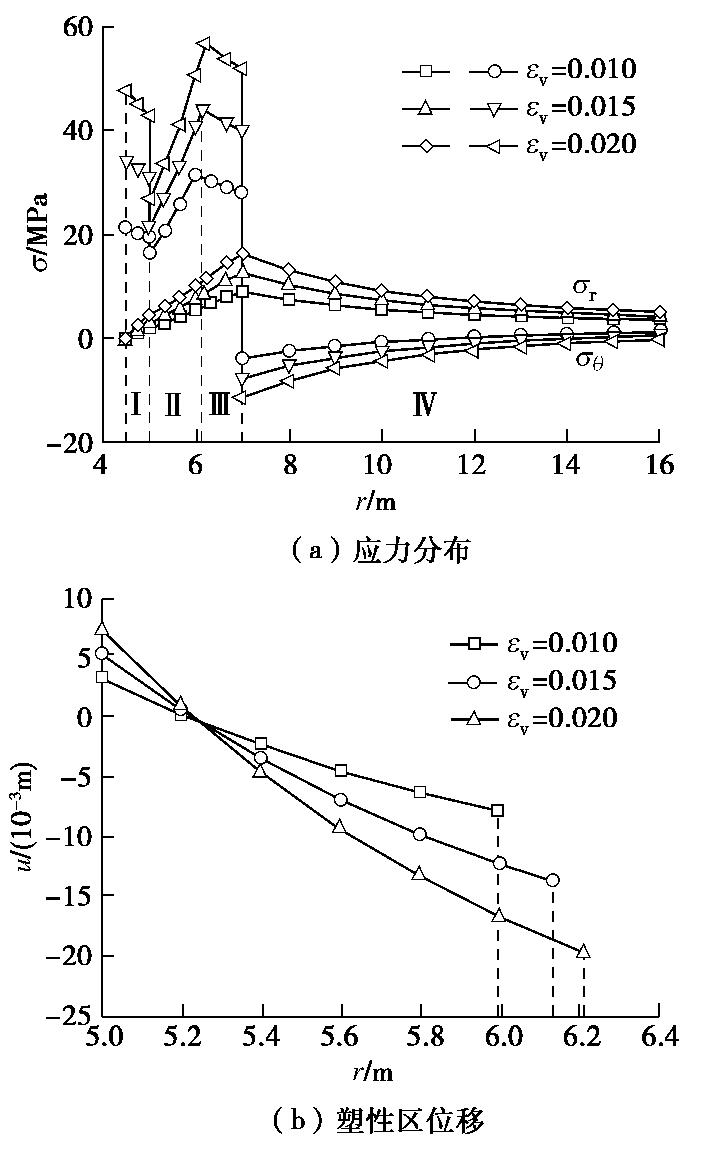
体积冻胀率 $ε_{v,f}$ 代表寒区隧道的冻结膨胀程度,图7为b=0.5,k=1.5, $ε_{v,f}$ =0.01,0.015和0.02时寒区隧道应力分布和塑性区位移的变化规律。

图 7 体积冻胀率的影响

Figure 7. Influences of volumetric frost-heave strain

下载: 全尺寸图片幻灯片

由图7可以看出,围岩体积冻胀率的增加,对各区域应力分布和塑性区位移的影响非常显著,将对寒区隧道结构安全与运营环境都十分不利,应采取有效保温措施予以缓解寒区隧道的整体冻胀效应。

5. 结论

（1）所建立的寒区隧道应力和位移塑性统一解综合考虑了中间主应力效应和横观各向同性冻胀的影响,可退化为有关文献中众多的已有解答,具有广泛的适用性和很好的可比性,同时给出了冻结围岩塑性状态的判定方法即适用条件与应用步骤,可为寒区隧道工程设计提供理论指导。

（2）通过与有关文献的寒区隧道应力的MC准则解答和外接圆DP准则解答的对比,验证了本文所得统一解的正确性。MC准则解答因忽略中间主应力效应而偏于保守,相反外接圆DP准则解答因高估中间主应力效应而偏于危险,可根据工程实际情况合理应用本文统一解。

（3）中间主应力效应和围岩冻胀特性对寒区隧道应力分布与塑性区位移的影响显著,应充分利用冻结围岩因中间主应力效应而获得的承载潜能,重视寒区隧道实际存在的横观各向同性冻胀,并采用有效保温措施降低隧道的整体冻胀效应。

图 1 寒区隧道的塑性力学模型

Figure 1. Plastic mechanical model for a tunnel in cold regions

下载: 全尺寸图片幻灯片

图 2 寒区隧道的弹性力学模型

Figure 2. Elastic mechanical model of a cold region tunnel

下载: 全尺寸图片幻灯片

图 3 b=0时与文献[8]解答的对比

Figure 3. Comparison between results from this study with b=0 and those in Reference [8]

下载: 全尺寸图片幻灯片

图 4 b=1时与文献[4]解答的对比

Figure 4. Comparison between results from this study with b=1 and those in Reference [4]

下载: 全尺寸图片幻灯片

图 5 中间主应力的影响

Figure 5. Influences of intermediate principal stress

下载: 全尺寸图片幻灯片

图 6 不均匀冻胀系数的影响

Figure 6. Influences of anisotropic frost-heave coefficient

下载: 全尺寸图片幻灯片

图 7 体积冻胀率的影响

Figure 7. Influences of volumetric frost-heave strain

下载: 全尺寸图片幻灯片

参考文献(15)

[1]	LAI Y M, WU H, WU Z W. Analytical viscoelastic solution for frost force in cold-region tunnels[J]. Cold Regions Science and Technology, 2000, 31(3): 227-234. doi: 10.1016/S0165-232X(00)00017-3
[2]	GAO G Y, CHEN Q S, ZHANG Q S, et al. Analytical elastic-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels[J]. Cold Regions Science and Technology, 2012, 72(1): 50-57.
[3]	FENG Q, JIANG B S, ZHANG Q, et al. Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels[J]. Cold Regions Science and Technology, 2014, 108: 59-68. doi: 10.1016/j.coldregions.2014.08.001
[4]	甄田田. 基于黏弹塑性理论的冻结壁与井壁共同作用机理分析[D]. 合肥: 安徽理工大学, 2017. ZHEN Tian-tian. Analysis of Interaction Mechanism Between Freezing Wall and Shaft Lining Based on Visco-Elastic-Plastic Theory[D]. Hefei: Anhui University of Science and Technology, 2017. (in Chinese)
[5]	夏才初, 李强, 吕志涛, 等. 各向均匀与单向冻结条件下饱和岩石冻胀变形特性对比试验研究[J]. 岩石力学与工程学报, 2018, 37(2): 274-281. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201802002.htm XIA Cai-chu, LI Qiang, LÜ Zhi-tao, et al. Comparative experimental study on frost deformation characteristics of saturated rock under uniform freezing and uni-directional freezing conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 274-281. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201802002.htm
[6]	LÜ Z T, XIA C C, LI Q, et al. Empirical frost heave model for saturated rock under uniform and unidirectional freezing conditions[J]. Rock Mechanics and Rock Engineering, 2019, 52(3): 955-963. doi: 10.1007/s00603-018-1666-z
[7]	XIA C C, LÜ Z T, LI Q, et al. Transversely isotropic frost heave of saturated rock under unidirectional freezing condition and induced frost heaving force in cold region tunnels[J]. Cold Regions Science and Technology, 2018, 152: 48-58. doi: 10.1016/j.coldregions.2018.04.011
[8]	LÜ Z T, XIA C C, WANG Y S, et al. Analytical elasto-plastic solution of frost heaving force in cold region tunnels considering transversely isotropic frost heave of surrounding rock[J]. Cold Regions Science and Technology, 2019, 163: 87-97. doi: 10.1016/j.coldregions.2019.04.008
[9]	YANG Y G, GAO F, LAI Y M. Modified Hoek-Brown criterion for nonlinear strength of frozen soil[J]. Cold Regions Science and Technology, 2013, 86: 98-103. doi: 10.1016/j.coldregions.2012.10.010
[10]	CHEN D, WANG D, MA W, et al. A strength criterion for frozen clay considering the influence of stress Lode angle[J]. Canadian Geotechnical Journal, 2018, 56(11): 1557-1572.
[11]	LIU X Y, LIU E L. Application of new twin-shear unified strength criterion to frozen soil[J]. Cold Regions Science and Technology, 2019, 167: 102857. doi: 10.1016/j.coldregions.2019.102857
[12]	俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC402.000.htm YU Mao-hong. Unified strength theory for geomaterials and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC402.000.htm
[13]	俞茂宏. 双剪理论及其应用[M]. 北京: 科学出版社, 1998. YU Mao-hong. Twin-Shear Theory and Its Application[M]. Beijing: Science Press, 1998. (in Chinese)
[14]	ZHANG C G, ZHAO J H, ZHANG Q H, et al. A new closed-form solution for circular openings modeled by the Unified Strength Theory and radius-dependent Young's modulus[J]. Computers and Geotechnics, 2012, 42: 118-128. doi: 10.1016/j.compgeo.2012.01.005
[15]	张常光, 祁航, 蔡明明, 等. 基于统一强度理论的煤层平动冲击失稳解答[J]. 煤炭学报, 2019, 44(8): 2589-2595. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201908034.htm ZHANG Chang-guang, QI Hang, CAI Ming-ming, et al. Instability solution of translatory coal seam bumps based on the unified strength theory[J]. Journal of China Coal Society, 2019, 44(8): 2589-2595. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201908034.htm