土–水特征曲线对非饱和砂土抗剪强度的影响

翟钱; 戴国亮; 赵学亮

doi:10.11779/CJGE202007018

土–水特征曲线对非饱和砂土抗剪强度的影响 English Version

翟钱^{1, 2,},
戴国亮^{1, 2},
赵学亮^{1, 2}

1.
东南大学混凝土及预应力混凝土结构教育部重点实验室,江苏　南京　210096
2.
东南大学土木工程学院,江苏　南京　210096

基金项目:

中国华能集团有限公司科技项目 HNKJ19-H17

国家电网鲁能集团有限公司科技项目 SGDC0000KXJS1900137

国家自然科学基金项目 51878160

详细信息

作者简介:
翟钱(1982—),男,博士,副教授,主要从事非饱和土力学等方面的教学和科研工作。E-mail：101012332@seu.edu.cn

中图分类号: TU42;P66
计量
- 文章访问数: 350
- HTML全文浏览量: 22
- PDF下载量: 206
出版历程
- 收稿日期: 2019-07-24
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-06-30

Effect of soil-water characteristic curve on shear strength of unsaturated sandy soils

ZHAI Qian^{1, 2,},
DAI Guo-liang^{1, 2},
ZHAO Xue-liang^{1, 2}

1.
Key Laboratory of Concrete and Prestressed Concrete Structure of Ministry of Education, Southeast University, Nanjing 210096, China
2.
School of Civil Engineering, Southeast University, Nanjing 210096, China

摘要

摘要: 因非饱和土的剪切试验设备成本比较高,通过间接手段估测非饱和土抗剪强度的方法日受欢迎,其中通过土–水特征曲线进行估测的方法最为普遍。通过修正传统毛细模型,结合概率统计学理论,为通过土–水特征曲线估测非饱和土抗剪强度的计算方法提供理论依据,并提出相关数学表达式。对比公式的估算值和现有文献的试验数据,发现估算值和试验数据基本吻合。此外,还发现很多文献中土–水特征曲线试验土样和非饱和土剪切试验土样并不在同一应力状态,如果忽略这样的应力状态差异,会增大估测的误差。因此,建议对传统张力仪或压力板试验的土–水特征曲线进行相关修正后再用以估测非饱和土抗剪强度。
- 孔径分布 /
- 非饱和土抗剪强度 /
- 修正毛细模型 /
- 土–水特征曲线 /
- 统计模型
Abstract: The experimental measurements of the shear strength of unsaturated soils are uncommonly emloyed in the practical engineering because the unsaturated experimental measurements are time-consuming and costly. Instead, the shear strength of unsaturated soils is commonly estimated from the soil-water characteristic curve (SWCC). In this study, an improved capillary model and a new mathematical equation are proposed for the estimation of the shear strength of unsaturated soils from the SWCC. The proposed equation is verified by the experimental data from the published literatures. It is observed that the soil specimen prepared for the SWCC tests may not be in the same stress state as that prepared for the shearing tests. In other words, the measured SWCC from the conventional Tempe cell and pressure plate may not agree with that of the specimen in the shearing tests. As a result, errors may be introduced in the estimated results of the shear strength of unsaturated soils. Consequently, the SWCCs obtained from the conventional method should be corrected for the estimation of the shear strength of the unsaturated soils with a high confining pressure.
- pore-size distribution /
- shear strength of unsaturated soils /
- improved capillary model /
- soil-water characteristic curve /
- statistical model

HTML全文

0. 引言

蒸发作为大气–土体相互作用的主要方式之一,在干旱、半干旱地区的水循环与能量平衡中扮演着至关重要的角色^[1]。干旱环境中大气–土体界面上的蒸汽压梯度较高,导致土体水分的蒸发强度较大,水分的蒸发会直接改变土体的含水率及水分场的空间分布状态,而土体的工程性质对含水率变化非常敏感,从而诱发龟裂、盐碱化、土质退化、地面沉降等岩土工程和环境工程地质问题^[2]。近年来,受全球气候变化影响,大范围的水文变化加剧了世界上许多地区的旱情。极端干旱气候的频发使得蒸发诱因的区域性岩土/地质工程问题或灾害更加显著,如地基土收缩变形引起的差异沉降导致地面基础设施大面积受损,土体开裂引起力学性质弱化及渗透性增加导致工程结构稳定性降低等,从而造成国民经济损失。因此,土体水分的蒸发过程及机理近年引起了学界的极大关注。

与纯水不同,水分在土体内的存在形式十分复杂,其蒸发和运移过程受土体结构及外部环境等诸多因素的制约。目前对土体水分蒸发的研究主要集中在各种影响因素方面,如环境温湿度、风速、土体成分、土体结构和含水率等^[3-12]。然而,传统的土体蒸发量化研究手段如蒸渗仪、土柱、土盒试验等的数据采集大多为点线式^[13-17],获取的数据也较为离散,且在经济成本和时间成本上耗费较大。同时,水分测量设备的埋设会破坏局部土体结构,扰动水分迁移路径,在一定程度上会影响研究结果的准确性,进而限制理论研究的进展。因此,目前学界对于土体蒸发模型的理论推导,尤其是黏性土方面,还鲜有报道。

土体水分蒸发的本质是其孔隙中的液态水通过吸收外部环境提供的能量,汽化为水蒸气后外逸的物理过程。水分子在离开土体表面的同时,会以潜热的形式带走土中的热量,导致土体温度产生相应的变化。蒸发的水分越多,消耗的潜热越多,土体降温也越大。因此,理论上可以通过监测土体的温度变化来评价土体水分的蒸发速率或者蒸发量。然而,目前学界关于土体蒸发过程中的温度变化以及温度与蒸发之间理论关系的研究还较为鲜见,这其中的关键问题是如何准确获得土体表面的温度场。红外热成像技术作为一种无接触、可视化、数据采集便捷的测温手段^[18-19],能够精确地获取物体表面的温度分布。近年来,该技术已经被广泛的运用到了环境、地质、岩土等领域的研究中,例如岩石在受荷载条件下的破坏及变形监测、红外探水、地热场监测等^[20-22]。但目前还尚未见基于红外热成像技术的土体水分蒸发研究。

为此,本文采用红外热成像技术对不同初始条件的土体蒸发特性开展了一系列室内试验研究,旨在提出一种无损、便捷、精确的土体蒸发研究新方法。试验中,为了计算蒸发速率,监测了蒸发失水导致的试样质量变化,并采用红外热成像仪实时记录了试样蒸发过程中的表面温度场演化。根据相关理论,分析了土体表面温度的变化过程以及对蒸发的响应机制。基于土–气交互的能量守恒模型推导了土体蒸发速率与土表界面温差之间的理论关系,并对其合理性和准确性进行了讨论和验证。

1. 试验材料与方法

1.1 试验材料

（1）试验土

本次试验采用南京地区的下蜀土作为研究对象,取土深度约0.5～1.5 m,其颜色为褐黄色。下蜀土广泛分布于长江中下游地区,其黏土矿物主要由伊利石和伊利-蒙脱石层间矿物组成^[23]。表1给出了试验土的基本物理性质。图1,2给出了该土的颗粒级配累计曲线及击实曲线。由图2可知,下蜀土的最优含水率为16.5%,对应最大干密度为1.70 g/cm^-3。根据美国ASTM协会的土体分类标准（ASTM,2011）,下蜀土可被划分为低液限黏土（CL）。

表 1 下蜀土基本物理性质

Table 1. Physical properties of Xiashu soil

相对质量密度 $G_{s}$	液限 $w_{L}$ /%	塑限 $w_{P}$ /%	塑性指数 $I_{P}$	最优含水率 $w_{opt}$ /%	最大干密度 $ρ_{d}$ /(g·cm^-3 )	黏粒含量（d<0.005 mm）/%
2.73	36.5	19.5	17	16.5	1.70	22

下载: 导出CSV

| 显示表格

图 1 下蜀土颗粒级配累计曲线

Figure 1. Cumulative grain-size distribution curve of Xiashu soil

下载: 全尺寸图片幻灯片

图 2 下蜀土击实曲线

Figure 2. Compaction curve of Xiashu soil

下载: 全尺寸图片幻灯片

（2）红外热成像仪

本研究使用的红外热成像仪型号为FLIR-T620,该仪器工作波段为7.8～14 μm,相机分辨率640 pix ×480 pix,温度测量灵敏度可达±0.04℃,精度可达±0.1℃。红外热成像技术的基本原理是物质温度在绝对零度（-273.15℃）以上时,物质不断地向外辐射电磁波^[24]。当物质温度发生变化,电磁波的辐射强度与波长分布特性也会随之改变。波长介于2.0～1000.0 μm的电磁波被称为热红外线。在辐射过程中由于大气的阻隔,仅在3～5 μm和8～12 μm两个波段的热红外线具有较好的穿透能力^[25]。通过捕获这两个波段的热红外线,并标定其辐射强度与物质温度之间的量化关系,即可实现对目标物体温度的反演。

1.2 试样制备

将取回的土样风干粉碎,过2 mm筛,以去除原状土体内的大颗粒杂质。过筛后的土样通过与蒸馏水混合并充分搅拌配制成含水率为55%和65%的两组泥浆样。随后,在振动台上振动泥浆5 min,排除搅拌过程中其内部产生的气泡。利用薄膜将泥浆密封在容器中,静置48 h。待泥浆沉积稳定后,抽去表面清液。将配制好的泥浆样缓慢地倒入圆形铝盒后,采用保鲜膜密封整个试样,静置于试验环境内72 h,以保证试样初始温度与环境温度一致。考虑到试样尺度过大可能更容易受到外界环境及土结构非均质性的影响,从而造成的土表局部蒸发不均匀,因此本次试验使用的铝盒内径为4 cm。此外,由于土体水分蒸发速率受到初始含水率和初始厚度等因素的影响^[26],本次试验中共设计了2种不同初始含水率（55%,65%）和2种不同初始厚度（1 cm,2 cm）的试样进行对比试验,以研究不同土体性质条件下的蒸发特性。具体的试样参数如表2所示。

表 2 土样参数

Table 2. Parameters of samples

试样编号	初始含水率/%	直径/cm	厚度/cm
S1	65	4	1
S2	55	4	1
S3	55	4	2

下载: 导出CSV

| 显示表格

1.3 试验方法

将试样表面密封材料揭去,在铝盒侧壁及底部包裹隔热保鲜膜后,置于温度31±1℃,湿度75%±2%的恒温室内干燥。通过试样正上方的红外热成像仪来记录土体蒸发过程中的表面温度变化,试验装置示意图如图3所示。与此同时,通过高精度电子天平（精度±0.005 g）实时获取土体在蒸发过程中的质量变化,从而计算各时刻土体对应的蒸发速率和含水率。为了排除自然光周期性变化造成的外辐射干扰,本次试验在恒定光源下进行。

图 3 红外热成像综合试验装置

Figure 3. Schematic drawing of experimental setup

下载: 全尺寸图片幻灯片

2. 结果与讨论

2.1 水分蒸发过程

在干燥环境下,由于大气–土界面存在蒸汽压梯度,当大气相对湿度低于土体的相对湿度时,土体内的液态孔隙水不断汽化向外逸出,即土体水分蒸发。土体的质量也随之逐渐减小。图4给出了不同初始含水率和不同初始厚度试样的蒸发速率随干燥时间的变化。可以发现,试样在不同的初始含水率和厚度条件下,蒸发速率变化的总体趋势一致,主要由3个阶段组成^[27-29]：

图 4 试样在干燥过程中蒸发速率随时间的变化

Figure 4. Changes in evaporation rate of soil samples during desiccation

下载: 全尺寸图片幻灯片

（1）常速率阶段：该阶段试样水分蒸发速率较为稳定,数值上趋于某一常数。例如试样S1（含水率65%,厚度1 cm）在该阶段的蒸发速率大约为0.14 mm/h。这一现象的原因在于,该阶段土体处于饱和或接近饱和状态,土体内部有充足的水分供给蒸发的需要,大气–土界面的蒸汽压差基本保持恒定。此时的土体蒸发主要受环境因素主导（如风速、温湿度、能量供给等）^[30]。

（2）减速率阶段：该阶段试样的蒸发速率随着干燥时间而逐渐减小。这是因为随着干燥的持续进行,土颗粒间的孔隙水不断减少产生毛细作用,诱导粒间吸力的形成。已有学者发现在土体由常速率蒸发阶段过渡到减速率阶段的过程中,土体状态从饱和转化为非饱和状态^[31]。在非饱和状态下,土体内部吸力随着含水率的减小而显著上升^[32-34]。吸力能抑制孔隙水的迁移,是土体持水能力的体现。吸力越大,土体持水能力越强^[35]。并且,土体内部吸力的增加,孔隙中的相对湿度降低,会导致大气–土界面上的蒸汽压梯度减小,从而减弱了土体水分蒸发的驱动力^[30]。因此,在土体蒸发经过常速率阶段以后,由于吸力的形成与发展,蒸发速率逐渐降低。此外,随着土体含水率或饱和度的下降,土体发生收缩变形,孔径及渗透系数减小,孔隙水由连续向非连续过渡,水分迁移由液相传输逐渐向气相扩散转变,这些也是导致蒸发速率减小的重要原因。

（3）残余阶段：该阶段试样的蒸发速率逐渐趋近为零。主要原因在于该阶段土体孔隙水含量很低,孔隙水的赋存状态以结合水为主,高吸力使得土体具备较高的持水能力^[36-37]。并且,大气–土界面之间的蒸汽压接近相等,导致缺少足够的驱动力或能量使土体孔隙水汽化^[30]。因此,该阶段土体内水分变化较小^[38]。

此外,通过对不同初始条件下的试样蒸发速率曲线进行对比,可发现在相同初始厚度,不同初始含水率条件下（S1和S2）,初始含水率越高,试样在常速率阶段的蒸发速率越大。这是因为初始含水率较高的土样可供蒸发的水量多,孔径相对较大,对应的持水能力较弱。此外,相同初始含水率条件下,试样厚度越厚,常速率阶段蒸发速率越高。部分学者针对土体厚度对其蒸发的影响也开展了一系列试验,发现厚度对常速率阶段蒸发速率大小的影响不是很明显^[27]。这与本文所得现象有所不同,其原因可能在于本次试验中S1和S2的初始厚度（1 cm）略低于容器壁高度,容器壁阻碍了由试样蒸发产生的蒸汽在其表面的流动。因此,土体表面的相对湿度较高,导致大气–土界面之间的蒸汽压梯度相比于S3偏小,水分蒸发受到一定抑制。

2.2 温度变化过程

图5给出了土样表面温度场随时间的变化过程。可以看出,在蒸发初期（对应常速率阶段）（图5（a）,（b）,（e）,（f）,（i）～（j））,土表温度随时间的变化幅度不大。随着蒸发的持续进行,土表温度逐渐升高。蒸发结束后,试样的表面温度与环境温度趋于一致。由于试验土样表面积较小,不同时刻下土表温度场分布均匀（图5）。因此,取土表温度的平均值与环境温度之间的差值与蒸发时间建立关系,可以得到大气与土界面上的温度差随干燥时间的变化曲线,如图6所示。从图6可发现,界面温差与蒸发速率随时间的变化趋势具有很好的一致性,各阶段转折点所对应的时间点基本相同,这说明土表温度的变化能同步响应其蒸发过程。出现这种现象的原因在于,土体水分蒸发是一个吸热过程,蒸发强度越大,土表的释热作用越剧烈,相应的表面温度也越低。对应于蒸发速率演化的三阶段,在干燥过程中土体表面温度的变化也可大致分为3个阶段：

图 5 不同土性试样在干燥过程中的表面温度场随时间的变化

Figure 5. Changes in surface temperature field of soil samples during desiccation

下载: 全尺寸图片幻灯片

图 6 试样在干燥过程中的界面温差随时间的变化

Figure 6. Changes in temperature difference between soil surface and atmosphere during desiccation

下载: 全尺寸图片幻灯片

（1）恒定低温阶段：对应于蒸发的常速率阶段。该阶段土体内部的液相自由水含量较高,外界辐射和热传递提供的能量几乎全部传递给土体内的液相,引起液相的熵增。当熵增至某一阈值以后,液相自由水发生相变转化为气相水蒸气,即土体水分蒸发。由于液相水在相变过程中引起了其内部热能的损耗,导致土体内液相与固相之间的热力学平衡被打破,两者之间形成热力梯度,固相不断向液相提供能量。这使得土体固相的热量减少,土体温度下降,土/气界面温差较大。并且,伴随着恒定的蒸发速率,上述环境以及土体液相和固相之间的热传递较为稳定。作为结果,土体在该阶段保持着恒定低温。

（2）升温阶段：对应于蒸发的减速率阶段。由于前期蒸发导致土体内的自由水逐渐减少,结合水的占比逐渐上升。结合水在分子间范德华力,偶极力等引力的作用下,与土颗粒之间紧密贴合,并具有一定的固相性质。相比较与自由水,结合水的物质混乱度和熵值较低,因此激发结合水发生相变,即转化为气相所需的能量越高。这解释了随着结合水在土体内的占比逐渐升高,在外界环境热辐射一定的条件下,土体蒸发速率逐渐降低的原因。蒸发速率降低意味着单位时间内蒸发的水量及消耗的热量降低。此外,随着自由水的减小,结合水以及固相土颗粒与外界环境的接触面积增大。土/气间环境–液相（自由水）的热交换逐渐转化为环境–固相（结合水与土颗粒）的热交换。因此,该阶段土表温度的逐步上升。

（3）稳定阶段：对应于蒸发的残余阶段。该阶段蒸发速率趋近于0,环境与土体的热交换趋于稳定,达到热力学平衡,因此土体温度与环境温度趋于一致,不再发生变化。

2.3 蒸发速率与温度的理论关系

土体蒸发过程中,土/气间能量交互服从能量守恒定理。如果假定大气横向对流的影响可忽略不计,可采用能量平衡模型估算土体水分的蒸发量^[39-40]：

$L_{e} E = R_{n} - G - H$ 。

(1)

式中 $L_{e}$ 为土水蒸发潜热（水由液相转化为气相吸收的热量）（J/kg）； $E$ 为蒸发速率（mm/d）； $R_{n}$ 为地表净辐射通量（环境提供的热量）（J/m²s）； $G$ 为土体热通量（土体吸收的热量）（J/m²s）； $H$ 为感热通量（传导及散射到大气中的热量）（J/m²s）。对于蒸发速率而言,水分蒸发为正,水汽凝结为负；对地表净辐射而言,入射为正,散射为负；对土体热通量而言,能量引起土体温度上升为正,下降为负；对感热通量而言,能量用于加热空气为正,空气冷却失去能量为负。地表净辐射量 $R_{n}$ 由入射的太阳短波辐射、大气散射和出射的地面反射、地面长波辐射共同组成,如图7所示。

图 7 水分蒸发过程中土体表面辐射平衡示意图^[42]

Figure 7. Diagram of radiation balance on soil surface during Evaporation^[42]

下载: 全尺寸图片幻灯片

当忽略大气散射的影响, $R_{n}$ 可表示为^[41-42]

$R_{n} = (1 - α) R_{s} - Δ R_{l}$ ,

(2)

式中, $R_{s}$ 为太阳短波辐射量, $α$ 为土体反照率, $Δ R_{l}$ 为地表长波辐射量。感热通量 $H$ 可表示为^{[39, 43]}

$H = ρ C_{p} h (T_{s} - T_{a}) = ρ C_{p} \frac{T_{s} - T_{a}}{r_{α}}$ ,

(3)

式中, $ρ$ 为空气密度, $C_{p}$ 为空气的定压比热容, $h$ 为空气的乱流导温率, $r_{α}$ 为空气的单位热阻,其值与 $h$ 互为倒数, $T_{s}$ 为土体表面温度, $T_{a}$ 为参考高度处的空气温度。

Tanner等^[44]对式（1）～（3）进行了整理,提出了用于估算蒸发速率的温差模型：

$L_{e} E = (R_{n} - G) - \frac{ρ C_{p}}{r_{α}} (T_{s} - T_{a})$ 。

(4)

Qiu等在砂性土的水分蒸发试验中发现,粗砂在干燥过程中的土体热通量G可近似为地表净辐射 $R_{n}$ 的1/5,即 $G = 0.2 R_{n}$ ^[45]。鉴于黏性土在失水过程中的物理性质变化与砂性土具有一定差别,对本次试验中下蜀土的热通量值,可假设为： $G = γ R_{n}$ 。式中的参数 $γ$ 是一个与土性相关的常量。通过此假设,式（4）可表示为

$E = \frac{(1 - γ) R_{n}}{L_{e}} - \frac{ρ C_{p}}{r_{α} L_{e}} (T_{s} - T_{a})$ ,

(5)

若蒸发过程中的环境温湿度和辐射强度（恒定光照）条件均保持恒定,即 $\frac{ρ C_{p}}{L_{e}}$ 的值为常量,则式（5）可进一步简化为

$E = α - β (T_{s} - T_{a}) = α - β Δ T$ 。

(6)

即在恒定光照或温湿度的环境中,土体水分蒸发时大气与土表的蒸发速率 $E$ 和界面温差 $Δ T$ 的变化将近似呈线性关系。式（6）中 $α$ 为与辐射强度和土性有关的常数, $β$ 为与空气单位热阻有关的常数。

为了证明上述理论关系式的准确性,在图8中给出了本次试验中各组试样蒸发过程蒸发速率与土表温度的关系散点图。由图8可知,试样的蒸发速率与界面温差间存在良好的对应关系,且初始含水率与厚度的区别对其关系影响较小。对3组数据进行线性拟合,得到本文研究的下蜀土的蒸发速率与界面温差之间的定量关系如下：

图 8 土/气界面温差–速率关系拟合图线

Figure 8. Fitting curves of temperature difference and evaporation rate

下载: 全尺寸图片幻灯片

$E = 0.0086 - 0.0578 Δ T (R^{2} = 0.94)$ 。

(7)

式（7）的确定系数 $R^{2}$ 值为0.94,可见该拟合优度较高,蒸发速率与界面温差之间存在较好的线性关系,这与理论公式得出的结论相吻合,即在恒定的环境温度条件下,土表界面温差与蒸发速率的变化线性相关。

上述试验现象和理论关系表明,土表温度的变化可以很好地响应土体水分蒸发过程,可以利用土表温度数据直接反演量化土体水分蒸发速率。因此,土表温度可以作为一种量化参数指示土体的蒸发特性。本文提出的基于红外热成像技术研究土体蒸发特性是可行的,后期需要围绕该技术及土体蒸发问题开展更系统和细致的研究。

3. 结论

通过开展一系列室内干燥试验,基于红外热成像技术研究了土体在蒸发过程中的蒸发速率和表面温度的演化规律,并探讨了两者之间的内在联系,得到以下主要结论：

（1）对于初始饱和的土体,水分蒸发速率随干燥时间呈现3个典型阶段,即常速率阶段、减速率阶段和残余阶段。其阶段性变化主要与干燥过程中土的持水能力、孔隙水的赋存状态及传输特征有关。

（2）土体蒸发过程中,土体表面的温度变化也呈现3个典型阶段,即恒定低温阶段、升温阶段和稳定阶段,且与蒸发阶段一一对应。这主要与水分蒸发过程中的热能消耗及热能在不同介质中的传递效应有关。

（3）在恒定的环境温湿度或辐射强度（光照）条件下,蒸发速率E和土体表面与大气的温差 $Δ T$ 之间具有线性关系： $E = α - β Δ T$ ,式中的常参数 $α$ 与的外界辐射强度和土体自身性质有关, $β$ 与空气单位热阻有关。对于同一种土,土层厚度和初始含水率对参数 $α$ 和 $β$ 取值没有明显影响。

本文研究成果表明,利用红外热成像技术开展土体蒸发特性研究是可行的。该技术具有便捷和无损的优点,能够快速、精确且实时地获取土体干燥条件下表面温度场的变化特征,进而可以反演量化土体的蒸发过程,评价土体的干湿状态。此外,本次试验成果也为未来开展原位土体在气候作用下蒸发/水分场的时空演化特征研究提供了新的技术思路。

图 1 传统毛细模型^[31]

Figure 1. Conventional capillary model^[31]

下载: 全尺寸图片幻灯片

图 2 水分在孔隙中的迁移过程

Figure 2. Movement of water in pores

下载: 全尺寸图片幻灯片

图 3 不规则孔隙简化为系列不同尺寸的毛细管

Figure 3. Simplification of irregular pores into a series of capillary tubes with different radii

下载: 全尺寸图片幻灯片

图 4 土体单元孔隙的简化

Figure 4. Simplification of soil element

下载: 全尺寸图片幻灯片

图 5 孔径分布函数和土水特征曲线的关系

Figure 5. Illustration of pore-size distribution function and soil-water characteristic curve

下载: 全尺寸图片幻灯片

图 6 土颗粒间的弯液面

Figure 6. Illustration of meniscus between two soil particles

下载: 全尺寸图片幻灯片

图 7 弯液面简化分析模型

Figure 7. Simplified model for meniscus

下载: 全尺寸图片幻灯片

图 8 土体在不同吸力状态下因弯液面造成对土颗粒框架的压缩应力^[11]

Figure 8. Illustration of compression on soil skeleton due to meniscus under different suction levels^[11]

下载: 全尺寸图片幻灯片

图 9 土颗粒周围不同状态的水^[32]

Figure 9. Illustration of different types of water around soil particles^[32]

下载: 全尺寸图片幻灯片

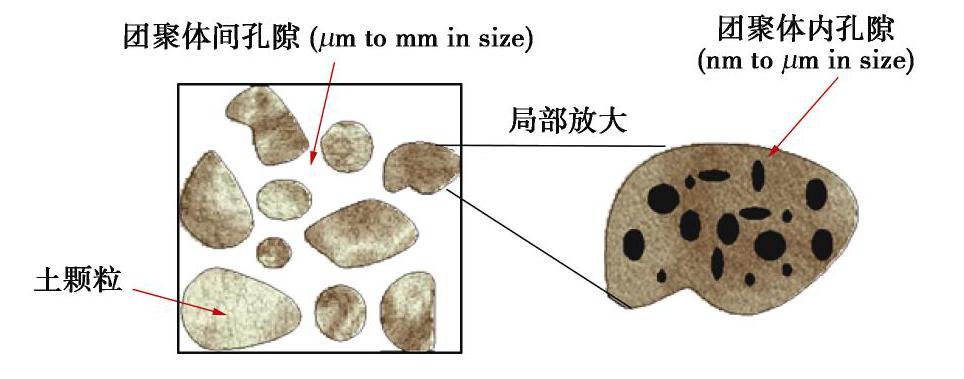
图 10 团聚体间孔隙和团聚体内孔隙^[33]

Figure 10. Illustration of inter-aggregate and intra-aggregate pores

下载: 全尺寸图片幻灯片

图 11 修正后的土–水特征曲线

Figure 11. Illustration of modified soil-water characteristic curve

下载: 全尺寸图片幻灯片

图 12 压实高岭土、风化花岗岩和印度Head Till的土–水特征曲线

Figure 12. Experimental data of soil-water characteristic curve for compacted kaolin, weathered granite and Indian Head Till

下载: 全尺寸图片幻灯片

图 13 压实高岭土、风化花岗岩和印度Head Till的抗剪强度试验数据

Figure 13. Experimental data of shear strength of unsaturated compacted kaolin, weathered granite, and Indian Head Till

下载: 全尺寸图片幻灯片

图 14 压实高岭土、风化花岗岩和印度Head Till估测抗剪强度和试验数据的比较

Figure 14. Comparison between estimated results and measured data of shear strength for unsaturated compacted kaolin, weathered granite, and Indian Head Till

下载: 全尺寸图片幻灯片

图 15 选用单一土–水特征曲线估测风化花岗岩和印度Head Till估测抗剪强度和试验数据的比较

Figure 15. Comparison between estimated results using single SWCC and measured data of shear strength for unsaturated weathered granite and Indian Head Till

下载: 全尺寸图片幻灯片

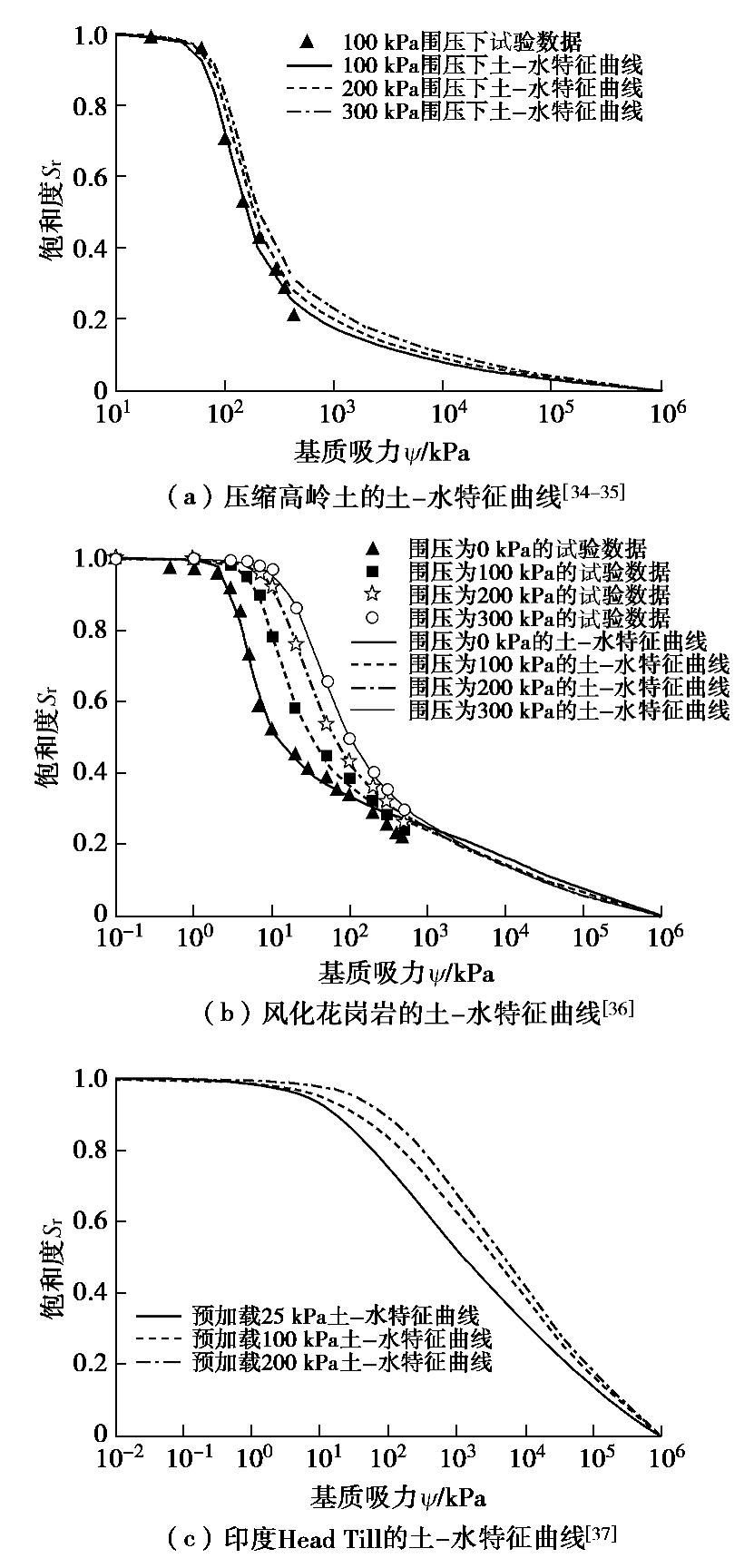
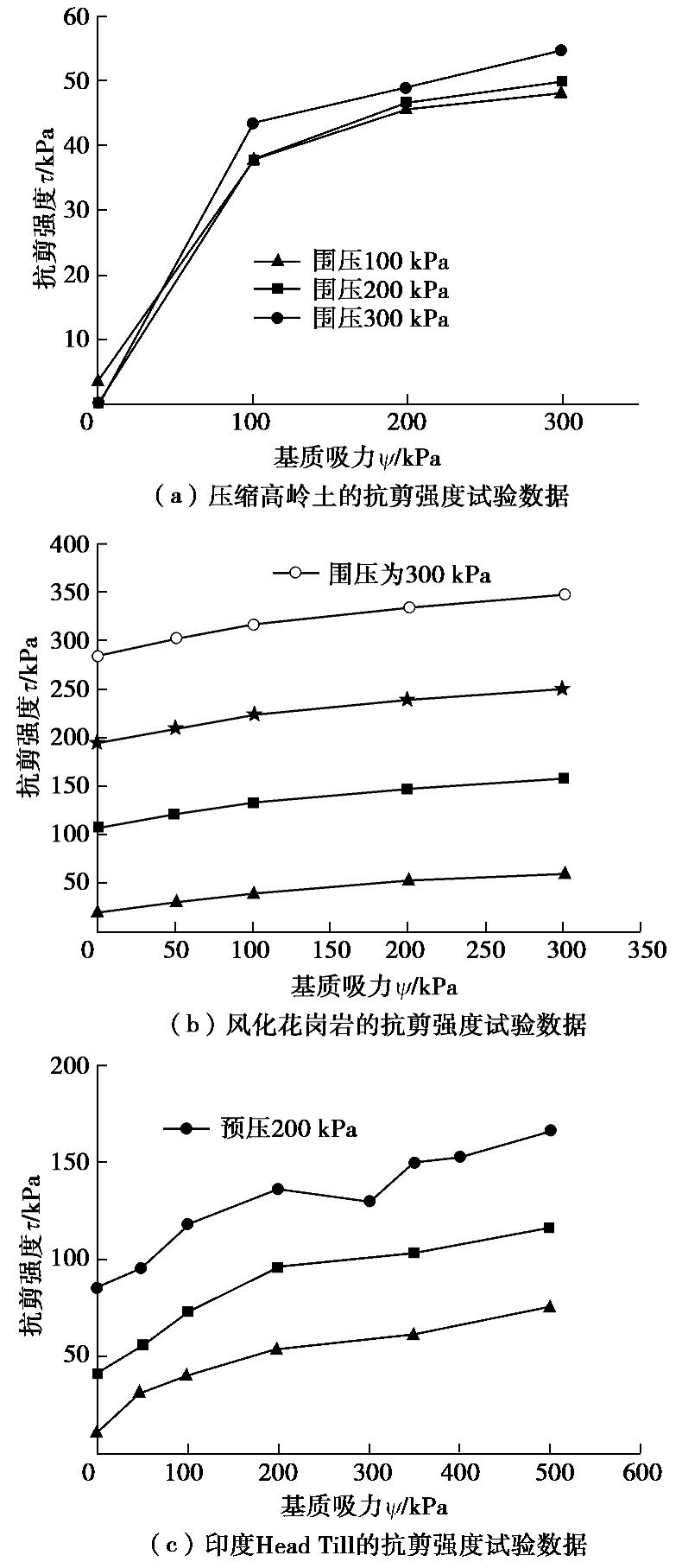
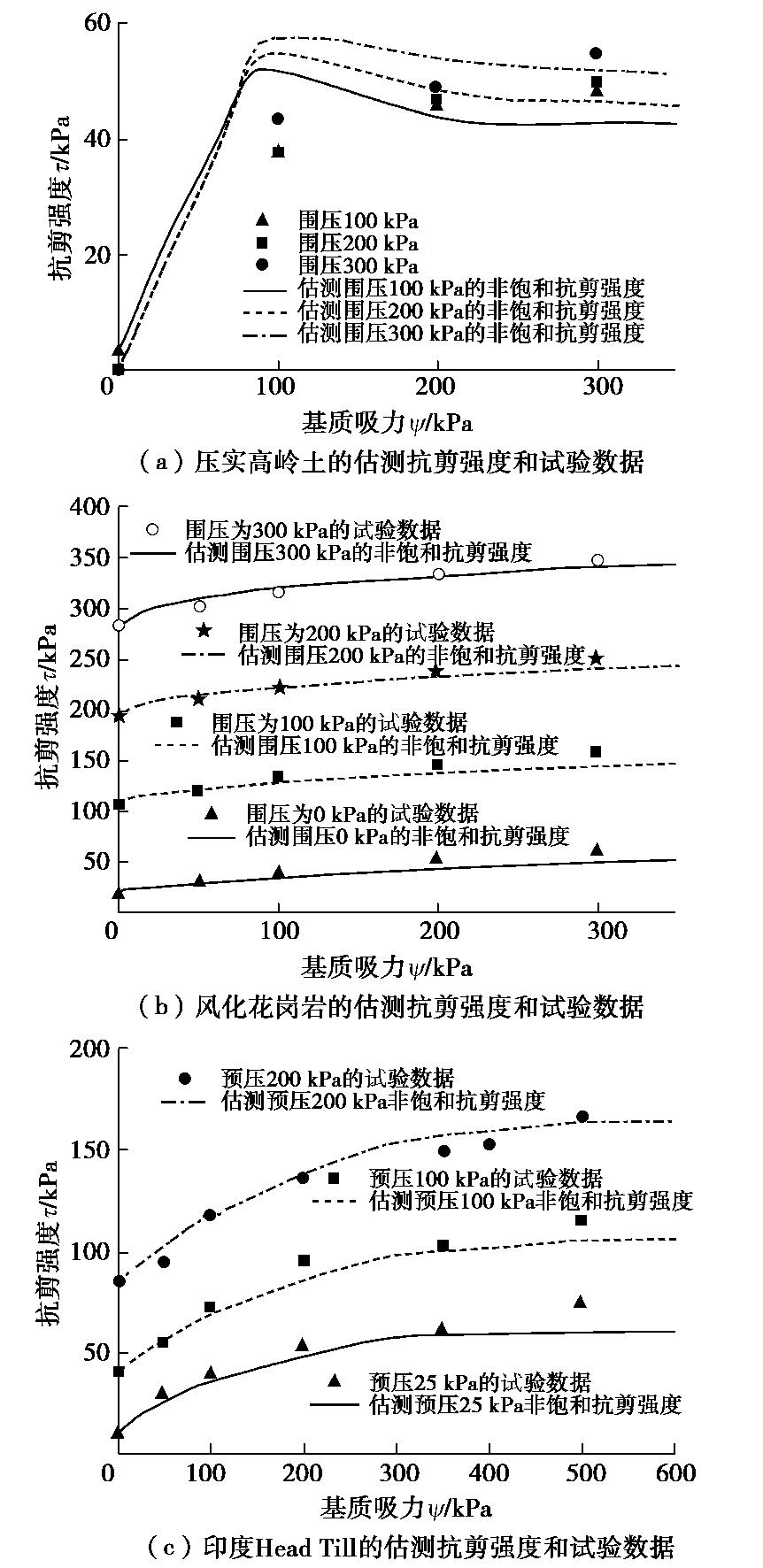
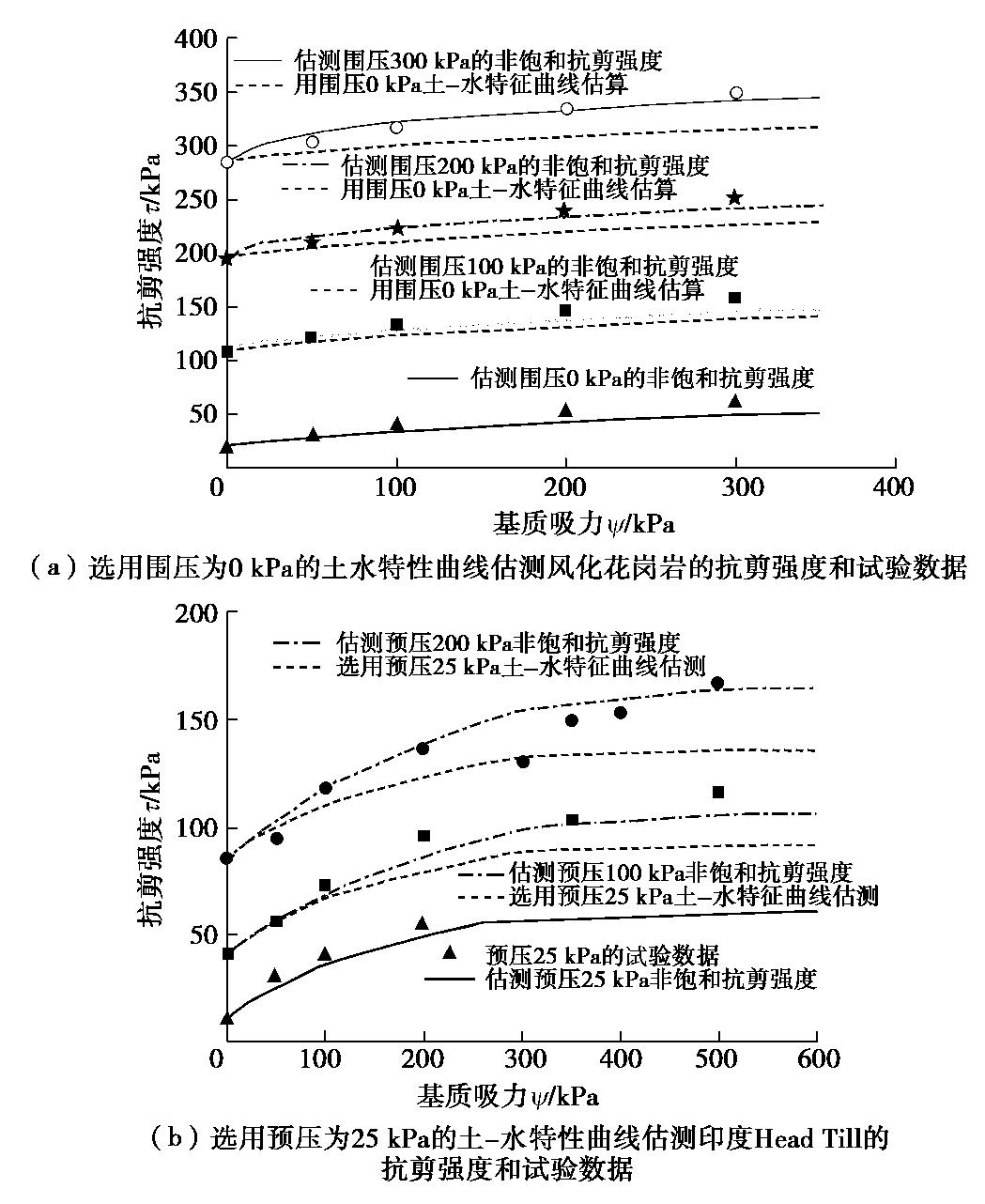
表 1 压实高岭土、风化花岗岩和印度Head Till土水特性曲线的拟合参数

Table 1 The SWCC fitting parameters for compacted kaolin, weathered granite and Indian Head Till

土样	围压/kPa	F-X模型^[21]参数
土样	围压/kPa	a/kPa	n	m	C_r
压缩高岭土	100	83.40	3.76	0.74	1500
压缩高岭土	200	95.00	3.80	0.70	1500
压缩高岭土	300	101.00	3.80	0.65	1500
风化花岗岩	0	3.26	4.12	0.41	1500
风化花岗岩	100	7.67	2.60	0.53	1500
风化花岗岩	200	14.72	2.07	0.61	1500
风化花岗岩	300	23.85	1.89	0.65	1500
印度Head Till	预压25	34.10	0.80	0.57	3000
印度Head Till	预压100	71.40	0.66	0.54	3000
印度Head Till	预压200	125.20	0.81	0.45	3000

下载: 导出CSV

参考文献(38)

[1]	FREDLUND D G, RAHARDJO H. Soil Mechanics for Unsaturated Soil[M]. New York: Wiley, 1993.
[2]	FREDLUND D G, RAHARDJO H, FREDLUND M D. Unsaturated Soil Mechanics in Engineering Practice[M]. New York: Wiley, 2012.
[3]	BISHOP A W. The principle of effective stress[J]. Teknisk Ukeblad, Norwegian Geotechnical Institute, 1959, 106(39): 859-863.
[4]	BIOT M A. General theory for three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. doi: 10.1063/1.1712886
[5]	JENNINGS J E B, BURLAND J B. Limitations to the use of effective stresses in partly saturated soils[J]. Géotechnique, 1962, 12(2): 125-144. doi: 10.1680/geot.1962.12.2.125
[6]	FREDLUND D G, MORGENSTERN N R, WIDGER A, et al. Shear strength of unsaturated soils[J]. Can Geotech J, 1978, 15: 313-321 doi: 10.1139/t78-029
[7]	FUNG Y C. Foundations of Solid Mechanics[M]. Englewood Cliffs: Prentice-Hall, 1965.
[8]	FUNG Y C. A First Course in Continuum Mechanics[M]. 2nd ed. Englewood Cliffs: Prentice-Hall, 1977.
[9]	陈正汉. 非饱和土与特殊土力学的基本理论研究[J]. 岩土工程学报, 2014, 36(2): 201-272. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm CHEN Zheng-han. On basic theories of unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 201-272. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm
[10]	陈正汉, 秦冰. 非饱和土的应力状态变量研究[J]. 岩土力学, 2012, 33(1): 1-11. doi: 10.3969/j.issn.1000-7598.2012.01.001 CHEN Zheng-han, QIN Bing. On stress state variables of unsaturated soils[J]. Rock and Soil Mechanics, 2012, 33(1): 1-11. (in Chinese) doi: 10.3969/j.issn.1000-7598.2012.01.001
[11]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Estimation of unsaturated shear strength from soil-water characteristic curve[J]. Acta Geotechnica, 2019, 14(6): 1977-1990. doi: 10.1007/s11440-019-00785-y
[12]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Role of pore-size distribution function on the water follow in soil[J]. Journal of Zhejiang University (Science A), 2019, 20(1): 10-20. doi: 10.1631/jzus.A1800347
[13]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. A pore-size distribution function based method for estimation of hydraulic properties of sandy soils[J]. Engineering Geology, 2018, 246: 288-292. doi: 10.1016/j.enggeo.2018.09.031
[14]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Estimation of air permeability from soil-water characteristic curve[J]. Canadian Geotechnical Journal, 2019, 56(4): 505-513. doi: 10.1139/cgj-2017-0579
[15]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Uncertainty in the estimation of hysteresis of soil-water characteristic curve[J]. Environmental Geotechnics, 2019, 6(4): 204-213. doi: 10.1680/jenge.17.00008
[16]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Effect of bimodal soil-water characteristic curve on the estimation of permeability function[J]. Engineering Geology, 2017, 230: 142-151. doi: 10.1016/j.enggeo.2017.09.025
[17]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Effects of residual suction and residual water content on the estimation of permeability[J]. Geoderma, 2017, 303: 165-177. doi: 10.1016/j.geoderma.2017.05.019
[18]	ZHAI Q, RAHARDJO H, SATYANAGA A, et al. Variability in unsaturated hydraulic properties of residual soil in Singapore[J]. Engineering Geology, 2016, 209: 21-29. doi: 10.1016/j.enggeo.2016.04.034
[19]	ZHAI Q, RAHARDJO H. Estimation of permeability function from the Soil-Water Characteristic Curve[J]. Engineering Geology, 2015, 199: 148-156. doi: 10.1016/j.enggeo.2015.11.001
[20]	DIAMOND S. Pore size distributions in clay[J]. Clays & Clay Minerals, 1970, 18: 7-23.
[21]	FREDLUND D G, XING A. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(3): 521-532.
[22]	陈正汉. 重塑非饱和黄土的变形、强度、屈服和水量变化特性[J]. 岩土工程学报, 1999, 21(1): 82-90. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC901.016.htm CHEN Zheng-han. Deformation, strength, yield and moisture change of a remolded unsaturated loess[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(1): 82-90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC901.016.htm
[23]	黄海, 陈正汉, 李刚. 非饱和土在P-S平面上的屈服轨迹及土–水性特征曲线的探讨[J]. 岩土力学, 2000, 21(4): 316-321. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200004002.htm HUANG Hai, CHEN Zheng-han, LI Gang. A study on yield locus of unsaturated soils on p-s plane and soil-water characteristic curve[J]. Rock and Soil Mechanics, 2000, 21(4): 316-321. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200004002.htm
[24]	方祥位, 陈正汉, 孙树国, 等. 剪切对非饱和土土水特征曲线影响的研究[J]. 岩土力学, 2004, 25(9): 1451-1454. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX20040900N.htm FANG Xiang-wei, CHEN Zheng-han, SUN Shu-guo, et al. A study on effect of shear on soil-water characteristic curve of an unsaturated soil[J]. Rock and Soil Mechanics, 2004, 25(9): 1451-1454. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX20040900N.htm
[25]	章峻豪, 陈正汉. 南水北调中线工程安阳段渠坡换填土广义土–水特征曲线的试验研究[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3987-3994. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2123.htm ZHANG Jun-hao, CHEN Zheng-han. Test research on generalized SWCC for the backfill soil of the canal slope in Anyang district of South-to-North Water Diversion Project[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3987-3994. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2123.htm
[26]	MENDES J D, TOLL G. Influence of initial water content on the mechanical behavior of unsaturated sandy clay soil[J]. Int J Geomech, 2016, 16(6): D4016005. doi: 10.1061/(ASCE)GM.1943-5622.0000594
[27]	WIJAYA M, LEONG E C. Modelling the effect of density on the unimodal soil-water characteristic curve[J]. Géotechnique, 2017, 67(7): 637-645.
[28]	GAO Y, SUN D A, ZHU A C, et al. Hydromechanical behavior of unsaturated soil with different initial densities over a wide suction range[J]. Acta Geotechnica, 2019, 14: 417-428.
[29]	MILINGTON R J, QUIRK J P. Permeability of porous media[J]. Nature, 1961, 183: 387-388.
[30]	MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resour Res, 1976, 12(3): 513-522.
[31]	TULLER M, OR D. Retention of water in soil and soil-water characteristic curve[J]. Encyclopedia of Soils in the Environment, 2004(4): 278-289.
[32]	PLASTER E J. Soil Science and Management[M]. Clifton Park, NY: Delmar, 2009.
[33]	PEPPER I L, GERBA C P, GENTRY T J, et al. Environmental Microbiology[M]. 2nd ed. Pittsburgh: Academic Press, 2009.
[34]	THU T M, RAHARDJO H, LEONG E C, et al. Critical state behavior of a compacted silt specimen[J]. Soils and Foundations, 2007, 47(4): 749-755.
[35]	THU T M, RAHARDJO H, LEONG E C, et al. Soil–water characteristic curve and consolidation behavior for a compacted silt[J]. Can Geotech J, 2008, 44: 266-275.
[36]	LEE I M, SUNG S G, CHO G C, et al. Effect of stress state on the unsaturated shear strength of a weathered granite[J]. Canadian Geotechnical Journal, 2005, 42(2): 624-631.
[37]	VANAPALLI S K, FREDLUND D G, PUFAHL D E, et al. Model for the prediction of shear strength with respect to soil suction[J]. Can Geotech J, 1996, 33: 379-392.
[38]	陈正汉, 郭楠. 非饱和土与特殊土力学及工程应用研究的新进展[J]. 岩土力学, 2019, 40(1): 1-54. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901002.htm CHEN Zheng-han, GUO Nan. New developments of mechanics and application for unsaturated soils and special soils[J]. Rock and Soil Mechanics, 2019, 40(1): 1-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201901002.htm

施引文献(40)

期刊类型引用(25)

1.	GUO Fei，XU Zhizhen，HU Jilei，DOU Jie，LI Xiaowei，YI Qinglin. Forecasting step-like landslide displacement through diverse monitoring frequencies. Journal of Mountain Science. 2025(01): 122-141 . 必应学术
2.	周一骥，党超，王建平，马思哲. 陡倾片麻岩滑坡影响因素分析——以兰陵溪滑坡为例. 三峡大学学报(自然科学版). 2025(02): 41-47 . 百度学术
3.	张家旭，易庆林，邓茂林，安知利，彭云飞，雷玉. 三峡库区三门洞滑坡复活机理及韧性变形研究. 人民长江. 2024(04): 160-168 . 百度学术
4.	范大波. 三峡库区香溪河流域滑坡类型及发育规律. 科技通报. 2024(04): 15-19+25 . 百度学术
5.	汪标，易庆林，邓茂林，童权，刘开心. 基于累积位移特征与时间序列组合模型的滑坡位移预测. 工程地质学报. 2024(05): 1629-1639 . 百度学术
6.	明成涛，张晶鑫，郭飞. 基于Massflow的三峡库区堆积层滑坡运动特性研究. 水利水电技术(中英文). 2024(S2): 678-684 . 百度学术
7.	汪标，易庆林，邓茂林，童权，刘开心. 降雨与库水作用下谭家河滑坡变形响应规律分析. 人民长江. 2023(04): 141-149 . 百度学术
8.	王国法，邓茂林，周露露，董汉青. 三峡库区白家包滑坡变形机理与预警模型研究. 三峡大学学报(自然科学版). 2023(04): 45-53 . 百度学术
9.	柯唯，杨亮. 库水下降条件下靠椅形滑坡的变形规律和稳定性. 陕西水利. 2023(06): 15-18 . 百度学术
10.	李忠文，李俊峰，张小琼，杨宇驰，周平根，韩冰. 大渡河瀑布沟水库红岩子滑坡变形特征与机理分析. 中国地质灾害与防治学报. 2023(04): 1-10 . 百度学术
11.	易庆林，汪标，邓茂林，童权，刘开心，张家旭，赖雪梅. 三峡库区降雨抬升地下水诱发滑坡变形特征及机理研究. 三峡大学学报(自然科学版). 2023(05): 105-115 . 百度学术
12.	周露露，邓茂林，易庆林，王国法，梁之康，万航. 三峡库区卧沙溪次级滑体变形机理与阈值研究. 地震工程学报. 2023(05): 1125-1132 . 百度学术
13.	汪标，易庆林，牛岩，邓茂林，童权，刘开心. 地下水动态作用下大型碎裂顺层岩质滑坡变形响应规律分析. 岩石力学与工程学报. 2023(S2): 4140-4151 . 百度学术
14.	朱智杰，卢书强，梅军. 基于有效降雨量的滑坡位移-降雨相关性研究. 长江科学院院报. 2023(12): 162-168+187 . 百度学术
15.	何伟，吴冠仲，范宣梅，王文松，柳杨. 水库淹没区岩土体文物遗址保护方案研究——以皎平渡山洞遗址为例. 成都理工大学学报(自然科学版). 2023(06): 734-743+755 . 百度学术
16.	刘清，甘建军，陈浩，李小明，徐仁山. 持续降雨下阳高山滑坡变形机理与稳定性分析. 南昌工程学院学报. 2023(06): 52-58 . 百度学术
17.	张翔宇，孟永东，蔡征龙，田斌，程祥，秦毅. 基于北斗短报文通讯和物联网的滑坡监测系统研究. 地球物理学进展. 2022(02): 911-919 . 百度学术
18.	ZHANG Fu-ling，DENG Mao-lin，YI Qing-lin，LU Shu-qiang，ZHENG Wei-jun，HUANG Hai-feng，ZHU Xing. Deformation characteristics and thresholds of the Tanjiawan landslide in the Three Gorges Reservoir Area, China. Journal of Mountain Science. 2022(05): 1370-1385 . 必应学术
19.	尚敏，熊德兵，张惠强，赵国飞. 基于时间序列与混合核函数SA-SVR的滑坡位移预测模型研究. 工程地质学报. 2022(02): 575-588 . 百度学术
20.	张海艳，简文星，杨涛，杨新志，沈铭，李喜. 降雨作用下三峡库区秭归谭家湾滑坡监测预警研究. 安全与环境工程. 2022(04): 129-138 . 百度学术
21.	杨玲，魏静，许子伏. 基于平滑先验法-麻雀搜索算法-支持向量机回归模型的滑坡位移预测——以三峡库区八字门和白水河滑坡为例. 地球科学与环境学报. 2022(06): 1096-1110 . 百度学术
22.	张富灵，邓茂林，周剑，李卓骏，林琰. 长江三峡库区谭家湾滑坡基本变形特征及机理分析. 长江科学院院报. 2021(01): 78-83 . 百度学术
23.	胡国平，周清勇，刘智，熊磊. 某水利枢纽近坝库岸滑坡体稳定分析及评价. 水电与新能源. 2021(03): 39-42+46 . 百度学术
24.	李高，谭建民，王世梅，林旭，陈勇，王力，郭飞. 滑坡对降雨响应的多指标监测及综合预警探析：以赣南罗坳滑坡为例. 地学前缘. 2021(06): 283-294 . 百度学术
25.	梁宇，严磊，苏培东，邱鹏，龙伟，汪意凌. 溪洛渡库区河口滑坡变形特征和形成机制. 科学技术与工程. 2021(34): 14500-14507 . 百度学术