Application of numerical manifold method in crack propagation
-
摘要: 针对传统的断裂准则难以模拟混合型多裂纹扩展问题,在已有数值流形法程序基础上,对已有的裂纹扩展准则进行改进使数值流形法能够适应于多种类型裂纹扩展模拟。研究中以莫尔–库仑准则和最大周向应力准则为基础,将二者结合确定裂纹扩展方向。采用C语言开发相应计算程序计算了半圆盘拉伸试验和四点双边剪切试验,数值模拟和试验结果的裂纹扩展路径一致,并且裂纹能够穿过流形单元内部。随后模拟了重力坝开裂问题,发现重力坝开裂主要是拉伸破坏,并且裂纹扩展路径与有限元结果近似。最后通过模拟边坡滑移问题,计算结果与DEM和其他方法对比具有高度一致性。结果不仅验证了提出的强度准则在模拟各类型的裂纹扩展问题是有效的,同时为NMM模拟工程实际问题打下基础。Abstract: In order to solve the problem that the traditional fracture criterion is difficult to simulate the mixed multi-crack propagation, based on the existing numerical manifold method program, the existing crack propagation criterion is improved so that the numerical manifold method can be adapted to the simulation of various types of crack propagation. Based on the Mohr-Coulomb criterion and the maximum circumferential stress criterion, the crack propagation direction is determined by combining the two criteria. The corresponding program developed by C language is used to calculate the half disk tensile tests and four-point bilateral shear tests. The crack propagation paths of the numerical simulation and test results are consistent, and the crack can pass through the interior of manifold element. Subsequently, the cracking problem of gravity dams is simulated, and it is found that the cracking of gravity dams is mainly tensile failure, and the crack propagation path is similar to the finite element results. Finally, by simulating the slope slip problem, the calculated results are highly consistent with those by DEM and other methods. The results of this study verify the effectiveness of the proposed strength criterion in simulating various types of crack propagation problems and lay a foundation for NMM to simulate practical engineering problems.
-
Keywords:
- numerical manifold method /
- crack propagation /
- stretching /
- shear /
- slope
-
0. 引言
中国是一个水资源严重短缺的国家,且水资源时空分布不均,呈现出南丰北缺、东多西少的显著特点。为了调节水资源的地域分布,国家相继修建了一大批长距离调水工程[1]。其中,北疆输水渠道缓解了乌鲁木齐、克拉玛依等地区水资源短缺的问题,是名副其实的生命线工程[2]。
北疆输水渠道为季节性供水,在渠道渗漏的区域,渠基土会经历“湿干”循环；北疆冬季气温低,最低温度可达-20℃,渠基土会经历“冻融”循环[3-4]。渠道多年运行结果表明,膨胀土渠段滑坡频发,每年需要耗费大量的人力物力进行维修,主要原因在于膨胀性渠基土性质不稳定,在“湿干”循环、“冻融”循环作用下强度衰减,最终导致滑坡[5-7]。为了解决这一难题,建管部门对渠道进行了改造,主要包括如下两条改造措施：①对渠坡的膨胀土进行换填,表层换为0.5 m厚碎石层,中间层为1.5 m厚白砂岩,内部依然为膨胀土；②在渠底设置排水设施,先将渠道渗漏的水集中到渠底,然后通过渠道沿线布置的竖向排水井进行抽排,避免渗水堆积造成对渠基土的劣化。
渠道改造前后,渠坡稳定性是否得到显著提高,目前尚无系统研究。首先,根据监测资料,改造前渠基土每年都会经历明显的干湿循环作用,导致渠道内部的膨胀土强度发生不可逆转的衰减,引起边坡稳定性系数的下降。其次,渠道在供水末期水位逐渐降低至0,在水位下降过程中,渠坡稳定性如何变化,是需要探索的问题。最后,渠道改造前大多数断面都存在不同高度的膜后水,改造后设置了排水系统,需要考察膜后水的存在对于渠坡稳定性的影响。
基于此,本文首先白砂岩开展了系列室内试验研究,测试了其强度指标在“干湿”循环、“冻融”循环条件下的变化规律,在此基础上分析了渠道改造措施对渠坡稳定性的影响,为渠道的建设和管理提供参考。
1. 渠基土的强度特性
1.1 渠道换填改造方案
渠道换填之前,渠道总高度为7.5 m,上层为1.9 m厚白砂岩,下部都为膨胀土,典型断面如图1（a）所示。由于渠水入渗导致膨胀土强度衰减,渠道滑坡时有发生,因此,管理部门对渠坡进行了改造。主要包括两条措施：①将渠坡表层膨胀土置换为0.5 m厚碎石层和1.5 m厚白砂岩,如图1（b）所示。②在渠底设置排水设施,及时对渗水进行抽排,避免渗水堆积造成对渠基土的劣化,如图1（b）所示。
1.2 膨胀土强度特性
在室内单元试验中,“湿润”阶段是在常温下将初始状态的试样装在三瓣模中抽气饱和2 h,再浸泡12 h使试样达到饱和状态；“干燥”阶段为了使试样快速达到含水率wD（渠基土在自然风干状态下的含水率,约为最优含水率的0.7倍）,采用在温度设定为60℃的烘箱中烘干,通过实时监测含水率实现；“冻结”阶段则以-20℃冻结为准,-20℃基本可以反映北疆地区冬季的平均温度；“融化”阶段以20℃状态下自然融化24 h为标准。则“湿干冻融”4个阶段的边界条件如表1所示。
表 1 湿干冻融边界条件Table 1. Conditions of wetting-drying and freeze-thaw cycle状态 温度 时间 湿润 常温 抽气饱和 干燥 60℃ 至含水率wD为止 冻结 -20℃ 24 h 融化 20℃ 24 h 朱洵等[3],蔡正银等[4]对膨胀土开展了“湿干”循环和“湿干冻融”循环下的三轴试验,以干密度1.48 g/cm3,最优含水率24.1%的土样为例,得到抗剪强度指标c,φ值与循环次数N的关系为[3-4]
cWD=17.64+4.4⋅e−2.04N, (1) cWDFT=12.79+8.77⋅e−1.27N, (2) φ=11.51+3.33⋅e−0.39N, (3) 式中,
cWD 为“湿干”循环下的黏聚力（kPa）,cWDFT 为“湿干冻融”循环下的黏聚力（kPa）,φ为“湿干”循环或“湿干冻融”循环下的内摩擦角。根据式（1）～（3）绘制了膨胀土在“湿干”循环和“湿干冻融”循环下c,φ值的衰减曲线,如图2所示。由图2可得,膨胀土c,φ值在“湿干”循环或“湿干冻融”循环5次后基本衰减到稳定状态。其中,“湿干冻融”循环下的黏聚力c值由22 kPa衰减至13 kPa左右,“湿干”循环下的黏聚力c值由22 kPa衰减至18 kPa左右；“湿干”循环与“湿干冻融”循环下的φ值衰减规律相同,由15°衰减至12°。
对渠道稳定性进行计算时,膨胀土的强度参数c,φ值根据所处的环境,按照式（1）～（3）进行折减,自然密度为1.84 g/cm3,饱和密度为1.92 g/cm3。
1.2 白砂岩强度特性
笔者先后从不同的料场采集了两批白砂岩土样,编号分别为#1白砂岩和#2白砂岩,主要区别在于细粒含量不同,如表2所示,#1白砂岩细粒含量为30.1%,#2白砂岩细粒含量为20.1%。
表 2 #1和#2白砂岩的粒组含量Table 2. Granular content of white sandstones No.1 and No. 2土料 细砾含量(5~2 mm) 砂粒含量(2~0.075 mm) 细粒含量(<0.075 mm) #1白砂岩 4.7 65.2 30.1 #2白砂岩 4.0 75.9 20.1 #1白砂岩开展了普通三轴CD试验,得到的强度参数值如表3所示。制样压实度由88.4%增大到96.%时,黏聚力c由12 kPa增大到40 kPa；内摩擦角φ则基本不变,为32°左右。
表 3 #1白砂岩的抗剪强度值Table 3. Strength values of white sandstone No. 1试样状态 制样干密度（压实度）/% c/kPa φ/(°) 普通状态 88.4 12 31.8 普通状态 90.9 18 32.0 普通状态 93.4 30 31.9 普通状态 96.0 41 32.0 #1白砂岩开展了干湿、冻融循环下的三轴CD试验,具体操作是先根据表1中的边界条件将试样养护至预定循环次数,然后再进行三轴加载剪切。得到的强度参数c,φ值与循环次数N的关系如表4所示。
表 4 干湿循环、冻融循环条件下#2白砂岩的强度值Table 4. Strength values under wetting-drying cycle and freeze-thaw cycle试样状态 试样编号 c/ kPa φ/(°) 普通状态 Y1-1 3.9 33.2 干湿循环1次 W1-1 4.7 33.6 干湿循环1次 W1-2 2.0 31.9 干湿循环3次 W3-1 3.9 31.8 干湿循环3次 W3-2 9.2 32.3 干湿循环7次 W7-1 5.1 33.2 干湿循环7次 W7-2 3.2 32.5 冻融循环1次 F1-1 3.7 33.1 冻融循环1次 F1-2 6.0 33.4 冻融循环3次 F3-1 0.5 32.8 冻融循环3次 F3-2 8.9 31.4 冻融循环7次 F7-1 1.0 33.0 冻融循环7次 F7-2 5.4 32.9 注： 进行了平行试验,试样编号-1和-2表示的平行试样。两批土料的物理性质相近,但是,由于#2白砂岩的细颗粒含量更低,为20.1%,低于#1白砂岩的30.1%。因此,三轴CD试验结果表明,#2白砂岩的黏聚力c显著低于#1白砂岩。其中#1白砂岩的压实度都为95%,普通状态下（编号Y1-1）的c为3.9 kPa,内摩擦角为33.2°,如表4所示。对白砂岩试样分别进行1,3,7次干湿循环、冻融循环后,黏聚力c与干湿、冻融循环次数之间未呈现相关关系,甚至平行试验之间的差异都大于不同循环次数之间的差异；干湿循环、冻融循环下试样的内摩擦角φ则基本较为稳定,为32°左右。
综上所述,干湿循环、冻融循环条件下白砂岩的强度参数c,φ值与循环次数之间未呈现出明显的相关关系,即干湿循环、冻融循环对白砂岩的强度影响不大。因此,利用白砂岩进行换填,可以认为白砂岩的强度不会随着渠道运行年份而改变。
对渠道稳定性进行计算时,综合两种白砂岩土料试验所得的c值范围为0～40 kPa,将计算的c值取平均值,为20 kPa；白砂岩的φ较为稳定,定为φ=32°；自然密度为1.89 g/cm3,饱和密度为2.13 g/cm3。
2. 渠坡稳定性
2.1 计算方案
渠坡稳定性计算采用有限元强度折减法[8],渠道断面有限元网格如图3所示。计算中基本假设如下：
（1）实际监测结果表明,北疆渠道冻深在2 m以内,因此,2 m深度以内的土体才会经历“冻融”循环,该区域内的土体所采用的强度参数为“冻融”循环作用下的强度参数。
（2）若渠道发生渗漏,防渗膜后浸润线以下的饱和区域会经历“湿干”循环,该区域内的土体所采用的强度参数为“湿干”循环作用下的强度参数。
（3）同时满足（1）和（2）的区域土体会经历“湿干冻融”循环,所采用的土体强度参数为“湿干冻融”循环作用下的强度参数。
（4）若膜后水位为0,即渠道没有发生渗漏,渠基土没有经历“湿干”循环作用；土体没有水分补充,则“冻融”作用的影响也较小。因此,膜后水位为0,渠道土体都采用N=0时的强度参数。
计算主要涉及3种土料,白砂岩的强度参数为c=20 kPa,φ=32°,自然密度为1.89 g/cm3,饱和密度为2.13 g/cm3。砂砾石的初始强度参数为c=0 kPa,φ=40°,自然密度为2.30 g/cm3,饱和密度为2.53 g/cm3。膨胀土的强度参数随着工况的变化而变化,按照式（1）～（3）确定,自然密度为1.84 g/cm3,饱和密度为1.92 g/cm3。
实践表明,退水时为渠坡稳定最危险工况,此时渠水快速降低至0,但渗漏区域的膜后水位并未消散。因此,渠坡稳定性计算选择的工况为渠水位为0,计算年份为0～5 a,膜后水位高度为0～5 m,综合不同运行年数和不同膜后水位高度,共产生6×6=36种典型工况,并分别计算了改造前和改造后不同工况下的渠坡稳定性系数,如表5,6所示。
表 5 渠道换填前各工况下渠坡稳定性系数Table 5. Stability of canals under various conditions before reconstructionN/次 膜后水位 0 m 1 m 2 m 3 m 4 m 5 m 0 1.78 1.73 1.67 1.61 1.56 1.50 1 1.78 1.49 1.43 1.38 1.33 1.28 2 1.78 1.42 1.37 1.31 1.27 1.22 3 1.78 1.39 1.34 1.29 1.24 1.19 4 1.78 1.37 1.32 1.28 1.23 1.18 5 1.78 1.35 1.31 1.26 1.22 1.17 注： N表示循环次数,一年表示渠基土经历一次“湿干”、“冻融”或“湿干冻融”循环。表 6 渠道换填后各工况下渠坡稳定性系数Table 6. Stability of canals under various conditions after reconstructionN/次 膜后水位 0 m 1 m 2 m 3 m 4 m 5 m 0 1.82 1.76 1.71 1.65 1.60 1.53 1 1.82 1.56 1.51 1.46 1.39 1.35 2 1.82 1.51 1.46 1.41 1.36 1.31 3 1.82 1.48 1.44 1.39 1.34 1.29 4 1.82 1.47 1.42 1.38 1.33 1.28 5 1.82 1.46 1.41 1.37 1.32 1.27 以表5中N=0、膜后水位为0 m的工况为例,由强度折减法计算得到滑弧如图4（a）所示,滑弧由渠底贯通至渠顶。选取渠道现场典型滑坡断面,如图4（b）所示,滑坡从渠底贯通到渠顶马道,滑弧范围与有限元计算结果相匹配。由此可见,本文采取的计算方案是合理的。
《建筑边坡工程技术规范》（GB50330—2013）[9]规定,边坡稳定性状态分为稳定、基本稳定、欠稳定和不稳定4种状态,如表7所示。
表 7 边坡稳定性状态划分Table 7. Division of slope stability states稳定性系数Fs Fs<1.0 1≤Fs<1.05 1.05≤Fs<Fst Fs>Fst 稳定性状态 不稳定 欠稳定 基本稳定 稳定 注： Fst为边坡稳定安全系数,一级、二级和三级安全等级的永久边坡,一般工况对应的Fst分别为1.35,1.30,1.25。本计算边坡取Fst=1.35。若以Fs是否大于1.35来划分渠道是否稳定,由表5可见,在渠坡改造前,由17种工况下的渠坡Fs小于1.35,主要集中在膜后水位高、循环次数大的工况；表6可见,渠坡改造后,减小到只有7种工况下的渠坡Fs小于1.35。从这个角度分析,渠坡改造在一定程度上提高了渠道的稳定性。
2.2 膜后水位的影响
根据表5中渠坡改造前的计算结果,以N为0,1,2,5为例,绘制了Fs随膜后水位高度的变化曲线,如图5所示。
由图5可得,渠坡稳定性的变化规律受到膜后水位高度的显著影响,呈现如下3大特点：
（1）膜后水位为0的断面在多年运行期内的渠坡稳定性系数Fs保持不变,都为1.78,大于1.35,渠坡处于稳定状态。这是由于膜后水位为0,渠基土始终保持干燥状态,自重不变；且未经历干湿循环作用,强度指标不变,因此,渠坡稳定性系数不变。
（2）膜后水位为0～1 m的断面,在多年运行期内Fs大于1.35,渠坡处于基本稳定状态。
（3）膜后水位大于1 m的断面,经过多年运行以后,Fs会小于1.35大于1.05,渠坡处于基本稳定状态。
2.3 仅白砂岩换填
仅考虑白砂岩换填的影响,不考虑纵横向排水体系的作用,即相对于改造前只需要将换填层的计算参数进行修改,计算结果见表6。其中,以膜后水位为0,1,5 m时的工况为例,渠坡稳定性系数Fs与N的关系曲线如图6所示。
![]()
图 6 换填前后渠坡稳定性系数Figure 6. Stability coefficient of canals before and after replacement图6（a）表明,若渠道不发生渗漏,膜后水位为0,渠道换填后的Fs保持在1.82,相比于换填前的Fs=1.78,略有提高。图6（b）,（c）表明,在相同的膜后水位下,换填前和换填后的Fs都会随着N的增加而降低,在相同工况下,换填后的Fs都略高于换填前,平均约提高0.1。
由图6可见,仅换填对于渠坡稳定性系数Fs的提高效果并不明显。主要原因在于,换填的碎石层和白砂岩层,虽然强度性质较为稳定,不会随着“湿干”或“冻融”作用而衰减。但是,由图4（a）可见,滑弧是由渠底贯通到渠顶,主要穿过内部的膨胀土层,渠坡表层共2 m厚的换填层起到的抗滑作用较低。
2.4 白砂岩换填且渗水抽排
理论上讲,若渠道防渗体系完好,防渗膜后应当不存在水的集聚。然而,实际观测表明,一旦发生渗漏,渗漏水将会集聚在渠道防渗膜后。因此,在对北疆输水渠道进行改造时,除了对渠坡表层膨胀土进行换填之外,还在渠道设置了排水系统,将渗漏的渠水及时抽排,降低渗漏水位,减小甚至杜绝渗水对渠基土强度的衰减作用。
根据监测资料,2017年运行期内膜后水位在2 m以上的断面占比较大,断面最高水位几乎与同时刻渠道内运行水位相同。相比较而言,2018年在渠道运行期内加强了渗水抽排作业,抽排效果显而易见,监测结果表明运行期间膜后水位相比去年同期有着较大程度的下降,膜后水位多集中在2 m以下。以里程为10～18 km渠段为例,对2017年和2018年膜后水位监测结果进行对比,如图7所示。2017年渠道沿线膜后水位大都在2～5 m；2018年加强渗水抽排作业以后,膜后水位基本都降低到2 m以内,其中,约一半的井点降低到了1 m以内。
![]()
图 7 2017年和2018年膜后水位监测结果Figure 7. Monitoring results of post-membrane water level in 2017 and 2018以表5,6中的结果为依据,若换填后经过渗水抽排作业,将膜后水位保持在2 m以下,如图8（a）所示,经过多年运行,渠坡稳定性系数Fs都保持在1.41以上,大于1.35,渠坡处于稳定状态。若渗水抽排能保持膜后水位在1 m以下,如图8（b）所示,经过多年运行后,Fs都保持在1.46以上,大于1.35,渠坡处于稳定状态。相反,在渠道改造前渠底没有设置排水系统,膜后渗水无法排出,膜后水位的可能高度范围为0～5 m,由图8可见,渠坡改造前只要出现膜后水位,即便膜后水位仅为1 m,经过多年运行以后Fs也会低于1.35,渠坡将处于欠稳定状态。
![]()
图 8 换填及渗水抽排后渠坡稳定性系数Figure 8. Coefficient of slope stability after filling replacement and drainage modification经过渠坡换填及渗水抽排改造,近几年运行结果表明,渠道滑坡显著减少。结合换填计算结果和渠道运行事实,渠道滑坡发生量减小、渠坡稳定性提高,主要是排水体系的作用,将渗水及时抽排,降低膜后水位,保障了渠道内部膨胀土性质不再劣化,显著提高了渠道的稳定性；相反,换填土体本身性质的改变对提高渠坡稳定性的作用有限。
3. 结论和建议
（1）白砂岩在干湿循环、冻融循环条件下,强度参数c值略有变化,φ值则基本保持在32°左右,因此,可以认为,白砂岩的强度基本不受干湿循环、冻融循环的影响。
（2）滑弧由渠底贯通到渠顶,主要穿过内部的膨胀土层,而膨胀土的性质会随着“湿干”循环而劣化,渠坡表层0.5 m厚的碎石和1.5 m厚的白砂岩换填层起到的抗滑作用较低。
（3）渠道改造后滑坡发生量减小、渠坡稳定性提高,主要是排水体系的作用,将渗水及时抽排,降低膜后水位,保障了渠道内部膨胀土性质不再劣化,显著提高了渠道的稳定性。
（4）为了保障渠道的长期稳定性,建议对渠道渗水进行持续抽排作业,将膜后水位控制在2 m以内。
-
![]()
图 5 半圆盘弯曲拉伸试验结果和NMM模拟对比
Figure 5. Comparison of bending tensile test results of half disc and NMM simulation
-
[1] ZHANG G X, SUGIURA Y, KOZO S. Failure simulation of foundation by manifold method and comparison with experiment[J]. Journal of Applied Mechanics, 1998(1): 427-436. http://www.onacademic.com/detail/journal_1000040291858710_fed7.html
[2] 陈远强, 杨永涛, 郑宏, 等. 饱和–非饱和渗流的数值流形法研究与应用[J]. 岩土工程学报, 2019, 41(2): 149-158. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902014.htm CHEN Yuan-qiang, YANG Yong-tao, ZHENG Hong, et al. Saturated-unsaturated seepage by numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 149-158. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902014.htm
[3] MA G, AN X, HE L E I. The numerical manifold method: a review[J]. International Journal of Computational Methods, 2010, 7(1): 1-32. doi: 10.1142/S0219876210002040
[4] 徐栋栋, 郑宏, 杨永涛. 线性无关高阶数值流形法[J]. 岩土工程学报, 2014, 36(3): 482-488. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403015.htm XU Dong-dong, ZHENG Hong, YANG Yong-tao. Linearly independent higher-order numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 482-488. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403015.htm
[5] 李伟, 郑宏. 基于数值流形法的渗流问题边界处理新方法[J]. 岩土工程学报, 2017, 39(10): 1867-1873. doi: 10.11779/CJGE201710015 LI Wei, ZHENG Hong. New boundary treatment for seepage flow problem based on numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1867-1873. (in Chinese) doi: 10.11779/CJGE201710015
[6] NING Y J, AN X M, MA G W. Footwall slope stability analysis with the numerical manifold method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(6): 964-975. doi: 10.1016/j.ijrmms.2011.06.011
[7] WU Z, WONG L N Y. Frictional crack initiation and propagation analysis using the numerical manifold method[J]. Computers and Geotechnics, 2012, 39: 38-53. doi: 10.1016/j.compgeo.2011.08.011
[8] TI K S, HUAT B B, NOORZAEI J, et al. A review of basic soil constitutive models for geotechnical application[J]. Electronic Journal of Geotechnical Engineering, 2009, 14: 1-18.
[9] HACKSTON A, RUTTER E. The Mohr–Coulomb criterion for intact rock strength and friction – a re-evaluation and consideration of failure under polyaxial stresses[J]. Solid Earth, 2016, 7(2): 493-508. doi: 10.5194/se-7-493-2016
[10] AN X, NING Y, MA G, et al. Modeling progressive failures in rock slopes with non-persistent joints using the numerical manifold method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(7): 679-701. doi: 10.1002/nag.2226
[11] XU Y, DAI F, XU N W, et al. Numerical investigation of dynamic rock fracture toughness determination using a semi-circular bend specimen in split hopkinson pressure bar testing[J]. Rock Mechanics and Rock Engineering, 2015, 49(3): 731-745.
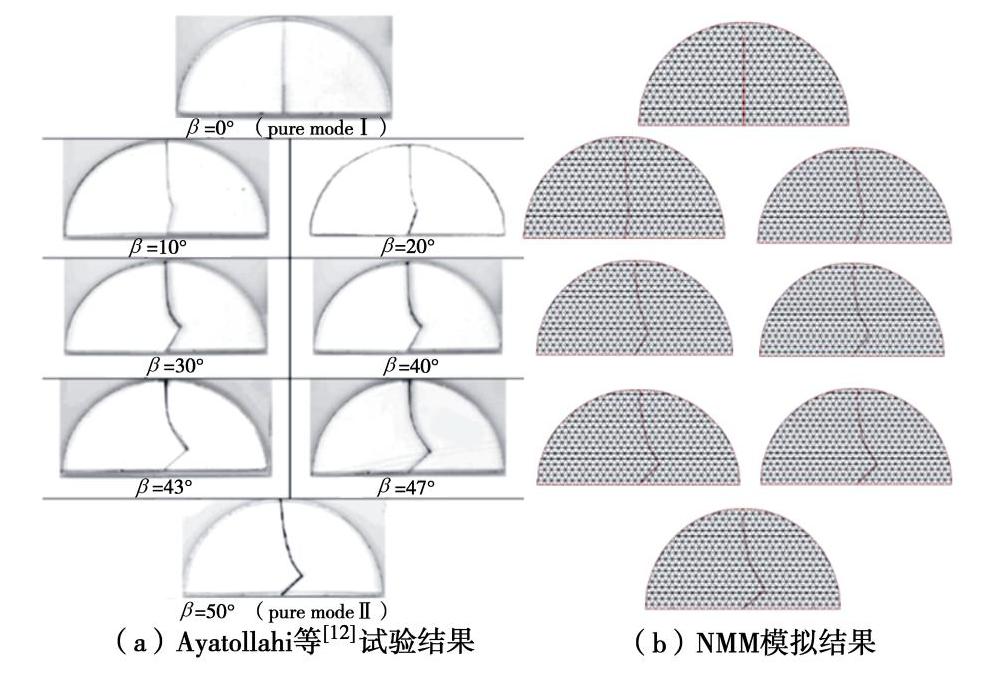
[12] AYATOLLAHI M R, ALIHA M R M, HASSANI M M. Mixed mode brittle fracture in PMMA—An experimental study using SCB specimens[J]. Materials Science and Engineering: A, 2006, 417(1/2): 348-356.
[13] XIE Y, CAO P, JIN J, et al. Mixed mode fracture analysis of semi-circular bend (SCB) specimen: A numerical study based on extended finite element method[J]. Computers and Geotechnics, 2017, 82: 157-172. doi: 10.1016/j.compgeo.2016.10.012
[14] BERGARA A, DORADO J I, MART N-MEIZOSO A, et al. Fatigue crack propagation in complex stress fields: experiments and numerical simulations using the extended finite element method (Xfem)[J]. International Journal of Fatigue, 2017, 103: 112-121. doi: 10.1016/j.ijfatigue.2017.05.026
[15] LANG C, MAKHIJA D, DOOSTAN A, et al. A simple and efficient preconditioning scheme for heaviside enriched XFEM[J]. Computational Mechanics, 2014, 54(5): 1357-1374. doi: 10.1007/s00466-014-1063-8
[16] BOCCA P, CARPINTERI A, VALENTE S. Size effects in the mixed mode crack propagation: softening and snap-back analysis[J]. Engineering Fracture Mechanics, 1990, 35(1): 159-170.
[17] GEERS M G D, BORST R D, PEERLINGS R H J. Damage and crack modeling in single-edge and double-edge notched concrete beams[J]. Engineering Fracture Mechanics, 2000, 65(2/3): 247-261.
[18] ZHU W C, TANG C A. Numerical simulation on shear fracture process of concrete using mesoscopic mechanical model[J]. Construction & Building Materials, 2002, 16(8): 453-463.
[19] OLIVER J, HUESPE A E, SAMANIEGO E, et al. Continuum approach to the numerical simulation of material failure in concrete[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2004, 28: 609-632.
[20] DIAS I F, OLIVER J, LEMOS J V, et al. Modeling tensile crack propagation in concrete gravity dams via crack-path-field and strain injection techniques[J]. Engineering Fracture Mechanics, 2016, 154: 288-310. doi: 10.1016/j.engfracmech.2015.12.028
[21] ROTH S-N, L GER P, SOULA MANI A. A combined XFEM-damage mechanics approach for concrete crack propagation[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 923-955.
[22] CAMONES L A M, VARGAS E D A, DE FIGUEIREDO R P, et al. Application of the discrete element method for modeling of rock crack propagation and coalescence in the step-path failure mechanism[J]. Engineering Geology, 2013, 153: 80-94.
[23] LI T, PENG Y, ZHU Z, et al. Discrete element method simulations of the inter-particle contact parameters for the mono-sized iron ore particles[J]. Materials, 2017, 10(5): 520.
[24] WONG L N Y, WU Z. Application of the numerical manifold method to model progressive failure in rock slopes[J]. Engineering Fracture Mechanics, 2014, 119: 1-20.
-
期刊类型引用(6)
1. 张德沧，毛佳，戴妙林，邵琳玉，赵兰浩. 圆化离散单元法的改进及其在岩体断裂过程中的应用. 岩土工程学报. 2024(09): 1974-1983 . 
本站查看
2. 何荣兴，张智源，张星宇，章雅雯. 诱导下岩体裂隙扩展规律研究存在问题及对策. 中国矿业. 2024(10): 168-176 . 百度学术
3. 刘洋，吴志军，储昭飞，翁磊，徐翔宇，周原，高波，毛春光. 基于FDEM的围压条件下机械冲击破岩机理研究. 中南大学学报(自然科学版). 2023(03): 866-879 . 百度学术
4. 杨奎斌，朱彦鹏. 考虑后缘裂缝影响的均质土坡滑动面形式及搜索研究. 应用基础与工程科学学报. 2022(05): 1216-1227 . 百度学术
5. 张亚军，莫思阳，张友良. 基于修正牛顿-拉普森迭代的数值流形法. 计算机仿真. 2022(09): 394-397+440 . 百度学术
6. 韩笑. 基于高阶块体元-有限元建模的混凝土细观数值分析. 粉煤灰综合利用. 2021(03): 56-63 . 百度学术
其他类型引用(7)
下载:
计量
- 文章访问数: 297
- HTML全文浏览量: 23
- PDF下载量: 91
- 被引次数: 13
