微生物处理砂土不排水循环三轴剪切CFD-DEM模拟

蒋明镜; 孙若晗; 李涛; 杨涛; 谭亚飞鸥

doi:10.11779/CJGE202001002

微生物处理砂土不排水循环三轴剪切CFD-DEM模拟 English Version

蒋明镜^{1, 2, 3, 4, 5,},
孙若晗^{1, 2},
李涛^{1, 2},
杨涛⁵,
谭亚飞鸥⁵

1.
天津大学建筑工程学院土木系,天津300072
2.
天津大学水利工程仿真与安全国家重点试验室,天津300072
3.
同济大学土木工程防灾国家重点试验室,上海200092
4.
同济大学土木工程学院地下建筑与工程系,上海200092
5.
上海理工大学环境与建筑学院,上海200093

基金项目:

国家自然科学基金重大项目 51890911

国家自然科学基金重点项目 51639008

详细信息

作者简介:
蒋明镜（1965— ）,男,教授,博士生导师,国家杰出青年基金获得者,主要从事天然结构性黏土、砂土、非饱和土、太空土和深海能源土宏观微观试验、本构模型和数值分析研究工作。E-mail：mingjing.jiang@tju.edu.cn

中图分类号: TU43
计量
- 文章访问数: 1153
- HTML全文浏览量: 61
- PDF下载量: 753
出版历程
- 收稿日期: 2019-03-11
- 网络出版日期: 2022-12-07
- 刊出日期: 2019-12-31

CFD-DEM simulation of microbially treated sands under undrained consolidated cyclic triaxial tests

JIANG Ming-jing^{1, 2, 3, 4, 5,},
SUN Ruo-han^{1, 2},
LI Tao^{1, 2},
YANG Tao⁵,
TAN Ya-fei-ou⁵

1.
Department of Civil Engineering, School of Civil Engineering, Tianjin University, Tianjin 300072, China
2.
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
3.
State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
4.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
5.
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China

摘要

摘要: 微生物诱导碳酸钙沉积是一种新型的地基处理技术,处理后的土体可以看成一种结构性土。首先,在已有三维含颗粒抗转动和抗扭转模型及三维胶结破坏准则的基础上,通过考虑颗粒碰撞接触过程中颗粒本身的塑性变形及率相关性的接触黏滞阻尼,建立考虑循环荷载作用下的三维胶结模型；然后,参考已有研究,建立了反硝化反应在加固砂土中的时效性关系。并引入CFD-DEM耦合程序,用以模拟分析不同胶结含量以及不同气泡含量下,微生物处理砂土在固结不排水循环剪切试验中的力学特性；最后,从宏微观角度分析生物胶结与生物气泡对砂土抗液化性能的影响及其作用机理。研究表明,胶结和气泡共同存在对抗液化能力的提升并没有起到“1+1=2”的效果；胶结的存在提高了非饱和砂土的抗液化能力,明显抑制孔压比和轴向应变的发展,力学配位数得到了提升；而气泡的存在却降低了胶结砂土的抗液化能力,使得胶结砂土达到初始液化的振次减少,轴向应变向受拉方向大幅增长,力学配位数下降明显。
- 微生物诱导碳酸钙沉积 /
- CFD-DEM耦合 /
- 不排水循环三轴剪切 /
- 地基液化 /
- 离散单元法
Abstract: The microbially induced calcite precipitation is a promising technology to improve ground, and the treated soil can be regarded as the structural one. In this study, firstly, based on the three-dimensional (3D) contact model for granulates incorporating rolling and twisting resistances and 3D bonds failure criteria, and considering both the slight plastic deformation of particles during collisions and the rate-dependency, a cyclic bonded contact model is established. A time-dependent relationship is then proposed to describe the denitrification reaction in reinforced sand. Next, the mechanical responses of microbially treated sands at different cementation and bubble contents are investigated by the coupled CFD-DEM in undrained-consolidated cyclic triaxial tests. The effects of biological bond and biological bubbles on the liquefaction resistance of sands are analyzed in link with the mechanism from macroscopic and microscopic scales. The results show that the coexistence of cementation and bubble does not increase the liquefaction resistance as expected in the form of "1+1=2". The presence of cementation enhances the liquefaction resistance of unsaturated sands evidenced by the decrease of excess pore water pressure ratio and axial strain, and the increase of coordination number. However, the presence of bubbles reduces the liquefaction resistance of cemented sands, where the number of cycles to the initial liquefaction decreases, the axial strain increases significantly in the tensile direction, and the coordination number decreases significantly.
- microbially induced calcite precipitation /
- coupled CFD-DEM /
- undrained cyclic triaxial test /
- ground liquefaction /
- distinct element method

HTML全文

0. 引言

砂土液化是指土体在振动作用下,孔隙水压力上升,土颗粒受重力影响向下沉落,使土颗粒处于悬浮状态,导致土体抗剪强度完全消失的现象。砂土液化通常会引起建筑物基础的不均匀沉降及结构的破坏,甚至造成严重灾害和人员伤亡。沈珠江^[1]曾指出砂土液化理论是现代土力学三大问题之一。目前,改善地基抗液化能力主要有夯实压密地基的物理处理方法和使用人工化学材料的化学处理方法,但传统的物理、化学地基处理方法都存在许多弊端,例如能量效率低下和人工化学材料的环境污染等问题。而微生物岩土技术创造性的利用丰富的无毒害的微生物资源,通过改变不良岩土体微观结构与组成来改善其工程力学性质,其中,又以微生物诱导钙质胶结（microbially induced calcite precipitation,MICP）技术的研究最为广泛^[2-3]。

针对微生物岩土技术抗液化能力的研究,较多研究着重于生物胶结的作用。如Inagaki等^[4]对MICP胶结砂土进行了固结排水三轴压缩试验与离心机试验,结果表明微生物胶结砂土有更高的抗压强度,超静孔隙水压力更低,残余变形更小,而加速度响应更大。Han等^[5]对MICP胶结砂土的抗液化强度进行了动三轴试验研究,发现通过MICP注浆来提高抗液化强度是可行有效的。刘汉龙等^[6]通过动三轴试验和SEM微观结构试验,研究了不同胶结程度和不同动应力水平下的动强度、动变形、动孔压、有效应力路径的发展规律和MICP胶结的微观机理。结果表明MICP胶结的钙质砂动剪应力比和抵抗变形的能力明显提高。

在微生物处理过程中,不仅碳酸钙沉淀形成的胶结对抗液化性能有影响,产生的气泡同样可以提高土体的抗液化能力。气泡提高土体抗液化强度的机理在于气泡的存在可以降低土体的饱和度,土体中含气泡的孔隙流体压缩性大大提高,使得在不排水过程中孔隙流体压力上升缓慢,最终导致土体抗液化强度的提升。Rebeta-Landa等^[7]通过多组室内试验观察表明生物气泡可以有效降低土体的剪切刚度,提高抗液化能力。He^[8]对使用生物气泡防止液化进行了大量试验研究,结果表明：饱和度降低时,松砂的不排水抗剪强度会提高；当B值从0.95降到0.30时,抗剪强度在压缩试验中提高了2.1倍,在拉伸试验中提高了1.7倍。

然而,对于胶结和气泡共同作用对MICP砂土抗液化能力的影响还鲜有研究。因此,有必要定性定量地评价两种微生物处理作用对砂土抗液化能力的影响。

近年来,针对MICP胶结砂土抗液化能力的研究多通过室内试验进行分析。然而室内试验存在试样制取耗时长、成本高和重复性差上的不足,因此有必要采用数值模拟方法进行分析。离散单元法（distinct element method,DEM）^[9]是研究颗粒材料的数值方法,可以避开传统有限元方法所需要的复杂本构模型,通过建立颗粒之间的接触模型来反映土体的宏微观力学性质。Khoubani等^[10]对MICP胶结砂土进行了三轴试验DEM模拟。根据模拟得到的应力应变曲线,分析了胶结试样与无胶结试样的强度与刚度特性。Feng等^[11]运用三维离散元软件PFC^3D（particle flow code）模拟MICP胶结砂土的力学性质,分析了宏观力学响应并输出了部分微观信息。

计算流体动力学（computational fluid dynamics,CFD）是流体力学的一个分支,是用特定的数值方法和算法求解与流体流动相关的问题^[12]。CFD已被广泛应用于模拟空气流动^[13]和湍流^[14]等复杂流体问题并取得了丰硕成果,表明该程序能够正确地对流体进行模拟。

将DEM方法与CFD软件进行耦合,能够较好反映砂土液化过程中颗粒与孔隙水之间的相互作用,对于研究砂土液化现象有着独特的优势。Shamy等^[15]采用CFD-DEM耦合分析方法研究颗粒试样在受临界向上孔隙流体流动和基础动力激励时发生液化的微观机理,揭示了岩土颗粒材料液化和相应的刚度、强度丧失的微观力学机制。蒋明镜等^[16]在传统的CFD流体运动控制方程外又基于大量室内试验结果引入了考虑流体弱可压缩性的流体状态方程,建立了流体密度与压力时间的关系,利用FISH语言将CFD与PFC^2D离散元计算耦合起来,用以对饱和砂土的固结不排水剪切试验进行模拟。

本文在宏微观土力学^[17]研究思路框架内,首先在已有三维含颗粒抗转动和抗扭转模型及三维胶结破坏准则的基础上,通过考虑颗粒碰撞接触过程中颗粒本身的塑性变形及率相关性的接触黏滞阻尼,建立考虑循环荷载作用下的三维胶结模型,模型中胶结半径比例系数 $η$ 用以模拟生物胶结的影响；然后结合CFD-DEM耦合程序,进行循环三轴剪切试验模拟,其中流体压缩系数C用以描述生物气泡的影响。参考已有研究,通过 $η$ 和C建立反硝化反应在加固砂土中的时效性关系。最后通过跟踪试样的液化振次、孔压比、轴向应变和配位数在加载过程中的变化情况,从宏微观角度分析了不同胶结含量和气泡含量下微生物处理砂土的固结不排水循环剪切力学特性,探究生物胶结和生物气泡对砂土抗液化性能的影响及其作用机理,为未来推广微生物地基处理方法提供借鉴。

1. 接触模型介绍

本文接触模型是在本团队之前的三维含颗粒抗转动和抗扭转模型^[18]及三维胶结铝球试验^[19]的基础上,进一步考虑循环荷载对于MICP胶结砂土粒间胶结及颗粒接触力学特性的影响,提出的适用于研究MICP胶结砂土在循环荷载作用下的力学特性的三维离散元微观模型。其中,通过引入考虑率相关性的接触黏滞阻尼,加入了黏滞力项。此外,颗粒接触部分还考虑了循环荷载作用下颗粒在碰撞过程中的微小塑性变形。

1.1 力与位移法则

（1）颗粒部分

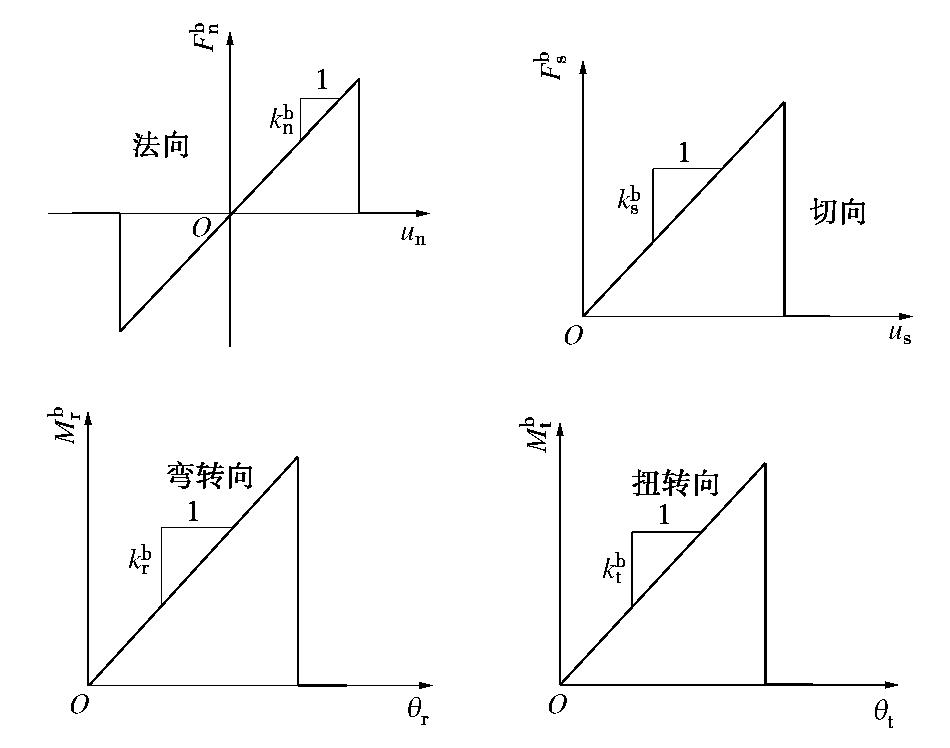
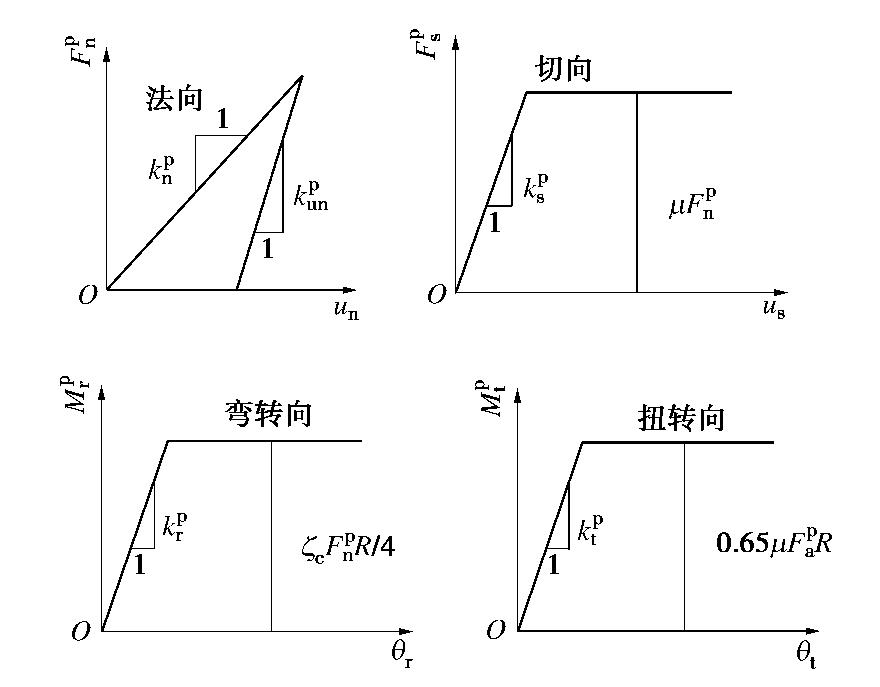
本文的三维离散元模型颗粒部分是在三维含颗粒抗转动和抗扭转模型^[18]基础上得到的。而为了考虑循环荷载作用下的微小塑性变形^[20],本文在法向接触分量采用线性滞回性接触模型,即加卸载刚度不同,这样可以考虑颗粒在循环荷载作用下碰撞产生的塑性变形耗散能。切向和转动向仍然采用理想弹塑性模型。颗粒部分的力学响应如图1所示。

图 1 颗粒部分的力学响应

Figure 1. Mechanical responses of contact between particles

下载: 全尺寸图片幻灯片

颗粒法向力采用全量法计算,如下式：

$F_{n} = k_{n}^{p} α,$

(1)

$F_{un} = k_{un}^{p} (α - α_{0}),$

(2)

式中, $k_{n}^{p}$ 为法向加载刚度, $k_{un}^{p}$ 为法向卸载刚度, $α$ 为颗粒法向重叠量, $α_{0}$ 为法向力卸载至0时的颗粒法向重叠量。加卸载刚度的比值记为 $e_{n}$ ：

$e_{n} = k_{n}^{p} / k_{un}^{p}$

(3)

颗粒切向接触力通过增量法计算（见式（4））,随着切向位移增加线性增长,当达到峰值时,切向力保持不变。

$F_{s}^{p} \leftarrow F_{s}^{p} + k_{s}^{p} Δ u_{s}^{p} F_{s}^{p} \leq μ F_{n}^{p},$

(4)

式中, $k_{s}^{p}$ 为颗粒接触的切向刚度, $Δ u_{s}^{p}$ 为单位时间的切向位移增量, $μ$ 为颗粒之间的摩擦系数。

颗粒弯转向接触弯矩通过增量法计算（见式（5））,随着弯转角的增加线性增长,当达到弯矩峰值时,弯矩保持不变。

$M_{r}^{p} \leftarrow M_{r}^{p} + k_{r}^{p} Δ θ_{r}^{p} M_{r}^{p} \leq ζ_{c} F_{n}^{p} \bar{R} / 4,$

(5)

式中, $k_{r}^{p}$ 为颗粒接触的弯转刚度, $Δ θ_{r}^{p}$ 为单位时间的弯转角增量, $ζ_{c}$ 为考虑颗粒局部破损的参数,取值范围为 $1 \leq ζ_{c} \leq 4$ , $\bar{R} = β R$ 为颗粒接触面半径, $β$ 为颗粒抗转动系数, $R$ 为颗粒接触的等效半径。

颗粒扭转向接触扭矩通过增量法计算（见式（6））,随着扭转角的增加线性增长,当达到扭矩峰值时,扭矩保持不变。

$M_{t}^{p} \leftarrow M_{t}^{p} + k_{t}^{p} Δ θ_{t}^{p} M_{t}^{p} \leq 0.65 μ F_{n}^{p} \bar{R},$

(6)

式中, $k_{t}^{p}$ 为颗粒接触的扭转刚度, $Δ θ_{t}^{p}$ 为单位时间的扭转角增量。

（2）胶结部分

类似于颗粒部分,胶结部分的力学响应可分为法向、切向、弯转向以及扭转向^[21]。图2为胶结部分在4个方向上的力与位移法则示意图。其中

图 2 胶结部分的力学响应

Figure 2. Mechanical responses of bond

下载: 全尺寸图片幻灯片

$F_{n}^{b} \leftarrow F_{n}^{b} + k_{n}^{b} Δ u_{n}^{b} (F_{n}^{b} \leq R_{n}^{b}),$

(7)

$F_{s}^{b} \leftarrow F_{s}^{b} + k_{s}^{b} Δ u_{s}^{b} (F_{s}^{b} \leq R_{s}^{b}),$

(8)

$M_{r}^{b} \leftarrow M_{r}^{b} + k_{r}^{b} Δ θ_{r}^{b} (M_{r}^{b} \leq R_{r}^{b}),$

(9)

$M_{t}^{b} \leftarrow M_{t}^{b} + k_{t}^{b} Δ θ_{t}^{b} (M_{t}^{b} \leq R_{t}^{b}) 。$

(10)

式中 $F_{n}^{b}$ , $F_{s}^{b}$ , $M_{r}^{b}$ , $M_{t}^{b}$ 分别为胶结法向力、切向力、胶结弯矩和扭矩, $k_{n}^{b}$ , $k_{s}^{b}$ , $k_{r}^{b}$ , $k_{t}^{b}$ 分别为胶结法向、切向、弯转向和扭转向刚度, $Δ u_{n}^{b}$ , $Δ u_{s}^{b}$ , $Δ θ_{r}^{b}$ , $Δ θ_{t}^{b}$ 分别为单位时间的胶结法向、切向位移增量,胶结弯转角度和扭转角度增量； $R_{n}^{b}$ 为胶结法向峰值荷载（包括胶结抗压强度 $R_{nc}^{b}$ 和胶结抗拉强度 $R_{nt}^{b}$ ）, $R_{s}^{b}$ , $R_{r}^{b}$ , $R_{t}^{b}$ 分别为胶结抗剪、抗弯和抗扭强度。

1.2 胶结强度准则

本文三维离散元模型胶结部分采用由金树楼^[19]通过试验提炼出的强度准则。

该胶结强度准则结合了简化椭圆公式与室内三维微观接触力学试验,认为胶结物的抗拉强度 $R_{nt}^{b}$ 、抗压强度 $R_{nc}^{b}$ 、抗剪强度 $R_{s}^{b}$ 、抗弯强度 $R_{r}^{b}$ 和抗扭强度 $R_{t}^{b}$ 分别为

$R_{nt}^{b} = 0.25 σ_{t} π B^{2},$

(11)

$R_{nc}^{b} = 0.25 σ_{c} π B^{2},$

(12)

$R_{s}^{b} = 0.145 \sqrt{{(R_{nt}^{b} + R_{nc}^{b})}^{2} - {(2 F_{n}^{b} - R_{nc}^{b} + R_{nt}^{b})}^{2}},$

(13)

$R_{r}^{b} = 0.175 R_{b} \sqrt{{(R_{nt}^{b} + R_{nc}^{b})}^{2} - {(2 F_{n}^{b} - R_{nc}^{b} + R_{nt}^{b})}^{2}},$

(14)

$R_{t}^{b} = 0.189 R_{b} \sqrt{{(R_{nt}^{b} + R_{nc}^{b})}^{2} - {(2 F_{n}^{b} - R_{nc}^{b} + R_{nt}^{b})}^{2}},$

(15)

式中, $B = 2 η \min [R_{1}, R_{2}]$ ,为胶结宽度,其中 $R_{1}$ , $R_{2}$ 分别为两个土颗粒的半径, $η$ 为胶结半径比例系数,取值范围为[0,1]。 $σ_{t}$ 和 $σ_{c}$ 分别为胶结的抗拉强度和抗压强度, $F_{n}^{b}$ 由式（7）得到。

式（11）～（15）中的强度表达式均为胶结在受单一方向上的荷载的峰值强度,实际情况中,胶结物的受力情况往往非常复杂。因此,基于室内复杂加载条件下的试验结果,构建了由峰值剪切荷载、弯矩、扭矩耦合控制的屈服面,且屈服面大小由法向力控制：

${(\frac{‖ F_{s}^{b} ‖}{R_{s}^{b}})}^{2} + {(\frac{‖ M_{r}^{b} ‖}{R_{r}^{b}})}^{2} + {(\frac{‖ M_{t}^{b} ‖}{R_{t}^{b}})}^{2} \leq 1 。$

(16)

1.3 接触黏滞阻尼

本文为考虑循环荷载下MICP胶结砂土的率相关性,在接触模型中加入黏滞阻尼。接触处的黏滞阻尼通过黏壶单元确定,同样可以分为法向、切向、弯转向和扭转向。其中,

$F_{n}^{v} = - c_{n} {\dot{u}}_{n} c_{n} = 2 β_{n} \sqrt{m k_{n}},$

(17)

$F_{s}^{v} = - c_{s} {\dot{u}}_{s}, c_{s} = 2 β_{s} \sqrt{m k_{s}},$

(18)

$M_{r}^{v} = - c_{r} {\dot{θ}}_{r} c_{r} = 0.25 c_{n} {\bar{R}}^{2},$

(19)

$M_{t}^{v} = - c_{t} {\dot{θ}}_{t} c_{t} = 0.5 c_{s} {\bar{R}}^{2} 。$

(20)

式中 $F_{n}^{v}$ , $F_{s}^{v}$ , $M_{r}^{v}$ , $M_{t}^{v}$ 分别代表法向、切向阻尼力,弯转向和扭转向阻尼力矩； $c_{n}$ , $c_{s}$ , $c_{r}$ , $c_{t}$ 分别为法向、切向、弯转向和扭转向黏滞系数； ${\dot{u}}_{n}$ , ${\dot{u}}_{s}$ , ${\dot{θ}}_{r}$ , ${\dot{θ}}_{t}$ 分别为法向、切向、弯转向和扭转向相对速度； $β_{n}$ , $β_{s}$ 分别为法向和切向临界阻尼比,m为接触的两个颗粒的等效质量。

了解详细的模型抽象过程、公式物理意义等可参考文献[18～22]。

2. CFD-DEM耦合计算

本文采用笔者团队^[23]开发的CFD-DEM耦合方法。与传统的流固耦合方法相比,该耦合技术考虑了不排水试验中的边界移动以及流体的可压缩性,适用于本文考虑生物气泡引起流体压缩系数变化的不排水循环三轴模拟。在本文的流固耦合研究中,土体为颗粒集合体,因此被视为非连续介质并采用DEM进行模拟,孔隙水被视为连续介质采用CFD进行模拟。

DEM的控制方程为牛顿第二定律和粒间接触模型。通过对第一节三维离散元胶结接触模型进行微观参数标定^[22],本文接触模型主要微观参数如表1所示。

表 1 胶结颗粒模型微观参数

Table 1. Microscopic parameters of model for bond grains

组成	参数名称	数值
颗粒部分	颗粒模量E_p/Pa	3×10⁸
	颗粒法向与切向刚度比 $ξ$	1.5
	颗粒摩擦系数 $μ$	0.5
	颗粒抗转动系数 $β$	0.2
	颗粒局部破损系数 $ξ_{c}$	2.1
	颗粒法向接触加卸载刚度比 $e_{n}$	0.95
胶结部分	胶结半径比例系数 $η$	(0.5)*
	胶结模量E_b/Pa	2×10⁸
	胶结泊松比 $ν_{b}$	0.2
	胶结抗拉强度 $σ_{t}$ /Pa	1.6×10⁶
	胶结抗压强度 $σ_{c}$ /Pa	8×10⁷
黏滞阻尼	法向临界阻尼比 $β_{n}$	0.6
黏滞阻尼	切向临界阻尼比 $β_{s}$	0.6
注：胶结半径比例系数 $η$ 在标定过程中取0.5,在此后的模拟中为控制胶结含量的研究变量。

下载: 导出CSV

| 显示表格

CFD基本控制方程为连续性方程、动量方程和能量方程。3个方程分别来源于3个物理学基本定律：质量守恒定律、牛顿第二定律和能量守恒定律。

在不考虑温度和压力耦合的情况下,能量方程是自动满足的,仅靠动量方程和连续性方程无法闭合求解。因此,本文引入了流体的状态方程：

$ρ_{f} - ρ_{f0} = ρ_{f} C (p - p_{0})$

(21)

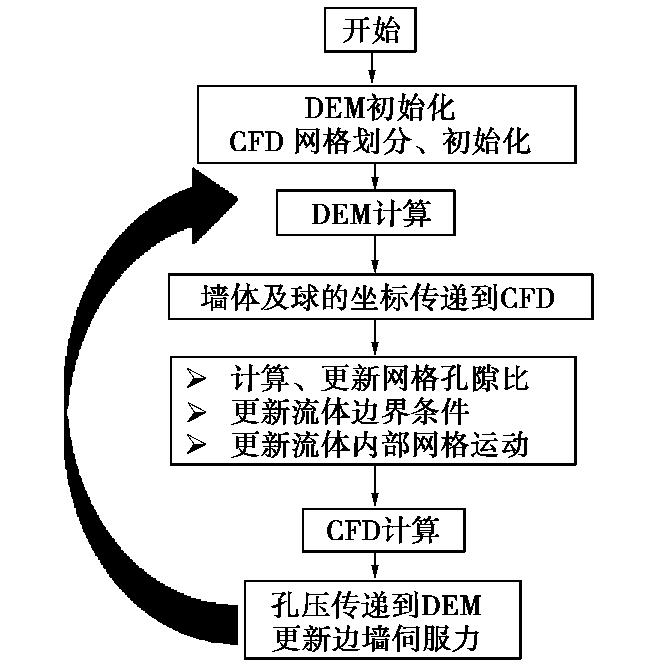
式中, $ρ_{f0}$ 和 $ρ_{f}$ 分别为流体初始密度和当前密度,p和 $p_{0}$ 分别表示流体初始孔压和当前孔压,C为液体压缩系数。

本文不排水剪切试验模拟CFD-DEM耦合流程主要步骤如图3所示。

图 3 CFD-DEM耦合流程

Figure 3. Flow chart of coupled CFD-DEM method

下载: 全尺寸图片幻灯片

图3中流体内部网格采用简单的均匀变形方式移动,以x方向为例,内部网格的运动控制方程为

$V_{x}^{i} = V_{x}^{1} + \frac{i - 1}{n - 1} \cdot (V_{x}^{n} - V_{x}^{1}),$

(22)

式中, $V_{x}^{i}$ 为第 $i$ 个网格的移动速度, $V_{x}^{1}$ 和 $V_{x}^{n}$ 为边界网格的移动速度。

此外,本文的CFD网格内孔隙比计算采用精确解析解法^[24]。该方法将跨网格的颗粒精确剖分于对应网格,较圆心定位法、外接正方体法计算得到的网格内孔隙比更为精确。

3. 微生物处理过程时效性计算

与人工形成胶结、人工注射气泡相比,微生物处理过程（尤其是反硝化反应）往往需要长时间的反应时间才能得到理想的胶结含量和气泡含量。此前分别根据van Paassen等^[25]和He^[8]的研究,得到了室内试验中反硝化反应胶结的生成速率为91 mmol/d。由于篇幅限制,本节仅据此反应速率,计算数值模拟试样中反硝化反应2 d后的胶结与气泡含量,并通过数值模拟中对应参数的值进行描述,应用于之后的不排水循环剪切模拟。

Al Qabany^[26]通过SEM试验,观察到MICP胶结砂土有时间依赖性特征,即小的方解石沉淀首先覆盖在砂粒表面,然后将两粒砂粒堆积并黏结在一起。而本文接触模型中的胶结半径比例系数 $η$ 可用来控制试样中胶结的含量并模拟方解石沉淀的堆积。这种时间依赖性可通过建立时间t和 $η$ 的关系式得到：

$\begin{array}{l} η = - 0.00118 + 0.23802 (\frac{t}{1000}) - 0.27795 {(\frac{t}{1000})}^{2} + 0.30913 \cdot \\ {(\frac{t}{1000})}^{3} - 0.23393 {(\frac{t}{1000})}^{4} + 0.11172 {(\frac{t}{1000})}^{5} - 0.03258 {(\frac{t}{1000})}^{6} + \\ 0.00561 {(\frac{t}{1000})}^{7} - 0.00052 {(\frac{t}{1000})}^{8} + 0.00002 {(\frac{t}{1000})}^{9} 。 \end{array}$

(23)

对于反硝化反应生成胶结,本文碳酸钙胶结的体积增长速率为0.359 mm³/d,反应2 d后的胶结含量为0.718 mm³,反应2 d对应的胶结半径比例系数 $η$ 为0.231。

对于反硝化反应生成气泡,本文的数值模拟试样中2 d后的气泡含量为2.46 mm³,对应的饱和度为98.3%。为了计算简便,将该气泡体积与饱和度转换为数值模拟中的流体压缩系数C。

Schuurman^[27]提出了一个被广泛认可的含气泡的孔隙流体的压缩系数计算方法：

$C = \frac{1}{V_{a} + V_{w}} {\frac{(V_{a0} + V_{s}) u_{a0}}{{(V_{a} + V_{s})}^{2}} - \frac{2 q}{3 r_{0}} \frac{1}{V_{a}} {[\frac{V_{a0}}{V_{a}}]}^{1 / 3}}^{- 1},$

(24)

式中,下标0代表初始状态, $V_{a}$ 为气泡体积, $u_{a}$ 为气泡压力。

刘侃等^[28]认为以Dorsey^[29]的试验结果为参考,将溶于水的气体和水作为整体确定压缩系数更为合理。在不考虑表面张力的情况下,得到了含气泡孔隙流体压缩系数的表达式为

$C = \frac{1}{V_{a0} + V_{w0}} {\frac{V_{a0}}{V_{a}^{2}} (u_{w0} + p_{a})}^{- 1} + S_{0} C_{0},$

(25)

式中, $S_{0}$ 为饱和度, $C_{0}$ 为饱和情况下的压缩系数,取4.5×10^-7。根据式（25）数值模拟试样经过微生物处理2 d后的压缩系数为3.87×10^-5。

至此,得到本文数值模拟试样微生物处理过程时效性对应的参数。最终的参数计算结果如表2所示。

表 2 数值模拟试样微生物处理过程时效性

Table 2. Time-dependent characteristics of microbial processing of numerical simulation samples

反应时间/d	微生物处理生成胶结		微生物处理生成气泡
反应时间/d	胶结体积/mm³	胶结半径比例系数η	气泡体积/mm³	饱和度S_r/%	孔隙流体压缩系数C
0	0	0	0	100	4.5×10^-7
2	0.718	0.231	2.46	98.3	3.87×10^-5

下载: 导出CSV

| 显示表格

4. 微生物处理砂土不排水循环剪切CFD-DEM耦合模拟

本节根据适用于MICP胶结砂土的三维微观胶结模型,结合CFD-DEM耦合程序,模拟分析不同胶结含量以及不同气泡含量下,微生物处理砂土的固结不排水循环剪切力学特性。前3个阶段均只采用DEM完成,循环剪切阶段采用CFD-DEM耦合。

4.1 模拟步骤

微生物处理砂土不排水循环三轴剪切试验的模拟步骤包括成样、预压、固结、循环剪切4个阶段。

（1）成样

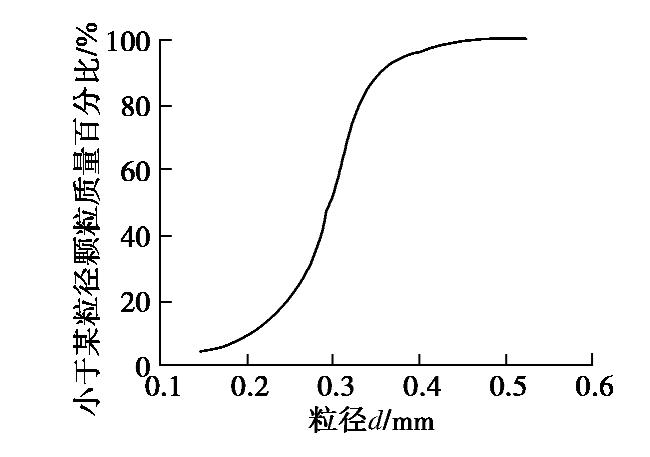
本文选用文献[30]的Ottawa 50-70砂为基砂（为进行MICP反应所选用的无胶结砂）,其级配曲线如图4所示。采用分层欠压法^[31]分10层制备离散元试样,初始孔隙比为0.73,欠压比选取1.1。

图 4 渥太华50-70砂级配

Figure 4. Grain-size distribution of Ottawa 50-70 sand

下载: 全尺寸图片幻灯片

（2）预压

制得均匀试样后,首先将模型颗粒参数施加到试样当中,然后固定四道侧墙,并通过伺服系统对上下墙施加12.5 kPa应力预压。

（3）固结

预压稳定后,再次通过伺服系统对试样进行等向固结。固结试样的平均有效主应力p为100 kPa,偏应力q为0。固结试样如图5所示。当试样固结平衡后,施加模型胶结参数到试样中,模拟室内试验的MICP处理过程,其中胶结半径比例系数 $η$ 如表3所示。

图 5 试样固结示意图

Figure 5. Schematic diagram of sample consolidation

下载: 全尺寸图片幻灯片

表 3 微生物处理砂土循环三轴数值模拟工况与结果列表

Table 3. Simulation program and main results of cyclic triaxial compression tests on different microbial treatment time on sand

试样编号	模拟工况					模拟结果
试样编号	土体种类	微生物处理时间/d	胶结半径比例系数η	孔隙流体压缩系数C	循环应力比CSR	破坏振次N_L	破坏模式
L0	净砂	0	0		0.15	1	I.L.
MU2-1	非饱和MICP胶结砂土	2	0.273	3.87×10^-5	0.30	45+	—
MU2-6	非饱和MICP胶结砂土	2	0.273	3.87×10^-5	0.60	3	I.L.
MP2-2	MICP胶结砂土	2	0.273		0.60	5	I.L.
US2-4	非饱和砂土	2		3.87×10^-5	0.30	2	I.L.

下载: 导出CSV

| 显示表格

（4）循环剪切

该阶段加入了CFD模块进行耦合模拟。DEM时步为1×10^-6 s/cycle,DEM与CFD的交换频率为25（即DEM计算25次,CFD计算1次）,CFD时步为2.5×10^-5 s/cycle。液体初始密度1000 kg/m³,压缩系数为4.5×10^-7。流体网格数目为6×6×12（长×宽×高）。CFD网格边界与DEM中六道墙体的坐标一致。采用文献[32]等幅循环加载的方法,即应变控制,等应力幅加载,加载程序如图6所示。上下墙匀速加载,当偏应力达到应力幅值q_cyc时,上下墙反向继续运动,直到达到相反方向的应力幅值q_cyc则再次反向。循环加载前施加100 kPa反压。侧墙仍然采用伺服系统控制,伺服应力为围压减去孔压后的有效应力。流体边界采用速度边界,与墙的速度一致。CFD参数孔隙流体压缩系数C取值如表3所示。

图 6 等应力幅循环剪切加载过程

Figure 6. Loading program for uniform-amplitude cyclic triaxial compression tests

下载: 全尺寸图片幻灯片

4.2 模拟方案

为研究不同胶结含量及气泡含量微生物处理砂土试样的抗液化强度,选取微生物处理2 d后的MICP胶结砂土、非饱和砂土及非饱和MICP胶结砂土进行对比。详细工况见表3。其中,循环应力比 $CSR = q_{cyc} /$ $2 p_{c}$ , $p_{c}$ 为固结后的平均有效应力,即100 kPa。为方便描述,对所有试样进行编号,L0代表初始固结偏应力为0 kPa的净砂,MP（US/MU）2分别代表微生物处理2 d的MICP胶结（含生物气泡的非饱和/非饱和MICP胶结）砂土试样,MP（US/MU）2-1/2/3又分别代表了对微生物处理2 d砂土试样的不同循环应力比循环三轴试验。破坏模式分为两种,初始液化破坏记为I.L.,累积应变破坏记为R.S.。

4.3 模拟结果对比分析

（1）抗液化强度

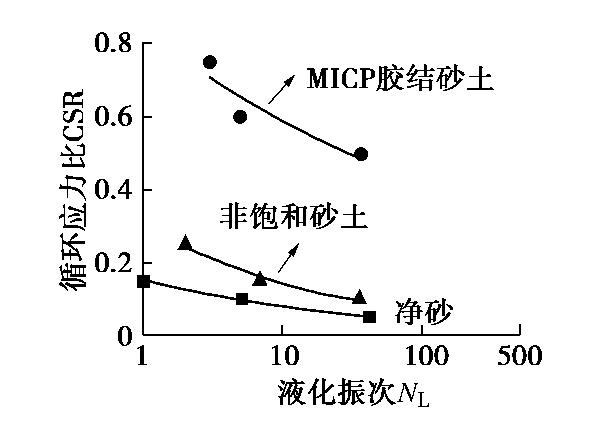
将微生物处理2 d得到的MICP胶结砂土和非饱和砂土试样的液化振次N_L与循环应力比CSR分别绘制于半对数坐标下,并与未进行生物处理的净砂试样进行对比,如图7所示。从图中可以看出微生物处理后的MICP胶结砂土及非饱和砂土的抗液化强度均较净砂试样有大幅度提升。

图 7 微生物处理砂土试样循环应力比-液化振次曲线

Figure 7. Cyclic stress ratio-cycles to initial liquefaction curves of sand samples treated by microorganism

下载: 全尺寸图片幻灯片

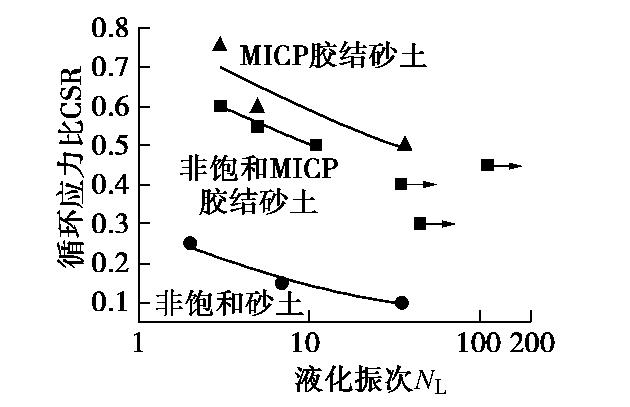
图8将微生物处理2 d得到的非饱和MICP胶结砂土试样的液化振次N_L与循环应力比CSR分别绘制于半对数坐标下,并与非饱和砂土和MICP胶结砂土试样进行对比。从图8可以看出,在相同处理时间下,同时考虑微生物处理的胶结作用和气泡作用时,非饱和MICP胶结砂土的抗液化强度并没有更进一步提升。相反,非饱和MICP胶结砂土的抗液化强度介于非饱和净砂和饱和MICP胶结砂土之间,高于非饱和净砂而低于饱和MICP胶结砂土。即胶结的存在可以提升非饱和砂土的抗液化能力,而气泡的存在反而抑制了MICP胶结砂土的抗液化能力。由于胶结与气泡共同作用的抗液化效果并没有起到“1+1=2”的效果,甚至比胶结单独作用的抗液化效果还要差。以下将胶结与气泡共同作用的试样与单独作用的试样分别进行对比,从孔压比、轴向应变、力学配位数的角度进行分析。

图 8 胶结与气泡共同作用与单一作用砂土试样液化线对比（箭头代表试样在该振次下仍未破坏）

Figure 8. Comparison of liquefaction lines of sand samples under single and combined actions of cementation and bubbles (arrows represents that sample is still intact under this vibration)

下载: 全尺寸图片幻灯片

（2）孔压比

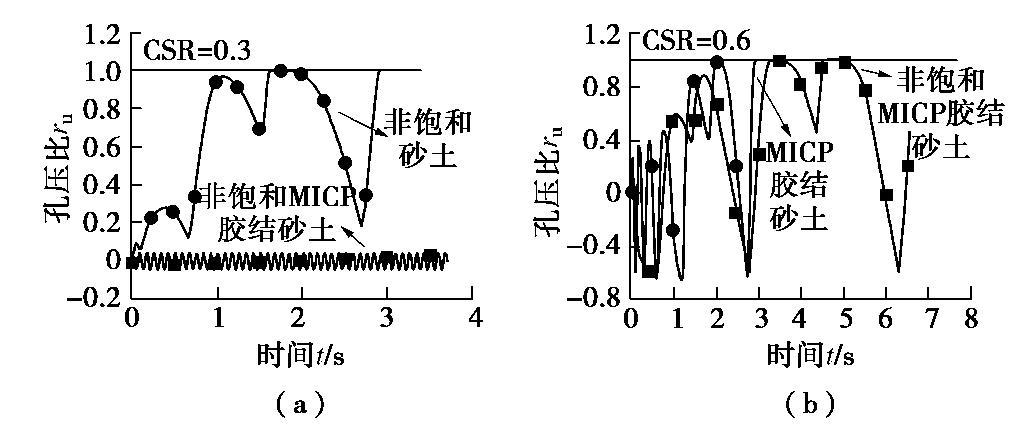
孔压比是指在循环应力作用下试样的孔隙水压力增量与侧向有效固结应力的比值。图9（a）对比了胶结与气泡共同作用和气泡单独作用的试样在相同CSR下的孔压比演化规律,由于篇幅限制,本文仅给出微生物处理2 d后的结果。可以看出,非饱和试样的孔压比随着加载的进行而累积上升。但在相同CSR下非饱和胶结试样的孔压比却不再累积,而是在正孔压和负孔压间交替变化。即胶结的存在会大大抑制非饱和试样的孔压比的发展。

图 9 胶结与气泡共同作用和单一作用砂土试样孔压比对比

Figure 9. Pore pressure ratios of sand samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

图9（b）对比了胶结与气泡共同作用和胶结单独作用的试样在相同CSR下的孔压比演化规律,并给出了微生物处理2 d的结果。可以看出,对于微生物处理2 d的试样,气泡的存在使得胶结试样达到初始液化所需的时间更长,而振次却由5次减少为3次,使得胶结试样的抗液化能力减弱。因此,气泡的存在降低了胶结试样的抗液化能力。

（3）轴向应变

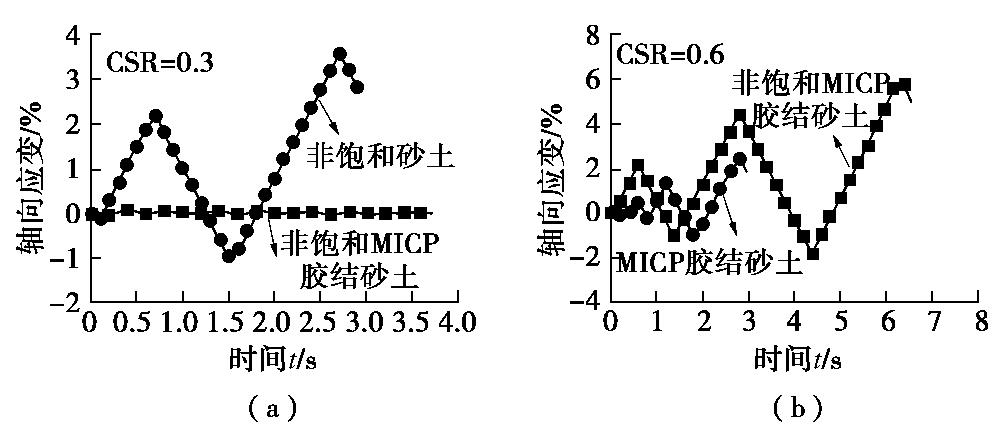
图10（a）对比了胶结与气泡共同作用和气泡单独作用的试样在相同CSR下的轴向应变演化规律。可以看出,随着加载的进行,非饱和试样轴向应变会向受拉方向累积增长。而在相同CSR下,非饱和胶结试样的轴向应变却只有小幅度的波动变化。即胶结的存在会大大抑制非饱和试样轴向应变的发展。

图 10 胶结与气泡共同作用与单一作用试样轴向应变对比

Figure 10. Axial strains of samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

图10（b）对比了胶结与气泡共同作用和胶结单独作用的试样在相同CSR下的轴向应变演化规律。对于微生物处理2 d的试样,气泡的存在使得胶结试样的轴向应变大大增加,非饱和MICP胶结砂土试样在循环2次后就接近达到了5%的累积应变破坏,与MICP胶结砂土试样相比,破坏振次减少,抗液化能力变弱。

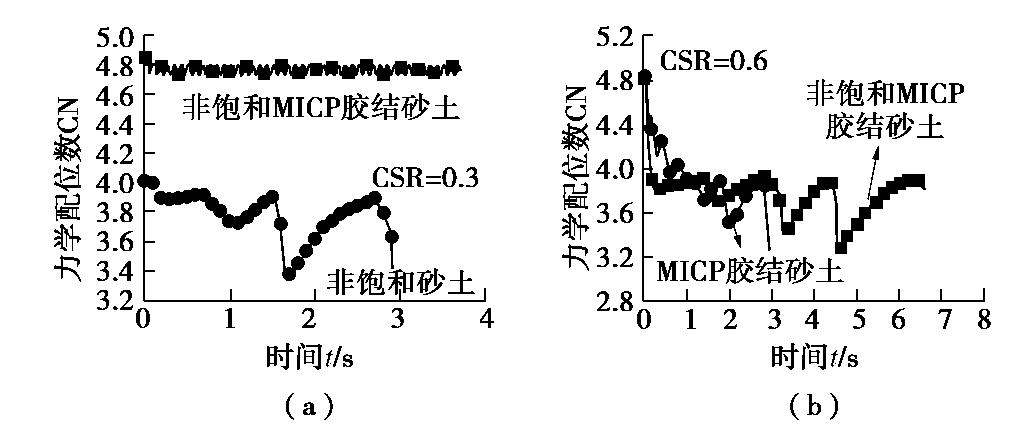
（4）力学配位数

力学配位数是指单个颗粒所含有接触力的数目,通常要求每个接触的法向接触力大于零。其曲线可以表征加载过程中试样的微观变化。图11（a）对比了胶结与气泡共同作用和气泡单独作用的试样在相同CSR下的力学配位数演化规律。可以看出,胶结的存在大大提高了非饱和试样的力学配位数,并且在加载过程中,力学配位数变化幅度很小。这也说明胶结的存在使得非饱和试样内部的传力更加稳定,更不容易破坏。

图 11 胶结与气泡共同作用和单一作用试样力学配位数对比

Figure 11. Mechanical coordination number of samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

图11（b）对比了胶结与气泡共同作用和胶结单独作用的试样在相同CSR下的力学配位数演化规律,并给出了微生物处理2 d后的结果。可以看出,气泡的存在使得胶结试样的力学配位数下降更快,即含气泡的胶结试样在加载过程中破坏更为迅速。

5. 结论

本文在团队已有三维含颗粒抗转动模型及三维胶结破坏准则的基础上,通过考虑颗粒碰撞接触过程中颗粒本身的塑性变形及率相关性的接触黏滞阻尼,建立了考虑循环荷载作用下的三维胶结模型；通过模型中参数胶结半径比例系数 $η$ 考虑生物胶结的影响,通过流体压缩系数C考虑生物气泡的影响,在建立反硝化反应在加固砂土中时效性关系的基础上,分别进行了考虑胶结单独作用的MICP胶结砂土、考虑气泡单独作用的非饱和砂土和考虑胶结及气泡共同作用的非饱和MICP胶结砂土不排水循环三轴试验模拟；对微生物处理砂土试样在循环荷载下的力学响应及微观信息进行了分析。主要得出以下结论：

（1）单独含微生物胶结砂土和单独含微生物气泡的非饱和砂土的抗液化强度均较非饱和净砂高。

（2）非饱和MICP胶结砂土的抗液化能力介于MICP胶结砂土和非饱和砂土之间,并没有起到“1+1=2”的效果。胶结的存在提高了非饱和砂土的抗液化能力,孔压比和轴向应变都受到了明显的抑制。微观层面胶结的存在提高了力学配位数,且在加载过程中下降幅度很小。气泡的存在降低了胶结砂土的抗液化能力,对于微生物处理2 d的试样,孔压比和轴向应变累积上升的幅度更大。微观层面气泡的存在使得力学配位数的下降更为剧烈。

沈珠江院士^[1]指出的结构性模型可能是针对准静态荷载作用下一般结构性土体,而未涉及循环荷载作用下同时考虑生物胶结和气泡作用的胶结生物土。故本文的模拟成果将帮助理解、拓展结构性模型。

图 1 颗粒部分的力学响应

Figure 1. Mechanical responses of contact between particles

下载: 全尺寸图片幻灯片

图 2 胶结部分的力学响应

Figure 2. Mechanical responses of bond

下载: 全尺寸图片幻灯片

图 3 CFD-DEM耦合流程

Figure 3. Flow chart of coupled CFD-DEM method

下载: 全尺寸图片幻灯片

图 4 渥太华50-70砂级配

Figure 4. Grain-size distribution of Ottawa 50-70 sand

下载: 全尺寸图片幻灯片

图 5 试样固结示意图

Figure 5. Schematic diagram of sample consolidation

下载: 全尺寸图片幻灯片

图 6 等应力幅循环剪切加载过程

Figure 6. Loading program for uniform-amplitude cyclic triaxial compression tests

下载: 全尺寸图片幻灯片

图 7 微生物处理砂土试样循环应力比-液化振次曲线

Figure 7. Cyclic stress ratio-cycles to initial liquefaction curves of sand samples treated by microorganism

下载: 全尺寸图片幻灯片

图 8 胶结与气泡共同作用与单一作用砂土试样液化线对比（箭头代表试样在该振次下仍未破坏）

Figure 8. Comparison of liquefaction lines of sand samples under single and combined actions of cementation and bubbles (arrows represents that sample is still intact under this vibration)

下载: 全尺寸图片幻灯片

图 9 胶结与气泡共同作用和单一作用砂土试样孔压比对比

Figure 9. Pore pressure ratios of sand samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

图 10 胶结与气泡共同作用与单一作用试样轴向应变对比

Figure 10. Axial strains of samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

图 11 胶结与气泡共同作用和单一作用试样力学配位数对比

Figure 11. Mechanical coordination number of samples under single and combined actions of cementation and bubbles

下载: 全尺寸图片幻灯片

表 1 胶结颗粒模型微观参数

Table 1 Microscopic parameters of model for bond grains

组成	参数名称	数值
颗粒部分	颗粒模量E_p/Pa	3×10⁸
	颗粒法向与切向刚度比 $ξ$ $ξ$	1.5
	颗粒摩擦系数 $μ$ $μ$	0.5
	颗粒抗转动系数 $β$ $β$	0.2
	颗粒局部破损系数 $ξ_{c}$ $ξ_{c}$	2.1
	颗粒法向接触加卸载刚度比 $e_{n}$ $e_{n}$	0.95
胶结部分	胶结半径比例系数 $η$ $η$	(0.5)*
	胶结模量E_b/Pa	2×10⁸
	胶结泊松比 $ν_{b}$ $ν_{b}$	0.2
	胶结抗拉强度 $σ_{t}$ $σ_{t}$ /Pa	1.6×10⁶
	胶结抗压强度 $σ_{c}$ $σ_{c}$ /Pa	8×10⁷
黏滞阻尼	法向临界阻尼比 $β_{n}$ $β_{n}$	0.6
黏滞阻尼	切向临界阻尼比 $β_{s}$ $β_{s}$	0.6
注：胶结半径比例系数 $η$ $η$ 在标定过程中取0.5,在此后的模拟中为控制胶结含量的研究变量。

下载: 导出CSV

表 2 数值模拟试样微生物处理过程时效性

Table 2 Time-dependent characteristics of microbial processing of numerical simulation samples

反应时间/d	微生物处理生成胶结		微生物处理生成气泡
反应时间/d	胶结体积/mm³	胶结半径比例系数η	气泡体积/mm³	饱和度S_r/%	孔隙流体压缩系数C
0	0	0	0	100	4.5×10^-7
2	0.718	0.231	2.46	98.3	3.87×10^-5

下载: 导出CSV

表 3 微生物处理砂土循环三轴数值模拟工况与结果列表

Table 3 Simulation program and main results of cyclic triaxial compression tests on different microbial treatment time on sand

试样编号	模拟工况					模拟结果
试样编号	土体种类	微生物处理时间/d	胶结半径比例系数η	孔隙流体压缩系数C	循环应力比CSR	破坏振次N_L	破坏模式
L0	净砂	0	0		0.15	1	I.L.
MU2-1	非饱和MICP胶结砂土	2	0.273	3.87×10^-5	0.30	45+	—
MU2-6	非饱和MICP胶结砂土	2	0.273	3.87×10^-5	0.60	3	I.L.
MP2-2	MICP胶结砂土	2	0.273		0.60	5	I.L.
US2-4	非饱和砂土	2		3.87×10^-5	0.30	2	I.L.

下载: 导出CSV

参考文献(32)

[1]	沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhu-jiang. Theoretical Soil Mechanics[M]. Beijing: China Water and Power Press, 2000. (in Chinese)
[2]	GAO Y F, HANG L, HE J, et al. Mechanical behaviour of biocemented sands at various treatment levels and relative densities[J]. Acta Geotechnica, 2019, 14(3): 697-707. doi: 10.1007/s11440-018-0729-3
[3]	WANG Y, SOGA K, DEJONG J T, et al. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP)[J]. Géotechnique, 2019, 69(12): 1-9.
[4]	INAGAKI Y, TSUKAMOTO M, MORI H, et al. A centrifugal model test of microbial carbonate precipitation as liquefaction countermeasure[J]. Japanese Geotechnical Journal, 2011, 6(2): 157-167. doi: 10.3208/jgs.6.157
[5]	HAN Z G, CHENG X H, MA Q. An experimental study on dynamic response for MICP strengthening liquefiable sands[J]. Earthquake Engineering and Engineering Vibration, 2016, 15(4): 673-679. doi: 10.1007/s11803-016-0357-6
[6]	刘汉龙, 肖鹏, 肖扬, 等. MICP胶结钙质砂动力特性试验研究[J]. 岩土工程学报, 2018, 40(1): 38-45. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. Dynamic behaviors of MICP-treated calcareous sand in cyclic tests[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 38-45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm
[7]	REBATA-LANDA V, SANTAMARINA J C. Mechanical effects of biogenic nitrogen gas bubbles in soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(2): 128-137. doi: 10.1061/(ASCE)GT.1943-5606.0000571
[8]	HE J. Mitigation of liquefaction of sand using microbial methods[D]. Singapore: Nanyang Technological University, 2013.
[9]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[10]	KHOUBANI A, EVANS T M, MONTOYA B M. Particulate simulations of triaxial tests on bio-cemented sand using a new cementation model[C]//Proceedings of GeoChicago: Sustainability, Energy, and the Geoenvironment. Chicago, 2016: 1-10.
[11]	FENG K, MONTOYA B M, EVANS T M. Discrete element method simulations of bio-cemented sands[J]. Computers and Geotechnics, 2017, 85: 139-150. doi: 10.1016/j.compgeo.2016.12.028
[12]	ANDERSON J D, WENDT J. Computational Fluid Dynamics[M]. New York: McGraw-Hill, 1995.
[13]	CHANG C Y, SCHMIDT J, DÖRENKÄMPER M, et al. A consistent steady state CFD simulation method for stratified atmospheric boundary layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 172: 55-67. doi: 10.1016/j.jweia.2017.10.003
[14]	PAREKH J, RZEHAK R. Euler-Euler multiphase CFD-simulation with full Reynolds stress model and anisotropic bubble-induced turbulence[J]. International Journal of Multiphase Flow, 2018, 99: 231-245. doi: 10.1016/j.ijmultiphaseflow.2017.10.012
[15]	EL SHAMY U, ZEGHAL M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(8): 712-729. doi: 10.1016/j.soildyn.2006.12.010
[16]	蒋明镜, 张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报, 2014, 36(5): 793-801. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm JIANG Ming-jing, ZHANG Wang-cheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 793-801. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm
[17]	蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[18]	JIANG M J, SHEN Z F, WANG J F. A novel three- dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[19]	金树楼. 结构性砂土三维微观接触力学试验及离散元数值模拟[D]. 上海: 同济大学, 2016. JIN Shu-lou. Three Dimensional Experimental and Numerical Study on Micro- and Macro-mechanical Behaviors of Structural Sands[D]. Shanghai: Tongji University, 2016. (in Chinese)
[20]	THORNTON C, CUMMINS S J, CLEARY P W. An investigation of the comparative behavior of alternative contact force models during inelastic collisions[J]. Powder Technology, 2013, 233(3): 30-46.
[21]	SHEN Z F, JIANG M J, THORNTON C. DEM simulation of bonded granular material: Part I contact model and application to cemented sand[J]. Computers & Geotechnics 2016, 75: 192-209.
[22]	谭亚飞鸥. 考虑循环荷载的三维微观胶结模型及微生物处理砂土循环三轴CFD-DEM耦合模拟[D]. 上海: 上海理工大学, 2018. TAN Ya-fei-ou. A Novel Three-dimensional Bonded Contact Model Incorporating the Effect of Cyclic Loads and CFD-DEM Simulation of Microbially Treated Sands Under Undrained Consolidated Cyclic Triaxial Tests[D]. Shanghai: University of Shanghai for Science and Technology, 2018. (in Chinese)
[23]	ZHANG A, JIANG M J. Numerical simulation of undrained triaxial tests for granular soil using a coupled CFD-DEM method with moving mesh[J]. Acta Geotechnica, 2019. (to be submitted)
[24]	ZHAO T. Investigation of Landslide-induced Debris Flows by the DEM and CFD[D]. Oxford: University of Oxford, 2014.
[25]	VAN PAASSEN L A, DAZA C M, STAAL M, et al. Potential soil reinforcement by biological denitrification[J]. Ecological Engineering, 2010, 36(2): 168-175.
[26]	AL QABANY A, SOGA K, SANTAMARINA C, et al. Factors affecting efficiency of microbially induced calcite precipitation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(8): 992-1001.
[27]	SCHUURMAN I E. The compressibility of an air/water mixture and a theoretical relation between the air and water pressures[J]. Géotechnique, 1966, 16(4): 269-281.
[28]	刘侃, 朱小军, 张帆舸, 等. 含气泡土的孔隙流体压缩系数计算分析[J]. 岩土工程学报, 2017, 39(增刊2): 120-123. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm LIU Kan, ZHU Xiao-jun, ZHANG Fan-ge, et al. Calculation of coefficient of compressibility for air-water mixture in gassy soils[J]. Chinese Journal of Geotechnical Engineering,2017, 39(S2): 120-123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm
[29]	DORSEY N E. Properties of Ordinary Water-Substance[M]. New York: Reinhold Publishing Corporation, 1940.
[30]	FENG K, MONTOYA B M. Influence of confinement and cementation level on the behavior of microbial-induced calcite precipitated sands under monotonic drained loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1): 04015057.
[31]	JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(5): 579-597.
[32]	KUHN M R, RENKEN H E, MIXSELL A D, et al. Investigation of cyclic liquefaction with discrete element simulations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(12): 04014075.

施引文献(18)

期刊类型引用(6)

1.	梁旭之，郑世伦，刘斌，王云进，肖平. 矿区道路排水设施设计研究. 能源与环保. 2022(06): 279-284 . 百度学术
2.	唐辉明. 重大滑坡预测预报研究进展与展望. 地质科技通报. 2022(06): 1-13 . 百度学术
3.	张伏光，聂卓琛，陈孟飞，冯怀平. 不排水循环荷载条件下胶结砂土宏微观力学性质离散元模拟研究. 岩土工程学报. 2021(03): 456-464 . 本站查看
4.	李涛，高颖，张嘉睿，李殿鑫，陈伟，张鹏，李博，梅奥然. 陕北保水采煤背景下MICP再造隔水土层的试验研究. 煤炭学报. 2021(09): 2984-2994 . 百度学术
5.	田威，李腾，贾能，张旭东，贺礼. 固化剂在黄土路基工程中的研究进展. 公路. 2021(11): 45-52 . 百度学术
6.	戴轩，霍海峰，程雪松，郭旺，冯兴. 高水压作用下水砂耦合流失的DEM-CFD分析. 工业建筑. 2020(11): 82-90 . 百度学术