强震损伤格栅墙处理地基抗液化性能离心模型试验研究

周燕国; 曹渊; 石川明; 陈云敏

doi:10.11779/CJGE2024S10050

强震损伤格栅墙处理地基抗液化性能离心模型试验研究 English Version

1.
浙江大学软弱土与环境土工教育部重点实验室, 浙江大学岩土工程研究所, 浙江大学超重力研究中心, 浙江杭州 310058
2.
清水建设技术研究所, 日本东京 135-8530

基金项目:

国家自然科学基金项目 51988101

国家自然科学基金项目 52278374

国家自然科学基金项目 51978613

高等学校学科创新引智计划（111计划）项目 B18047

详细信息

作者简介:
周燕国(1978—)，男，博士，教授，主要从事土动力学与地震工程、岩土工程防震减灾、地下基础设施性能设计与抗震韧性以及离心物理模拟方向的研究工作。E-mail: qzking@zju.edu.cn

中图分类号: TU411
计量
- 文章访问数: 102
- HTML全文浏览量: 17
- PDF下载量: 26
出版历程
- 收稿日期: 2024-04-28
- 刊出日期: 2024-07-31

Centrifuge model tests on liquefaction mitigation performance of soil-cement grid-improved ground subjected to earthquake pre-shaking history

1.
MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Institute of Geotechnical Engineering, Center for Hypergravity Experiment and Interdisciplinary Research, Zhejiang University, Hangzhou 310058, China
2.
Institute of Technology, Shimizu Corporation, Tokyo, Japan

摘要

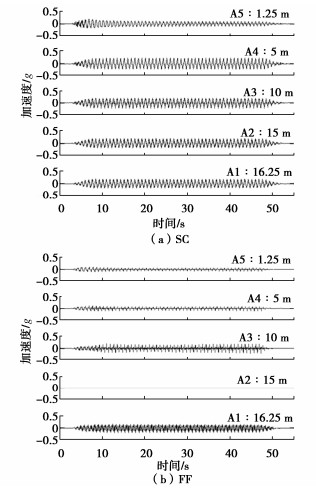
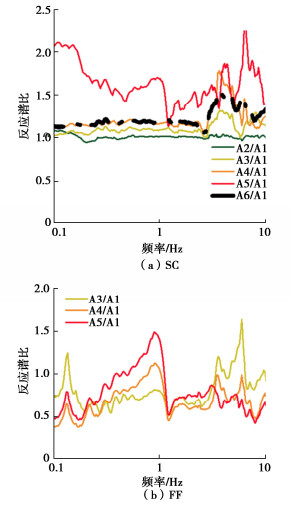
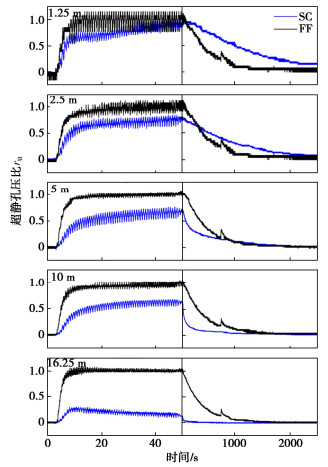
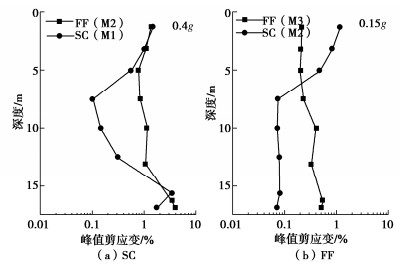
摘要: 水泥土格栅墙能有效减缓被围束土体在地震作用下的剪切荷载及变形，已广泛应用为一种高效的抗液化对策。针对其长期服役过程，开展了两组超重力离心模型试验以研究强振历史对水泥土格栅墙内被围束土体液化响应的影响。两组模型均由15米厚的易液化含黏粒砂土和2.5 m厚的粗砂层组成。其中，一组模型采用水泥土格栅墙对易液化层进行加固；另一组模型则未进行处理，作为自由场地对照组。两组模型均经历振幅为0.15g的振动事件，且在0.15g振动事件前，对两组模型施加振幅为0.4g的振动事件作为强振历史。试验结果表明，格栅墙在强振下主要的损伤模式表现为竖向贯穿型裂缝，并部分伴随有局部斜向裂缝，且外侧格室对于中心格室表现出类似于群桩基础的“遮蔽效应”。强振历史后，格栅墙中心格室内被围束土体的超静孔压显著低于自由场地，损伤后格栅墙仍具有良好的抗液化效果。同时，格栅墙由于强振后整体刚度的削弱，其与下卧粗砂层间的剪切变形显著减小。
- 地震液化 /
- 水泥土格栅墙 /
- 地基处理 /
- 离心机模型试验 /
- 地震历史
Abstract: The soil-cement grid has been widely applied as an effective liquefaction countermeasure due to its capability to effectively mitigate the shear load and deformation of the enclosed soil under seismic loadings. In terms of its long service period, two dynamic centrifuge model tests are conducted to study the effects of strong shaking history on the liquefaction responses of the enclosed soil. The model ground consists of a 15 m-thick liquefiable clayey fine sand and an underlain 2.5 m-thick coarse sand layer. The liquefiable layer is improved by the soil-cement grid in one model, while the other without any improvement affording a contrast. Both models are subjected to a sinusoidal input motion with amplitude of 0.15g. Several more severe shaking events with amplitude of 0.4g are applied to the models prior to this 0.15g event as strong shaking history. The results imply that the damage patterns of the walls are mainly vertical penetrating cracks, partly accompanied by local diagonal cracks, and the outer cells show a "shielding effect" on the center cell similar to that of a group pile foundation. After the strong vibration history, the central cell of the soil-cement grid still has satisfactory anti-liquefaction effects, leading to a much lower excess pore pressure than free field. At the same time, due to the weakening of the overall stiffness of the soil-cement grid, the shear deformation between the soil-cement grid and the underlying coarse sand layer is significantly reduced.
- soil liquefaction /
- soil-cement grid /
- ground improvement /
- centrifuge model test /
- earthquake pre-shaking history

HTML全文

0. 引言

随着中国建设的推进，盾构法隧道越来越广泛应用于城市地下公路、铁路、地铁、各类通道等设施建设。然而，城市化发展常常导致已建成隧道处于复杂周边环境状态，如周边超载^[1-2]、近接穿越^[3]、围岩劣化^[4]等意外情况。而受周边环境影响，隧道在全寿命周期中往往将面临诸多复杂受荷状态如注浆、偏载、偏转等非对称偏不利工况。当前部分隧道在结构设计时已考虑到这些不利影响，但更多的研究还是主要聚焦于隧道结构在简单对称荷载条件下的力学性能，既有与结构复杂非对称受力性能相关的研究也仅针对部分异型盾构隧道如双圆隧道^[5]。

为研究盾构隧道结构的力学性能，开展模型试验往往是最为直观也最为有效的手段。其中缩尺模型试验的成本较低，可对结构的多种状态进行复现^[6]，但研究也一定程度上受制于尺寸效应。原型试验研究对象为1︰1原型试件，故而其研究成果也更具参考价值。2000年左右，德国、荷兰和日本分别针对4th Elbe隧道^[7]、Botlek隧道^[8]和京都地铁大断面圆角矩形隧道^[9]开展原型结构试验研究，中国也相继针对双圆隧道^[10]、矩形隧道^[11]、类矩形隧道^[12-13]等异型隧道和各地越江隧道^[14-16]、排蓄水隧道^[17-19]和地铁隧道^[20]等圆形隧道开展了试验研究，获得了诸多宝贵的隧道结构力学性能研究成果，为隧道实际工程的设计、施工、运维提供了指导。

为了通过原型试验研究盾构隧道结构在复杂受荷条件下的力学性能，高精度多组群控的试验系统和基于多独立荷载组的试验荷载设计方法都是必不可少的。从试验系统和试验手段来看，随着技术发展，试验系统对结构所受荷载条件的模拟也愈发精确和全面。如封坤等^[15]采用环箍钢绞线模拟隧道所受高水压，Liu等^[11]、Zhang等^[13]均基于站立式试验平台，用弹性橡胶支座模拟了基底反力，充分考虑了管片自重的影响，朱瑶宏等^[21]通过PID控制器使部分千斤顶荷载位移关系遵循土体本构曲线，以模拟土-隧道结构相互作用。整体而言，原型试验对实际结构受荷状态的模拟愈发精确，同时试验需求和技术的发展也促进了基于云服务和本地实时交互控制的试验系统的发展。

从试验荷载设计方法来看，荷载设计原则整体从荷载等效逐渐向内力等效发展。如Vervuurt等^[8]开展的Botlek隧道试验和王彪等^[14]的上海崇明隧道试验均采用了荷载等效原则设计试验荷载。黄鸿浩^[19]在地铁盾构隧道试验中，采用了弹性阶段综合考虑内力等效，非线性阶段荷载等效的试验原则，揭示了隧道结构的弹塑性力学性能演化机制。刘威等^[18]在深埋排蓄水隧道整环试验中采用外压荷载点和内拉荷载点分别模拟外部水土荷载和内水压，并给出了基于内力等效原则和修正惯用法计算模型的试验荷载设计方法。

原型结构试验平台如今已具备了高精度集群控制、多方案、多独立荷载组加载等性能，对隧道结构力学性能的探究也从设计弹性阶段逐渐过渡至弹塑性阶段或整体失稳阶段。但现有研究主要关注隧道结构在简单对称荷载状态下的力学响应，而未拓展至复杂受荷状态。事实上隧道在施工、运维期将面临周边地质变化、临近施工等诸多影响，处于复杂受荷状态，其中大部分情况下均为更为不利的非对称荷载状态。但需要注意的是，非对称状态模拟的关键不在于通过试验手段施加非对称荷载，而是使试验荷载下的结构状态能与待模拟非对称荷载下的结构状态相匹配。这就要求试验系统必须包含较多的独立荷载组数，对应荷载设计方法也应具备适用性，而当前试验技术的发展也使对结构复杂受荷状态的模拟成为了可能。

为了对盾构隧道结构开展复杂受荷状态力学性能研究，将首先介绍相关试验平台的开发，包含试验平台装置和试验荷载设计方法两部分。之后基于该试验平台对类矩形盾构隧道、双圆隧道和圆形隧道开展原型结构试验的实证应用，以偏载荷载状态为例，探究隧道结构力学性能的同时也验证试验平台的适用性和可靠性。最后对试验方法的控制目标权重系数、计算模型、结构断面形式、试验边界形式等参数进行分析讨论，以拓展试验平台适用范围。

1. 试验平台装置

试验平台装置分为加载系统和监测系统两部分，其中加载系统负责根据荷载指令控制试验荷载。监测系统与加载系统独立，用于监测结构的受荷响应，同时对加载系统部分油压、顶力等参数进行独立监测。

1.1 加载系统

加载系统基于上海同禾科技股份有限公司研发技术，其整体控制架构包含云平台控制层、现场控制层和智能硬件层3层，其架构如图 1所示。

图 1 加载系统整体架构

Figure 1. Framework of loading system

下载: 全尺寸图片幻灯片

云平台控制层与中控主机、液压站、监测测项建立数据链路，基于云端优异的运算和访问速度，任意时刻、地址均可联网查阅和远程控制试验进度。中控主机通过嵌入式系统实时协同控制液压站，控制速率为1000次/s。集成液压站通过直流无刷电机、液压泵、液压控制阀的配合执行动作，实现液压千斤顶控制误差在3 kN以内的精准加、卸载及位移控制动作，可模拟土-结相互作用和结构塑性下降段，使试验综合控制误差低于2%，模拟更为精确。上述加载系统和试验试件、加载框架及其他辅助构件组合，形成试验平台，为足尺试验中实现盾构隧道结构的复杂受荷状态力学性能模拟提供硬件支撑，如图 2所示^[22]。

图 2 隧道原型结构试验平台

Figure 2. Prototype test platform

下载: 全尺寸图片幻灯片

1.2 监测系统

试验平台的监测内容，除常见的结构整体变形、环纵缝变形、材料应变等，还额外包含了对加载参数的监测及基于激光和机器视觉技术的结构变形测量。系列技术已成功运用于本课题组所开展的盾构隧道原型结构试验。

（1）加载参数独立监测。除加载系统本身监测，还额外布置油压传感器和称重传感器，以对千斤顶的油压和顶力进行实时监测和校核，保证系统稳定。

（2）基于激光扫描的结构变形测量。结合三维激光扫描和近距离摄影测量技术，通过设备自动获取隧道结构点云和图像，进一步基于机器学习方法得到高精度结构变形，识别结构损伤和缺陷。

（3）基于机器视觉测量技术的结构变形测量^[23]。通过机器视觉非接触式测量技术，在隧道结构上布置靶标以监测结构变形。该方法具有布设简单、测量精度高和数据可信度高等特点，同时可避免繁琐接线。其测量布置和实物识别如图 3所示。

图 3 机器视觉测量技术

Figure 3. Machine photogrammetry technology

下载: 全尺寸图片幻灯片

2. 试验荷载设计方法

2.1 荷载设计原则

开展盾构隧道结构力学性能原型试验研究，尤其是针对复杂受荷状态或新型结构，重点在于使试验荷载下结构状态能充分模拟复杂设计水土荷载下的结构状态。为此应明确设计水土荷载，根据一定原则计算试验荷载，以保证原型结构试验研究的顺利开展。本章节所提出的试验荷载设计方法可同时适用于任意对称和非对称荷载条件下的结构试验，适用于任意隧道断面形式及任意由千斤顶提供试验荷载的结构试验。

将结构所受设计水土荷载转化为试验荷载时，要满足两个基本原则。

（1）因所有试验荷载均由千斤顶提供，故所有试验荷载应满足自平衡条件，以确保试验系统的安全稳定。若所有试验荷载对任意点取合力、合力矩不为0，则易引入未知边界力，导致系统性误差。

（2）保证设计水土荷载和试验荷载下结构在控制目标处（如变形、内力）的误差在一定范围内。由于管片本体、接头设计时主要受弯矩控制，故而试验荷载设计时应以弯矩控制为主，并尽可能保证目标截面在试验荷载下的内力状态相比设计水土荷载下是危险的，以确保试验得到的验证性结果偏于保守。

2.2 试验荷载设计过程

设计主要分为3步：①基础加载组系确定；②控制目标确定；③试验荷载求解。

（1）基础加载组系确定

在所有千斤顶的布置位置和布置方向已确定的条件下，记加载点总数为N。（N个千斤顶视为N个点荷载）记包含所有加载点试验荷载的列向量为F（元素数为N，也是最后要求解的试验荷载向量）。以试验结构中心为原点设置平面直角坐标系，如图 4所示。

图 4 不同断面隧道试验荷载点分布示意图

Figure 4. Test loads of tunnel specimens with different cross-sections

下载: 全尺寸图片幻灯片

记第i个加载点作用单位荷载时其x方向、y方向荷载分量和相对原点的力矩分别为e_xi，e_yi和e_Oi，合并记为列向量e_Fi。根据原则（1），有

$\left(\begin{array}{ccc}{e}_{x1}& \mathrm{...}& {e}_{xN}\\ {e}_{y1}& \mathrm{...}& {e}_{yN}\\ {e}_{O1}& \mathrm{...}& {e}_{ON}\end{array}\right)\left(\begin{array}{c}{F}_{1}\\ \mathrm{...}\\ {F}_{N}\end{array}\right)=(\begin{array}{ccc}\boldsymbol{e}_{F1}& \mathrm{...}& \boldsymbol{e}_{FN}\end{array})\left(\begin{array}{c}F_1 \\ \cdots \\ F_N\end{array}\right)=\boldsymbol{e}_F \cdot \boldsymbol{F}=\left(\begin{array}{l}0 \\ 0 \\ 0\end{array}\right)。$

(1)

满足式（1）时，记N个试验荷载F₁~F_N自由度数（独立数）由N降为n。假定千斤顶施荷方向均垂直于管片，当试验试件为类矩形、双圆等异型隧道时，易有n的值为N-3。当试验试件为圆形时，所有试验荷载所在直线都经过圆心，易满足合力矩为0的条件，自由度数n的值为N-2。根据线性代数基本概念，对任意满足原则（1）的一组试验荷载F，总能将其表示为n组互相独立的自平衡基础加载组的线性组合，有

$\boldsymbol {F} = \left( {\begin{array}{*{20}{c}} {{ {F}_1}} \\ {...} \\ {{F_N}} \end{array}} \right) = (\begin{array}{*{20}{c}} {{\boldsymbol {P}_1}}& \cdots &{{\boldsymbol{P}_n}} \end{array})\left( {\begin{array}{*{20}{c}} {{x_1}} \\ {...} \\ {{x_n}} \end{array}} \right) = \boldsymbol{P} \cdot \boldsymbol{ x} 。$

(2)

式中： ${\boldsymbol{P}_i}$ 代表一种基础加载组，是含N个元素的列向量， ${\boldsymbol{P}_i}$ 的第j个元素代表第i组基础加载组中第j个加载点的荷载值。x代表所有基础加载组对应的系数向量，元素数为n。

P满足两个条件：

（1）n个 ${\boldsymbol{P}_1}$ ~ ${\boldsymbol{P}_n}$ 是线性无关的，保证了F在N维向量空间中的自由度数为n。

（2）因F总是满足式（1），又由于x_i是任意的。则对所有 ${\boldsymbol{P}_i}$ ，都有

${\boldsymbol{e}_F} \cdot {\boldsymbol{P}_i} = 0 。$

(3)

由于P属于N维向量空间，且矩阵秩为n。故而满足式（3）所求得的 ${\boldsymbol{P}_1}$ ~ ${\boldsymbol{P}_n}$ 是不唯一的。但由线性代数常识可知，只要找到符合条件的较为简单的一组基础解系作为基础加载组系，即可用式（2）表示所有满足式（1）的试验荷载组合F。即对找到的一组P和任意的F，F总能由 ${P_1}$ ~ ${P_n}$ 唯一线性表示，即x是唯一确定的。在设备可控情况下，本文推荐 ${P_i}$ 中的非零向量不多于4个，即每个基础加载组中的千斤顶尽可能少，以便于计算。在确定了基础加载组系后，试验荷载设计问题也就从求解F转变成了求解x。

（2）控制目标确定

为模拟复杂水土荷载，根据原则（2），选取部分变形、管片内力等作为试验荷载设计控制目标。记控制目标总计p个，其中可能包含荷载、收敛变形、相对转角、截面弯矩、截面轴力、截面剪力等任意指标。采用弹性计算模型（如等效刚度均质环法）进行计算，记设计水土荷载状态下所有p个控制目标处的计算值为b₁~b_p。对所有p个控制目标赋以权值 ${\omega _1}$ ~ ${\omega _p}$ ，以表征不同控制目标的重要性程度。（一般而言，变形权重高于弯矩权重高于结构顶部轴力权重高于结构底部轴力权重）为使试验能在全环范围而不仅仅是部分截面达到较好的模拟效果，控制目标数量p建议远高于自由度数n，以避免局部过拟合导致的整体失真。

（3）试验荷载求解

对于已确定的基础加载组系，采用同样的计算模型获得每组基础加载组对应试验荷载下结构在p个控制目标处的响应，得到n个列向量 ${\boldsymbol{M}_1}$ ~ ${\boldsymbol{M}_n}$ ，其中M_i代表第i组基础加载组所对应的荷载下结构在所有p个控制目标处的结构响应。进而根据线弹性叠加原理，有初始控制方程

$(\begin{array}{*{20}{c}} {{\boldsymbol{M}_1}}& \cdots &{{\boldsymbol{M}_n}} \end{array})\left( {\begin{array}{*{20}{c}} {{x_1}} \\ {...} \\ {{x_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_1}} \\ {...} \\ {{b_p}} \end{array}} \right) 。$

(4)

定义权重矩阵：

$\boldsymbol{\omega} = {\rm diag}(\begin{array}{*{20}{c}} {{\omega _1}}& \cdots &{{\omega _p}} \end{array}) 。$

(5)

将式（4）改写为加权控制方程

$\boldsymbol{\omega} {\boldsymbol M} \cdot \boldsymbol{x} = \boldsymbol{\omega} \boldsymbol{b} 。。$

(6)

利用矛盾方程组求解方法，有

$\boldsymbol{x}=\left((\boldsymbol{\omega} \boldsymbol{M})^{\mathrm{T}} \cdot \boldsymbol{\omega} \boldsymbol{M}\right)^{-1} \cdot\left((\boldsymbol{\omega} \boldsymbol{M})^{\mathrm{T}} \cdot \boldsymbol{\omega} \boldsymbol{b}\right)$

(7)

求解得到系数向量x后，将其带入式（2）即可计算得到所有加载点的设计试验荷载向量F。

通过该方法计算得到的试验荷载能够在全环范围内达到令人满意的拟合度，适当调整权重系数也能达到局部和整体拟合度的平衡，且尤其适用于非对称等复杂受荷状态的结构试验。本方法当然也适用于对称荷载状态，相比于复杂非对称荷载状态，适当减少基础加载组的组数仍可保持足够的模拟精度。

2.3 试验荷载解的性质

基于式（7），基础加载组彼此的独立性保证了系数矩阵的非奇异性，线性方程组的表示形式保证了得到的系数向量和对应的试验荷载是存在且唯一的，同时随控制目标b（设计水土荷载下结构响应）的变化而连续变化。另一方面，由于结构的弯矩取决于外荷载的差值、结构的轴力取决于外荷载的绝对值，故而当结构轴力相较弯矩处于较高水平时，可以保证该方法计算出来的试验荷载总是为正值，说明该方法给出的解是适定且合理的，这一结论也得到了了迄今为止所有本课题组开展过的结构试验的验证。

而当结构轴力相较弯矩处于较低水平时，采用该方法易出现部分计算试验荷载为负的情况，说明解不适用（千斤顶压力为负不具备实际物理意义）。本文从试验设计层面和试验设备层面给出两种解决方法。

（1）试验设计方面，进行试验荷载设计时删去部分加载点，通过迭代计算方法，不断剔除计算值为负的加载点，计算剩余加载点的试验荷载，以保证所有荷载都是非负的。但该方法由于可用于加载的千斤顶数量的降低，试验的模拟精度也会随之降低。

（2）试验设备层面，通过千斤顶或其他加载形式从隧道内部施加荷载，通过内、外荷载组合施加的形式，以保证通过该方法计算的外部试验荷载的解仍然是合理适用的。这一工况与取排水隧道十分类似，即隧道结构同时受外部水土荷载和内水压荷载。针对此受荷状态的盾构隧道原型结构试验，本课题组已开发了新的内水压加载方式，并开展了探索性试验研究，将在后续的论文中介绍。

3. 复杂受荷状态原型结构试验实证

3.1 类矩形盾构隧道偏载试验

（1）设计水土荷载下结构响应

针对类矩形盾构隧道单侧偏载工况结构响应进行计算，荷载采用水土分算方法。隧道埋深17 m，水位地下0.5 m，侧压力系数取0.54，隧道上方20 kPa超载，单侧有30 kPa偏载，如图 5（a）所示，这也是设计常用考虑偏载的荷载模型。基于等效刚度均质环法结构模型，计算得到弯矩响应如图 5（b）所示。

图 5 类矩形盾构隧道设计偏载工况结构状态

Figure 5. Quasi-rectangular tunnel under eccentric loading design state

下载: 全尺寸图片幻灯片

（2）试验荷载设计过程

由于设备限制，30个千斤顶加载点最多分为16组独立液压站控制，如图 6（a）所示。但即使千斤顶液压站分组不均，只要加载系统满足不同液压荷载组可独立加载的要求，本方法亦可有效对试验荷载进行设计计算。根据2.2节所述方法，通过16组液压分组确定包含13组加载情况的基础加载组系，部分基础加载组情况如图 6（b）所示。

图 6 类矩形试验荷载布置示意

Figure 6. Test loads of quasi-rectangular tunnel

下载: 全尺寸图片幻灯片

本次试验选取全环在设计水土荷载下的弯矩和轴力作为控制目标，权重系数取值方式为轴力仅对上半环较小区域取为1，下半部分轴力不控制，弯矩权重系数取为弯矩绝对值的根号。根据式（7），计算得到P1~P16每组的荷载如表 1所示。

表 1 试验荷载表

Table 1. Values of test loads 单位: kN

P1	P2	P3	P4	P5	P6	P7	P8
466.0	285.0	388.1	483.6	294.6	402.6	588.0	276.1

P9	P10	P11	P12	P13	P14	P15	P16
347.7	573.7	308.3	310.6	267.1	583.6	472.1	333.7

下载: 导出CSV

| 显示表格

（3）试验验证

根据表 1试验荷载，将结构在设计水土荷载和在试验荷载下的结构内力对比绘制于图 7。

图 7 水土荷载、试验荷载、实证试验类矩形隧道结构对比

Figure 7. Comparison of internal forces of Quasi-rectangular tunnel under design distributed load, design test load and real test load

下载: 全尺寸图片幻灯片

进一步基于荷载设计结果开展了原型结构试验验证^[12]（图 8（a）），并将部分关键截面的弯矩、轴力实测结果注于图 7。

图 8 类矩形、双圆盾构隧道原型结构试验平台

Figure 8. Prototype tests on Quasi-rectangular tunnel and DOT tunnel

下载: 全尺寸图片幻灯片

设计水土荷载和试验荷载下结构内力的对比验证了试验荷载设计方法的可行性。从对比结果来看，结构弯矩在大部分位置都较为匹配，局部偏差主要出现在偏载侧正弯矩控制截面附近。这是由于模型中千斤顶作用被视为指向管片内部的点荷载，腰部负弯矩区域试验荷载整体小于角部正弯矩区域，进而导致剪力和弯矩误差均较小，这也侧面反映出了隧道结构内部正、负弯矩产生机理的区别。由轴力对比可知，结构顶部的拟合效果最好，腰部次之，底部最差。这是由于千斤顶加载方向垂直于管片，较难模拟设计水土荷载下底部侧向力通过管片切向提供的结构底部轴力，权重系数的设置时选择性忽略了底部的轴力，也是与这一原因相统一的。从另一方面来看，试验荷载下结构轴力整体低于设计工况，所以管片截面处于更危险内力状态，试验结果也更偏保守，与原则（2）一致。

实证试验得到的部分截面内力监测值同样与试验荷载下结构的内力理论值保持着相近的整体分布，证明试验平台及对应试验荷载设计方法有效模拟了盾构隧道结构在非对称荷载状态下的受力状态。当然，试验结果与理论值仍存在一定偏差，这是由于理论值计算基于等效刚度均质环模型，而实际类矩形隧道结构的受力性能还受纵缝接头和刚域等特征影响^[12]。

足尺试验结果显示，类矩形盾构隧道在单侧偏载受荷状态下较为危险的位置为偏载侧顶底角部正弯矩区与腰部负弯矩区，相较于另一侧弯矩高了一半左右，且结构底角部更为危险。设计时广泛采用的等效刚度均质环模型计算结果相比实际试验结果较高，说明设计出的结构更偏安全。另一方面，结构最大收敛变形出现在偏载侧短轴（向内），接头变形方面则是^#3，^#6，^#8，^#9等接头较为显著。试验研究结果表明，结构设计时应考虑单侧偏载工况，同时应重点关注前述模拟和试验所反映出来的薄弱区域，在设计时作为关键设计控制点。

3.2 双圆、圆形盾构隧道偏载试验

（1）双圆盾构隧道

与类矩形盾构隧道偏载试验类似，双圆盾构隧道的荷载计算模型如图 9（a）所示，其整环试验加载点和部分基础加载组布置如图 9（b）所示，原型结构试验平台图如图 8（b）所示。采用同样步骤计算得到试验荷载后，将结构在设计水土荷载和在试验荷载下的结构内力响应、原型结构试验实证试验的关键截面内力实测结果对比于图 10所示。

图 9 双圆盾构隧道设计状态及试验状态荷载简图

Figure 9. Design loading and test loads of DOT tunnel

下载: 全尺寸图片幻灯片

图 10 水土荷载、试验荷载、实证试验双圆隧道结构内力对比

Figure 10. Comparison of internal forces of DOT tunnel under design distributed load, design test load, and real test load

下载: 全尺寸图片幻灯片

（2）圆形盾构隧道

圆形盾构隧道的荷载计算模型如图 11（a）所示，其整环试验加载点和部分基础加载组布置如图 11（b）所示。将结构在设计水土荷载和在试验荷载下的结构内力响应对比于图 12所示，其设计适用性也将后续通过原型结构试验证明。

图 11 圆形盾构隧道设计状态及试验状态荷载简图

Figure 11. Design loading and test load of circular tunnel

下载: 全尺寸图片幻灯片

图 12 设计水土荷载、试验荷载下圆形盾构隧道结构内力对比

Figure 12. Comparison of internal forces of circular tunnel under design distributed load and design test load

下载: 全尺寸图片幻灯片

整体而言，类矩形盾构隧道、双圆隧道和圆形隧道的结构非对称力学性能试验证明了本文所提出的试验平台和荷载设计方法的适用性。在试验设计阶段，能通过试验荷载准确模拟结构在设计水土荷载下的结构响应，在试验实证阶段，试验结果证明了试验方法的适用性，并进一步真实反应了盾构隧道结构在非对称荷载状态下的力学性能。

当然，受限于千斤顶的点荷载加载效果，试验荷载下结构弯矩分布呈现出显著的“锯齿”效应，如图 10（a），12（a）所示。实际试验中千斤顶并非点荷载，具有实际作用面积，另一方面加密千斤顶布置，也都能有效缓解这一效应。

4. 试验关键参数分析讨论

4.1 控制目标权重系数

在给定结构断面、设计水土荷载及计算模型的情况下，控制目标如荷载、变形、弯矩、轴力等都是固定的，不同控制目标重要性均可通过权重系数来调整。根据控制方程（6）及求解方程（7），调整权重系数（不同的模拟侧重点）可以得到不同的试验荷载设计结果，从而达到不同的模拟效果。

如实证章节图 12（a）所示，由于权重系数的取法是使总弯矩方差最小，故而试验荷载下结构弯矩总是“缠绕”在设计水土荷载下结构弯矩周围，呈现出部分偏高部分偏低的效应。为了说明目标权重调整对模拟效果的控制，同样以圆形隧道试验设计为例，给出另外两种权重系数取值方法：①第一种保证试验荷载下结构内力更安全，即弯矩总是较低，轴力较高；②第二种保证内力更危险，即弯矩总是较高，轴力较低。将不同权重系数计算得到的结构内力对比绘制于图 13。

图 13 不同权重设计水土荷载、试验荷载下圆形盾构隧道结构内力对比

Figure 13. Comparison of internal forces of circular tunnel under design test loads with different weight coefficients

下载: 全尺寸图片幻灯片

如图 13（a）所示，内力安全权重弯矩（绿色）始终包络于设计水土荷载弯矩（蓝色）包络于内力危险权重弯矩（紫色）。如图 13（b）所示，内力危险权重轴力（紫色）始终包络于设计水土荷载轴力（蓝色）包络于内力安全权重轴力（绿色），其中本文更推荐内力危险权重轴力（紫色）方案，使验证性试验更为保守。对比结果表明，权重系数的调整能有效改变拟合效果。除了算例所述考虑全环的弯矩和轴力外，若试验重点关注接头响应，亦可调整权重系数使接头位置弯矩、内力组合满足模拟要求。总之，由于试验荷载条件和设计水土荷载条件存在天然物理区别，无法做到100%完美模拟，故而在试验设计时应把握主要矛盾，明确具体试验目的，选取更为合适的权重系数。

4.2 计算模型

基于等效刚度均质环法计算模型进行结构分析是最为常见且简单的，由于模型中结构处于完全弹性状态，故式（4）中不同基础加载组内力的线性叠加也是可行的。当计算模型取其他弹性模型如部分解析法模型或接头刚度固定的梁-弹簧模型时，本文所给出的方法仍然适用。但对于非线性计算模型如接头转角受弯矩、轴力影响的梁-弹簧模型，之前方法中给出的控制方程将不再适用。为解决此问题，给出一种迭代方法用于计算试验荷载，有如下步骤：

（1）基于等效刚度均质环模型计算得到试验荷载的系数向量x，作为初始系数向量x₀。

（2）初始系数向量x₀通过式（2）得到试验荷载F₀，输入非线性计算模型，得到所有控制目标处的计算值 ${\boldsymbol{b}_0}$ 。

（3）计算最大修正量 $\Delta \boldsymbol{x}$ ，参考式（7）有

$\Delta \boldsymbol{x}=\left((\boldsymbol{\omega} \boldsymbol{M})^{\mathrm{T}} \cdot \boldsymbol{\omega} \boldsymbol{M}\right)^{-1} \cdot\left((\boldsymbol{\omega} \boldsymbol{M})^{\mathrm{T}} \cdot \boldsymbol{\omega} \cdot\left(\boldsymbol{b}-\boldsymbol{b}_0\right)\right) 。$

(8)

（4）欲求解下一项系数向量，定义带权误差指标，表征当前计算值与目标值的带权误差，有

${\varGamma _{0, \eta }} = ({\omega _1} \cdots {\omega _p}) \cdot (\boldsymbol{b} - {\boldsymbol{b}_0}) 。$

(9)

参考牛顿下山法，计算下一项系数向量

${\boldsymbol{x}_1} = {\boldsymbol{x}_0} + \eta \Delta \boldsymbol{x} 。$

(10)

在0~1内搜索最大的修正系数η，使下一项系数向量控制目标计算值所对应的带权误差指标是下降的。

（5）重复步骤（2）~（4），直至带权误差下降到可接受水平。

（6）通过x_n计算得到试验荷载F_n，计算完成。

由于迭代操作是基于系数向量进行的，所以每一次迭代后的系数向量所对应的试验荷载均满足2.1节中所提的原则（1），故而所设计的试验荷载是适用于非线性计算模型的，同时也是自平衡的。

4.3 结构断面形式

在实证章节中针对类矩形、双圆和圆形盾构隧道均开展了试验荷载设计。为定量对比不同断面形式的试验拟合效果，采用变异系数对拟合效果进行描述，（此处仅将管片全截面弯矩作为控制目标）有

$\left.\begin{array}{l}\delta =\sigma /\mu \text{，}\\ \sigma =\sqrt{\frac{1}{p}}{\Vert \boldsymbol{b}-{\boldsymbol{b}}_{n}\Vert }_{2}\text{，}\\ {\mu }_{1}=\sqrt{\frac{1}{p}}{\Vert \boldsymbol{b}\Vert }_{2}\text{，}\\ {\mu }_{2}=\sqrt{\frac{1}{p}}{\Vert \boldsymbol{b}\Vert }_{1}。\end{array}\right\}$

(11)

式中： $\sigma$ 为标准差，分别用1，2范数计算均值μ，将根据式（11）计算得到的3种结构的拟合变异系数列于表 2，同时给出了正、负弯矩区的方差贡献。

表 2 不同断面拟合结果变异系数对比

Table 2. Fitting situations of different cross-sections

断面形式	类矩形	双圆	圆形	圆形	圆形	圆形	圆形
总加载点数	30	32	24	24	24	24	24
基础加载组数	13	21	22	13	10	8	6
δ₁	0.119	0.277	0.089	0.092	0.094	0.101	0.224
δ₂	0.148	0.344	0.100	0.103	0.106	0.113	0.251
正弯矩区贡献	0.756	0.423	0.578	0.580	0.621	0.511	0.390
负弯矩区贡献	0.244	0.577	0.422	0.420	0.379	0.489	0.610

下载: 导出CSV

| 显示表格

计算结果表明，圆形隧道拟合效果优于类矩形隧道优于双圆隧道，这也与图 7，10，12反映出的弯矩模拟情况是一致的。从感性认知角度来看，所模拟的结构内力变化越复杂，对试验加载系统的布置要求也就越高。圆形隧道结构顶底正弯矩、腰部负弯矩，内力分布最为简单，类矩形隧道结构由于中柱的存在使顶底T块位置为负弯矩，内力分布稍复杂。而相较类矩形隧道，双圆隧道结构海鸥块位置内力分布更为复杂多变^[24]，也进而导致拟合效果相对较差。

另一方面，随基础加载组数下降，圆形隧道的拟合变异系数逐渐上升，即拟合误差逐渐增大。当基础加载组数较大时，适当减少基础加载组数对拟合效果影响不大，但当加载组数降至8组左右后，变异系数迅速增大。这一现象说明对结构复杂受荷状态的模拟有最低临界组数要求，换言之模拟精度是受限于试验平台能提供的最大独立荷载组数的。总而言之，对于越复杂的结构，越复杂的荷载，结构试验要精确模拟结构状态所需要的独立荷载组数也越多。

4.4 试验边界形式

（1）橡胶支座支承

在计算模型中考虑橡胶支座，设置为被动边界。如果认为试验时橡胶支座为弹性或处于局部弹性状态，那么在模型中将其设置为弹性边界，试验荷载的设计方法与前述无异。若考虑其超弹性或复杂非线性，则可参考4.2节中的迭代算法，将带橡胶支座边界的计算模型考虑为非线性模型，采用迭代法对试验荷载进行计算。若采用站立式试验平台，设计荷载时在计算模型中额外考虑重力，也是较为容易的。

（2）钢绞线加载

相比于千斤顶施加的点荷载，环箍钢绞线对结构的作用以均布荷载形式传递，故而对于水压的模拟更为精确与实际。考虑环箍钢绞线作用，在第2章给出的基础加载组系中额外增加一组钢绞线加载组，即向量x的元素数和矩阵M的列数均增长为n+1，该加载组对结构弯矩无影响，仅产生均匀轴力。

仍以24点加载圆形盾构隧道偏载状态为算例，在增加钢绞线加载组后，图 14（a）显示绿线几乎与蓝线重合，说明试验荷载弯矩拟合效果非常好。但在2.3已分析过，轴力的存在保证了计算得到的试验荷载都是正的。而组合加载方案中千斤顶负责模拟弯矩，环箍钢绞线负责模拟轴力，虽然模拟精度提升，但也导致左右侧腰部共计12个千斤顶的试验荷载计算值为负值，（图 14（a）中红色加载点）说明解是不适用的。采用2.3节中所提方案（1）进行迭代修正计算，当删去右侧腰部P6和P7后（如图 14（b）所示）所有千斤顶的设计荷载均为正，试验荷载解是适用的。

图 14 千斤顶、钢绞线组合加载方案模拟效果

Figure 14. Simulation effects of loading model combining hoop strand with hydraulic jacks

下载: 全尺寸图片幻灯片

对比修正前方案，修正后方案中钢绞线提供的轴力从820 kN下降至698 kN，拟合变异系数δ₁从0.0097上升至0.0166。修正前部分由钢绞线提供的轴力现由千斤顶提供，从而保证了试验荷载的合理性。虽然删去部分千斤顶牺牲了一定的拟合度，但相比于表 2仅采用千斤顶加载的变异系数0.089，其模拟精度有显著提升。可以认为钢绞线、千斤顶组合加载方案的效果是较优的，本文所给出的修正方法也是适用的。

5. 结论

（1）开发了能用于盾构隧道原型结构试验研究的试验平台，该平台适用于不同断面盾构隧道结构和不同复杂荷载状态的模拟，针对类矩形盾构隧道、双圆隧道和圆形隧道的偏载荷载状态足尺试验研究也验证了试验平台和试验荷载设计方法的适用性。

（2）为模拟隧道结构所受复杂荷载状态，给出了基于多组独立液压分组加载的试验荷载设计方法，在给定控制目标和权重系数的条件下能得到较优的复杂荷载状态模拟效果。该设计方法不仅易满足自平衡条件，而且算法简单直观。

（3）试验荷载设计时应明确拟合目标，通过权重系数的调整以达到需要的模拟效果。本文建议使试验荷载下结构整体相比于设计水土荷载下更危险（弯矩整体更高、轴力整体更低），使验证性试验更为保守。

（4）本文设计方法基于弹性计算模型和边界支承条件提出，但采用迭代算法进行修正后，依然可适用于非线性计算模型或边界支承条件下的试验荷载求解。

（5）同样条件下，圆形隧道拟合精度高于类矩形隧道高于双圆隧道，对结构在复杂荷载状态下的模拟强烈依赖于试验装置所能提供的最大独立荷载组数（即所有加载点由多少组独立液压站控制）。对于越复杂的荷载状态、越复杂的结构和越复杂的内力状态，精确模拟所需的独立液压站组数也越高。

（6）钢绞线和千斤顶的组合加载模式能有效提升盾构隧道结构试验对复杂荷载状态的模拟精度，其拟合变异性可降低至仅采用千斤顶加载模式的1/5。但在试验荷载设计时需要考虑试验荷载的非负性，删去部分加载点以使计算得到的试验荷载是合理且适用的。

整体而言，本文所提出的试验平台和荷载设计方法适用于大部分的弹性、部分弹塑性阶段盾构隧道结构原型试验研究，但仍有一些问题亟待解决。如在给定有限液压站分组和加载点数（千斤顶数）条件下，如何对加载点进行分组和布置位置优化，以达到给定条件下的最好模拟效果。如对其他异型盾构隧道如马蹄形、圆角矩形等，所提方法的适用性也有待后续研究进一步优化发展及实践检验。

图 1 深层搅拌水泥土格栅处理地基

Figure 1. Deep soil mixing (DSM) grid-improved ground

下载: 全尺寸图片幻灯片

图 2 超重力离心模型试验布置图

Figure 2. Schematic diagram of centrifuge models

下载: 全尺寸图片幻灯片

图 3 福建砂+10%高岭土及福建粗砂颗分曲线

Figure 3. Grain-size distribution curves of Fujian sand with Kaolin clay of 10% and Fujian coarse sand

下载: 全尺寸图片幻灯片

图 4 水泥土格栅墙振后损伤状态

Figure 4. Post-shaking conditions of soil-cement grid

下载: 全尺寸图片幻灯片

图 5 加速度时程

Figure 5. Time histories of acceleration

下载: 全尺寸图片幻灯片

图 6 加速度反应谱比

Figure 6. Spectral acceleration ratios

下载: 全尺寸图片幻灯片

图 7 超静孔压比时程

Figure 7. Time histories of excess pore pressure ratio

下载: 全尺寸图片幻灯片

图 8 峰值剪应变剖面

Figure 8. Profile of peak shear strain

下载: 全尺寸图片幻灯片

表 1 福建砂+10%高岭土及福建粗砂物性参数表

Table 1 Physical properties of Fujian sand with Kaolin clay of 10% and Fujian coarse sand

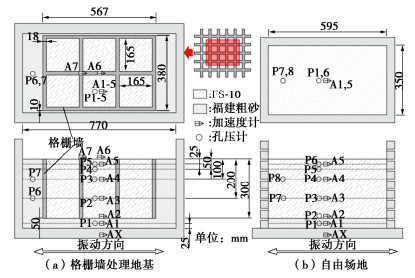
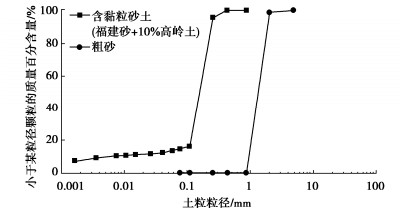
物性参数	符号	单位	FS-10	福建粗砂
土粒密度	ρ_s	g/cm³	2.651	2.648
最大孔隙比	e_max	—	1.143	0.801
最小孔隙比	e_min	—	0.60	0.568
细粒含量	F_c	%	15	0.2
平均粒径	D₅₀	mm	0.1578	1.31
渗透系数	k	m/s	8.04×10^-6	7.14×10^-3

下载: 导出CSV

表 2 振动事件

Table 2 Shaking events

模型	振动顺序	设计PBA/g	实际PBA/g	I_a/(m·s^-1)
SC	M1	0.40	0.45	32.8
SC	M2	0.15	0.20	7.8
FF	M1	0.15	0.22	7.4
	M2	0.40	0.50	34.6
	M3	0.15	0.21	7.0

下载: 导出CSV

参考文献(9)

[1]	KITAZUME M, TERASHI M. The Deep Mixing Method[M]. Florida: CRC Press, the United States of America, 2013.
[2]	ISHIKAWA A, ASAKA Y. Seismic responses of column and grid-type improved grounds[C]//Proceedings of the 6th International Conference on Physical Modelling in Geotechnics, Hong Kong, R P China, 2006: 521-526.
[3]	RAYAMAJHI D, TAMURA S, KHOSRAVI M, et al. Dynamic centrifuge tests to evaluate reinforcing mechanisms of soil-cement columns in liquefiable sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(6): 04015015. doi: 10.1061/(ASCE)GT.1943-5606.0001298
[4]	SUZUKI Y, SAITOH S, ONIMARU S, et al. Grid-shaped stabilized ground improved by deep cement mixing method against liquefaction for abuilding foundation[J]. Journal of the Japanese Society of Soil Mechanics and Foundation Engineering, 1996, 44(3): 46-48.
[5]	TOKIMATSU K, MIZUNO H, KAKURAI M. Building damage associated with geotechnical problems[J]. Soils and Foundations-Special Issue, 1996, 1: 219-234.
[6]	李艳, 程谦恭, 张建磊, 等. 倾斜可液化场地中矩形闭合型地下连续墙桥梁基础动力特性研究[J]. 岩土工程学报, 2019, 41(5): 959-966. doi: 10.11779/CJGE201905020 LI Yan, CHENG Qiangong, ZHANG Jianlei, et al. Seismic behavior of rectangular closed diaphragm walls as bridge foundations in slope liquefiable deposits[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(5): 959-966. (in Chinese) doi: 10.11779/CJGE201905020
[7]	许成顺, 汪洋筱珊, 杜修力, 等. 分体柱在地下车站结构中的减震效果研究[J]. 岩土工程学报, 2021, 43(4): 624-633. doi: 10.11779/CJGE202104004 XU Chengshun, WANG Yangxiaoshan, DU Xiuli, et al. Seismic mitigation effects of split columns in underground station structures[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(4): 624-633. (in Chinese) doi: 10.11779/CJGE202104004
[8]	张梓鸿, 许成顺, 闫冠宇, 等. 液化夹层场地地铁车站结构离心机振动台试验方案设计[J]. 岩土工程学报, 2022, 44(5): 879-888. doi: 10.11779/CJGE202205011 ZHANG Zihong, XU Chengshun, YAN Guanyu, et al. Experimental design for dynamic centrifuge tests on a subway station structure in liquefied interlayer site[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(5): 879-888. (in Chinese) doi: 10.11779/CJGE202205011
[9]	CAO Y, KURIMOTO Y, ZHOU Y G, et al. Centrifuge model tests on liquefaction mitigation effect of soil-cement grids under large earthquake loadings[J]. Bulletin of Earthquake Engineering, 2023, 21(9): 4217-4236.

施引文献(41)

期刊类型引用(19)

1.	许博闻，兰恒星，刘世杰. 界面形态对黄土-泥岩接触面剪切力学特性影响研究. 工程地质学报. 2024(02): 448-462 . 百度学术
2.	黄晓虎，魏兆亨，易武，郭飞，黄海峰，肖宇煌. 裂隙优势流入渗诱发堆积层滑坡浅层破坏机理研究. 岩土工程学报. 2024(06): 1136-1145 . 本站查看
3.	赵宽耀，许强，陈婉琳，彭大雷，高登辉. 黄土塬边漫灌区土体水入渗过程研究. 岩土力学. 2024(09): 2754-2764 . 百度学术
4.	王立朝，任三绍，李金秋. 降雨作用下古滑坡复活机理物理模拟试验研究. 中国地质灾害与防治学报. 2024(05): 21-31 . 百度学术
5.	王诏楷. 地下水人工回灌颗粒沉积研究进展. 江淮水利科技. 2023(01): 9-14 . 百度学术
6.	周峙，罗易，张家铭，孙狂飙. 考虑裂隙面积率的裂隙性黏土优势流双域入渗规律研究. 安全与环境工程. 2023(02): 109-118 . 百度学术
7.	吴玮江，宋丙辉，刘迪，安亚鹏. 黄土塬区包气带水分运移特征研究. 水文地质工程地质. 2023(03): 12-22 . 百度学术
8.	曾鹏，王宇豪，张天龙，张琳，南骁聪. 基于NSGA-Ⅱ遗传算法的黄土滑坡参数反分析与稳定性预测. 地球科学. 2023(05): 1675-1685 . 百度学术
9.	冯乐涛，吴玮江，刘兴荣，宿星，万朝东. 黄土高原降水入渗方式与引发滑坡研究——以甘肃黄土地区为例. 科学技术与工程. 2023(14): 5937-5945 . 百度学术
10.	许增光，李海洋，柴军瑞，曹成，陈东来. 堤坝内集中渗漏通道与周围介质水量交换研究. 水力发电学报. 2023(07): 12-23 . 百度学术
11.	赵宽耀，许强，高登辉，刘方洲，彭大雷，陈婉琳. 坡底饱和型黄土滑坡离心模拟试验. 岩土力学. 2023(11): 3213-3223 . 百度学术
12.	赵鲁庆，彭建兵，马鹏辉，冷艳秋，朱兴华. 黄土细观界面及其灾害效应研究初探. 工程地质学报. 2023(06): 1783-1798 . 百度学术
13.	许强，陈婉琳，蒲川豪，袁爽，刘佳良. 基于自然的解决方案在黄土高原重大工程灾变防控中的理论与实践. 工程地质学报. 2022(04): 1179-1192 . 百度学术
14.	宁瑞浩，冷艳秋，何芝远，李泽坤，马哲. 基于CT的黄土孔隙尺度优先流特性. 科学技术与工程. 2022(23): 9927-9936 . 百度学术
15.	蒋小虎，黄跃廷，胡海军，陈铄，陈锐，王崇华，汪慧，康顺祥. 基于原位双环、试坑浸水试验和数值模拟反演的Q_3黄土饱和渗透系数对比研究. 岩土力学. 2022(11): 2941-2951 . 百度学术
16.	李同录，汪颖，胡向阳，李萍，王宇. 厚层非饱和黄土中优势流和活塞流的讨论. 工程地质学报. 2022(06): 1842-1848 . 百度学术
17.	张永双，吴瑞安，任三绍. 降雨优势入渗通道对古滑坡复活的影响. 岩石力学与工程学报. 2021(04): 777-789 . 百度学术
18.	孙恒飞，朱兴华，成玉祥，张智锋，张卜平，蔡佳乐. 黄土优势渗流研究进展与展望. 自然灾害学报. 2021(06): 1-12 . 百度学术
19.	侯孝东，涂国祥，邱潇，李明，王清，钱昭宇. 汉源九襄地区深厚砾石层渗透特性研究. 水利与建筑工程学报. 2020(04): 192-197 . 百度学术