Characteristics of compressive bearing capacity and resistance to foundation freeze-thaw of the isolation helical pile
-
摘要: 基于针对竖向承载并消除地基冻融影响需求所设计的隔离式螺旋桩，结合物理模型试验与有限元数值方法，从桩体受力视角对比揭示了两种特征螺旋桩（S/D＜S/Dcr与S/D≥S/Dcr）受压沉降时桩身受力演化、荷载传递与地基响应特征，以及桩体几何参数对单桩承载力的影响规律及机理；验证了该新型桩抵抗地基冻融变形性能。结果表明：①两种特征桩型底螺旋及以下桩身在受荷沉降过程具有相同受力及演化特征，而其余上部螺旋端阻和螺旋间桩侧摩阻大小及演化特征差异显著。②S/D≥S/Dcr桩各螺旋端阻相当，且螺旋对下卧土施加附加应力显著提高了其下桩侧摩阻力，并主导了螺旋间桩侧摩阻自上而下近指数衰减趋势；S/D＜S/Dcr桩上部螺旋端阻仅约为1/5底螺旋端阻。③两种特征桩型单桩承载力随顶螺旋埋深比、螺旋直径与螺旋数量增长线性提升，随中心桩桩径增长先线性增大后加速衰减，桩型参数对S/D≥S/Dcr桩承载力影响更显著；S/D＜S/Dcr桩承载力随S/D增长显著提升，相反S/D≥S/Dcr桩承载力线性衰减。④螺旋桩较传统桩具有显著抗地基冻融变形影响优势，在冻土深度内设置隔离套可进一步消除影响。Abstract: Based on the isolation helical piles designed to resist vertical loads and eliminate the effects of freeze-thaw of foundation, the characteristics of force evolution, load transfer, and foundation response of two typical types of helical piles (S/D < S/Dcr and S/D≥S/Dcr) during settlement, as well as the influences and mechanisms of pile geometries on the bearing capacity of the single pile are revealed from the perspective of pile force. Furthermore, the performance of the new piles against freeze-thaw deformation of foundation is examined. The results show that: (1) The bottom helixes and the lower pile bodies of the two typical piles share the same stress characteristics during the settlement, whereas the stress magnitude and evolution characteristics of end resistances of the remaining upper helixes and side friction resistances of inter-helixe piles differ significantly. (2) The end resistance of each helix of piles with S/D≥S/Dcr is essentially equal, and the additional stress that the helixes exert on the underlying soil significantly enhances the side friction of piles. This also determines the top-down near-exponential decay trend of the pile side frictional resistance between the helixes. The end resistances of the upper helixes are only about 1/5 of the bottom ones for the piles with S/D < S/Dcr. (3) The compressive bearing capacities of the two types of piles all grow linearly as the embedment ratio, helix diameter and helix number increase, and linearly increase first and then decrease rapidly with the increment of pile diameters. These pile geometries possess heavier impacts on the bearing capacity of piles with S/D≥S/Dcr. The bearing capacity of piles with S/D < S/Dcr increases significantly with the increase of S/D, whereas that of piles with S/D≥S/Dcr decreases linearly. (4) The helical pile has a significant advantage over the conventional pile in resisting the impact of freeze-thaw deformation of foundation. The impact can be further eliminated by installing an isolation sleeve on the pile within the frozen soil depth.
-
0. 引言
螺旋桩通过在等直径桩体上增设螺旋叶片实现了其单桩承载力的显著提高，并具有可快速、弱扰动沉桩，以及环保、经济等功能性优点[1-2]。随着近几十年液压扭矩机械的发展，螺旋桩正在被广泛研究应用于各种抗拔[3-4]、抗压[5]与抗侧向力[6]场景中。
然而，螺旋桩相比传统等直径桩更为复杂的桩体几何也导致能显著影响其承载能力的桩体几何参数众多，影响特征与机理更为复杂。螺旋间距比（S/D，螺旋间距与螺旋直径比）是影响螺旋桩最终地基破坏模式的关建桩型参数：在某临界螺旋间距比（S/Dcr）前后，地基破坏分别呈现为底部和顶部螺旋之间筒状土体剪切破坏，以及各螺旋下卧土独立受压破坏，相应承载力设计方法分别称为圆柱面剪切法与单盘承载法[7]。不同地基破坏模式是桩体受荷时荷载传递特征差异的最终宏观展现，进而使得相同情况下两种特征桩型的单桩承载力往往差距明显。大量研究[8-10]尝试找到引起螺旋桩承载特性转变的确切临界S/D值，但目前各研究结果间仍存在不同程度差异。另外，顶螺旋埋深比[11]、中心桩桩径[12]、螺旋直径[13]、螺旋数量[14]等其余众多桩型参数同样显著影响着螺旋桩承载特性。各种因素的交织影响为形成准确的螺旋桩承载力设计方法带来了挑战[15]。
目前对螺旋桩的应用研究多集中于各种抗拔场景，但其同样优异的竖向承载能力使其具有代替传统桩成为建筑领域，特别是需要快速施工的临时建筑邻域主流基桩的潜力[16-17]。已有针对螺旋桩在不同土质条件中受压的临界S/D值、荷载-位移特征、荷载传递特征与桩型参数影响特征研究[18-19]。但现有研究侧重于宏观分析地基土响应与荷载-位移曲线特征，缺少对承载过程中桩体受力演化分析，以及从桩体受力视角认识螺旋桩荷载传递特征及其机理，不利于更准确的单桩承载力计算方法的实现。此外，在保持其它因素相同情况下，顶螺旋埋深比、中心桩桩径、螺旋直径、螺旋数量、螺旋间距比等桩型参数变化对两种特征桩型螺旋桩（S/D＜S/Dcr与S/D≥S/Dcr）各自承载特性的影响特征及机理的对比分析更是缺乏。中国对螺旋桩研究起步较晚，亟需研究积累相关设计与应用经验。
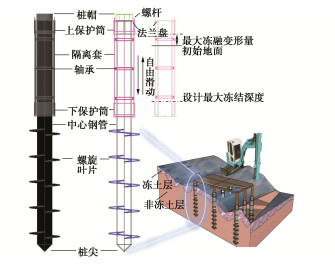
以针对某寒区山地赛场临时看台工程快速施工，有效提高地基承载力，并消除地基冻融变形影响需求所研制的一种隔离式抗冻融循环螺旋钢桩[20]为基础桩型（图 1），结合室内物理模型试验与数值模拟试验，首先查明所设计螺旋桩在试验条件下的S/Dcr值，进而从桩体受力视角对比揭示两种特征桩型螺旋桩（S/D＜S/Dcr与S/D≥S/Dcr）各自在竖向受荷沉降过程中的桩身受力演化、荷载传递与地基响应特征，阐明顶螺旋埋深比、中心桩桩径、螺旋直径、螺旋数量、螺旋间距比等桩型参数对两种特征桩型单桩承载力的影响规律及其机理。建立水-热-力多场耦合数值分析模型，探究桩基在冻融循环作用下的桩体位移响应特征，验证其抵抗地基冻融变形能力。研究成果可丰富螺旋桩抗压承载设计与使用经验，并为广阔寒区抗冻融地基处理提供新参考方案。
1. 试验材料及方法
1.1 土体及桩-土界面参数
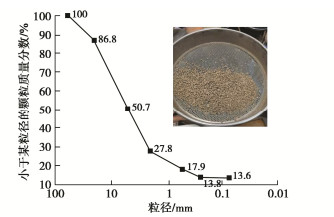
取工程现场土根据《土工试验方法标准》（GB/T 50123—2019）开展室内土工试验确定土样基本物性参数（表 1），其中土样颗粒级配曲线如图 2所示，根据《土的工程分类标准》（GB/T 50145—2007）可确定为含细粒土砾。
表 1 土样的基本物性参数Table 1. Basic physical parameters of soil sample塑限wP/% 液限wL/% 塑性指数IP 最优含水率wOP/% 最大干密度ρd max/(g∙cm-3) 11.3 21.5 10.2 9.7 2.07 进一步开展土体及桩-土界面直剪试验，提供数值试验所需力学参数。直剪土体含水率控制为土样最优含水率，干密度控制为95%土样最大干密度。制作与环刀等直径、1/2环刀高度钢垫块，称取环刀样1/2体积所需质量的土样倒入内含垫块的环刀中，进而静压制样形成钢-土界面以开展桩-土界面直剪试验。
1.2 单桩抗压试验
（1）物理模型试验
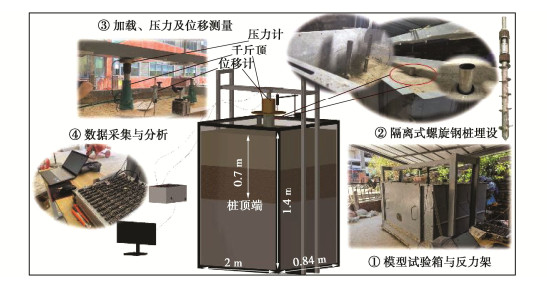
制作0.8 m试验桩（沉桩0.7 m）、长×宽×高=2 m×0.84 m×1.4 m的模型箱开展单桩抗压物理模型试验（图 3），以获得螺旋桩荷载-沉降特征，并指导、验证数值模型建立。桩与模型箱边界距离大于5倍桩径, 箱深2倍于桩埋深。通过沿桩体轴心放置的千斤顶实现桩端加载，压力与位移分别由千斤顶与反力架之间设置的压力计，千斤顶底部设置的位移计监测，并通过数据采集系统实时记录。采用等量分级加载，第一级加载取1/5预估承载力，后续分级荷载取1/10预估承载力，在前一级载荷下桩体沉降速率呈收敛趋势后施加下一级荷载。通过压力计实时读数反馈微调千斤顶顶盘外升或回缩实现荷载维持。
![]()
图 3 单桩抗压物理模型试验系统Figure 3. Physical model test system for compression of a single pile（2）数值分析试验
a）计算参数
利用ABAQUS有限元平台开展单桩抗压数值试验。桩体采用弹性模型，土体采用Mohr-Coulomb弹塑性模型考虑土体塑性。具体材料及界面参数见表 2。
表 2 数值模型材料参数Table 2. Material parameters of numerical model参数 密度ρ/(kg∙m-3) 弹性模量E/GPa 泊松比$ \nu $ 内摩擦角φ/(°) 黏聚力c/kPa 钢桩 7850 200 0.3 — — 土体 2157 0.02 0.3 36.87 8.51 桩土界面 — — — 23.27 0.20 b）几何模型与边界条件
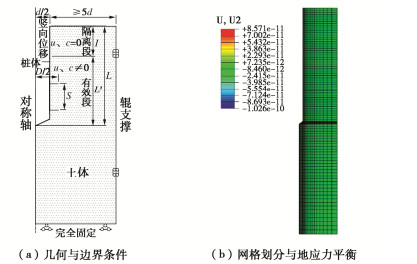
数值试验几何模型与边界条件如图 4（a）所示。为合理简化计算，忽略隔离套下保护筒外伸圆盘承载力贡献，将隔离段视为与中心桩等直径；螺旋螺距小，对单桩承载特性几乎无影响[11]，故将螺旋视为完整圆盘。最终桩体简化为二维轴对称模型。设置土体深度不小于2倍桩埋深，土体半径不小于10倍桩半径。
![]()
图 4 数值试验的几何模型、边界条件与网格划分Figure 4. Geometries, boundary conditions and meshing of numerical tests桩身隔离段桩-土界面设置为无摩擦接触，以模拟由可沿中心桩自由滑动隔离套所实现的阻断中心承载钢管与四周土体切向力传递效果；其余有效段桩身与周围土体摩擦接触。通过在中心钢管上端面施加竖向位移边界模拟竖向加载。模型网格划分与地应力平衡效果如图 4（b）所示。
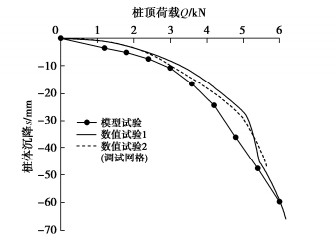
为检验网格划分对试验结果的影响，进行了不同网格划分情况下的单桩抗压数值分析试验。对比相同条件下数值分析与物理模型试验所得Q-s曲线（图 5），可认为试验结果在误差允许范围内符合度较高，所建立数值分析模型可较准确反应实际承载特性。
1.3 桩基冻融数值分析试验
利用COMSOL有限元平台，考虑孔隙冰含量和未冻水含量与土体负温、水分迁移之间的动态平衡关系建立冻土水-热全耦合模型，再引入水分迁移、相变与土体应变关系搭建冻土水-热-力多场耦合模型[21]。
考虑冰-水相变潜热的传热方程为
$$ \rho C(\theta )\frac{{\partial T}}{{\partial t}} = \lambda (\theta ){\nabla ^2}T + L \cdot {\rho _{\rm{i}}}\frac{{\partial {\theta _{\rm{i}}}}}{{\partial t}} 。 $$ (1) 式中：ρ，$ {\rho _{\rm{i}}} $分别为土体与冰的密度；C(θ)为比热容；T为温度；$ t $为时间；$ \lambda (\theta ) $为导热系数；L为水相变潜热；θ，θi分别为土体体积含水量与孔隙冰体积含量；$ \nabla $为微分算子。
考虑桩体传热影响，其热传导方程为
$$ {\rho _{\rm{p}}}{C_{\rm{p}}}\frac{{\partial T}}{{\partial t}} = {\lambda _{\rm{p}}}{{\mathit{\nabla}} ^2}T 。 $$ (2) 式中：ρp，Cp，$ {\lambda _{\rm{p}}} $分别为桩密度、比热容与导热系数。
冻土中水分迁移方程为
$$ \frac{{\partial {\theta _{\rm{u}}}}}{{\partial t}} + \frac{{{\rho _{\rm{i}}}}}{{{\rho _{\rm{w}}}}}\frac{{\partial {\theta _{\rm{i}}}}}{{\partial t}} = \nabla \left[ {D({\theta _{\rm{u}}})\nabla {\theta _{\rm{u}}} + k({\theta _{\rm{u}}})} \right] 。 $$ (3) 式中：D(θu)为冻土中水的扩散率，
$$ D({\theta _{\rm{u}}}) = k({\theta _{\rm{u}}})/c({\theta _{\rm{u}}}) \cdot I \text{, }\; $$ (4) $$ k({\theta _{\rm{u}}}) = {k_{\rm{s}}} \cdot {S^l}{\left[ {1 - {{(1 - {S^{1/m}})}^m}} \right]^2} \text{, }\; $$ (5) $$ c({\theta _{\rm{u}}}) = {a_0}m/(1 - m) \cdot {S^{1/m}}{(1 - {S^{1/m}})^m} , $$ (6) $$ I = {10^{ - 10{\theta _{\rm{i}}}}} \text{, }\; $$ (7) $$ S = {{({\theta _{\rm{u}}} - {\theta _{\rm{r}}})} / {({\theta _{\rm{s}}} - {\theta _{\rm{r}}})}} 。 $$ (8) 式中：k(θu)为非饱和土渗透系数；ks为饱和土渗透系数；c(θu)为比水容量；I为孔隙冰对未冻水的阻滞系数；S为冻土相对饱和度；θr为残余含水量，θs为饱和含水量；l，m，a0为受土性影响的参数。
水、热联系方程为
$$ {B_I} = \frac{{{\theta _{\rm{i}}}}}{{{\theta _{\rm{u}}}}} = \left\{ \begin{gathered} 1.1{(T/{T_{\rm{f}}})^B} - 1.1\begin{array}{*{20}{c}} {}&{} \end{array}(T < {T_{\rm{f}}}) \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array}0\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{} \end{array}\;\;\;\;\;\;\;\;(T \geqslant {T_{\rm{f}}})} \end{array}} \end{array} \hfill \\ \end{gathered} \right. 。 $$ (9) 式中：BI为固液比；B为由土性所决定的常数；Tf为土体冻结温度。
仅考虑水分相变和迁移导致的土体应变εv将力场与水热场联系起来，通过下式计算[22]：
$$ {\varepsilon _{\rm{v}}} = 0.09({\theta _0} + \Delta \theta - {\theta _{\rm{u}}}) + \Delta \theta - n 。 $$ (10) 式中：θ0为前一状态含水量；Δθ为迁移水量；n为冻土孔隙率。
为在满足研究需求的基础上合理简化计算，忽略土体比热容与导热系数在冻融过程中的变化，计算所用热力学与水力学参数见表 3[23]。
表 3 桩基冻融数值分析试验参数Table 3. Parameters of numerical tests on freeze-thaw of foundation参数 C/(J∙kg-1∙K-1) λ/(W∙m-1∙K-1) ks/(m∙s-1) l m 土(桩) 890(475) 1.38(44.50) 10-6 0.50 0.14 参数 a0 θr θs B Tf/℃ 土(桩) 0.66 0.05 0.42 0.53 -0.18 2. 桩身受力演化与荷载传递
2.1 桩身受力演化与地基破坏特征
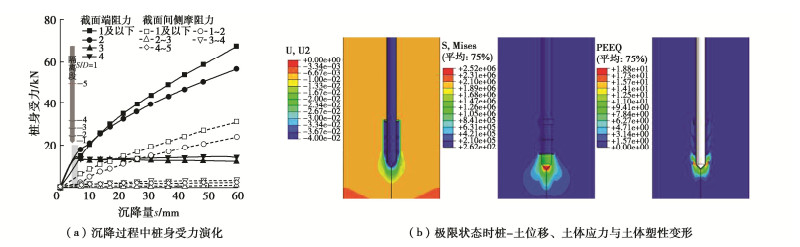
试验中发现当螺旋桩S/D增大至3时，地基破坏模式从螺旋间筒状土体剪切破坏转变为各螺旋下卧土独立受压破坏，故确定S/Dcr=3为试验条件下螺旋桩的临界螺旋间距比。如图 6（a）所示，S/D < S/Dcr桩的桩端和底螺旋端阻在桩体受荷沉降过程中持续增长，且由于桩端埋深更大，其端阻增长速率大于底螺旋端阻增长率，在桩体达一定沉降量后（约10 mm）桩端端阻保持为单桩承载力最大来源。特别的，中间及顶层螺旋端阻力大小与变化趋势在桩体沉降全过程中几乎保持一致，二者在沉降约5 mm后停止增长，而后几乎不再变化。摩擦力对单桩承载力的贡献明显小于端阻力贡献。其主要来源于底螺旋以下桩身侧摩阻，并在沉降过程中保持较大增长趋势。各螺旋间桩身几乎无侧摩阻，且由于试验桩尺寸、土体黏聚力小，顶螺旋以上较长的有摩擦桩身对承载力贡献同样微小。桩体隔离段由于隔离套隔绝了中心受力桩身与土体的切向力传递, 未起承载作用。
![]()
图 6 S/D＜S/Dcr时桩身受力与地基破坏特征Figure 6. Characteristics of pile force and foundation failure when S/D < S/Dcr在此桩身受力特征下，地基宏观响应为桩端及底螺旋下卧土体出现显著高应力、高塑性变形区，结合端阻力演化特征可判断桩端及底螺旋共同起着端承作用，其下卧土为桩体荷载的主要持力土体；中间螺旋与顶螺旋下卧土体应力小，且螺旋间所夹筒状土体外缘出现显著的贯通塑性变形区，综合中间螺旋与顶螺旋端阻，以及螺旋间桩身侧摩阻变化趋势，符合该筒状土体受剪特征（图 6（b））。最终，地基中桩端应力泡范围内土体，以及螺旋叶片间及其附近筒状土体组合形成“子弹状”较大沉降土体。地基破坏模式呈现螺旋叶片间筒状土体早早发生剪切破坏，而后桩体继续沉降直至桩端与底螺旋下卧土受压破坏。
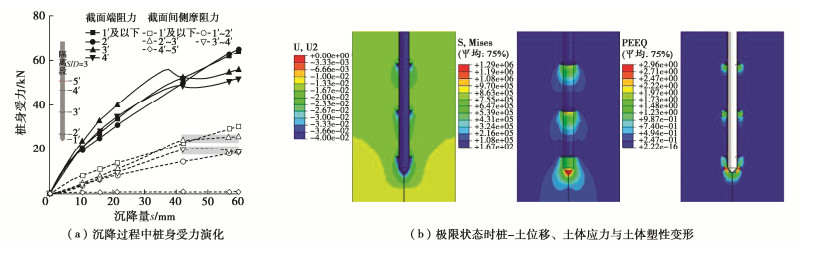
如图 7（a）所示，S/D≥S/Dcr桩的桩端和底螺旋端阻大小及其相互关系随桩体沉降的变化趋势均与S/D < S/Dcr桩相同，但明显不同的是其底螺旋以上各螺旋的端阻力在沉降全过程中均保持总体增长趋势，并且在达到下卧土极限状态前其端阻力大小与桩端和底螺旋端阻力相当。此外，螺旋间桩身同底螺旋以下桩身一样具有较大侧摩阻，但其在顶层及中间螺旋下卧土体达极限状态后停止了随沉降过程的增长趋势。
![]()
图 7 S/D≥S/Dcr时桩身受力与地基破坏特征Figure 7. Characteristics of pile force and foundation failure when S/D≥S/Dcr此时地基中除因试验桩型桩端与底螺旋距离较小，二者下卧土体出现应力重叠外，其余螺旋下卧土体均出现独立的显著高应力、高塑性变形区，呈现各部位独立起端承作用的地基土持力特征（图 7（b））。相应的，各独立端承部位应力泡范围内地基土组合形成“串珠状”较大沉降土体，最终地基破坏模式呈现为各螺旋及桩端下卧土体先后受压破坏。
2.2 荷载传递特征及机理
以上分析表明在试验土质条件下，不同桩型螺旋桩抗压承载力均主要由桩端及螺旋端阻力贡献，并且多端阻效应使其竖向受荷Q-s曲线相较于普通等直径桩具有更明显的缓变特征[19]。该类型桩常按控制沉降量（40~60 mm）确定其极限承载力[24]，故后文取40 mm作为特征沉降量开展承载特性分析。
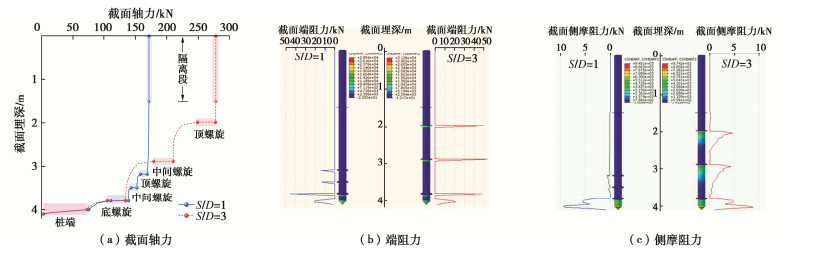
图 8（a）中显示了两种特征桩型在受荷沉降达40 mm时各自的桩身轴力分布情况。可见尽管两种桩型在沉降过程中受力演化与地基破坏模式差别显著，但其桩身轴力分布总体特征基本一致，沿桩尖自下而上：桩尖端阻与侧摩阻组合使桩身轴力在桩端部位平稳增长；桩端至底螺旋，及各螺旋之间呈加速增大的桩身侧摩阻导致桩身轴力相应加速增大；各螺旋端阻力引起桩身截面轴力突增，轴力分布曲线在相应截面深度处出现轴力增长平台；顶螺旋以上摩擦段桩身微小侧摩阻力引起轴力连续的微小增长；隔离段桩身无侧摩阻、无端阻，桩身轴力等于桩顶竖向荷载。
![]()
图 8 桩身轴力、端阻力与侧摩阻力分布Figure 8. Distribution of axial force, end resistance and side friction of piles然而两种桩型底螺旋以上各螺旋端阻力（图 8（b））及螺旋间桩身侧摩阻力（图 8（c））大小的显著差异，最终导致S/D=3桩的单桩承载力较S/D=1桩提高了62%。造成承载力差异的根本原因是两种桩型底螺以上各螺旋端阻力来源不同。当S/D＜S/Dcr时，底螺以上各螺旋端阻来源于螺旋间所夹筒状土体受剪反力，最大端阻力等于筒状土体抗剪强度；当筒状土体剪切破坏后，端阻力来源于筒状土体与周围土体的摩擦力。而当S/D≥S/Dcr时，各螺旋下卧土体受压破坏无法形成贯通的破坏面，各自独立起着端承作用。此时螺旋端阻力源于下卧土体侧限受压反力，最大端阻力等于下卧土体侧限抗压强度，明显高于S/D＜S/Dcr时筒状土体抗剪强度及其与周围土体的摩擦力。
另外，桩身侧摩阻力大小受桩周土体侧压力影响。与普通等直径桩只存在唯一端承部位（桩端），其下再无摩擦桩身不同，螺旋叶片端承作用将荷载传递至地基土中时对土体施加着附加应力，地基土侧向膨胀会增大其以下桩身侧摩阻。S/D≥S/Dcr桩更明显的螺旋端承作用向其下卧地基土施加着更大附加应力，进而更明显增大螺旋以下桩身侧摩阻力。因此，在荷载作用范围内地基土中附加应力沿深度增加而加速衰减规律也主导了螺旋以下桩身侧摩阻力自上而下加速衰减的变化趋势。现有螺旋桩承载力计算方法[15]往往未考虑螺旋下卧土附加应力对桩身侧摩阻力的贡献。
3. 桩型参数对承载力的影响及机理
设置如表 4所示的初始桩型参数，开展仅改变所探讨桩型参数、保持其余参数为初始值的单因素试验，对比分析顶螺旋埋深比（顶螺旋埋深与螺旋直径比H/D，通过改变桩长L实现）、中心桩桩径d、螺旋直径D、螺旋数量n和螺旋间距比S/D对两种特征桩型螺旋桩（S/D < S/Dcr，S/D≥S/Dcr）单桩承载力的影响特征与影响机理。
表 4 初始桩型参数Table 4. Original parameters of pilesL/m d/m D/m n/片 S/D 4.0 0.2 0.3 2 1或3 注：隔离段和底螺旋距桩底距离分别保持为1.5，0.2 m。 3.1 顶螺旋埋深比H/D的影响
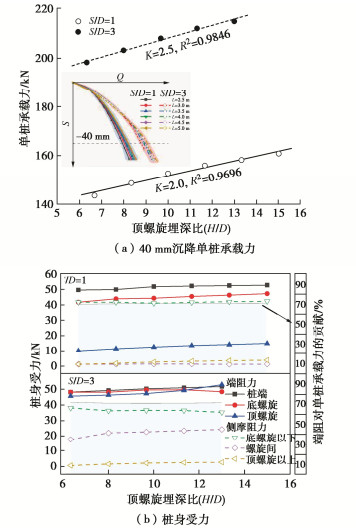
顶螺旋埋深比H/D对两种特征桩型螺旋桩单桩承载力的影响特征如图 9所示。由于在保持其它桩型参数不变情况下，H/D增大代表着中心桩桩长增大，桩端及各螺旋叶片埋深都相应增大，所以无论是S/D < S/Dcr桩螺旋间筒状土体抗剪强度还是S/D≥S/Dcr桩各螺旋下卧土体抗压强度都随之线性增长；同时更长的桩身也有利于总侧摩阻力的增长。所以两种特征桩型的单桩承载力皆随H/D增大呈线性增长趋势，并且相似的H/D变化对桩身受力影响特征导致了两种桩型近乎平行的承载力增长线（图 9（a））。
![]()
图 9 顶螺旋埋深比对两种特征桩型单桩承载力的影响Figure 9. Influences of top helix embedment ratio on bearing capacity of two typical types of helical piles但S/D≥S/Dcr桩各螺旋下卧土抗压强度随埋深增大而增长的趋势较S/D < S/Dcr桩螺旋间筒状土体抗剪强度增长更明显，相应能提供更大的螺旋端阻，并对其下地基土施加更大的附加应力，进而使得螺旋间桩身侧摩阻力增长更明显（图 9（b）），最终引起S/D=3桩的承载力增长率略大于S/D=1桩。两种特征桩型螺旋桩总端阻对单桩抗压承载力的贡献都几乎不受H/D影响，维持在70%左右。
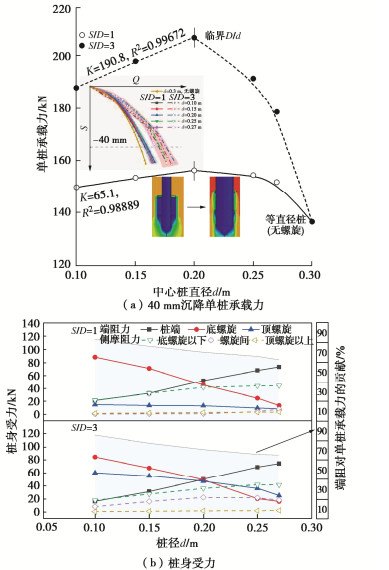
3.2 中心桩桩径d的影响
由图 10（a）可知两种桩型的单桩承载力随中心桩桩径d增大皆表现为先线性增大后加速衰减两段式发展特征。中心桩桩径增大直接提高着桩端端阻与侧摩阻，以及其余桩身因土体自重侧向应力提供的侧摩阻力；但同时，桩径增大而螺旋直径保持不变会使得螺旋外伸面积减小，底螺旋端阻力因此显著衰减。不同的是，S/D＜S/Dcr桩除底螺旋以外的螺旋端阻源于螺旋间筒状土体抗剪反力，而筒状土体受剪面积在桩径增大过程保持不变，所以其未发生明显改变；但此时S/D≥S/Dcr桩的各螺旋下承压土体面积减小导致了其端阻力的显著降低（图 10（b））。
![]()
图 10 桩径对两种特征桩型单桩承载力影响Figure 10. Influences of pile diameter on bearing capacity of two typical types of helical piles故当桩径在小于某临时值（本试验D/dcr=1.2~1.5）范围内增长时，桩端阻力与桩侧摩阻力的提高尚能填补螺旋端阻力损失，此时单桩承载力随桩径增长呈线性增大趋势。并且由于S/D≥S/Dcr桩螺旋间桩-土摩擦本就较S/D < S/Dcr桩大，此范围内桩径增大引起了前者螺旋间桩身侧摩阻力较后者更明显的增长，最终前者承载力增长率大于后者。但当桩径超过临时值继续增长时，各螺旋端阻力损失超过桩端端阻力与侧摩阻力增长，此时桩径增长导致单桩承载力加速衰减。尤其是S/D≥S/Dcr桩底螺旋以上螺旋端阻损失更为显著，再加上进而引发的螺旋间桩身侧摩阻力衰减，其承载力急剧降低。两种螺旋桩总端阻对单桩承载力的贡献相当，且皆随中心桩桩径增长而快速降低。
特别的，随着中心桩直径增大，螺旋叶片外伸面积减小，原本S/D＜S/Dcr桩螺旋间筒状土体剪切破坏的地基破坏模式逐渐向着同S/D≥S/Dcr桩一样的螺旋下卧土独立受压破坏转变（图 10（a））。这说明在不同试验条件下单独以S/D值来判断桩体受力特征与最终地基破坏模式是不完备的。分析认为，出现两种地基破坏模式差异的本质在于螺旋下卧土体抗压强度与相邻螺旋间筒状土体抗剪强度的大小关系，即当下卧土体抗压强度大于螺旋间筒状土体抗剪强度时则地基最终呈现为螺旋间筒状土体剪切破坏；反之则呈现螺旋下卧土独立受压破坏。这是更为全面的囊括了地基土性质、螺旋埋深、中心桩与螺旋直径相关关系、以及螺旋间距比等桩型参数综合影响的判别标准，可一定程度上解释大量针对不同土质、不同桩型条件研究所得临界S/D值存在不同程度出入的现象[8-10]。
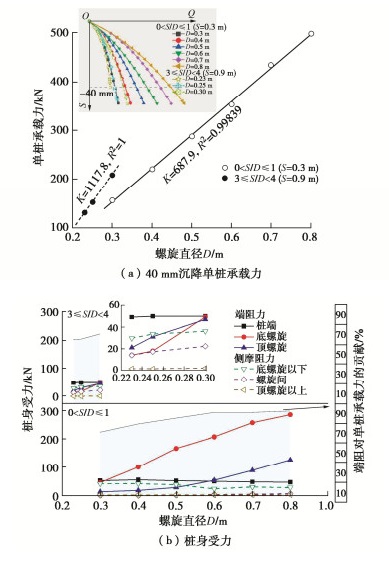
3.3 螺旋直径D的影响
螺旋直径D增大带来了螺旋下卧端承土体面积和螺旋间筒状土体受剪面积的指数增长，各螺旋端阻力显著提高，两种特征桩型单桩承载力均随螺旋直径增大呈显著线性增长趋势（图 11（a））。其中，S/D≥S/Dcr桩各螺旋，特别是顶螺旋的端阻增长率明显大于S/D＜S/Dcr桩，并由此引起了螺旋间侧摩阻力的增长（图 11（b）），最终导致其承载力增长率明显更大。但螺旋叶片外伸长度增长也会使得其自身弯曲应力，尤其是其与桩身连接处应力急剧增长，需要注意螺旋叶片屈服破坏。两种特征桩型螺旋桩总端阻对单桩承载力的贡献皆随螺旋直径增大而快速提升，但在总端阻贡献超过90%后，其提升幅度趋于收敛。
![]()
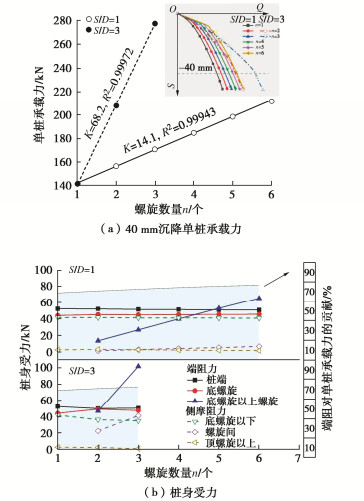
图 11 螺旋直径对两种特征桩型单桩承载力影响Figure 11. Influences of helix diameter on bearing capacity of two typical types of helical piles3.4 螺旋数量n的影响
两种特征桩型单桩承载力均随螺旋增多而线性增大（图 12（a））。螺旋数量n改变并没有引起桩端、原有螺旋叶片及其间桩身的受力特征变化，单桩承载力增长来自新增螺旋的端阻贡献。其中，S/D≥S/Dcr桩单个新增螺旋的端阻明显高于S/D < S/Dcr桩，并且新增螺旋下的桩身侧摩阻力也相较之前因土体自重侧向应力提供的侧摩阻力明显增长（图 12（b））。这些差异使得S/D≥S/Dcr桩单桩承载力随螺旋数量增大呈现出更显著的增长趋势。两种螺旋桩总端阻对单桩承载力的贡献皆随螺旋数量增长稳定提升。
![]()
图 12 螺旋数量对两种特征桩型单桩承载力影响Figure 12. Influences of helix number on bearing capacity of two typical types of helical piles3.5 螺旋间距比S/D的影响
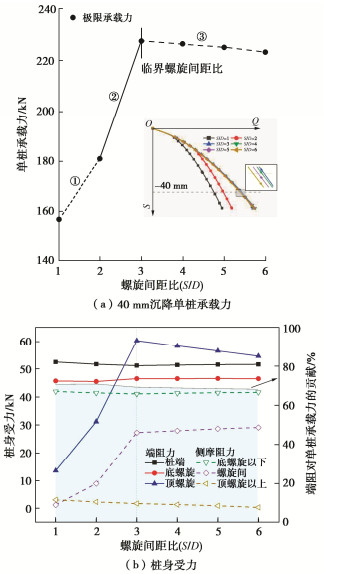
单桩承载力随螺旋间距比S/D增长的变化趋势总体表现为达S/Dcr前显著增长与达S/Dcr后小幅度降低两阶段发展特征。其中，S/D从小于S/Dcr跨越至S/Dcr时的单桩承载力提升更为显著（图 13（a））。
![]()
图 13 螺旋间距比对两种特征桩型单桩承载力影响Figure 13. Influences of helix spacing ration on bearing capacity of two typical types of helical piles由图 13（b）可知，S/D在小于S/Dcr范围内增长时所带来的承载力提升效果得益于螺旋间筒状土体受剪面积增大带来的底螺旋以上各螺旋端阻力提升，以及螺旋间桩身长度与螺旋端阻力的同时增长引起的螺旋间桩身侧摩阻力相应增长。当继续增大至达S/Dcr时，底螺旋以上各螺旋端阻力来源从筒状土体剪切反力转换为螺旋下卧土体受压反力，此时端阻力与螺旋间桩身侧摩阻力更明显增长，进而实现单桩承载力更为显著的提升。但若S/D在达到S/Dcr以后继续增大，螺旋总体埋深减小会导致其端阻力降低，单桩总体承载力相应衰减。S/D在小于S/Dcr范围内增长时，桩体总端阻力对单桩承载力的贡献有所提升，但达到S/Dcr后的S/D增长导致总端阻贡献缓慢降低。
4. 隔离式螺旋桩抗地基冻融特征
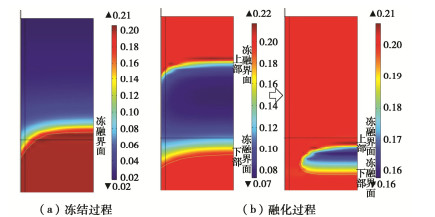
桩基冻融过程中水分场响应特征如图 14所示。地表温度通过桩、土传热不断向深层土体传递，引起地基土冻融变化。由于钢比土的导热性强，桩侧土温度变化较同一深度处远离桩的土体更迅速，桩侧土率先发生冻结或融化。特别的，冻结过程中土层积蓄的冷量导致下部冻融界面在早期融化过程中继续加深。
![]()
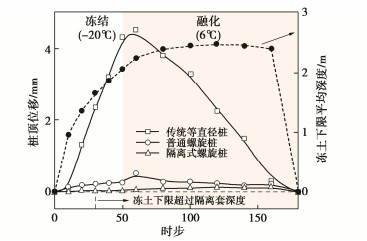
图 14 冻融过程中桩基水分场（未冻水含量）响应Figure 14. Response of water field (unfrozen water content) of pile foundation during freeze-thaw process图 15中显示了相同桩径（0.2 m）与桩长（4 m）条件下传统等直径桩、普通螺旋桩（无隔离套）与隔离式螺旋桩各自在地基土冻融变形过程中的桩体位移情况。土体在地表负温影下逐渐向深层冻结，引起了传统等直径桩明显的冻拔位移；在地基土早期融化过程中，下部冻融界面的继续加深使得桩体冻拔位移相应继续有所增大；随着地基土继续融化，桩体位移逐渐恢复。最终，传统等直径桩在整个地基冻融变形过程中发生显著桩体位移。相比之下，普通螺旋桩桩体位移大幅降低。对于隔离式螺旋桩，在冻融界面未超过隔离套深度范围时，地基土冻融变形几乎未引起桩体位移，在冻融界面超过隔离套深度范围后，冻土与桩身摩擦才引起了微小桩体位移。试验结果展现了螺旋桩显著的抗地基土冻融变形优势，并且通过进一步在冻土深度范围内设置隔离套形成隔离式螺旋桩，切断冻土与中心承载桩体的切向力传递，具有消除地基土冻融对桩体位移影响的理论可行性。
![]()
图 15 地基土冻融过程中的桩体竖向位移Figure 15. Vertical displacements of piles during freeze-thaw process of foundation soil5. 结论
结合物理模型试验与有限元方法从桩身受力视角对比揭示了两种特征桩型螺旋桩受压沉降时桩身受力演化、荷载传递与地基响应特征，以及各桩型几何参数对单桩抗压承载力的影响特征及机理；探讨了隔离式螺旋桩抵抗地基冻融变形性能。得到4点主要结论。
（1）受荷沉降过程中，两种特征桩型螺旋桩底螺旋及其以下桩身受力（端阻、侧摩阻）大小相当且均呈增长趋势；S/D＜S/Dcr桩底螺旋以上各螺旋端阻在螺旋间筒状土体剪切破坏前不断增长，而后保持远小于桩端与底螺旋端阻水平，螺旋间桩侧摩阻保持低水平，地基破坏模式为螺旋间筒状土体早先剪切破坏，最终桩端及底层螺旋下卧土体受压破坏；S/D≥S/Dcr桩上层螺旋端阻在其下卧土体达极限状态前保持与桩端及底螺旋端阻相当大小与增长趋势，螺旋间桩侧摩阻较大且随螺旋端阻同步增长，地基破坏模式为各螺旋及桩端下卧土自上而下独立受压破坏。
（2）两种特征桩型达极限状态时桩身轴力分布总体特征基本一致。桩端与各螺旋端承作用导致相应桩身截面轴力突增，S/D＜S/Dcr桩上层螺旋端阻仅约为1/5底螺旋端阻，而S/D≥S/Dcr桩各螺旋端阻相当。S/D≥S/Dcr桩螺旋对下卧土体显著施加附加应力，导致明显增大且自上而下指数衰减的螺旋间桩侧摩阻力。相同条件下，更大上层螺旋端阻及螺旋间桩侧摩阻赋予了S/D≥S/Dcr桩更强的抗压承载性能。
（3）两种特征桩型单桩抗压承载力皆随桩长、螺旋直径与螺旋数量增长线性提升，随中心桩桩径增长先线性增大后加速衰减两段式发展。但S/D≥S/Dcr桩单桩承载力受以上桩型参数变化影响较S/D＜S/Dcr桩更显著。在不超过S/Dcr范围内增大S/D可显著提升单桩承载力，但超过S/Dcr后继续增大反而导致承载力线性衰减。
（4）通过在冻土深度范围内设置可轴向滑动的隔离套，具有切断冻土与中心持力桩体切向力传递，消除地基冻融变形对桩体位移影响的理论可行性。
-
![]()
图 3 单桩抗压物理模型试验系统
Figure 3. Physical model test system for compression of a single pile
![]()
图 4 数值试验的几何模型、边界条件与网格划分
Figure 4. Geometries, boundary conditions and meshing of numerical tests
![]()
图 6 S/D＜S/Dcr时桩身受力与地基破坏特征
Figure 6. Characteristics of pile force and foundation failure when S/D < S/Dcr
![]()
图 7 S/D≥S/Dcr时桩身受力与地基破坏特征
Figure 7. Characteristics of pile force and foundation failure when S/D≥S/Dcr
![]()
图 8 桩身轴力、端阻力与侧摩阻力分布
Figure 8. Distribution of axial force, end resistance and side friction of piles
![]()
图 9 顶螺旋埋深比对两种特征桩型单桩承载力的影响
Figure 9. Influences of top helix embedment ratio on bearing capacity of two typical types of helical piles
![]()
图 10 桩径对两种特征桩型单桩承载力影响
Figure 10. Influences of pile diameter on bearing capacity of two typical types of helical piles
![]()
图 11 螺旋直径对两种特征桩型单桩承载力影响
Figure 11. Influences of helix diameter on bearing capacity of two typical types of helical piles
![]()
图 12 螺旋数量对两种特征桩型单桩承载力影响
Figure 12. Influences of helix number on bearing capacity of two typical types of helical piles
![]()
图 13 螺旋间距比对两种特征桩型单桩承载力影响
Figure 13. Influences of helix spacing ration on bearing capacity of two typical types of helical piles
![]()
图 14 冻融过程中桩基水分场（未冻水含量）响应
Figure 14. Response of water field (unfrozen water content) of pile foundation during freeze-thaw process
![]()
图 15 地基土冻融过程中的桩体竖向位移
Figure 15. Vertical displacements of piles during freeze-thaw process of foundation soil
表 1 土样的基本物性参数
Table 1 Basic physical parameters of soil sample
塑限wP/% 液限wL/% 塑性指数IP 最优含水率wOP/% 最大干密度ρd max/(g∙cm-3) 11.3 21.5 10.2 9.7 2.07 
下载: 导出CSV
表 2 数值模型材料参数
Table 2 Material parameters of numerical model
参数 密度ρ/(kg∙m-3) 弹性模量E/GPa 泊松比$ \nu $ 内摩擦角φ/(°) 黏聚力c/kPa 钢桩 7850 200 0.3 — — 土体 2157 0.02 0.3 36.87 8.51 桩土界面 — — — 23.27 0.20
下载: 导出CSV
表 3 桩基冻融数值分析试验参数
Table 3 Parameters of numerical tests on freeze-thaw of foundation
参数 C/(J∙kg-1∙K-1) λ/(W∙m-1∙K-1) ks/(m∙s-1) l m 土(桩) 890(475) 1.38(44.50) 10-6 0.50 0.14 参数 a0 θr θs B Tf/℃ 土(桩) 0.66 0.05 0.42 0.53 -0.18
下载: 导出CSV
表 4 初始桩型参数
Table 4 Original parameters of piles
L/m d/m D/m n/片 S/D 4.0 0.2 0.3 2 1或3 注：隔离段和底螺旋距桩底距离分别保持为1.5，0.2 m。
下载: 导出CSV
-
[1] PERKO H A. Helical Piles: a Practical Guide to Design and Installation[M]. Hoboken: J Wiley, 2009.
[2] DEBNATH A, SINGH V P. Analysis and design methods of helical piles: a critical review with emphasis on finite element method[J]. Arabian Journal of Geosciences, 2022, 15(18): 1-31.
[3] 郝冬雪, 王磊, 陈榕, 等. 冻融循环下粉砂中螺旋锚抗拔稳定模型试验研究[J]. 岩土工程学报, 2023, 45(1): 57-65. doi: 10.11779/CJGE20211293 HAO Dongxue, WANG Lei, CHEN Rong, et al. Experimental investigation on uplift stability of helical anchors in silty sand under freeze-thaw cycles[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(1): 57-65. (in Chinese) doi: 10.11779/CJGE20211293
[4] 王腾飞, 刘建坤, 邰博文, 等. 螺旋桩冻拔特性的模型试验研究[J]. 岩土工程学报, 2018, 40(6): 1084-1092. doi: 10.11779/CJGE201806014 WANG Tengfei, LIU Jiankun, TAI Bowen, et al. Model tests on frost jacking behaviors of helical steel piles[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1084-1092. (in Chinese) doi: 10.11779/CJGE201806014
[5] KHAN U, SIDDIQUA S. Study of compressive loading capacities of helical piles using torque method and induced settlements[J]. Environmental Earth Sciences, 2018, 77(1): 22. doi: 10.1007/s12665-017-7199-z
[6] ELKASABGY M, EL NAGGAR M H. Lateral performance and p-y curves for large-capacity helical piles installed in clayey glacial deposit[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(10): 04019078. doi: 10.1061/(ASCE)GT.1943-5606.0002063
[7] SAKR M. Performance of helical piles in oil sand[J]. Canadian Geotechnical Journal, 2009, 46(9): 1046-1061. doi: 10.1139/T09-044
[8] AYDIN M, BRADKA T D, KORT D A. Osterberg cell load testing on helical piles[C]//Geo-Frontiers 2011. Dallas, 2011.
[9] LUTENEGGER A J. Cylindrical shear or plate bearing? —uplift behavior of multi-helix screw anchors in clay[C]// Contemporary Topics in Deep Foundations. Orlando, 2009.
[10] RAWAT S, GUPTA A K. Numerical modelling of pullout of helical soil nail[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(4): 648-658. doi: 10.1016/j.jrmge.2017.01.007
[11] GEORGE B E, BANERJEE S, GANDHI S R. Numerical analysis of helical piles in cohesionless soil[J]. International Journal of Geotechnical Engineering, 2020, 14(4): 361-375. doi: 10.1080/19386362.2017.1419912
[12] MERIFIELD R S. Ultimate uplift capacity of multiplate helical type anchors in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(7): 704-716. doi: 10.1061/(ASCE)GT.1943-5606.0000478
[13] ARAÚJO P N G, DA SILVA COSTA J P, COSTA Y D J. Numerical study of geometric characteristics of helical piles subjected to uplift[C]// Proceedings of the ⅩⅩⅩⅧ Iberian Latin American Congress on Computational Methods in Engineering. Florianopolis, 2017.
[14] MITTAL S, MUKHERJEE S. Behaviour of group of helical screw anchors under compressive loads[J]. Geotechnical and Geological Engineering, 2015, 33(3): 575-592. doi: 10.1007/s10706-015-9841-4
[15] MOHAJERANI A, BOSNJAK D, BROMWICH D. Analysis and design methods of screw piles: a review[J]. Soils and Foundations, 2016, 56(1): 115-128. doi: 10.1016/j.sandf.2016.01.009
[16] VIGNESH V, MAYAKRISHNAN M. Design parameters and behavior of helical piles in cohesive soils—a review[J]. Arabian Journal of Geosciences, 2020, 13(22): 1194. doi: 10.1007/s12517-020-06165-1
[17] POLISHCHUK A I, MAKSIMOV F A. Improving the design of screw piles for temporary building foundations[J]. Soil Mechanics and Foundation Engineering, 2016, 53(4): 282-285. doi: 10.1007/s11204-016-9399-z
[18] ALWALAN M F, EL NAGGAR M H. Load-transfer mechanism of helical piles under compressive and impact loading[J]. International Journal of Geomechanics, 2021, 21(6): 04021082. doi: 10.1061/(ASCE)GM.1943-5622.0002037
[19] NOWKANDEH M J, CHOOBBASTI A J. Numerical study of single helical piles and helical pile groups under compressive loading in cohesive and cohesionless soils[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(5): 4001-4023. doi: 10.1007/s10064-021-02158-w
[20] 杨忠平, 李绪勇, 李诗琪, 等. 一种隔离式抗冻融循环桩及其设计方法: CN113502812A[P]. 2022-05-03. YANG Zhongping, LI Xuyong, LI Shiqi, et al. Isolation Type Freeze-Thaw Resistant Circulating Pile and Design Method Thereof: CN113502812A[P]. 2022-05-03. (in Chinese)
[21] 白青波, 李旭, 田亚护, 等. 冻土水热耦合方程及数值模拟研究[J]. 岩土工程学报, 2015, 37(增刊2): 131-136. doi: 10.11779/CJGE2015S2026 BAI Qingbo, LI Xu, TIAN Yahu, et al. Equations and numerical simulation for coupled water and heat transfer in frozen soil[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 131-136. (in Chinese) doi: 10.11779/CJGE2015S2026
[22] 李洪升, 刘增利, 梁承姬. 冻土水热力耦合作用的数学模型及数值模拟[J]. 力学学报, 2001(5): 621-629. doi: 10.3321/j.issn:0459-1879.2001.05.005 LI Hongsheng, LIU Zengli, LIANG Chengji. Mathematical model for coupled moisture, heat and stress field and numerical simulation of frozen soil[J]. Acta Mechanica Sinica, 2001(5): 621-629. (in Chinese) doi: 10.3321/j.issn:0459-1879.2001.05.005
[23] 王晓刚. 冻土区桩土体系冻胀融沉特性研究[D]. 西安: 西安科技大学, 2019. WANG Xiaogang. Study on Characteristics of Frost Heave and Thawing Settlement of Pile-Soil System in Permafrost Regions[D]. Xi'an: Xi'an University of Science and Technology, 2019. (in Chinese)
[24] 龚晓南. 桩基工程手册[M]. 2版. 北京: 中国建筑工业出版社, 2016. GONG Xiaonan. Handbook of Pile Foundation Engineering[M]. 2nd ed. Beijing: China Architecture & Building Press, 2016. (in Chinese)
-
其他相关附件
计量
- 文章访问数: 367
- HTML全文浏览量: 42
- PDF下载量: 100
