Distribution characteristics and evolution laws of liner cracks in underground caverns for compressed air energy storage
-
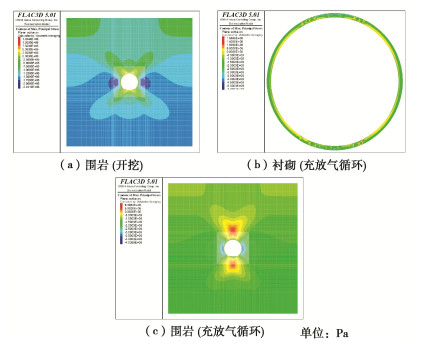
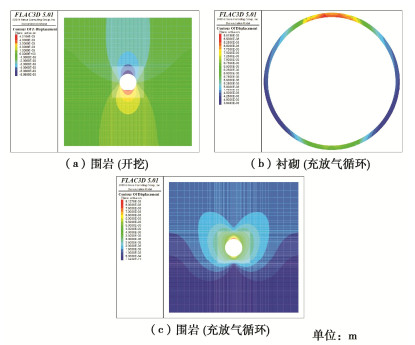
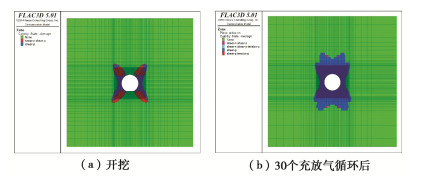
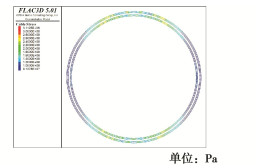
摘要: 地下储气库衬砌的主要作用是将内压传递给围岩,且同时作为柔性密封层的附着基层。高内压作用下衬砌开裂可导致密封层出现反射型裂缝,进而引起高压气体的泄漏。为深入认识地下储气库衬砌的开裂特征,开发了基于FLAC3D平台的衬砌裂缝分析程序,研究了衬砌配筋方式、配筋率、钢筋保护层厚度、围岩类别和温压循环荷载作用等因素对衬砌开裂演化特征的影响。研究成果表明:对衬砌采取合理的配筋方式和改善围岩质量的措施可有效控制衬砌裂缝的宽度;采用分区配筋的方式可有效控制圆形断面隧洞式储气库衬砌中的最大裂缝宽度,同时降低衬砌的配筋量。空气压力和温度同步变化引起的热力耦合效应还有助于减小衬砌中出现的裂缝宽度。Abstract: The liner of underground gas storage cavern is used to transfer the internal pressure to the surrounding rock, and at the same time serves as the base of flexible sealing layer. The excessively wide cracks due to the high internal pressure may lead to generation of reflective cracks in the sealing layer, thus causing the leakage of high-pressure gas. To deeply understand the characteristics of liner cracking in high-pressure underground gas storage cavern, a routine for cracking analysis of a liner based on the FLAC3D platform is developed, and the influences of reinforcement mode and ratio, concrete cover thickness, surrounding rock type and effect of temperature-pressure cyclic loading on cracking evolution characteristics are studied. The research results show that the crack width of the liner can be effectively controlled by reasonable reinforcement of concrete liner and improvement of the surrounding rock quality. For a circular cross-section tunnel gas storage cavern, it is possible to control the maximum crack opening in the liner by differentiated reinforcement mode, so as to reasonably reduce the reinforcement quantity in the liner. The thermo-mechanical coupling effects due to the simultaneous change of compressed air pressure and temperature are helpful to reduce the crack width in the liner.
-
0. 引言
随着中国对环境和生态的日益重视,全国主要的河流湖泊基本都已开展了底泥清淤和疏浚,例如太湖第一轮清淤已经将3600万m3污染底泥全部清除,而正在开展的太湖第二轮清淤,疏浚工程量仍然高达1800万m3。根据中国的底泥疏浚国情,固化方法仍然是处理大量疏浚淤泥的主要方法[1-3]。目前中国的淤泥固化处理主要以低含水率水平下固化再进行适当碾压为主,控制含水率在较低水平主要是为了减少固化材料的用量,但这种碾压方式的固化淤泥施工,经常会受限于固化设备的处理能力,并且碾压后固化淤泥的强度会有很大损失,不利于大规模固化淤泥施工[4-6]。
国外例如日本、美国,除了上述碾压方式的固化淤泥常用作筑堤以外[7-8],对于造岛、机场跑道等大规模的淤泥固化处理工程,更多的是采用流动固化的方式[9],该方法采用高浓度泥浆输送,经过调理以后加入固化剂,固化剂在管道输泥的过程中经过气流混合形成流动性的固化淤泥,直接浇筑在场地内形成人工岛[10]。此种方法从清淤到固化浇筑主要都在管道内完成,效率高,固化淤泥一次成型,因此强度大、变形小,是未来大规模淤泥固化处理技术的发展方向[11]。
国内对固化淤泥的流动性研究已有不少学者开始关注,丁建文等[12]研究了不同初始含水率和不同固化材料添加量下固化淤泥的流动性,建立了流动值的预测方法。黄英豪[11]、朱伟等[13]研究了淤泥固化之后流动性的变化模式,并提出了固化淤泥的流动浇筑和碾压施工的选择方法。顾欢达等[9]通过调整淤泥含水率,使得固化淤泥保持一定的流动性,从而实现淤泥的回填或者回灌处理的技术要求。陆强[14]研究了海水环境下固化淤泥的流动性。纪文栋等[15]采用高吸水材料来改善淤泥的流动性,但其目的是为了减少流动性以便于淤泥的运输和周转。
本文采用两种疏浚淤泥,研究了淤泥加入水泥固化之后流动性和黏滞性的变化,并建立了流动性和黏滞性之间的内在关系,以期对淤泥的流动固化施工技术发展有所助益。
1. 试验材料和方法
1.1 试验材料
研究所用淤泥分别取自淮安白马湖和太湖梅梁湖,淤泥的主要物理性质指标如表 1所示,根据土的分类方法,均属于高液限黏土(CH)。考虑到目前大规模淤泥固化处理采用的固化材料主要为水泥,为了减少影响因素,本文只采用#32.5普通硅酸盐水泥,没有和其他固化材料进行复合。
表 1 试验用淤泥物理性质指标Table 1. Physical properties of test soils淤泥名称 天然含水率wn/% 密度ρ/(g·cm-3) 相对质量密度Gs 黏粒含量/% 液限wL/% 塑限wP/% 有机质含量/% 白马湖 98 1.48 2.65 47.4 76.5 30 0.4 梅梁湖 80 1.53 2.68 26.3 56 27 3.5 1.2 试验方法
流动性测试采用的是新鲜搅拌的固化淤泥,即刚搅拌完成,水泥尚未完成初凝的固化淤泥,本文称之为新拌固化淤泥。试验时先按照设计配比将固化材料和淤泥在容积为6 L的砂浆搅拌机中强制搅拌10 min,使其混合均匀,刚搅拌完成的固化淤泥立即进行流动性和黏滞性的测试。
固化淤泥流动性测试目前在中国尚没有标准方法,学者多借鉴日本的圆柱筒容器测量水平扩展度。本文为了使得淤泥的流出更加顺畅,借鉴采用水泥砂浆流动性测试所采用的的截锥圆模装置,截锥圆模上底直径7 cm,下底直径10 cm,高6 cm。试验时把截锥模放置在水平玻璃板上,截锥模内壁和玻璃板上涂薄层凡士林,将新拌的固化淤泥装入到截锥圆模中,装入的过程不进行振捣,完全靠自身重力作用下流动充满至圆模,用刮泥刀削平截锥模上表面溢出的固化淤泥,将截锥圆模垂直向上轻轻提起,测定固化淤泥在互相垂直两个方向的流动直径,取其平均值作为新拌固化淤泥的流动度。
在流体力学中,流体的流变特性一般是采用旋转黏度计来测试,由于流体力学中的流变特性和土力学中常讲的土体的流变特性含义不尽相同,为了避免本专业人员的误解,本文采用黏滞特性一词来代替流变特性。黏滞性测试采用NXS-11A型旋转黏度计,它是一种通用的同轴圆筒上旋式黏度计,可用来测量各种牛顿流体和非牛顿流体的黏滞特性,为了测量不同黏度的的物质,仪器带有5个转子,选择不同的上旋转子和外筒及转速,可测量黏度不同黏度和不同剪切应力范围的的流体参数,如图 1所示。
为了考察不同含水率下新拌固化淤泥的流动性和黏滞性,将白马湖淤泥的初始含水率分别调至液限的不同倍数,具体为76%,98%,118%,153%,190%,228%,296%,456%,912%;将梅梁湖淤泥初始含水率分别调至56%,65%,87%,99%,130%,163%,343%,674%,856%。为了考察水泥添加量对流动性和黏滞性的影响,设定50,100,200 kg/m3三个水泥添加量。
2. 新拌固化淤泥的流动性
2.1 淤泥的流动性
这里含水率用w表示,并定义流动度D为淤泥或者新拌固化淤泥坍落稳定后在水平面内投影的直径(单位为cm,精确到mm)。图 2给出了梅梁湖淤泥典型的流动性的试验照片,(白马湖淤泥的照片类似,限于篇幅不再展示),对两种淤泥的流动性试验结果进行分析,发现有以下共同规律:①当含水率非常高,w≥6.0wL左右时,虽然还未提起截锥模,但已经有少量淤泥从截锥模的下底面流出,这主要是因为淤泥的稠度过小;②当含水率很高,2.5wL≤w<6.0wL时,流动稳定后淤泥的形态呈现非常规则的薄圆饼状,并且竖直方向的高度要远小于水平方向的扩展度;③当含水率较高,2.0wL≤w<2.5wL时,流动稳定后淤泥的形态虽然仍呈现圆饼状,但竖直方向的高度相比于前一阶段要显著增大;④当含水率较低,wL≤w<2.0wL时,淤泥的流动性非常小,流动稳定后的淤泥形态呈现圆台状;⑤当含水率很低,w<wL时,淤泥已经不具有流动性,并且从定义看,含水率小于液限的土体已经不属于淤泥的范畴。
图 3所示为白马湖淤泥和梅梁湖淤泥的流动度随含水率的变化,可见,两种泥的流动度随含水率降低都急剧减小,并且在相同含水率下两种泥的流动度相差不大,表明含水率是决定淤泥流动度的重要因子。另一方面,流动度随含水率变化的过程可以比较明显地分为两段,对白马湖淤泥当含水率w < 150%时,淤泥的流动度随着含水率的增加有很少量的增大,而当含水率w > 150%时,淤泥的流动度随着含水率的增加迅速增大。对梅梁湖淤泥,也同样存在这样的临界点,只不过临界含水率w′在110%左右。
如果将淤泥的含水率转化为其相应的液限倍数,从流动度随液限倍数的变化图来看,则流动度的变化规律更为明显,如图 3(b)所示。可以看出,无论对于白马湖淤泥还是梅梁湖淤泥,在w=2.0wL左右时,淤泥的流动度变化速率开始呈现差别。当w<2.0wL时,两种泥的流动度相差很小,并且随着含水率的变化改变不明显。当w>2.0wL时,两种泥的流动度都随着含水率增大而显著增加,但两种泥的流动度曲线并不重合,显示出液限对淤泥的流动度有一定影响,同样的液限倍数时,梅梁湖淤泥流动度要小于白马湖淤泥的流动度。这是因为白马湖淤泥的液限要高于梅梁湖淤泥的液限,使得液限倍数相同时白马湖淤泥的含水率要高于梅梁湖淤泥,后文将进一步从淤泥的黏滞性进行分析。
2.2 新拌固化淤泥的流动性
(1)初始含水率对新拌固化淤泥流动性影响
将两种淤泥调至不同含水率,分别加入50,100,200 kg/m3的固化材料,考察流动性的变化。如图 4所示,可以看出在水泥添加量相同时,初始含水率越高,新拌固化淤泥的流动度越大,和未加入水泥处理的原泥的流动度相比,加入水泥后的新拌固化淤泥的流动度要有很大程度的减小。这说明水泥的加入能显著增大淤泥的稠度,减小淤泥的流动性能。从流动度的变化趋势上来看,新拌固化淤泥的流动度变化也可以分为两段,只不过流动度变化的临界含水率点相比于原泥有明显增大,对于新拌白马湖固化淤泥,临界含水率w′s约为220%,对于新拌梅梁湖固化淤泥,临界含水率w′s约为150%,小于临界含水率时流动度变化很小。
如果将初始含水率用液限的倍数来表示,则新拌固化淤泥的流动性变化规律则更加明显,见图 4(c)所示。可以看出两种新拌固化淤泥的流动度都大致在同一临界点发生变化,该临界点的值约为w′s=2.8wL。小于该临界点时,两种固化淤泥的流动度相差很小,超过临界值之后,流动度迅速增大,并且同样的液限倍数下新拌白马湖固化淤泥的流动度要大于梅梁湖固化淤泥的流动度。
由前文分析可知,对未处理的淤泥,当w<2.0wL时,两种淤泥的流动度变化缓慢且相差不大,而对于新拌的固化淤泥,当w<2.8wL时,两种新拌固化淤泥的流动度变化缓慢且也相差不大。如果把两种原泥的流动度和水泥量为50 kg/m3的新拌固化淤泥的流动度随初始含水率的变化对比,如图 5所示。由图 5可见,所有的原泥的流动度都近似在一条直线上,而所有的新拌固化淤泥的流动度都在淤泥流动度的下方,并且也大致成一直线。对淤泥和新拌固化淤泥的流动度结果进行回归分析,可得如下关系:
D=11.34w(ac=0), (1) D=7.61w(ac=50)。 (2) 由式(1),(2)可知,对于流动度比较大的淤泥和新拌固化淤泥,流动度和初始含水率间都有很简单的线性正相关关系,比较而言,淤泥的流动度随初始含水率的变化速率要高于新拌固化淤泥的流动度变化速率。即淤泥经过固化之后,它的流动度会显著降低,在大流动度的情况下,新拌固化淤泥的流动度约为淤泥流动度的0.67倍,即加入50 kg/m3的水泥后,淤泥的流动度会减小1/3。
(2)水泥添加量对新拌固化淤泥流动性影响
由前文分析可知,初始含水率对新拌固化淤泥的流动度有显著影响。为了进一步考察不同水泥添加量对新拌固化淤泥流动度的影响,分别对白马湖淤泥和梅梁湖淤泥添加不同的水泥量,试验结果如图 6所示。由图 6可见,水泥量对流动度的影响主要发生在添加量小于50 kg/m3的阶段,而超过此水泥量后,继续添加水泥对流动度的影响很小。表明只要有少量水泥的添加,就会显著降低淤泥的流动性能。
3. 新拌固化淤泥的黏滞性
淤泥固化后的流动度有很大程度的降低,为了进一步探究为何淤泥固化后的流动性会变化如此之大,本节从旋转黏度计测得的淤泥的黏滞性方面进一步研究。
3.1 流体黏滞特性的划分
流体流动时有速度梯度存在,因此运动较慢的液层阻滞着较快层的运动,因此产生流动阻力,切应力的作用就是克服这流动阻力,以维持一定的速度梯度而流动。表达剪切力和剪切速率之间关系的数学方程称为黏滞方程,它们之间的图解关系称为黏滞曲线。流体的黏滞曲线主要可以分为4个类型:牛顿流体、宾汉姆流体、幂律流体、带屈服值的幂律流体,具体见图 7。图 7中,τ为切应力(Pa);μ为液体的黏度(Pa·s);˙γ为剪切速率(s-1);τ0为剪切屈服应力,通常也可称为为动切力;n为流动指数,n值小于1,是非牛顿性的量度,与1相差越多,非牛顿性越强。
3.2 淤泥的黏滞特性
和前述测试淤泥流动度的试验方案相对应,分别对白马湖淤泥和梅梁湖淤泥的黏滞性测试,典型的试验结果如图 8所示(限于篇幅,仅只给出3幅白马湖淤泥的典型结果图)。综合分析两种淤泥的试验结果可以发现无论对于白马湖淤泥还是梅梁湖淤泥,在淤泥的含水率由高到底的变化过程中,淤泥的黏滞特性逐渐发生变化,可分为3种不同的类型。
(1)当淤泥的含水率w>12.0wL,淤泥的黏滞曲线基本为通过原点的直线,表明此时可以认为淤泥是牛顿流体,黏性特征不显著。这主要是因为淤泥的含水率非常高,土颗粒在水中分布形成悬液,土颗粒之间尚没有形成连接作用,淤泥的剪切应力的大小只与剪切速率相关。
(2)当淤泥的含水率2.0wL≤w≤12wL,淤泥的黏滞曲线为不通过原点的直线,表明在此范围内淤泥为宾汉姆流体。在这个阶段,溶液中的土颗粒数量增多,使得土颗粒之间能够形成连接作用,淤泥要实现流动,首先必须克服这种连接作用,也就是要克服初始动切力τ0的作用。
(3)当淤泥的含水率w<2.0wL,淤泥的黏滞曲线呈现出带屈服值的伪塑性流体的特征,剪切应力和剪切速率之间基本为幂函数关系。在这个阶段,淤泥的稠度已经很大,土颗粒间的作用非常强烈。
一般工程实际中,需要固化处理的淤泥含水率不会大于12倍液限含水率。疏浚工程中采用绞吸式挖泥船清淤出的泥浆的含水率多为液限的几倍。因此,工程实际中的刚刚吹填的淤泥一般属于宾汉姆流体。能表征宾汉姆流体特征的两个黏滞参数是动切力τ0和黏滞系数μ,对白马湖淤泥和梅梁湖淤泥,当淤泥属于宾汉姆流体时的动切力和黏滞系数进行分析,图 9为梅梁湖淤泥的动切力τ0和黏滞系数μ随淤泥初始含水率的变化。
由图 9可见,当淤泥属于宾汉姆流体时,它的黏滞系数都比较小,并且两种淤泥的黏滞参数随含水率的变化都呈现指数关系变化:
μ=ae−0.02w (3) τ0=be−0.02w (4) 式中,e为自然常数,w为淤泥的含水率,a和b分别为常数。由关系式可知,指数都为-0.02,表明两种淤泥的黏滞参数随着含水率的升高而降低的速率相同,但参数a和b则不同,说明了不同淤泥种类对黏滞系数的影响。白马湖淤泥的黏滞系数参数a为0.70,而梅梁湖淤泥的黏滞系数参数a为0.91;白马湖淤泥的动切力参数b为768,梅梁湖淤泥的动切力参数b为560。另一方面,白马湖淤泥的黏粒含量为47.4%,而梅梁湖淤泥的黏粒含量为26.3%,可见参数a和黏粒含量负相关,而参数b和黏粒含量呈现正相关。
从流动度的试验中知道,当淤泥的含水率w<2.0wL时,淤泥的流动度随着含水率的增加变化不大,而当淤泥的含水率w>2.0wL时,淤泥的流动度随着含水率的增加迅速增大。从淤泥的黏滞性试验中知道,当淤泥的含水率w<2.0wL时,淤泥属于带屈服值的幂律流体,而当淤泥的含水率w>2.0wL时,淤泥属于宾汉姆流体。这表明,当淤泥的黏滞特性属于宾汉姆流体时,它的流动性会很大,而当淤泥属于屈服值的幂律流体时,它的流动性很小。
3.3 新拌固化淤泥的黏滞特性
(1)初始含水率对新拌固化淤泥黏滞性影响
对新拌固化淤泥黏滞特性的研究分为两种情况:①固定水泥添加量为50 kg/m3,研究不同初始含水率下固化淤泥的黏滞特性;②在确定新拌固化淤泥的黏滞曲线类型之后,选择有代表性的初始含水率,研究不同水泥添加量对黏滞特性的影响。典型的白马湖新拌固化淤泥黏滞性试验结果见图 10。可见在水泥添加量为50 kg/m3的情况下,新拌固化淤泥的黏滞特性显著受到初始含水率的影响并且对于白马湖淤泥和梅梁湖淤泥有一样的规律。在含水率由高到底变化过程中,新拌固化淤泥的黏滞曲线可以显著的分为两个阶段、两种类型。
a)对白马湖淤泥,当初始含水率w≥228%;对梅梁湖淤泥,当淤泥的初始含水率w≥163%,固化淤泥的黏滞特性为宾汉姆流体。可以近似认为当淤泥的初始含水率w≥2.8wL时,新拌固化淤泥的黏滞特性表现为宾汉姆流体。
b)当淤泥的初始含水率w<2.8wL时,无论对于白马湖淤泥,还是对于梅梁湖淤泥,新拌固化淤泥的黏滞性都已经不符合宾汉姆流体,近似为带屈服值的幂律流体。
由新拌固化淤泥的流动度试验知道,新拌固化淤泥的流动度显著受到淤泥初始含水率的影响,并可以分为两个阶段。当w<2.8wL时,固化淤泥的流动度随含水率的增加变化不大;当w>2.8wL时,固化淤泥的流动度随着含水率的增加迅速增大。对比固化淤泥的黏滞性试验结果可以得出,当w>2.8wL时,新拌固化淤泥属于宾汉姆流体,这个阶段固化淤泥的流动性很大,并且初始含水率对固化淤泥的流动性影响很显著;当w<2.8wL时,新拌固化淤泥属于带屈服值的伪塑性流体,这个阶段固化淤泥的流动性很小。
当新拌固化淤泥属于宾汉姆流体时,黏滞系数μ和动切力τ0是表征其流动特性的两个参数,新拌白马湖固化淤泥的黏滞系数μ和动切力τ0随初始含水率的变化见图 11,原泥的宾汉姆流体参数也放在了一起以便于比较分析。由图 11可以看出,固化淤泥的动切力和黏滞系数都要大于相应原泥的参数,说明淤泥经过固化之后,黏性增强,动切力增大。并且固化淤泥的动切力和黏滞系数随初始含水率增大也在减小,但减小的速率要明显大于未处理的原泥,说明初始含水率对新拌固化淤泥的黏滞特性有非常显著的影响。
(2)水泥添加量对新拌固化淤泥黏滞性影响
为了研究不同水泥添加量对固化淤泥黏滞特性的影响,对白马湖淤泥选择296%,190%,118%三个不同初始含水率,对梅梁湖淤泥选择130%的初始含水率,进一步研究分别添加100,200 kg/m3的水泥后的固化淤泥的黏滞性,上述含水率范围可以涵盖淤泥为宾汉姆流体和幂律流体两种情况。通过分析发现在初始含水率相同的情况下,不同水泥添加量会对淤泥的黏滞特性产生影响,但在水泥添加量从50 kg/m3提高到200 kg/m3时,固化淤泥黏滞曲线的形态并没有明显变化,仅列出初始含水率为296%,水泥添加量为100 kg/m3时的新拌白马湖固化淤泥的黏滞特性试验结果,可见呈现出典型宾汉姆流体的特征,见图 12。
虽然不同的水泥添加量下固化淤泥的黏滞曲线形态相同,但对黏滞参数的影响需要进一步明确,以新拌固化淤泥属于宾汉姆流体时来考察不同水泥添加量对宾汉姆流体参数的影响。图 13给出了初始含水率为296%的白马湖淤泥分别添加不同水泥量下新拌固化淤泥的黏滞系数和动切力的变化曲线。由图 13可见,水泥添加量对新拌固化淤泥黏滞系数和动切力的影响主要发生在水泥量小于50 kg/m3的范围内,水泥添加量继续增加,只能使固化淤泥的黏滞系数和动切力有少量的增大。因此,水泥添加量对淤泥黏滞性的影响,主要发生在水泥量小于50 kg/m3的范围。前面的研究已经表明,水泥对新拌固化淤泥流动度的影响也主要发生在水泥量50 kg/m3的范围,原因也就在于水泥对淤泥黏滞性的影响主要发生在这个范围内。
4. 基于滨汉姆流体时的流动性和黏滞性的关系
从淤泥和新拌固化淤泥的流动度试验结果知道,对于淤泥当含水率w>2.0wL时,淤泥的流动性会随着含水率的增加而快速增大,并且坍落稳定后的形态呈现圆饼状;对于新拌固化淤泥当淤泥的初始含水率w>2.8wL时,固化淤泥的流动特性表现出和上述淤泥相类似的特征。从黏滞性试验结果知道,淤泥和固化淤泥之所以会表现出比较大的流动性,原因在于此种状态下淤泥或者新拌固化淤泥属于宾汉姆流体。
表征宾汉姆流体特征的两个参数是黏滞系数μ和动切力τ0,黏滞系数可以认为是流体开始流动后流动快慢的表征,而动切力的大小则决定了流体在外力的作用下能否进行流动。本文中的流动度试验是淤泥或者固化淤泥完全在自身重力作用下的流动,如果淤泥(固化淤泥)的动切力小于自身重力所产生的应力时,那么提起坍落度筒(截锥圆模)后,淤泥在自身重力作用下会向四周流动。因此,黏滞参数是反映流体流动特性的内在原因,而流动度只是这种流动特性的宏观表现。对于流动性比较大的属于宾汉姆流体时的淤泥或者新拌固化淤泥,有理由相信黏滞参数和流动度之间有内在联系,换句话讲,如果知道了宾汉姆流体参数也就应该可以知道流动度的结果。
当淤泥或新拌固化淤泥的流动性很大时,稳定状态后的水平流动度要远大于竖直方向的坍落度。淤泥在坍落度筒中时有一个自由表面,对于这种有自由表面的流体的流动,可采用浅水长波方程求解。坍落度筒中的淤泥在自重作用下的流动,可以看作恒定体积的黏性液体在水平面上的释放,初始淤泥的形状是截锥状,可以看作轴对称问题来求解,采用如图 14所示柱坐标系统(O,r,θ,z),并作以下假设:①流体是不可压缩的,密度是恒定不变的;②水平方向的扩展距离远大于竖直方向的坍落距离;③坍落流动过程中水固分离过程忽略不计;④在自重作用下流动稳定后,在水平面上的投影是规则的圆形。
按照浅水长波方程,可得平衡方程为
∂p∂r=∂τ∂z, (5) ∂p∂z=−ρg。 (6) 淤泥或者新拌固化淤泥在流动时,其黏滞特性满足Bingham方程,即满足
τ=τ0+μ˙γ, (7) 式中,ρ为淤泥的密度,g为重力加速度。τ为淤泥的剪切应力,τ0为淤泥的动切力,˙γ为剪切速率。则有
˙γ=∂Vr∂z。 (8) 假设淤泥压力p的分布符合流体静力学,则可得
p=ρg(h(r)−z), (9) 式中,h(r)为淤泥的深度,z=h(r)处的压力为大气压力,假设气液交界面的表面张力相对于动切力可以忽略不计。联立式(5),(6),并考虑边界条件z=0和z=h得
ρgh(r)dh(r)dr=−τ0−f(˙γ)|z=0。 (10) 在停止的时刻,˙γ=0,式(10)可以简化为
ρgh(r)dh(r)dr=τ0。 (11) 进一步考虑边界条件h(r=R)=0,可得坍落稳定后的淤泥高度为
h(r)=[2τ0(R−r)ρg]12。 (12) 淤泥的体积V可以通过积分得到:
V=∫2π 0∫R0h(r)rdθ=8√2τ0π R5215√ρg。 (13) 则可得坍落稳定后半径R的表达式为
R=(225ρgV2128π 2τ0)15。 (14) 流动度D为流动稳定后的直径,所以
D=2R=2(225ρgV2128π 2τ0)15。 (15) 由式(15)可知,流动度可以根据试样体积、屈服应力、重度来进行预测。同时也可以看出,当淤泥或者新拌固化淤泥满足宾汉姆流体方程时,屈服应力和流动度之间有唯一对应的关系,和淤泥的种类无关,并且对于新拌固化淤泥也有这样的对应关系。对于本文中所有的含水率在2wL以上的淤泥和初始含水率在2.8wL以上的新拌固化淤泥,如果把黏滞性试验中得到的动切力τ0作为已知条件,则可以根据式(15)对淤泥或者新拌固化淤泥的流动度进行预测,其中截锥的体积V=344 cm3。按照此种方法得到的流动度和动切力的关系见图 15。可见根据动切力预测的流动度和实测的流动度之间吻合得很好,说明此种方法可以有效地把两者之间联系起来。
5. 结论
采用白马湖和梅梁湖的淤泥,选择水泥作为固化材料,通过截锥圆模流动度试验和旋转黏度计试验,研究了淤泥和新拌固化淤泥的流动性和黏滞特性,得到以下6点结论。
(1)初始含水率对淤泥的流动性影响显著,并存在临界含水率w′≈2.0wL,当淤泥初始含水率高于2.0wL时,淤泥的流动性迅速增大。
(2)淤泥固化后,流动性降低,初始含水率相同时,水泥添加量越高,新拌固化淤泥流动性越小,且主要发生在水泥添加量ac≤50 kg/m3。初始含水率对新拌固化淤泥流动性的影响也存在临界含水率w′s,w′s和水泥添加量有关,当ac=50 kg/m3,w′s≈2.8wL,此时新拌固化淤泥的流动性约为未固化淤泥流动性的2/3。
(3)黏滞性试验表明,含水率w>12.0wL,淤泥为牛顿流体;2.0wL≤w≤12wL,为宾汉姆流体;w<2.0wL,为带屈服值的伪塑性流体。当淤泥的初始含水率w≥2.8wL时,新拌固化淤泥为宾汉姆流体;当w<2.8wL时,新拌固化淤泥近似为带屈服值的幂律流体。
(4)新拌固化淤泥的黏滞系数μ和动切力τ0都随初始含水率增大而减小,并且都大于对应原泥的黏滞参数,水泥添加量对对黏滞参数数的影响主要发生在水泥添加量ac≤50 kg/m3。
(5)对于淤泥,当含水率w≥2.0wL时,或者对于新拌固化淤泥,当初始淤泥含水率w≥2.8wL时,即当淤泥或者新拌固化淤泥满足宾汉姆流体方程时,根据浅水方程推导得到了屈服应力和流动度之间的唯一关系,即流动度可以由试样体积、重度和屈服应力获得,也说明黏滞特性参数是决定淤泥宏观流动性的内在原因。
(6)流动度和黏滞性试验联合表明,新拌固化淤泥流动性小于淤泥,根本原因在于固化材料的加入使得水泥和水发生化学反应从而成为振凝性流体,随着时间的延长,固化淤泥逐渐从流体变成为固体状态,从而实现了淤泥的固化作用。本文的规律性结论是基于两种淤泥,水泥作为单一固化材料通过大量试验得出的,后续需要对更多的淤泥进行研究,以检验结论是否有普适性,但无疑,本文对于大规模淤泥流动固化浇筑施工具有重要参考价值。
-
表 1 岩体计算参数
Table 1 Computational parameters of rock
计算参数 重度γ/ (kN·m-3) 变形模量E/GPa 泊松比ν 黏聚力c/MPa 内摩擦角φ/(°) 抗拉强度T/MPa 热传导系数/ (W·m-1·K-1) 比热/ (J·kg-1·K-1) 线膨胀系数/(K-1) 换热系数/(W·m-2·K-1) 围岩 26 18 0.200 1.50 50 2.00 3.00 771 1×10-5 — C30混凝土 25 30 0.167 3.08 55 2.01 1.74 800 1×10-5 6 表 2 钢筋计算参数
Table 2 Computational parameters for rebar
弹性模量/ GPa 屈服强度/ MPa 剪切刚度/ GPa 200 400 10 表 3 计算方案表
Table 3 Computational schemes
影响因素 布置方式 钢筋直径/mm 钢筋间距/ mm 保护层厚度/mm 围岩变形模量/ GPa 基准方案 单层钢筋 22 250 50 18 对比方案 无钢筋、双层钢筋 16,28,32 125,165 60,70,80,90,100 9,12,15,30 表 4 配筋率与裂缝特征值关系表
Table 4 Relationship between crack eigenvalue and percentage of reinforcement
钢筋直径/ mm 钢筋间距/ mm 配筋率/% 平均裂缝宽度/mm 最大裂缝宽度/mm 宏观裂缝条数 单筋 双筋 单筋 双筋 单筋 双筋 单筋 双筋 16 125 0.34 0.67 0.639 0.518 1.490 1.287 38 32 165 0.27 0.54 0.637 0.534 1.623 1.189 39 33 250 0.20 0.40 0.713 0.584 2.037 1.613 35 33 22 125 0.63 1.27 0.625 0.507 1.346 1.074 39 29 165 0.51 1.01 0.624 0.512 1.425 1.171 41 31 250 0.38 0.76 0.634 0.528 1.709 1.151 38 30 28 125 1.03 2.05 0.569 0.457 1.046 1.029 41 28 165 0.82 1.64 0.573 0.490 1.131 1.066 42 30 250 0.62 1.23 0.590 0.508 1.168 1.112 44 30 32 125 1.34 2.68 0.584 0.399 1.090 0.711 35 30 165 1.07 2.14 0.600 0.418 1.096 0.844 38 31 250 0.80 1.61 0.608 0.429 1.207 0.909 43 31 -
[1] 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010, 30(25): 1-9. ZHANG Liying, YE Tinglu, XIN Yaozhong, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE, 2010, 30(25): 1-9. (in Chinese)
[2] KIM H M, RUTQVIST J, RYU D W, et al. Exploring the concept of compressed air energy storage (CAES) in lined rock Caverns at shallow depth: a modeling study of air tightness and energy balance[J]. Applied Energy, 2012, 92: 653-667. doi: 10.1016/j.apenergy.2011.07.013
[3] 夏才初, 张平阳, 周舒威, 等. 大规模压气储能洞室稳定性和洞周应变分析[J]. 岩土力学, 2014, 35(5): 1391-1398. XIA Caichu, ZHANG Pingyang, ZHOU Shuwei, et al. Stability and tangential strain analysis of large-scale compressed air energy storage cavern[J]. Rock and Soil Mechanics, 2014, 35(5): 1391-1398. (in Chinese)
[4] 蒋中明, 秦双专, 唐栋. 压气储能地下储气库围岩累积损伤特性数值研究[J]. 岩土工程学报, 2020, 42(2): 230-238. doi: 10.11779/CJGE202002003 JIANG Zhongming, QIN Shuangzhuan, TANG Dong. Numerical study on accumulative damage characteristics of underground rock Caverns for compressed air energy storage[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(2): 230-238. (in Chinese) doi: 10.11779/CJGE202002003
[5] JIANG Z M, LI P, TANG D, et al. Experimental and numerical investigations of small-scale lined rock cavern at shallow depth for compressed air energy storage[J]. Rock Mechanics and Rock Engineering, 2020, 53(6): 2671-2683. doi: 10.1007/s00603-019-02009-x
[6] 蒋中明, 李鹏, 赵海斌, 等. 压气储能浅埋地下储气库性能试验研究[J]. 岩土力学, 2020, 41(1): 235-241, 252. JIANG Zhongming, LI Peng, ZHAO Haibin, et al. Experimental study on performance of shallow rock cavern for compressed air energy storage[J]. Rock and Soil Mechanics, 2020, 41(1): 235-241, 252. (in Chinese)
[7] 邓建, 肖明, 陈俊涛. 高压引水隧洞运行期复杂承载过程数值分析[J]. 中南大学学报(自然科学版), 2017, 48(5): 1261-1267. DENG Jian, XIAO Ming, CHEN Juntao. Numerical analysis for complex bearing process of high pressure diversion tunnel at runtime[J]. Journal of Central South University (Science and Technology), 2017, 48(5): 1261-1267. (in Chinese)
[8] 苏凯, 王博士, 王文超, 等. 水-温作用下水工隧洞钢筋混凝土衬砌开裂特性[J]. 华中科技大学学报(自然科学版), 2020, 48(12): 114-120. SU Kai, WANG Boshi, WANG Wenchao, et al. Study on cracks of reinforced concrete lining of hydraulic tunnel under the combined action of water pressure and temperature load[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(12): 114-120. (in Chinese)
[9] 韩峰, 徐磊, 金永苗. 输水隧洞内压作用下衬砌结构破坏分析[J]. 人民长江, 2020, 51(增刊1): 149-152. HAN Feng, XU Lei, JIN Yongmiao. Failure analysis on water diversion tunnel lining under internal pressure[J]. Yangtze River, 2020, 51(S1): 149-152. (in Chinese)
[10] 张广权, 曾大乾, 范照伟, 等. 利用地应力评价地下储气库断层密封性方法及应用[J]. 天然气地球科学, 2021, 32(6): 923-930. ZHANG Guangquan, ZENG Daqian, FAN Zhaowei, et al. Method and application of in situ stress field to evaluate fault sealing of underground gas storage traps[J]. Natural Gas Geoscience, 2021, 32(6): 923-930. (in Chinese)
[11] 张娟霞, 唐春安, 周秀艳, 等. 基于高性能计算的钢筋混凝土构件等间距裂缝形成过程研究[J]. 工程力学, 2009, 26(3): 161-167. ZHANG Juanxia, TANG Chunan, ZHOU Xiuyan, et al. Study on fracture spacing formation process of reinforced concrete specimen based on high performance calculation[J]. Engineering Mechanics, 2009, 26(3): 161-167. (in Chinese)
[12] 任晓丹, 李杰. 基于损伤理论的钢筋混凝土结构裂缝分析[J]. 同济大学学报(自然科学版), 2015, 43(8): 1129-1134. REN Xiaodan, LI Jie. Damage theory based analysis of crack opening width for RC structures[J]. Journal of Tongji University (Natural Science), 2015, 43(8): 1129-1134. (in Chinese)
[13] 陆新征. FRP-混凝土界面行为研究[D]. 北京: 清华大学, 2005. LU Xinzheng. Studies on FRP-Concrete Interface[D]. Beijing: Tsinghua University, 2005. (in Chinese)
[14] MA F J, KWAN A K H. Crack width analysis of reinforced concrete members under flexure by finite element method and crack queuing algorithm[J]. Engineering Structures, 2015, 105: 209-219.
[15] 王新敏, 李义强, 许宏伟. ANSYS结构分析单元与应用[M]. 北京: 人民交通出版社, 2011. WANG Xinmin, LI Yiqiang, XU Hongwei. ANSYS Structural Analysis Unit and its Application[M]. Beijing: China Communications Press, 2011. (in Chinese)
[16] 张飞, 马建勋, 南燕. 混凝土塑性损伤模型参数的选取与验证计算[J]. 混凝土与水泥制品, 2021(1): 7-11, 29. ZHANG Fei, MA Jianxun, NAN Yan. Parameters selection and verification calculation of concrete plastic damage model[J]. China Concrete and Cement Products, 2021(1): 7-11, 29. (in Chinese)
[17] 康清梁. 钢筋混凝土有限元分析[M]. 北京: 中国水利水电出版社, 1996: 130-146. KANG Qingliang. RC Finite Element Analysis[M]. Beijing: China Water & Power Press, 1996: 130-146. (in Chinese)
[18] KOUSKSOU T, ARID A, JAMIL A, et al. Thermal behavior of building material containing microencapsulated PCM[J]. Thermochimica Acta, 2012, 550: 42-47.
[19] 杨侗伟. 钢衬钢筋混凝土压力管道裂缝宽度计算模型研究[D]. 武汉: 湖北工业大学, 2020. YANG Dongwei. Research on Calculation Model of Crack Width of Steel Lined Reinforced Concrete Ppenstocks[D]. Wuhan: Hubei University of Technology, 2020. (in Chinese)
-
期刊类型引用(1)
1. 谭明伦,仝令帅,周鸣亮,张乐,黄宏伟. 数物双驱动的水下隧道围岩稳定性分析. 现代隧道技术. 2024(S1): 183-193 .  百度学术
百度学术
其他类型引用(1)
-
本文视频
-
49634c50c4b8625f7b197e9bacf65917Video Player is loading.
This is a modal window.
The media could not be loaded, either because the server or network failed or because the format is not supported. -
804c0dcee66a2af710af2eb3aa3ef115Video Player is loading.
This is a modal window.
The media could not be loaded, either because the server or network failed or because the format is not supported.
其他相关附件
-



 下载:
下载: