饱和砂-黏及砂-粉-黏混合土动孔压特性

李涛; 唐小微; 曾铃; 杨钢

doi:10.11779/CJGE2023S20044

饱和砂-黏及砂-粉-黏混合土动孔压特性 English Version

李涛^{1, 2,},
唐小微²,
曾铃¹,
杨钢²

1.
长沙理工大学土木工程学院, 湖南长沙 410114
2.
大连理工大学海岸和近海工程国家重点实验室, 辽宁大连 116024

基金项目:

国家自然科学基金项目 52308339

海岸和近海工程国家重点实验室开放基金项目 LP2110

桥梁工程安全控制教育部重点实验室开放基金项目 23ZDXK10

湖南省教育厅一般项目 22C0143

详细信息

作者简介:
李涛(1989—)，男，博士，讲师，主要从事混合砂土液化试验及理论等方面的研究工作。E-mail: litao@csust.edu.cn

中图分类号: TU435
计量
- 文章访问数: 126
- HTML全文浏览量: 25
- PDF下载量: 27
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Dynamic pore water pressure characteristics of saturated sand-clay and sand-silt-clay mixtures

1.
School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China
2.
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China

摘要

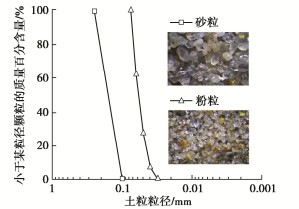
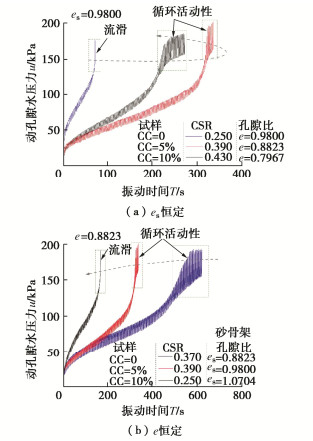
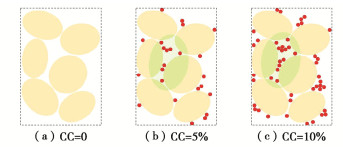
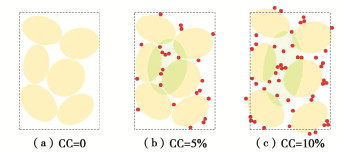
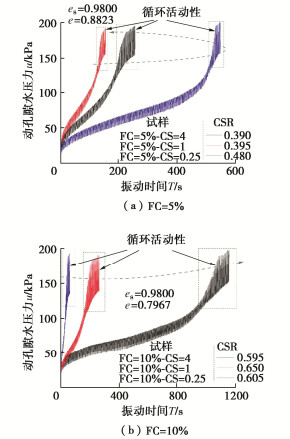
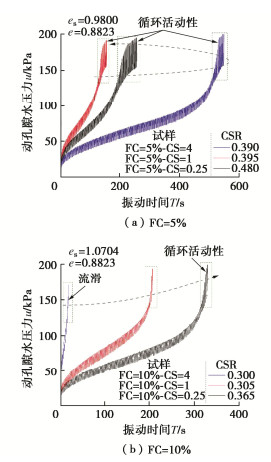
摘要: 含细粒砂土在吹填土中广泛分布，其在长期服役过程中可能经受波浪及车辆荷载的循环作用，掌握含细粒砂土动孔隙水压力的变化特性对于评价吹填土在循环荷载作用下的安全性及稳定性尤为重要。通过对饱和重塑砂-黏混合土及砂-粉-黏混合土开展室内固结不排水循环三轴试验，研究了不同黏粒含量、细粒含量、黏粉比和孔隙比下砂-黏混合土及砂-粉-黏混合土动孔压的发展特征。结合不同混合土内部颗粒赋存状态光学显微镜图像及颗粒赋存状态理论，揭示了黏粒含量、细粒含量、黏粉比和孔隙比对混合土动孔压发展的影响规律及影响机理。试验结果表明：对于砂骨架孔隙比与孔隙比恒定的砂-黏混合土来说，随着黏粒含量的增加，动孔压在振动后期的波动性增长趋势分别增强、减弱；对于砂-粉-黏混合土来说，随着细粒中粉粒含量增多（黏粒含量减少），FC=5%试样动孔压在振动后期的波动性增长趋势呈现非单调变化规律，不同孔隙比下FC=10%试样动孔压在振动后期的波动性增长趋势单调增强；提出了适用于砂-黏混合土以及砂-粉-黏混合土动孔压发展的Mod-Baziar模型，该模型不仅扩展了动孔压的预测范围，而且具有更高的预测精度，其可以更好反映动孔压的整体发展趋势以及孔压在振动后期的细节变化；当采用Mod-Baziar模型分别对不同孔隙比下的纯砂、砂-黏混合土以及砂-粉-黏混合土动孔压进行预测时，模型中各个参数的取值范围依次增大。初步分析认为上述试验结果是由不同颗粒间复杂的黏结、摩擦及填充作用所致。
- 混合土 /
- 黏粒含量 /
- 细粒含量 /
- 黏粉比 /
- 动三轴试验 /
- 动孔压模型
Abstract: The sand-fines mixtures are widely distributed in hydraulic fill soil and may be subjected to the cyclic action of wave and vehicle loads during their long-term service. It is very important to know the dynamic pore water pressure changing characteristics of the sand-fines mixtures for evaluating the safety and stability of hydraulic fill soil under cyclic loading. The consolidated undrained cyclic triaxial tests are carried out on the saturated reconstituted sand-clay and sand-silt-clay mixtures to investigate the development features of dynamic pore water pressure of mixed soil with different clay contents, fines contents, clay silt ratios and void ratios. By combining with the optical microscope images of soil particles and the theory of soil particles occurrence modes, the influence laws and mechanisms of clay content, fines content, clay silt ratio and void ratio on the dynamic pore water pressure of mixed soils are revealed. It is find that for the sand-clay mixtures (constant e and constant e_s), with the increasing clay contents, the fluctuation growth trend of dynamic pore water pressure at the later stage of vibration increases and weakens respectively. For the sand-silt-clay mixtures, with the increasing silt contents (decreasing clay contents), the fluctuation growth trend of the dynamic pore water pressure at the later stage of vibration of specimens with FC of 5% changes nonmonotonously. While the fluctuation growth trend of the dynamic pore water pressure at the later stage of vibration of specimens with FC of 10% increases monotonically under different void ratios. The Mod-Baziar model applied to the development of dynamic pore water pressure of sand-clay mixtures and sand-silt-clay mixtures is proposed, which extends the prediction range of dynamic pore water pressure and has higher prediction accuracy. The Mod-Baziar model can better reflect the overall development trend and detail change at the later stage of dynamic pore water pressure. By comparing the values of each parameter in the Mod-Baziar model, it is found that when the Mod-Baziar model is used to predict the dynamic pore water pressure of sand, sand-clay mixtures and sand-silt-clay mixtures with different void ratios respectively, the value range of each parameter in the model increases successively. The preliminary analysis suggests that the above results are attributed to the complex bonding, friction and filling between different particles.
- mixed soil /
- clay content /
- fines content /
- clay silt ratio /
- dynamic triaxial test /
- dynamic pore water pressure model

HTML全文

0. 引言

改革开放以来,中国高土石坝筑坝技术的快速提升,为满足不断增长的能源需求和改善能源结构的重要选择,一大批大型水利工程已建成或者在建,如糯扎渡、双江口、如美等300 m级高土石坝^[1],但是这些高坝大多数位于中国西南地震强度和频率很高的区域,一旦遭受强震失事,将会极大损害人民生命及财产安全^[2]。因此实时监测大坝的健康状况,并基于大坝真实特性分析大坝抗震安全是水电行业高度关注的关键性问题,其中大坝抗震安全动力分析主要采用有限元法,而坝体的模态参数,包括频率、阻尼比等,以及动力模型中参数等反映坝体的动态特征^[3],是更新大坝抗震分析有限元模型的重要参数,也是大坝在长期运行期间健康状况的评价指标。这些参数一般通过室内试验、现场试验或借鉴其他工程的参数确定,然而由于室内和现场条件的不确定性以及不同工程场地的差异,通过上述方法确定的参数和实际值往往会存在差异^[4],因此这些参数的合理选择和识别对于抗震安全十分重要。

许多学者基于地震记录和强迫振动试验进行大坝的模态参数识别。Alves等^[5]采用MODE-ID方法,基于地震数据确定了Pacoima拱坝的前两阶振动模式。Loh等^[6-7]采用带外源输入的自回归（auto regressive eXogenous, ARX）模型算法,基于强迫振动数据和地震记录识别了翡翠拱坝的模态参数。Yang等^[8]和李帅等^[9]基于地震数据采用ARX模型和频域法识别了二滩拱坝的模态参数。谯雯等^[10]和Cheng等^[3]基于地震数据,分别采用希伯特-黄变换方法和矢量自回归滑动平均模型模型对水口重力坝进行了模态参数识别。综上所述,可以看出模态参数的识别研究主要在于混凝土坝中,鲜有基于地震数据对土石坝进行模态识别。然而位于强震地区的一些土石坝也获得了大量的地震数据^[11-16],充分利用这些地震资料进行土石坝的模态参数识别,对土石坝的抗震安全评价有很重要的意义。

目前,主要有频域分解法和时域类等方法应用于基于环境激励的模态参数识别中^[17]。其中在频域内容易造成个别频率丢失,而时域类方法具有较好的识别精度和鲁棒性强等优点,并且随着计算机技术的快速发展,时域内根据结构的振动响应进行模态识别得到了大量应用^[18-23]。高土石坝是一种规模宏大的工程结构,其自由度高,模态密集。时域内的协方差驱动的随机子空间（stochastic subspace identification, SSI）可以较好识别密集模态,其假定激励源为高斯白噪声,在桥梁和高层建筑等结构广泛应用^[18,22-25],本文将其应用于高土石坝模态参数识别,取得了较好计算精度。

本文基于高土石坝的地震观测数据,提出了一种基于协方差驱动的随机子空间模型和改进的稳定图,以及谱系聚类的模态参数自动识别方法。首先,通过假定坝体上各个测点的监测数据满足白噪声序列来构造随机子空间模型；然后,构建并计算多个不同维度的Hankel矩阵所对应的SSI模型来获得稳定图,这样可以较好地剔除虚假模态,并且可以获得较为清晰的稳定轴；最后,采用谱系聚类分析自动准确识别出模态参数。通过两个数值算例对提出的模态识别方法进行了验证,获得了较好的结果,并将其应用于糯扎渡心墙堆石坝模态参数识别,验证了所提出的方法在工程应用上的可靠性和有效性,可以为高土石坝抗震安全评价提供有效的动力计算依据。

1. 协方差驱动的随机子空间算法

1.1 离散型随机状态空间模型

对于一个n维自由度系统,其离散型随机状态空间模型为

。

$\begin{array}{l} x_{k + 1} = A x_{k} + w_{k}, \\ y_{k} = C x_{k} + v_{k} 。 \end{array}}$

(1)

式中 $x_{k} \in R^{n \times 1}$ , $y_{k} \in R^{l \times 1}$ 分别为系统离散时间的状态矢量x和输出矢量y在k时刻的值,l为系统输出的数目； $A \in R^{n \times n}$ , $C \in R^{l \times n}$ 分别为系统状态空间方程的状态矩阵和输出矩阵； $w_{k} \in R^{n \times 1}$ , $v_{k} \in R^{l \times 1}$ 分别为系统建模过程噪声w和测量噪声v在k时刻的值,其亦为均值为零的白噪声。

定义输出协方差矩阵R_i：

$R_{i} = E [y_{k + i} \cdot y_{k}^{T}]$ ,

(2)

定义状态-输出协方差矩阵G：

$G = E [x_{k + 1} \cdot y_{k}^{T}]$ ,

(3)

可证明如下关系成立：

$R_{i} = C A^{i - 1} G$ 。

(4)

式（1）～（4）详细推导见文献[19]。

1.2 求解状态矩阵及输出矩阵

定义Hankel矩阵 $Y_{p} \in R^{l i \times j}$ , $Y_{f} \in R^{l i \times j}$ 为

$Y_{p} = \frac{1}{\sqrt{j}} [\begin{matrix} y_{0} & y_{1} & y_{2} & \dots & y_{j - 1} \\ y_{1} & y_{2} & y_{3} & \dots & y_{j} \\ y_{2} & y_{3} & y_{4} & \dots & y_{j + 1} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ y_{i - 1} & y_{i} & y_{i + 1} & \dots & y_{i + j - 1} \end{matrix}]$ ,

(5)

$Y_{f} = \frac{1}{\sqrt{j}} [\begin{matrix} y_{i} & y_{i + 1} & y_{i + 2} & \dots & y_{i + j} \\ y_{i + 1} & y_{i + 2} & y_{i + 3} & \dots & y_{i + j + 1} \\ y_{i + 2} & y_{i + 3} & y_{i + 4} & \dots & y_{i + j + 2} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ y_{2 i - 1} & y_{2 i} & y_{2 i + 1} & \dots & y_{2 i + j - 1} \end{matrix}]$ ,

(6)

$Y_{f +} = \frac{1}{\sqrt{j}} [\begin{matrix} y_{i + 1} & y_{i + 2} & y_{i + 3} & \dots & y_{i + j + 1} \\ y_{i + 2} & y_{i + 3} & y_{i + 4} & \dots & y_{i + j + 2} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ y_{2 i - 1} & y_{2 i} & y_{2 i + 1} & \dots & y_{2 i + j + 1} \\ y_{2 i} & y_{2 i + 1} & y_{2 i + 2} & \dots & y_{2 i + j} \end{matrix}]$ 。

(7)

式中 i,j分别为矩阵的行块数和列块数,理论上 $j \to \infty$ ；l为通道数,在本文中为监测点的个数,假定地震激励为白噪声序列；则y_i表示第i时刻各通道记录的输出信号构成的系列,即 $y_{i} \in R^{l \times 1}$ ；下标p,f分别表示“past”,“future”。

由（5）～（7）可得Toeplitz矩阵 $T_{1 | i} \in R^{l i \times l i}$ ：

$T_{1 | i} = Y_{f} Y_{p}^{T}$ ,

(8)

$T_{2 | i + 1} = Y_{f +} Y_{p}^{T}$ 。

(9)

结合式（2）中协方差矩阵的定义,式（8）为

$T_{1 | i} = [\begin{matrix} R_{i} & R_{i - 1} & R_{i - 2} & \dots & R_{1} \\ R_{i + 1} & R_{i} & R_{i - 1} & \dots & R_{2} \\ R_{i + 2} & R_{i + 1} & R_{i} & \dots & R_{3} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ R_{2 i - 1} & R_{2 i - 2} & R_{2 i - 3} & \dots & R_{i} \end{matrix}]$ 。

(10)

此外,结合式（3）和（4）,Toeplitz矩阵 $T_{1 | i}$ 可进一步改写为

$T_{1 | i} = O_{i} M_{i}$ 。

(11)

式中, $O_{i} = [\begin{matrix} C \\ C A \\ ⋮ \\ C A^{i - 1} \end{matrix}] \in R^{l i \times n}$ 为观测矩阵, $M_{i} =$ $(A^{i - 1} G A^{i - 2} G \dots G) \in R^{n \times l a}$ 为控制矩阵。

对Toeplitz矩阵 $T_{1 | i}$ 进行SVD分解可得

$T_{1 | i} = [\begin{matrix} U_{1} & U_{2} \end{matrix}] [\begin{matrix} S_{1} & 0 \\ 0 & S_{2} \end{matrix}] [\begin{matrix} V_{1}^{T} \\ V_{2}^{T} \end{matrix}] \approx U_{1} S_{1} V_{1}^{T}$ ,

(12)

式中, $U_{1} \in R^{l i \times n}$ , $V_{1} \in R^{l i \times n}$ 均为正交矩阵, $S_{1} =$ $d i a g [σ_{s}]$ , $σ_{1} \geq σ_{2} \geq \dots \geq σ_{n} \geq 0$ 为降序排列的n个主奇异值对角阵。

联立式（11）,（12）可求得矩阵的估计值：

$\begin{array}{l} O_{i} = U_{1} S_{1}^{1 / 2}, \\ M_{i} = S_{1}^{1 / 2} V_{1}^{T} 。 \end{array}}$

(13)

式中, $O_{i}$ 的前l行为输出矩阵C。由式（9）,（11）可得

$T_{2 | i + 1} = O_{i} A M_{i}$ 。

(14)

将式（13）代入式（14）可得

$A = {(O_{i}^{})}^{+} T_{2 | i + 1} {(M_{i}^{})}^{+} = (S_{1}^{- 1 / 2} U_{1}^{T}) T_{2 | i + 1} (V_{1} S_{1}^{- 1 / 2})$ ,

(15)

式中, ${(•)}^{+}$ 表示伪逆运算。

1.3 求解模态参数

对离散系统状态矩阵 $A$ 进行特征值分解

$A = ϕ Λ ϕ^{- 1}$ ,

(16)

式中, $Λ = d i a g (z_{s})$ （s=1,2,3,…,n）为由离散时间复特征值 $z_{s}$ 组成的n阶对角矩阵, $ϕ$ 为复特征向量组成的矢量矩阵。实际的系统是连续的,设 $λ_{s}$ 为 $z_{s}$ 对应的第s个连续时间特征值, $Δ t$ 为采样间隔,则有 $λ_{s} = \frac{\ln z_{s}}{Δ t}$ 。

系统的固有频率和阻尼比进而可以表示为

$\begin{array}{l} f_{i} = \frac{| λ_{i} |}{2 π}, \\ ξ_{i} = \frac{- Re (λ_{i})}{| ω_{i} |} 。 \end{array}}$

(17)

式中,Re表示取实部。

2. 模态参数的自动识别

稳定图作为一种有效剔除虚假模态的工具,假定系统有不同的阶次,通过计算可以得到每个阶次的模态参数,然后对各个阶次按照提前设置的条件进行参数识别,对于某一模态频率出现次数较多的点则为稳定点,由稳定点进而组成稳定轴。然而,在实际工程中,由于有时候激励源为地震波,此外噪声的干扰和结构的复杂性,传统的稳定图中仍会出现虚假模态,此外计算得到稳定极点较少时,难以获得清晰的稳定轴,对工程人员辨识模态参数造成干扰。

为能有效地移除虚假极点,同时避免一些稳定极点在某一维度Hankel矩阵中未识别到,造成稳定轴不清楚,本文通过构造多组不同维度的Hankel矩阵（根据经验,一般取5～10组就可以获得较好的结果）,将不同组辨识的结果在同一阶次进行两两对比,来剔除不稳定的极点,主要依据是稳定极点受构造矩阵行数影响较小,而计算模态或虚假模态受其影响较大,基本思路：假设有L组矩阵,在系统阶次p时,首先根据第i组(1≤i≤L)中第m个极点对应的模态参数组合 $(f_{p, m}^{i}, ξ_{p, m}^{i})$ ,在第j组(1≤j≤L)中选定与第i组中所选极点的固有频率最近极点n,其对应的模态参数组合 $(f_{p, n}^{j}, ξ_{p, n}^{j})$ ,然后按照式（18）进行计算,在两两计算循环结束后,满足条件式（18）最多的点作为稳定极点予以保留。

$\begin{array}{l} {(\frac{f_{m}^{i} - f_{n}^{j}}{Δ f})}^{2} + {(\frac{ξ_{m}^{i} - ξ_{n}^{j}}{Δ ξ})}^{2} + {(\frac{1 - M A C (Φ_{m}^{i}, Φ_{n}^{j})}{Δ m a c})}^{2} < 1, \\ Δ f = \min (δ_{f} \max (f_{m}^{i}, f_{n}^{j})), \\ Δ ξ = \min (δ_{ξ} \max (ξ_{m}^{i}, ξ_{n}^{j})) 。 \end{array}}$

(18)

式中 f, $ξ$ , $Φ$ 分别为极点处的固有频率、阻尼比和模态振型； $M A C (Φ_{m}^{i}, Φ_{n}^{j})$ 为 $Φ_{m}^{i}$ 与 $Φ_{n}^{j}$ 模态置信准则值； $δ_{f}$ 为频率相对偏差,取值5%； $δ_{ξ}$ 为阻尼比相对偏差,取值10%； $Δ m a c$ 为模态置信准则值绝对偏差,取值2%。

借助谱系聚类的方法对挑选出的稳定极点进行自动选择,将距离在一定范围内的数据进行聚类,认为同一类中的数据属于同一模态,最后选择元素个数大于一定值的类作为识别结果。

步骤（1）：假设由SSI方法识别得到的稳定极点总数为N,令N个样本自成一类。通过计算各极点之间的距离（相似性）d_ij：

$d_{i j} = {(\frac{f_{m}^{i} - f_{n}^{j}}{Δ f})}^{2} + {(\frac{ξ_{m}^{i} - ξ_{n}^{j}}{Δ ξ})}^{2} + {(\frac{1 - M A C (Φ_{m}^{i}, Φ_{n}^{j})}{Δ m a c})}^{2},$

(19)

即可得到初始距离矩阵D₀。

步骤（2）：通过判断距离矩阵D₀中的各数值大小来实现相同模态的聚类,设定距离阈值为1,即当 $d_{i j} \leq 1$ 时,则认为第F_i和F_j的模态为同一类,将其合并为新的一类F_ij。并与其余类建立新的分类。

步骤（3）：通过最短距离法得到新的距离矩阵D₁^[20],然后跳转步骤（2）,重复计算并合并,当D_k的最小分量超过1,算法停止,此时将N个样本分成了k类。

步骤（4）：统计每一类中聚类元素的个数,并设定聚类数目阈值X,若每一类中元素个数大于X,则判定为稳定极点,予以保留,并将其绘制于稳定图中。最后采用每一类中统计均值作为最终的模态参数估计值。其中,X=N/3,N为系统阶数。

3. 算例验证

为了讨论随机子空间法和模态参数自动识别方法的可靠性,本文采用一个双自由度系统和一个均质堆石坝在非平稳随机激励下的动力反应进行模态参数识别两个算例。

3.1 双自由度模型

双自由度模型如图1所示,利用Newmark-β方法求解地震情况下各质点的反应。模型参数分别为^[26]：质量 $m_{1} = 0.050 t \cdot s^{2} / c m$ , $m_{2} = 0.055 t \cdot s^{2} / c m$ ；刚度 $k_{1} = k_{2} =$ $120 t / c m$ ；阻尼系数 $c_{1} = 1.0 t \cdot s / c m$ , $c_{2} =$ $0.6 t \cdot s / c m$ 。根据模型参数,通过特征值法计算系统的理论模态参数,结构的固有频率分别为f₁=4.653 Hz,f₂=12.458 Hz；振型阻尼比 $ξ_{1} = 0.107$ , $ξ_{2} = 0.234$ 。地面输入的非平稳激励为EI Centro波南北向地震动记录,如图2所示。

图 1 双自由度系统模型

Figure 1. Two degrees of freedom system model

下载: 全尺寸图片幻灯片

图 2 EI Centro地震波

Figure 2. EI Centro seismic waves

下载: 全尺寸图片幻灯片

为满足协方差驱动的随机子空间法的识别需求,模型Hankel矩阵的行数i $＞$ N/l,且列数j $＞$ 20i^[17]。在算例中,构造协方差的振动数据是两个质点的水平向的加速度,因此通道数l=2。分析时最大阶次为100,则Y_p矩阵的最小行数i_min为50。假定每个通道信号的总采样长度为L,则利用所有数据点来构造矩阵Y_p和Y_p+1的列数为j=L-2i,输入的非平稳激励是EI centro地震波前30 s数据,其采用长度L=400 Hz×30 s=12000,取构造矩阵行数i=60,则j=11880,利用随机子空间识别方法,得到传统稳定图如图3所示。由图3可以看出,存在较多的虚假极点,并且出现了虚假的稳定轴。采用第2节提出的方法对虚假极点进行剔除生成清晰的稳定图,并自动识别模态参数,分析时构造5组不同行数的Hankel矩阵,矩阵的行数为i=50+randn(50,5）,获得的稳定图如图4所示,可以看出虚假极点基本被剔除,并且相对于原始稳定图来说稳定轴更为连续,较好地避免了稳定极点的在某一组计算时的丢失；为了较好看出各个频率下的阻尼比关系,并以频率和阻尼比建立簇分析图,如图5所示,稳定点被聚集到2个簇中；采用参数统计均值法计算模态结果,如表1所示,可以看出识别得到的频率值和阻尼比与理论值十分接近,说明本文方法对激励源为地震波情况下的结构进行模态参数识别具有较好的精度。

图 3 原始稳定图(i=60)

Figure 3. Original stable graph

下载: 全尺寸图片幻灯片

图 4 剔除虚假极模态后稳定图

Figure 4. Stable graph after removing false polar modes

下载: 全尺寸图片幻灯片

图 5 频率–阻尼比簇分析图

Figure 5. Cluster analysis chart of frequency-damping ratio

下载: 全尺寸图片幻灯片

表 1 双自由度模态参数识别结果

Table 1. Identified model parameters of two degrees of freedom system model

振型	频率/Hz		阻尼比
振型	理论值	计算值	理论值	计算值
1阶	4.653	4.614	0.107	0.105
2阶	12.458	12.856	0.234	0.246

下载: 导出CSV

| 显示表格

3.2 均质堆石坝模型

均质堆石坝断面有限元网格如图6所示,坝高150 m,上下游坝坡均为1∶2。为获得动力计算需要的初始应力场,采用邓肯-张E-B模型进行静力填筑计算,模型参数^[27]： $ρ$ =2.2 g/cm^-3, $φ_{0}$ =51.8, $Δ φ$ =10.4°,K=1100,n=0.35,R_f=0.82,K_b=600,m=0.1。动力计算采用等效黏弹性模型,计算参数：K=3000,n=0.5。堆石料的归一化动剪应变和阻尼比与动剪应变的关系采用孔宪京等^[28]建议的平均值,其中阻尼比在小应变10^-5时约为0.02。有限元计算得到的大坝前四阶频率见表2。地面输入的非平稳激励仍为EI Centro波南北向地震动记录,由于堆石坝在弱震时近似线弹性变化,因此调整峰值为0.05 m/s²进行动力计算。

图 6 堆石坝网格图

Figure 6. FEM mesh of rockfill dam

下载: 全尺寸图片幻灯片

表 2 均质堆石坝模态参数识别结果

Table 2. Identified model parameters of homogeneous rockfill dam

振型	频率/Hz		阻尼比
振型	计算值	FEM	计算值	FEM
1阶	1.11	1.09	0.023	0.020
2阶	1.75	1.76	0.016	0.020
3阶	1.93	1.96	0.022	0.020
4阶	2.20	2.24	0.015	0.020

下载: 导出CSV

| 显示表格

坝体下游坝坡按照等高设置3个测点,利用3个测点的水平向加速度记录作为输入,构造Hankel矩阵,通道数l=3,每个通道长度为30 s,频率为400 Hz,矩阵行数i=100,j=11800,通过协方差驱动的随机子空间法可以获得图7所示的稳定图,可以看出原始的稳定图中出现了较多的虚假极点,采用第2节提出的剔除虚假极点和谱系聚类筛选法,分析时构造5组不同行数的Hankel矩阵,矩阵的行数为i=100+ randn(100,5）,获得图8所示的稳定图,可以看出不仅剔除了虚假极点,还使稳定图中的稳定轴相对于原始稳定图更为清晰连续。图9是频率和阻尼比的簇分析图。最终的模态参数统计均值如表2所示。识别得到的结果和有限元计算值十分接近,说明本文方法对激励源为地震波情况下的堆石坝进行模态参数识别也具有较好的精度。

图 7 原始稳定图(i=100)

Figure 7. Original stable graph (i=100)

下载: 全尺寸图片幻灯片

图 8 剔除虚假极模态后稳定图

Figure 8. Stable graph after removing false polar modes

下载: 全尺寸图片幻灯片

图 9 频率–阻尼比簇分析图

Figure 9. Cluster analysis chart of frequency-damping ratio

下载: 全尺寸图片幻灯片

4. 糯扎渡心墙堆石坝模态参数识别

4.1 工程概况

糯扎渡水电站位于澜沧江下游普洱市思茅区和澜沧县交界处,坝址区位于青藏地震区的滇西南地震带,区内地震活动比较强烈,其地震基本烈度为Ⅶ。该工程主体挡水结构为高261.5 m的心墙堆石坝,是目前国内已建成的最高的土石坝。坝顶高程824.1 m,坝顶长630 m,宽18 m,上游坡度比为1.9∶1,下游坡度比为1.8∶1,大坝水库正常蓄水位812 m。为了监测大坝受地震情况下的影响,根据结构物对地震的反应特征,在大坝典型断面安置了若干个强震监测仪,坝体典型断面及强震仪布置如图10所示,在典型断面坝顶是T2测点,下游坝坡780高程处是T6测点,下游坝坡高程701高程处是T7测点,下游坝坡高程626高程处是T8测点,这些测点在2014年10月7日发生的6.6级景谷地震中均测到并记录了完整的加速度时程,图11给出了各个测点顺河向的地震动记录。

图 10 坝体典型断面及强震仪布置图

Figure 10. Typical cross-section with material zones in Nuozhadu core-wall rockfill dam

下载: 全尺寸图片幻灯片

图 11 坝体T2、T6、T7、T8测站的顺河向加速度记录

Figure 11. Downstream acceleration records of dam body at monitoring points T2, T6, T7 and T8

下载: 全尺寸图片幻灯片

4.2 基于SSI的坝体模态参数识别

选取坝体上4个测点的顺河向加速度记录作为输入,构造Hankel矩阵,通道数l=4,每个通道长度为35 s,采用频率为400 Hz,矩阵行数i=60,j=13880,通过协方差驱动的随机子空间法可以获得图12所示的稳定图,可以看出原始的稳定图中出现了较多的虚假极点,对于模态识别增加了干扰。采用第2节提出的剔除虚假极点和谱系聚类筛选法,分析时构造5组不同行数的Hankel矩阵,矩阵的行数为i=50+ randn(50,5）,获得图13所示的稳定图,在0～4 Hz范围内,有4类模态参数被识别出来。图14是频率和阻尼比的簇分析图,可以清楚地看出不同阶次下频率和阻尼比的分布情况。最终的模态参数统计均值如表3所示。此外并和有限元分析结果对比,分别采用相互作用模型和刚性边界有限元模型进行分析,相互作用模型如图15所示,刚性边界模型为图中去除地基部分模型,并采用文献[12]根据坝体实测响应反演得到的坝料参数,采用“直接滤频法”求解特征方程,得到坝体的前四阶坝体频率,如表3所示。

图 12 糯扎渡大坝原始稳定图

Figure 12. Original stable graph of Nuozhadu dam

下载: 全尺寸图片幻灯片

图 13 糯扎渡大坝剔除虚假极模态后稳定

Figure 13. Stable graph after removing false polar modes

下载: 全尺寸图片幻灯片

图 14 糯扎渡频率–阻尼比簇分析图

Figure 14. Cluster analysis chart of frequency-damping ratio

下载: 全尺寸图片幻灯片

表 3 糯扎渡大坝模态参数识别结果

Table 3. Identified model parameters of Nuozhadu dam

振型	频率/Hz			阻尼比
振型	计算值	FEM1	FEM2	计算值	FEM
1阶	1.15	1.10	1.22	0.051	0.04
2阶	1.35	1.27	1.42	0.034	0.04
3阶	1.83	1.54	1.73	0.027	0.04
4阶	2.37	1.74	1.96	0.043	0.04
注：FEM1为相互作用有限元模型,FEM2为刚性边界模型。

下载: 导出CSV

| 显示表格

图 15 糯扎渡大坝三维有限元模型

Figure 15. 3D FEM of Nuozhadu dam

下载: 全尺寸图片幻灯片

从表3中可以看出,SSI法识别的前三阶模态频率基本上是一致的,第四阶模态频率较大。分析产生的原因可能是在弱震情况下,很难激发坝体的某些高阶振型,对于土石坝这种密频结构在坝体响应中未能完整体现。进一步计算刚性边界有限元模型较高阶频率,得到第5阶频率为2.13 Hz,第6阶频率为2.30 Hz,对比可以发现在景谷地震中未能识别出实际的第4和5阶振型。但是在土石坝进行抗震稳定性分析时,一般比较关心的前两阶频率,SSI方法可以较好地识别出坝体基频和第二阶频率,可以为大坝抗震安全性评价提供一定的依据。此外有限元模拟时阻尼比计算采用的是糯扎渡大坝室内动三轴试验得到的阻尼比与动剪应变幅值之间的关系曲线,根据试验曲线在动剪应变幅值为10^-5时堆石料阻尼比约为0.04,心墙料阻尼比约为0.03^[29],考虑到堆石料占大坝主要部分,认为大坝在弱震情况下阻尼比为0.04。对比识别的模态参数,坝体前几阶的阻尼比都在0.05左右,和室内试验值也较为接近,符合坝体在弱震情况下的一般规律,也说明景谷地震对坝体的影响不大,处于弹性范围内。

楚金旺等^[30]通过考虑三维河谷效应对国内外20余座土石坝的实测基本自振周期资料进行了统计分析,提出了大坝一阶自振周期计算公式,根据此公式糯扎渡大坝的一阶自振频率约为1.1 Hz。毛文娟^[31]对不同坝坡和河谷地形因素研究指出300级均质坝自振频率在0.84～1.06 Hz,由于其所采用地震工况峰值为0.2g,地震时坝体进入非线性使得自振频率偏小。杨玉生等^[32]对300 m级双江口心墙堆石坝模型试验研究指出双江口原型坝在弱震情况下一阶自振频率在0.8～1.2 Hz。通过对比以上学者研究,本文识别得到的糯扎渡心墙堆石坝的自振频率在合理范围内,这也说明本文提出的高土石坝模态参数识别方法是合理的。

5. 结语

本文利用地震情况下坝体测点反应构建协方差驱动的随机子空间模型,通过构造多组不同维度的Hankel矩阵,不仅可以很好地剔除虚假模态,同时也避免了稳定极点的在某一组计算时的丢失,采用谱系聚类的筛选方法,可以有效的识别坝体的固有频率和阻尼比,并且实现了物理模态参数的自动获取,规避了人为选择引入的误差,保障了识别结果的稳定性。

在两个数值算例中,改进后的稳定图很好地剔除了虚假极点,也使得稳定轴较为清晰,并且获得的模态参数与模型的实际模态分析结果较为一致,说明在利用地震波的非平稳环境激励下,本文方法仍可以获得较好的模态参数识别精度。

根据景谷地震的地震监测数据,将其应用于糯扎渡心墙堆石坝的模态参数识别,较好地识别坝体的固有频率和阻尼比,可以进一步根据模态参数来识别坝体动力参数,为土石坝抗震安全评价提供一种新的方法。

随着大坝高度向300 m级建设,在强震情况下大坝的监测在水利工程中受到很大的关注,在本文的基础上进一步研究基于强震记录的大坝模态识别方法,可以为大坝运行期的健康监测和抗震安全分析提供基础,也具有重要的理论意义和工程应用价值。

图 1 试验所用砂粒和粉粒的颗粒级配曲线

Figure 1. Grain-size distribution curves of sand and silt

下载: 全尺寸图片幻灯片

图 2 混合土细观特征观测流程

Figure 2. Observation process of micro-characteristics of mixed soil

下载: 全尺寸图片幻灯片

图 3 砂-黏混合土动孔压试验结果

Figure 3. Dynamic pore water pressures of sand-clay mixtures

下载: 全尺寸图片幻灯片

图 4 砂-黏混合土细观特征图像

Figure 4. Microscopic feature images of sand-clay mixtures

下载: 全尺寸图片幻灯片

图 5 砂-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 5. Contact states of sand-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

图 6 砂-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 6. Contact states of sand-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

图 7 砂-粉-黏混合土动孔压试验结果（e_s恒定）

Figure 7. Dynamic pore water pressures of sand-silt-clay mixtures (constant e_s)

下载: 全尺寸图片幻灯片

图 8 砂-粉-黏混合土动孔压试验结果（e恒定）

Figure 8. Dynamic pore water pressures of sand-silt-clay mixtures (constant e)

下载: 全尺寸图片幻灯片

图 9 砂-粉-黏混合土细观特征图像^[13]

Figure 9. Microscopic feature images of sand-silt-clay mixtures^[13]

下载: 全尺寸图片幻灯片

图 10 砂-粉-黏混合土颗粒接触状态示意图

Figure 10. Contact states of sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

图 11 砂-粉-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 11. Contact states of sand-silt-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

图 12 砂-粉-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 12. Contact states of sand-silt-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

图 13 三模型对混合土动孔压的拟合结果

Figure 13. Fitting results of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

图 14 三模型对各个试样动孔压的拟合度

Figure 14. R-squared of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

图 15 饱和砂-黏、砂-粉-黏混合土动孔压发展

Figure 15. Development of dynamic pore water pressure for saturated sand-clay and sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

图 16 Mod-Baziar模型中各个参数取值范围

Figure 16. Value ranges of each parameter in Mod-Baziar model

下载: 全尺寸图片幻灯片

表 1 试验设计方案

Table 1 Design schemes of dynamic tests

试验编号	细粒含量FC/%	细粒中黏、粉占比/%		黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
试验编号	细粒含量FC/%	黏粒	粉粒	黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
D1	0	－	－	－	200	0.9800	0.9800
D2	5	20	80	0.25	200	0.9800	0.8823
D3		50	50	1	200	0.9800	0.8823
D4		80	20	4	200	0.9800	0.8823
D5		100	0	－	200	0.9800	0.8823
D6	10	20	80	0.25	200	0.9800	0.7967
D7		50	50	1	200	0.9800	0.7967
D8		80	20	4	200	0.9800	0.7967
D9		100	0	－	200	0.9800	0.7967
D10	0	－	－	－	200	0.8823	0.8823
D11	10	20	80	0.25	200	1.0704	0.8823
D12		50	50	1	200	1.0704	0.8823
D13		80	20	4	200	1.0704	0.8823
D14		100	0	－	200	1.0704	0.8823

下载: 导出CSV

表 2 Mod-Baziar模型拟合参数取值范围

Table 2 Fitting parameter ranges of Mod-Baziar model

土体	模型参数
土体	θ	β	γ	ω
纯砂	1.5430~2.0362	-0.0057~-0.2760	0.1152 ~0.5637	0.4136~1.9222
砂-黏	1.3227~2.3576	-0.1089~-0.4709	0.0132~1.4852	-2.0889~2.7362
砂-粉-黏	1.2490~2.4263	-0.0510~-0.4252	-0.5369~1.8854	-2.8496~3.8353

下载: 导出CSV

参考文献(13)

[1]	SASAKI Y, TOWHATA I, MIYAMOTO K, et al. Reconnaissance report on damage in and around river levees caused by the 2011 off the Pacific coast of Tohoku earthquake[J]. Soils and Foundations, 2012, 52(5): 1016-1032. doi: 10.1016/j.sandf.2012.11.018
[2]	SEED H B, MARTIN P P, LYSMER J. Pore-water pressure changes during soil liquefaction[J]. Journal of the Geotechnical Engineering Division, 1976, 102(4): 323-346. doi: 10.1061/AJGEB6.0000258
[3]	BOOKER J R, RAHMAN M S, SEED H B. Gadflea: a computer program for the analysis of pore pressure generation and dissipation during cyclic or earthquake loading[R]. Berkeley, CA: Earthquake Engineering Research Center, University of California, 1976.
[4]	BAZIAR M, SHAHNAZARI H, SHARAFI H. A laboratory study on the pore pressure generation model for Firouzkooh silty sands using hollow torsional test[J]. International Journal of Civil Engineering, 2011, 9: 126-134.
[5]	许成顺, 王冰, 杜修力, 等. 循环加载频率对砂土液化模式的影响试验研究[J]. 土木工程学报, 2021, 54(11): 109-118. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202111011.htm XU Chengshun, WANG Bing, DU Xiuli, et al. Experimental study on effect of cyclic loading frequency on liquefaction mode of sand[J]. China Civil Engineering Journal, 2021, 54(11): 109-118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202111011.htm
[6]	董青, 周正华, 苏杰, 等. 基于对数动骨架考虑可逆孔压的有效应力本构研究[J]. 岩土工程学报, 2020, 42(12): 2322-2329. doi: 10.11779/CJGE202012020 DONG Qing, ZHOU Zhenghua, SU Jie, et al. Constitutive model for effective stress based on logarithmic skeleton curve considering reversible pore pressure[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2322-2329. (in Chinese) doi: 10.11779/CJGE202012020
[7]	王桂萱, 桑野二郎, 竹村次朗. 循环荷载下砂质混合土孔隙水压力特性研究[J]. 岩土工程学报, 2004, 26(4): 541-545. doi: 10.3321/j.issn:1000-4548.2004.04.023 WANG Guixuan, JiRO Kuwano, JIRO Takemura. Study on excess pore water pressures of sands mixed with clays under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 541-545. (in Chinese) doi: 10.3321/j.issn:1000-4548.2004.04.023
[8]	吴琪, 王路阳, 刘启菲, 等. 基于剪切应变特征的饱和珊瑚砂超静孔压发展模型试验研究[J]. 岩土工程学报, 2023, 45(10): 2091-2099. doi: 10.11779/CJGE20220956 WU Qi, WANG Luyang, LIU Qifei, et al. Experimental study on development model of excess pore pressure for saturated coral sand based on shear strain characteristics[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(10): 2091-2099. (in Chinese) doi: 10.11779/CJGE20220956
[9]	张伏光, 聂卓琛, 陈孟飞, 等. 不排水循环荷载条件下胶结砂土宏微观力学性质离散元模拟研究[J]. 岩土工程学报, 2021, 43(3): 456-464. doi: 10.11779/CJGE202103008 ZHANG Fuguang, NIE Zhuochen, CHEN Mengfei, et al. DEM analysis of macro- and micro-mechanical behaviors of cemented sand subjected to undrained cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 456-464. (in Chinese) doi: 10.11779/CJGE202103008
[10]	王志华, 何健, 高洪梅, 等. 基于触变流体理论的可液化土体振动孔压模型[J]. 岩土工程学报, 2018, 40(12): 2332-2340. doi: 10.11779/CJGE201812023 WANG Zhihua, HE Jian, GAO Hongmei, et al. Dynamic pore water pressure model for liquefiable soils based on theory of thixotropic fluid[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2332-2340. (in Chinese) doi: 10.11779/CJGE201812023
[11]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[12]	刘洋, 吴顺川, 周健. 循环荷载下砂土变形的细观数值模拟Ⅱ: 密砂试验结果[J]. 岩土工程学报, 2007, 29(11): 1676-1682. doi: 10.3321/j.issn:1000-4548.2007.11.014 LIU Yang, WU Shunchuan, ZHOU Jian. Micro-numerical simulation of cyclic biaxial test Ⅱ: results of dense sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1676-1682. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.11.014
[13]	LI T, TANG X W. Influences of low fines content and fines mixing ratio on the undrained static shear strength of sand-silt-clay mixtures[J]. European Journal of Environmental and Civil Engineering, 2022, 26(9): 3706-3728. doi: 10.1080/19648189.2020.1813206

施引文献(13)

期刊类型引用(7)

1.	刘华仁，佟大威，余佳，苏哲. 基于模糊聚类和随机子空间的高土石坝模态参数自动识别. 水力发电学报. 2025(02): 107-115 . 百度学术
2.	蔡正银，范开放，朱洵. 基于现场试验的海上筒型基础风电结构动力特性研究. 岩土工程学报. 2025(03): 443-452 . 本站查看
3.	张翰，张锋，谭尧升，姚孟迪，邓检华. 基于运行时模态分析和代理模型的大坝力学参数反演方法. 粉煤灰综合利用. 2025(01): 163-166 . 百度学术
4.	王晓澎，张浩，李欣，肖森，刘璇. 基于随机子空间法的滑动轴承运行模态参数识别. 噪声与振动控制. 2024(01): 126-133 . 百度学术
5.	樊圆，卢文胜，虞终军，任祥香. 多次地震作用下高层建筑结构动力特性识别和响应分析. 建筑结构学报. 2023(01): 225-234 . 百度学术
6.	翟世龙，刘萍，黄静，艾萨·伊斯马伊力，毛玉剑. 基于大坝地震反应台阵的土石坝模态参数识别. 内陆地震. 2023(04): 353-361 . 百度学术
7.	黄嘉思，徐文城，段元锋，章红梅. 基于随机子空间方法的向量式有限元索网模型模态识别. 结构工程师. 2022(06): 1-6 . 百度学术