深部冲击地压煤层水射流割缝卸压参数优化研究

胡阳; 曹安业; 秦续峰; 薛成春; 郭文豪; 刘耀琪; 彭雨杰

doi:10.11779/CJGE20220451

深部冲击地压煤层水射流割缝卸压参数优化研究 English Version

胡阳^{1, 2,},
曹安业^{2, 3, ,},
秦续峰^{4, 5},
薛成春²,
郭文豪²,
刘耀琪²,
彭雨杰²

1.
云南煤矿安全技术中心有限公司, 云南昆明 650000
2.
中国矿业大学矿业工程学院, 江苏徐州 221116
3.
中国矿业大学江苏省矿山地震监测工程实验室, 江苏徐州 221116
4.
山东新河矿业有限公司山东济宁 272499
5.
内蒙古仲泰能源伊旗分公司, 内蒙古鄂尔多斯 017200

基金项目:

国家自然科学基金项目 U21A20110

国家自然科学基金项目 51734009

山东省重大科技创新工程项目 2019SDZY02

详细信息

作者简介:
胡阳(1995—)，男，云南玉溪人，硕士，主要从事冲击地压方面的研究工作。E-mail: 1598826049@qq.com

通讯作者:
曹安业, E-mail: caoanye@163.com

中图分类号: TU43;TD713
计量
- 文章访问数: 244
- HTML全文浏览量: 54
- PDF下载量: 45
出版历程
- 收稿日期: 2022-04-17
- 网络出版日期: 2023-02-19
- 刊出日期: 2023-06-30

On optimization of pressure-relief parameters of water jet slots in deep rockburst coal seams

HU Yang^{1, 2,},
CAO Anye^{2, 3, ,},
QIN Xufeng^{4, 5},
XUE Chengchun²,
GUO Wenhao²,
LIU Yaoqi²,
PENG Yujie²

1.
Yunnan Coal Mine Safety Technology Center Co., Ltd., Kunming 650000, China
2.
School of Mining Engineering, China University of Mining and Technology, Xuzhou 221116, China
3.
Jiangsu Mine Earthquake Monitoring Engineering Laboratory, China University of Mining and Technology, Xuzhou 221116, China
4.
Shandong Xinhe Mining Co., Ltd., Jining 272499, China
5.
Inner Mongolia Zhongtai Energy Yiqi Branch, Ordos 017200, China

摘要

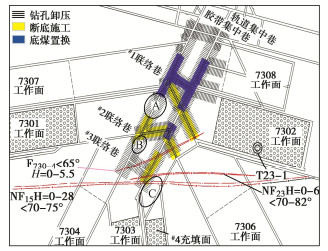
摘要: 为确定深部冲击地压煤层高压水射流割缝卸压最优参数，采用数值模拟、理论推导剖析了高压水射流割缝卸压防冲原理，构建了钻孔间距、割缝半径等4个因素的参数优化理论模型，以某矿730采区集中巷为研究对象，基于动静载叠加原理，研究揭示了集中巷冲击地压机理，获得了各影响因素的理论参数值，并揭示了不同理论参数下应力、塑性区及冲击危险指数的异同。研究结果表明：各影响因素对高压水射流割缝卸压效果均有较大影响，且各因素之间存在显著的交互作用；采用卸压后平均垂直应力、弹性能密度、冲击危险指数及卸压成本为卸压参数的有效性及经济性指标，评估了不同参数卸压效果的优劣，获得该煤层物理力学性质下高压水射流割缝卸压最优参数；研究成果在730采区^#3联络巷应用后，现场微震频次、总能量及微震空间集中度均大幅降低，为工作面安全回采提供了技术保障。
- 冲击地压 /
- 煤矿巷道 /
- 水射流割缝 /
- 参数优化 /
- 数值模拟
Abstract: In order to determine the optimal parameters of pressure relief by high-pressure water jet slotting in deep rockburst coal seams, the principles of pressure relief and impact prevention are analyzed through numerical simulation and theoretical deduction. The theoretical model for parameter optimization for four factors, such as drilling spacing and slot radius, is established. Based on the principles of dynamic and static load superpositions, the mechanism of rockburst in the concentrated roadway in mining area No. 730 of a mine is studied, the theoretical parameter values of each influencing factor are obtained, and the similarities and differences of stress, plastic zone and impact risk index under different theoretical parameters are revealed. The results show that all the influencing factors have a great influence on the pressure-relief effects of high-pressure water jet slotting, and there is a significant interaction between the factors. The average vertical stress after pressure relief, elastic energy density, impact danger index and pressure relief cost are used as the effectiveness and economic indexes of pressure-relief parameters, and the advantages and disadvantages of the pressure-relief effects of different parameters are evaluated so as to obtain the optimal pressure-relief parameters of high-pressure water jet slotting under the physical and mechanical properties of the coal seam. After the application of the research results in the contact lane No. 3 of the mining area No. 730, the frequency, total energy and spatial concentration of microearthquakes in the site are greatly reduced, which provides technical support for the safe mining of the working face.
- rockburst /
- coal mine roadway /
- water jet slot /
- parameter optimization /
- numerical simulation

HTML全文

0. 引言

相较于传统的单台盾构掘进方式，盾构地中对接法的最大优点是无需设置中间到达井，两台盾构机相向掘进有效解决了盾构机掘进能力不足的问题，并且可大幅降低施工工期。1997年建成的东京湾海底隧道是早期实现盾构对接解体的经典工程案例^[1]，中国则是在2011年建成的广东狮子洋隧道上首次应用该方法^[2-3]。盾构对接法通常施工流程如下：先行盾构掘进至对接点、对接点注浆加固、后行盾构掘进至对接点、洞内拆解刀盘等设备、浇筑二次衬砌。刀盘拆卸后，对接段临空面拱顶发生下沉，围岩应力重新分布。为了保证地层稳定性，隧道围岩有限的变形并不能使压力拱充分发展，由于抗剪应力未达到极限条件，此时的成拱效应称为“不完全拱效应”，探究不完全拱的上覆围岩压力计算方法有助于更好指导实际工程。

明确压力拱拱体的范围是准确计算隧道围岩压力的必要前提。傅鹤林等^[4]根据隧道围岩弹塑性应力分布特点，提出以切向应力高于原岩应力区域作为拱体范围。王家全等^[5]提出以最大主应力最大值为内边界，以大小主应力偏转点为外边界。李奎^[6]认为以最大主应力最大值作为内边界是不充分的，提出根据水平应力减小区域判定内边界，以最大主应力矢量流线确定拱体外边界。Kong等^[7]提出以水平应力相较于初始状态进行判定隧道上方压力拱内外边界，但缺少对两侧边界的判定。Chen等^[8]通过计算水平应力和垂直应力在扰动后与初始状态之比区分对拱顶、拱脚范围。从上述研究可知对于压力拱范围的确定主要有围岩弹塑性分区法、主应力偏转法和主应力矢量流线法^[9-10]，但大多都是单独讨论拱圈范围，如何划分起转移上部垂直荷载作用的主拱圈范围并不明确。

针对地层成拱作用下的围岩上覆围岩压力计算，叶飞等^[11]针对软弱围岩中隧道掌子面前方形成的不完全拱，假设水平微分土条上的垂直应力为定值，推导了砂土和低黏聚力岩体中拱顶上方垂直应力的计算方法。Chen等^[12]指出由于隧道拱顶沉降由中心向两端递减，实际拱体范围内的垂直应力呈现为向隧道内凹的形式，极限状态下的砂土大主应力拱迹线为圆弧形，其计算所得的侧压力系数和同一土条上的垂直应力分布系数更符合实际。徐长杰等^[13]进一步探讨了圆弧、抛物线和悬链线3种不同大主应力拱迹线的区别。上述关于主应力拱迹线的研究均是基于水平微分土条上各点应力莫尔圆相同的假设^[14-15]，这主要适用于浅埋隧道。但是，随着隧道埋深的增大，水平微分土条中点与两端的主应力大小差距越加明显。

本文依托青岛盾构地中对接工程，通过COMSOL Multiphysics建立三维数值模型，基于地层主应力矢量流线偏转和各向应力变化确定盾构地中对接段压力拱的主拱圈范围，并通过考虑大主应力不完全偏转和内摩擦角不完全调用推导上覆围岩压力计算公式。

1. 计算模型的建立

青岛地铁8号线工程全长约3.26 km，隧道外直径为6.7 m，内直径为6.0 m，盾构机直径6.98 m，对接段隧道埋深为17.5 m。该区域上覆地层为沿海地区常见的土岩复合地层，地层参数见表 1。三维计算模型如图 1所示。模型外部尺寸：长80.0 m，宽73.7 m，高44.3 m。内部尺寸：盾构主机长9.0 m，相当于6环管片宽，刀盘宽度1.0 m，管片外直径6.7 m，内直径6.0 m。结合青岛地铁8号线的现场施工结果，先、后行盾构机实际对接偏差小于10 mm，刀盘最小间隔10 cm，假设模拟开挖过程中先、后行盾构机轴线水平和高程位置始终保持一致，盾构对接间距设置为0。刀盘仅模拟其侧面，通过施加梯度水平压力模拟掌子面支撑作用^[16]。

表 1 材料物理力学参数

Table 1. Physical and mechanical parameters of materials

地层	H/m	g/(kg·m^-3)	E/MPa	μ	c/kPa	$\varphi$ /(°)
回填土	2.2	1750	20	0.35	15	10
含有机质粉质黏土	4.5	1800	15	0.36	9	7
粉质黏土	4.1	2000	28	0.34	17	13
强风化安山岩	2.1	2200	1600	0.33	45	21
微风化安山岩	32.3	2500	10500	0.30	300	36
管片	—	2500	27600	0.20	—	—
盾壳	—	7800	206000	0.25	—	—
注浆层	—	2000	100	0.25	—	—
注：H为层厚，g为密度，E为弹性模量，μ为泊松比，c为黏聚力， $\varphi$ 为内摩擦角。

下载: 导出CSV

| 显示表格

图 1 三维计算模型

Figure 1. Three-dimensional model

下载: 全尺寸图片幻灯片

盾构模型设计3个研究步骤：①步骤一为初始地应力平衡，模型侧面采用辊支承约束水平位移，底面采用固定约束，施加重力；②步骤二为先行隧道和后行隧道相向掘进开挖，通过循环移除两环开挖土体并施加盾尾管片及水平推力实现，单侧共循环开挖26环，该步骤主要是为了考虑开挖对对接段应力重分布的影响；③步骤三为对接点两侧盾构机刀盘同时拆除，采用稳态计算方式，通过去除刀盘宽度方向上的壳单位实现，以分析两侧刀盘拆除后围岩稳定后的规律。

2. 压力拱主拱圈范围的确定

选择对接点位置处的纵截面以及横截面作为观测截面，该位置处的地层沉降最大，其大主应力流线成拱效应最显著。通过图 2（a）所示对接点位置纵截面的最大主应力矢量流线偏转图可知，处于隧道外边沿的主应力由水平方向转变为竖直方向，可判定该区域为开挖卸荷导致的围岩松动区，但未见明显的流线成拱，围岩压力在拱顶附近有所下降。从图 2（b）所示对接点位置横截面的最大主应力矢量图可知，在拱顶微风化安山岩和强风化安山岩分界线处的最大主应力发生明显偏转，最大偏转角度约90°。相较于隧道纵截面，横截面成拱效应更为显著。

图 2 大主应力矢量流线偏转图

Figure 2. Streamline deflection of principal stress vector

下载: 全尺寸图片幻灯片

2.1 外边界的确定

从图 3所示刀盘拆卸后拱顶应力曲线可知，在拱顶以上5.5 m处水平应力突然增大，转变为最大主应力垂直应力。当刀盘拆除时，临空面顶部围岩下陷，由此导致隧道外边沿两侧围岩产生挤压作用。此时，上覆围岩压力在拱顶区域发生偏转。由于微风化岩层围岩强度较高，并且临空面两侧盾壳的支撑作用，拱顶围岩有限的沉降使得压力拱仅向上发展至软硬围岩分界面，而非像砂土的活动门试验，滑裂面一直延伸至地表。当超出分界面后，拱顶最大主应力由水平应力转换成垂直应力，表明强风化安山岩基本不承受压力拱水平挤压作用，压力拱外边界位于5.5 m处。

图 3 压力拱主拱圈外边界确定图

Figure 3. Determination of outer boundary main arch ring of pressure arch

下载: 全尺寸图片幻灯片

2.2 内边界的确定

定义水平应力变化指标A的表达式为

$A = \frac{{{\sigma_{x1}} - {\sigma_{x0}}}}{{{\sigma_{x0}}}} 。$

(1)

式中： ${\sigma_{x1}}$ 为刀盘拆卸后水平应力（kPa）； ${\sigma_{x0}}$ 为刀盘初始水平应力（kPa）。

从图 4（a）可知，在压力拱外边界，水平应力变化指标A达到最大，两侧围岩挤压程度最高，并随深度减小。具体分界可从图 4（b）水平应力变化指标曲线图得知，在隧道正上方0~0.5 m水平应力变化指标A呈现线性变化，当超出拱顶0.5 m后水平应力指标变化幅度缩小，并且水平应力由下降变成增大。根据上述分析确定主拱圈内边界位于拱顶0.5 m位置处，其并未与隧道拱顶上边沿重合。

图 4 压力拱主拱圈内边界确定图

Figure 4. Determination of inner boundary of main arch ring of pressure arch

下载: 全尺寸图片幻灯片

2.3 侧边界的确定

图 5中h表示水平监测截线与隧道拱顶间距。

${B_{\text{3}}} = D(1 + \cot \beta ) \text{，}$

(2)

$\beta = {45^ \circ } + \frac{\varphi }{2} 。$

(3)

图 5 隧道上部成拱区域围岩应力分布

Figure 5. Stress distribution of surrounding rock in upper arch area of tunnel

下载: 全尺寸图片幻灯片

式中：B₃为Terzarghi剪切面宽度（m）；D为隧道外直径（m）； $\varphi$ 为土体内摩擦角（°）。

图 5（a）所示剪应力分布表明，相较于按式（2），（3）计算所得Terzarghi地层剪切面^[17]宽度为9.8 m，数值计算得到的剪切面最大宽度仅6.0 m，并且随深度增加而减小，剪切面最小宽度为5.0 m，剪切面倾角与垂直面夹角为5.7°。

图 5（b）所示垂直应力分布图表明，在剪切面内垂直应力均出现下降，剪切面内侧围岩垂直应力通过剪切面转移至拱腰位置。图 5（c）所示水平应力分布图表明水平应力增大区域宽度相对较大，而在h=0.5 m截线处出现了水平应力下降的现象，说明围岩处于松动状态。

2.4 压力拱主拱圈模型

总结上述压力拱的主拱圈范围分析得出如图 6所示的简化模型。相较于传统砂土地层中不完全拱土拱的塔形滑移面，考虑一定黏聚力条件下的不完全压力拱的滑移面呈现出上大下小的盆状，这与叶飞等^[11]和吕伟华等^[18]通过模型试验观测的压力拱形状结果一致。同时，从图 6还可知压力拱外边界与拱顶沉降曲线存在一致性，拱顶沉降曲线的两个转折点分别发生在强风化安山岩和微风化安山岩分界线处。

图 6 压力拱主拱圈简化模型

Figure 6. Simplified model for main arch ring of pressure arch

下载: 全尺寸图片幻灯片

3. 不完全拱条件下的主拱圈围岩垂直压力计算

3.1 平均侧压力系数 ${K_\text{av}}$ 的确定

侧压力系数反映压力拱两侧稳定围岩对滑移面内围岩挤压程度，选取拱顶范围内任一水平微分土条，按下式计算土条上平均侧压力系数 ${K_\text{av}}$ ：

$K_{\mathrm{av}}=\frac{\sigma_{\mathrm{h}}^{\mathrm{A}}}{\sigma_{\mathrm{v}}^{\mathrm{av}}} 。$

(4)

式中： $\sigma_{\mathrm{h}}^{\mathrm{A}}$ 为水平微分土条上端点处的水平应力（kPa）； $\sigma_{\mathrm{v}}^{\mathrm{av}}$ 为微分土条上平均垂直应力（kPa）。

如所示，假设拱顶水平微分土条上各点均处于同一应力莫尔圆，土条上任意一点水平应力 ${\sigma_{\text{h}i}}$ 和垂直应力 ${\sigma_{\text{v}i}}$ 统一表达为关于最大主应力 ${\sigma_1}$ 偏转角 ${\theta_i}$ 的函数，即

${\sigma_{\text{h}i}} = {\sigma_1}{\cos ^2}{\alpha_i} + {\sigma_3}{\sin ^2}{\alpha_i} ={\sigma }_{1}({\mathrm{cos}}^{2}{\alpha }_{i}+{K}_\text{a}{\mathrm{sin}}^{2}{\alpha }_{i})\text{，}$

(5)

${\sigma_{\text{v}i}} = {\sigma_1}{\sin ^2}{\alpha_i} + {\sigma_3}{\cos ^2}{\alpha_i} = {\sigma_1}({\sin ^2}{\alpha_i} + {K_\text{a}}{\cos ^2}{\alpha_i}) \text{，}$

(6)

${K_\text{a}} = \frac{{{\sigma_3}}}{{{\sigma_1}}} = \frac{{1 - \sin \varphi }}{{1 + \sin \varphi }} = \frac{1}{{{K_\text{P}}}} \text{，}$

(7)

${\theta_i} = \frac{\pi }{2} - {\alpha_i} 。$

(8)

图 7 压力拱成拱机理

Figure 7. Forming mechanism of pressure arch

下载: 全尺寸图片幻灯片

式中： ${\sigma_1}$ ， ${\sigma_3}$ 分别为水平微分土条任意一点上的最大主应力和最小主应力（kPa）； ${\alpha_i}$ 为最大主应力与水平方向的夹角(°)，其值域为 $\left[ { - {\alpha_0}, {\alpha_0}} \right]$ ，其中， ${\alpha_i}$ 在水平微分土条中心位置等于0，在极限状态下滑移面位置等于 ${45^ \circ } + \varphi /{\text{2}}$ 。

从可知，随着最大主应力偏转角 ${\theta_i}$ 增大，水平应力逐渐增大，垂直应力逐渐减小，当 ${\theta_i} = {90^ \circ }$ 时，水平应力变为最大主应力，垂直应力变为最小主应力。因此，水平微分土条上端点处的水平应力 $\sigma_{\mathrm{h}}^{\mathrm{A}}$ 和垂直应力 $\sigma_{\mathrm{h}}^{\mathrm{A}}$ 可以表示为

$\sigma_{\mathrm{h}}^{\mathrm{A}} = {\sigma_1}{\cos ^2}{\alpha_0} + {\sigma_3}{\sin ^2}{\alpha_0} \text{，}$

(9)

$\sigma_{\mathrm{v}}^{\mathrm{A}} = {\sigma_1}{\sin ^2}{\alpha_0} + {\sigma_3}{\cos ^2}{\alpha_0} 。$

(10)

为了将平均垂直应力 $\sigma_{\mathrm{v}}^{\mathrm{av}}$ 表达为关于偏转角 ${\theta_i}$ 的函数，需要进一步明确最大主应力 ${\sigma_1}$ 的拱迹线。目前研究认为最大主应力拱迹线主要存在线性、圆弧形和抛物线形三种形式，最大主应力与水平方向夹角 ${\alpha_i}$ 与拱顶宽度B的关系表达式：

${\alpha_i} = \frac{{2y}}{B}\;(线性) ,$

(11)

$\sin {\alpha_i} = \frac{{2y}}{B}\sin {\alpha_0}\;(圆弧),$

(12)

$\tan {\alpha_i} = \frac{{2y}}{B}\tan {\alpha_0}\;(抛物线) 。$

(13)

在同一应力莫尔圆假设下，对水平微分土条上各点垂直应力进行积分可得平均垂直应力 $\sigma_{\mathrm{v}}^{\mathrm{av}}$ ，

$\sigma_{\mathrm{v}}^{\mathrm{av}} = \frac{1}{B}\int_{ - \frac{B}{{\text{2}}}}^{\frac{B}{{\text{2}}}} {({\sigma_1}{{\sin }^2}{\sigma_i} + {\sigma_3}{{\cos }^2}{\sigma_i})} \text{d}x$

$= \frac{{{\sigma_1}}}{B}\int_{ - \frac{B}{{\text{2}}}}^{\frac{B}{{\text{2}}}} {({{\sin }^2}{\sigma_i} + {K_{\text{a}}}{{\cos }^2}{\sigma_i})} \text{d}x 。$

(14)

结合式（11）可得 $\sigma_{\mathrm{v}}^{\mathrm{av}}$ 在线性、圆弧形和抛物线形拱迹线的表达式：

$\sigma_{\mathrm{v}}^{\mathrm{av}} = \frac{1}{2}{\sigma_1}\left[ {1 + {K_\text{a}} - \frac{{(1 - {K_\text{a}})\sin {\alpha_0} \cdot \cos {\alpha_0}}}{{{\alpha_0}}}} \right](线性),$

(15)

$\sigma_{\mathrm{v}}^{\mathrm{av}} = {\sigma_1}\left[ {1 + \frac{1}{3}(1 - {K_\text{a}}){{\sin }^2}{\alpha_0}} \right] \quad (圆弧),$

(16)

$\sigma_{\mathrm{v}}^{\mathrm{av}} = {\sigma_1}\left[ {1 + \frac{{({K_\text{a}} - 1)}}{{\tan {\alpha_0}}} \cdot {\alpha_0}} \right] \quad \quad (抛物线) 。$

(17)

将式（9），（17）代入式（4）即可求得平均侧压力系数 ${K_\text{av}}$ ，线性、圆弧和抛物线拱迹线的平均侧压力系数 ${K_\text{av}}$ 分别为

${K_\text{av}} = \frac{{2 \cdot ({{\cos }^2}{\alpha_0} + {K_\text{a}}{{\sin }^2}{\alpha_0})}}{{1 + {K_\text{a}} - (1 - {K_\text{a}}) \cdot \sin {\alpha_0} \cdot \cos {\alpha_0}/{\alpha_0}}} \;(线性),$

(18)

${K_\text{av}} = \frac{{{{\cos }^2}{\alpha_0} + {K_\text{a}}{{\sin }^2}{\alpha_0}}}{{{K_\text{a}} + 1/3 \cdot (1 - {K_\text{a}}) \cdot {{\sin }^2}{\alpha_0}}} \quad (圆弧)，$

(19)

${K_\text{av}} = \frac{{{{\cos }^2}{\alpha_0} + {K_\text{a}}{{\sin }^2}{\alpha_0}}}{{{K_\text{a}} \cdot {\alpha_0}/\tan {\alpha_0} + 1 - {\alpha_0}/\tan {\alpha_0}}} \quad (抛物线)。$

(20)

应当指出，上述拱迹线均是基于完全拱条件下得出的，而从前面分析可知盾构刀盘拆卸后形成的压力拱为不完全拱，实际最大主应力偏转程度小于上述3种拱迹线。

从所示应力莫尔圆可知，对于土条上任意计算单元，其最大主应力与水平方向夹角 ${\alpha_i}$ 可以表示为关于剪应力 ${\tau_{yz}}$ 、水平应力 ${\sigma_{\text{h}i}}$ 以及最小主应力 ${\sigma_3}$ 的函数，

${\tau_{yz}} = ({\sigma_{\text{h}i}} - {\sigma_3}) \cdot \tan {\alpha_i} 。$

(21)

根据式（21）计算得到如所示数值模拟结果下的最大主应力拱迹线，结合式（8）进一步反映最大主应力偏转角 ${\theta_i}$ 与地层成拱效应的显著程度。为了说明与不完全拱条件下拱迹线的区别，将数值模拟结果下的水平微分土条端点位置处的最大主应力与水平方向夹角 ${\alpha_0}$ 代入式（11）~（13），计算得到其余3种完全拱条件下的拱迹线。从可知，在h=5.5 m时的最大主应力偏转角 ${\theta_i}$ 基本在90°左右，并且由于监测截线中心偏转角和两侧偏转角相差并不大，所以不同形状拱迹线基本重合在一起；从可知，在h=4.5 m时最大主应力偏转角 ${\theta_i}$ 呈现为中间大两边小，最大偏转角 ${\theta_i} =$ 90°，各形状拱迹线差别并不明显；从图 8（c）可知，在h=3.5 m时的圆弧拱迹线条件下最大主应力偏转最显著，数值模拟的拱迹线居于第三位，说明地层压力拱的荷载传递能力出现下降；从图 8（d）~（f）可知，数值模拟拱迹线条件下最大主应力偏转程度随着埋深h减小而不断减小，说明成拱效应不断衰减。

图 8 最大主应力拱迹线

Figure 8. Arch traces of major principal stress

下载: 全尺寸图片幻灯片

根据式（4）计算得到如所示数值模拟结果下的平均侧压力系数 ${K_\text{av}}$ ，并将数值模拟结果下的水平微分土条端点位置处最大主应力与水平方向夹角 ${\alpha_0}$ 代入式（18）~（20），计算得到其余3种拱迹线条件下的平均侧压力系数 ${K_\text{av}}$ 。从可知，现有完全拱理论计算下的 ${K_\text{av}}$ 普遍偏大，高估了主拱圈两侧围岩的挤压作用，在计算上覆围岩压力时偏于不安全，特别是在距离拱顶较远位置，其偏差更加明显。其中，圆弧拱迹线的偏差最大，线性拱迹线的偏差次之，抛物线拱迹线偏差最小，这与前述拱迹线偏转程度的排序一致。

图 9 拱顶平均侧压力系数

Figure 9. Mean lateral pressure coefficients of arch vanlt

下载: 全尺寸图片幻灯片

3.2 调用内摩擦角 $\delta$ 的确定

由于围岩具有较大的黏聚力，压力拱滑移剪切面上的内摩擦角并未完全发挥，调用部分内摩擦角通常就能满足隧道开挖扰动引起的地应力再平衡。从所示的不完全压力拱条件下的应力莫尔圆可知，在无黏聚力情况下（即 ${\tau_\text{c}} - {O_\text{c}} - {\sigma_\text{c}}$ 坐标系），调用内摩擦角 $\delta$ 可表示为剪切面上的剪应力 $\tau_{yz}^\text{c}$ 和水平应力 $\sigma_\text{h}^\text{c}$ 的函数，

$\tau_{y z}^{\mathrm{c}}=\sigma_{\mathrm{h}}^{\mathrm{c}} \cdot \tan \delta 。$

(22)

图 10 不完全拱计算应力莫尔圆

Figure 10. Mohr circle of stress for calculation of incomplete arch

下载: 全尺寸图片幻灯片

在具有黏聚力情况下，通过向右平行移轴 $c \cdot \cot \varphi$ 的距离得到新的坐标系（即 $\tau - O - \sigma$ 坐标系），调用内摩擦角 $\delta$ 可进一步表示为新坐标系下剪切面上的剪应力 $\tau_{yz}^{}$ 和水平应力 $\sigma_\text{h}^{}$ 的函数，

$\tau_{y z}=\tau_{y z}^{\mathrm{c}}=\sigma_{\mathrm{h}}^{\mathrm{c}} \cdot \tan \delta=(\sigma+c \cdot \cot \varphi) \cdot \tan \delta。$

(23)

根据式（23）计算得到如所示距拱顶不同距离下的调用内摩擦角 $\delta$ 。从可知，在不完全拱的外边界（即h=5.5 m），地层调用的内摩擦角 $\delta$ 基本为0，可忽略不计。并且，随着距拱顶距离的减小，调用内摩擦角 $\delta$ 逐渐增大；随着距隧道中心距离的增加，调用内摩擦角 $\delta$ 逐渐增大。在不完全拱的内边界（即h=0.5 m）两侧滑移面位置处，调用内摩擦角 $\delta$ 达到最大，大约为20°，仍然小于地层最大内摩擦角 $\varphi = {36^ \circ }$ 。这说明刀盘拆卸后地层强度仍有较大富余，并未达到极限平衡状态，再平衡后形成的压力拱能够有效保证地层稳定性。

图 11 调用内摩擦角

Figure 11. Call of internal friction angle

下载: 全尺寸图片幻灯片

3.3 拱顶平均垂直应力 $\sigma_{\mathrm{v}}^{\mathrm{av}}$ 的计算

针对不完全压力拱的滑移面呈现倾斜向上的形状，本文通过微分的思想将其分为若干矩形微分土条进行适当简化，每条微分土条的厚度为1 m，其受力分析如图 12所示。

图 12 微分土条受力分析

Figure 12. Force analysis of differential soil strips

下载: 全尺寸图片幻灯片

对于砂土，其垂直受力平衡满足如下方程：

$B \sigma_{\mathrm{av}}^{\mathrm{c}}+\gamma B \mathrm{~d} z=B\left(\sigma_{\mathrm{av}}^{\mathrm{c}}+\mathrm{d} \sigma_{\mathrm{av}}^{\mathrm{c}}\right)+2 \tau_{y z}^{\mathrm{c}} \mathrm{~d} z 。$

(24)

整理得

$\frac{\mathrm{d} \sigma_{\mathrm{av}}^{\mathrm{c}}}{\mathrm{~d} z}+\frac{2 \tau_{y z}^c}{B}=\gamma 。$

(25)

其中：

$\tau_{y z}^{\mathrm{c}}=\sigma_{\mathrm{h}} \tan \delta=K_{\mathrm{av}}^{\mathrm{c}} \sigma_{\mathrm{av}}^{\mathrm{c}} \tan \delta 。$

(26)

解上述微分方程得

$\sigma_{\mathrm{av}}^{\mathrm{c}}=\frac{\gamma B}{2 K_{\mathrm{av}}^{\mathrm{c}} \tan \delta}+C \cdot \mathrm{e}^{-2 K_{\mathrm{av}}^{\mathrm{c}} \cdot \tan \delta \cdot \frac{z}{B}} 。$

(27)

当压力拱外边界存在超载为 $q$ 时，代入初始条件 $\left.\sigma_{\mathrm{av}}^{\mathrm{c}}\right|_{z=0}=q$ 时，得到

$\sigma_{\mathrm{av}}^{\mathrm{c}}=\frac{\gamma B}{2 K_{\mathrm{av}}^{\mathrm{c}} \tan \delta}\left(1-\mathrm{e}^{-2 K_{\mathrm{av}}^{\mathrm{c}} \cdot \tan \delta \cdot \frac{z}{B}}\right)+q \cdot \mathrm{e}^{-2 K_{\mathrm{av}}^{\mathrm{c}} \cdot \tan \delta \cdot \frac{z}{B}} 。$

(28)

对于具有一定黏聚力的岩土体，通过图 10所示平行移轴进行处理，

$\sigma_{\mathrm{av}}+c \cot \varphi=\sigma_{\mathrm{av}}^{\mathrm{c}} 。$

(29)

将式（30）代入式（24）得

$\gamma B \mathrm{~d} z=B \mathrm{~d} \sigma_{\mathrm{av}}+2 K_{\mathrm{av}}^{\mathrm{c}} \cdot\left(\sigma_{\mathrm{av}}+c \cot \varphi\right) \cdot \tan \delta \cdot \mathrm{d} z 。$

(30)

整理得

$\frac{\mathrm{d} \sigma_{\mathrm{av}}}{\mathrm{~d} z}+\frac{2 K_{\mathrm{av}}^{\mathrm{c}} \sigma_{\mathrm{av}} \tan \delta}{B}=\gamma-\frac{2 K_{\mathrm{av}}^{\mathrm{c}} c \cot \varphi \tan \delta}{B} 。$

(31)

解上述微分方程得

$\sigma_{\mathrm{av}}=q \cdot \mathrm{e}^{-2 K_{\mathrm{av}}^{\mathrm{c}} \tan \delta \cdot \frac{Z}{B}}+ \\ \frac{\left(1-\mathrm{e}^{-2 K_{\mathrm{av}}^{\mathrm{c}} \tan \delta \cdot \frac{z}{B}}\right) \cdot\left(\gamma B-2 K_{\mathrm{av}}^{\mathrm{c}} \cdot c \cot \varphi \cdot \tan \delta\right)}{2 K_{\mathrm{av}}^{\mathrm{c}} \tan \delta} 。$

(32)

其中，边界条件 $\sigma_\text{av}^{}\left| {_{z = 0} = } \right.q$ 与压力拱外边界上覆围岩压力有关，按照地层初始垂直应力取值。

所示为拱顶平均垂直应力计算参数。其中，平均侧压力系数 ${K_\text{av}}$ 和调用内摩擦角 $\delta$ 分别根据式（4），（23）确定。从可以看出，拱顶平均侧压力系数 ${K_\text{av}}$ 在压力拱内边界和外边界位置处相对较大，而在拱圈范围内有所减小；拱顶调用内摩擦角 $\delta$ 随着拱顶距离增大而减小，在压力拱的外边界达到0。将上述计算参数代入式（33）可以得到如图 13所示的拱顶各微分土条平均垂直应力。从图 13可知，通过考虑大主应力拱迹线不完全偏转，相较于抛物线、线性、圆弧形拱迹线的17.7%，25.0%，28.6%的最大误差，采用本文理论计算的结果与数值模拟最大误差进一步缩小为10.5%，能够更合理地反映地层不完全成拱状态下上覆围岩压力的计算。总体而言，通过数值模型计算和理论分析可以得出，在微风化安山岩地层中弃壳解体，原则上无需进行加固就可形成自承拱，其压力拱拱圈内垂直应力下降明显，内边界从初始的346 kPa减小为113 kPa（理论计算结果）或119 kPa（数值模型结果），相当于初始围压压力的1/3，能够有效保证刀盘拆卸后临空面的稳定性。

表 2 拱顶平均垂直应力计算参数

Table 2. Parameters of mean vertical stress of arch vault

距拱顶距离/m	土条宽度/m	平均侧压力系数	调用内摩擦角/(°)
5.5	6.0	0.956	0
4.5	5.8	0.895	7.48
3.5	5.6	0.858	11.13
2.5	5.4	0.847	13.59
1.5	5.2	0.861	15.54
0.5	5.0	0.950	17.07

下载: 导出CSV

| 显示表格

图 13 压力拱间平均垂直应力

Figure 13. Mean vertical stresses between arches

下载: 全尺寸图片幻灯片

4. 结论

依托青岛盾构地中对接工程，通过COMSOL Multiphysics建立三维数值模型，确定盾构地中对接过程中压力拱的主拱圈范围，并通过理论推导主拱圈范围内围岩压力计算方法，主要得出4点结论。

（1）由于刀盘厚度相对隧道直径较小，盾构对接段沿隧道轴向的大主应力未见矢量流线成拱，沿隧道径向的成拱效应更为显著。

（2）压力拱外边界位于软硬围岩分界面处，由于拱顶存在松动区域，内边界并未与隧道上边沿重合，而是距离拱顶一定高度，压力拱两侧边界倾斜向上，主拱圈总体上呈现为盆状。

（3）在刀盘拆卸后形成的不完全拱中，采用既有圆弧、线性、抛物线形拱迹线均高估了最大主应力偏转角度，相应所得的平均侧压力系数偏大，计算上覆围岩压力时偏于不安全。并且，随着距拱顶距离的减小，调用内摩擦角 $\delta$ 逐渐增大；随着离隧道中心距离的增加，调用内摩擦角 $\delta$ 逐渐增大。

（4）通过数值模型计算和理论分析得出在微风化安山岩地层中弃壳解体原则上无需进行加固，其压力拱拱圈内垂直应力下降明显，拱圈内边界垂直应力相当于初始围压压力的1/3。

图 1 730采区集中巷布置图

Figure 1. Layout of centralized roadway in mining area No. 730

下载: 全尺寸图片幻灯片

图 2 卸压前后应力变化规律图

Figure 2. Variation of stress before and after pressure relief

下载: 全尺寸图片幻灯片

图 3 卸压前后能量变化规律图

Figure 3. Variation of energy before and after pressure relief

下载: 全尺寸图片幻灯片

图 4 钻孔间距-割缝半径理论模型图

Figure 4. Theoretical model for drilling spacing and slot radius

下载: 全尺寸图片幻灯片

图 5 钻孔深度-割缝长度理论模型图

Figure 5. Theoretical model for drilling depth and slot length

下载: 全尺寸图片幻灯片

图 6 三维数值模型及卸压区域示意图

Figure 6. 3D numerical model and schematic diagram of pressure-relief area

下载: 全尺寸图片幻灯片

图 7 巷帮煤体有效卸压区域图

Figure 7. Effective pressure-relief areas of roadway coal

下载: 全尺寸图片幻灯片

图 8 巷帮煤体应力场变化规律图

Figure 8. Variation of stress field of roadway coal

下载: 全尺寸图片幻灯片

图 9 塑性区变化规律图

Figure 9. Variation of plastic zone

下载: 全尺寸图片幻灯片

图 10 冲击危险指数K值变化规律图

Figure 10. Variation ofK value of shock risk index

下载: 全尺寸图片幻灯片

图 11 应力场变化规律图

Figure 11. Variation of stress field

下载: 全尺寸图片幻灯片

图 12 塑性区变化规律图

Figure 12. Variation of plastic zone

下载: 全尺寸图片幻灯片

图 13 冲击危险指数K值变化规律图

Figure 13. Variation of K value of shock risk index

下载: 全尺寸图片幻灯片

图 14 水射流割缝卸压布置图

Figure 14. Layout of pressure relief by water jet slotting

下载: 全尺寸图片幻灯片

图 15 微震空间集中度统计图

Figure 15. Statistical map of spatial concentration of microseism

下载: 全尺寸图片幻灯片

表 1 煤岩层物理力学参数

Table 1 Physical and mechanical parameters of coal strata

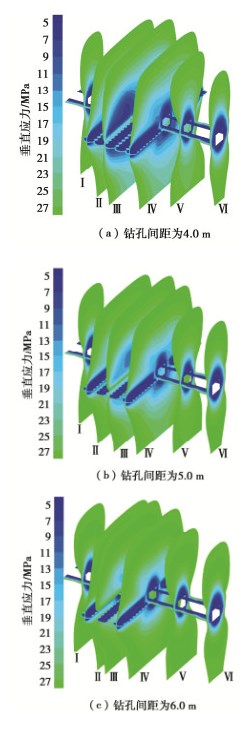
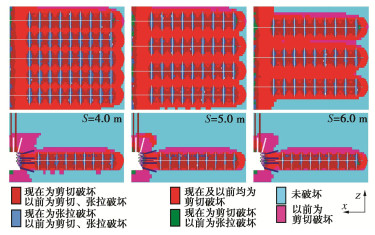
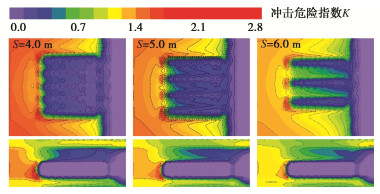
煤岩名称	体积模量/GPa	剪切模量/GPa	密度/ (kg·m^-3)	内摩擦角/ (°)	内聚力/ MPa
^#3煤	2.41	0.98	1400	32	1.0
泥岩	3.55	1.82	2380	38	2.2
粉砂岩	5.22	3.38	2446	38	8.0
细粒砂岩	6.44	3.35	2600	36	8.5

下载: 导出CSV

表 2 钻孔间距-割缝半径参数条件下卸压效果数据表

Table 2 Data of pressure-relief effects under drilling spacing and slot radius

钻孔间距 S/m	割缝半径 R_c/m	平均垂直应力 /MPa	平均弹性能密度/MJ	巷道冲击危险指数	卸压成本预估
3.0	1.5	11	0.053	0.82	70个割缝槽
4.0	2.0	9	0.048	0.75	50个割缝槽
5.0	2.0	13	0.063	0.98	40个割缝槽

下载: 导出CSV

参考文献(17)

[1]	窦林名, 田鑫元, 曹安业, 等. 我国煤矿冲击地压防治现状与难题[J]. 煤炭学报, 2022, 47(1): 152-171. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202201011.htm DOU Linming, TIAN Xinyuan, CAO Anye, et al. Present situation and problems of coal mine rock burst prevention and control in China[J]. Journal of China Coal Society, 2022, 47(1): 152-171. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202201011.htm
[2]	XUE C C, CAO A Y, GUO W H, et al. Mechanism and energy evolution characteristics of coal burst in mining thick, deep, and large inclined coal seams: a case study from a Chinese coal mine[J]. Geofluids, 2022, 2022: 1-18.
[3]	王高昂, 朱斯陶, 姜福兴, 等. 高应力厚煤层大巷孤立煤体蠕变失稳冲击机理及防治研究[J]. 岩土工程学报, 2022, 44(9): 1689-1698, 9. doi: 10.11779/CJGE202209014 WANG Gaoang, ZHU Sitao, JIANG Fuxing, et al. Creep instability rock burst mechanism and prevention technology of isolated coal mass in roadways of high-stress thick coal seam[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(9): 1689-1698, 9. (in Chinese) doi: 10.11779/CJGE202209014
[4]	袁亮, 林柏泉, 杨威. 我国煤矿水力化技术瓦斯治理研究进展及发展方向[J]. 煤炭科学技术, 2015, 43(1): 45-49. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201501013.htm YUAN Liang, LIN Baiquan, YANG Wei. Research progress and development direction of gas control with mine hydraulic technology in China coal mine[J]. Coal Science and Technology, 2015, 43(1): 45-49. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201501013.htm
[5]	周新超, 马小晶, 廖翔云, 等. 磨料水射流冲击孔隙岩体的SPH模拟研究[J]. 岩土工程学报, 2022, 44(4): 731-739. doi: 10.11779/CJGE202204016 ZHOU Xinchao, MA Xiaojing, LIAO Xiangyun, et al. Numerical simulation of abrasive water jet impacting porous rock based on SPH method[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(4): 731-739. (in Chinese) doi: 10.11779/CJGE202204016
[6]	YANG Z, DOU L, LIU C, et al. Mechanism of rock burst in roadway side wall and the application of water jet pressure relief technology in deep mine[J]. Journal of Mining & Safety Engineering, 2017, 34(4): 670-677, 729.
[7]	潘俊锋, 马文涛, 刘少虹, 等. 坚硬顶板水射流预制缝槽定向预裂防冲技术试验[J]. 岩石力学与工程学报, 2021, 40(8): 1591-1602. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202108008.htm PAN Junfeng, MA Wentao, LIU Shaohong, et al. A prevention technology of rock burst based on directional presplitting of water jet prefabricated slot in hard roof[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(8): 1591-1602. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202108008.htm
[8]	刘生龙, 朱传杰, 林柏泉, 等. 水力割缝空间分布模式对煤层卸压增透的作用规律[J]. 采矿与安全工程学报, 2020, 37(5): 983-990. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL202005016.htm LIU Shenglong, ZHU Chuanjie, LIN Baiquan, et al. The effect of spatial distribution mode of hydraulic slotting on pressure relief and permeability enhancement of the coal seam[J]. Journal of Mining & Safety Engineering, 2020, 37(5): 983-990. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL202005016.htm
[9]	张永将, 郭寿松. 高压水射流环形割缝深度理论模型及应用[J]. 煤炭学报, 2019, 44(增刊1): 126-132. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB2019S1014.htm ZHANG Yongjiang, GUO Shousong. Theoretical model of annular slotting depth for high pressure water jet and its application[J]. Journal of China Coal Society, 2019, 44(S1): 126-132. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB2019S1014.htm
[10]	林柏泉, 刘厅, 邹全乐, 等. 割缝扰动区裂纹扩展模式及能量演化规律[J]. 煤炭学报, 2015, 40(4): 719-727. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201504001.htm LIN Baiquan, LIU Ting, ZOU Quanle, et al. Crack propagation modes and energy evolution within slotting disturbed zone[J]. Journal of China Coal Society, 2015, 40(4): 719-727. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201504001.htm
[11]	镐振, 郭林峰, 赵希栋, 等. 回采巷道围岩冲击破坏能量特征分析[J]. 煤炭学报, 2020, 45(12): 3995-4005. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202012004.htm HAO Zhen, GUO Linfeng, ZHAO Xidong, et al. Analysis of burst failure energy characteristics of mining roadway surrounding rock[J]. Journal of China Coal Society, 2020, 45(12): 3995-4005. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202012004.htm
[12]	贾传洋, 蒋宇静, 张学朋, 等. 大直径钻孔卸压机理室内及数值试验研究[J]. 岩土工程学报, 2017, 39(6): 1115-1122. doi: 10.11779/CJGE201706018 JIA Chuanyang, JIANG Yujing, ZHANG Xuepeng, et al. Laboratory and numerical experiments on pressure relief mechanism of large-diameter boreholes[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1115-1122. (in Chinese) doi: 10.11779/CJGE201706018
[13]	刘少虹. 动载冲击地压机理分析与防治实践[D]. 北京: 煤炭科学研究总院, 2014. LIU Shaohong. The Study on the Mechanism and Prevention of Dynamic-Loading Rockburst[D]. Beijing: China Coal Research Institute, 2014. (in Chinese)
[14]	李云鹏, 张宏伟, 朱志洁, 等. 冲击危险煤层卸压钻孔安全参数研究[J]. 中国安全科学学报, 2018, 28(11): 122-128. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201811020.htm LI Yunpeng, ZHANG Hongwei, ZHU Zhijie, et al. Study on safety parameters of pressure relief borehole in rockburst coal seam[J]. China Safety Science Journal, 2018, 28(11): 122-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201811020.htm
[15]	王志强, 王鹏, 石磊, 等. 基于沿空巷道围岩应力分析的防冲机理研究[J]. 中国矿业大学学报, 2020, 49(6): 1046-1056. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD202006003.htm WANG Zhiqiang, WANG Peng, SHI Lei, et al. Research on prevention of rock burst based on stress analysis of surrounding rock of gob-side entry[J]. Journal of China University of Mining & Technology, 2020, 49(6): 1046-1056. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD202006003.htm
[16]	李铀, 袁亮, 刘冠学, 等. 圆形巷道围岩扰动区及其临界破坏深度的确定[J]. 采矿与安全工程学报, 2016, 33(5): 795-799. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201605005.htm LI You, YUAN Liang, LIU Guanxue, et al. Determination of disturbed region and critical failure depth of surrounding rock in circular roadway[J]. Journal of Mining & Safety Engineering, 2016, 33(5): 795-799. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201605005.htm
[17]	赵阳升, 冯增朝, 万志军. 岩体动力破坏的最小能量原理[J]. 岩石力学与工程学报, 2003, 22(11): 1781-1783. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200311004.htm ZHAO Yangsheng, FENG Zengchao, WAN Zhijun. Least energy priciple of dynamical failure of rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1781-1783. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200311004.htm