隧道下穿施工引起既有隧道及地层变形预测的改进随机介质理论模型

徐强; 朱永全; 雷升祥; 刘勇; 赵伟; 方智淳; 王聪; 徐硕

doi:10.11779/CJGE20211447

隧道下穿施工引起既有隧道及地层变形预测的改进随机介质理论模型 English Version

徐强^{1, 2,},
朱永全^{1, 2, ,},
雷升祥^{1, 3},
刘勇¹,
赵伟⁴,
方智淳¹,
王聪¹,
徐硕¹

1.
石家庄铁道大学土木工程学院, 河北石家庄 050043
2.
石家庄铁道大学交通工程结构力学行为与系统安全国家重点实验室, 河北石家庄 050043
3.
中国铁建股份有限公司, 北京 100855
4.
中铁十八局集团有限公司, 天津 300222

基金项目:

国家重点研发计划项目 2018YFC0808703

国家重点研发计划项目 2018YFC0808704

国家自然科学基金项目 52178391

石家庄铁道大学研究生创新资助项目 YC2022001

详细信息

作者简介:
作者简介：徐强(1994—)，男，博士研究生，主要从事隧道与地下工程方面的研究工作。E-mail: xuqiang@stdu.edu.cn

通讯作者:
朱永全, E-mail: 7935526@163.com

中图分类号: TU45
计量
- 文章访问数: 314
- HTML全文浏览量: 74
- PDF下载量: 93
出版历程
- 收稿日期: 2021-12-04
- 网络出版日期: 2023-02-23
- 刊出日期: 2023-01-31

Improved stochastic medium theoretical model for predicting deformation of existing tunnels and strata caused by excavation of new undercrossing tunnels

XU Qiang^{1, 2,},
ZHU Yongquan^{1, 2, ,},
LEI Shengxiang^{1, 3},
LIU Yong¹,
ZHAO Wei⁴,
FANG Zhichun¹,
WANG Cong¹,
XU Shuo¹

1.
School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
3.
China Railway Construction Corporation Limited, Beijing 100855, China
4.
China Railway 18th Bureau Group Co., Ltd., Tianjin 300222, China

摘要

摘要: 新建隧道下穿既有隧道施工时，由于传统随机介质理论无法考虑既有隧道的影响，地层变形预测结果易出现较大误差。考虑隧道开挖后断面的非均匀收敛，基于随机介质理论与Peck公式两者关键参数之间的关系，对传统随机介质理论进行了简化和改进；应用隧道衬砌抗弯刚度等效及当层法，对非均质地层和既有隧道进行了等效处理，提出了隧道下穿施工引起的既有隧道及地层变形预测模型，结合相关典型工程验证了该理论模型的准确性。结果表明：与传统随机介质理论相比，预测模型对既有隧道及地层的变形预测曲线均呈“宽而浅”的特点，与数值计算及现场实测结果的关联度更大，具有更高的合理性和准确性，为隧道下穿施工引起的既有隧道及地层变形预测提供了理论依据。
- 下穿 /
- 随机介质理论 /
- 抗弯刚度等效 /
- 当层法 /
- 非均质地层
Abstract: During the construction of new tunnels undercrossing the existing tunnels, the predicted results of the stratum deformation are prone to large errors since the traditional stochastic medium theory cannot consider the influences of the existing tunnel. Considering the non-uniform convergence of the tunnel section after excavation, the traditional stochastic medium theory is simplified and improved based on the relationship between the key parameters of the stochastic medium theory and those of the Peck's formula. The heterogeneous strata and existing tunnels are equated by applying the bending stiffness of an existing tunnel and the equivalent layer method. A prediction model for the deformation of the existing tunnels and strata caused by the excavation of new undercrossing tunnels is proposed, and based on the relevant typical project, its accuracy is validated. The results show that compared with those of the traditional stochastic medium theory, the predicted curves of the proposed model are "wide and shallow" and have a greater correlation with the numerical calculations and the field measurements, and they have a higher rationality and accuracy, which may provide a theoretical basis for the prediction of the deformation of the existing tunnels and strata caused by the excavation of undercrossing tunnels.
- undercrossing /
- stochastic medium theory /
- equivalent bending rigidity /
- equivalent layer method /
- heterogeneous stratum

HTML全文

0. 引言

在“双碳”目标牵引下，中国海上风电工程的建设已进入快速发展阶段。海上环境比陆地复杂，海上风电桩基会承受更大的运行荷载。目前，海上风电机常用的基础形式为5~10 m大直径钢管桩基础。然而，现在的桩基承载力设计预测方法往往基于小直径柔性桩，不适用于大直径刚性桩。本文研究钢桩-软黏土界面的剪切特性，来对海上大直径刚性桩基的设计预测方法进行优化。

国内外学者对桩-土接触面的剪切特性展开了一系列室内研究。Potyondy^[1]通过大量试验研究了不同土样与包括钢在内的各种界面之间的摩阻力。夏红春等^[2]研究了不同粗糙程度的混凝土结构面与砂土的剪切力学特性，并采用归一化方法获得了剪切强度和剪切位移之间的相关关系。冯大阔等^[3]研究了粗粒土与人造三维粗糙钢板的剪切特性以及循环剪切时的剪切特性。朱俊高等^[4]利用改进的直剪仪对不同密实度的粗粒土与不锈钢毛坯板进行直剪试验，研究接触面本构模型。郭聚坤等^[5]研究了不同含水率、固结时间下的海洋黏土与钢板的剪切特性。

相较于室内试验，离散元数值模拟更能反映细观结构与宏观力学反应之间的联系，并获得配位数、接触力链等细观力学信息。赵亦凡等^[6]对粗粒土与接触面往返剪切试验进行数值模拟，研究剪胀特性与颗粒平移、旋转、破碎的关系及体应变可逆性和不可逆性规律。王超^[7]从可视化模型试验、离散元数值分析两方面入手，研究了圆桩桩土相互作用在微观层面的机理，对比了不同桩径、桩间距及深度对桩土相互作用的影响。许多学者^[8-9]采用PFC2D软件模拟了土工格栅拉拔试验、混凝土-海洋黏土大型接触面剪切试验，并对细观机理进行分析。

以往研究表明钢桩-软黏土接触面的剪切特性受多种因素影响。其中，对法向应力、含水率等变量的研究较多，但现有结论大多为定性结论，并且现有研究在法向静力荷载条件下居多，考虑法向循环荷载作用下接触面剪切特性的较少。基于此，本文通过钢桩-软黏土大型接触面剪切试验和数值模拟软件研究手段，研究海上风浪耦合荷载作用下钢桩-软黏土接触面的剪切特性以及细观机理，从而为海上风电桩基承载力的准确预测提供理论基础。

1. 试验方法与数值模型建立

已有研究^[10]设计了大规模桩土界面剪切试验，分析法向循环荷载作用下桩土界面剪切强度特性。图 1为实际海上风电机组单桩情况及相应的桩土界面剪切试验概化示意图。界面剪切试验中的法向荷载由海上风机的侧向土压力（静荷载）和风浪荷载（动荷载）组成。设计的大型接触面剪切试验对应的是桩基上不同深度的界面。本研究的影响因素包括动荷载频率和动荷载幅值。

图 1 海上风力桩基和桩-土界面剪切试验

Figure 1. Pile foundation of offshore wind power and generalized pile-soil interface shear tests

下载: 全尺寸图片幻灯片

研究也设计了一组直剪试验，一方面验证大型接触面剪切试验的试样质量，另一方面标定数值模型中黏性土的参数。最终，数值模拟的具体参数设置如表 1所示。

表 1 法向荷载数值模拟参数设置

Table 1. Normal loading conditions in numerical simulation

编号	法向应力/kPa	频率/Hz	振幅/kPa
1	300	0	0
2	300	0.1	20
3		0.2
4		0.3
5	300	0.2	10
6			20
7			30

下载: 导出CSV

| 显示表格

1.1 试验材料

桩基材料选择实际桩基采用的DH36高强度钢材制成的光滑钢板。研究土样的参数与上海第④层软黏土接近，如表 2所示。试验中采用泥浆法，控制密度和预压固结过程制备重塑黏性土样。首先，取土，晒（烘）干，粉碎过筛成土粉。然后，称量所需质量的干土粉与水，混合并搅拌均匀成湿土备用。在木制模具中分五次填入黏性土，并分层振捣排出气泡。最后，将平板置于土样表面，通过放置重物和使用固结仪进行预压，使土样固结。使用千分表观测固结沉降量，在50 kPa荷载下，当沉降量小于0.1 mm/d时，视为土样已经固结完毕。

表 2 黏性土样三相比例指标

Table 2. Basic physical and mechanical properties of clay

湿重度/(kN·m^-3)	含水率/%	饱和度/%	孔隙比	固结快剪试验
湿重度/(kN·m^-3)	含水率/%	饱和度/%	孔隙比	黏聚力/kPa	摩擦角/(°)
17.0	40	100	1.34	13	11.3

下载: 导出CSV

| 显示表格

1.2 试验方法

大型接触面剪切试验采用的仪器为大型接触面剪切仪，如图 2所示。上下剪切盒的内部尺寸均为600 mm×400 mm×100 mm（长×宽×高）。在进行剪切试验时，钢板置入下剪切盒中，土样置于上剪切盒内，由加载板提供法向压力，上剪切盒固定，拉拔头带动下剪切盒移动，在剪切盒长度方向上完成剪切。

图 2 大型接触面剪切仪

Figure 2. Large direct shear apparatus

下载: 全尺寸图片幻灯片

在试样安装完毕后，对试样施加法向循环荷载。试样剪切速度为1 mm/s。大型接触面剪切试验可以研究循环荷载下土与钢结构接触面的受力特性、变形机理和破坏形式等，是之后数值模型接触面参数标定不可或缺的一环。

1.3 数值模型建立与参数标定

利用离散元模拟钢与土的大型接触面剪切试验，首先需生成三道墙体用来模拟剪切盒的顶板和左右两侧墙体，土体长为600 mm，高为100 mm。在剪切过程中为了避免颗粒溢出墙体，造成试验误差，应保证上侧墙体比试样长度略长，左、右两侧墙体比试样高度略高。本文中所生成的墙体两端均比试样本身长出1.5倍。钢板采用clump单元来模拟，其由一系列重叠的颗粒组成，这样可以在提供足够粗糙度的前提下保证计算结果的稳定性。在整个加载的过程中，整个clump相当于一个刚体，其不会产生变形，也不会发生断裂，它将作为一个整体一起以速度1 mm/s向右移动。本次接触面剪切试验的数值模拟中，试样的颗粒粒径为1.6~2.4 mm，采用颗粒粒径均匀分布，共生成颗粒3936颗。最终生成的钢与黏性土接触面剪切试验模型如图 3所示。

图 3 钢-黏性土接触面剪切试验模型

Figure 3. Numerical model for large-scale interface shear tests

下载: 全尺寸图片幻灯片

基于直剪试验与大型接触面剪切试验获得的应力应变曲线，黏性土细观参数、钢与黏性土接触面细观参数最终标定如表 3所示。

表 3 模型细观参数

Table 3. Mesoscopic parameters of model

类型	有效模量	刚度比	摩擦系数	黏结有效模量	黏结刚度比	黏结强度	抗拉强度	摩擦角
黏性土	1×10⁶	1	0.9	1×10⁶	1	5×10⁴	1.5	10
接触面	1×10⁶	1	0.95	1×10⁶	1	1×10³	1.5	10

下载: 导出CSV

| 显示表格

钢与黏性土接触面剪切试验数值模拟与实际试验对比如图 4所示。在140，200，300 kPa法向应力下数值模拟的应力应变曲线与实际试验曲线拟合较好，峰值强度、峰值强度对应的剪切位移以及稳定强度都非常接近。可认为该模型能较好的模拟钢与黏性土接触面剪切试验。因此，可以通过该模型进一步研究钢-软黏土界面在不同动载荷频率和动荷载振幅下的剪切特性。

图 4 细观参数标定

Figure 4. Calibration of mesoscopic parameters

下载: 全尺寸图片幻灯片

2. 试验结果分析与讨论

2.1 动荷载频率的影响

相同法向应力（300 kPa）、动荷载幅值（20 kPa）不同动荷载频率的黏性土样试验结果如图 5所示。可以发现，动荷载频率与黏性土的接触面强度成负相关，这与实际试验在较低振动频率下所得到的规律一致。钢与黏性土接触面在动荷载频率为0.1，0.2，03 Hz时，峰值强度分别为28.922，27.939，27.326 kPa。同时也可以发现，动荷载频率对黏性土接触面强度的影响较小。

图 5 不同动荷载频率下接触面剪切应力-剪切位移结果

Figure 5. Numerical simulation results with different frequencies

下载: 全尺寸图片幻灯片

2.2 动荷载幅值的影响

相同法向应力（300 kPa）、动荷载频率（0.2 Hz）不同动荷载幅值的试验结果如图 6所示。可以发现，动荷载幅值与黏性土的接触面强度成负相关。动荷载幅值为10，20，30 kPa时，接触面峰值强度分别为30.643，28.026，26.489 kPa，稳定强度分别为29.830，28.026，26.011 kPa。以动荷载幅值为横坐标轴，峰值强度、稳定强度作为纵坐标轴，绘制散点图并进行线性拟合。可以发现，在不同动荷载幅值下，幅值与接触面强度存在较为明显的负相关性。

图 6 不同动荷载幅值下接触面剪切应力-剪切位移结果

Figure 6. Numerical simulation results with different amplitudes

下载: 全尺寸图片幻灯片

2.3 细观机理分析

图 7为钢与黏性土接触面不同动荷载频率和幅值下剪切位移为15 mm时的颗粒位移结果。图 8为300 kPa法向应力下剪切位移为15 mm时试样不同高度处颗粒的平均水平位移变化规律。可以发现动荷载频率和幅值越大，黏性土颗粒位移越小，并且动荷载幅值对黏性土颗粒位移的影响比动荷载频率的影响更明显。随着动荷载频率和幅值的增加，接触界面处颗粒位移降低，且同一高度处颗粒发生水平位移的范围也显著降低。这是因为动荷载频率和幅值越大，黏性土颗粒与接触面受到的扰动越大，导致黏性土颗粒越不容易随接触面发生移动。

图 7 钢-黏性土接触面颗粒位移图

Figure 7. Displacements of particles

下载: 全尺寸图片幻灯片

图 8 试样不同高度处颗粒的平均水平位移变化

Figure 8. Average displacements of particles at different heights

下载: 全尺寸图片幻灯片

根据实际试验数据，静荷载下的接触面剪切应力要大于动荷载，因此静荷载下接触面附近的黏性土颗粒位移应该要大于动荷载下的颗粒位移。但是，取静荷载和动荷载下剪切位移为10 mm时的颗粒位移图进行对比，发现动荷载下黏性土颗粒的位移要明显大于静荷载下颗粒的位移，如图 9所示。这说明法向方向上的动荷载使黏性土颗粒与钢、颗粒与颗粒间的接触受到扰动，并且频率和幅值越大造成的扰动也越大，最终导致动荷载的颗粒位移较大但剪切应力较小。

图 9 静荷载和动荷载下颗粒位移

Figure 9. Displacements of particles under statistic and dynamic normal loads

下载: 全尺寸图片幻灯片

图 10显示的力链分布情况也证明了这一点。颜色越深说明颗粒之间的作用力越大。可以看出，在静荷载条件下颗粒之间的作用力相对较大。力链网络中，力链以平均接触力为标准可分为强接触力链和弱接触力链，而强接触力链主要起抵抗变形的作用，弱接触力链主要起维稳的作用^[11]。整体上看，动荷载下黏性土颗粒间强接触力链明显少于静荷载下的黏性土，说明动荷载导致黏性土颗粒间的接触受到扰动，传力性能降低，导致剪切应力降低。

图 10 静荷载和动荷载下力链分布图

Figure 10. Force chains under statistic and dynamic normal loads

下载: 全尺寸图片幻灯片

3. 结论

为了分析动荷载频率和动荷载幅值对钢-软黏土界面剪特性的影响，进行了一系列大型接触面剪切试验数值模拟。试验结果从宏观和微观两个角度进行了分析。主要得到以下3点结论。

（1）钢与黏性土接触面剪切试验数值模拟模型在不同法向应力下的接触面强度特性与大型接触面剪切试验较为符合，说明该数值模型能较好的模拟实际试验。

（2）数值模拟结果表明：随着动荷载频率和幅值增加，钢与黏性土的接触面强度减小，其中动荷载幅值的影响较为明显。

（3）通过细观分析可以发现：动荷载频率和幅值越大，黏性土颗粒位移越小；静荷载下黏性土颗粒间作用力比动荷载下的作用力大；动荷载会导致颗粒间的扰动，使接触面强度减小。

图 1 随机介质理论模型

Figure 1. Stochastic medium theoretical model

下载: 全尺寸图片幻灯片

图 2 非均匀收敛计算模式示意图

Figure 2. Schematic diagram of non-uniform convergence model

下载: 全尺寸图片幻灯片

图 3 既有隧道抗弯刚度等效示意图

Figure 3. Schematic diagram of equating bending stiffness of an existing tunnel

下载: 全尺寸图片幻灯片

图 4 非均质地层当层法应用

Figure 4. Diagram of equivalent layered method in heterogeneous strata

下载: 全尺寸图片幻灯片

图 5 有限元模型示意图

Figure 5. Diagram of finite element model

下载: 全尺寸图片幻灯片

图 6 理论预测与数值计算结果对比

Figure 6. Comparison between theoretical predictions and numerical results

下载: 全尺寸图片幻灯片

图 7 理论预测与现场实测结果对比

Figure 7. Comparison between theoretical predictions and measured results

下载: 全尺寸图片幻灯片

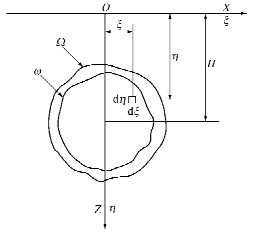
表 1 非均匀收敛计算模式下随机介质理论积分界限

Table 1 Integral bounds of non-uniform convergence model of stochastic medium theory

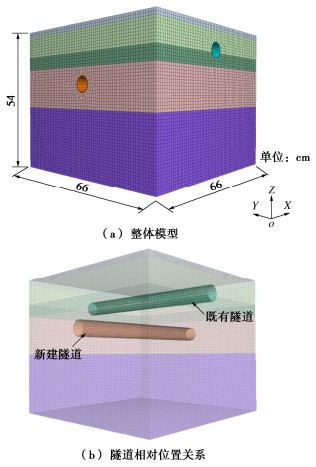
开挖变形前积分界限		开挖变形后积分界限
a	$H - R$	e	$H + {u_{\text{v}}} - (R - {u_{\text{g}}} - {u_{\text{o}}}) = H - (R - {u_{\text{1}}})$
b	$H + R$	f	$H + {u_{\text{v}}} + (R - {u_{\text{g}}} - {u_{\text{o}}}) = H + (R - {u_{\text{2}}})$
c	$- \sqrt {{R^2} - {{(\eta - H)}^2}}$	g	$- (R - {u_{\text{g}}} + {u_{\text{o}}})\sqrt {{\text{1}} - {{(\frac{{\eta - H - {u_{\text{v}}}}}{{R - {u_{\text{g}}} - {u_{\text{o}}}}})}^2}} = - (R - {u_3})\sqrt {{\text{1}} - {{\left( {\frac{{\eta - H - ({u_1} - {u_{\text{2}}})/2}}{{R - ({u_1} + {u_{\text{2}}})/2}}} \right)}^2}}$
d	$- c$	h	$- g$

下载: 导出CSV

表 2 地层及主要结构材料参数

Table 2 Parameters of soils and structural materials in model

材料名称	重度/ (kN·m^-3)	内摩擦角/(°)	黏聚力/ kPa	弹性模量/MPa	泊松比
回填土	18.0	15	25	10	0.42
淤泥质粉质黏土	20.0	20	35	30	0.32
卵石	22.0	40	—	40	0.25
强风化板岩	23.6	33	60	100	0.26
中风化板岩	25.0	38	75	300	0.23
衬砌	26.0	—	—	30000	0.20
注浆参数	20.0	—	—	0.033	0.20

下载: 导出CSV

参考文献(23)

[1]	张治国, 张成平, 奚晓广. 双线隧道不同布置方式下相互作用影响的地层位移解析[J]. 岩土工程学报, 2019, 41(2): 262-271. doi: 10.11779/CJGE201902003 ZHANG Zhiguo, ZHANG Chengping, XI Xiaoguang. Closed solutions to soil displacements induced by twin-tunnel excavation under different layout patterns[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 262-271. (in Chinese) doi: 10.11779/CJGE201902003
[2]	陈仁朋, 曾巍, 吴怀娜, 等. 盾构隧道下穿引起砌体结构建筑沉降损伤实例研究[J]. 岩土工程学报, 2020, 42(12): 2301-2307. doi: 10.11779/CJGE202012017 CHEN Renpeng, ZENG Wei, WU Huaina, et al. Case study of tunneling-induced settlement and damage of masonry buildings[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2301-2307. (in Chinese) doi: 10.11779/CJGE202012017
[3]	刘国琛, 廖国华. 煤矿地表移动的基本规律[M]. 北京: 中国工业出版社, 1965. LIU Baochen, LIAO Guohua. Basic law of coal mine surface movement[M]. Beijing: China Architecture and Building Press, 1965. (in Chinese)
[4]	韩煊, 李宁. 隧道开挖不均匀收敛引起地层位移的预测模型[J]. 岩土工程学报, 2007, 29(3): 347-352. doi: 10.3321/j.issn:1000-4548.2007.03.006 HAN Xuan, LI Ning. A predicting model for ground movement induced by non-uniform convergence of tunnel[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 347-352. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.03.006
[5]	CAI H B, LIU Z, LI S, et al. Improved analytical prediction of ground frost heave during tunnel construction using artificial ground freezing technique[J]. Tunnelling and Underground Space Technology, 2019, 92: 103050. doi: 10.1016/j.tust.2019.103050
[6]	齐永洁, 朱建才, 周建, 等. 土岩复合地层中盾构施工引起的地表位移预测[J/OL]. 岩土工程学报, 2022: 1-10. (2022-06-20). https://kns.cnki.net/kcms/detail/32.1124.TU.20220616.1831.008.html. QI Yongjie, ZHU Jiancai, ZHOU Jian, et al. Prediction of surface displacement caused by shield construction in soil-rock composite stratum[J/OL]. Chinese Journal of Geotechnical Engineering, 2022: 1-10. (2022-06-20). https://kns.cnki.net/kcms/detail/32.1124.TU.20220616.1831.008.html. (in Chinese)
[7]	刘波, 杨伟红, 张功, 等. 基于隧道不均匀变形的地表沉降随机介质理论预测模型[J]. 岩石力学与工程学报, 2018, 37(8): 1943-1952. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201808017.htm LIU Bo, YANG Weihong, ZHANG Gong, et al. A prediction model based on stochastic medium theory for ground surface settlement induced by non-uniform tunnel deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(8): 1943-1952. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201808017.htm
[8]	伍振志. 基于非均匀收敛模式的隧道地表变形的随机介质预测模型[J]. 中南大学学报(自然科学版), 2010, 41(5): 2005-2010. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201005060.htm WU Zhenzhi. Stochastic medium predicting model of ground movement tunneling based on non-uniform convergence mode[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 2005-2010. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201005060.htm
[9]	阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M]. 北京: 中国铁道出版社, 2002. YANG Junsheng, LIU Baochen. Ground Movement and Deformation Caused by Urban Tunnel Construction[M]. Beijing: China Railway Publishing House, 2002. (in Chinese)
[10]	GONZÁLEZ C, SAGASETA C. Patterns of soil deformations around tunnels. Application to the extension of Madrid Metro[J]. Computers and Geotechnics, 2001, 28(6/7): 445-468.
[11]	YANG X L, WANG J M. Ground movement prediction for tunnels using simplified procedure[J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462-471. doi: 10.1016/j.tust.2011.01.002
[12]	LOGANATHAN N, POULOS H G. Analytical prediction for tunneling-induced ground movements in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846-856.
[13]	童磊, 谢康和, 程永锋, 等. 考虑椭圆化地层变形影响的浅埋隧道弹性解[J]. 岩土力学, 2009, 30(2): 393-398. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200902023.htm TONG Lei, XIE Kanghe, CHENG Yongfeng, et al. Elastic solution of sallow tunnels in clays considering oval deformation of ground[J]. Rock and Soil Mechanics, 2009, 30(2): 393-398. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200902023.htm
[14]	韩煊. 隧道施工引起地层位移及建筑物变形预测的实用方法研究[D]. 西安: 西安理工大学, 2007. HAN Xuan. The Analysis and Prediction of Tunnelling-Induced Building Deformations[D]. Xi'an: Xi'an University of Technology, 2007. (in Chinese)
[15]	VERRUIJT A, BOOKER J R. Surface settlements due to deformation of a tunnel in an elastic half plane[J]. Géotechnique, 1996, 46(4): 753-756.
[16]	SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301-320.
[17]	艾传志, 王芝银. 既有路基下浅埋隧道开挖引起地层的位移及应力解析解[J]. 岩土力学, 2010, 31(2): 541-546. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201002039.htm AI Chuanzhi, WANG Zhiyin. An analytical solution for displacement and stress caused by shallow buried tunnel excavation under existing highway foundation[J]. Rock and Soil Mechanics, 2010, 31(2): 541-546. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201002039.htm
[18]	欧阳文彪, 丁文其, 谢东武. 考虑建筑刚度的盾构施工引致沉降计算方法[J]. 地下空间与工程学报, 2013, 9(1): 155-160. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201301026.htm OUYANG Wenbiao, DING Wenqi, XIE Dongwu. Calculation method for settlement due to shield tunnelling considering structure stiffness[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(1): 155-160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201301026.htm
[19]	ZHOU Z, CHEN Y, LIU Z Z, et al. Theoretical prediction model for deformations caused by construction of new tunnels undercrossing existing tunnels based on the equivalent layered method[J]. Computers and Geotechnics, 2020, 123: 103565.
[20]	龚晓南. 土力学[M]. 北京: 中国建筑工业出版社, 2002. GONG Xiaonan. Soil Mechanics[M]. Beijing: China Architecture & Building Press, 2002. (in Chinese)
[21]	雷华阳, 刘旭, 施福硕, 等. 顶管工程聚合物改性膨润土泥浆配比优化研究[J]. 岩土工程学报, 2021, 43(增刊2): 51-55. doi: 10.11779/CJGE2021S2012 LEI Huayang, LIU Xu, SHI Fushuo, et al. Proportional optimization of polymer-modified bentonite slurry in pipe jacking[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S2): 51-55. (in Chinese) doi: 10.11779/CJGE2021S2012
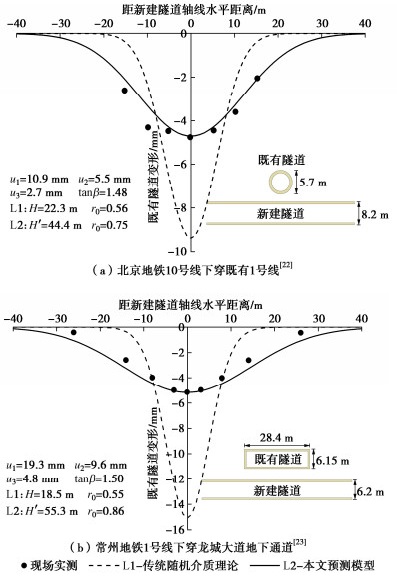
[22]	王剑晨, 刘运亮, 张顶立, 等. 下穿施工影响下既有隧道和地层的位移解析解[J]. 地下空间与工程学报, 2016, 12(增刊2): 678-683. WANG Jianchen, LIU Yunliang, ZHANG Dingli, et al. The displacement solution of existing tunnel and ground by traversing construction[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(S2): 678-683. (in Chinese)
[23]	韩文君, 严红霞, 欧建军. 富水地层盾构下穿城市快速路隧道影响分析[J]. 常州工学院学报, 2020, 33(6): 9-13. HAN Wenjun, YAN Hongxia, OU Jianjun. An analysis of the impact of shield tunnel on silt strata under urban expressway tunnel[J]. Journal of Changzhou Institute of Technology, 2020, 33(6): 9-13. (in Chinese)

施引文献(35)

期刊类型引用(12)

1.	曹小为. 双线盾构区间侧穿既有建筑物加固方案分析. 运输经理世界. 2025(03): 97-100 . 百度学术
2.	周鹏远，宋战平，王军保，张玉伟，田小旭. 基于随机介质理论的偏压隧道地表沉降预测方法. 岩土工程学报. 2025(03): 589-598 . 本站查看
3.	顾章川. 基于Midas GTS有限元软件的下穿既有轨道交通结构安全保护研究. 城市轨道交通研究. 2025(03): 181-185+191 . 百度学术
4.	徐峰. 不同工法下双孔隧道施工引起地表沉降的随机预测研究. 铁道建筑技术. 2024(04): 103-107 . 百度学术
5.	张治国，沃巍，朱正国，韩凯航，孙苗苗. 考虑衬砌截面协调变形约束的既有隧道受盾构下穿施工影响的Fourier能量变分解. 岩土力学. 2024(05): 1397-1411+1422 . 百度学术
6.	王荣桥，彭珠辉. 基于有限元模型的共建隧道开挖施工影响分析. 黑龙江交通科技. 2024(08): 139-142 . 百度学术
7.	王理想，刘四进，王军，段其广. 盾构下穿引起的既有隧道沉降变形研究. 力学季刊. 2024(03): 855-866 . 百度学术
8.	刘志坚，曹伍富，黄俊鸿，寇鼎涛，邵小康，王炳禄，江玉生. 盾构隧道超近间距下穿运营盾构隧道管片环变形规律研究. 铁道标准设计. 2024(09): 132-139 . 百度学术
9.	申庆梦，杨玉坤，李越，李涛，王晓龙，李峰. 基于改进GA-PSO的双线隧道开挖地表沉降的智能反分析法. 河南科技大学学报(自然科学版). 2024(06): 69-80+122 . 百度学术
10.	郭延辉，李顺银. 隧道双线盾构-暗挖近距下穿湖底安全性研究. 地下空间与工程学报. 2024(S2): 900-906 . 百度学术
11.	张逆进，姚胜泉. 基于量测数据频率分布的隧道变形分析与预测方法. 铁道建筑技术. 2023(04): 126-129+135 . 百度学术
12.	韩伟，唐钱龙. 富水饱和区盾构隧道施工地表沉降计算方法. 力学与实践. 2023(05): 1057-1066 . 百度学术