上方基坑开挖引起下卧隧道纵向变形分析方法

黄茂松; 李豪; 俞剑; 张陈蓉; 倪雨萍

doi:10.11779/CJGE20220780

上方基坑开挖引起下卧隧道纵向变形分析方法 English Version

黄茂松^{1, 2,},
李豪^{1, 2},
俞剑^{1, 2, ,},
张陈蓉^{1, 2},
倪雨萍^{1, 2}

1.
同济大学地下建筑与工程系, 上海 200092
2.
同济大学岩土及地下工程教育部重点实验室, 上海 200092

基金项目:

国家自然科学基金重点项目 51738010

国家重点研发计划课题 2016YFC0800202

详细信息

作者简介:
黄茂松(1965—)，男，博士，教授，博士生导师，从事岩土工程方面的教学与科研工作。E-mail: mshuang@tongji.edu.cn

通讯作者:
俞剑, E-mail: 002yujian@tongji.edu.cn

中图分类号: TU43
计量
- 文章访问数: 712
- HTML全文浏览量: 91
- PDF下载量: 332
出版历程
- 收稿日期: 2022-06-19
- 网络出版日期: 2023-05-29
- 刊出日期: 2023-10-31

Approach for evaluating longitudinal deformation of underlying tunnels due to excavation of upper foundation pit

HUANG Maosong^{1, 2,},
LI Hao^{1, 2},
YU Jian^{1, 2, ,},
ZHANG Chenrong^{1, 2},
NI Yuping^{1, 2}

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China

摘要

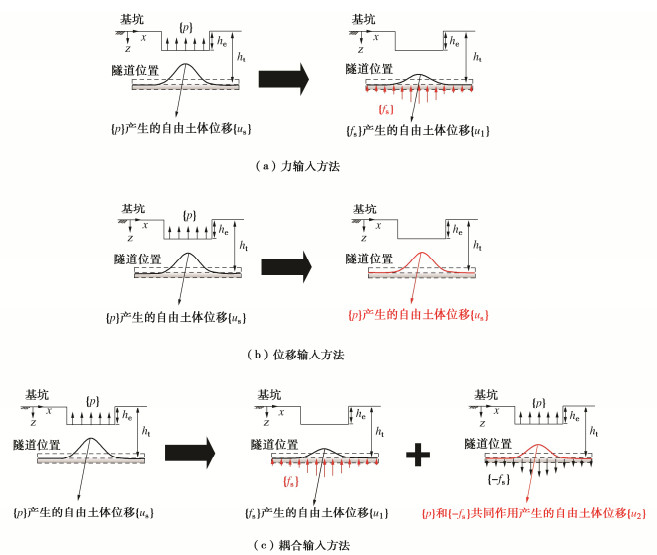
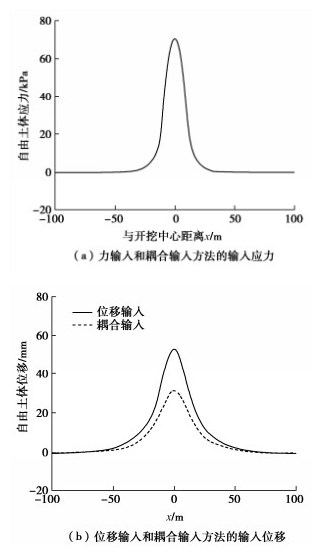
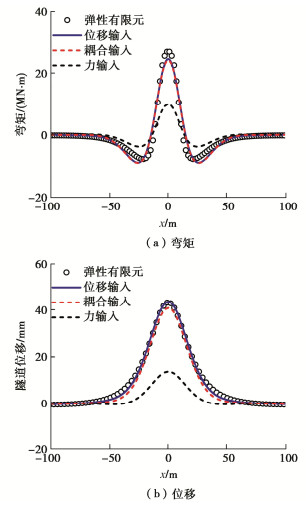
摘要: 上方基坑开挖引起下卧隧道纵向响应的分析方法大多将基坑开挖处理为基底简单卸荷作用，采用基底卸荷引起的隧道轴线处自由土体的附加应力作为输入条件，视之为隧道所受到的荷载。然而，这种力输入条件并非隧道受到的真实荷载，导致得不到合理的隧道响应。为此，首先从理论上分析当前的力输入条件的不足以及位移输入条件较为合理的原因，并对两种输入条件下Winkler地基模量进行区分，指出位移输入条件和力输入条件应分别采用被动和主动Winkler地基模量。其次，通过对比有限元和Winkler方法得到的隧道响应，验证了位移输入条件的合理性，而当前的力输入条件会低估隧道的响应。最后，鉴于力输入方法的工程实用性，提出利用荷载放大系数调整输入荷载的大小，以获得合理的隧道响应。利用大量的有限元算例进行研究，确定了荷载放大系数的简化计算公式，通过与工程案例的实测结果对比，验证了所提出方法的可行性。
- 上方基坑 /
- 隧道 /
- 纵向变形 /
- 输入条件 /
- Winkler地基模量
Abstract: For most of the analysis methods for the longitudinal response of underlying tunnels, excavation of the foundation pits is treated as a simple unloading of the base and the additional stress of the greenfield soil at the tunnel axis is taken as the input condition. However, this force input condition is not the real load to which the tunnel is subjected, resulting in an unreasonable tunnel response. To this end, the reasons why the current force input condition is insufficient and the displacement input condition is more reasonable are firstly analyzed theoretically, and the Winkler subgrade moduli of the two input conditions are distinguished. It is proposed that the passive and active Winkler subgrade moduli should be used for the displacement and pressure input conditions, respectively. Secondly, by comparing the tunnel response obtained by the finite element model and the Winkler methods, it is verified that the displacement input condition is reasonable, while the current force input condition would underestimate the tunnel response. Finally, given the engineering practicality of the force-based method, it is proposed to adjust the magnitude of the force input condition by using the load amplification factor to obtain a reasonable tunnel response. Using a large number of finite element calculations for parametric studies, a simplified formulation for the load amplification factor is proposed. The feasibility of the proposed method is verified by comparing with the field measurements of a case study.
- upper foundation pit /
- tunnel /
- longitudinal deformation /
- input condition /
- Winkler subgrade modulus

HTML全文

0. 引言

全断面岩石隧道掘进机(以下简称TBM)是集机、电、液和自动化控制于一体，能够实现破岩、掘进、出渣与隧道支护的大型掘进装备，其具有对围岩扰动小、能连续作业、环境污染小、安全性能高、成硐质量好等优点^[1]。然而，随着TBM向“三高”等(高原岩围压、高岩石强度、高石英含量)等极端恶劣地层推广应用，TBM的核心破岩刀具——盘形滚刀(以下简称滚刀)失效严重，从而导致TBM掘进效率低、施工成本高等问题^[2]。为了克服上述TBM的性能瓶颈，在当前材料科学与制备技术的约束下，鉴于激光技术在石油钻探领域已取得的良好效果，将激光发生器耦合安装到TBM刀盘上，进行激光预钻孔/预切槽条件下滚刀滚压破碎掌子面岩石，理论上有望实现新型热-机械高效破岩之目的^[3]。

目前，一方面由于激光破岩过程涉及到新物质生成、岩石物性改变、热裂纹衍生与扩展等，难以借助理论工具予以准确描述，另一方面由于热-机械耦合效应解耦困难，有关激光辅助滚刀破岩机理的理论建模研究尚不多见。学术界主要针对滚刀及激光的破岩过程分别予以了研究。

(1) 滚刀破岩方面

JI A史莱涅、Hertz、Boussinesq和Davies等对平底压头、半球形压头及楔形压头等不同压头形式侵入岩石过程中的应力分布公式进行了推导^[4]。在上述压头侵岩理论的基础上，不少学者基于滚压破岩试验，相继建立了滚刀破岩载荷预测模型。Evans等^[5]认为垂直力与侵岩投影面积成正比且将该面积按抛物线围成面积的一半计算。Rostami^[6]将垂直力分为压碎下方岩石所需作用力和剪切相邻刀间距间岩石所需作用力两部分，并按三角形面积来确定刀岩接触面积，建立了经典的CSM模型。国内许多科研院所也进行了滚刀破岩预测模型的研究工作^[7-9]。但由于对于刀岩作用过程认识的局限性，加之岩石本构行为的复杂性，导致上述模型并未考虑刀岩作用过程中密实核的衍生效应^[10]。密实核的衍生效应在滚刀切削破岩过程中的影响是不可忽略的。当滚刀作用于岩石表面时，刃底的岩石表面由于承压产生凹陷，并衍生出微裂纹；随着刀具的不断侵入，裂纹内部的岩石不断受到压缩和剪切的作用，形成了由岩石碎屑粉末组成的密实核；由于密实核的膨胀和变形，密实核周围的岩石持续受压，继而产生剪切破坏并形成破碎区^[11]。Alehossein等^[12]将刀具侵岩时在裂纹形成之前岩石内部分为密实核区、弹塑性失效区和弹性变形区3个应力区，并基于腔体膨胀理论建立了钝刀侵岩模型。在此基础上，张魁等^[13]进一步建立了考虑密实核衍生现象的常截面(CCS)滚刀侵岩载荷模型。有许多学者也通过侵岩^[14]、滚压破岩^[15]等试验方法，对滚刀破岩机理进一步探究完善。

(2) 激光破岩方面

为了研究激光破岩机理，学者们搭建了诸多试验平台，其中使用的激光器主要为光纤激光器，功率为50 W~9 kW。研究表明：利用激光器发射高能激光束照射在岩石表面，可使岩石在在局部高温作用下发生升温、熔化、汽化和凝固过程，并伴随着热爆裂现象的产生，其表面存在固液气多相混化合物^[16]。当激光作用在岩石表面时间较短，岩石表温度未超过其熔点时，其破碎方式主要为热力破碎，破碎后脱落的碎屑可由高压辅助气流带出；当岩石持续吸收激光束的能量，并不断积累超过一定阀值时，岩石就会熔化甚至汽化，此时岩石因为在极短时间内吸收大量能量发生相变，导致体积膨胀，产生热爆裂现象；当熔融物和汽化物不能及时被辅助气体吹出带走时，岩石表面会重新凝固成玻璃状物质，该物质会阻碍激光束能量的进一步传递，不利于激光孔洞的扩张，但在另一方面，该玻璃物质可以加固松散程度较高、力学性能不好的岩石^[17-19]。近年来，随着科技的不断进步，人们对激光破岩技术的研究也逐渐深入。由于现有试验设备难以观察和测量破岩过程中激光与岩石相互作用界面的具体形貌，以及熔体-蒸汽界面处的温度状态，大量的学者着力于用理论模型和数值仿真方法研究激光破岩机理^[20-22]。研究表明构建激光破岩数值模型能有效观察激光破岩过程中岩石温度和应力场分布，对分析岩石微观和宏观性质变化的有效方法，对指导激光破岩试验测试有重要意义。综上所述，为了用理论描述预制激光孔条件下滚刀侵岩过程，基于小孔应力集中理论的弹性应力状态计算方法，在空腔膨胀模型基础上，拟建立一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型，并开展激光辅助缩尺比例滚刀侵岩试验，尝试从侵岩垂直力的角度，通过理论与试验结果的对比验证，讨论理论模型的正确性。

1. 理论基础与理论建模

1.1 基本假设

如图 1所示，在高能量激光照射下，岩石表面发生了弱化、碎化、熔化和汽化现象，继而形成了孔洞状等损伤形貌，并在孔洞周围产生了热影响区域；同时，在孔底附着有玻璃釉物质。可见，激光预钻孔条件下滚刀滚压破碎掌子面岩石，属于一种典型的机械破碎-热破碎耦合作用过程。为了便于建模，现作出如下7点简化假设。

图 1 激光破岩示意图

Figure 1. Schematic diagram of laser-assisted rock breaking

下载: 全尺寸图片幻灯片

(1) 忽略激光钻孔时序对孔径、孔深等形貌尺寸及围岩物理力学性能的影响。

(2) 忽略激光热源所产生热应力对岩石试样强度的削弱作用。

(3) 忽略所述玻璃釉对滚刀破岩机理的影响。

(4) 将岩石试样视为各向同性的线弹性体，满足平面应变条件。

(5) 假定岩石试样尺寸远大于激光孔径，且刀孔距大于两倍激光孔径。

(6) 假定激光孔孔深不小于滚刀侵深。

(7) 假设刀孔距远大于激光孔孔径后，滚刀对激光孔的合力为均布载荷。

基于上述简化假设，认定在受原岩围压以及滚刀机械应力的综合作用下，激光孔周围存在小孔应力集中现象。根据小孔应力集中理论可知：激光孔周围的局部最大应力甚至会达到平均应力水平的(2~3)倍；当超出孔中心一定范围时，应力集中现象消失；小孔应力集中现象只与小孔形状有关，与小孔尺寸无关。

1.2 考虑密实核衍生效应的滚刀侵岩模型

文献[]基于密实核衍生现象，认为滚刀侵岩时刃底向密实核区施加了挤压应力，而刃侧对岩壁产生了剪切挤压应力。为此，如所示，滚刀所受垂直侵岩力 ${F_{\rm{v}}}$ 与刃底密实核对滚刀所施加挤压力 ${F_1}$ 和刃侧岩体对滚刀所施加挤压力 ${F_2}$ 的合力相关。其中， ${F_1}$ 可分解为沿垂直方向的 ${F'_{\rm{v}}}$ 和沿水平方向的 ${F'_{\rm{c}}}$ 两个分力； ${F_2}$ 可分解为沿垂直方向的 ${F''_{\rm{v}}}$ 和沿水平方向的 ${F''_{\rm{c}}}$ 两个分力。

图 2 滚刀侵岩过程中的受力示意图

Figure 2. Schematic diagram of forces involved during rock penetration by a disc cutter

下载: 全尺寸图片幻灯片

中， ${F'_{\rm{v}}}$ 和 ${F'_{\rm{c}}}$ 可由考虑密实核效应的常截面(CCS)滚刀侵岩载荷模型计算给出^[13]，其中密实核对岩体的垂直挤压力 ${F'_{\rm{v}}}$ 为

${F'_{\rm{v}}}{\text{ = }}2\int_0^\psi {2{P_{\rm{s}}}bR\cos {\text{(}}\psi - \beta {\text{)}}} {\text{d}}\beta 。$

(1)

式中：P_s为密实核区应力； ${\text{d}}\beta$ 为滚刀微元的位置角；R为滚刀半径；2 $\psi$ 为刀岩接触角，

$\psi = \arccos [(R - h')/R] 。$

(2)

密实核对岩体的水平挤压力 ${F'_{\rm{c}}}$ 为

${F'_{\rm{c}}}{\text{ = }}{P_{\rm{s}}}{S_{\rm{s}}} 。$

(3)

式中： ${S_{\rm{s}}}$ 为密实核与岩体接触部分投影面积，

${S_{\rm{s}}} = R\arccos \frac{{R - h'}}{R}b 。$

(4)

如所示， $b$ 为密实核区半径，其值等于1/2刃宽； $h'$ 为侵深； ${S_{\rm{t}}}$ 为滚刀与岩体接触部分投影面积，

${S_{\rm{t}}} = {R^2}\arccos \frac{{R - h'}}{R} - (R - h')\sqrt {{R^2} - {{(R - h')}^2}} 。$

(5)

图 3 刀岩作用过程中的纵向截面图

Figure 3. Longitudinal section during rock penetration

下载: 全尺寸图片幻灯片

中 ${F''_{\rm{v}}}$ ， ${F''_{\rm{c}}}$ 可由考虑刃侧挤压与剪切效应的CCS滚刀侵岩载荷模型计算给出^[23]：

${F_{\rm{v}}}^{\prime \prime }{\text{ = }}2\int_0^\psi {R\left[ {{{P'}_1}{\text{cos}}(\left| \varphi \right| - {\theta _0}) + {P_1}''\cos ({\theta _0} + \varphi )} \right]} {\text{d}}\beta \text{，}$

(6)

${F}_{c}{}^{\prime \text{}\prime }\text{=}2R{\displaystyle {\int }_{0}^{\psi }\left[-{{P}^{\prime }}_{1}\mathrm{sin}(\left|\phi \right|-{\theta }_{0})+{{P}^{″}}_{1}\mathrm{sin}({\theta }_{0}+\phi )\right]}\text{cos(}\psi -\beta \text{)d}\beta 。$

(7)

式中： ${P_1}^\prime$ 为等效剪切破岩力； ${P_1}^{\prime \prime }$ 为等效挤压破岩力。

${P}_{1}\text{'}=\text{2}\tau \text{cos}\phi [R-(R-{h}^{\prime })/\mathrm{cos}(\psi -\beta )]/(n+1)(1-\mathrm{cos}2\psi )\text{，}$

(8)

${P_1}{\text{''}} = {\sigma _{\rm{c}}}[R - (R - h')/\cos (\psi - \beta )]/\cos {\theta _0}\cos \varphi 。$

(9)

式中： $\varphi$ 为内摩擦角； ${\sigma _{\rm{c}}}$ 为岩石最大抗压强度。

故滚刀单侧所受侧向侵岩力 ${F_{\text{c}}}$ 及滚刀所受垂直侵岩力 ${F_{\rm{v}}}$ 为

${F_{\rm{c}}} = {F_{\rm{c}}}^\prime + {F''_{\rm{c}}} \text{，}$

(10)

${F_{\rm{v}}} = {F'_{\rm{v}}}{\text{ + }}2{F''_{\rm{v}}} 。$

(11)

1.3 激光预钻孔条件下滚刀侵岩模型

(1) 基于小孔应力集中的单个激光孔周围应力分布

假设岩石初始受双向对称围压作用。当滚刀侵入激光孔一侧岩石，由于滚刀机械应力参与作用，打破了围岩所受双向对称围压状态，使其转换为双向非对称围压状态，如所示。 ${p_0}$ 为激光孔总应力； ${p_{\rm{w}}}$ 为侧向围压应力； ${p_{\rm{z}}}$ 为正向围压应力， ${p_{\rm{z}}} = {p_{\rm{w}}}$ ； ${F'_{\rm{c}}}$ 为密实核对岩体的水平挤压力； ${F''_{\text{c}}}$ 为滚刀刃侧对岩壁的水平作用力。

图 4 激光辅助滚刀侵岩过程的受力图

Figure 4. Force diagram of rock penetration by laser-assisted disc cutter

下载: 全尺寸图片幻灯片

激光孔的总应力为刃侧切向应力和刃底密实核挤压应力之和：

${P_0} = ({F_{\rm{c}}}{\text{ + }}{F'_{\rm{c}}})/({S_{\rm{t}}}{\text{ + }}{S_{\rm{s}}}) 。$

(12)

式中： ${S_{\rm{t}}}$ 为滚刀与岩体接触部分面积； ${S_{\rm{s}}}$ 为密实核与岩体接触部分面积。

假设激光孔仅受围压及 ${P_0}$ 作用，此时将双向非对称围压状态转换成双向轴对称围压状态和等应力单向受拉单向受压状态，如所示。 ${R_0}$ 为激光孔半径；r为任意点到激光孔圆心的距离； $\theta$ 为任意点到激光孔圆心连线与x轴的夹角； $\lambda$ 为应力系数( $\lambda$ < 1)； $P$ 为轴对称围压应力； $P'$ 为刃底密实核挤压应力。

图 5 激光孔受力情况简化图

Figure 5. Simplified diagram of forces on laser hole

下载: 全尺寸图片幻灯片

应力系数 $\lambda$ 定义为正向压应力与侧向压应力之比。轴对称围压应力状态是滚刀-激光辅助破岩的特例(即 $\lambda = 1$ 时)，但在滚刀破岩过程中，刃侧及刃底对岩石的挤压作用总是会打破这个平衡，使得 $\lambda < 1$ 。

在轴对称围压应力状态下激光孔周边岩石的应力解^[24]为

$\left. \begin{array}{l}{\sigma }_{\text{θ}}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1\pm \frac{{R}_{0}^{2}}{{r}^{2}}\right)\text{ }\text{，}\\ {\sigma }_{r}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1\pm \frac{{R}_{0}^{2}}{{r}^{2}}\right)\text{ }。\end{array} \right\}$

(13)

在等应力单向受拉单向受压状态下，激光孔周边岩石的应力解为

$\left. \begin{array}{l}{\sigma }_{r}=\frac{1}{2}(1-\lambda ){P}_{0}\left(1-4\frac{{R}_{0}^{2}}{{r}^{2}}+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\sigma }_{\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\tau }_{r\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+2\frac{{R}_{0}^{2}}{{r}^{2}}-3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{sin}2\theta 。\end{array} \right\}$

(14)

式中： ${\sigma _r}$ 为激光孔径向正应力； ${\sigma _\theta }$ 为激光孔切向正应力； ${\tau _{r\varphi }}$ 为激光孔切向应力。

基于应力场叠加原理，由式(13)，(14)可得双向非对称围压状态下激光孔周边岩石应力计算式：

$\left. \begin{array}{l}{\sigma }_{r}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1-\frac{{R}_{0}^{2}}{{r}^{2}}\right)-\frac{1}{2}(1-\lambda ){P}_{0}\left(1-4\frac{{R}_{0}^{2}}{{r}^{2}}+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\sigma }_{\theta }=\frac{1}{2}(1+\lambda ){P}_{0}\left(1+\frac{{R}_{0}^{2}}{{r}^{2}}\right)+\frac{1}{2}(1-\lambda ){P}_{0}\left(1+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\tau }_{r\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+2\frac{{R}_{0}^{2}}{{r}^{2}}-3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{sin}2\theta 。 \end{array} \right\}$

(15)

由式(15)可知，当 $r \approx {R_0}$ 时，激光孔边的应力分布为

${\sigma _r} = {\tau _{r\theta }} = 0 \text{，}$

(16)

${\sigma _\theta } = (1 + \lambda ){P_0} + 2(1 - \lambda ){P_0}\cos 2\theta 。$

(17)

在 $\theta {\text{ = }}{0^ \circ }$ 处，激光孔边存在最大压应力，其应力解为

${\sigma _\theta } = (3 - \lambda ){P_0} > 0 。$

(18)

在 $\theta {\text{ = 9}}{0^ \circ }$ 处，激光孔边存在最小应力，其应力解为

${\sigma _\theta } = (3\lambda - 1){P_0} 。$

(19)

当 $0 < \lambda < \frac{1}{3}$ 时，激光孔周围存在拉应力；当 $\frac{1}{3} < \lambda < 1$ 时，激光孔周围只存在压应力；当TBM位于深层岩石掘进时，由于岩石围压力 ${P_{\rm{z}}}$ 较大， $\lambda$ 一般为 $\frac{1}{3} < \lambda < 1$ 。

(2) 基于小孔应力集中的激光孔排周围应力分布

当多个激光孔以给定孔距排列时，激光孔排的应力分布如所示。其中k为小孔应力集中系数，一般 $k = 1.5 \sim 2$ ，则 $k{R_0}$ 为应力集中边界^[25]。基于小孔应力集中理论，激光孔应力集中边界最大压应力为

${\sigma }_{k{R}_{0}}{{}_{, }}_{0}=\left[3(1-\lambda )/2{k}^{4}+(1+\lambda )/2{k}^{2}+1\right]{P}_{0} > {P}_{0} 。$

(20)

图 6 激光孔排的应力分布图

Figure 6. Distribution of stress of multiple laser holes

下载: 全尺寸图片幻灯片

当激光孔应力集中边界处最大压应力达到岩石最大抗压强度 ${\sigma _{\text{c}}}$ 时，该边界处岩体被破坏，即

${\sigma _{k{R_0}, 0}} = \left[ {3(1 - \lambda )/2{k^4} + (1 + \lambda )/2{k^2} + 1} \right]{P_0}{\text{ = }}{\sigma _{\text{c}}} \text{，}$

(21)

${P_{0\min }}{\text{ = }}\sigma c/[3(1 - \lambda )/2{k^4} + (1 + \lambda )/2{k^2} + 1] 。$

(22)

式中：P_0min为激光孔破坏时的临界应力。

此时，应力系数 $\lambda$ 进一步给出为

$\lambda = {P_{\rm{z}}}/[({P_{\rm{t}}}{S_{\rm{t}}} + {P_{\rm{s}}}{S_{\rm{s}}})/({S_{\rm{t}}} + {S_{\rm{s}}}) + {P_{\rm{w}}}] 。$

(23)

待激光孔被破坏后，激光孔间剩余未被破坏岩石，处于三面临空、两面受压状态，并假定其承受压力 ${P_0}$ 。如所示，当激光孔被破坏的瞬间，假定滚刀切削力保持不变。由于激光孔破碎，岩石承载面积由原本的 $(a - 2{R_0})h$ 骤减到 $(a - 2k{R_0})h$ ，因此该处岩石压力重新分布为

$\sigma = {P_0}(a - 2{R_0})/(a - 2k{R_0}) 。$

(24)

图 7 激光孔周边岩石的破碎情况分析

Figure 7. Analysis of rock fragmentation around laser hole

下载: 全尺寸图片幻灯片

令式(24)等于 ${\sigma _{\rm{c}}}$ ，即可求得破坏剩余部分岩石所需应力P₀：

${P_0} = {\sigma _{\text{c}}}(a - 2k{R_0})/(a - 2{R_0}) 。$

(25)

当激光孔被破坏时，剩余岩石同时发生破坏，此时破岩效果最佳，则

${P_0}{\text{ = }}{P_{0\min }} 。$

(26)

可求得激光辅助滚刀侵岩时最优孔距 ${a_0}$ 为

${a_0} = {\text{2}}{R_0}({P_{0\min }} - k{\sigma _{\rm{c}}}{\text{)/(}}{P_{0\min }} - {\sigma _{\rm{c}}}{\text{)}} (2k{R_0} < a < 10{R_0}) 。$

(27)

(3) 综合建模

由式(27)求得最佳孔距为 ${a_0}$ ，当 $a < {a_0}$ 时，由于孔距较小，其所对应的侵岩载荷和所需能量均较大，不再适用于小孔应力集中问题，故此处不做计算。当 $a > {a_0}$ 时，可得滚刀对激光孔排总应力 ${P_{\text{0}}}^\prime$ ：

${P'_0} = {F_{\rm{c}}}/({S_{\rm{t}}} + {S_{\rm{s}}}) 。$

(28)

由平衡公式可得

${P_0} = {P_0}^\prime 。$

(29)

即

${\sigma _{\rm{c}}}(a - 2k{R_0})/(a - 2{R_0}) = ({F_{\rm{c}}} + {F'_{\text{c}}})/({S_{\rm{s}}} + {S_{\rm{t}}}) 。$

(30)

密实核区处于静水压力状态，可将密实核区应力 ${P_{\rm{s}}}$ 视为均值，可求得

${P_{\rm{s}}} = \left\{ {{\sigma _{\rm{c}}}{\text{(}}{S_{\rm{s}}} + {S_{\rm{t}}}{\text{)}}(a - 2k{R_0})/(a - 2{R_0}) + \mathop {}\limits_{} } \right.$

$2R{\displaystyle {\int }_{0}^{\psi }\left[{P}_{1}\text{'sin}(\left|\varphi \right|-{\theta }_{0})-{P}_{1}\text{'}\text{'}\mathrm{sin}({\theta }_{0}+\varphi )\right]}\text{cos(}\psi -\beta \text{)d}\beta \}/{S}_\text{s}\text{ }。$

(31)

当求得 ${P_{\rm{s}}}$ 后，即可联立式(1)，(6)，(8)求出 ${F_{\rm{v}}}$ ；联合式(3)，(7)，(9)求出 ${F_{\rm{c}}}$ 。

2. 理论分析

(1) 孔距对密实核区应力和侵岩垂直力的影响

为了便于后续试验验证，本节理论计算所用的滚刀按1︰3的比例对17英寸工程用滚刀进行缩小，以花岗岩为试验对象，并给定刃宽d为3 mm，刃倾角 ${\theta _{\text{0}}}$ 为8°，得出滚刀侵岩作用下不同孔距对密实核区应力和侵岩垂直力的影响规律图，如所示。由式(27)根据前述理论可以求出最优孔距 ${a_0}$ 为4.3 mm。当 $a < {a_0}$ 时，由于孔距较小，所对应的侵岩载荷和所需能量均较大，且不适用于小孔应力集中问题，因此，只对 $a > {a_0}$ 的条件下进行求解。

图 8 不同孔距对密实核区应力和侵岩垂直力的影响规律曲线

Figure 8. Curves of influences of hole spacing on stress in dense core area and vertical force of rock penetration

下载: 全尺寸图片幻灯片

由图可知，当 $a > {a_0}$ 时，密实核区应力及侵岩垂直力随孔距的增加，增加速率趋于平缓。随着孔距的增加，孔与孔之间剩余岩体的相对面积增加，应力集中区域的面积则相对减小，激光孔排逐渐趋近于没有激光辅助滚刀侵岩的情况，因此，其增加速率趋于平缓，最终将会无限趋近于无激光孔辅助滚刀侵岩的密实核区应力及侵岩垂直力。这也说明了，激光孔可影响滚刀侵岩过程中的密实核区应力及侵岩垂直力，并可通过激光孔距来优化滚刀破岩过程。

(2) 刃宽对密实核区应力和侵岩垂直力的影响

由式(2)~(16)计算可得最优孔距，再将最优孔距取整为4 mm，刃倾角 ${\theta _{\text{0}}}$ 为8°，得出不同刃宽对密实核区应力和侵岩垂直力的影响规律图，如图 9所示。由图可知，随刃宽的增加，密实核区应力与侵岩垂直力均近似呈线性增加。相对而言，侵岩垂直力的增加速率在刃宽较小时略有降低。这与实际情况中侵岩垂直力随刃宽增加而指数增加是相符合的^[26]。

图 9 不同刃宽对密实核区应力和侵岩垂直力的影响规律图

Figure 9. Curve of influences of edge width on stress in dense core area and vertical force of rock penetration

下载: 全尺寸图片幻灯片

3. 试验验证

3.1 试验方案

为了进一步验证上述理论模型，本节以YWYA- 2000型全自动伺服岩石抗压抗剪试验机为基础试验平台，开展了激光预钻孔条件下缩尺比例滚刀压头侵岩试验，如图 10所示。图 10中采用与理论分析相同尺寸的缩尺比例滚刀压头；选取板状长沙花岗岩作为岩石试样，岩样尺寸为150 mm×150 mm×24 mm；激光功率设置为100 W，激光频率为60 kHz，激光作用时间为1 s，采用E1309M型高速精密激光切割机在岩石试样表面沿岩石厚度方向预钻出激光孔排；孔距分别设置为2，3，4，5，6 mm。

图 10 侵岩试验示意图

Figure 10. Schematic diagram of rock penetration tests

下载: 全尺寸图片幻灯片

采用如图 11所示的具有自主知识产权的双侧围压装置夹持岩石试样，并将双侧围压装置设置于全自动伺服岩石抗压抗剪试验机工作平台上，再将高速摄像仪的镜头正对双侧围压装置的观测窗口。图 11中，双侧围压装置包括基座、正向围压部件、侧向围压部件和液压部件。其中，基座上装夹有岩石物料，正向围压部件对称压装于岩石物料的前后两面，侧向围压部件对称压装于岩石物料的左右两侧面，岩石物料与两侧正向围压部件之间对称压装有观测板，前后两个加载板及压板中部均开设有观测窗口，液压部件分别压紧正向围压部件及侧向围压部件，由于基座具有上述技术特征，使得在模拟滚刀压头侵岩过程中，本试验装置既可实现岩石试样围压状态的模拟加载，又可实现刃底密实核动态衍生现象的在线观测。

图 11 双侧围压装置

Figure 11. Test devices

下载: 全尺寸图片幻灯片

随后，采用全自动伺服岩石抗压抗剪试验机进行静压侵岩试验，将板状岩石安装于密实核衍生观测装置上，并放置好滚刀压头，监测设备沿试验装置的观测窗口架设，录制静压侵岩动态全过程。此外，还设置了一组无激光孔的侵岩对照试验。

3.2 试验结果分析

(1) 激光破岩后的岩石损伤形貌观测

如图 12，13所示，分别为激光预钻孔后花岗岩试样表面形貌图和激光孔横截面形貌图。由图 12，13可知，所获激光孔呈上部孔径大、底部孔径小的“倒锥形”形貌。这是由于在试验中，岩石所含矿物质受热熔化后无法及时排出，附着在孔壁上并形成玻璃釉物质；同时，玻璃釉物质的生成也限制了孔径与孔深的继续增大，进而导致了位于激光热源中心处的花岗岩去除量大于周边岩样。

图 12 孔距为3 mm时的岩石损伤形貌图

Figure 12. Morphology of rock damage at hole spacing of 3 mm

下载: 全尺寸图片幻灯片

图 13 激光孔横截面损伤形貌图

Figure 13. Morphologies of cross-sectional damage of laser hole

下载: 全尺寸图片幻灯片

(2) 密实核及岩石裂纹衍生扩展过程观测

如图 14所示，为密实核及裂纹衍生扩展过程观测图。由图 14(b)可知，在滚刀压头刃底出现了明显的白色密实核现象，且其半径大致为刃宽的一半，而在其周围出现了大量裂纹。其中，在激光孔一侧，表面裂纹延伸至激光孔排处，并与之贯穿，形成破碎岩块。由图 14(d)可知，从俯视侵岩形貌可以看出，在压头压痕与激光孔之间产生了较多破碎的岩块。

图 14 滚刀侵岩过程观测图

Figure 14. Observation images of rock penetration process by disc cutter

下载: 全尺寸图片幻灯片

(3) 侵岩垂直力分析

如图 15所示，为给定滚刀刃宽d为3 mm时，不同孔距下及无激光孔对照组所测滚刀峰值侵岩垂直力。由图 15可知，预制激光孔后，侵深及侵岩垂直力均小于无激光孔侵岩对照试验。这是由于激光孔排对局部岩石产生了弱化效应，降低了该处岩石强度，并在激光孔附近形成应力集中现象，峰值侵岩垂直力大大减小。而随着孔距的增加，侵岩垂直力呈先减小后增加的趋势，这是因为孔距过小时，应力集中区域重叠，岩石被过度破碎，在压头刃底更多的岩粉被重复压实，形成密实核，吸收了更多的破岩能量，侵岩垂直力也随之升高。因此第2节中的激光辅助滚刀侵岩模型不适用于孔距较小的情况。而随着孔距的增大，小孔应力集中区域不再重叠，岩石破碎时，岩碴多为较大的岩块，岩石没有被过度破碎，侵岩垂直力也随之下降至最小值，当孔距增大至4 mm时，峰值破岩力最小。随着孔距继续增加，小孔应力集中效应逐渐减弱，侵岩垂直力再次上升。

图 15 滚刀侵岩垂直力随孔距变化的曲线图

Figure 15. Curves of vertical force with spacing of cutter hole

下载: 全尺寸图片幻灯片

3.3 理论与试验结果的对比分析

为验证第2节中激光激光预钻孔条件下滚刀侵岩理论模型的正确性，将理论模型的结果曲线与试验结果曲线进行对比分析。

如图 16所示，为花岗岩在不同孔距条件下理论与试验侵岩垂直力对比图。如前所述第2节中的激光激光预钻孔条件下滚刀破岩模型不适用于孔距较小的情况，故理论组仅对孔距大于最优孔距的值进行理论分析。

图 16 理论与试验侵岩垂直力对比图

Figure 16. Comparison between theoretical and experimental vertical forces

下载: 全尺寸图片幻灯片

由图可知，试验组侵岩垂直力略大于理论组，且随着孔距的增加，两组曲线的变化趋势相同，均为逐渐放缓的上升趋势，且破岩力最小处均在孔距为4 mm处。由于试验中激光作用于岩石表面，岩石表面受到损伤而形成激光孔洞，同时熔融的岩石矿物质会覆盖在激光孔洞表面形成更加硬的玻璃釉层，而在理论中忽略了的玻璃釉对后续侵岩的影响；同时在理论中，假设了密实核区的半径为1/2刃宽，而在试验中由于岩石的破碎情况不同，形成的密实核半径并不是保持不变的，故造成了试验与理论的侵岩垂直力有较小的差别。

4. 结论

基于小孔应力集中理论的弹性应力状态计算方法及滚刀侵岩过程中的空腔膨胀模型，建立了一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型，并基于具有自主知识产权的双侧围压装置，开展激光辅助缩尺比例滚刀侵岩试验，从侵岩垂直力的角度，验证理论模型的正确性。

(1) 建立了一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型。随后对该模型进行数值建模分析后发现，随滚刀刃宽增加，密实核区应力呈线性增加，最大侵岩垂直力指数上升；随孔距的增加，密实核区应力、最大侵岩垂直力均呈先下降后上升趋势。

(2) 开展双侧围压下的激光辅助缩尺比例滚刀侵岩试验，并将得出的试验结果与理论分析结果进行对比，发现破岩垂直力在总体上较为吻合。由于在理论模型中未考虑激光破岩中产生的玻璃釉物质对后续侵岩的影响以及假设密实核区的半径为一个固定值，因此理论模型的预测精度有待进一步提升。

综上所述，本文所建立滚刀侵岩理论模型，具有一定的准确性，未来可将滚刀空间运动纳入考察，建立满足工程应用要求的激光辅助TBM破岩预测模型，为激光器-滚刀耦合刀盘的设计提供理论指导。

图 1 基坑开挖引起隧道轴线处自由土体附加应力与位移

Figure 1. Additional stresses and displacements of free soil at tunnel axis caused by excavation of foundation pit

下载: 全尺寸图片幻灯片

图 2 隧道结构有限差分示意图

Figure 2. Finite difference diagram of tunnel structure

下载: 全尺寸图片幻灯片

图 3 有限元得到的输入条件

Figure 3. Input conditions obtained by finite element method

下载: 全尺寸图片幻灯片

图 4 有限元与Winkler方法对比

Figure 4. Comparison of results by Winkler and finite element methods

下载: 全尺寸图片幻灯片

图 5 上方基坑与隧道相对位置

Figure 5. Relative position of above foundation pit and tunnel

下载: 全尺寸图片幻灯片

图 6 荷载放大系数影响因素

Figure 6. Influencing factors for load amplification factor

下载: 全尺寸图片幻灯片

荷载放大系数 ${Q_{\text{F}}}$ 的归一化处理

Normalization of load amplification factor ${Q_{\text{F}}}$

下载: 全尺寸图片幻灯片

图 8 基坑开挖示意图

Figure 8. Diagram of excavation of foundation pit

下载: 全尺寸图片幻灯片

图 9 实测、HS-Small模型和弹性模型的结果

Figure 9. Results of measurement, HS-Small model and elastic model

下载: 全尺寸图片幻灯片

图 10 Winkler方法与实测的对比结果

Figure 10. Comparison between Winkler method and measure ment

下载: 全尺寸图片幻灯片

表 1 模型工况

Table 1 Working conditions

基坑面积/m²	基坑尺寸(长×宽)/m	S/L_w
900	18×50	0/0.2/0.4
	22.5×40
	30×30
	40×22.5
	50×18	0/0.2/0.4/0.8
1600	32×50	0/0.2/0.4
	40×40	0/0.2/0.4
	50×32	0/0.2/0.4/0.8
2500	30×83	0/0.2/0.4
	40×62.5	0/0.2/0.4
	50×50	0/0.2/0.4/0.8
	62.5×40
	83×30

下载: 导出CSV

参考文献(21)

[1]	陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 91-94. doi: 10.3969/j.issn.1673-0836.2005.01.020 CHEN Yu, LI Yongsheng. Calculation of tunnel heaving due to unloading of pit excavation[J]. Underground Space, 2005, 1(1): 91-94. (in Chinese) doi: 10.3969/j.issn.1673-0836.2005.01.020
[2]	张治国, 黄茂松, 王卫东. 邻近开挖对既有软土隧道的影响[J]. 岩土力学, 2009, 30(5): 1373-1380. doi: 10.3969/j.issn.1000-7598.2009.05.033 ZHANG Zhiguo, HUANG Maosong, WANG Weidong. Responses of existing tunnels induced by adjacent excavation in soft soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1373-1380. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.05.033
[3]	姜兆华, 张永兴. 基坑开挖对邻近隧道纵向位移影响的计算方法[J]. 土木建筑与环境工程, 2013, 35(1): 7-11, 39. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201301003.htm JIANG Zhaohua, ZHANG Yongxing. Calculation of influence on longitudinal deformation of adjacent tunnels due to excavation[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(1): 7-11, 39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201301003.htm
[4]	梁荣柱, 林存刚, 夏唐代, 等. 考虑隧道剪切效应的基坑开挖对邻近隧道纵向变形分析[J]. 岩石力学与工程学报, 2017, 36(1): 223-233. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201701020.htm LIANG Rongzhu, LIN Cungang, XIA Tangdai, et al. Analysis on the longitudinal deformation of tunnels due to pit excavation considering the tunnel shearing effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(1): 223-233. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201701020.htm
[5]	应宏伟, 程康, 俞建霖, 等. 考虑地基变形连续的基坑开挖诱发邻近盾构隧道位移预测[J]. 浙江大学学报(工学版), 2021, 55(2): 318-329. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202102012.htm YING Hongwei, CHNEG Kang, YU Jianlin, et al. Prediction of shield tunnel displacement due to adjacent basement excavation considering continuous deformation of ground[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(2): 318-329. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202102012.htm
[6]	魏纲, 洪文强, 魏新江, 等. 基坑开挖引起邻近盾构隧道转动与错台变形计算[J]. 岩土工程学报, 2019, 41(7): 1251-1259. doi: 10.11779/CJGE201907009 WEI Gang, HONG Wenqiang, WEI Xinjiang, et al. Calculation of rigid body rotation and shearing dislocation deformation of adjacent shield tunnels due to excavation of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1251-1259. (in Chinese) doi: 10.11779/CJGE201907009
[7]	刘建文, 施成华, 雷明锋, 等. 基坑开挖对下卧地铁隧道影响的解析计算方法[J]. 中南大学学报(自然科学版), 2019, 50(9): 2215-2225. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201909018.htm LIU Jianwen, SHI Chenghua, LEI Mingfeng, et al. Analytical method for influence analysis of foundation pit excavation on underlying metro tunnel[J]. Journal of Central South University (Science and Technology), 2019, 50(9): 2215-2225. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201909018.htm
[8]	徐国元, 黄思源. 基坑开挖对下卧盾构隧道变形影响的计算分析[J]. 重庆交通大学学报(自然科学版), 2021, 40(9): 78-85. doi: 10.3969/j.issn.1674-0696.2021.09.12 XU Guoyuan, HUANG Siyuan. Calculation and analysis of the influence of foundation pit excavation on the deformation of the underlying shield tunnel[J]. Journal of Chongqing Jiaotong University (Natural Science), 2021, 40(9): 78-85. (in Chinese) doi: 10.3969/j.issn.1674-0696.2021.09.12
[9]	ZHANG J F, CHEN J J, WANG J H, et al. Prediction of tunnel displacement induced by adjacent excavation in soft soil[J]. Tunnelling and Underground Space Technology, 2013, 36: 24-33.
[10]	周泽林, 陈寿根, 涂鹏, 等. 基坑开挖对邻近隧道影响的耦合分析方法[J]. 岩土力学, 2018, 39(4): 1440-1449. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201804037.htm ZHOU Zelin, CHEN Shougen, TU Peng, et al. Coupling method for analyzing the influence on existing tunnel due to adjacent foundations pit excavation[J]. Rock and Soil Mechanics, 2018, 39(4): 1440-1449. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201804037.htm
[11]	程康, 徐日庆, 应宏伟, 等. 既有隧道在上覆基坑卸荷下的形变响应简化算法[J]. 岩石力学与工程学报, 2020, 39(3): 637-648. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202003019.htm CHENG Kang, XU Riqing, YING Hongwei, et al. Simplified method for evaluating deformation responses of existing tunnels due to overlying basement excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(3): 637-648. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202003019.htm
[12]	黄栩, 黄宏伟, 张冬梅. 开挖卸荷引起下卧已建盾构隧道的纵向变形研究[J]. 岩土工程学报, 2012, 34(7): 1241-1249. http://www.cgejournal.com/cn/article/id/14632 HUANG Xu, HUANG Hongwei, ZHANG Dongmei. Longitudinal deflection of existing shield tunnels due to deep excavation[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1241-1249. (in Chinese) http://www.cgejournal.com/cn/article/id/14632
[13]	ZHANG C R, ZHU J R, HUANG M S, et al. Winkler load-transfer analysis for pipelines subjected to surface load[J]. Computers and Geotechnics, 2019, 111: 147-156.
[14]	俞剑, 张陈蓉, 黄茂松. 被动状态下地埋管线的地基模量[J]. 岩石力学与工程学报, 2012, 31(1): 123-132. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201201017.htm YU Jian, ZHANG Chenrong, HUANG Maosong. Subgrade modulus of underground pipelines subjected to soil movements[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 123-132. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201201017.htm
[15]	VESIĆ A B. Bending of beams resting on isotropic elastic solid[J]. Journal of the Engineering Mechanics Division, 1961, 87(2): 35-53.
[16]	KLAR A, VORSTER T E B, SOGA K, et al. Soil-pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions[J]. Géotechnique, 2005, 55(6): 461-466.
[17]	张治国, 黄茂松, 王卫东. 层状地基中隧道开挖对临近既有隧道的影响分析[J]. 岩土工程学报, 2009, 31(4): 600-608. http://www.cgejournal.com/cn/article/id/13226 ZHANG Zhiguo, HUANG Maosong, WANG Weidong. Analysis on response of existing tunnels due to adjacent tunneling in multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 600-608. (in Chinese) http://www.cgejournal.com/cn/article/id/13226
[18]	郑刚, 王琦, 邓旭, 等. 不同围护结构变形模式对坑外既有隧道变形影响的对比分析[J]. 岩土工程学报, 2015, 37(7): 1181-1194. doi: 10.11779/CJGE201507003 ZHENG Gang, WANG Qi, DENG Xu, et al. Comparative analysis of influences of different deformation modes of retaining structures on deformation of existing tunnels outside excavations[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1181-1194. (in Chinese) doi: 10.11779/CJGE201507003
[19]	李志高, 刘浩, 刘国彬, 等. 基坑开挖引起下卧隧道位移的实测分析[J]. 地下空间与工程学报, 2005, 1(4): 619-623. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SHTM200509001033.htm LI Zhigao, LIU Hao, LIU Guobin, et al. Influence analysis of deep-dip excavation on down tunnel based on the measured displacement[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(4): 619-623. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SHTM200509001033.htm
[20]	倪雨萍. 基于小应变非线性弹性模型的基坑开挖诱发隧道变形数值模拟[D]. 上海: 同济大学, 2019. NI Yuping. Simulation of Tunnel Deformations Adjacent to Excavation Based on a Small Strain Non-Linear Hypoelastic Model[D]. Shanghai: Tongji University, 2019. (in Chinese)
[21]	POULOS H G, DAVIS E H. Pile Foundation Analysis and design[M]. New York: Wiley, 1980.

施引文献(7)

期刊类型引用(5)

1.	孙海忠. 复杂环境下基坑开挖对邻近设施的影响分析. 建筑施工. 2024(02): 225-228 . 百度学术
2.	吴忠立. 异型深基坑开挖对既有地铁车站的影响研究. 工程技术研究. 2024(05): 28-31 . 百度学术
3.	江名华. 基坑放坡开挖引起下卧地铁隧道隆起变形的模拟分析及应对措施. 四川水泥. 2024(07): 225-227 . 百度学术
4.	刘源，陈仁朋，程红战，吴怀娜，张凯. 门式抗浮框架作用下上方开挖既有盾构隧道响应解析解. 岩土工程学报. 2024(08): 1675-1684 . 本站查看
5.	王荣桥，彭珠辉. 基于有限元模型的共建隧道开挖施工影响分析. 黑龙江交通科技. 2024(08): 139-142 . 百度学术