Displacement laws of grout-water two-phase flow in a rough-walled rock fracture through visualization tests
-
摘要: 富水裂隙岩体中的注浆是一个将浆液压入裂隙内空腔并驱替地下水的过程，开展浆液–水两相流驱替渗流规律研究对优化工程注浆方案具有重要意义。研发了基于粒子图像测速技术（PIV）的可视化驱替试验系统与方法，获取了3D打印的透明粗糙裂隙内的流场分布以及流速与压差的关系；基于有限元法求解Navier-Stokes偏微分方程组模拟驱替过程，与试验测试结果进行了对比验证。结果表明：在恒定流速条件下，注浆压力会随着时间的增加呈现先缓慢增大再加速增大，最终趋于一个定值的演变趋势；浆液首先沿优势渗流通道驱替水，在到达出口后压力增速减缓，随后在较长的时间内逐渐驱替残余水；残余水的分布主要集中在连通主要渗流通道边缘的盲端孔隙和开度大小发生突变的细小孔隙处，具有较低的流速；采用平行平板模型评价具有相同开度的粗糙裂隙中的注浆过程将低估注浆压力达45%。注浆压力是工程注浆中的一个关键控制参数，在理论计算中应充分考虑粗糙度的影响以确定合理的注浆压力，提升注浆效果。Abstract: The grouting in water-rich fractured rock masses is a process in which the pressurized grouts gradually displace the existing water. It is important to thoroughly investigate the grout-water displacement laws for improving the engineering grouting efficiency. In this study, a visualization technique that incorporates the particle image velocimetry (PIV) into the grout-water displacement tests is established, and is used to capture the flow field distribution in a 3D-printed transparent rough-walled fracture along with the flow velocity and hydraulic pressure measurements. The Navier-Stokes equations are solved based on the finite element method to simulate the displacement process, and the simulation is compared with the experimental observations. The results show that under the constant flow rate, the injection pressure first increases gently, followed by a rapid increase stage, and finally approaches a constant value. The grouts preferentially flow through some major channels, and the injection pressure tends to increase gently after the grout reaches the outlet. The residual water is mainly distributed in the dead end close to the edge of main flow channels and the locations where sudden changes in aperture happen. The parallel-plate model can underestimate the injection pressure by up to 45% comparing to the corresponding rough-walled model. It is therefore necessary to consider fracture roughness in the theoretical assessment of grouting pressures to achieve better grouting performance.
-
Keywords:
- rough-walled fracture /
- grouting /
- two-phase flow /
- PIV /
- displacement
-
0. 引言
注浆技术广泛应用于解决裂隙岩体中隧道突涌水、地基渗漏等问题，是增强地下岩土体强度、防止地下工程灾害的有效方法之一。在高放废物地质处置库建设中，注浆是封堵核素可能的运移通道，增强围岩密封性从而控制长期储存中环境污染风险的重要手段之一。地下水普遍存在于天然岩体中，通过注入浆液驱替地下水，从而降低岩体的渗透性，提高其强度是裂隙岩体注浆的首要目的。由于地下深部岩体结构以及所处应力、渗流状态复杂，有必要通过理论分析、基础试验和数值模拟等方法深入探究岩石裂隙中浆液驱替地下水的基本作用机制，为提高地下工程岩体注浆加固效率提供技术支撑[1-4]。
注浆封堵是一个复杂隐蔽的工程，浆液注入岩体后的扩散过程和规律难以直接观察，同时工程中常用注浆材料自身具有时变性、触变性、非线性等复杂多元的特性[5-6]。早期研究受到技术条件的限制，一般将浆液的流体性质进行简化来探究其在裂隙中的渗流扩散规律。如Baker[7]基于牛顿流体的渗流特性建立了裂隙内浆液扩散方程；王渊[8]通过试验研究和数值模拟建立了多孔介质内牛顿流体注浆数值模型；Wrobel[9]提出一种高效计算细通道内牛顿流体平稳流动的算法。近年来的研究逐渐考虑了浆液的非牛顿流体特性，如Amadei等[10]基于光滑裂隙模型，建立了裂隙中Bingham流体的一维瞬态流动数值模型；章敏等[11]在总结分析不同性质流体扩散规律的基础上，讨论了注浆压力和裂隙开度对光滑裂隙内Herschel-Bulkley（H-B）流体渗流扩散特性的影响；Sui等[12]采用室内试验，研究了化学浆液在光滑裂隙中动水条件下的注浆封堵效率。
天然岩石裂隙具有粗糙的表面特征，其中的流体在复杂的裂隙空腔结构内曲折流动，采用光滑的平行平板模型计算裂隙内浆液的渗流扩散特性容易导致较大的偏差[13]，因此学者们在研究中引入了粗糙度的影响。李训刚等[14]建立了岩石粗糙节理面几何模型，基于Navier-Stokes方程分析了粗糙裂隙内浆液渗流特性；熊加路[15]通过室内试验对比分析了不同粗糙度对浆液扩散形态的影响；崔溦等[16]将平行板模型中的流体流动规律扩展到粗糙裂隙，探究了注浆压力以及裂隙面几何特征对流体运动过程的影响; Wang等[17]设计了室内试验装置并研究了浆液在粗糙裂隙中的流动过程。上述研究主要集中于粗糙裂隙内的单相流，未考虑浆液与水两相之间的作用。
针对岩体裂隙内的两相流驱替过程，学者们开展了一些初步的探索，例如，王中才[18]研究了真实多孔介质中两相流驱替过程中压力梯度的变化规律；Zou等[19-20]提出了基于雷诺方程的均质含水饱和裂隙中浆液流动的数值模型，研究了浆液与水黏度比对浆液扩散长度的影响以及裂隙结构特征与水力传导性之间的关系；李昊宸等[21]模拟毛细管内流体在相互驱替时界面运动的全过程，探究了流速与渗透压差之间的关系；张鹏伟等[22]通过建立岩体孔隙模型研究复杂多孔介质中流体流动特性，在单相流的基础上研究了孔隙内两相流动态运动过程。柳崎等[23]运用有限元软件模拟地下流体在多孔介质裂隙中的两相流体渗流，建立了流速和渗透压差之间的关系；Amiri等[24]研究发现对于计算两（多）相流，相场法相较于水平集法更准确省时且适用范围更广。
然而，真实粗糙裂隙内的空腔结构受应力和表面特征的控制，内部渗流难以直接观测，目前尚缺乏对粗糙裂隙内浆液–水两相流驱替规律的高精度数值分析及试验验证。20世纪70年代末发展起来的PIV（particle image velocimetry）技术，能在同一瞬态记录大量空间点上的速度分布信息，并可提供丰富的流场空间结构以及流动特性，近年来在岩土力学和水力学测试中得到了应用。例如，李振亚等[25]在非饱和黏性土冻结过程中结合PIV技术，实现了对冻土图像的采集；姜彤等[26]借助PIV技术，对黄土原状样和重塑样进行劈裂试验，进而研究其结构性和初始干密度对抗拉强度的影响；祁沛垚等[27]基于PIV技术研究了低雷诺数条件下通道内充分发展段的流场特征。然而目前PIV技术尚未在岩石裂隙注浆的研究中得到应用。
针对上述问题，本文首先建立具有真实空腔几何特征的裂隙三维数值模型，采用3D打印技术制作透明裂隙试样；其次开展模拟浆液的非牛顿流体在不同流速条件下的渗流试验，研究裂隙内浆液–水两相流驱替特性；然后利用有限元法进行两相流数值模拟，并将数值结果与试验结果对比验证；最后从流场特征与注浆压力演化相结合的角度分析两相流驱替规律。
1. 试验方法与验证
1.1 粗糙裂隙模型的建立
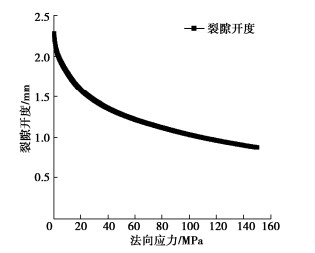
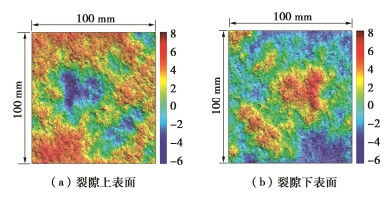
采集中粒花岗岩试样，通过劈裂生成单裂隙。采用分辨率为0.1 μm的高精度光学轮廓仪（Keyence VR）扫描裂隙表面，得到如图 1所示的裂隙表面形貌。该表面的JRC值在15~16之间，代表了较为粗糙的裂隙面。基于MATLAB编制了计算粗糙裂隙表面接触体弹塑性变形破坏过程的程序，在以往研究中已通过与试验结果的对比验证了其计算精度[28-31]。为了得到更复杂的内部空腔结构，将上下表面在水平方向进行2 mm的错位，然后基于该程序，计算裂隙受法向压力至150 MPa的变形破坏过程，得到其平均开度随应力的变化规律，如图 2所示。随着法向应力的增大，裂隙开度逐渐减小，变化速率逐渐降低，符合Barton-Bandis模型的规律。通过该计算得到0~150 MPa之间任意应力作用下裂隙内空腔结构的高精度数值模型。
选取应力为20 MPa时对应的裂隙空腔结构，利用透明的光敏树脂打印材料（VeroClear）基于Object 500 Connex3系统进行3D打印，制作含单裂隙的物理模型，如图 3所示。由于PIV试验中的激光对于被照射物的折射率很敏感，在非光滑的粗糙面上折射后将产生较大偏差。为解决该问题，裂隙模型由一个粗糙面和一个光滑的平面构成，渗流图像由光滑面采集。因此，该模型可视作沿裂隙中间面剖开的半空间模型。
1.2 驱替试验
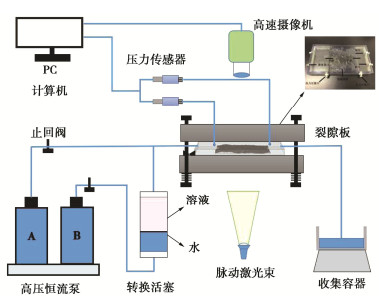
试验系统主要由注液系统、PIV测试系统、数据采集系统组成，包括ISCO柱塞泵（ISCO 260D）、高精度压力计（Keller PR-41X）、高速相机等仪器，如图 4所示。将3D打印模型固定在试验台上，裂隙光滑一面向上，粗糙一面向下放置，高速相机放置在模型上方连续拍摄，激光由模型侧面射入并保持与裂隙面平行。模型两端分别连接注水管和出水管，模型侧壁连接两个压力传感器测量入口和出口间的压力差，出水管末端连接收集容器。试验前，将模型裂隙中充满水并排除气泡，保证裂隙内处于饱和状态；试验开始后通过柱塞泵将模拟浆液以恒定的流速注入到裂隙模型中，此时非牛顿流体（浆液）作为入侵相，水作为被驱替相产生两相流；数据采集系统连续采集驱替过程中的图像和出入口压力的变化值。改变流速重复上述试验过程，得到不同流速下的测试结果。
开展两组驱替试验，第一组试验周期较短，主要用于拍摄裂隙模型内的流场特征，在主要流路中的驱替完成后即停止；第二组为了与平行平板模型进行对比，选取1.67×10-8，3.33×10-8，6.66×10-8 m3/s 3种不同的入口流量进行了较长时间的测试，直到压力完全稳定为止，每个试验的具体时长与流速相关。
采用水溶性高分子化合物聚丙烯酸钠质量分数为0.2%的溶液模拟浆液的行为，该溶液具有显著的剪切稀化特征，符合浆液的非牛顿流体特性。采用旋转流变仪测量溶液的动力黏度等基本参数用于数值模拟。在溶液中加上质量浓度为0.1 g/mL，直径为7 μm的荧光颗粒，在激光照射下这些颗粒的轨迹可被高速相机捕捉，从而获取裂隙内的流场信息。
1.3 基于平行平板模型的试验方法验证
采用光滑的平行平板模型对试样制作及测试设备的可靠性和精度进行验证。对于黏性的不可压缩流体，平行平板内的流量与压力梯度线性相关，符合下式所示的立方定律：
Q=−we3h12μ∇P， (1) 式中，Q为流量，eh为等效水力开度，μ为动力黏滞系数，∇P为压力梯度，w为裂隙宽度。
通过3D打印制作力学开度为1.12 mm的平行平板模型，密封两侧并开展一系列流速条件下的渗流试验；采用纯净水作为流体，黏度为1.03×10-3 Pa·s。将试验测得的入口流量和出入口压力差代入立方定律，计算得到等效水力开度和雷诺数Re，如表 1所示。
表 1 平行平板模型渗流测试结果Table 1. Hydraulic testing results of a parallel-plate modelQ △P eh Re /(m3·s-1) /Pa /mm 8.33×10-9 0.70 1.14 0.09 3.33×10-8 3.00 1.11 0.34 6.66×10-8 7.00 1.06 0.69 9.99×10-8 9.00 1.11 1.03 1.33×10-7 12.00 1.11 1.37 1.67×10-7 16.00 1.09 1.72 3.33×10-7 31.00 1.10 3.43 平均值 1.11 试验测得的平均等效水力开度与模型设计的力学开度吻合性较好，相对误差小于1%。这一结果验证了本研究所采用的试验方法，包括3D打印试样制作、传感器校正、试验流程等的可靠性。
2. 数值模型
根据图 2所示的平均开度与法向应力的关系，选取平均力学开度为1.54 mm条件下的裂隙内部空腔结构点云数据，在COMSOL中进行数值建模，得到三维粗糙裂隙数值模型，如图 5所示，图中白色部分为接触面。模型尺寸大小为98 mm×98 mm，采样点距为0.5 mm，点与点之间再划分10个以上的三角形单元，保证求解的精度。为了与试验直接对比，数值模型也将构成裂隙的其中一个表面换成光滑的平面，在保持平均开度不变的情况下建立半空间模型。
![]()
图 5 法向应力作用下的三维粗糙裂隙数值模型Figure 5. Numerical model of a 3D rough-walled fracture subject to a normal stress采用COMSOL Multiphysics模拟驱替过程，该软件以有限元法为基础，通过求解偏微分方程（单场）或偏微分方程组（多场）来实现对物理现象的模拟[32]。采用层流（spf）接口求解质量守恒的连续方程以及动量守恒的Navier-Stokes方程组计算渗流，同时采用相场接口模拟非混溶两相流的流体流动。
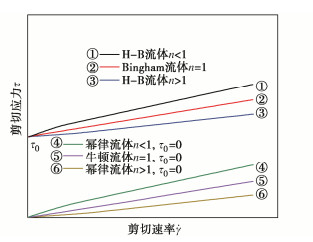
以往研究根据流体的剪切速率和剪切力构建了一系列浆液扩散的本构方程，用于描述不同性质的流体，如牛顿流体、幂律流体、Bingham流体、H-B流体等，其基本特征如图 6所示。
在数值计算中，Herschel-Bulkley-Papanastasiou（HBP）模型可以较好地描述浆液等H-B流体的渗流特性，其在一般情况下（τ0≠0）的本构方程为[33]
˙γ=0(τ<τ0) ，τ=τ0[1−exp(−m˙γ)]+k˙γn(τ≥τ0) ，} (2) 式中，τ0为屈服应力，k为稠度系数，n为流变指数，˙γ为剪应变率，m为流体一致性系数。
本研究配置的溶液为典型的H-B流体，可基于流变仪的测试结果拟合得到流体的基本参数，其中屈服应力τ0为0.689 N/m³，流体稠度系数k为0.961 kg/(m·s)，流动特性指数n为0.412。将模型中两个相对的边界分别设置为入口和出口，忽略岩石基质的渗透性，将其余边界设定为非透水边界。在入口边界上设定恒定的流量Q，设置出口压力为0 Pa。在COMSOL中求解HBP本构方程，得到出入口的压差以及内部相场的分布。数值模拟参数见表 2。
表 2 数值模拟参数表Table 2. Parameters used in numerical simulation参数 表达式（单位） 取值 密度 ρ/(kg·m-3) 987.1 重力加速度 g/(m·s-2) 9.81 力学开度 em/mm 1.54 入口流量 Q/(m3·s-1) 1.67×10−8，3.33×10-8， 6.66×10−8，9.99×10-8， 1.33×10−7，1.67×10-7 Re 0.168，0.337，
0.675，1.013，1.35，1.69 3. 结果与分析
3.1 流场图对比分析
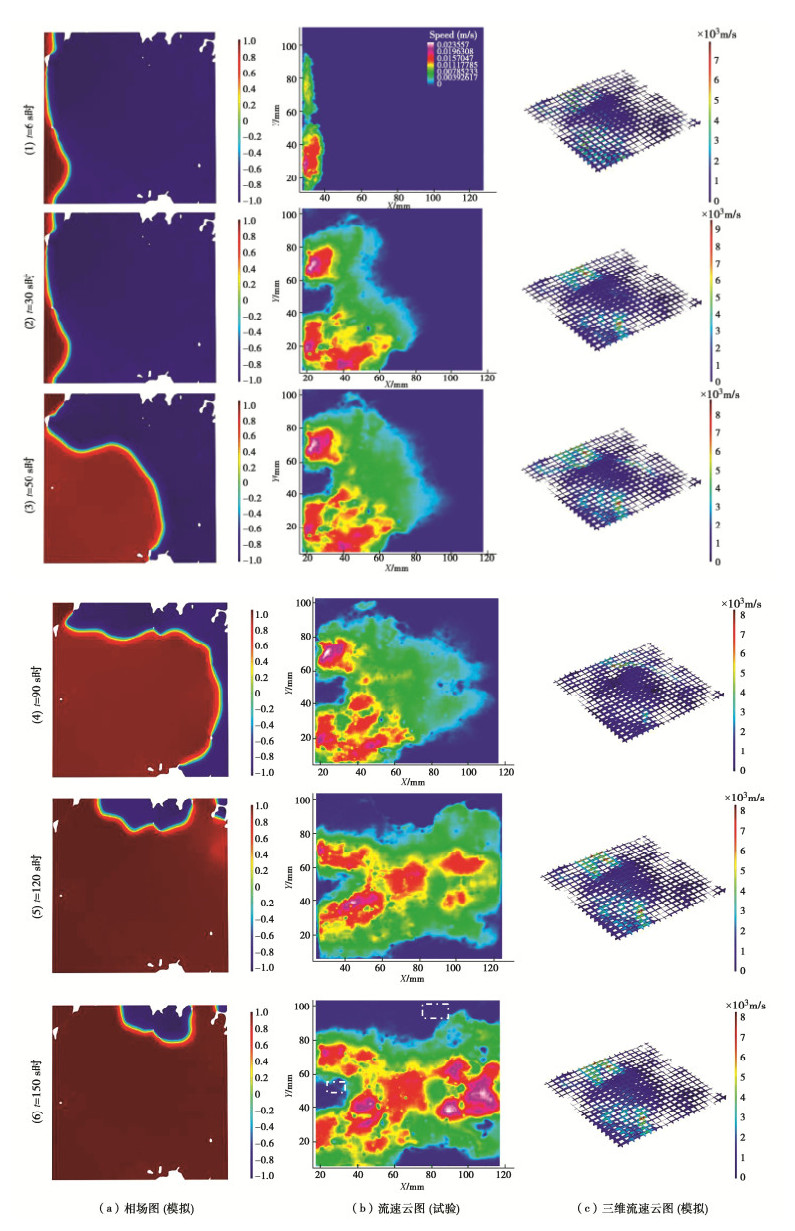
图 7为流量1.67×10-7 m3/s条件下粗糙裂隙模型中的驱替过程，包括了PIV测试与数值模拟结果的对比。图中蓝色代表水，其他颜色代表浆液，颜色越偏红色代表流速越大。由图 7可见，注浆开始后，浆液沿着入口附近两处主要的通道（红色区域）流入，局部开度较小处出现较大的流速。初始驱替前缘形状为弧形，其凹凸性受局部空腔结构的控制；随着驱替的进行，凸型前缘向平稳型前缘转化；浆液会优先选择开度较大的优势通道流动，表现出显著的沟槽流特征；一些空腔在较长时间内无法被入侵，成为残余水的赋存空间。统计各个时间点上的最大和最小流速，发现：当t=6 s时，vmax= 6.9×10-3 m/s，vmin=1.1×10-3 m/s；当t=18 s时，vmax=7.7×10-3 m/s，vmin=1.3×10-3 m/s；当t=125 s时，vmax=2.4×10-2 m/s，vmin=3.9×10-3 m/s。最大和最小流速随时间呈逐渐上升的趋势，说明浆液进入复杂空腔结构后局部的流速整体提升，当t=150 s时，vmax=2.2×10-2 m/s，vmin=3.6×10-3 m/s，流速趋于稳定，表明裂隙内主要通道内的水被驱替。
相比流场图，数值模拟得到的相场图在局部，特别是靠近两侧边界的位置显示出更多的浆液侵入。这是因为PIV试验（图 7（b））得到的是流速的分布，一旦驱替完成，流场趋于静止，则不再显示，而数值模拟（图 7（a））展示的是相场图，反映的是两相流体的分布特征。图 7中时序（5）和（6）对应图两侧的差异显示这些部分流速较低，优势渗流通道集中在裂隙中间的部分。结合相场图和流场图可以看出，残余水主要集中在两种结构中：一是连通主要渗流通道边缘的盲端空腔（静水区，图 7（b）中白色虚线框所示处），这类空腔往往不具备完整的流通出口或在压力传导的方向上不具备流动优势；第二类残余水分布于裂隙开度大小发生突变的细小空腔处，水在通过窄小孔道时受到附加阻力产生滞留，如图 7（b）中的入口附近产生的静水区。在图 7（c）中，开度较大的位置横截面的厚度也较大，如每张图的中间部分。可以看出，开度较小的位置，局部流速较大（红色代表较大的流速）。图 7（c）展示的三维流速分布与PIV测试结果在优势渗流通道上具有较好的一致性。
3.2 压力短期演变规律
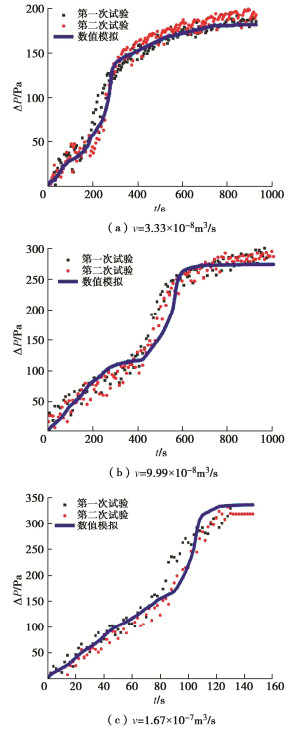
由于驱替过程中的两相流难以用一个渗透系数统一描述，这里统计恒定流速条件下出入口压力差即注浆压力随时间的演化来反映裂隙内的两相渗流特性，如图 8所示。与之类似，在工程注浆中，如采用恒流模式，一般也通过监测注入压力来反映浆液的渗流和扩散情况。每种条件下开展两次测试以确保数据的可靠度。图 8中展示了3种流速的测试结果，这里以入口流速为1.67×10-7 m3/s为例进行说明。可见，压差随着时间呈非线性增大的趋势，且整条曲线可分为3个阶段，第一阶段为初始增压阶段（0 < t < 90 s），第二阶段为快速增压阶段（90 < t < 120 s），第三阶段为稳定增压阶段（t > 120 s），各自特征如下：
（1）初始增压阶段：在注浆开始后，浆液首先沿着阻力较小的通道（优势通道）驱替水，同时带动其他低流速区域驱动水流向出口，此时压力以一个较缓且较为恒定的速率上升。
（2）快速增压阶段：在浆液充分侵入优势通道并达到出口边界后（见图 7），逐渐向开度较小的低流速区域扩展，此时需要更大的压力才能驱替出较小空腔中的水，因此压力曲线迅速变陡。
（3）稳定增压阶段：在浆液驱替出大部分的水后，压力和流场逐渐进入稳定阶段，此时仅有静水区内少许的残余水被逐渐驱替。在流速较大的情况下，压力迅速趋于稳定，而流速较小的情况下，则需要一个较长的过程来驱替残余水。
3.3 压力全周期演变规律
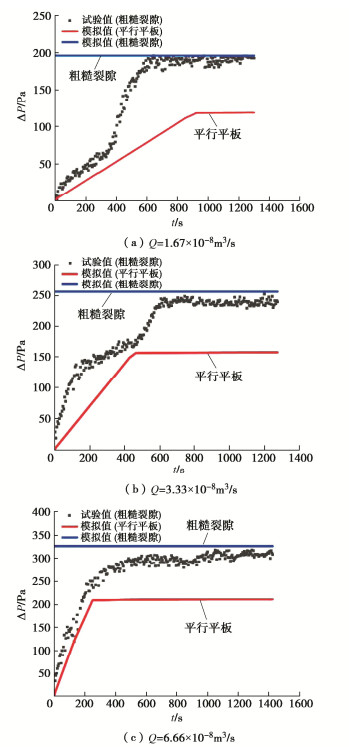
由图 8可以看出，进入稳定增压阶段后，压差随着时间仍然保持较小的上升趋势。为了掌握该阶段的长期发展规律，选取3种较低的流速进行长周期试验，并与稳态条件下的数值模拟结果进行对比，如图 9所示。图中蓝线代表粗糙裂隙稳态数值模拟结果，此时不考虑驱替，仅计算浆液充满裂隙的渗流，因此压力为一个定值。可见，只要注入浆液的时间足够长，最终压差会趋于一个稳定值，该值与稳态数值模拟得到的压差相吻合，说明此时裂隙内的水已经完全被浆液所驱替；流速越大，达到稳定值也越快。为了定量研究裂隙粗糙表面对注浆过程的影响，将试验结果与基于平行平板模型（平板开度等于粗糙裂隙的平均开度）的两相流数值计算结果进行了对比，如图中红色曲线所示。结果表明在增压阶段，基于平行平板模型的压差增量是关于时间的线性函数，这与试验压差在发展规律上有较大的偏差，并在压力稳定后的最终压差上差别较大。流速越大，两者的相对偏差逐渐减小。
![]()
图 8 短期驱替过程中压差随时间的演变规律Figure 8. Evolution of pressure difference during short-term displacement tests![]()
图 9 长期驱替过程中压差随时间的演变规律Figure 9. Evolution of pressure difference during long-term.displacement与牛顿流体渗流一致，由于粗糙度的影响，粗糙裂隙的有效渗透系数一般低于相应的平行平板模型，因此在恒定流速条件下需要更大的压力来驱动流体。目前在岩石注浆工程实践中，仍经常采用基于平行平板模型的解析解对浆液流动过程进行预测。本文结果表明，采用平行平板模型将高估浆液的扩散长度或大幅低估注浆压力（> 45%，其中偏差值=（平行平板模拟值-粗糙裂隙模拟值）/粗糙裂隙模拟值），从而对注浆效果评估造成较大偏差。同时，如图 9所示，流速较大时曲线的转折点更接近平行平板的预测值，表明在一定的流速范围内（如Re数接近1时）平行平板模型有可能预测上节所述第二阶段驱替的结束时间。另一方面，在富水条件下的注浆作业往往选取早凝浆液，因此在驱替的早期阶段浆液即开始逐渐凝固，容易导致残余水的滞留。如何优化注浆手段以有效排除残余水尚需进一步的试验论证。
4. 结论
基于扫描的天然岩石裂隙面形貌数据和弹塑性接触模型计算生成具有复杂空腔结构的三维裂隙模型，开展不同流速条件下的浆液-水两相流驱替可视化试验和数值模拟，研究浆液在饱和粗糙裂隙中的驱替特性，并通过试验与数值计算结果的对比定量分析了整个驱替过程中的压力演化规律。主要结论如下：
（1）将3D打印与粒子图像测速技术相结合，获取了真实粗糙裂隙内两相流驱替过程中的高精度流场分布，为裂隙岩体注浆测试技术提供了新思路。
（2）浆液首先驱替开度较大、连通较好的通道中的水并形成优势驱替通道，驱替前缘呈弧形，并受局部空腔结构特征的影响；在连通主要渗流通道边缘的盲端和开度发生突变的细小空腔处容易产生残余水。
（3）驱替过程中，注浆压力会随时间的增加呈先先缓慢增大再加速增大，最终逐渐趋于一个稳定值的演化规律；最终压力值与稳态计算得到的压力值一致。
（4）裂隙表面粗糙度对注浆过程和注浆压力影响较大，采用传统的平行平板模型将低估注浆压力达45%以上（针对JRC=15~16的表面），从而对注浆效果评估带来较大偏差。
注浆压力是影响注浆效果的重要因素之一，对于动水条件下的裂隙岩体，若注浆压力不足，注入的浆液在尚未固化时可能被水冲走；对于早凝型注浆材料，若注浆压力不足，则浆液尚未达到有效位置即开始凝固，导致注浆加固达不到预期效果。本研究的计算表明，大流量注浆有利于快速驱除残余水，然而同时也将导致注浆压力的迅速升高，容易撑开裂隙，增大注浆成本和工程风险。今后将测试具有不同流动和凝固特性的浆液，并注入具有不同粗糙度的裂隙研究其驱替特性，促进工程注浆的精细化控制。
-
![]()
图 5 法向应力作用下的三维粗糙裂隙数值模型
Figure 5. Numerical model of a 3D rough-walled fracture subject to a normal stress
![]()
图 8 短期驱替过程中压差随时间的演变规律
Figure 8. Evolution of pressure difference during short-term displacement tests
![]()
图 9 长期驱替过程中压差随时间的演变规律
Figure 9. Evolution of pressure difference during long-term.displacement
表 1 平行平板模型渗流测试结果
Table 1 Hydraulic testing results of a parallel-plate model
Q △P eh Re /(m3·s-1) /Pa /mm 8.33×10-9 0.70 1.14 0.09 3.33×10-8 3.00 1.11 0.34 6.66×10-8 7.00 1.06 0.69 9.99×10-8 9.00 1.11 1.03 1.33×10-7 12.00 1.11 1.37 1.67×10-7 16.00 1.09 1.72 3.33×10-7 31.00 1.10 3.43 平均值 1.11 
下载: 导出CSV
表 2 数值模拟参数表
Table 2 Parameters used in numerical simulation
参数 表达式（单位） 取值 密度 ρ/(kg·m-3) 987.1 重力加速度 g/(m·s-2) 9.81 力学开度 em/mm 1.54 入口流量 Q/(m3·s-1) 1.67×10−8，3.33×10-8， 6.66×10−8，9.99×10-8， 1.33×10−7，1.67×10-7 Re 0.168，0.337，
0.675，1.013，1.35，1.69
下载: 导出CSV
-
[1] 熊峰, 姜清辉, 陈胜云, 等. 裂隙–孔隙双重介质Darcy-Forchheimer耦合流动模拟方法及工程应用[J]. 岩土工程学报, 2021, 43(11): 2037–2045. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111012.htm XIONG Feng, JIANG Qing-hui, CHEN Sheng-yun, et al. Modeling of coupled Darcy-Forchheimer flow in fractured porous media and its engineering application[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2037–2045. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111012.htm
[2] STILLE H. Rock Grouting-Theories and Applications[M]. Stockholm: BeFo, Rock Engineering Research Foundation, 2015.
[3] HÄSSLER L, HÅKANSSON U, STILLE H. Computer-simulated flow of grouts in jointed rock[J]. Tunnelling and Underground Space Technology, 1992, 7(4): 441–446. doi: 10.1016/0886-7798(92)90074-R
[4] ERIKSSON M, STILLE H, ANDERSSON J. Numerical calculations for prediction of grout spread with account for filtration and varying aperture[J]. Tunnelling and Underground Space Technology, 2000, 15(4): 353–364. doi: 10.1016/S0886-7798(01)00004-9
[5] HÅKANSSON U, HÄSSLER L, STILLE H. Rheological properties of microfine cement grouts[J]. Tunnelling and Underground Space Technology, 1992, 7(4): 453–458. doi: 10.1016/0886-7798(92)90076-T
[6] HÅKANSSON U. Rheology of Fresh Cement Based Grouts[D]. Stockholm: Royal Institute of Technology, Sweden, 1993.
[7] BAKER C. Comments on Paper Rock Stabilization in Rock Mechanics[M]. New York: Springer-Verlag NY, 1974: 22–57.
[8] 王渊. 基于多孔介质迂曲度的牛顿流体渗透注浆机制研究[D]. 昆明: 昆明理工大学, 2020. WANG Yuan. Study on Newtonian Fluid Infiltration Grouting Mechanism Based on Tortuosity of Porous Media[D]. Kunming: Kunming University of Science and Technology, 2020. (in Chinese)
[9] WROBEL M. An efficient algorithm of solution for the flow of generalized Newtonian fluid in channels of simple geometries[J]. Rheologica Acta, 2020, 59(9): 651–663. doi: 10.1007/s00397-020-01228-2
[10] AMADEI B, SAVAGE W Z. An analytical solution for transient flow of Bingham viscoplastic materials in rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(2): 285–296. doi: 10.1016/S1365-1609(00)00080-0
[11] 章敏, 王星华, 汪优. Herschel-Bulkley浆液在裂隙中的扩散规律研究[J]. 岩土工程学报, 2011, 33(5): 815–820. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201105028.htm ZHANG Min, WANG Xing-hua, WANG You. Diffusion of Herschel-Bulkley slurry in fractures[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 815–820. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201105028.htm
[12] SUI W H, LIU J Y, HU W, et al. Experimental investigation on sealing efficiency of chemical grouting in rock fracture with flowing water[J]. Tunnelling and Underground Space Technology, 2015, 50(22): 239–249. http://www.researchgate.net/profile/Jinyuan_Liu/publication/281101597_Experimental_investigation_on_sealing_efficiency_of_chemical_grouting_in_rock_fracture_with_flowing_water/links/5650ed3b08aefe619b1563cc.pdf
[13] 李博, 蒋宇静. 岩石单节理面剪切与渗流特性的试验研究与数值分析[J]. 岩石力学与工程学报, 2008, 27(12): 2431–2439. doi: 10.3321/j.issn:1000-6915.2008.12.007 LI Bo, JIANG Yu-jing. Experimental study and numerical analysis of shear and flow behaviors of rock with single joint[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(12): 2431–2439. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.12.007
[14] 李训刚, 唐超, 张帅, 等. 基于纳米材料的水泥浆液粗糙裂隙注浆数值模拟[J]. 矿业研究与开发, 2021, 41(6): 66–71. https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202106013.htm LI Xun-gang, TANG Chao, ZHANG Shuai, et al. Numerical simulation of cement slurry grouting in rough cracks based on nano-materials[J]. Mining Research and Development, 2021, 41(6): 66–71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202106013.htm
[15] 熊加路. 考虑岩体裂隙粗糙度的动水注浆模拟试验[D]. 徐州: 中国矿业大学, 2017. XIONG Jia-lu. Experimental Investigation on Grouting into Rock Fracture with Flowing Water by Considering its Roughness[D]. Xuzhou: China University of Mining and Technology, 2017. (in Chinese)
[16] 崔溦, 王利新, 江志安, 等. 基于修正立方定律的岩体粗糙裂隙网络注浆过程模拟研究[J]. 岩土力学, 2021, 42(8): 2250–2258. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108020.htm CUI Wei, WANG Li-xin, JIANG Zhi-an, et al. Numerical simulation of grouting process in rock mass with rough fracture network based on corrected cubic law[J]. Rock and Soil Mechanics, 2021, 42(8): 2250–2258. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108020.htm
[17] WANG X C, XIAO F, ZHANG Q S, et al. Grouting characteristics in rock fractures with rough surfaces: apparatus design and experimental study[J]. Measurement, 2021, 184: 109870. doi: 10.1016/j.measurement.2021.109870
[18] 王中才. 微尺度毛细管中不相溶两相驱替特性的实验研究[D]. 武汉: 武汉大学, 2011. WANG Zhong-cai. Experimental Studies on the Characteristics of Immiscible Displacements in Microscale Quartz Capillaries[D]. Wuhan: Wuhan University, 2011. (in Chinese)
[19] ZOU L C, HÅKANSSON U, CVETKOVIC V. Cement grout propagation in two-dimensional fracture networks: impact of structure and hydraulic variability[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 115: 1–10. doi: 10.1016/j.ijrmms.2019.01.004
[20] ZOU L C, HÅKANSSON U, CVETKOVIC V. Two-phase cement grout propagation in homogeneous water-saturated rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 106: 243–249. doi: 10.1016/j.ijrmms.2018.04.017
[21] 李昊宸, 马智, 郭同翠, 等. 毛细管内两相流体驱替规律研究[J]. 科学技术与工程, 2015, 15(36): 155–158, 178. doi: 10.3969/j.issn.1671-1815.2015.36.026 LI Hao-chen, MA Zhi, GUO Tong-cui, et al. The new study of two-phase fluid displacement model[J]. Science Technology and Engineering, 2015, 15(36): 155–158, 178. (in Chinese) doi: 10.3969/j.issn.1671-1815.2015.36.026
[22] 张鹏伟, 胡黎明, MEEGODA J N, 等. 基于岩土介质三维孔隙结构的两相流模型[J]. 岩土工程学报, 2020, 42(1): 37–45. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001008.htm ZHANG Peng-wei, HU Li-ming, MEEGODA J N, et al. Two-phase flow model based on 3D pore structure of geomaterials[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 37–45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001008.htm
[23] 柳崎, 索丽敏. 地下岩体内多孔介质中裂隙流运移过程的COMSOL Multiphysics仿真模拟[J]. 系统仿真技术, 2019, 15(3): 184–187, 197. doi: 10.3969/j.issn.1673-1964.2019.03.005 LIU Qi, SUO Li-min. COMSOL multiphysics simulation of fracture flow migration in porous media in underground rock mass[J]. System Simulation Technology, 2019, 15(3): 184–187, 197. (in Chinese) doi: 10.3969/j.issn.1673-1964.2019.03.005
[24] AKHLAGHI AMIRI H A, HAMOUDA A A. Evaluation of level set and phase field methods in modeling two phase flow with viscosity contrast through dual-permeability porous medium[J]. International Journal of Multiphase Flow, 2013, 52(3): 22–34. http://www.onacademic.com/detail/journal_1000036079789310_b9af.html
[25] 刘振亚, 刘建坤, 李旭, 等. PIV技术在非饱和冻土冻胀模型试验中的实现与灰度相关性分析[J]. 岩土工程学报, 2018, 40(2): 313–320. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802015.htm LIU Zhen-ya, LIU Jian-kun, LI Xu, et al. Application of PIV in model tests on frozen unsaturated soils and grayscale correlation analysis[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 313–320. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802015.htm
[26] 姜彤, 翟天雅, 张俊然, 等. 基于粒子图像测速技术的黄土径向劈裂试验研究[J]. 岩土力学, 2021, 42(8): 2120–2126, 2140. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108008.htm JIANG Tong, ZHAI Tian-ya, ZHANG Jun-ran, et al. Diametric splitting tests on loess based on particle image velocimetry technique[J]. Rock and Soil Mechanics, 2021, 42(8): 2120–2126, 2140. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202108008.htm
[27] 祁沛垚, 邓坚, 谭思超, 等. 基于PIV技术的低雷诺数下棒束通道流场研究[J]. 核动力工程, 2021, 42(1): 18–22. https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG202101006.htm QI Pei-yao, DENG Jian, TAN Si-chao, et al. Research on flow field in rod bundle channel under low Reynolds number using PIV technique[J]. Nuclear Power Engineering, 2021, 42(1): 18–22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG202101006.htm
[28] 莫洋洋. 法向应力作用下粗糙岩石裂隙变形行为研究[D]. 绍兴: 绍兴文理学院, 2020. MO Yang-yang. Study on Deformation Behavior of Rough-Walled Rock Fracture Subject to Normal Stress[D]. Shaoxing: Shaoxing University, 2020. (in Chinese)
[29] 李博, 崔逍峰, 莫洋洋, 等. 法向应力作用下砂岩错位裂隙变形行为研究[J]. 岩土力学, 2021, 42(7): 1850–1860. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202107010.htm LI Bo, CUI Xiao-feng, MO Yang-yang, et al. Deformation behavior of dislocated sandstone fractures subject to normal stresses[J]. Rock and Soil Mechanics, 2021, 42(7): 1850–1860. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202107010.htm
[30] ZOU L C, LI B, MO Y Y, et al. A high-resolution contact analysis of rough-walled crystalline rock fractures subject to normal stress[J]. Rock Mechanics and Rock Engineering, 2020, 53(5): 2141–2155. doi: 10.1007/s00603-019-02034-w
[31] LI B, ZHAO Z H, JIANG Y J, et al. Contact mechanism of a rock fracture subjected to normal loading and its impact on fast closure behavior during initial stage of fluid flow experiment[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(13): 1431–1449. doi: 10.1002/nag.2365
[32] 陈如梦. 粗糙岩石裂隙中非牛顿流体非线性渗流规律研究[D]. 绍兴: 绍兴文理学院, 2021. CHEN Ru-meng. Study on Nonlinear Seepage Law of Non Newtonian Fluid in Rough Rock Fractures[D]. Shaoxing: Shaoxing University, 2021. (in Chinese)
[33] MITSOULIS E. Numerical simulation of calendering viscoplastic fluids[J]. Journal of Non-Newtonian Fluid Mechanics, 2008, 154(2/3): 77–88. http://www.onacademic.com/detail/journal_1000034089822310_4cc8.html
-
期刊类型引用(10)
1. 张翔，陈莹，雷真，范翔，赵彦淇. 高温冷热循环对花岗岩物理力学性能的影响. 科学技术与工程. 2025(02): 737-752 . 
百度学术
2. 翟明磊，李振华，杜锋，白海波，王文强. 考虑浆液渗流–岩体变形耦合作用的裂隙注浆模拟试验系统研制与应用. 岩石力学与工程学报. 2024(04): 878-889 . 百度学术
3. 周新，盛建龙，叶祖洋. 基于LBM的粗糙裂隙内两相驱替渗流特性模拟研究. 力学学报. 2024(05): 1475-1487 . 百度学术
4. 崔溦，裴介渲，江志安. 动水作用下岩体裂隙中颗粒运动规律的试验研究. 岩土力学. 2024(10): 2870-2878 . 百度学术
5. 罗涛，黄正濛，李兵磊，刘谦，刘辉，陈志强. 含二维和三维预制裂隙的脆性岩石试样的破坏特征数值验证. 南昌大学学报(工科版). 2024(03): 345-350 . 百度学术
6. 孙强，高千，张玉良，胡建军，耿济世，周书涛，袁士豪. 干热岩开发中高温水-岩作用下岩石应力腐蚀及多场损伤问题. 地球科学与环境学报. 2023(03): 460-473 . 百度学术
7. 张乐 ，杨志兵 ，李东奇 ，陈益峰 . 浆液在透明复制裂隙中驱替行为的可视化试验研究. 岩土力学. 2023(06): 1708-1718 . 百度学术
8. 孔德森，赵明凯，时健，滕森. 基于分形维数特征的岩石介质气-水相对渗透率预测模型研究. 岩土工程学报. 2023(07): 1421-1429 . 本站查看
9. 吕鑫，杨科，方珏静，段敏克，王于，张寨男. 采空区破碎岩体负压注浆加固试验研究与机制分析. 岩石力学与工程学报. 2023(S2): 4174-4188 . 百度学术
10. 李奔，刘汉乐，李培华，程锡治，王清，黄仕龙，刘新宇，金明哲. 碳酸盐岩石裂隙中DNAPL污染物迁移过程的电阻率成像. 地球物理学进展. 2023(06): 2704-2713 . 百度学术
其他类型引用(6)
计量
- 文章访问数: 289
- HTML全文浏览量: 58
- PDF下载量: 113
- 被引次数: 16
