狭窄河谷面板堆石坝坝体底部应力拱效应的形成机理及影响范围研究

杨超; 薛海斌; 党发宁; 王辉

doi:10.11779/CJGE2021S1039

狭窄河谷面板堆石坝坝体底部应力拱效应的形成机理及影响范围研究 English Version

杨超^1,,
薛海斌^{2, 3, ,},
党发宁²,
王辉¹

1.
北方民族大学土木工程学院,甘肃　银川　750021
2.
西安理工大学西北旱区生态水利国家重点试验室,陕西　西安　710048
3.
陕西省水利电力勘测设计研究院,陕西　西安　710001

基金项目:

北方民族大学校级重点科研项目 2019KJ33

宁夏回族自治区重点研发项目（引才专项） 2019BEB04035

北方民族大学科研启动项目

国家自然科学基金项目 51979225

详细信息

作者简介:
杨超（1987— ）,男,博士,讲师,主要从事岩土工程数值计算方面的研究。E-mail：yckevin5.163.com

通讯作者:
薛海斌, E-mail：xhbyts2013@163.com

中图分类号: TV641.4
计量
- 文章访问数: 185
- HTML全文浏览量: 24
- PDF下载量: 59
出版历程
- 收稿日期: 2020-12-14
- 网络出版日期: 2022-12-05
- 刊出日期: 2021-06-30

Mechanism and influence range of stress arching effect of CFRD in narrow valley regions

1.
School of Civil Engineering, North Minzu University, Yinchuan 750021, China
2.
State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi'an University of Technology, Xi'an 710048, China
3.
Shaanxi Province Water Conservancy and Electric Power Survey and Design Institute, Xi'an 710001, China

摘要

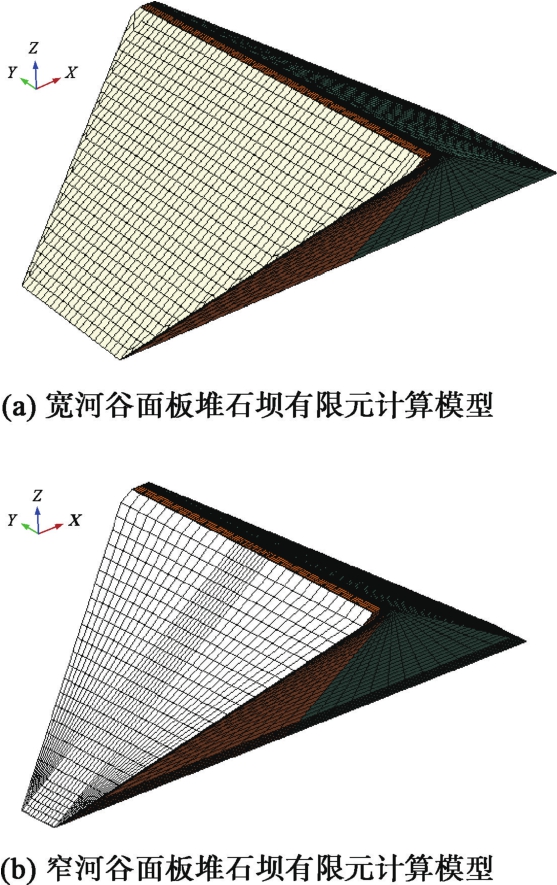
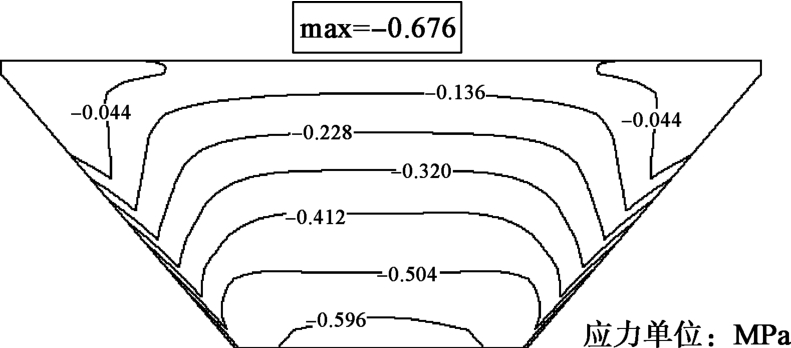
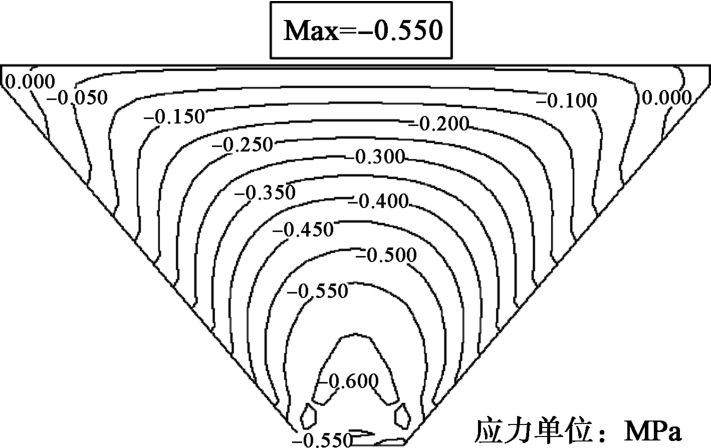
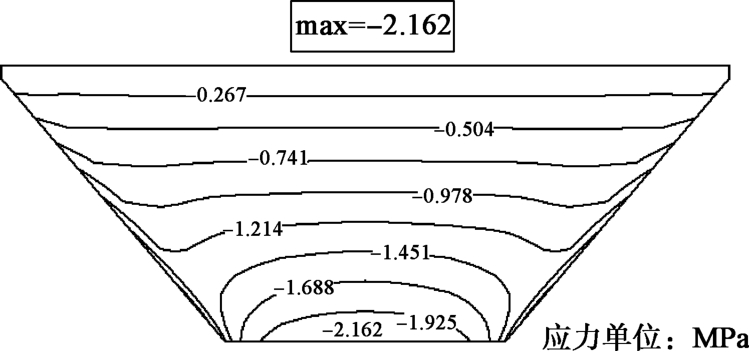
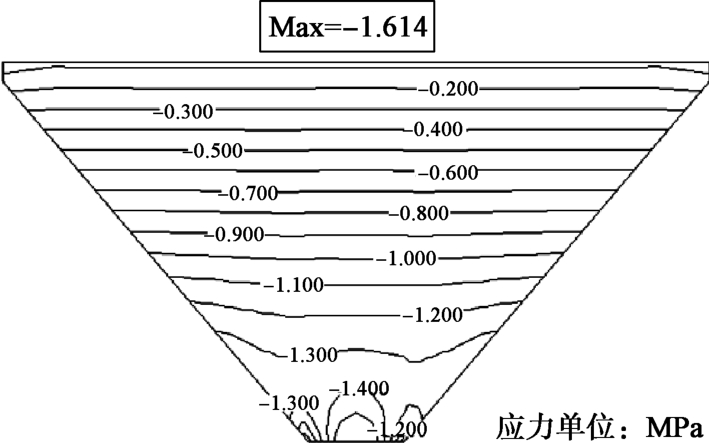
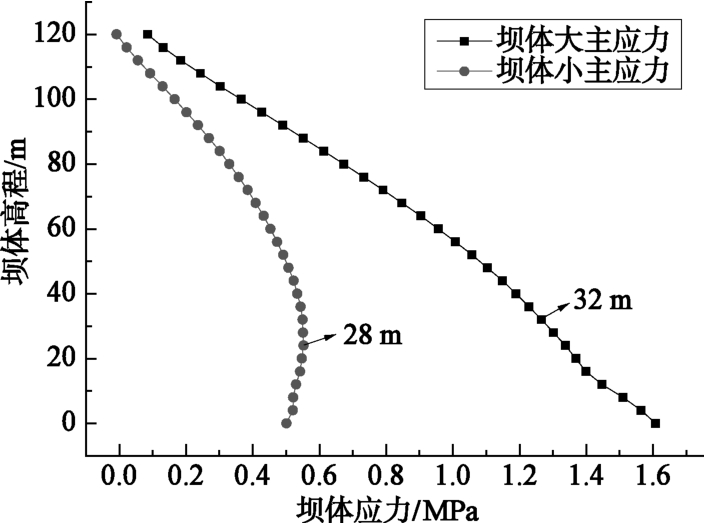
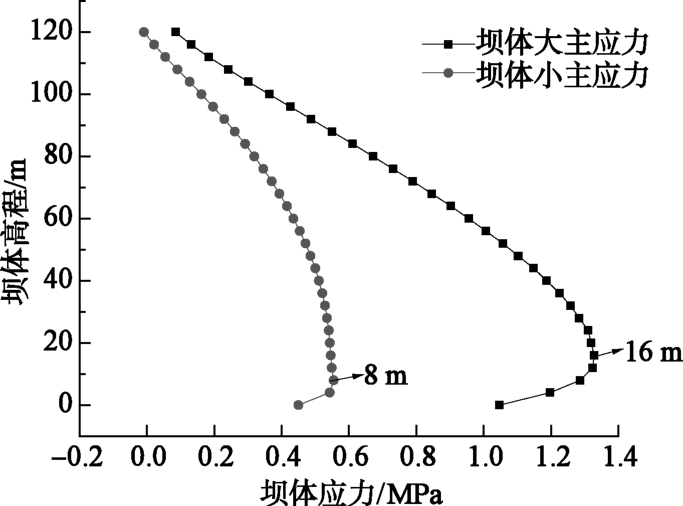
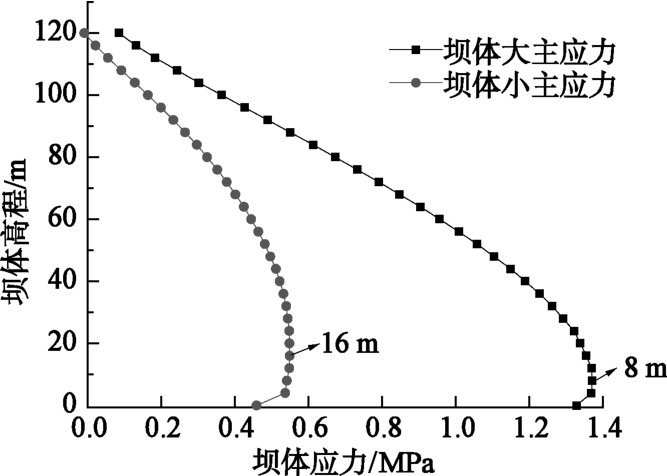
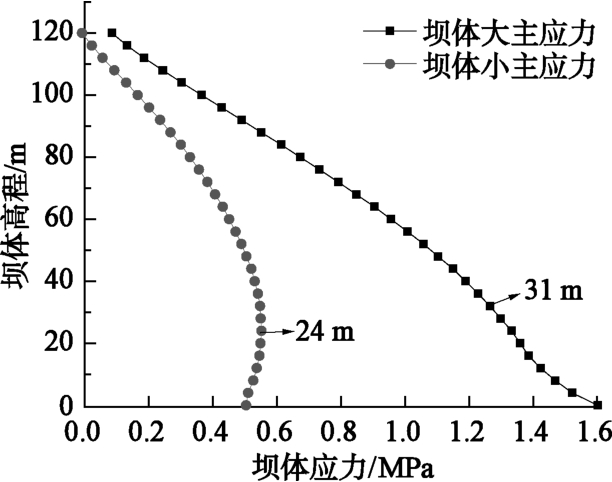
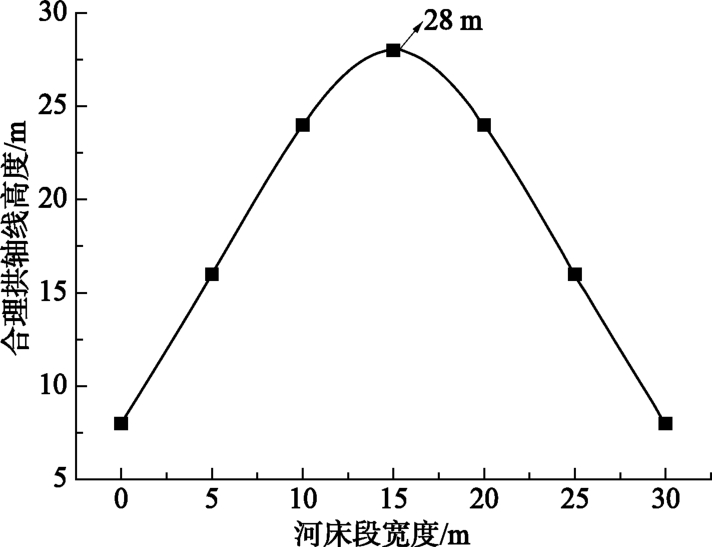
摘要: 受狭窄河谷地形的影响,峡谷地区修建的面板堆石坝工程会在跨河方向上出现应力拱效应问题,造成坝体底部堆石体难以被充分碾压密实,大坝蓄水后沉降变形增大,危及大坝安全。从应力拱效应的形成条件出发,分析峡谷地区面板堆石坝在跨河方向上应力拱效应的形成条件。采用有限元数值模拟方法,通过对比分析宽、窄河谷中面板堆石坝大、小主应力的大小及分布规律,揭示峡谷地区面板堆石坝坝体内部应力拱效应的形成机理。研究了峡谷地区面板坝坝体底部应力拱效应合理拱轴线的分布形态及范围,在河谷中心处的坝体底部堆石体受到应力拱效应的影响最大,影响范围约占坝体整体高度的23%。研究成果为采用工程措施减弱应力拱效应对面板堆石坝的不利影响提供参考依据。
- 狭窄河谷 /
- 面板堆石坝 /
- 应力拱效应 /
- 影响范围
Abstract: Influenced by canyon topography, the CFRD built in canyon areas will cause the stress arching effect in the rivercrossing direction.The stress arching effect makes it difficult for the rockfill to be fully compacted at the bottom of the dam.Starting from the forming conditions, 3-D FEM is used to compare the distribution of the major and minor principal stresses of the CFRD with wide narrow valley, in order to reveal the formation mechanism of internal stress arching effect of CFRD in canyon regions.The distribution form and range of reasonable arch axis of stress arching effect at the bottom of CFRD are studied.The bottom rockfill at the center of the valley is most affected by the stress arching effect.The influence area accounts for about 23%of the overall height of the dam.The research results may provide a reference for reducing the adverse effect of stress arching effect of CFRD in canyon area.
- narrow valley /
- CFRD /
- stress arching effect /
- influence range

HTML全文

0. 引言

全断面岩石隧道掘进机(以下简称TBM)是集机、电、液和自动化控制于一体，能够实现破岩、掘进、出渣与隧道支护的大型掘进装备，其具有对围岩扰动小、能连续作业、环境污染小、安全性能高、成硐质量好等优点^[1]。然而，随着TBM向“三高”等(高原岩围压、高岩石强度、高石英含量)等极端恶劣地层推广应用，TBM的核心破岩刀具——盘形滚刀(以下简称滚刀)失效严重，从而导致TBM掘进效率低、施工成本高等问题^[2]。为了克服上述TBM的性能瓶颈，在当前材料科学与制备技术的约束下，鉴于激光技术在石油钻探领域已取得的良好效果，将激光发生器耦合安装到TBM刀盘上，进行激光预钻孔/预切槽条件下滚刀滚压破碎掌子面岩石，理论上有望实现新型热-机械高效破岩之目的^[3]。

目前，一方面由于激光破岩过程涉及到新物质生成、岩石物性改变、热裂纹衍生与扩展等，难以借助理论工具予以准确描述，另一方面由于热-机械耦合效应解耦困难，有关激光辅助滚刀破岩机理的理论建模研究尚不多见。学术界主要针对滚刀及激光的破岩过程分别予以了研究。

(1) 滚刀破岩方面

JI A史莱涅、Hertz、Boussinesq和Davies等对平底压头、半球形压头及楔形压头等不同压头形式侵入岩石过程中的应力分布公式进行了推导^[4]。在上述压头侵岩理论的基础上，不少学者基于滚压破岩试验，相继建立了滚刀破岩载荷预测模型。Evans等^[5]认为垂直力与侵岩投影面积成正比且将该面积按抛物线围成面积的一半计算。Rostami^[6]将垂直力分为压碎下方岩石所需作用力和剪切相邻刀间距间岩石所需作用力两部分，并按三角形面积来确定刀岩接触面积，建立了经典的CSM模型。国内许多科研院所也进行了滚刀破岩预测模型的研究工作^[7-9]。但由于对于刀岩作用过程认识的局限性，加之岩石本构行为的复杂性，导致上述模型并未考虑刀岩作用过程中密实核的衍生效应^[10]。密实核的衍生效应在滚刀切削破岩过程中的影响是不可忽略的。当滚刀作用于岩石表面时，刃底的岩石表面由于承压产生凹陷，并衍生出微裂纹；随着刀具的不断侵入，裂纹内部的岩石不断受到压缩和剪切的作用，形成了由岩石碎屑粉末组成的密实核；由于密实核的膨胀和变形，密实核周围的岩石持续受压，继而产生剪切破坏并形成破碎区^[11]。Alehossein等^[12]将刀具侵岩时在裂纹形成之前岩石内部分为密实核区、弹塑性失效区和弹性变形区3个应力区，并基于腔体膨胀理论建立了钝刀侵岩模型。在此基础上，张魁等^[13]进一步建立了考虑密实核衍生现象的常截面(CCS)滚刀侵岩载荷模型。有许多学者也通过侵岩^[14]、滚压破岩^[15]等试验方法，对滚刀破岩机理进一步探究完善。

(2) 激光破岩方面

为了研究激光破岩机理，学者们搭建了诸多试验平台，其中使用的激光器主要为光纤激光器，功率为50 W~9 kW。研究表明：利用激光器发射高能激光束照射在岩石表面，可使岩石在在局部高温作用下发生升温、熔化、汽化和凝固过程，并伴随着热爆裂现象的产生，其表面存在固液气多相混化合物^[16]。当激光作用在岩石表面时间较短，岩石表温度未超过其熔点时，其破碎方式主要为热力破碎，破碎后脱落的碎屑可由高压辅助气流带出；当岩石持续吸收激光束的能量，并不断积累超过一定阀值时，岩石就会熔化甚至汽化，此时岩石因为在极短时间内吸收大量能量发生相变，导致体积膨胀，产生热爆裂现象；当熔融物和汽化物不能及时被辅助气体吹出带走时，岩石表面会重新凝固成玻璃状物质，该物质会阻碍激光束能量的进一步传递，不利于激光孔洞的扩张，但在另一方面，该玻璃物质可以加固松散程度较高、力学性能不好的岩石^[17-19]。近年来，随着科技的不断进步，人们对激光破岩技术的研究也逐渐深入。由于现有试验设备难以观察和测量破岩过程中激光与岩石相互作用界面的具体形貌，以及熔体-蒸汽界面处的温度状态，大量的学者着力于用理论模型和数值仿真方法研究激光破岩机理^[20-22]。研究表明构建激光破岩数值模型能有效观察激光破岩过程中岩石温度和应力场分布，对分析岩石微观和宏观性质变化的有效方法，对指导激光破岩试验测试有重要意义。综上所述，为了用理论描述预制激光孔条件下滚刀侵岩过程，基于小孔应力集中理论的弹性应力状态计算方法，在空腔膨胀模型基础上，拟建立一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型，并开展激光辅助缩尺比例滚刀侵岩试验，尝试从侵岩垂直力的角度，通过理论与试验结果的对比验证，讨论理论模型的正确性。

1. 理论基础与理论建模

1.1 基本假设

如图 1所示，在高能量激光照射下，岩石表面发生了弱化、碎化、熔化和汽化现象，继而形成了孔洞状等损伤形貌，并在孔洞周围产生了热影响区域；同时，在孔底附着有玻璃釉物质。可见，激光预钻孔条件下滚刀滚压破碎掌子面岩石，属于一种典型的机械破碎-热破碎耦合作用过程。为了便于建模，现作出如下7点简化假设。

图 1 激光破岩示意图

Figure 1. Schematic diagram of laser-assisted rock breaking

下载: 全尺寸图片幻灯片

(1) 忽略激光钻孔时序对孔径、孔深等形貌尺寸及围岩物理力学性能的影响。

(2) 忽略激光热源所产生热应力对岩石试样强度的削弱作用。

(3) 忽略所述玻璃釉对滚刀破岩机理的影响。

(4) 将岩石试样视为各向同性的线弹性体，满足平面应变条件。

(5) 假定岩石试样尺寸远大于激光孔径，且刀孔距大于两倍激光孔径。

(6) 假定激光孔孔深不小于滚刀侵深。

(7) 假设刀孔距远大于激光孔孔径后，滚刀对激光孔的合力为均布载荷。

基于上述简化假设，认定在受原岩围压以及滚刀机械应力的综合作用下，激光孔周围存在小孔应力集中现象。根据小孔应力集中理论可知：激光孔周围的局部最大应力甚至会达到平均应力水平的(2~3)倍；当超出孔中心一定范围时，应力集中现象消失；小孔应力集中现象只与小孔形状有关，与小孔尺寸无关。

1.2 考虑密实核衍生效应的滚刀侵岩模型

文献[]基于密实核衍生现象，认为滚刀侵岩时刃底向密实核区施加了挤压应力，而刃侧对岩壁产生了剪切挤压应力。为此，如所示，滚刀所受垂直侵岩力 ${F_{\rm{v}}}$ 与刃底密实核对滚刀所施加挤压力 ${F_1}$ 和刃侧岩体对滚刀所施加挤压力 ${F_2}$ 的合力相关。其中， ${F_1}$ 可分解为沿垂直方向的 ${F'_{\rm{v}}}$ 和沿水平方向的 ${F'_{\rm{c}}}$ 两个分力； ${F_2}$ 可分解为沿垂直方向的 ${F''_{\rm{v}}}$ 和沿水平方向的 ${F''_{\rm{c}}}$ 两个分力。

图 2 滚刀侵岩过程中的受力示意图

Figure 2. Schematic diagram of forces involved during rock penetration by a disc cutter

下载: 全尺寸图片幻灯片

中， ${F'_{\rm{v}}}$ 和 ${F'_{\rm{c}}}$ 可由考虑密实核效应的常截面(CCS)滚刀侵岩载荷模型计算给出^[13]，其中密实核对岩体的垂直挤压力 ${F'_{\rm{v}}}$ 为

${F'_{\rm{v}}}{\text{ = }}2\int_0^\psi {2{P_{\rm{s}}}bR\cos {\text{(}}\psi - \beta {\text{)}}} {\text{d}}\beta 。$

(1)

式中：P_s为密实核区应力； ${\text{d}}\beta$ 为滚刀微元的位置角；R为滚刀半径；2 $\psi$ 为刀岩接触角，

$\psi = \arccos [(R - h')/R] 。$

(2)

密实核对岩体的水平挤压力 ${F'_{\rm{c}}}$ 为

${F'_{\rm{c}}}{\text{ = }}{P_{\rm{s}}}{S_{\rm{s}}} 。$

(3)

式中： ${S_{\rm{s}}}$ 为密实核与岩体接触部分投影面积，

${S_{\rm{s}}} = R\arccos \frac{{R - h'}}{R}b 。$

(4)

如所示， $b$ 为密实核区半径，其值等于1/2刃宽； $h'$ 为侵深； ${S_{\rm{t}}}$ 为滚刀与岩体接触部分投影面积，

${S_{\rm{t}}} = {R^2}\arccos \frac{{R - h'}}{R} - (R - h')\sqrt {{R^2} - {{(R - h')}^2}} 。$

(5)

图 3 刀岩作用过程中的纵向截面图

Figure 3. Longitudinal section during rock penetration

下载: 全尺寸图片幻灯片

中 ${F''_{\rm{v}}}$ ， ${F''_{\rm{c}}}$ 可由考虑刃侧挤压与剪切效应的CCS滚刀侵岩载荷模型计算给出^[23]：

${F_{\rm{v}}}^{\prime \prime }{\text{ = }}2\int_0^\psi {R\left[ {{{P'}_1}{\text{cos}}(\left| \varphi \right| - {\theta _0}) + {P_1}''\cos ({\theta _0} + \varphi )} \right]} {\text{d}}\beta \text{，}$

(6)

${F}_{c}{}^{\prime \text{}\prime }\text{=}2R{\displaystyle {\int }_{0}^{\psi }\left[-{{P}^{\prime }}_{1}\mathrm{sin}(\left|\phi \right|-{\theta }_{0})+{{P}^{″}}_{1}\mathrm{sin}({\theta }_{0}+\phi )\right]}\text{cos(}\psi -\beta \text{)d}\beta 。$

(7)

式中： ${P_1}^\prime$ 为等效剪切破岩力； ${P_1}^{\prime \prime }$ 为等效挤压破岩力。

${P}_{1}\text{'}=\text{2}\tau \text{cos}\phi [R-(R-{h}^{\prime })/\mathrm{cos}(\psi -\beta )]/(n+1)(1-\mathrm{cos}2\psi )\text{，}$

(8)

${P_1}{\text{''}} = {\sigma _{\rm{c}}}[R - (R - h')/\cos (\psi - \beta )]/\cos {\theta _0}\cos \varphi 。$

(9)

式中： $\varphi$ 为内摩擦角； ${\sigma _{\rm{c}}}$ 为岩石最大抗压强度。

故滚刀单侧所受侧向侵岩力 ${F_{\text{c}}}$ 及滚刀所受垂直侵岩力 ${F_{\rm{v}}}$ 为

${F_{\rm{c}}} = {F_{\rm{c}}}^\prime + {F''_{\rm{c}}} \text{，}$

(10)

${F_{\rm{v}}} = {F'_{\rm{v}}}{\text{ + }}2{F''_{\rm{v}}} 。$

(11)

1.3 激光预钻孔条件下滚刀侵岩模型

(1) 基于小孔应力集中的单个激光孔周围应力分布

假设岩石初始受双向对称围压作用。当滚刀侵入激光孔一侧岩石，由于滚刀机械应力参与作用，打破了围岩所受双向对称围压状态，使其转换为双向非对称围压状态，如所示。 ${p_0}$ 为激光孔总应力； ${p_{\rm{w}}}$ 为侧向围压应力； ${p_{\rm{z}}}$ 为正向围压应力， ${p_{\rm{z}}} = {p_{\rm{w}}}$ ； ${F'_{\rm{c}}}$ 为密实核对岩体的水平挤压力； ${F''_{\text{c}}}$ 为滚刀刃侧对岩壁的水平作用力。

图 4 激光辅助滚刀侵岩过程的受力图

Figure 4. Force diagram of rock penetration by laser-assisted disc cutter

下载: 全尺寸图片幻灯片

激光孔的总应力为刃侧切向应力和刃底密实核挤压应力之和：

${P_0} = ({F_{\rm{c}}}{\text{ + }}{F'_{\rm{c}}})/({S_{\rm{t}}}{\text{ + }}{S_{\rm{s}}}) 。$

(12)

式中： ${S_{\rm{t}}}$ 为滚刀与岩体接触部分面积； ${S_{\rm{s}}}$ 为密实核与岩体接触部分面积。

假设激光孔仅受围压及 ${P_0}$ 作用，此时将双向非对称围压状态转换成双向轴对称围压状态和等应力单向受拉单向受压状态，如所示。 ${R_0}$ 为激光孔半径；r为任意点到激光孔圆心的距离； $\theta$ 为任意点到激光孔圆心连线与x轴的夹角； $\lambda$ 为应力系数( $\lambda$ < 1)； $P$ 为轴对称围压应力； $P'$ 为刃底密实核挤压应力。

图 5 激光孔受力情况简化图

Figure 5. Simplified diagram of forces on laser hole

下载: 全尺寸图片幻灯片

应力系数 $\lambda$ 定义为正向压应力与侧向压应力之比。轴对称围压应力状态是滚刀-激光辅助破岩的特例(即 $\lambda = 1$ 时)，但在滚刀破岩过程中，刃侧及刃底对岩石的挤压作用总是会打破这个平衡，使得 $\lambda < 1$ 。

在轴对称围压应力状态下激光孔周边岩石的应力解^[24]为

$\left. \begin{array}{l}{\sigma }_{\text{θ}}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1\pm \frac{{R}_{0}^{2}}{{r}^{2}}\right)\text{ }\text{，}\\ {\sigma }_{r}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1\pm \frac{{R}_{0}^{2}}{{r}^{2}}\right)\text{ }。\end{array} \right\}$

(13)

在等应力单向受拉单向受压状态下，激光孔周边岩石的应力解为

$\left. \begin{array}{l}{\sigma }_{r}=\frac{1}{2}(1-\lambda ){P}_{0}\left(1-4\frac{{R}_{0}^{2}}{{r}^{2}}+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\sigma }_{\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\tau }_{r\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+2\frac{{R}_{0}^{2}}{{r}^{2}}-3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{sin}2\theta 。\end{array} \right\}$

(14)

式中： ${\sigma _r}$ 为激光孔径向正应力； ${\sigma _\theta }$ 为激光孔切向正应力； ${\tau _{r\varphi }}$ 为激光孔切向应力。

基于应力场叠加原理，由式(13)，(14)可得双向非对称围压状态下激光孔周边岩石应力计算式：

$\left. \begin{array}{l}{\sigma }_{r}=\frac{1}{2}(1+\lambda ){P}_{0}\left(1-\frac{{R}_{0}^{2}}{{r}^{2}}\right)-\frac{1}{2}(1-\lambda ){P}_{0}\left(1-4\frac{{R}_{0}^{2}}{{r}^{2}}+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\sigma }_{\theta }=\frac{1}{2}(1+\lambda ){P}_{0}\left(1+\frac{{R}_{0}^{2}}{{r}^{2}}\right)+\frac{1}{2}(1-\lambda ){P}_{0}\left(1+3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{cos}2\theta \text{，}\\ {\tau }_{r\theta }=\frac{1}{2}(1-\lambda ){P}_{0}\left(1+2\frac{{R}_{0}^{2}}{{r}^{2}}-3\frac{{R}_{0}^{4}}{{r}^{4}}\right)\mathrm{sin}2\theta 。 \end{array} \right\}$

(15)

由式(15)可知，当 $r \approx {R_0}$ 时，激光孔边的应力分布为

${\sigma _r} = {\tau _{r\theta }} = 0 \text{，}$

(16)

${\sigma _\theta } = (1 + \lambda ){P_0} + 2(1 - \lambda ){P_0}\cos 2\theta 。$

(17)

在 $\theta {\text{ = }}{0^ \circ }$ 处，激光孔边存在最大压应力，其应力解为

${\sigma _\theta } = (3 - \lambda ){P_0} > 0 。$

(18)

在 $\theta {\text{ = 9}}{0^ \circ }$ 处，激光孔边存在最小应力，其应力解为

${\sigma _\theta } = (3\lambda - 1){P_0} 。$

(19)

当 $0 < \lambda < \frac{1}{3}$ 时，激光孔周围存在拉应力；当 $\frac{1}{3} < \lambda < 1$ 时，激光孔周围只存在压应力；当TBM位于深层岩石掘进时，由于岩石围压力 ${P_{\rm{z}}}$ 较大， $\lambda$ 一般为 $\frac{1}{3} < \lambda < 1$ 。

(2) 基于小孔应力集中的激光孔排周围应力分布

当多个激光孔以给定孔距排列时，激光孔排的应力分布如所示。其中k为小孔应力集中系数，一般 $k = 1.5 \sim 2$ ，则 $k{R_0}$ 为应力集中边界^[25]。基于小孔应力集中理论，激光孔应力集中边界最大压应力为

${\sigma }_{k{R}_{0}}{{}_{, }}_{0}=\left[3(1-\lambda )/2{k}^{4}+(1+\lambda )/2{k}^{2}+1\right]{P}_{0} > {P}_{0} 。$

(20)

图 6 激光孔排的应力分布图

Figure 6. Distribution of stress of multiple laser holes

下载: 全尺寸图片幻灯片

当激光孔应力集中边界处最大压应力达到岩石最大抗压强度 ${\sigma _{\text{c}}}$ 时，该边界处岩体被破坏，即

${\sigma _{k{R_0}, 0}} = \left[ {3(1 - \lambda )/2{k^4} + (1 + \lambda )/2{k^2} + 1} \right]{P_0}{\text{ = }}{\sigma _{\text{c}}} \text{，}$

(21)

${P_{0\min }}{\text{ = }}\sigma c/[3(1 - \lambda )/2{k^4} + (1 + \lambda )/2{k^2} + 1] 。$

(22)

式中：P_0min为激光孔破坏时的临界应力。

此时，应力系数 $\lambda$ 进一步给出为

$\lambda = {P_{\rm{z}}}/[({P_{\rm{t}}}{S_{\rm{t}}} + {P_{\rm{s}}}{S_{\rm{s}}})/({S_{\rm{t}}} + {S_{\rm{s}}}) + {P_{\rm{w}}}] 。$

(23)

待激光孔被破坏后，激光孔间剩余未被破坏岩石，处于三面临空、两面受压状态，并假定其承受压力 ${P_0}$ 。如所示，当激光孔被破坏的瞬间，假定滚刀切削力保持不变。由于激光孔破碎，岩石承载面积由原本的 $(a - 2{R_0})h$ 骤减到 $(a - 2k{R_0})h$ ，因此该处岩石压力重新分布为

$\sigma = {P_0}(a - 2{R_0})/(a - 2k{R_0}) 。$

(24)

图 7 激光孔周边岩石的破碎情况分析

Figure 7. Analysis of rock fragmentation around laser hole

下载: 全尺寸图片幻灯片

令式(24)等于 ${\sigma _{\rm{c}}}$ ，即可求得破坏剩余部分岩石所需应力P₀：

${P_0} = {\sigma _{\text{c}}}(a - 2k{R_0})/(a - 2{R_0}) 。$

(25)

当激光孔被破坏时，剩余岩石同时发生破坏，此时破岩效果最佳，则

${P_0}{\text{ = }}{P_{0\min }} 。$

(26)

可求得激光辅助滚刀侵岩时最优孔距 ${a_0}$ 为

${a_0} = {\text{2}}{R_0}({P_{0\min }} - k{\sigma _{\rm{c}}}{\text{)/(}}{P_{0\min }} - {\sigma _{\rm{c}}}{\text{)}} (2k{R_0} < a < 10{R_0}) 。$

(27)

(3) 综合建模

由式(27)求得最佳孔距为 ${a_0}$ ，当 $a < {a_0}$ 时，由于孔距较小，其所对应的侵岩载荷和所需能量均较大，不再适用于小孔应力集中问题，故此处不做计算。当 $a > {a_0}$ 时，可得滚刀对激光孔排总应力 ${P_{\text{0}}}^\prime$ ：

${P'_0} = {F_{\rm{c}}}/({S_{\rm{t}}} + {S_{\rm{s}}}) 。$

(28)

由平衡公式可得

${P_0} = {P_0}^\prime 。$

(29)

即

${\sigma _{\rm{c}}}(a - 2k{R_0})/(a - 2{R_0}) = ({F_{\rm{c}}} + {F'_{\text{c}}})/({S_{\rm{s}}} + {S_{\rm{t}}}) 。$

(30)

密实核区处于静水压力状态，可将密实核区应力 ${P_{\rm{s}}}$ 视为均值，可求得

${P_{\rm{s}}} = \left\{ {{\sigma _{\rm{c}}}{\text{(}}{S_{\rm{s}}} + {S_{\rm{t}}}{\text{)}}(a - 2k{R_0})/(a - 2{R_0}) + \mathop {}\limits_{} } \right.$

$2R{\displaystyle {\int }_{0}^{\psi }\left[{P}_{1}\text{'sin}(\left|\varphi \right|-{\theta }_{0})-{P}_{1}\text{'}\text{'}\mathrm{sin}({\theta }_{0}+\varphi )\right]}\text{cos(}\psi -\beta \text{)d}\beta \}/{S}_\text{s}\text{ }。$

(31)

当求得 ${P_{\rm{s}}}$ 后，即可联立式(1)，(6)，(8)求出 ${F_{\rm{v}}}$ ；联合式(3)，(7)，(9)求出 ${F_{\rm{c}}}$ 。

2. 理论分析

(1) 孔距对密实核区应力和侵岩垂直力的影响

为了便于后续试验验证，本节理论计算所用的滚刀按1︰3的比例对17英寸工程用滚刀进行缩小，以花岗岩为试验对象，并给定刃宽d为3 mm，刃倾角 ${\theta _{\text{0}}}$ 为8°，得出滚刀侵岩作用下不同孔距对密实核区应力和侵岩垂直力的影响规律图，如所示。由式(27)根据前述理论可以求出最优孔距 ${a_0}$ 为4.3 mm。当 $a < {a_0}$ 时，由于孔距较小，所对应的侵岩载荷和所需能量均较大，且不适用于小孔应力集中问题，因此，只对 $a > {a_0}$ 的条件下进行求解。

图 8 不同孔距对密实核区应力和侵岩垂直力的影响规律曲线

Figure 8. Curves of influences of hole spacing on stress in dense core area and vertical force of rock penetration

下载: 全尺寸图片幻灯片

由图可知，当 $a > {a_0}$ 时，密实核区应力及侵岩垂直力随孔距的增加，增加速率趋于平缓。随着孔距的增加，孔与孔之间剩余岩体的相对面积增加，应力集中区域的面积则相对减小，激光孔排逐渐趋近于没有激光辅助滚刀侵岩的情况，因此，其增加速率趋于平缓，最终将会无限趋近于无激光孔辅助滚刀侵岩的密实核区应力及侵岩垂直力。这也说明了，激光孔可影响滚刀侵岩过程中的密实核区应力及侵岩垂直力，并可通过激光孔距来优化滚刀破岩过程。

(2) 刃宽对密实核区应力和侵岩垂直力的影响

由式(2)~(16)计算可得最优孔距，再将最优孔距取整为4 mm，刃倾角 ${\theta _{\text{0}}}$ 为8°，得出不同刃宽对密实核区应力和侵岩垂直力的影响规律图，如图 9所示。由图可知，随刃宽的增加，密实核区应力与侵岩垂直力均近似呈线性增加。相对而言，侵岩垂直力的增加速率在刃宽较小时略有降低。这与实际情况中侵岩垂直力随刃宽增加而指数增加是相符合的^[26]。

图 9 不同刃宽对密实核区应力和侵岩垂直力的影响规律图

Figure 9. Curve of influences of edge width on stress in dense core area and vertical force of rock penetration

下载: 全尺寸图片幻灯片

3. 试验验证

3.1 试验方案

为了进一步验证上述理论模型，本节以YWYA- 2000型全自动伺服岩石抗压抗剪试验机为基础试验平台，开展了激光预钻孔条件下缩尺比例滚刀压头侵岩试验，如图 10所示。图 10中采用与理论分析相同尺寸的缩尺比例滚刀压头；选取板状长沙花岗岩作为岩石试样，岩样尺寸为150 mm×150 mm×24 mm；激光功率设置为100 W，激光频率为60 kHz，激光作用时间为1 s，采用E1309M型高速精密激光切割机在岩石试样表面沿岩石厚度方向预钻出激光孔排；孔距分别设置为2，3，4，5，6 mm。

图 10 侵岩试验示意图

Figure 10. Schematic diagram of rock penetration tests

下载: 全尺寸图片幻灯片

采用如图 11所示的具有自主知识产权的双侧围压装置夹持岩石试样，并将双侧围压装置设置于全自动伺服岩石抗压抗剪试验机工作平台上，再将高速摄像仪的镜头正对双侧围压装置的观测窗口。图 11中，双侧围压装置包括基座、正向围压部件、侧向围压部件和液压部件。其中，基座上装夹有岩石物料，正向围压部件对称压装于岩石物料的前后两面，侧向围压部件对称压装于岩石物料的左右两侧面，岩石物料与两侧正向围压部件之间对称压装有观测板，前后两个加载板及压板中部均开设有观测窗口，液压部件分别压紧正向围压部件及侧向围压部件，由于基座具有上述技术特征，使得在模拟滚刀压头侵岩过程中，本试验装置既可实现岩石试样围压状态的模拟加载，又可实现刃底密实核动态衍生现象的在线观测。

图 11 双侧围压装置

Figure 11. Test devices

下载: 全尺寸图片幻灯片

随后，采用全自动伺服岩石抗压抗剪试验机进行静压侵岩试验，将板状岩石安装于密实核衍生观测装置上，并放置好滚刀压头，监测设备沿试验装置的观测窗口架设，录制静压侵岩动态全过程。此外，还设置了一组无激光孔的侵岩对照试验。

3.2 试验结果分析

(1) 激光破岩后的岩石损伤形貌观测

如图 12，13所示，分别为激光预钻孔后花岗岩试样表面形貌图和激光孔横截面形貌图。由图 12，13可知，所获激光孔呈上部孔径大、底部孔径小的“倒锥形”形貌。这是由于在试验中，岩石所含矿物质受热熔化后无法及时排出，附着在孔壁上并形成玻璃釉物质；同时，玻璃釉物质的生成也限制了孔径与孔深的继续增大，进而导致了位于激光热源中心处的花岗岩去除量大于周边岩样。

图 12 孔距为3 mm时的岩石损伤形貌图

Figure 12. Morphology of rock damage at hole spacing of 3 mm

下载: 全尺寸图片幻灯片

图 13 激光孔横截面损伤形貌图

Figure 13. Morphologies of cross-sectional damage of laser hole

下载: 全尺寸图片幻灯片

(2) 密实核及岩石裂纹衍生扩展过程观测

如图 14所示，为密实核及裂纹衍生扩展过程观测图。由图 14(b)可知，在滚刀压头刃底出现了明显的白色密实核现象，且其半径大致为刃宽的一半，而在其周围出现了大量裂纹。其中，在激光孔一侧，表面裂纹延伸至激光孔排处，并与之贯穿，形成破碎岩块。由图 14(d)可知，从俯视侵岩形貌可以看出，在压头压痕与激光孔之间产生了较多破碎的岩块。

图 14 滚刀侵岩过程观测图

Figure 14. Observation images of rock penetration process by disc cutter

下载: 全尺寸图片幻灯片

(3) 侵岩垂直力分析

如图 15所示，为给定滚刀刃宽d为3 mm时，不同孔距下及无激光孔对照组所测滚刀峰值侵岩垂直力。由图 15可知，预制激光孔后，侵深及侵岩垂直力均小于无激光孔侵岩对照试验。这是由于激光孔排对局部岩石产生了弱化效应，降低了该处岩石强度，并在激光孔附近形成应力集中现象，峰值侵岩垂直力大大减小。而随着孔距的增加，侵岩垂直力呈先减小后增加的趋势，这是因为孔距过小时，应力集中区域重叠，岩石被过度破碎，在压头刃底更多的岩粉被重复压实，形成密实核，吸收了更多的破岩能量，侵岩垂直力也随之升高。因此第2节中的激光辅助滚刀侵岩模型不适用于孔距较小的情况。而随着孔距的增大，小孔应力集中区域不再重叠，岩石破碎时，岩碴多为较大的岩块，岩石没有被过度破碎，侵岩垂直力也随之下降至最小值，当孔距增大至4 mm时，峰值破岩力最小。随着孔距继续增加，小孔应力集中效应逐渐减弱，侵岩垂直力再次上升。

图 15 滚刀侵岩垂直力随孔距变化的曲线图

Figure 15. Curves of vertical force with spacing of cutter hole

下载: 全尺寸图片幻灯片

3.3 理论与试验结果的对比分析

为验证第2节中激光激光预钻孔条件下滚刀侵岩理论模型的正确性，将理论模型的结果曲线与试验结果曲线进行对比分析。

如图 16所示，为花岗岩在不同孔距条件下理论与试验侵岩垂直力对比图。如前所述第2节中的激光激光预钻孔条件下滚刀破岩模型不适用于孔距较小的情况，故理论组仅对孔距大于最优孔距的值进行理论分析。

图 16 理论与试验侵岩垂直力对比图

Figure 16. Comparison between theoretical and experimental vertical forces

下载: 全尺寸图片幻灯片

由图可知，试验组侵岩垂直力略大于理论组，且随着孔距的增加，两组曲线的变化趋势相同，均为逐渐放缓的上升趋势，且破岩力最小处均在孔距为4 mm处。由于试验中激光作用于岩石表面，岩石表面受到损伤而形成激光孔洞，同时熔融的岩石矿物质会覆盖在激光孔洞表面形成更加硬的玻璃釉层，而在理论中忽略了的玻璃釉对后续侵岩的影响；同时在理论中，假设了密实核区的半径为1/2刃宽，而在试验中由于岩石的破碎情况不同，形成的密实核半径并不是保持不变的，故造成了试验与理论的侵岩垂直力有较小的差别。

4. 结论

基于小孔应力集中理论的弹性应力状态计算方法及滚刀侵岩过程中的空腔膨胀模型，建立了一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型，并基于具有自主知识产权的双侧围压装置，开展激光辅助缩尺比例滚刀侵岩试验，从侵岩垂直力的角度，验证理论模型的正确性。

(1) 建立了一种考虑密实核衍生效应的激光预钻孔条件下滚刀侵岩理论模型。随后对该模型进行数值建模分析后发现，随滚刀刃宽增加，密实核区应力呈线性增加，最大侵岩垂直力指数上升；随孔距的增加，密实核区应力、最大侵岩垂直力均呈先下降后上升趋势。

(2) 开展双侧围压下的激光辅助缩尺比例滚刀侵岩试验，并将得出的试验结果与理论分析结果进行对比，发现破岩垂直力在总体上较为吻合。由于在理论模型中未考虑激光破岩中产生的玻璃釉物质对后续侵岩的影响以及假设密实核区的半径为一个固定值，因此理论模型的预测精度有待进一步提升。

综上所述，本文所建立滚刀侵岩理论模型，具有一定的准确性，未来可将滚刀空间运动纳入考察，建立满足工程应用要求的激光辅助TBM破岩预测模型，为激光器-滚刀耦合刀盘的设计提供理论指导。

图 1 有限元计算模型

Figure 1. FEM model

下载: 全尺寸图片幻灯片

图 2 宽河谷计算模型坝体小主应力等值线图

Figure 2. Contour map of minor principal stress of dam for wide valley model

下载: 全尺寸图片幻灯片

图 3 窄河谷计算模型坝体小主应力等值线图

Figure 3. Contour map of minor principal stress of dam for narrow valley model

下载: 全尺寸图片幻灯片

图 4 宽河谷计算模型坝体大主应力等值线图

Figure 4. Contour map of major principal stress of dam for wide valley model

下载: 全尺寸图片幻灯片

图 5 窄河谷计算模型坝体大主应力等值线图

Figure 5. Contour map of major principal stress of dam for narrow valley model

下载: 全尺寸图片幻灯片

图 6 窄河谷时河谷中心点处主应力随坝体高程变化曲线

Figure 6. Variation curves of principal stress with dam height at center point of narrow valley

下载: 全尺寸图片幻灯片

图 7 (0, 0)点处坝体主应力随坝体高程变化

Figure 7. Variation curves of principal stress with dam height at point(0, 0)

下载: 全尺寸图片幻灯片

图 8 (5, 0)处坝体主应力随坝体高程变化

Figure 8. Variation curves of principal stress with dam height at point(5, 0)

下载: 全尺寸图片幻灯片

图 9 (10, 0)处坝体主应力随坝体高程变化

Figure 9. Variation curves of principal stress with dam height at point(10, 0)

下载: 全尺寸图片幻灯片

图 10 窄河谷计算模型中坝体底部应力拱的合理拱轴线

Figure 10. Reasonable arch axis of stress arching at dam bottom for narrow valley model

下载: 全尺寸图片幻灯片

表 1 邓肯模型材料参数

Table 1 Parameters of Duncan-Chang model

材料	K	n	R_f	c/KPa	φ/(°)	△φ/(°)	K_b	m	K_ur	ρ/(g·cm^-3)
上游堆石料	1422	0.28	0.70	300	50	11.8	768	0.03	2701	2.09
下游堆石料	1198	0.29	0.70	293	50	12.2	768	0.03	2276	2.12
过渡料	1055	0.3	0.62	315	51	12.0	627	0.12	2113	2.32
垫层料	1165	0.3	0.62	315	51	12.0	627	0.47	2213	2.34

下载: 导出CSV

参考文献(11)

[1]	蒋国澄, 傅志安, 凤家骥. 混凝土面板坝工程[M]. 武汉: 湖北科学技术出版社, 1997. JIANG Guo-cheng, FU Zhian, FENG Jia-yi. Concrete Face Rockfill Dam Engineering[M]. Wuhan: Hubei Science and Technology Press, 1997. (in Chinese)
[2]	蒋国澄, 曹克明. 中国的混凝土面板堆石坝[C]//国际高土石坝学术研讨会论文集.1993, 北京. JIANG Guocheng, CAO Ke-ming. Concrete face rockfill dam in China[C]//Proceedings of the International Symposium on High Earth Rockfill Dams.1993, Beijing. (in Chinese)
[3]	WILKINS J K, MITCHELL W R, FITZPATRICK M D, et al. The design of cethana concrete face rockfill dams[C]//11th ICOLD Congress.1973, Madrid.
[4]	汪小刚. 高土石坝几个问题探讨[J]. 岩土工程学报, 2018, 40(2): 203-222. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802002.htm WANG Xiao-gang. Discussion on some problems observed in high earth-rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 203-222. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802002.htm
[5]	曾奕滔, 沈振中, 甘磊, 等. 反滤层对高心墙堆石坝拱效应影响研究[J]. 水利水电技术, 2018, 49(1): 90-95. https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ201801013.htm ZENG Yi-tao, SHEN Zhen-zhong, GAN Lei, et al. Influence from filter layer on arching effect of high rockfill dam with core wall[J]. Water Conservancy and Hydropower Technology, 2018, 49(1): 90-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ201801013.htm
[6]	高昂, 苏怀智, 刘春高. 超高心墙堆石坝拱效应分析[J]. 水力发电学报, 2015, 34(9): 138-145. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201509018.htm GAO Ang, SU Huai-zhi, LIU Chun-gao. Analysis of soil arching in high core-wall rockfill dam[J]. Journal of Hydroelectric Engineering, 2015, 34(9): 138-145. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201509018.htm
[7]	林江, 胡万雨, 孟凡理, 等. 瀑布沟大坝心墙拱效应分析[J]. 岩土力学, 2013, 34(7): 2031-2035. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307031.htm LIN Jiang, HU Wan-yu, MENG Fan-li, et al. Arching effect analysis of core wall in Pubugou dam[J]. Rock and Soil Mechanics, 2013, 34(7): 2031-2035. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201307031.htm
[8]	张岩. 猴子岩狭窄河谷高面板堆石坝拱效应及其控制措施研究[C]//水电2013大会——中国大坝协会2013学术年会暨第三届堆石坝国际研讨会论文集.2013, 昆明. ZHANG Yan. Study on arch effect and control measures of high concrete face rockfill dam in Houziyan narrow valley[C].//Hydropower 2013 Conference——Proceedings of the 2013 Annual Conference of China Dam Associaion and the Third International Symposiumon Rockfill Dam.2013, Kunming. (in Chinese)
[9]	党发宁, 杨超, 薛海斌, 等. 河谷形状对面板堆石坝变形特性的影响研究[J]. 水利学报, 2014, 45(4): 435-442. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201404008.htm DANG Fa-ning, YANG Chao, XUE Hai-bin, et al. The effect of valley topography on deformation properties of CFRD[J]. Journal of Hydraulic Engineering, 2014, 45(4): 435-442. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201404008.htm
[10]	狄文龙, 屈楚杰, 蒋宽鹏. 狭窄河谷高面板堆石坝拱效应计算分析[J]. 水利科技与经济, 2016, 22(6): 7-12. https://www.cnki.com.cn/Article/CJFDTOTAL-SLKY201606003.htm DI Wen-long, QU Chu-jie, JIANG Kuan-peng. Analysis of arch effect of high CFRD built in narrow valley[J]. Water Conservancy Science and Technology and Economy, 2016, 22(6): 7-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLKY201606003.htm
[11]	KARL T. Theoretical Soil Mechanics[M]. 4th ed. New York: John Wiley&Sons, 1947.

施引文献(4)

期刊类型引用(2)

1.	韩成，张康成，陈振宇，彭赐彩，张魁. 基于LS-DYNA的激光-TBM滚刀破岩仿真方法及试验验证. 力学与实践. 2025(01): 179-188 . 百度学术
2.	汪鼎华，江彪，徐国强，张魁. 移动激光预切槽辅助TBM滚刀破岩的仿真研究. 陕西科技大学学报. 2024(06): 151-156+179 . 百度学术