裂缝边坡三维极限上限拓展分析

饶平平; 吴健; 崔纪飞; 赵琳学

doi:10.11779/CJGE202109005

裂缝边坡三维极限上限拓展分析 English Version

1.
上海理工大学土木工程系,上海　200093
2.
悉尼大学土木工程学院,澳大利亚　悉尼　2008

基金项目:

国家自然科学基金项目 42077435

详细信息

作者简介:
饶平平(1984— ),男,博士,副教授,主要从事岩土力学教学与科研工作。E-mail：raopingping@usst.edu.cn

中图分类号: TU431
计量
- 文章访问数: 343
- HTML全文浏览量: 72
- PDF下载量: 206
出版历程
- 收稿日期: 2020-12-14
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Extended three-dimensional analysis of cracked slopes using upper-bound limit method

1.
Department of Civil Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
2.
School of Civil Engineering, The University of Sydney, Sydney 2008, Australia

摘要

摘要: 裂缝的存在会降低边坡稳定性,而在边坡宽度受到限制时三维效应更加显著,因此有必要对裂缝边坡稳定性进行评估。针对裂缝边坡三维稳定性研究,基于极限分析上限定理,在三维破坏机构中引入一条垂直张拉裂缝,并引进机构参数拓展裂缝边坡三维破坏模式,包括坡面破坏和坡底破坏,建立能量平衡方程并通过优化算法求解裂缝边坡稳定系数上限解。根据g-line图像法绘制裂缝边坡稳定性图表以便读取安全系数。分析了边坡宽高比、坡角以及土体内摩擦角对裂缝边坡破坏模式和裂缝深度及位置的影响规律。结果表明：对于确定的边坡几何形态以及土体参数,存在最小边坡宽高比B/H^*,当边坡宽高比小于B/H^*,边坡发生坡面破坏且坡顶裂缝的影响可以忽略；内摩擦角φ小于5°时,边坡发生坡底破坏,而对于裂缝边坡,仅在φ=1°左右发生坡底破坏；随着边坡宽高比的增大,裂缝深度逐渐增加,裂缝位置逐渐远离坡肩,但对于坡角为75°的边坡裂缝深度先增大后减小。
- 边坡稳定性 /
- 极限分析 /
- 裂缝 /
- 安全系数 /
- 图表法
Abstract: The existence of cracks will reduce the stability of a slope and the three-dimensional effect is more significant when its width is limited. Therefore, it is necessary to evaluate the stability of cracked slopes. In order to study the three-dimensional stability of cracked slopes, based on the upper-bound theorem of limit analysis, a vertical tensile crack is introduced into the three-dimensional failure mechanism, and the mechanism parameters are introduced to extend the three-dimensional failure mode of slopes, including face failure and base failure. The energy balance equation is established, and the upper bounds of stability number of cracked slopes are obtained by the optimization algorithm. The stability charts of cracked slopes are established based on the g-line graphical method to read the factor of safety conveniently. The influences of slope width-to-height ratio, slope angle and internal friction angle of soils on the failure mechanism of cracked slopes and the crack depth and location are analyzed. The results show that for the specific slope geometry and soil parameters, there is a minimum slope width B/H^*. When the slope width is less than B/H^*, the failure surface passes above the slope toe, and the influences of the crack on the upper surface of the slope can be ignored. When the internal friction angle φ is less than 5°, the failure surface passes below the slope toe; for the cracked slope, only when φ=1°, failure surface passes below the slope. As the width of the slope increases, the crack depth gradually increases, and the crack location gradually moves away from the slope crest, while the crack depth of the slope with inclination 75° increases first and then decreases.
- slope stability /
- limit analysis /
- crack /
- factor of safety /
- graphical method

HTML全文

0. 引言

中国山地分布面积广,存在着大量的天然边坡。同时随着城市的持续发展,大量的铁路、公路以及矿山等工程建设会形成众多的人工边坡。边坡稳定性问题的研究,不仅仅关系到建筑物的正常使用,更直接与区域内人民群众的生命安全息息相关^[1-2]。目前边坡稳定性分析研究中,极限分析以其独特的优势被广泛运用^[3-6]。极限分析可表述为不必分析弹塑性变形全过程,通过建立运动学许可的速度场直接求解极限状态下的极限荷载,所得到的极限荷载是不小于真实值的上限解。Chen^[7]运用极限分析详细论述了岩土边坡的稳定性。而岩土体为受压材料,其抗拉强度较小,当拉应力超过其抗拉强度时,边坡坡顶会出现张拉裂缝同时降低边坡的稳定性。Terzaghi^[8]提出诸多稳定性分析受到拉应力区的影响。Spencer^[9]在圆弧滑动面中引入一条张拉裂缝并给出裂缝深度公式,表明裂缝深度与土的重度以及有效黏聚力和内摩擦角有关。Cousins^[10]认为垂直黏性土坡的张拉裂缝小于坡高的一半。Michalowski^[11]通过将裂缝类比为垂直边坡给出裂缝深度表达式,并研究了坡内孔隙水作用下了既有裂缝以及裂缝形成过程对边坡稳定性的影响,得出孔隙水作用下裂缝的深度会有所增加；对于陡坡或较大孔隙水压力情况下,存在裂缝的边坡的稳定性将明显下降。

Utili^[12]综合分析了裂缝对边坡稳定性的影响,讨论了裂缝的3种不同状态（裂缝位置与深度均未知、裂缝位置已知以及裂缝深度已知）对二维边坡稳定性的影响。Zhao等^[13]采用拟静力法将地震效应引入二维裂缝边坡稳定性分析中,证明了地震效应将显著降低裂缝边坡的稳定性。何毅等^[14]考虑坡顶倾角对地震作用下裂缝边坡稳定性的影响,研究表明,坡顶倾角越大边坡稳定系数减小百分比越大,裂缝深度逐渐增加且远离坡肩。周志军等^[15]建立单裂缝与多裂缝滑动模型推导出黄土边坡倾斜坡顶垂直裂隙极限深度的计算公式。

以上文献都是基于二维平面应变机制。但当边坡周围存在既有土工建筑或者坚硬岩石层,发生破坏时边坡宽度将受到约束,三维效应较为明显,若继续按照平面应变机制求解边坡稳定性将过于保守。故对裂缝边坡进行三维稳定性分析是非常有必要的。Michalowski等^[16]首次提出牛角状对数螺旋锥体破坏机构进行边坡三维稳定性分析。He等^[17]通过构建裂缝边坡三维破坏机构,指出随着边坡宽度的增加,最不利裂缝对于边坡稳定性的不利影响显著降低。在此基础上,Li等^[18]通过拟静力法将地震效应考虑进三维裂缝稳定性分析中,得出地震效应将大幅度减低边坡稳定性。

上述裂缝边坡三维稳定性分析中,边坡破坏模式仅仅考虑了破坏面通过边坡坡趾的情况（坡趾破坏）。但根据Gao等^[19]对边坡三维破坏模式拓展研究,得出在边坡宽高比很小时破坏面会通过边坡坡面（坡面破坏）以及对于较小的坡角与内摩擦角的情况破坏面会通过边坡坡底（坡底破坏）。本文基于极限分析上限定理,引入机构参数对裂缝边坡三维破坏模式进行拓展分析,包括坡面破坏和坡底破坏,并对不同破坏模式下裂缝边坡进行三维稳定性分析。利用蒙特卡罗模拟法与模式搜索法相结合的优化方法求解边坡稳定系数,同时绘制出相应的稳定性图表；在此基础上分析边坡宽高比、坡角及土体内摩擦角等参数对裂缝边坡三维稳定性、破坏模式和裂缝深度及位置的影响规律。

1. 基本原理和计算模型

1.1 基本原理

极限分析上限定理可表述为：对于任一运动学许可的破坏机构,令外力所作功率等于内部能量耗散率,得到的破坏荷载或极限荷载不小于真实极限荷载,即

$\int_{V} σ_{i j} {\dot{ε}}_{i j}^{*} d V = \int_{S} T_{i} v_{i}^{*} d S + \int_{V} F_{i} v_{i}^{*} d V$ 。

(1)

式中 T_i和F_i分别使机构边界S上的面力和体积V中的体力； $ε_{i j}^{*}$ 为运动学许可速度场中的塑性应变速率； $σ_{i j}^{*}$ 为通过相关联流动法则与 $ε_{i j}^{*}$ 相关联的应力场； $v_{i j}^{*}$ 为与 $ε_{i j}^{*}$ 满足几何相容条件的速度场。

本文采用极限分析上限定理对裂缝边坡进行三维稳定性分析,假设边坡为均质土体,土体满足理想弹塑性模型,服从莫尔库仑屈服准则和相关联流动法则。同时仅将土体自重作为外功率,土体内能耗散作为内功率,通过外功率等于内功率求解边坡稳定系数上限解。并基于g-line图像法和强度折减法建立裂缝边坡三维稳定性图表以便快速读取安全系数。

1.2 计算模型

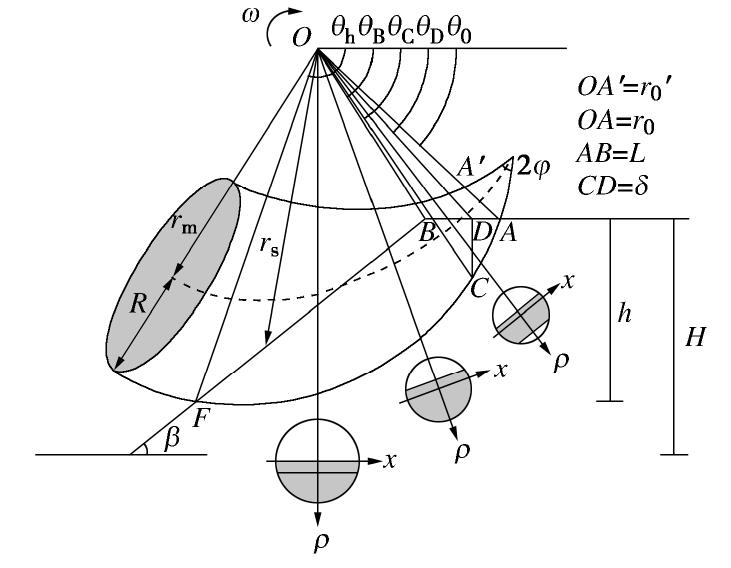
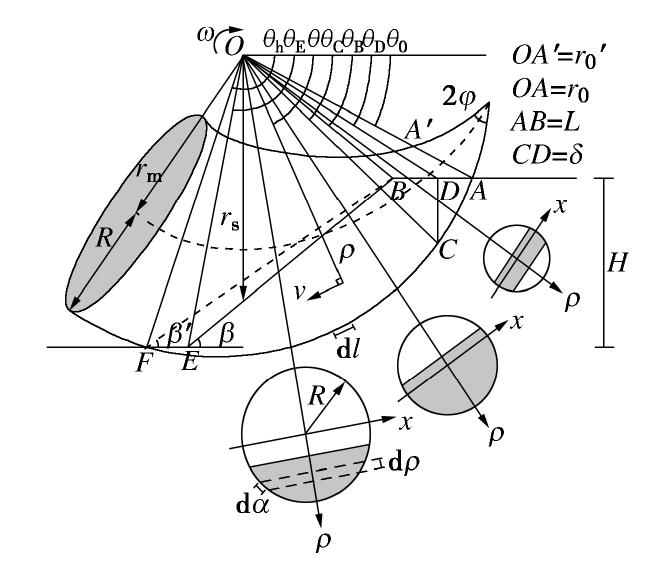
Michalowski等^[16]提出一种牛角状对数螺旋旋转破坏机构来描述边坡三维破坏状态,如图1所示。该机构是由顶角为2φ的对称曲线椎体构成,该锥体的对称面由上下两条对数螺旋线表示,分别为r= r₀exp[(θ-θ₀)tanφ]和r'=r₀'exp[-(θ-θ₀)tanφ]。基准线OA与OF对应的角度分别为θ₀和θ_h,长度为r₀和r_h。O为该机构的旋转轴。该牛角状对数螺旋锥体的横截面为一系列半径不断增大的圆截面,圆截面半径R= (r-r')/2,圆心轨迹r_m=(r+r')/2。边坡坡顶为L,坡高为H。由于所研究的对象是裂缝边坡,为消除拉应力的影响,在坡顶处引入一条竖直张拉裂缝CD,裂缝深度为δ。C为裂缝与下方对数螺旋线的交点,对应角度为θ_C,长度为r_C。ρ为土体内任意一点到旋转轴O的半径,对应破坏机构圆截面与旋转轴O的夹角为θ。对数螺旋锥体与边坡土体的相交部分为滑移块体,该块体视为刚性块体并绕着旋转轴O转动,转动角速度为ω,块体内部任意一点的滑移线速度v=ωρ,为了满足运动学许可的要求,滑动面处块体线速度与滑动面的夹角为土体内摩擦角φ。

图 1 裂缝边坡三维旋转破坏机构

Figure 1. Three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

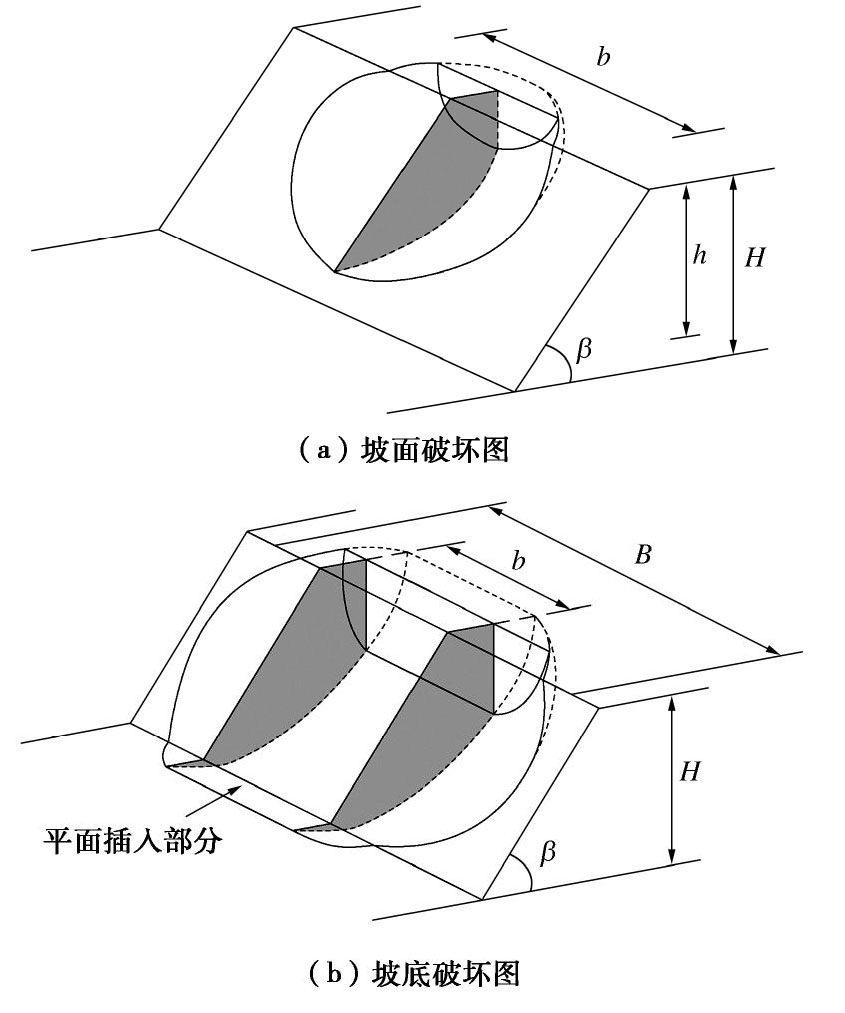
由于是对裂缝边坡破坏模式进行拓展分析,因此,引入机构参数n=h/H与β'用以判断边坡破坏模式,如图1和2所示。n<1时边坡发生坡面破坏；β'=β时边坡发生坡趾破坏；β'<β时边坡发生坡底破坏。

图 2 裂缝边坡三维旋转破坏拓展机构

Figure 2. Extended three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

当边坡周围存在土工建筑或坚硬岩石层时,边坡发生破坏时宽度变化范围有限,此时三维效应较明显,采用上述牛角状对数螺旋锥体机构来描述边坡破坏是较为合理的。但当边坡破坏时宽高比很大时,其破坏机制更接近与平面应变机制,对应于二维破坏模式。基于此,为了使边坡破坏能从三维模式转变为二维模式,在牛角状对数螺旋锥体对称面处插入横截面与对称面一致且宽度为b的块体,此时,边坡宽度为B,如图3所示。

图 3 平面应变机制插入示意图

Figure 3. Schematic diagram of insert portion of plane-strain mechanism

下载: 全尺寸图片幻灯片

2. 外功率和内功率

根据极限分析上限定理,通过建立能量平衡方程,可以得到极限荷载的上限解。本文仅考虑滑动土体自重作为外功率。由于将滑动块体视为刚性块体,发生在破坏面上的土体内能耗散作为内功率。能量平衡方程表达式为

$W_{γ} = D$ ,

(2)

式中,W_γ为土体自重功率,D为滑动土体沿破坏面内能耗散率。

2.1 外功率

根据上述裂缝边坡三维破坏机构,滑动土体自重功率分为两部分,其一为三维部分牛角状对数螺旋破化机构对应滑动土体自重功率W_γ^3D,其二为插入的二维部分平面应变机制对应土体自重功率W_γ^2D：

$W_{γ} = W_{γ}^{3D} + b \cdot W_{γ}^{2D}$ 。

(3)

二维部分土重所做功率采用Michalowski^[11]中的计算方法,此处不再赘述。三维部分土重功率可视为边坡ACEFB土重功率W_s1减去边坡ADC土重功率W_s2：

$W_{γ}^{3D} = W_{s1} - W_{s2}$ 。

(4)

在极坐标下,边坡ACEFB与边坡ADC轮廓线可用分段函数r_s1和r_s2表示,并将r_s1和r_s2统称为r_s：

$r_{s1} (θ) = {\begin{cases} r_{0} \frac{\sin θ_{0}}{\sin θ} θ_{0} < θ \leq θ_{B} \\ r_{0} \frac{\sin θ_{0} \sin (θ_{B} + β)}{\sin θ_{B} \sin (θ + β)} θ_{B} < θ \leq θ_{E} \\ r_{h} \frac{\sin θ_{h}}{\sin θ} θ_{E} < θ \leq θ_{h} \end{cases}$ ,

(5)

$r_{s2} (θ) = {\begin{cases} r_{0} \frac{\sin θ_{0}}{\sin θ} θ_{0} < θ \leq θ_{D} \\ r_{C} \frac{\cos θ_{C}}{\cos θ} θ_{D} < θ \leq θ_{C} \end{cases}$ 。

(6)

式中

$r_{C} = r_{0} e^{(θ_{C} - θ_{0}) \tan φ}$ ,

(7)

$θ_{B} = \arctan (\frac{r_{0} \sin θ_{0}}{r_{0} \cos θ_{0} - L})$ ,

(8)

$θ_{E} = \arctan (\frac{r_{h} \sin θ_{h}}{r_{0} \cos θ_{0} - L - H \cot β})$ ,

(9)

$θ_{D} = \arctan (\frac{r_{0} \sin θ_{0}}{r_{C} \cos θ_{C}})$ ,

(10)

$H = r_{h} \sin θ_{h} - r_{0} \sin θ_{0}$ ,

(11)

$L = \frac{1}{\sin β} [r_{0} \sin (θ_{0} + β) - r_{h} \sin (θ_{h} + β)]$ 。

(12)

取土体内任意一点,ρ为该点到旋转轴O的长度,对应角度为θ,速度为ωρ。则土体体积微元可表示为

$d V = 2 ρ \sqrt{R^{2} - {(ρ - r_{m})}^{2}} d ρ d θ$ ,

(13)

土重功率微元可由下式表示：

$d W = ω γ ρ^{2} \sqrt{R^{2} - {(ρ - r_{m})}^{2}} \cos θ d ρ d θ$ ,

(14)

式中, $γ$ 为土体重度。因此边坡ACEFB与边坡ADC土重功率表达式分别为^[20]

$W_{s1} = 2 ω γ \int_{θ_{0}}^{θ_{h}} \int_{r_{s1}}^{r} ρ^{2} \sqrt{R^{2} - {(ρ - r_{m})}^{2}} \cos θ d ρ d θ$ ,

(15)

$W_{s2} = 2 ω γ \int_{θ_{0}}^{θ_{C}} \int_{r_{s2}}^{r} ρ^{2} \sqrt{R^{2} - {(ρ - r_{m})}^{2}} \cos θ d ρ d θ$ 。

(16)

2.2 内功率

由于将滑移土体视为作刚体旋转破坏,土体发生剪胀的能量耗散率可忽略不计。土体内能耗散只发生在破坏面上。同样,土体内能耗散率由三维部分D^3D和二维部分D^2D组成

$D = D^{3D} + b \cdot D^{2D}$ 。

(17)

二维部分土体内能耗散率采用Michalowski^[11]中的计算方法,故此处不再赘述。同样,三维部分土体内能耗散率可视为边坡ACEFB内能耗散率D_s1减去边坡ADC内能耗散率D_s2：

$D^{3D} = D_{s1} - D_{s2}$ ,

(18)

取面积微元dS：

$d S = d l \cdot d α = \frac{ρ}{\cos θ} \frac{R}{\sqrt{R^{2} - {(ρ - r_{m})}^{2}}} d ρ d θ$ ,

(19)

因此边坡ACEFB与边坡ADC土体内能耗散率表达式分别为^[20]

$D_{s1} = 2 c ω \int_{θ_{0}}^{θ_{h}} \int_{r_{s1}}^{r} ρ^{2} \frac{R}{\sqrt{R^{2} - {(ρ - r_{m})}^{2}}} d ρ d θ$ ,

(20)

$D_{s2} = 2 c ω \int_{θ_{0}}^{θ_{C}} \int_{r_{s2}}^{r} ρ^{2} \frac{R}{\sqrt{R^{2} - {(ρ - r_{m})}^{2}}} d ρ d θ$ ,

(21)

式中,c为土体黏聚力。

2.3 安全系数

边坡稳定性分析常采用强度折减法,将土体的实际抗剪强度c和φ与维持土体极限平衡所需的黏聚力c_d和内摩擦角φ_d的比值定义为安全系数 $F_{S}$ ：

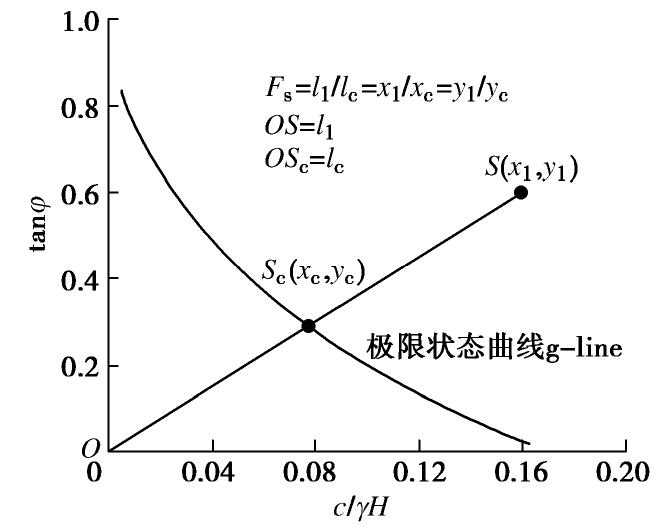
$F_{S} = \frac{c}{c_{d}} = \frac{\tan φ}{\tan φ_{d}}$ 。

(22)

一些学者提出了无须迭代即可计算边坡安全系数的稳定性图表^[21-26]。本文基于g-line图像法^[27],建立裂缝边坡三维稳定性图表。从图表中可以方便读取一个特定的边坡安全系数。读取安全系数方法如图4所示,S(x₁, y₁)代表土体的实际抗剪强度参数组合c/γH和tanφ,其与原点O的连线与极限状态曲线（g-line）相较于S_c(x_c, y_c)。安全系数可表示为

图 4 读取安全系数示意图

Figure 4. Schematic diagram of reading factor of safety

下载: 全尺寸图片幻灯片

$F_{S} = \frac{l_{1}}{l_{c}} = \frac{x_{1}}{x_{c}} = \frac{y_{1}}{y_{c}}$ ,

(23)

式中,l₁和l_c分别为OS和OS_c的长度。根据极限分析上限定理,令外功率等于内功率,可以得到边坡稳定系数N_S：

$\frac{γ H}{c} = N_{S} (θ_{0}, θ_{C}, θ_{h}, \frac{r_{0}^{'}}{r_{0}}, n, β^{'})$ 。

(24)

为了得到稳定系数N_S最小值,本文采用Chen^[28]中提到的优化方法进行求解。利用蒙特卡洛模拟法得到一个较为合理的初值x₀,再运用模式搜索法利用此初值x₀求其最优上限解,进而可得到c/γH的最大值。

3. 对比验证

验证本文模型和公式推导的正确性,将本文所求结果与现有文献结果进行对比。一般边坡宽高比B/H为0.5～3.0时,边坡破坏时三维效应较为明显,在不考虑坡顶存在裂缝情况下,计算所得三维边坡的稳定系数γH/c与文献[19]和文献[20]的结果进行对比,如表1所示。由表1可以看出,本文求解边坡的稳定系数的结果与文献[19]和文献[20]具有良好的一致性,且结果与文献[20]的结果更为接近。原因在于相比于文献[19]采用的内外功率计算公式,本文所推导的计算公式更为严谨,在优化过程中不必考虑几何约束r_m≤r_s的影响,避免了影响最危险破坏面的搜索,如图5所示。在考虑坡顶存在垂直张拉裂缝情况下,将本文结果与文献[17]的结果进行对比,如表2所示。从表2可知,本文的结果略高于文献[17]的结果且两者最大误差不超过1%。对比结果说明本机构在求解裂缝边坡三维稳定性方面是有效的,充分证明了本文模型和所导公式的正确性。

表 1 不考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 1. Comparison of 3D stability factors of slopes without cracks

β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	γH/c
β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	本文解答	文献[19]解答	文献[20]解答
30	15	0.5	53.69	97.25	0.941	73.106^a	73.156^a	73.120^a
45	15	0.5	30.39	89.54	0.888	32.184^a	32.371^a	32.198^a
	30	0.8	57.27	95.34	0.856	62.121	62.213	62.121
60	15	0.5	14.43	80.14	0.843	20.889^a	21.512^a	20.805^a
	30	0.8	42.14	87.18	0.739	26.464	26.486	26.464
注：^a坡面破坏。

下载: 导出CSV

| 显示表格

图 5 几何约束对三维破坏机构的影响

Figure 5. Influences of geometric constraints on 3D failure mechanism

下载: 全尺寸图片幻灯片

表 2 考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 2. Comparison of 3D stability factors of slopes with cracks

β/(°)	φ/(°)	B/H	γH/c
β/(°)	φ/(°)	B/H	本文解答	文献[17]解答
30	10	0.8	28.00	27.74
	20	3.0	47.81	47.75
45	10	0.8	15.82	15.68
	20	3.0	17.54	17.53
60	10	0.8	11.15	11.07
	20	3.0	10.60	10.59
70	10	0.8	8.33	8.26
	20	3.0	7.02	7.01

下载: 导出CSV

| 显示表格

4. 结果与分析

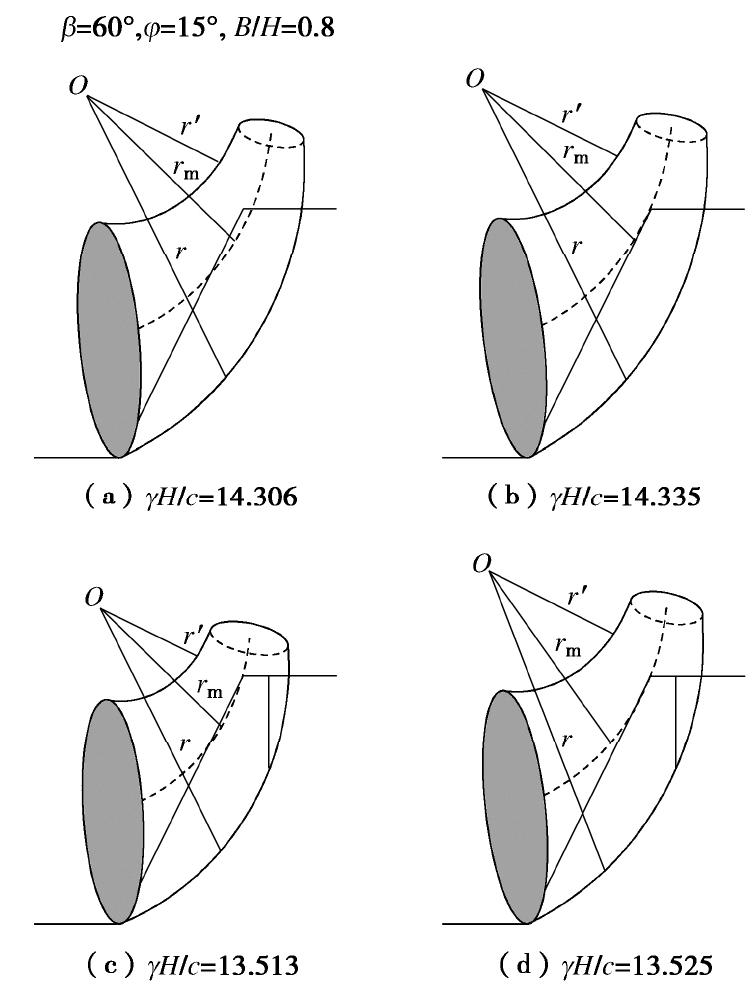
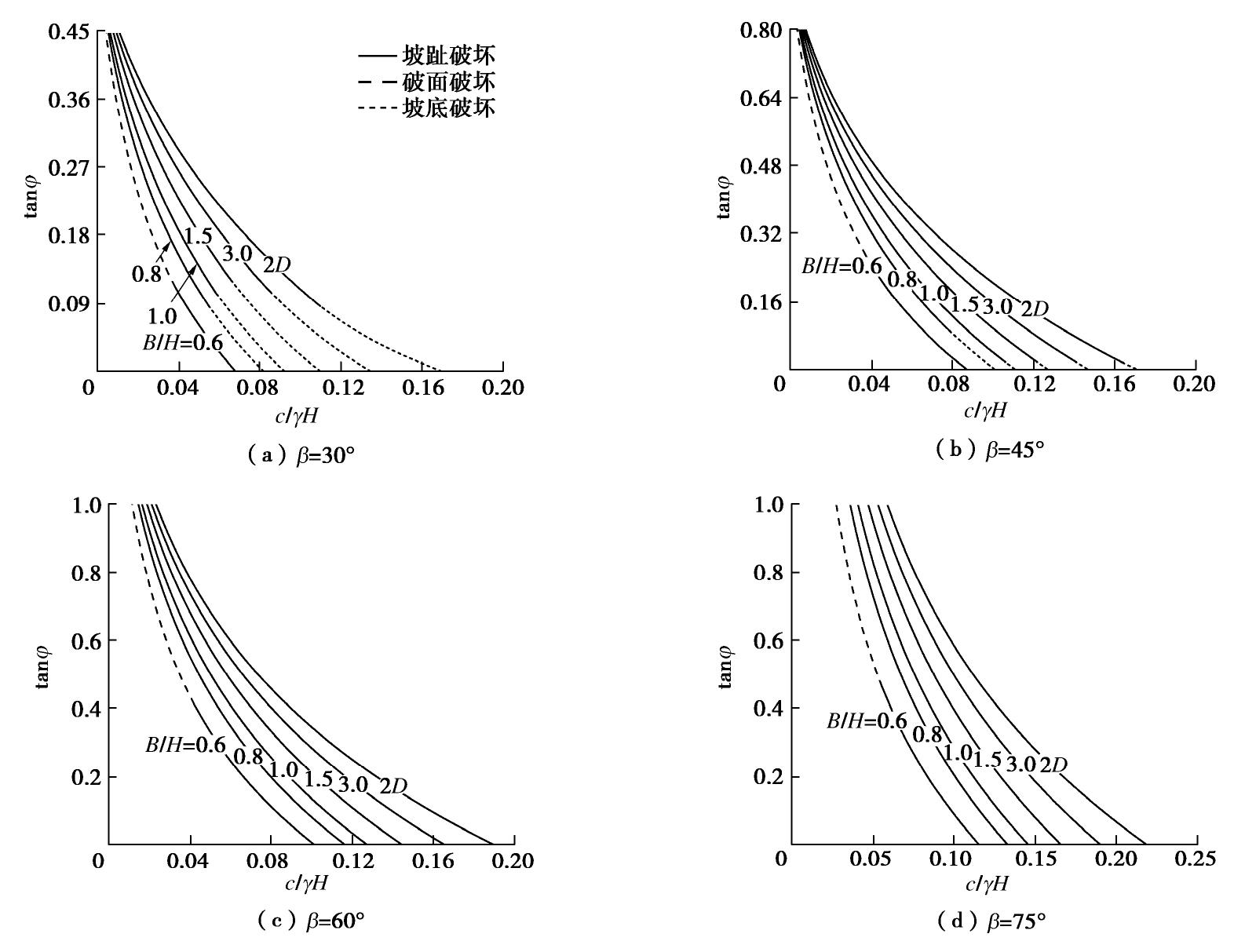
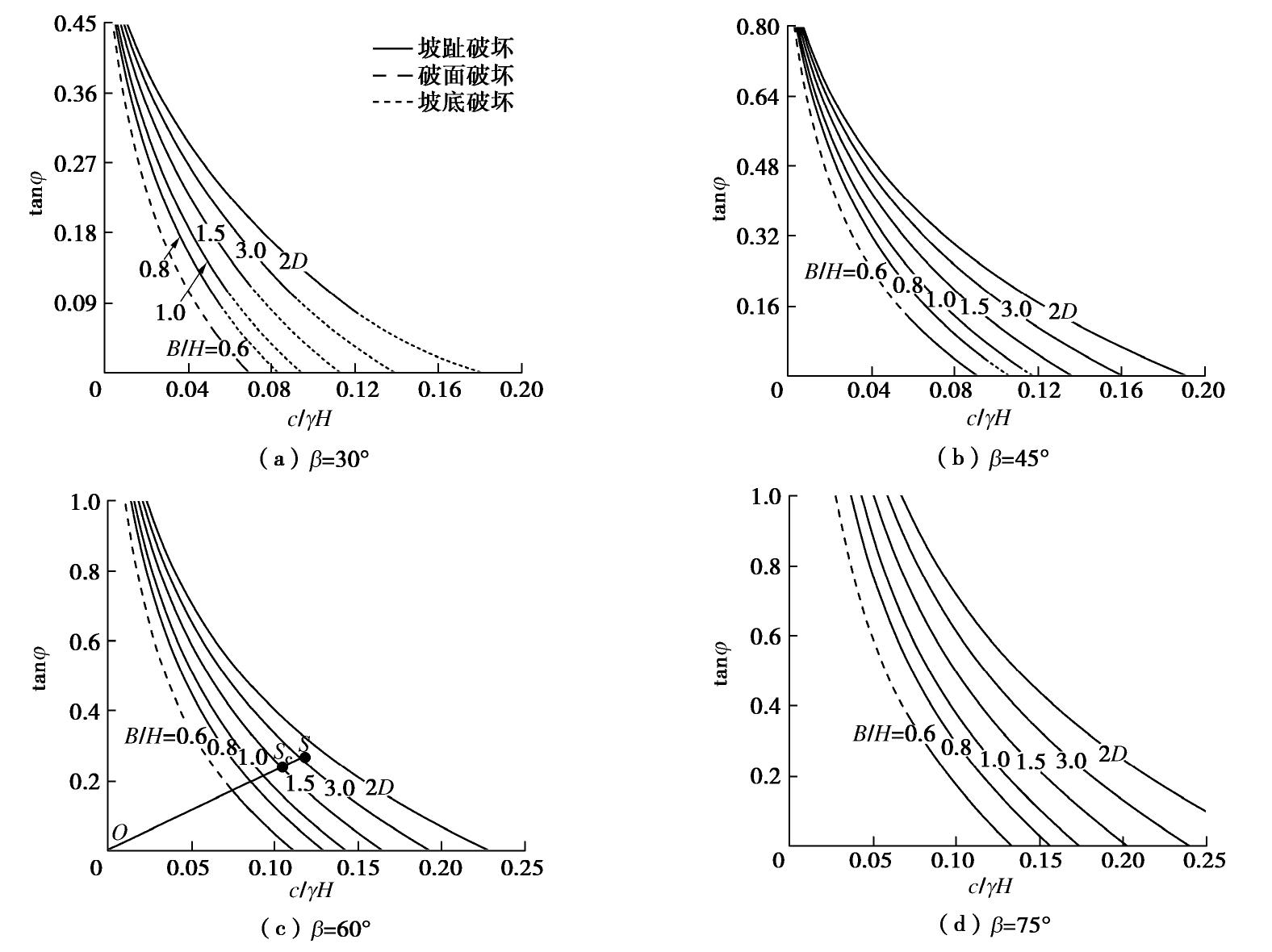
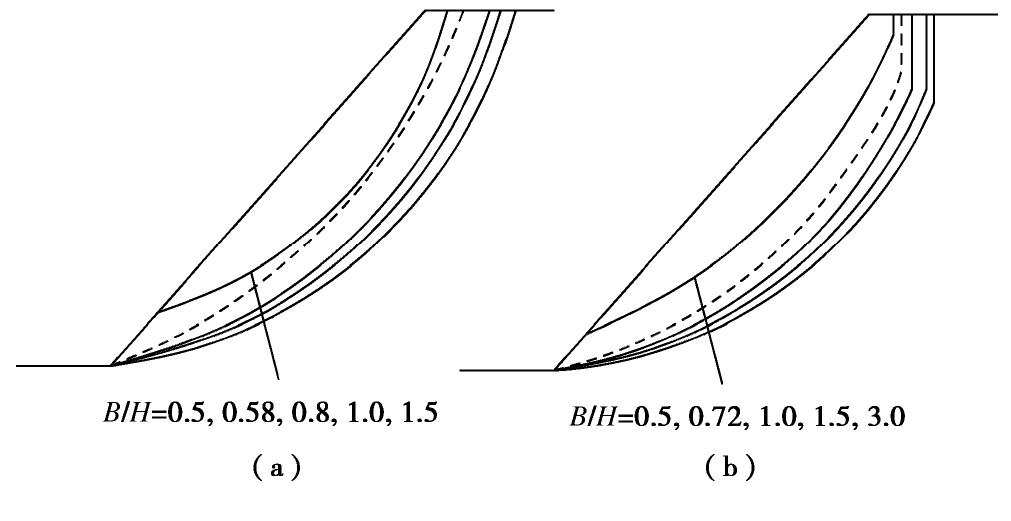
根据g-line图表法绘制出边坡稳定性图表,分别取不同的坡角β为30°,45°,60°和75°。如图6和7所示。当β=90°时,即垂直边坡,在求解边坡稳定系数最优上限解过程中,参数裂缝深度δ/H接近于1,即裂缝深度与边坡高度基本相等,将导致稳定系数接近于0,故此处未给出垂直边坡坡顶存在裂缝的稳定性图表。从图6和7可以看出,裂缝的存在将降低边坡的稳定性,且裂缝的不利影响随着坡角β的增大而增大。随着内摩擦角φ的增加,c/γH的值减小,且随着边坡宽高比B/H的增大,c/γH减小的幅度增加,即随着φ的增大,边坡稳定系数增加,边坡更加稳定。当B/H=0.6时,随着φ的增大,破坏模式从坡趾破坏逐渐转向坡面破坏,且随着β的增大,破坏模式由坡趾破坏转向坡面破坏所需的内摩擦角也逐渐增加。同时边坡宽高比B/H对破坏模式也有所影响。如同文献[27]中提到,由于在B/H减小时,三维破坏机构中二维插入块体宽度逐渐减小至0,并随着B/H进一步缩小,三维破坏机构无法形成迫使边坡发生坡面破坏,此时参数n<1。如图8所示,随着B/H的减小,三维破坏机构下方对数螺旋破坏线逐渐向坡面靠近,图8中虚线表示坡趾破坏模式与坡面破坏模式的分界线,相当于文献[27]中提到的B/H^*,即B/H < B/H^*时,边坡发生坡面破坏。同时,三维破坏机构内边坡土体体积逐渐减小。对于边坡而言,稳定系数N_S越大,相当于边坡发生坍塌时的破坏规模要越小,显然这种概率很小,故稳定系数越大的边坡较难发生破坏。当β=30°时,在B/H处于0.8～3.0之间,随着内摩擦角φ的增大,边坡破坏模式从坡底破坏逐渐转向坡趾破坏,且在B/H=1.5时,破坏模式转化所需内摩擦角较大。而在β=45°,仅在φ<5°情况下发生坡底破坏,对于坡顶存在裂缝,基本上都是坡趾破坏。而相对于β≥45°的边坡来说,其破坏模式都是坡趾破坏。

图 6 不考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 6. Stability charts of 3D slopes without cracks on upper surface

下载: 全尺寸图片幻灯片

图 7 考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 7. Stability charts of 3D slopes with cracks on upper surface

下载: 全尺寸图片幻灯片

图 8 边坡宽度对三维破坏机构的影响

Figure 8. Influences of slope width on 3D failure mechanism

下载: 全尺寸图片幻灯片

根据绘制的稳定性图表可以快速读取边坡的安全系数,以文献[20]为例,考虑坡角β=60°,坡高H=10 m的土坡。土体抗剪强度参数分别是黏聚力c=20 kPa和内摩擦角φ=15°,土体重度 $γ$ =17 kN/m³。故c/γH=0.118和tanφ=0.268,如图7（c）所示,OS的斜率为2.281,与B/H=1.5相交于S_c,其横坐标为0.104。则安全系数 $F_{S}$ =0.118/0.104≈1.13。与文献[20]中不考虑坡顶裂缝情况下边坡的安全系数F≈1.20相比,再次表明了裂缝的存在会降低边坡的稳定性。

表3和表4给出来了在φ=15°和φ=30°情况下边坡的稳定系数N_S以及对应的裂缝深度和位置。图10表明了三维效应对裂缝深度的影响。由表3和表4可知,对于β=30°的边坡,坡顶产生的裂缝深度都很小,基本上接近于0,例如B/H=0.5和B/H=3.0时,φ=30°,坡顶裂缝的裂缝深度δ/H分别为0.001和0.098,且此时的稳定系数与坡顶无裂缝情况非常接近,因此对于具有β≤30°的边坡,可不考虑坡顶是否存在裂缝。可以从图8（b）、图9和图10可以看出,随着β和B/H的增大,裂缝深度逐渐增大,且裂缝位置逐渐远离坡肩。表明当三维效应逐渐趋近于0时,裂缝的存在对陡坡的影响较大,且裂缝深度随着B/H的增大而增大。但对于β=75°的边坡,裂缝深度随着B/H的增大先增大再减小,例如,φ=15°,B/H=0.6时裂缝裂缝深度最大,δ/H=0.599,分别比B/H=0.5和B/H=3.0高出25.58%和11.13%。

表 3 边坡稳定系数(φ=15°)

Table 3. Stability factors of slopes (φ=15°)

B/H		β/(°)
		30			45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	73.155^a	0.003	0.043	31.978^a	0.126	0.041	19.903^a	0.331	0.041	14.085^a	0.477	0.070
0.5	IN	73.106^a	—	—	32.184^a	—	—	20.889^a	—	—	15.834^a	—	—
0.6	PC	61.199^a	0.015	0.075	26.685	0.145	0.043	16.670	0.389	0.057	11.713	0.599	0.082
0.6	IN	61.002^a	—	—	26.725	—	—	17.482	—	—	13.322	—	—
0.8	PC	46.051	0.021	0.107	20.913	0.186	0.111	13.524	0.392	0.117	9.598	0.587	0.126
0.8	IN	46.071	—	—	21.220	—	—	14.306	—	—	10.936	—	—
1.0	PC	38.698	0.046	0.123	18.230	0.211	0.136	11.965	0.386	0.148	8.505	0.571	0.150
1.0	IN	38.795	—	—	18.648	—	—	12.786	—	—	9.797	—	—
1.5	PC	30.874	0.084	0.145	15.298	0.234	0.173	10.190	0.382	0.186	7.217	0.553	0.182
1.5	IN	31.126	—	—	15.855	—	—	11.087	—	—	8.503	—	—
3.0	PC	25.124	0.114	0.170	12.994	0.248	0.207	8.722	0.379	0.220	6.111	0.539	0.211
3.0	IN	25.540	—	—	13.686	—	—	9.714	—	—	7.433	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

| 显示表格

表 4 边坡稳定系数(φ=30°)

Table 4. Stability factors of slopes (φ=30°)

B/H		β/(°)
		45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	96.560^a	0.001	0.040	40.219^a	0.125	0.041	23.673^a	0.389	0.029
0.5	IN	96.417^a	—	—	40.590^a	—	—	25.446^a	—	—
0.6	PC	80.718^a	0.021	0.061	33.511^a	0.187	0.042	19.361^a	0.552	0.016
0.6	IN	80.287^a	—	—	33.935^a	—	—	21.226^a	—	—
0.8	PC	61.978	0.045	0.067	25.882	0.263	0.061	15.137	0.523	0.081
0.8	IN	62.121	—	—	26.464	—	—	16.534	—	—
1.0	PC	53.724	0.068	0.069	22.644	0.250	0.092	13.261	0.491	0.107
1.0	IN	54.066	—	—	23.398	—	—	14.647	—	—
1.5	PC	45.243	0.088	0.076	19.260	0.251	0.115	11.186	0.466	0.134
1.5	IN	45.836	—	—	20.216	—	—	12.652	—	—
3.0	PC	39.061	0.098	0.084	16.677	0.252	0.132	9.516	0.452	0.156
3.0	IN	39.864	—	—	17.830	—	—	11.120	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

| 显示表格

图 9 三维效应下边坡坡角对裂缝深度的影响

Figure 9. Influences of slope inclination on crack depth under 3D condition

下载: 全尺寸图片幻灯片

图 10 三维效应对裂缝深度的影响

Figure 10. Influences of three-dimensional effects on crack depth

下载: 全尺寸图片幻灯片

5. 结论

基于极限分析上限定理,在三维牛角状旋转破坏机构引入一条张拉裂缝研究裂缝边坡的稳定性,并对边坡破坏模式进行拓展分析,运用g-line图像法绘制出边坡稳定性图表以便直接获取边坡安全系数。所得主要结论如下：

（1）无论坡顶是否存在裂缝,对于任意一个特定的边坡,都存在一个B/H^*,当边坡宽高比B/H < B/H^*时,边坡只能发生坡面破坏,且此时裂缝的影响可以忽略不计。

（2）在φ<5°情况下,边坡更倾向于发生坡底破坏；考虑裂缝存在时,该破坏模式发生的范围变小。随着B/H的增大,β=30°的边坡发生坡底破坏的所需的内摩擦角先增大后减小,而对于β≥45°的边坡来说,只有在φ=1°左右时发生坡底破坏。

（3）对于β≤30°的边坡可以忽略裂缝的影响。且随着β和B/H的增大,裂缝深度逐渐增加,裂缝位置逐渐远离坡肩。β=75°的边坡裂缝深度随B/H的增大先增大后减小,并在B/H=0.6时,裂缝深度达到最大。

图 1 裂缝边坡三维旋转破坏机构

Figure 1. Three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

图 2 裂缝边坡三维旋转破坏拓展机构

Figure 2. Extended three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

图 3 平面应变机制插入示意图

Figure 3. Schematic diagram of insert portion of plane-strain mechanism

下载: 全尺寸图片幻灯片

图 4 读取安全系数示意图

Figure 4. Schematic diagram of reading factor of safety

下载: 全尺寸图片幻灯片

图 5 几何约束对三维破坏机构的影响

Figure 5. Influences of geometric constraints on 3D failure mechanism

下载: 全尺寸图片幻灯片

图 6 不考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 6. Stability charts of 3D slopes without cracks on upper surface

下载: 全尺寸图片幻灯片

图 7 考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 7. Stability charts of 3D slopes with cracks on upper surface

下载: 全尺寸图片幻灯片

图 8 边坡宽度对三维破坏机构的影响

Figure 8. Influences of slope width on 3D failure mechanism

下载: 全尺寸图片幻灯片

图 9 三维效应下边坡坡角对裂缝深度的影响

Figure 9. Influences of slope inclination on crack depth under 3D condition

下载: 全尺寸图片幻灯片

图 10 三维效应对裂缝深度的影响

Figure 10. Influences of three-dimensional effects on crack depth

下载: 全尺寸图片幻灯片

表 1 不考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 1 Comparison of 3D stability factors of slopes without cracks

β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	γH/c
β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	本文解答	文献[19]解答	文献[20]解答
30	15	0.5	53.69	97.25	0.941	73.106^a	73.156^a	73.120^a
45	15	0.5	30.39	89.54	0.888	32.184^a	32.371^a	32.198^a
	30	0.8	57.27	95.34	0.856	62.121	62.213	62.121
60	15	0.5	14.43	80.14	0.843	20.889^a	21.512^a	20.805^a
	30	0.8	42.14	87.18	0.739	26.464	26.486	26.464
注：^a坡面破坏。

下载: 导出CSV

表 2 考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 2 Comparison of 3D stability factors of slopes with cracks

β/(°)	φ/(°)	B/H	γH/c
β/(°)	φ/(°)	B/H	本文解答	文献[17]解答
30	10	0.8	28.00	27.74
	20	3.0	47.81	47.75
45	10	0.8	15.82	15.68
	20	3.0	17.54	17.53
60	10	0.8	11.15	11.07
	20	3.0	10.60	10.59
70	10	0.8	8.33	8.26
	20	3.0	7.02	7.01

下载: 导出CSV

表 3 边坡稳定系数(φ=15°)

Table 3 Stability factors of slopes (φ=15°)

B/H		β/(°)
		30			45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	73.155^a	0.003	0.043	31.978^a	0.126	0.041	19.903^a	0.331	0.041	14.085^a	0.477	0.070
0.5	IN	73.106^a	—	—	32.184^a	—	—	20.889^a	—	—	15.834^a	—	—
0.6	PC	61.199^a	0.015	0.075	26.685	0.145	0.043	16.670	0.389	0.057	11.713	0.599	0.082
0.6	IN	61.002^a	—	—	26.725	—	—	17.482	—	—	13.322	—	—
0.8	PC	46.051	0.021	0.107	20.913	0.186	0.111	13.524	0.392	0.117	9.598	0.587	0.126
0.8	IN	46.071	—	—	21.220	—	—	14.306	—	—	10.936	—	—
1.0	PC	38.698	0.046	0.123	18.230	0.211	0.136	11.965	0.386	0.148	8.505	0.571	0.150
1.0	IN	38.795	—	—	18.648	—	—	12.786	—	—	9.797	—	—
1.5	PC	30.874	0.084	0.145	15.298	0.234	0.173	10.190	0.382	0.186	7.217	0.553	0.182
1.5	IN	31.126	—	—	15.855	—	—	11.087	—	—	8.503	—	—
3.0	PC	25.124	0.114	0.170	12.994	0.248	0.207	8.722	0.379	0.220	6.111	0.539	0.211
3.0	IN	25.540	—	—	13.686	—	—	9.714	—	—	7.433	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

表 4 边坡稳定系数(φ=30°)

Table 4 Stability factors of slopes (φ=30°)

B/H		β/(°)
		45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	96.560^a	0.001	0.040	40.219^a	0.125	0.041	23.673^a	0.389	0.029
0.5	IN	96.417^a	—	—	40.590^a	—	—	25.446^a	—	—
0.6	PC	80.718^a	0.021	0.061	33.511^a	0.187	0.042	19.361^a	0.552	0.016
0.6	IN	80.287^a	—	—	33.935^a	—	—	21.226^a	—	—
0.8	PC	61.978	0.045	0.067	25.882	0.263	0.061	15.137	0.523	0.081
0.8	IN	62.121	—	—	26.464	—	—	16.534	—	—
1.0	PC	53.724	0.068	0.069	22.644	0.250	0.092	13.261	0.491	0.107
1.0	IN	54.066	—	—	23.398	—	—	14.647	—	—
1.5	PC	45.243	0.088	0.076	19.260	0.251	0.115	11.186	0.466	0.134
1.5	IN	45.836	—	—	20.216	—	—	12.652	—	—
3.0	PC	39.061	0.098	0.084	16.677	0.252	0.132	9.516	0.452	0.156
3.0	IN	39.864	—	—	17.830	—	—	11.120	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

参考文献(28)

[1]	陈祖煜. 土质边坡稳定分析：原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu. Soil Slope Stability Analysis[M]. Beijing: China Water Power Press, 2003. (in Chinese)
[2]	陈曦, 刘春杰. 有限元强度折减法中安全系数的搜索算法[J]. 岩土工程学报, 2010, 32(9): 1443-1447. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201009028.htm CHEN Xi, LIU Chun-jie. Search algorithms for safety factor in finite element shear strength reduction method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1443-1447. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201009028.htm
[3]	DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157-165. doi: 10.1090/qam/48291
[4]	刘锋, 芮勇勤, 张春. 坡顶张拉裂缝对边坡稳定性影响[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(9): 949-954. https://www.cnki.com.cn/Article/CJFDTOTAL-FXKY201609010.htm LIU Feng, RUI Yong-qin, ZHANG Chun. Influence of tension cracks of slope crest on the stability of slope[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35(9): 945-954. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FXKY201609010.htm
[5]	秦会来, 周予启, 黄茂松, 等. 基于上限理论的预留土支护基坑极限抗力分析[J]. 岩土工程学报, 2020, 42(6): 1101-1107. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006017.htm QIN Hui-lai, ZHOU Yu-qi, HUANG Mao-song, et al. Passive earth pressure analysis of berm-retained excavation by upper bound method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 1101-1107. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006017.htm
[6]	吴梦喜, 杨家修, 湛正刚. 边坡稳定分析的虚功率法[J]. 力学学报, 2020, 52(3): 663-672. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202003007.htm WU Meng-xi, YANG Jia-xiu, ZHAN Zheng-gang. A virtual power slope stability analysis method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 663-672. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202003007.htm
[7]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Science, 1975.
[8]	TERZAGHI K. Theoretical Soil Mechanics[M]. New York: Wiley, 1943.
[9]	SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11-26. doi: 10.1680/geot.1967.17.1.11
[10]	COUSINS B F. Stability charts for simple earth slopes allowing for tension cracks[C]//Proceedings of the Third Australia-New Zealand Conference on Geomechanics, 1980, Wellington.
[11]	MICHALOWSKI R L. Stability assessment of slopes with cracks using limit analysis[J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021. doi: 10.1139/cgj-2012-0448
[12]	UTILI S. Investigation by limit analysis on the stability of slopes with cracks[J]. Géotechnique, 2013, 63(2): 140-154. doi: 10.1680/geot.11.P.068
[13]	ZHAO L H, CHENG X, ZHANG Y, et al. Stability analysis of seismic slopes with cracks[J]. Computers and Geotechnics, 2016, 77: 77-90. doi: 10.1016/j.compgeo.2016.04.007
[14]	何毅, 余军炎, 袁冉, 等. 考虑坡顶倾角的土质裂隙边坡稳定性分析[J]. 中国公路学报, 2021, 34(5): 45-54. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105005.htm HE Yi, YU Jun-yan, YUAN Ran, et al. Stability analysis of soil slope with cracks considering upper slope inclination angle[J]. China Jouranl of Highway and Transport, 2021, 34(5): 45-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105005.htm
[15]	周志军, 朱林楦, 陈磊. 倾斜坡顶黄土边坡垂直裂隙深度计算方法[J]. 中国公路学报, 2021, 34(5): 37-44. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105004.htm ZHOU Zhi-jun, ZHU Lin-xuan, CHEN Lei. Calculation method of vertical crack depth of loess slope with inclined crest[J]. China Journal of Highway and Transport, 2021, 34(5): 37-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105004.htm
[16]	MICHALOWSKI R L, DRESCHER A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839-850.
[17]	HE Y, LIU Y, ZHANG Y, et al. Stability assessment of three-dimensional slopes with cracks[J]. Engineering Geology, 2019, 252: 136-144.
[18]	LI Z W, YANG X L, LI T Z. Static and seismic stability assessment of 3D slopes with cracks[J]. Engineering Geology, 2019, 265: 105450.
[19]	GAO Y F, ZHANG F, LEI G H, et al. An extended limit analysis of three-dimensional slope stability[J]. Géotechnique, 2013, 63(6): 518.
[20]	DOWON P, MICHALOWSKI R L. Intricacies in three-dimensional limit analysis of earth slopes[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(17): 2109-2129.
[21]	SUN J, ZHAO Z. Stability charts for homogenous soil slopes[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2013, 139(12): 2212-2218.
[22]	孙超伟, 柴军瑞, 许增光, 等. 求解三维均质边坡安全系数的稳定性图表法研究[J]. 岩土工程学报, 2018, 40(11): 2068-2077. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201811015.htm SUN Chao-wei, CHAI Jun-rui, XU Zeng-guang, et al. Stability charts for determining safety factors of 3D homogeneous slopes[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2068-2077. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201811015.htm
[23]	GAO Y F, ZHANG F, LEI G H, et al. Stability charts for 3D failures of homogeneous slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1528-1538.
[24]	LI A J, MERIFIELD R S, LYAMIN A V. Three-dimensional stability charts for slopes based on limit analysis methods[J]. Canadian Geotechnical Journal, 2010, 47(12): 1316-1334.
[25]	RAO P P, ZHAO L X, CHEN Q S, et al. Three-dimensional limit analysis of slopes reinforced with piles in soils exhibiting heterogeneity and anisotropy[J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 194-199.
[26]	MICHALOWSKI R L. Stability charts for uniform slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(4): 351-355.
[27]	QIN C, CHIAN S C. New perspective on seismic slope stability analysis[J]. International Journal of Geomechanics, 2018, 18(7): 1-8.
[28]	CHEN Z Y. Random trials used in determining global minimum factors of safety of slopes[J]. Canadian Geotechnical Journal, 1992, 29(2): 225-233.

施引文献(13)

期刊类型引用(7)

1.	刘华仁，佟大威，余佳，苏哲. 基于模糊聚类和随机子空间的高土石坝模态参数自动识别. 水力发电学报. 2025(02): 107-115 . 百度学术
2.	蔡正银，范开放，朱洵. 基于现场试验的海上筒型基础风电结构动力特性研究. 岩土工程学报. 2025(03): 443-452 . 本站查看
3.	张翰，张锋，谭尧升，姚孟迪，邓检华. 基于运行时模态分析和代理模型的大坝力学参数反演方法. 粉煤灰综合利用. 2025(01): 163-166 . 百度学术
4.	王晓澎，张浩，李欣，肖森，刘璇. 基于随机子空间法的滑动轴承运行模态参数识别. 噪声与振动控制. 2024(01): 126-133 . 百度学术
5.	樊圆，卢文胜，虞终军，任祥香. 多次地震作用下高层建筑结构动力特性识别和响应分析. 建筑结构学报. 2023(01): 225-234 . 百度学术
6.	翟世龙，刘萍，黄静，艾萨·伊斯马伊力，毛玉剑. 基于大坝地震反应台阵的土石坝模态参数识别. 内陆地震. 2023(04): 353-361 . 百度学术
7.	黄嘉思，徐文城，段元锋，章红梅. 基于随机子空间方法的向量式有限元索网模型模态识别. 结构工程师. 2022(06): 1-6 . 百度学术