0.   引言

为确保高堆石坝的安全并达到经济合理地建坝的目标,通常需要预测堆石坝的应力变形性状,针对性地采取工程设计和施工措施。因此,研究堆石料的力学特性,寻求能真实反映其应力变形特性的本构模型,达到较真实地预测堆石坝尤其是高堆石坝的应力变形性状一直是岩土力学和水工结构工程科技人员研究解决的课题^[1]。

堆石料的应力应变关系受到堆石料母岩特性、颗粒级配、密实程度、应力状态、颗粒破碎、材料湿化和劣化等等多因素的影响。虽然有试料的缩制和应力路径的限制,在研究缩制方法、缩尺效应的影响、提高测试技术的基础上,三轴压缩试验一直是测定堆石料力学特性和建立其本构模型的主要手段。

中国的堆石坝坝高已经达到300 m级,实测结果表明高坝的变形随坝高显著增加,工程界常用的邓肯E–B非线性弹性模型和南水双屈服面弹塑性模型预测的高土石坝的变形往往偏小。为此,学者们提出了一些考虑高应力下堆石料颗粒破碎的弹塑性本构模型,以期望高堆石坝的数值分析结果更符合实际^[2-15]。蔡正银等^[16]指出了堆石料颗粒级配和破碎对其临界状态的影响。张丙印等^[17]提出将修正Rowe剪胀方程引入到南水模型中来改善南水模型在高应力水平和轴向应变较大时拟合${\epsilon }_{\text{v}}$–${\epsilon }_{\text{i}}$的效果。Wan等^[18-19]基于能量损耗原理修正了Rowe剪胀方程、成功拟合Sacramento河砂三轴压缩试验成果。

三轴压缩试验是研究堆石料应力变形特性以及构建颗粒破碎本构模型的基础。高质量的三轴试验数据得来不易。首先,为了达到临界状态,高围压下试样的轴向应变通常要超过规程规定的15%,最好能做到25%。其次,由于堆石试料有尖锐棱角,试验中乳胶膜易被刺破,压力室的水进入试样会导致试验失败。因此,目前已取得的周围压力3.5 MPa、轴向应变25%、轴向应变速率小于0.1%/min的试验数据极少。颗粒破碎本构模型大多缺少高围压2～3.5 MPa且轴向应变20%以上的试验数据支撑。

本文进行水布垭面板堆石坝的堆石料三轴压缩试验,取得了周围压力0.2～3.5 MPa、轴向应变达到25%、轴向应变速率<0.1%/min的31组试验成果,研究了在不同围压条件下堆石料的颗粒破碎特性和剪胀特性,分析了堆石料达到临界状态的判断标准,进一步修正了Rowe剪胀方程,以期使考虑高应力下堆石料颗粒破碎的本构方程更适宜预测300 m级高堆石坝的应力变形性状。

1.   堆石料三轴压缩试验

试料为水布垭面板堆石坝料场采集的茅口组灰岩堆石料。其物理性质为：相对密度为2.73,岩块密度为2.69 g/cm³,饱和吸水率为0.76%,饱和时极限抗压强度为68.1 MPa,干态极限强度为87.3 MPa,软化系数为0.78。试料依照《土工试验规程》SL 237—1999要求采用混合法制备,试样干密度2.18,2.20 g/cm³。

采用三峡大学1500 kN微机控制电液伺服静态大型三轴试验机,进行固结排水三轴压缩试验,该仪器最大围压为4 MPa,轴应变量程30%。试样直径300 mm,高600 mm。

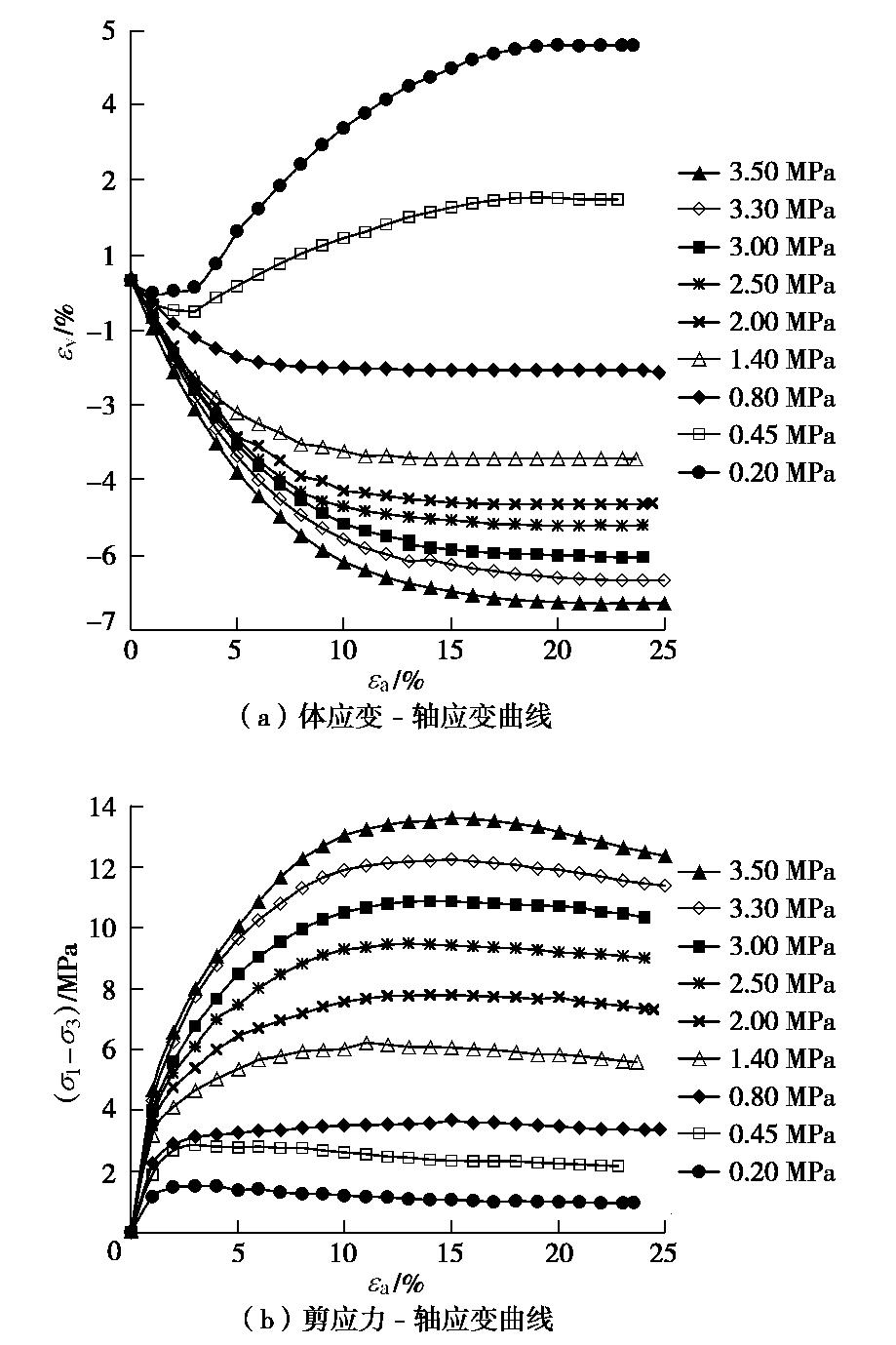
试验轴向应变速率取0.083%/min（即轴向变形速率0.5mm/min）,周围压力0.2,0.45,0.8,1.4,2.0,2.5,3.0,3.3,3.5 MPa。典型试验曲线见图1。

图  1  体应变、剪应力–轴应变曲线

Figure  1.  Relationship among volumetric strain shear stress and axial strain

下载: 全尺寸图片 幻灯片

依据图1所示试验结果,本文可将三轴试验的0.8 MPa以下围压称为低围压,0.8 MPa<${\sigma }_3$≤3.0 MPa围压称为高围压,3.0 MPa以上围压称为超高围压。

2.   堆石料的剪胀特性

2.1   临界状态线

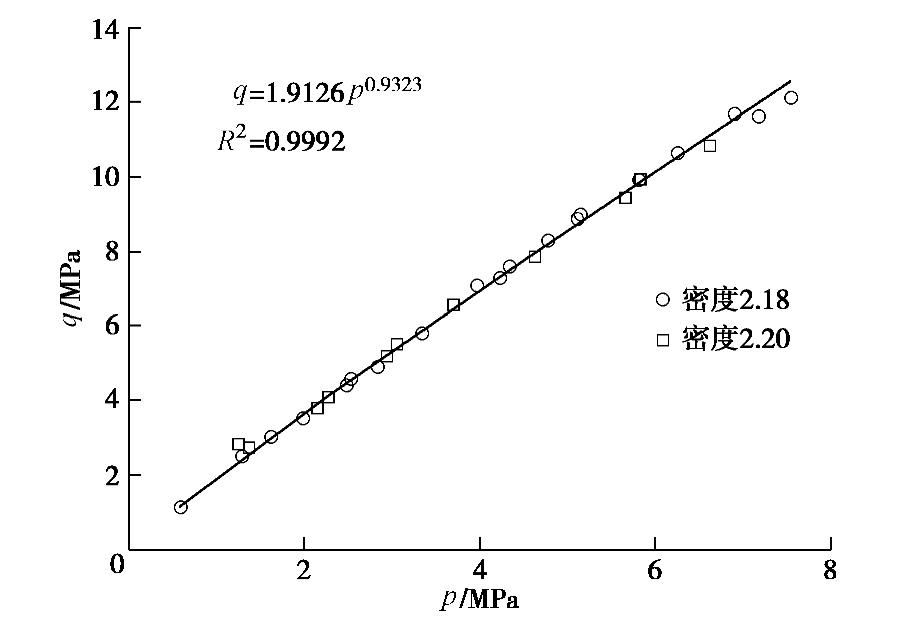
根据31组大型三轴压缩试验数据,整理得到了临界状态剪应力q与平均主应力$p$的关系曲线,见图2所示。两者之间呈幂函数关系：

图  2  剪应力q与平均主应力p幂函数关系

Figure  2.  Power relationship between shear stress and main stress

下载: 全尺寸图片 幻灯片

幂函数拟合方差为0.9992。当$p$=0,q=0,拟合的幂曲线,像经典的剑桥模型^[20]中的临界状态线那样经过原点,随着围压${\sigma }_3$增大,临界状态应力比$M_{\text{f}}$减小。围压${\sigma }_3$=0.2 MPa时,临界状态应力比$q/p=$$M_{\text{f}}$= 1.967；围压${\sigma }_3$=3.5 MPa时,临界状态应力比$M_{\text{f}}$= 1.608。

300 m级高堆石坝自重应力很大,例如拟建的315 m的如美堆石坝,坝底处最大自重应力约为6.9 MPa。大多数三轴试验最大的围压是1.5～3.0 MPa,由于试验设备限制、本文三轴试验最大围压${\sigma }_3$也仅3.5 MPa。因此式（1）可用来预测围压超过3.5 MPa的临界状态应力比$M_{\text{f}}$。将公式$q=1.9126p^{0.9323}$改写为$q/p=$$M_{\text{f}}=1.9126/p^{0.0673}$。可以看出随着周围压力的增大,堆石料将发生更多的颗粒破碎,临界状态应力比$M_{\text{f}}$显著减小。

2.2   颗粒破碎率与围压关系

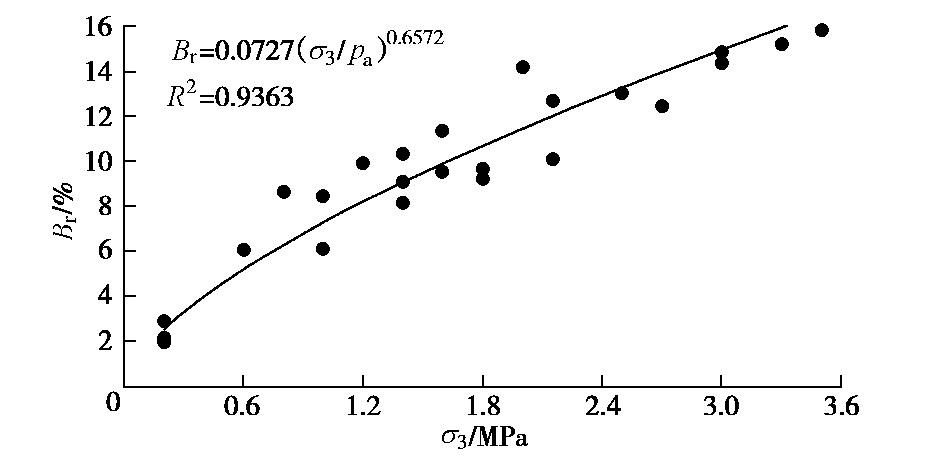
本文选用Hardin颗粒破碎率$B_{\text{r}}$作为颗粒破碎的度量指标,研究颗粒破碎的影响需要先扣除制备试样造成的颗粒破碎,扣除方法是在制样完成后再卸样,晾干后筛分得到由于制样引起的颗粒破碎。本次试验得到：试样干密度2.18 g/cm³（孔隙比e₀=0.234）的制样造成颗粒破碎率$B_{\text{r}}$为1.95%。可与文献[21]中的$e_0=0.25$,$B_{\text{r}}$=1.61%,相互印证。

从31组试验得到颗粒破碎率$B_{\text{r}}$与围压${\sigma }_3$的关系见图3所示,两者之间呈幂函数关系：

图  3  围压与相对破碎率幂函数曲线

Figure  3.  Power relationship between confining pressure and relative breakage ratio

下载: 全尺寸图片 幻灯片

幂曲线拟合的方差为0.9363。

2.3   临界状态应力比与围压关系

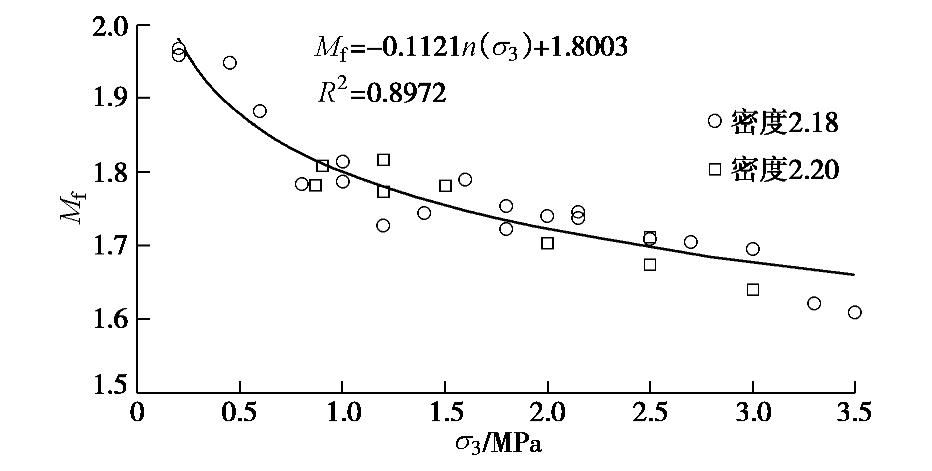
依据25组干密度2.18 g/cm³试验数据,得到临界状态应力比$M_{\text{f}}$与围压${\sigma }_3$的关系见图4所示,两者之间呈对数函数关系：

图  4  临界状态应力比M_f –${\sigma }_3$关系

Figure  4.  Relationship between confining pressure and stress ratio in critical state

下载: 全尺寸图片 幻灯片

由图4可见,随着围压${\sigma }_3$的增大,堆石料颗粒破碎加剧,导致$M_{\text{f}}$减小。从图4中自然对数函数拟合曲线的弯曲程度逐渐减弱可以看出：随着围压${\sigma }_3$的增大、颗粒破碎引起的临界状态应力比减小的程度逐渐变小。

由于目前没有围压超过3.5 MPa的三轴试验数据,为此可用式（3）进行预测。结果为：围压3.5 MPa时,$M_{\text{f}}$=1.66；围压7.0 MPa时,$M_{\text{f}}$=1.58。这表明围压3.5～7.0 MPa区间颗粒破碎的影响程度逐渐减弱。

2.4   临界状态判断标准

在黏土的剑桥模型中,临界状态的判断标准是“体应变不变”和“剪应力不变”。而堆石料因为密度与当前应力状态不像黏土那样存在一一对应关系,并且剪切时堆石料发生一定程度的颗粒破碎,因此本文试验得到的应力应变试验曲线（见图1）与正常固结黏土的有所不同。

由图1可见,低围压（${\sigma }_3$≤0.8 MPa）“体应变不变”和“剪应力不变”点基本对应于同一个轴应变${\epsilon }_{\text{a}}$,由图3可知0.8 MPa围压下堆石料的相对破碎率$B_{\text{r}}$=6.3%。

高围压（0.8 MPa<${\sigma }_3$≤3.0 MPa）下堆石料剪应力值达到峰值后有一定程度的降低,表现为图1（b）中曲线达到峰值后下弯,其中1.4 MPa围压的曲线切线与水平线最大夹角约为5°,3.0 MPa围压的曲线切线与水平线最大夹角约为9°。这与蔡正银等^[16]固结排水剪切试验得到的堆石料剪应力–轴向应变曲线也是向下微弯的现象相互印证。这种现象是由于试验中颗粒发生破碎导致强度降低引起的^[4]。由于基本不存在“剪应力不变”段,所以“剪应力不变”的临界状态判断标准无法应用。但是,图1（a）中随着轴应变的增加,体应变${\epsilon }_{\text{v}}$逐渐会达到一个定值,因此,“体应变不变”的临界状态判断标准依然有效。

由图3可知,1.8 MPa围压下堆石料的相对破碎率$B_{\text{r}}$=10.7%,2.5 MPa围压下堆石料的相对破碎率$B_{\text{r}}$=13.3%,3.0 MPa围压下堆石料的相对破碎率$B_{\text{r}}$=15.0%。说明高压下堆石料发生了较多的颗粒破碎,此时应力状态判断标准不宜采用“剪应力不变”。

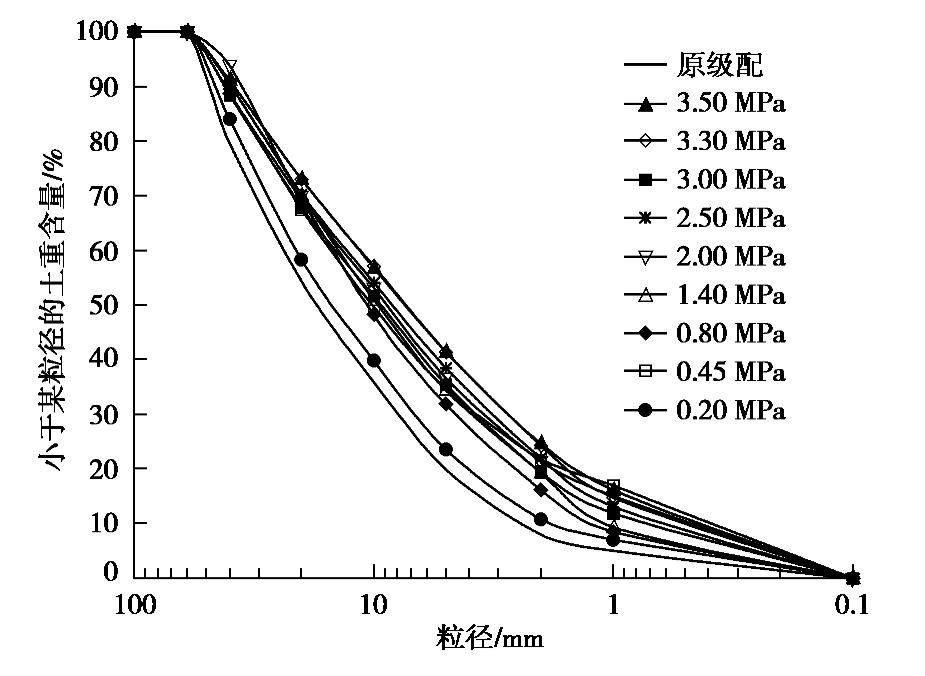
超高围压（${\sigma }_3$>3.0 MPa）下,图1（b）中剪应力曲线达到峰值后下弯明显,其中围压3.3 MPa的曲线切线与水平线最大夹角约为10°,围压3.5 MPa的曲线切线与水平线最大夹角约为15°,不存在“剪应力不变”段。但是,图1（a）中曲线的体应变${\epsilon }_{\text{v}}$会达到一个定值,因此,“体应变不变”的临界状态判断标准依然有效。由图3（a）中曲线,可知3.3 MPa围压下堆石料相对破碎率$B_{\text{r}}$=15.9%,3.5 MPa围压下堆石料的相对破碎率$B_{\text{r}}$=16.6%,堆石料颗粒破碎剧烈,此时临界状态判别标准更不宜采用“剪应力不变”。

堆石料试验前、后颗粒级配曲线见图5,可以看出：围压越大、试验后弓弦形颗粒级配曲线的弯曲程度越小,与原颗粒级配曲线相差越大、颗粒破碎越显著。

图  5  试验前后级配曲线

Figure  5.  Grading curves before and after tests

下载: 全尺寸图片 幻灯片

综上所述,三轴试验过程中随着轴向应变${\epsilon }_{\text{a}}$的增大,堆石料逐渐发生颗粒破碎,颗粒破碎程度与围压密切相关导致图1（b）中高围压下剪应力$q$有一定程度的下弯,超高围压下剪应力$q$下弯明显。因此,对于高–超高围压下发生大量颗粒破碎的堆石料,“体应变不变”仍是判断临界状态的标准,但不宜采用“剪应力不变”标准。低围压下堆石料的临界状态判定仍可同时考虑“剪应力不变”标准。

2.5   Wan-Guo硬化法则的修正

罗维（Rowe）令等效摩擦角${\overline{\phi }}_{\text{f}}$等于${\phi }_{\text{cv}}$。罗维剪胀方程用下式表示：

式中,${\phi }_{\text{m}}=({\sigma }_1-{\sigma }_3)/({\sigma }_1+{\sigma }_3)$,${\phi }_{\text{cv}}$为体积不变时摩擦角,${\phi }_{\text{m}}$为库仑摩擦角。当${\psi }_{\text{m}}$值小于零时,动摩擦角${\phi }_{\text{m}}<{\phi }_{\text{cv}}$,代表体积压缩；当${\psi }_{\text{m}}$值大于零时,动摩擦角${\phi }_{\text{m}}>{\phi }_{\text{cv}}$,代表体积膨胀。

${\overline{\phi }}_{\text{f}}$不是一个常量,为此,Wan等^[18-19]依据Sacramento河砂三轴试验结果提出了砂的修正罗维方程：

在修正罗维方程基础上,Wan等^[18-19]提出了含有塑性剪应变${\epsilon }_{\text{s}}^{\text{p}}$和孔隙比$e$的动摩擦角${\phi }_{\text{m}}$的简单表达式：

式中,${\epsilon }_{\text{s}}^{\text{p}}$为塑性剪应变,$e_{\text{cr}}$是临界状态孔隙比,${\phi }_{\text{cv}}$是体积保持恒定不变时的临界状态摩擦角,${\phi }_{\text{m}}$为库仑摩擦角,$a$和$\beta$是硬化参数。

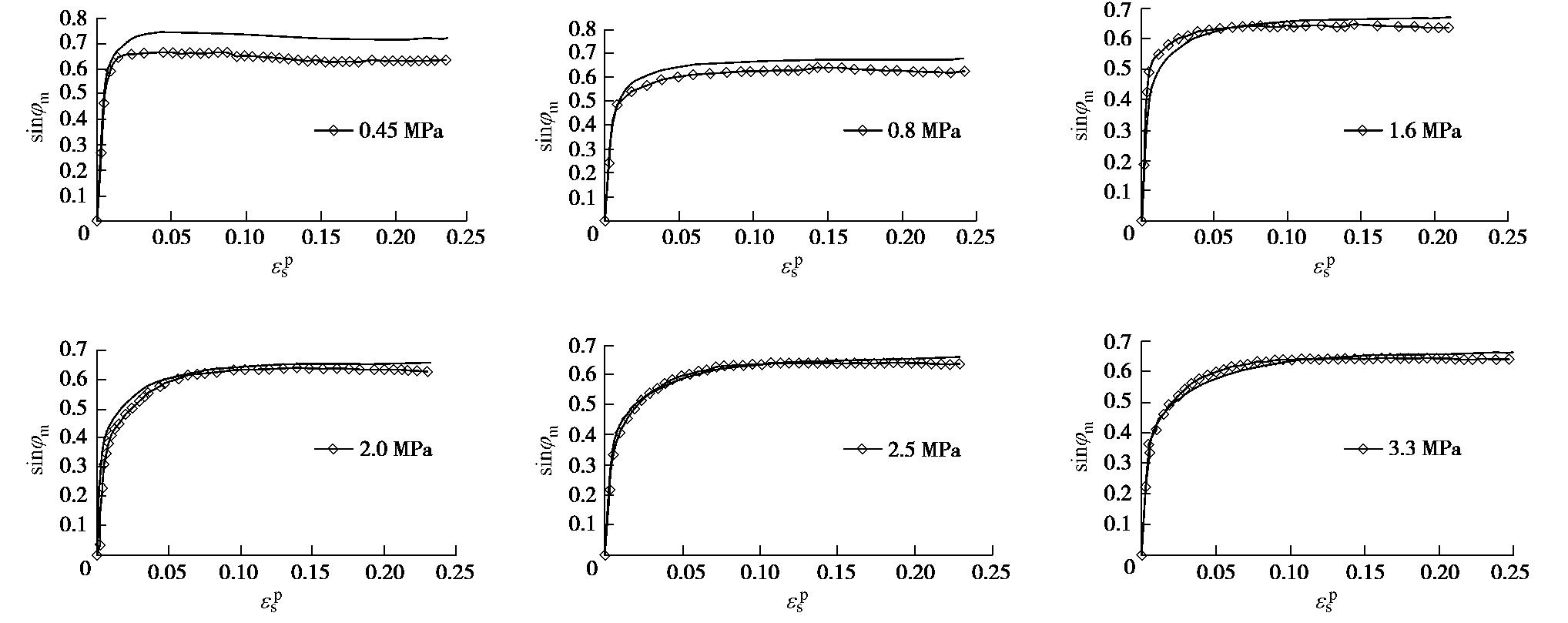
式（6）为双曲线形式,当砂受到剪切、孔隙比趋近临界状态孔隙比$e\to e_{\text{cr}}$时,塑性剪应变${\epsilon }_{\text{s}}^{\text{p}}$达到最大值,动摩擦角${\phi }_{\text{m}}$最大程度的接近临界状态摩擦角${\phi }_{\text{cv}}$。随着${\epsilon }_{\text{s}}^{\text{p}}$的变化,根据剪胀方程,孔隙比$e$也发生变化。

由于Wan等修正罗维方程未考虑砂的颗粒破碎影响,近年来堆石料力学特性的研究和本文试验研究结果都表明堆石料存在不可忽视的颗粒破碎,因此罗维（Rowe）剪胀方程应该进一步修正。

本文引入含颗粒破碎率$B_{\text{r}}$和围压${\sigma }_3$的影响因子Y,对公式（6）修正。

式中

将式（2）$B_{\text{r}}=0.0727{({\sigma }_3/p_{\text{a}})}^{0.6572}$代入式（8）有

基于常规三轴试验曲线,峰值应力条件下取$\sin {\phi }_{\text{cv}}=\sin {\phi }_{\text{f}}$,式（7）变形为

由于常规三轴试验曲线的峰值应力条件下有$\text{d}(\sin {\phi }_{\text{m}})/\text{d}{\epsilon }_{\text{s}}^{\text{p}}=0$,从而得到

式中,${(\cdot )}_{\text{f}}$中的下标f代表峰值状态,$e_0$是初始孔隙比,$\sin {\psi }_{\max }=\text{d}{\epsilon }_{\text{v}}^{\text{p}}/\text{d}{\epsilon }_{\text{s}}^{\text{p}}$。

塑性体应变、剪应变、峰值摩擦角都可试验测得,联立解式（10）和（11）就可以得到硬化参数$\alpha$和$\beta$。图6是按式（10）得出的$\sin {\phi }_{\text{m}}-{\epsilon }_{\text{s}}^{\text{p}}$关系曲线,其中菱形代表试验数据点,连续实线为公式（10）拟合曲线。可以看出除低围压时稍有不足外、拟合效果好,说明本文建立的考虑高应力下颗粒破碎的修正罗维剪胀方程的硬化准则是合适的。

图  6  不同围压下拟合的$\sin {\phi }_{\text{m}}$-${\epsilon }_{\text{s}}^{\text{p}}$关系曲线

Figure  6.  Relationship between $\sin {\phi }_{\text{m}}$ and ${\epsilon }_{\text{s}}^{\text{p}}$ under different values of confining pressure

下载: 全尺寸图片 幻灯片

3.   结论

（1）提出了“体应变不变”是判断高—超高围压下堆石料临界状态的标准。由于剪应力达到峰值后随着颗粒破碎发展而减小,导致剪应力曲线下弯,几乎找不到“剪应力不变”段。因此“剪应力不变”标准不再适用于高–超高围压下发生大量颗粒破碎的堆石料。

（2）试验成果验证了堆石料临界状态剪应力$q$与平均主应力$p$为幂函数关系,而不是线性关系。

（3）临界状态下,堆石料颗粒破碎率$B_{\text{r}}$与围压${\sigma }_3$呈幂函数关系。

（4）堆石料临界状态剪应力$M_{\text{f}}$与围压${\sigma }_3$间的关系呈对数函数关系。围压3.0 MPa以上颗粒破碎引起的临界状态应力比$M_{\text{f}}$值的程度逐渐减弱。利用该公式可以预测围压3.5 MPa以上的临界状态应力比$M_{\text{f}}$。

（5）引入颗粒破碎因子,修正了罗维（Rowe）剪胀方程Wan-Guo硬化法则,高—超高围压下试验数据拟合好,为构建考虑高应力下颗粒破碎的堆石料状态相关本构模型提供了支持。