Numerical study on tunnel deformation under local thickness reduction in tunnel linings and destruction prediction
-
摘要: 隧道衬砌结构在施工过程中容易出现空洞区域，严重影响了隧道运营的长期稳定性，为研究衬砌结构局部减薄对隧道变形及力学特性的影响，开展了1000组不同隧道埋深、减薄位置角度、减薄长度及减薄厚度条件下的数值模拟计算，通过统计分析不同工况条件下的数值模拟计算结果发现：衬砌减薄位置对最大变形位置影响较小，隧道最大压应力主要集中在隧道的左右拱脚位置，其中多数情况下隧道右边局部减薄容易造成隧道左拱脚位置压应力集中。衬砌局部减薄有可能造成左拱脚及右拱脚处拉应力集中，而更多条件下衬砌局部减薄有可能造成局部减薄区域附近拉应力集中，对于拉应力集中主要为左右拱脚处及减薄区域附近。基于1000组数值模拟计算结果，建立了CART隧道破损预测模型，并通过2个算例验证该模型的合理性及有效性，该研究数值模拟研究可为隧道局部减薄力学分析及隧道稳定性预测提供依据。Abstract: The cavity area commonly appears in lining structures in engineering practice, which has great influences on the long-term stability of tunnel operation. In order to investigate the influences of thickness reduction of lining structures on displacement and mechanical characteristics of tunnels, 1000 groups of numerical simulations with different buried depths, angles of local thickness reduction location, reduction lengths and thicknesses of linings of tunnel the conducted. Through analysis of the numerical simulation results, it can be concluded that the local thickness reduction area has less influences on displacement. Tthe maximum compressive stress of the tunnel is mainly concentrated at the left and right arch feet of the tunnel, and local thinning at the right side of the tunnel is prone to causing stress concentration at the left arch feet of the tunnel. Local thinning of linings may cause tensile stress concentration at the left and right arch feets, while under more conditions, local thinning of linings may cause tensile stress concentration near the local thinning area. The tensile stress concentration mainly occurs at the left and right arch feets and near the thinning area. Based on the 1000 groups of numerical simulation results, the CART tunnel damage predictive model is established. Meanwhile, 2 numerical examples verify the validity of the predictive model. This study provide numerical simulation basis for the mechanical and stability analysis of tunnels under local thickness reduction.
-
Keywords:
- lining structure /
- local thinning /
- decision tree model /
- numerical simulation
-
0. 引言
随着中国公路、铁路的不断增加，目前运营的隧道每年总里程正以每年上千公里的速度增加。在隧道快速建设过程中，部分隧道服役状态存在衬砌空洞、衬砌厚度缺陷、渗水、漏水、开裂等[1]。与衬砌开裂、渗水、漏水等其他隧道缺陷不同，衬砌厚度不足、衬砌空洞，具有隐蔽性，难以被发现，但衬砌结构缺陷或局部减薄对隧道安全有直接影响。研究表明，衬砌结构空洞、衬砌结构局部减薄容易造成衬砌承载能力降低，从而引发灾害[2]，给人民和国家生命财产安全带来严重的威胁。
考虑隧道衬砌结构缺陷及局部减薄对隧道安全运营具有重要影响，国内外学者通过采用室内实验、理论推导及数值模拟计算对隧道衬砌结构局部减薄开展了一系列研究，取得了丰富的研究成果[3]。Ding等[4]通过大比例尺寸模型的实验，通过计算得到了考虑隧道衬砌结构局部减薄或局部空洞条件下衬砌承载力损失率的计算表示式，为工程应用提供经验公式，便于获取隧道运行安全状态。由于数值模拟计算具有可重复性的优点，采用数值模拟计算分析不同隧道减薄及空洞条件下隧道变形及应力集中现象，可为工程实践提供有力指导。李彬等[5]、张成平等[6]分析了衬砌结构局部减薄条件下衬砌安全系数变化，建立了隧道衬砌结构局部减薄或缺陷程度对衬砌结构安全系数之间的关系，为衬砌结构安全评价提供了数值模拟计算基础及方法。叶艺超等[7]采用有限元分析计算，研究了衬砌减薄尺寸、减薄位置及减薄厚度对衬砌结构应力及围岩应力分布情况，发现衬砌局部减薄区域，容易产生应力集中现象。李兰[8]对衬砌结构的拱顶和边墙进行局部减薄，共设计出6种减薄方案，获得了不同减薄位置对衬砌位移及裂隙参数的影响规律，其研究成果可为隧道厚度不足的风险评估提供数值模拟计算基础及技术支撑。
分析国内外研究已有成果可以发现，目前已有研究一般根据先前参考文献选取隧道衬砌结构特殊位置进行减薄处理，主要针对拱顶、拱腰及边墙，从而开展相关理论分析、数值模拟计算或室内试验。考虑到选取的工况（减薄位置、减薄厚度及减薄长度）非常有限，因此试验结果具有一定主观性，其研究成果对工程实践指导意义具有一定局限性。针对已有研究不足，该论文采用FLAC3D数值模拟计算软件，建立衬砌结构不同位置、不同减薄厚度、不同减薄长度及不同埋深下的数值模拟计算，各变量的选取服从均匀分布，不具有主观性，获取不同工况条件下的数值模拟计算结果，统计分析埋深、减薄位置、减薄长度及减薄厚度对隧道最大变形及最大应力位置变化的影响，同时提出了隧道破损预测模型，为隧道安全性评估提供有效的预测方法，具有重要的实际意义。
1. 数值模拟研究
1.1 数值模拟计算模型
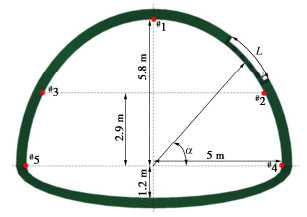
数值模拟计算模型如图 1所示，隧道模型巷道宽度为10 m，隧道上半部分高度为5.8 m，下半部分高度为1.5 m，衬砌厚度为0.4 m。其中减薄区域由减薄位置角度$ \alpha $、减薄长度L及减薄厚度t确定。其中位置角度范围为[0，90°]，减薄厚度的范围为0~0.35 m，衬砌减薄长度为0~3 m，隧道埋深的取值范围为10~200 m，为避免数值模拟计算过程中人为主观性，4个参数在指定范围内随机选取，且服从均匀分布。此外在数值模拟模型上布置5个监测点：#1、#2、#3、#4及#5，计算过程中对5个监测点的位移、剪切应力、拉应力、压应力进行监测，便于对数值模拟计算结果进行定量分析。
1.2 数值模拟计算过程
数值模拟计算采用FALC3D数值模拟计算软件，模拟计算首先对岩土体参数及衬砌结构进行力学参数赋值，其中岩土体参数及衬砌结构均采用莫尔库仑模型，其中力学参数见表 1。
表 1 岩土体及衬砌结构力学参数Table 1. Physical and mechanical parameters of main soils and lining strutures数值模拟计算过程中，对整个模型进行初始应力平衡，然后对隧道开挖区域进行开挖，对衬砌结构赋值力学参数，当数值模拟计算达到应力平衡或计算步数超过20000步时，则数值模拟计算结束，进行下一个数值模拟计算。通过随机选取不同隧道埋深、减薄位置角度、减薄长度及减薄厚度，共开展1000次数值模拟计算，分析隧道埋深、减薄位置角度、减薄长度及减薄厚度对衬砌结构变形及力学的影响。
2. 最大变形及最大应力位置分布情况
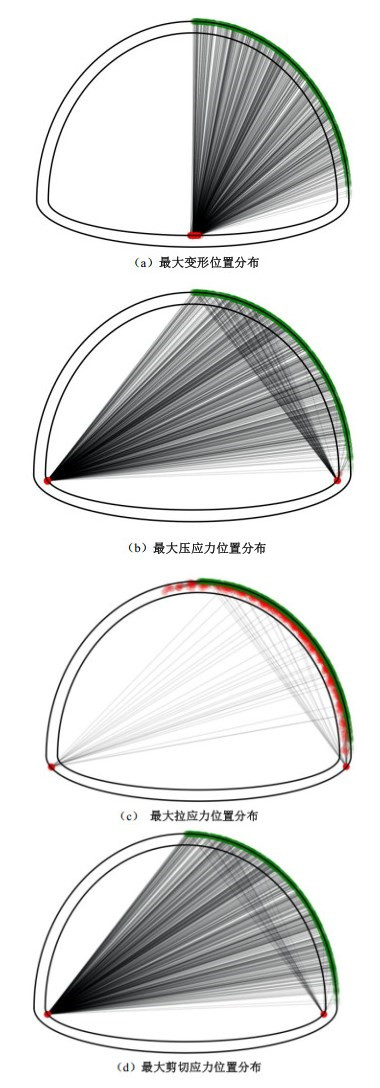
根据数值模拟计算结果得到了在不同位置减薄条件下最大变形位置、最大压应力位置、最大拉应力位置及最大剪切应力位置（图 2）。如图 2所示，绿色点表示减薄位置的中心位置，而红色点表示最大变形、最大压应力、最大拉应力及最大剪切应力位置，并采用直线将减薄位置的中心坐标点与位移或应力最大值坐标点连接起来。其中不同衬砌减薄位置条件下隧道最大变形位置均分布在仰拱的中心位置区域（图 2（a）），表明衬砌减薄位置对最大变形位置影响较小，因此仰拱中心位置的变形在工程应用中应引起足够重视。隧道最大压应力主要集中在隧道的左右拱脚位置（图 2（b）），其中多数情况下右边隧道局部减薄容易造成隧道左拱脚位置压应力集中，当衬砌减薄位置主要位于拱腰及拱顶位置时有可能造成右拱脚位置剪切应力集中，因此减薄区域位于右边时，要更多注意左拱脚位置剪切应力集中。最大拉应力集中位置（图 2（c））与最大位移、最大压应力及后续的最大剪切应力位置有明显不同，衬砌局部减薄有可能造成左拱脚及右拱脚处拉应力集中，而更多情况下右边衬砌局部减薄有可能造成局部减薄区域附近拉应力集中，拉应力集中主要为左右拱脚处及减薄区域附近。剪切应力集中与最大压应力集中位置较为雷同，右边衬砌减薄容易造成左拱脚处剪切应力集中，而当减薄区域位于拱顶或拱腰位置时，有可能造成右拱脚处的剪切应力集中，总体上来说，主要以左拱脚处的剪切应力集中为主。
![]()
图 2 衬砌不同减薄区域条件下最大变形、最大压应力、最大拉应力及最大剪切应力位置分布Figure 2. Locations of maximum displacement, maximum compression stress, maximum tensile stress and maximum shear stress3. 隧道破损严重预测模型
为进一步定量分析隧道埋深、减薄衬砌角度、减薄长度及减薄厚度对隧道稳定性影响，假定塑性区由边界区域扩展到剩余衬砌结构厚度一半时，则认为隧道衬砌破损严重，隧道需要修复。而当塑性区扩展程度不及衬砌厚度一半时，则认为隧道结构较为稳定，破损不严重，不需要修复。
基于不同隧道埋深、减薄衬砌位置角度、减薄长度、减薄厚度及数值模拟塑性区发育情况（是否达到衬砌结构厚度的50%）数据集（1000组数据），建立隧道衬砌局部减薄条件下隧道破损严重预测模型。
本论文中将采用CART（Classification and Regression Tree）算法建立隧道破损预测模型，该算法是由Breiman提出，广泛应用于决策树学习方法，该算法可用于分类及回归。由于隧道破损预测模型主要基于不同埋深、减薄位置角度、减薄长度及减薄厚度下隧道是否破损数值模拟数据集，建立分类模型（二分类模型），主要将隧道分为隧道破损严重及不严重，为便于数据处理，将隧道破损严重标识为“1”，破损不严重标识为“0”，基于该数据集，建立隧道破损预测模型。
在CART算法中分类树采用基尼指数作为选择最优特征指数，在分类问题中，如果最终结果有K类，数据样本点属于第k类的概率的基尼指数可表示为
$$ {\text{Gini}}(p) = \sum\nolimits_{K = 1}^K {{p_k}(1 - {p_k}) = 1 - } \sum\nolimits_{K = 1}^K {p_k^2} 。 $$ (1) 由于该论文中数值模拟计算结果只有两类，即隧道破损严重及隧道破损不严重，为典型的二分类问题。对于二分类问题，概率分布的基尼指数可表示为
$$ {\text{Gini}}(p) = 2p(1 - p) 。 $$ (2) 对于样本集合D的基尼指数可表示为
$$ {\text{Gini}}(D) = 1 - {\sum\nolimits_{K = 1}^K {\left( {\frac{{\left| {{c_k}} \right|}}{D}} \right)} ^2} 。 $$ (3) 式中，$ {c_k} $表示是样本D属于k类样本子集，本文中K为2。
当样本集合D根据特征A是否可能被某一值a分$ {D_1} $及$ {D_2} $：
$$ \left. \begin{array}{l} {D}_{1}=\left\{(x, y)\in D|A(x)=a\right\}\text{ }\text{,}\;\\ {D}_{2}=D-{D}_{1}\text{ }。 \end{array} \right\} $$ (4) 在特征A的条件下，集合D的基尼指数表示为
$$ {\text{Gini}}(D, A) = \frac{{\left| {{D_1}} \right|}}{D}{\text{Gini}}({D_1}) + \frac{{\left| {{D_2}} \right|}}{D}{\text{Gini}}({D_2}) 。 $$ (5) 式中：$ {\text{Gini}}(D) $表示集合D的不确定性，$ {\text{Gini}}(D, A) $表示A=$ a $分隔后集合D的不确定性。
CART决策树算法具体步骤如下：
（1）设置训练数据集D，计算现有特征数据集的基尼系数，该论文中数据集的特征主要有隧道埋深、衬砌减薄位置、减薄长度及减薄厚度。对每一个特征A可能的取值a，根据样本数据对A=$ a $的测试，将数据集D分为两个部分$ {D_1} $及$ {D_2} $，利用式（5）计算A=$ a $的基尼系数。
（2）在所有可能的特征A及所有可能的切割点a，获取基尼指数最小的特征及对应的切割点作为最优特征及最优切割点。根据该切割点，将数据分类，生成两个子节点。
（3）对两个子节点递归调用（1）和（2），直至满足条件。
（4）最终生成CART决策树。
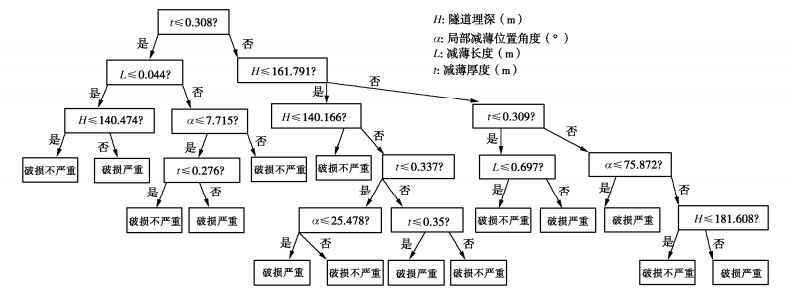
通过采用上述步骤，获得了隧道破损预测模型，如图 3所示。
为进一步说明该模型，给出2个具体算例，当隧道埋深H为52.853 m，减薄位置角度$ \alpha $为37.868°，减薄长度L为0.104 m，减薄厚度$ t $为0.06 m，根据图 3决策模型树，对该工况条件下隧道衬砌结构破损进行预测。
（1）根据模型树，首先从模型树的最顶端开始判断，t < =0.308不成立，因此转向右边节点。
（2）H≤161.791进行判断，H为52.853 m，该判断成立，因此进入下一步的右边节点。
（3）H≤140.166进行判断，H为52.853 m，该判断成立，达到了模型的终点位置，为破损不严重。
为进一步验证该模型的正确性，开展数值模拟计算，数值模拟计算结果塑性区分布如图 4所示。
![]()
图 4 塑性区分布情况（H =52.853 m；$ \alpha $ =37.868°，L = 0.104 m，t =0.06 m）Figure 4. Distribution of plastic zone (H =52.853 m; $ \alpha $=37.868°, L=0.104 m, t =0.06 m)根据预测模型，该隧道破损不严重，而通过数值模拟计算表明，衬砌结构上没有出现塑性区，表明该隧道是稳定的，预测模拟与数值模拟计算结果一致。
为进一步验证该模型，论文给出了另一算例，该算例相关参数为：隧道埋深H为196.052 m，减薄位置角度$ \alpha $为56.841°，减薄长度L为1.083 m，减薄厚度t为0.308 m，根据预测模型（图 3），预测该隧道的破损情况：①t≤0.308 m，算例中t=0.308 m，因此转向左节点；②L≤0.044 m，算例中L为1.083 m，不成立，转向右节点；③$ \alpha $≤7.715°，算例中减薄位置角度$ \alpha $为56.841o，不成立，转向右节点；④t≤0.276 m，算例中t为0.308 m，不成立，转向右节点，达到模型树的端点位置，结果为隧道破损严重。
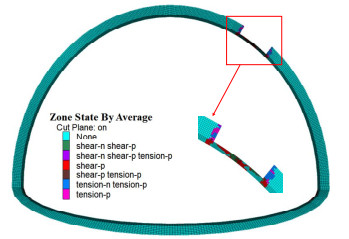
图 5给出了该算例条件下（H=196.052 m；$ \alpha $=56.841°，L =1.083 m，t =0.30819 m）塑性区分布情况，分析数值模拟计算结果发现，大面积塑性区出现在衬砌减薄区域，且塑性区完全贯穿了衬砌结构，表明隧道破损严重，通过验证预测模型与数值模拟计算结果一致，表明该预测模型具有一定可靠性。
![]()
图 5 塑性区分布（H =196.052m；$ \alpha $=56.841°，L =1.083 m，t=0.308 m）Figure 5. Distribution of plastic zone (H =196.052 m; $ \alpha $= 56.841°, L =1.083 m, t =0.308 m)4. 结论
为探讨隧道埋深、隧道减薄区域位置角度、隧道减薄长度及减薄厚度对隧道稳定性影响，共开展1000组不同埋深、隧道减薄区域位置角度、隧道减薄长度及减薄厚度下的数值模拟计算，统计分析了埋深、隧道减薄位置角度、隧道减薄长度及减薄厚度对衬砌结构稳定性影响，基于数值模拟计算结果，采用CART算法，建立隧道衬砌破损预测模型，得到以下2点结论。
（1）根据数值模拟计算结果得到了在不同位置减薄条件下最大变形位置、最大压应力位置、最大拉应力位置及最大剪切应力位置，分析数值模拟结果可知：衬砌减薄位置对最大变形位置影响较小，隧道最大压应力主要集中在隧道的左右拱脚位置，其中多数情况下隧道局部减薄容易造成隧道左拱脚位置压应力集中。衬砌局部减薄有可能造成左拱脚及右拱脚处拉应力集中，而更多情况下衬砌局部减薄有可能造成局部减薄区域附近拉应力集中，对于拉应力集中主要为左右拱脚处及减薄区域附近。剪切应力集中与最大压应力集中位置较为雷同，右边衬砌减薄容易造成左拱脚处剪切应力集中，而当减薄区域位于拱顶或拱腰位置时，有可能造成右拱脚处的剪切应力集中，总体上来说，主要以左拱脚处的剪切应力集中为主。
（2）根据塑性区扩展情况，基于1000组数值模拟计算结果，建立了以隧道埋深、隧道减薄位置角度、减薄长度及减薄厚度作为输入变量的CART决策预测模型，两个算例表明，预测模型结果与数值模拟计算结果一致，验证了该预测模型的有效性。
-
![]()
图 2 衬砌不同减薄区域条件下最大变形、最大压应力、最大拉应力及最大剪切应力位置分布
Figure 2. Locations of maximum displacement, maximum compression stress, maximum tensile stress and maximum shear stress
![]()
图 4 塑性区分布情况（H =52.853 m；α =37.868°，L = 0.104 m，t =0.06 m）
Figure 4. Distribution of plastic zone (H =52.853 m; α=37.868°, L=0.104 m, t =0.06 m)
![]()
图 5 塑性区分布（H =196.052m；α=56.841°，L =1.083 m，t=0.308 m）
Figure 5. Distribution of plastic zone (H =196.052 m; α= 56.841°, L =1.083 m, t =0.308 m)
-
[1] 吴江滨, 张顶立, 王梦恕. 铁路运营隧道病害现状及检测评估[J]. 中国安全科学学报, 2003, 13(6): 49-52. WU Jiangbin, ZHANG Dingli, WANG Mengshu. Current damage situation of railway operation tunnels and their inspection and evaluation[J]. China Safety Science Journal, 2003, 13(6): 49-52. (in Chinese)
[2] 殷洪波, 刘正初, 郭永发. 组合缺陷影响下衬砌结构受力特征分析[J]. 铁道科学与工程学报, 2020, 17(8): 2037-2045. YIN Hongbo, LIU Zhengchu, GUO Yongfa. Analysis of stress characteristics of lining structure under the influence of combined defects[J]. Journal of Railway Science and Engineering, 2020, 17(8): 2037-2045. (in Chinese)
[3] 佘健, 何川, 汪波, 等. 衬砌背后空洞对隧道结构承载力影响的模型试验研究[J]. 公路交通科技, 2008, 25(1): 104-110. SHE Jian, HE Chuan, WANG Bo, et al. Study on effect of cavities behind linings on bearing capacity of tunnel structure by model test[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 104-110. (in Chinese)
[4] DING Z D, JI X F, LI X Q, et al. Influence of symmetric and asymmetric voids on mechanical behaviors of tunnel linings: model tests and numerical simulations[J]. Symmetry, 2019, 11(6): 802. doi: 10.3390/sym11060802
[5] 李彬, 雷明锋, 李文华. 运营公路隧道病害对衬砌结构安全性的影响[J]. 铁道科学与工程学报, 2011, 8(5): 40-45. LI Bin, LEI Mingfeng, LI Wenhua. Safety influence of operating highway tunnel caused by sturcture disease[J]. Journal of Railway Science and Engineering, 2011, 8(5): 40-45. (in Chinese)
[6] 张成平, 张旭, 冯岗, 等. 衬砌厚度不足对隧道结构安全性的影响分析[J]. 现代隧道技术, 2017, 54(2): 137-143, 169. ZHANG Chengping, ZHANG Xu, FENG Gang, et al. Influence of insufficient lining thickness on the safety of a tunnel structure[J]. Modern Tunnelling Technology, 2017, 54(2): 137-143, 169. (in Chinese)
[7] 叶艺超, 彭立敏, 雷明锋, 等. 不同脱空模式下隧道结构安全状态分析[J]. 铁道科学与工程学报, 2018, 15(11): 2875-2883. YE Yichao, PENG Limin, LEI Mingfeng, et al. Safety analysis of tunnel structures with different patterns of voids behind lining[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2875-2883. (in Chinese)
[8] 李兰. 衬砌减薄位置对输水隧洞结构安全性影响的数值模拟研究[J]. 水利技术监督, 2020, 28(2): 180-183. LI Lan. Numerical simulation study on the influence of lining thinning position on the structural safety of water conveyance tunnel[J]. Technical Supervision in Water Resources, 2020, 28(2): 180-183. (in Chinese)
[9] 王明年, 魏龙海, 李海军, 等. 公路隧道围岩亚级物理力学参数研究[J]. 岩石力学与工程学报, 2008, 27(11): 2252-2259. WANG Mingnian, WEI Longhai, LI Haijun, et al. Research on mechanical parameters of subclassification rock mass of highway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2252-2259. (in Chinese)
[10] 张亚辉, 安洋, 郭唯伟, 等. 围岩空洞对重载铁路隧道动力稳定性的影响[J]. 铁道勘察, 2023, 49(4): 135-141. ZHANG Yahui, AN Yang, GUO Weiwei, et al. Influence of surrounding rock voids on the dynamic stability of heavy-haul railway tunnels[J]. Railway Investigation and Surveying, 2023, 49(4): 135-141. (in Chinese)
下载:
计量
- 文章访问数: 69
- HTML全文浏览量: 6
- PDF下载量: 14
