渗流条件下滨海地层人工冻结多场耦合理论模型

朱紫义; 任磊; 高国耀; 郭伟; 任宇晓; 冯守中; 祝显鹏

doi:10.11779/CJGE2024S20031

渗流条件下滨海地层人工冻结多场耦合理论模型 English Version

1.
天津大学建筑工程学院, 天津 300072
2.
安徽滁宁高速公路股份有限公司, 安徽滁州 239000
3.
滁州学院土木与建筑工程学院，安徽滁州 239000

基金项目:

国家自然科学基金项目 52171273

国家自然科学基金项目 52108335

国家自然科学基金项目 52078336

天津市科技计划项目 20JCJQJC00220

详细信息

作者简介:
朱紫义(1999—)，女，河北邯郸人，硕士，主要研究方向为岩土工程。E-mail: zhuzy@hfuu.edu.cn

通讯作者:
冯守中, E-mail: fsz63@vip.163.com

中图分类号: TU43
计量
- 文章访问数: 60
- HTML全文浏览量: 8
- PDF下载量: 13
出版历程
- 收稿日期: 2024-06-20
- 刊出日期: 2024-09-30

Multi-field coupling theoretical model for artificial freezing of coastal soils under seepage

1.
School of Civil Engineering, Tianjin University, Tianjin 300072, China
2.
Anhui Chuning Expressway Co., LTD, Chuzhou 239000, China
3.
College of Civil and Architecture Engineering, Chuzhou University, Chuzhou 239000, China

摘要

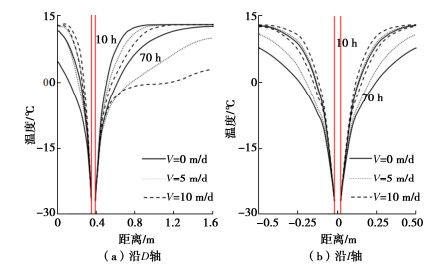
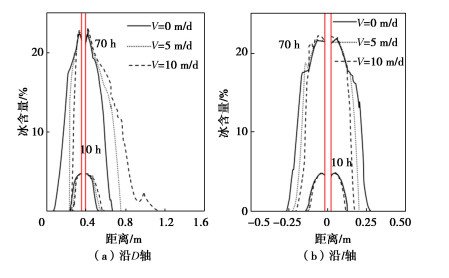
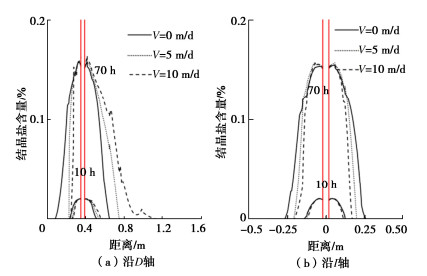
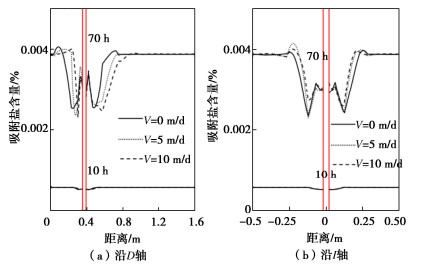
摘要: 采用Navier-Stokes方程考虑流体动量守恒对渗流过程的影响，建立了考虑渗流对滨海砂土地层人工冻结过程影响的水-盐-热-力学理论模型。理论模型的计算结果与试验吻合良好，验证了所提模型的准确性。通过参数分析，探讨了渗流速度对冰、盐空间分布的影响。研究发现，渗流削弱了冻结效果，随着渗流速度从0 m/d增加到10 m/d，冻结管左右两侧的土体位移降低了23.1%；冻结管左右两侧的结冰范围缩减了37.8%；冻结管左右两侧的盐分的析出范围缩减了42.7%；砂层上游的吸附盐突变位置向下游移动了52%，下游的吸附盐突变位置向下游移动了32%。
- 人工冻结 /
- 冻结管 /
- 渗流 /
- 砂地层 /
- 多场耦合
Abstract: A hydro-salt-thermal-mechanical theoretical model for the influences of seepage flow on the artificial freezing process in sand-clay stratum is derived. The influence of momentum conservation of fluid during seepage process is considered by using the Navier-Stokes equation. The good agreement between the results from the theoretical model and laboratory tests in the literature verifies the accuracy of the proposed model. The parametric studies are conducted to investigate the influences of the seepage velocities on the spatial distributions of ice and salinity. It is found that the seepage weakens the freezing effects. With the seepage velocity increases from 0 to 10 m/d, at the left and right sides of the freezing pipe, the soil displacement decreases by 23.1 %. The range of water freezing is reduced by 37.8 %. The range of salt precipitation is reduced by 42.7 %. The mutation position of the adsorbed salt in the upstream of the sand stratum moves by 52 % downstream, and that in the downstream moves downstream by 32 %.
- artificial freezing /
- frozen pipe /
- seepage flow /
- sand stratum /
- multi-field coupling theory

HTML全文

0. 引言

高桩码头是一种典型的沿海水工建筑物。高桩码头的岸坡在地震期间可能发生整体失稳、产生较大的侧向位移进而导致结构损坏。

在进行高桩码头抗震设计时，需对岸坡地震稳定性进行验算，并可采用拟静力法^[1]开展。在拟静力分析方法中，地震引起的荷载通过等效静态水平力施加，边坡的拟静力地震稳定性常用临界地震系数表示。针对边坡拟静力地震稳定性问题，Sarma^[2]在1973年提出了一种使用极限平衡法确定边坡临界地震系数的方法。Chang等^[3]采用极限分析法，确定了平面和对数螺旋两种破坏机制下边坡临界地震系数的严格上限解。Sloan^[4-5]基于有限元法将土体离散进行极限分析，并开发了适用于边坡稳定性分析的数值极限分析程序。Loukidis等^[6]使用有限元极限分析方法，评估了地震作用下边坡的稳定性。

考虑排桩稳定效果的高桩码头岸坡稳定性分析可采用有限元方法开展，但其计算较为复杂。Ito等^[7-8]使用塑性变形理论计算抗滑桩受到的极限侧向力，提出了多排抗滑桩边坡的设计方法。Lee等^[9]基于非耦合公式，分别考虑桩的响应和边坡稳定性，使用简化Bishop法寻找边坡的临界滑动面。Hassiotis等^[10]推广摩擦圆法，将反作用力纳入到边坡稳定性分析中，从而确定了边坡临界滑动面和安全系数。Ausilio^[11]采用极限分析上限法分析抗滑桩边坡稳定性，得出了给定安全系数条件下所需抗滑力的理论表达式。

针对考虑排桩加固的高桩码头岸坡稳定性，使用梯形分布抗滑力考虑排桩对岸坡的稳定作用，假设临界破坏面为穿过坡脚的对数螺旋面，基于极限分析上限法推导了岸坡临界地震系数的表达式。通过变量优化，得到临界地震系数最小上限解和对应的临界破坏面。进一步地，采用强度折减法计算给定水平地震加速度下高桩码头岸坡的安全系数，并分析不同因素对岸坡地震稳定安全系数和破坏模式的影响规律。

1. 高桩码头岸坡临界地震系数

根据极限分析上限定理，对于任何假定的破坏机制，若外力功率超过内部能量耗散速率，则土体不能承受施加的荷载。

${{\displaystyle \int }}_{S}{T}_{i}{v}_{i}\text{d}S+{{\displaystyle \int }}_{V}{X}_{i}{v}_{i}\text{d}V\le {{\displaystyle \int }}_{V}{\sigma }_{ij}{\epsilon }_{ij}\text{d}V\text{ }i,j=1,2,3 。$

(1)

式中：T_i为作用在边界S上的牵引力；X_i为作用在体积V上的体力；v_i为运动学容许的速度场； ${\varepsilon _{ij}}$ 为与v_i相容的应变速率场； ${\sigma _{ij}}$ 为与T_i和X_i相对应的应力场。

对岸坡地震稳定性的分析基于以下条件开展：土体为均质、各向同性；平面应变条件；拟静力地震荷载；土体服从莫尔-库伦破坏准则及关联流动法则。

使用极限分析上限法计算临界水平地震系数，假设破坏面为穿过坡脚的对数螺旋面，破坏面方程为

$r = {r_0}{{\text{e}}^{\left( {\theta - {\theta _0}} \right)\tan \varphi }}。$

(2)

式中：r为对数螺旋线的半径；φ为土体内摩擦角；r₀为对数螺旋线与坡顶面相交处的半径；θ₀和θ为r₀和r与水平线的夹角。

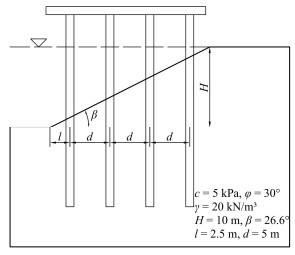
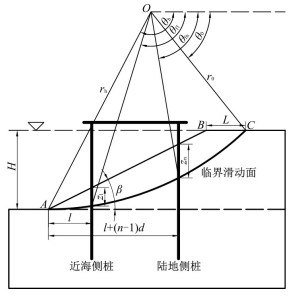
建立岸坡地震稳定性极限分析模型，如图 1所示。水位线与坡顶平齐，岸坡坡高为H，坡角为β。土体的总重度和有效重度分别为 $\gamma$ 和 $\gamma '$ 。破坏时ABC区域的土体作为刚体绕点O以角速度ω旋转，L为滑动土体顶面宽度，参数θ₀和θ_h用于确定滑动面的具体位置，θ_f1至θ_fn分别代表码头从近海侧到陆地侧的第i排桩在对数螺旋破坏机制中所处的位置(i=1, 2, $\cdots$ , n)。最靠近坡脚的一排桩与坡脚的距离为l，桩间距为d。

图 1 上限分析破坏机制

Figure 1. Failure mechanism of upper bound analysis

下载: 全尺寸图片幻灯片

破坏模式的几何关系如下：

$\frac{H}{{{r_0}}} = \left[ {\sin {\theta _{\text{h}}}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }} - \sin {\theta _0}} \right]\text{，}$

(3)

$\frac{L}{{{r_0}}} = \frac{{\sin (\beta + {\theta _0}) - {{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\sin ({\theta _{\text{h}}} + \beta )}}{{\sin \beta }}\text{，}$

(4)

$\begin{array}{c} \begin{gathered} {r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{\text{h}}} + l = {r_0}{{\text{e}}^{\left( {{\theta _{{\text{f1}}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{{\text{f1}}}}， \\ \text{······} \end{gathered} \\ {r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{\text{h}}} + l + (n - 1)d = {r_0}{{\text{e}}^{\left( {{\theta _{{\text{fn}}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{{\text{fn}}}} 。 \end{array}$

(5)

速度不连续面AC上能量耗散速率为

$D = \frac{{c{r_0}^2\omega }}{{2\tan \varphi }}\left( {{{\text{e}}^{2\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }} - 1} \right) 。$

(6)

极限状态下，作用在排桩上的侧向力可由Ito等^[7]提出的公式确定。排桩对单位宽度岸坡的反作用力可由排桩受力除以桩间距得到，故可将高桩码头岸坡稳定性问题简化为平面应变问题。将排桩对岸坡稳定作用等效为梯形分布力，表达为

$p = {\alpha _{\text{m}}}(a + bz)\text{，}$

(7)

式中：a和b为使用Ito等^[7]提出的公式计算出的参数； ${\alpha _{\text{m}}}$ 为群桩抗滑力系数；z为计算点距地表的深度。

近海侧到陆地侧排桩在滑动面以上产生抗滑力的有效深度z₁至 ${z_n}$ 分别为：

$\begin{array}{c}{z}_{1}={r}_{0}{\text{e}}^{\left({\theta }_{\text{f1}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{f1}}-{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}+l\mathrm{tan}\beta \text{ }，\\ \text{……}\\ {z}_{n}={r}_{0}{\text{e}}^{\left({\theta }_{\text{f}n}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{f}n}-{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}+\\ \left[ {l + {\text{(}}n - 1{\text{)}}d} \right]\tan \beta 。 \end{array}$

(8)

近海侧到陆地侧排桩的抗滑力做功功率W_f1至 ${W_{{\text{f}}n}}$ 分别为：

$\begin{array}{c}{W}_{\text{f1}}=-\omega {\alpha }_{\text{m}}\{\left(a{z}_{1}+\frac{b{z}_{1}{}^{2}}{2}\right)\left[{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}-l\mathrm{tan}\beta \right]+\\ \left(\frac{a{z}_{1}{}^{2}}{2}+\frac{b{z}_{1}{}^{3}}{3}\right)\}\text{ }，\\ \text{……}\\ {W_{{\text{f}}n}} = - \omega {\alpha _{\text{m}}}\left\{ {\left( {a{z_n} + \frac{{bz_n^2}}{2}} \right)\left[ {{r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\sin {\theta _{\text{h}}} - } \right.} \right. \\ \left. {\left[ {l + (n - 1)d} \right]\tan \beta } \right] + \left. {\left( {\frac{{az_n^2}}{2} + \frac{{bz_n^3}}{3}} \right)} \right\} 。 \end{array}$

(9)

ABC区滑动土体重力做功功率可由OAC、OBC和OAB区土体重力的功率（W₁-W₂-W₃）得到：

$\begin{array}{c} {W_1} = \frac{{\gamma 'r_0^3\omega }}{{3(1 + 9{{\tan }^2}\varphi )}}\left\{ {(3\tan \varphi \cos {\theta _{\text{h}}} + \sin {\theta _{\text{h}}}){{\text{e}}^{\left[ {3\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}} - } \right.\\ \left. {\mathop {}\limits_{} 3\tan \varphi \cos {\theta _0} - \sin {\theta _0}} \right\}\text{，} \end{array}$

(10)

${W_2} = \frac{{\gamma 'r_0^3\omega }}{6}\frac{L}{{{r_0}}}\left( {2\cos {\theta _0} - \frac{L}{{{r_0}}}} \right)\sin {\theta _0}\text{，}$

(11)

$\begin{array}{c} {W_3} = \frac{{\gamma 'r_0^3\omega }}{6}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}\left[ {\sin {\text{(}}{\theta _{\text{h}}} - {\theta _0}{\text{)}} - \frac{L}{{{r_0}}}\sin {\theta _{\text{h}}}} \right] \cdot \\ \left\{ {\cos {\theta _0} - \frac{L}{{{r_0}}} + \cos {\theta _{\text{h}}}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}} \right\}。 \end{array}$

(12)

ABC区域土体单位重力加速度的水平惯性力做功功率可同理可表示为（W₄-W₅-W₆）：

$\begin{array}{c} {W_4} = \frac{{\gamma r_0^3\omega }}{{3(1 + 9{{\tan }^2}\varphi )}}\left\{ {(3\tan \varphi \sin {\theta _{\text{h}}} - \cos {\theta _{\text{h}}}) \cdot \mathop {}\limits_{} } \right. \\ {\text{e}}^{\left[3\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi \right]}-3\mathrm{tan}\phi \mathrm{sin}{\theta }_{\text{h}}+\mathrm{cos}{\theta }_{0}\}\text{ }\text{，} \end{array}$

(13)

${W_5} = \frac{{\gamma r_0^3\omega }}{6}\frac{L}{{{r_0}}}\sin {\theta _0}\sin {\theta _0}\text{，}$

(14)

$\begin{array}{c} {W_6} = \frac{{\gamma r_0^3\omega }}{6}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}\left[ {\sin ({\theta _{\text{h}}} - {\theta _0}) - \frac{L}{{{r_0}}}\sin {\theta _{\text{h}}}} \right] \cdot \\ \left\{ {{\text{sin}}{\theta _0} + \sin {\theta _{\text{h}}}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}} \right\}。 \end{array}$

(15)

将内部能量耗散速率与外力做功的功率相等，可得到岸坡的临界地震系数k_c。

${k_{\text{c}}} = \frac{{D - {W_{{\text{f1}}}} - \ldots \ldots - {W_{{\text{f}}n}} - ({W_1} - {W_2} - {W_3})}}{{({W_4} - {W_5} - {W_6})}}。$

(16)

前述分析表明，临界地震系数k_c中有n+2个未知参数θ₀, θ_h, θ_f1, …, θ_fn。将式（5）中的n个几何关系作为非线性约束条件，对k_c进行优化，从而得到临界地震系数k_c的最小上限解和破坏模式参数θ₀和θ_h。

2. 高桩码头地震稳定性极限有限元分析

2.1 计算案例

地震作用下高桩码头岸坡断面如图 2所示，水位与坡顶地表平齐，岸坡坡高H = 10 m，坡度为1∶2。高桩码头在垂直海岸线的方向上有四排桩，近海排桩与坡脚的距离为2.5 m，排桩间距为5 m。在平行海岸线方向上，桩间距D₁ = 5 m，桩间净距D₂ = 3.8 m。岸坡土的黏聚力c = 5 kPa，内摩擦角φ = 30°重度γ = 20 kN/m³。群桩抗滑力系数α_m取0.5。

图 2 高桩码头结构断面

Figure 2. Cross section of pile-supported wharf

下载: 全尺寸图片幻灯片

使用本文理论方法求出临界地震系数k_c= 0.2521，对应的破坏面形态参数θ₀ = 1.3763、θ_h = 1.9883。

2.2 计算结果

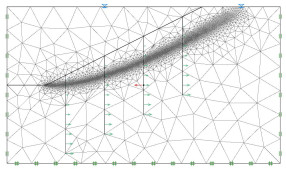
为验证本文方法所得结果的合理性，使用有限元极限分析软件OPTUM G2对案例进行计算。OPTUM G2通过网格自适应迭代技术来获得更为精确的上、下限解，有限元极限分析网格如图 3所示。

图 3 有限元极限分析网格

Figure 3. Meshes of finite element limit analysis

下载: 全尺寸图片幻灯片

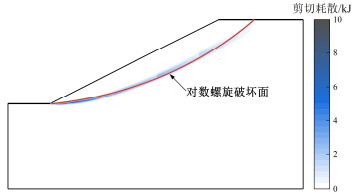
通过极限分析有限元上、下限分析计算得到的临界地震系数k_c分别为0.2493和0.2473。将上、下限解平均值作为精确解的估计，本文理论方法与有限元极限分析结果误差约为1.2%，这表明本文理论方法在计算岸坡临界地震系数方面的有效性。岸坡在拟静力地震荷载作用下的破坏模式可根据极限分析有限元上限分析得到的剪切耗散云图确定。理论方法得到的对数螺旋破坏面与有限元极限分析得到的剪切耗散分布如图 4所示，可看到对数螺旋破坏面与剪切耗散集中区域接近重合，证明了假设的破坏机制的合理性。

图 4 岸坡破坏机制对比

Figure 4. Comparison of failure mechanisms

下载: 全尺寸图片幻灯片

为进一步验证本文理论方法的合理性，分析了不同桩间净距与桩间距之比D₂/D₁、土体强度指标c和φ条件下理论分析方法与极限分析有限元方法得到的临界地震系数k_c，如表 1所示。从表 1可知，理论分析方法得到的临界地震系数k_c略大于极限分析上限有限元解，与本文方法上、下限解平均值误差均为1%左右，表明采用本文理论分析方法所得的岸坡临界地震系数合理。

表 1 临界地震系数对比

Table 1. Comparison of critical seismic coefficients

D₂/D₁	c/kPa	φ/(°)	k_c
D₂/D₁	c/kPa	φ/(°)	有限元下限解	有限元上限解	本文理论方法
0.76	5	30	0.2473	0.2493	0.2521
0.80	5	30	0.2269	0.2287	0.2303
0.84	5	30	0.2107	0.2122	0.2131
0.76	2.5	30	0.1722	0.1747	0.1760
0.76	7.5	30	0.3040	0.3061	0.3101
0.76	5	27.5	0.2164	0.2181	0.2201
0.76	5	32.5	0.2810	0.2837	0.2870

下载: 导出CSV

| 显示表格

3. 岸坡地震稳定性影响因素分析

强度折减法被广泛应用于边坡稳定性分析中，其通过安全系数 ${{F}_\text{S}}$ 折减土体强度指标c和φ，直至边坡达到临界状态，安全系数与土体强度参数的关系为

${{F}_\text{S}} = \frac{c}{{c{\text{'}}}} = \frac{{\tan \varphi }}{{\tan \varphi {\text{'}}}}\text{，}$

(17)

式中：c和φ为土体的黏聚力和内摩擦角， $c{\text{'}}$ 和 $\varphi {\text{'}}$ 为折减后的黏聚力和内摩擦角。

为分析土体强度参数c，φ和影响抗滑力的排桩布置参数D₂/D₁对稳定性和临界破坏面的影响，在岸坡拟静力稳定性分析中，使用临界地震系数k_c和0.15g水平地震作用下岸坡安全系数F_S评估其抗震性能。

3.1 排桩布置影响

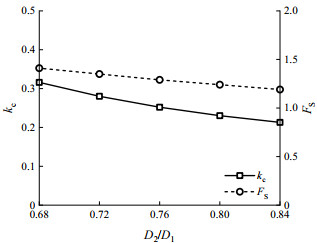
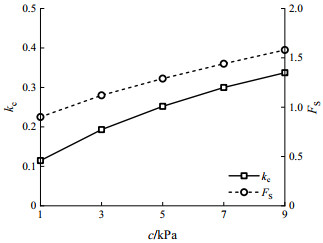
排桩抗滑力受桩间净距与桩间距之比D₂/D₁影响。分别计算不同D₂/D₁条件下岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数，桩间净距与桩间距之比D₂/D₁分别为0.84，0.80，0.76，0.72，0.68。得到D₂/D₁对岸坡稳定性影响如图 5所示，临界地震系数k_c和安全系数F_S随D₂/D₁增大而减小。

图 5 D₂/D₁对地震稳定性的影响

Figure 5. Influences of D₂/D₁ on seismic stability

下载: 全尺寸图片幻灯片

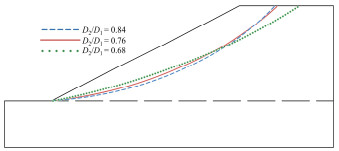
不同D₂/D₁对应的临界破坏面如图 6所示，图 6表明随着D₂/D₁增大，滑动土体在上部范围缩小而在中下部范围扩大，破坏面曲率增大，但D₂/D₁对破坏机制的影响并不显著。

图 6 D₂/D₁对破坏机制的影响

Figure 6. Influences of D₂/D₁ on failure mechanism

下载: 全尺寸图片幻灯片

3.2 黏聚力的影响

计算不同黏聚力条件下岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数F_S，其中，土体黏聚力c分别为1，3，5，7，9 kPa。黏聚力c的影响如图 7所示，图 7表明k_c和F_S随黏聚力c增大呈非线性增大，且随着黏聚力c增大，k_c和F_S增长速率降低。

图 7 黏聚力对地震稳定性的影响

Figure 7. Influences of cohesion on seismic stability

下载: 全尺寸图片幻灯片

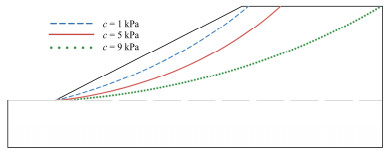
不同黏聚力c对应的岸坡破坏面如图 8所示，从图 8可知，随着黏聚力c增大，临界破坏面以上滑动土体的范围明显增大，这表明土体黏聚力对岸坡的破坏机制有较显著的影响。

图 8 黏聚力对破坏模式的影响

Figure 8. Influences of cohesion on failure mechanism

下载: 全尺寸图片幻灯片

3.3 内摩擦角的影响

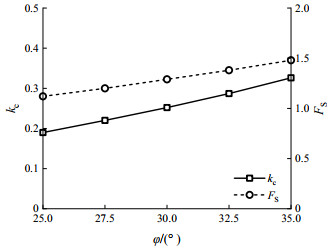
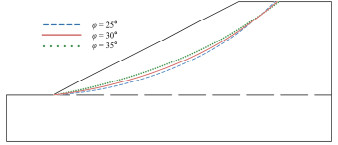
计算不同内摩擦角的岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数F_S，内摩擦角φ分别为25°，27.5°，30°，32.5°，35°，内摩擦角φ对岸坡地震稳定性的影响如图 9所示，图 9表明k_c和F_S均随内摩擦角增大而增大。

图 9 内摩擦角对地震稳定性的影响

Figure 9. Influences of friction angle on seismic stability

下载: 全尺寸图片幻灯片

不同内摩擦角对应的临界破坏面如图 10所示。从图 10可知随着内摩擦角增大，滑动土体在岸坡中下部范围减小，对数螺旋面曲率减小。内摩擦角对岸坡临界破坏面形态的影响在三个因素中最小。

图 10 内摩擦角对破坏机制的影响

Figure 10. Influences of friction angle on failure mechanism

下载: 全尺寸图片幻灯片

4. 结论

针对地震条件下高桩码头岸坡稳定性提出了一种理论分析方法，分析了高桩码头岸坡的破坏模式和安全系数及随主要因素的变化规律。

（1）将排桩对码头岸坡的稳定作用简化为梯形分布力，采用对数螺旋破坏机制推导出岸坡的临界地震系数，并确定临界地震系数的最小上限解和对应的临界破坏面，建立了适用于高桩码头岸坡地震稳定性的理论分析方法。

（2）采用提出的理论分析方法分析了一个高桩码头案例的临界地震系数和破坏机制，并与极限分析有限元结果进行对比，所得结果与有限元极限分析结果相符，验证了理论分析方法的合理性。

（3）采用建立的理论分析方法，分析得出排桩布置、黏聚力、内摩擦角等对临界地震系数和破坏机制的影响规律，并通过强度折减法计算0.15g水平地震加速度条件下岸坡的安全系数。

（4）高桩码头岸坡的临界地震系数和安全系数随桩间净距与桩间距之比增大而减小，随着土体黏聚力和内摩擦角增大而增大。桩间净距与桩间距之比、土体黏聚力和内摩擦角均影响岸坡的临界破坏模式，但土体黏聚力对破坏面模式的影响更明显。

图 1 Wang等^[14]的模型试验示意图

Figure 1. Sketch of model tests conducted by Wang et al.^[14]

下载: 全尺寸图片幻灯片

图 2 不同渗流速度下D轴上Wang等^[14]的试验中温度分布与理论验证

Figure 2. Verification of proposed theory with model tests conducted by Wang et al^[14] and spatial temperature distribution at (a) 0 m/d and (b) 3 m/d seepage velocity on D axis

下载: 全尺寸图片幻灯片

图 3 砂地层模型

Figure 3. Sketch of sand stratum model

下载: 全尺寸图片幻灯片

图 4 在不同渗流速度下，冻结10，75 h后，砂层中温度分布

Figure 4. Distribution of temperature along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

图 5 在不同渗流速度下，冻结10，75 h后，砂层中冰含量分布

Figure 5. Distribution of ice content along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

图 6 在不同渗流速度下，冻结10，75 h后，砂层中结晶盐含量分布

Figure 6. Distribution of crystalline salt content along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

图 7 在不同渗流速度下，冻结10，75 h后，砂层中吸附盐含量分布

Figure 7. Distribution of adsorbed salt content along (a) D axis and (b) Ⅰ axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

图 8 在不同渗流速度下，冻结10，75 h后，砂层中位移分布

Figure 8. Distribution of soil displacement along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

表 1 数值模型中物理参数^[12]

Table 1 Physical parameters for numerical simulation^[12]

名称	符号	值	单位	名称	符号	值	单位
吸附系数	k_ad	2.5×10^-4	s^-1	水冰相变潜热	L_wi	6.01	kJ·mol^-1
解吸系数	k_de	1.5×10^-4	s^-1	液相压缩率	β_lp	1×10^-7	kPa^-1
固相热膨胀系数	β_sT	7.8×10^-6	K^-1	液体热膨胀系数	β_lT	2.1×10^-4	K^-1
浓度依赖系数	β_lw	0.6923	—	液态水密度	$\rho _{\text{w}}^{\text{l}}$	1000	kg·m^-3
冰的密度	$\rho _{}^{\text{l}}$	917	kg·m^-3	摩尔气体常数	R	8.2	J·mol^-1·K^-1
结晶盐密度	$\rho _{}^{\text{p}}$	1460	kg·m^-3	结晶盐的物质的量	M_p	0.142	kg·mol^-1
盐的动力学参数	K_p	1.8×10^-3	s^-1	液相的物质的量	M_l	0.018	kg·mol^-1
吸湿膨胀系数	β_s	1.5×10^-4	—	固体热容	c_s	850	J·kg^-1·K^-1
冰的动力学参数	K_i	5.82×10^-3	s^-1	冰的热容	$c_{\text{i}}^{\text{i}}$	2090	J·kg^-1·K^-1
自由水结合水相变潜热	L_lp	73.04	kJ·mol^-1	结晶盐的热容	$c_{\text{p}}^{\text{p}}$	1743	J·kg^-1·K^-1
盐、结晶盐相变潜热	L_sc	2.34	kJ·mol^-1	固相压缩率	β_sp	2×10^-4	kPa^-1

下载: 导出CSV

表 2 参数分析中使用的目标参数

Table 2 Target parameters used in parametric studies

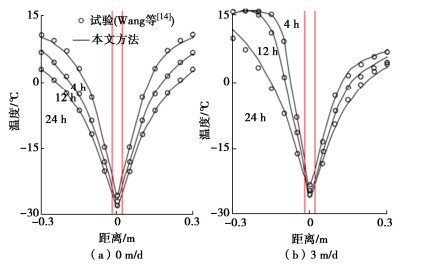
项目	P_l0/kPa	T_p/℃	T₀/℃	$w_{{\text{p0}}}^{\text{l}}$	$w_{\text{p}}^{\text{l}}$	渗流/(m·d^-1)
试验	$\gamma _{\text{w}}^{}\Delta H$	-30	10	—	—	0, 3
渗流	$\gamma _{\text{w}}^{}\Delta H$	-27	13	0.005	0.005	0, 5, 10

下载: 导出CSV

参考文献(14)

[1]	LIU X H, SUN Z Z, ZHU J P, et al. Study on stress-strain characteristics of pipeline-soil interaction under ground collapse condition[J]. Geofluids, 2022, 2022: 5778761.
[2]	ALZOUBI M A, XU M H, HASSANI F P, et al. Artificial ground freezing: a review of thermal and hydraulic aspects[J]. Tunnelling and Underground Space Technology, 2020, 104: 103534. doi: 10.1016/j.tust.2020.103534
[3]	PAPAKONSTANTINOU S, ANAGNOSTOU G, PIMENTEL E. Evaluation of ground freezing data from the Naples subway[J]. Proceedings of the Institution of Civil Engineers - Geotechnical Engineering, 2013, 166(3): 280-298. doi: 10.1680/geng.10.00099
[4]	CHEN K Z, HUANG S, LIU Y J, et al. Thermal, mechanical behavior and engineering response of frozen soil[J]. Geofluids, 2022, 7472284.
[5]	HU X D, YU J Z, REN H, et al. Analytical solution to steady-state temperature field for straight-row-piped freezing based on superposition of thermal potential[J]. Applied Thermal Engineering, 2017, 111: 223-231. doi: 10.1016/j.applthermaleng.2016.09.058
[6]	PIMENTEL E, SRES A, ANAGNOSTOU G. Large-scale laboratory tests on artificial ground freezing under seepage-flow conditions[J]. Géotechnique, 2012, 62(3): 227-241. doi: 10.1680/geot.9.P.120
[7]	HU X D, HONG Z Q, FANG T. Analytical solution to steady-state temperature field with typical freezing tube layout employed in freeze-sealing pipe roof method[J]. Tunnelling and Underground Space Technology, 2018, 79: 336-345. doi: 10.1016/j.tust.2018.06.014
[8]	MING F, CHEN L, LI D Q, et al. Estimation of hydraulic conductivity of saturated frozen soil from the soil freezing characteristic curve[J]. Science of the Total Environment, 2020, 698: 134132. doi: 10.1016/j.scitotenv.2019.134132
[9]	LI M K, CAI H B, LIU Z, et al. Research on frost heaving distribution of seepage stratum in tunnel construction using horizontal freezing technique[J]. Applied Sciences, 2022, 12(22): 11696. doi: 10.3390/app122211696
[10]	ZHANG X D, WU Y J, ZHAI E C, et al. Coupling analysis of the heat-water dynamics and frozen depth in a seasonally frozen zone[J]. Journal of Hydrology, 2021, 593: 125603. doi: 10.1016/j.jhydrol.2020.125603
[11]	YANG X, JI Z Q, ZHANG P, et al. Model test and numerical simulation on the development of artificially freezing wall in sandy layers considering water seepage[J]. Transportation Geotechnics, 2019, 21: 100293. doi: 10.1016/j.trgeo.2019.100293
[12]	ZHOU L Z, ZHOU F X, YING S, et al. Study on water and salt migration and deformation properties of unsaturated saline soil under a temperature gradient considering salt adsorption: Numerical simulation and experimental verification[J]. Computers and Geotechnics, 2021, 134: 104094. doi: 10.1016/j.compgeo.2021.104094
[13]	GAO G Y, GUO W, REN Y X. Numerical study on coupled modelling of artificial freezing marine soil[J]. Computers and Geotechnics, 2023, 159: 105409. doi: 10.1016/j.compgeo.2023.105409
[14]	WANG B, RONG C X, CHENG H, et al. Temporal and spatial evolution of temperature field of single freezing pipe in large velocity infiltration configuration[J]. Cold Regions Science and Technology, 2020, 175: 103080. doi: 10.1016/j.coldregions.2020.103080