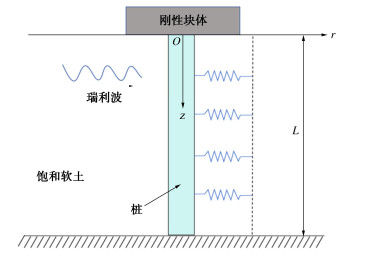
Horizontal dynamic analysis of a single pile in saturated soft soils under Rayleigh wave action consideringe effects of vertical loads
-
摘要: 桩在竖向荷载和瑞利波共同作用下产生水平振动,竖向荷载会因二阶效应导致水平位移增大。为研究桩在饱和软土地基中的水平动力响应,建立瑞利波作用下单桩动力响应的计算模型。基于Biot理论计算均匀自由场中饱和软土地基的水平动力响应。利用边界条件求得土体阻力封闭解。基于Timoshenko梁理论建立桩基动力微分方程,得到桩的水平位移、弯矩和转角的解析解。通过数值算例验证模型正确性,分析竖向荷载、无量纲频率对桩水平振动的影响。研究发现竖向荷载和桩长对水平振动影响较大。
-
关键词:
- 饱和软土 /
- 柔性约束 /
- 水平振动 /
- 瑞利波 /
- Timoshenko梁
Abstract: The pile generates horizontal vibration under the combined action of vertical loads and Rayleigh waves, and the vertical loads will increase the horizontal displacement due to the second-order effects. In order to study the horizontal dynamic response of piles in saturated soft soil foundation, a model for calculating the dynamic response of a single pile under the action of Rayleigh waves is established. Based on the Biot theory, the horizontal dynamic response of saturated soft soil foundation in a uniform free field is calculated. The boundary conditions are used to obtain the closure solution of soil resistance. Based on the Timoshenko beam theory, the dynamic differential equation for the pile foundation is established, and the analytical solutions of the horizontal displacement, bending moment and rotation angle of the pile are obtained. Numerical examples are used to verify the correctness of the model, and the influences of the vertical load and dimensionless frequency on the horizontal vibration of the pile are analyzed. It is found that the vertical load and pile length have a great influence on the horizontal vibration.-
Keywords:
- saturated soft soil /
- flexible constraint /
- horizontal vibration /
- Rayleigh wave /
- Timoshenko beam
-
0. 引言
以往研究中,通常采用循环三轴试验来研究软黏土变形特性[1, 2]。然而,两列相邻列车运行时存在一个间歇阶段,意味着轨道下卧土体经历间歇循环荷载作用[3-5]。例如,Yıldırım等[6]分析了间歇循环荷载作用下软黏土累积轴向应变的发展规律。此外,Li等[7]将间歇循环荷载作用下细粒土的变形模式分成了三种类型,并提出了一个考虑间歇循环荷载影响的累积轴向应变计算模型。Chen等[8]发现土体回弹模量随间歇停振阶段时长的增加而增大。值得注意的是,在这些研究当中,土体在间歇停振阶段处于不排水状态。然而,对于低渗透性的土体而言,其孔隙水在循环加载阶段和间歇停振阶段均可以部分排出,而且土体力学性质与循环荷载加载期间和加载后存余的超孔隙水压力密切相关[9]。因此,研究不同排水条件间歇循环荷载作用下的土体变形特性很有必要。
另一方面,交通荷载作用时土单元上的应力场存在着循环变化的轴向和水平应力[10]。一部分学者通过开展变围压循环三轴试验研究了土体力学性质[11-12]。例如,Wichtmann等[10]分析了有、无循环围压条件下循环载荷作用时土体应变发展的差异。而累积轴向应变随循环围压的变化规律还受到排水条件的影响:不排水条件下,累积轴向应变随循环围压增加而减少[13],而在部分排水条件下则增加[14]。
以往的研究中已经分析了间歇循环荷载对土体变形特性的影响。然而,未考虑循环偏应力和循环围压耦合作用对软黏土变形的影响,同时,也未考虑试验过程中排水条件的影响。本文主要由三部分组成:首先,针对软黏土开展间歇加载循环三轴试验;然后,分析循环围压和排水条件对软黏土变形特性的影响;最后,结合试验结果提出一个考虑循环围压和排水条件影响的计算间歇循环荷载作用下产生的累积轴向应变计算模型。
1. 试验土样及方案
1.1 试验土样
采用薄壁取土器在珠海地区进行取样,取样深度为12.0~14.0 m。按照《土工试验规程(GB/T 50123—2019)》,对试验土样进行了基本物性试验,其基本物理力学参数为:天然密度1.76 g/cm3,天然含水率和界限含水率分别为48.6%,51.9%(液限)和19.8%(塑限),渗透系数为2.26×10-7cm/s。
1.2 试验方案
采用GDS变围压动三轴试验系统开展试验。整个试验过程分为三个阶段:①饱和阶段;②固结阶段;③循环加载阶段。首先,按照《土工试验规程(GB/T 50123—2019)》制备一批直径38 mm,高76 mm的圆柱原状试样,并采用真空饱和、反压饱和的联合饱和方式对所有试样进行饱和。当试样B值至少达到0.95时,试样饱和完成。然后,对所有试样进行等向固结,当试样排水量小于100 mm3/h时,试样固结阶段完成。随后,对固结完成后的试样施加间歇循环荷载。
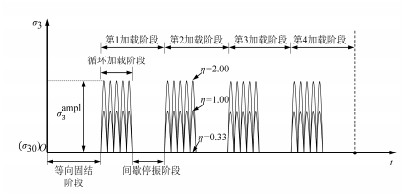
图 1为间歇循环加载过程示意图。从图 1可以看出,整个多阶段间歇循环加载过程由四个阶段组成,每个阶段由循环加载阶段和间歇停振阶段组成:在循环加载阶段,对固结完成后的试样同时施加循环偏应力和循环围压,二者波形均为半正弦波且其相位差为0。采用应力路径斜率η和循环应力比CSR分别表征循环围压幅值和循环偏应力幅值,其表达式见文献[13]所述。结合已有研究成果,拟定循环应力比CSR为0.20,应力路径斜率η分别为0.33,1.00,2.00。在此条件下,每个循环加载阶段振动次数为1000次。
另一方面,对于低渗透性土体而言,很难准确测量循环荷载作用下试样孔压,同时由于该试验系统中孔压的测量位置位于试样底部,若采用较大的加载频率进行试验,可能会导致试样内孔隙水压分布不均匀,测试不够准确。因此,结合文献[11]的研究成果,本试验中采用的加载频率为0.1 Hz。每个循环加载阶段以后,伴随着一个间歇停振阶段,结合文献[7]的研究成果,间歇停振阶段停振时长为3600 s。
以往研究中,由于软黏土渗透系数较低,在循环加载阶段和间歇停振阶段均认为处于不排水状态;而试样在循环加载和间歇停振阶段,不是完全处于不排水状态,而是处于不排水和完全排水状态之间,即部分排水状态。因此,为研究不同排水条件间歇循环荷载作用下软黏土的变形特性,将上述试验分为两种类型:第Ⅰ类试验,试样在循环加载和间歇停振阶段均处于不排水状态,此时排水阀门始终关闭;第Ⅱ类试验,试样在循环加载和间歇停振阶段均处于部分排水状态,结合已有研究成果,打开排水阀门以模拟该状态。
2. 试验结果与分析
2.1 循环围压对累积轴向应变的影响
图 2为部分排水条件下各个加载阶段所产生的累积应变增量随应力路径斜率的变化曲线。从图 2可以看出,各加载阶段累积轴向应变增量均随加载阶段的增加逐渐减小,但不同循环围压对应的试样累积应变增量随加载阶段的衰减程度不一。例如,从第1加载阶段至第4加载阶段时,恒定围压条件下(η=0.33)的试样累积轴向应变增量从4.207%下降到0.044%,而变围压试验条件下(η=2.00)的试样应变增量则从6.979%下降到0.054%。上述试验现象表明,部分排水条件下,变围压试验条件下(η=1.00,2.00)试样累积应变增量的衰减程度更为显著。另一方面,从图 2还可以看出,循环围压对应变增量的影响主要体现在第1加载阶段,后续加载阶段中,有、无循环围压条件下累积轴向应变增量基本相等。以第Ⅱ类试验为例,当η=0.33,1.00和2.00时,第1加载阶段产生的累积轴向应变增量分别为4.207%、5.190%和6.979%,而第4加载阶段产生的对应应变增量则为0.044%、0.089%和0.054%。
2.2 排水条件对累积轴向应变的影响
应变增量随加载阶段的变化曲线还受到排水条件的影响:在部分排水条件下(第Ⅱ类试验)应变增量随循环围压增加而增大,而在不排水条件下则下降(即第Ⅰ类试验)。发生上述试验现象的原因可能是:每个加载阶段的应变增量包括两部分,循环加载阶段循环荷载作用产生的变形和间歇停振阶段试样发生的变形。对于第Ⅰ类试验而言,循环加载阶段试样在循环荷载作用下发生形变,而在间歇停振阶段则会发生回弹变形;对于第Ⅱ类试验而言,循环加载阶段试样变形由循环荷载作用下发生的形变和因孔隙水的排出所发生的体变组成,而在间歇停振阶段则会因为孔隙水的继续排出发生附加体变。因此,相同循环围压条件下,部分排水条件下的间歇循环荷载作用所产生的试样累积应变增量要明显大于不排水条件下的对应应变增量。
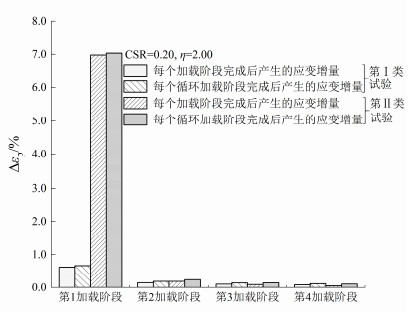
图 3为两种试验条件下每个循环加载阶段和每个加载阶段完成后的应变增量。如图 3所示,不同排水条件下,每个循环加载阶段和每个加载阶段完成后的累积应变增量均逐渐减小,但应变增量的衰减程度不同。以不同加载阶段循环荷载作用完成后两种试验条件下试样变形结果为例进行分析,第1循环加载阶段完成后应变增量分别为0.668%(不排水条件)和7.035%(部分排水条件),而最后一个循环加载阶段对应的应变增量为0.119%(不排水条件)和0.104%(部分排水条件)。部分排水条件下,循环加载阶段完成后试样应变增量的衰减幅度达到了98.52%,而不排水条件下对应应变增量衰减量则为82.18%。
2.3 间歇循环加载累积轴向应变计算模型
一定数量加载阶段所产生的总累积轴向应变εpn, η,可由每个加载阶段所产生的累积轴向应变增量(Δεpi, η)累加计算获得,即
εpn, η=n∑i=1Δεpi, η。 (1) 结合图 2,每个加载阶段所产生的累积轴向应变增量随加载阶段的增加呈幂函数变化趋势,即
Δεpi, η=Δεp1, η⋅ia, (2) 式中:a为拟合参数,Δεpi, η,Δεp1, η分别为第i阶段和第1加载阶段对应的累积轴向应变增量。采用回归分析,不排水状态下,当应力路径斜率η=0.33,1.00和2.00时,拟合参数a取值分别为-2.529,-2.455和-1.816;部分排水状态下,对应的拟合参数a取值分别为-4.647,-4.730和-5.085。不同排水条件下参数a随η的变化规律不一致:在不排水状态,参数a随η的增大而线性增大,而在部分排水状态时则随之线性减小。参数a随η的变化规律可由下式描述:
a=αη+β, (3) 式中,α,β为两个拟合参数。不排水状态下,两个拟合参数α,β的取值分别为0.443和-2.759;部分排水状态下α,β取值则分别为-0.270和-4.521。
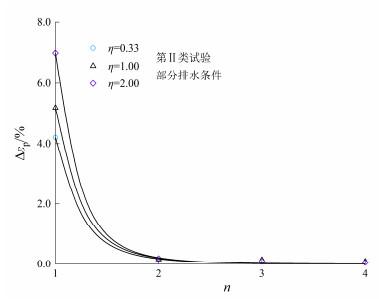
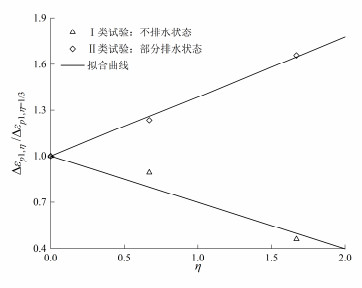
另一方面,图 4描述了不同排水状态下,第1加载阶段有、无循环围压条件下累积轴向应变增量比Δεp1, η/Δεp1, ηΔεp1, η=1/3Δεp1, η=1/3随应力路径斜率η的变化曲线。其中Δεp1, η、Δεp1, η=1/3分别代表变围压和恒围压条件下对应的累积轴向应变增量。从图 4可以看出,不排水状态下,应变增量比随应力路径斜率增大呈减小趋势,而在部分排水状态下,则呈线性增长趋势。二者均可用线性函数描述,但拟合参数有所不同,即
Δεp1, η/Δεp1, ηΔεp1, η=1/3Δεp1, η=1/3=b(η−1/3)+1, (4) 式中,b为拟合参数。通过回归分析,不排水和部分排水状态下的拟合参数取值分别为-0.301和0.388。
然后,将式(3),(4)代入式(2),即可得到不同排水条件下每个加载阶段软黏土累积轴向应变增量计算表达式,即
Δεpi, η=[b(η−1/133)+1]⋅iαη+β⋅Δεp1, η=1/3。 (5) 最后,将式(5)带入式(1)即可得到不同排水条件下间歇循环荷载作用下软黏土累积轴向应变计算表达式,即
εpn,η=n∑i=1Δεpi,η=n∑i=1[b(η−1/3)+1]⋅iαη+β⋅Δεp1,η=1/3。 (6) 表 1为不同排水条件间歇循环荷载作用下软黏土累积轴向应变计算值和试验值对比结果。从表 1中可以看出,计算值与试验值较为接近,表明式(6)可以较好地预测间歇循环荷载作用下软黏土累积轴向应变。
表 1 不同排水条件试样累积轴向应变试验值和预测值Table 1. Comparison between measured results and predicted accumulated axial strains of specimens under intermittent cyclic loading编号 η 排水条件 累积轴向应变 循环加载阶段 间歇停振阶段 实测值/% 计算值/% U1 0.33 不排水 1.760 1.715 U2 1.00 1.592 1.551 U3 2.00 0.954 0.936 P1 0.33 部分排水 4.478 4.408 P2 1.00 5.583 5.422 P3 2.00 7.313 7.217 3. 结论
本文通过两种类型的间歇加载循环三轴试验,分析了循环围压和排水条件对间歇循环荷载作用下软黏土变形特性的影响,主要结论如下:
(1)累积轴向应变的变化受循环围压的影响显著。累积应变增量随加载阶段的增加逐渐减小,但不同循环围压下应变增量的衰减程度不同。同时,不同循环围压下应变增量的差异性在第一个加载阶段中较为明显,而在后续加载阶段中则可以忽略。
(2)累积轴向应变的变化还受到排水条件的影响。在部分排水条件下,应变增量随循环围压增加而增大,而在不排水条件下则反之。同时,与不排水条件下的应变增量衰减幅度相比,部分排水条件下的应变增量的衰减程度更为显著。
(3)提出了一个考虑循环围压和排水条件影响的预测间歇循环荷载作用下软黏土累积应变的表达式。其中,不同排水条件下拟合参数的变化趋势不一致。
-
-
[1] 王磊, 赵成刚. 饱和土沉积谷场地对平面Rayleigh波的散射[J]. 岩土工程学报, 2007, 29(2): 204-211. http://www.cgejournal.com/article/id/12305 WANG Lei, ZHAO Chenggang. Scattering of plane Rayleigh waves in alluvial valleys with saturated soil deposits[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 204-211. (in Chinese) http://www.cgejournal.com/article/id/12305
[2] 肖薄, 刘争平, 黄云, 等. 瑞利面波地形效应的数值模拟研究[J]. 地球物理学进展, 2019, 34(3): 1221-1228. XIAO Bo, LIU Zhengping, HUANG Yun, et al. Study to the topographical effect of Rayleigh surface waves by numerical simulation[J]. Progress in Geophysics, 2019, 34(3): 1221-1228. (in Chinese)
[3] ATHANASOPOULOS G A, PELEKIS P C, ANAGNOSTOPOULOS G A. Effect of soil stiffness in the attenuation of Rayleigh-wave motions from field measurements[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(4): 277-288. doi: 10.1016/S0267-7261(00)00009-9
[4] 夏唐代, 颜可珍, 孙鸣宇. 饱和土层中瑞利波的传播特性[J]. 水利学报, 2004, 35(11): 81-84. XIA Tangdai, YAN Kezhen, SUN Mingyu. Propagation of Rayleigh wave in saturated soil layer[J]. Journal of Hydraulic Engineering, 2004, 35(11): 81-84. (in Chinese)
[5] YANG Z J, WU W B, LIU H, et al. Flexible support of a pile embedded in unsaturated soil under Rayleigh waves[J]. Earthquake Engineering & Structural Dynamics, 2023, 52(1): 226-247.
[6] CAI Y Q, DING G Y, XU C J, et al. Vertical amplitude reduction of Rayleigh waves by a row of piles in a poroelastic half-space[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(16): 1799-1821. doi: 10.1002/nag.789
[7] YANG Z, WU W, LIU H, et al. Flexible support of a pile embedded in unsaturated soil under Rayleigh waves[J]. Earthquake Engineering & Structural Dynamics, 2023, 52(1): 226-247.
[8] ZHANG M, WANG X H, YANG G C, et al. Solution of dynamic Green's function for unsaturated soil under internal excitation[J]. Soil Dynamics and Earthquake Engineering, 2014, 64: 63-84. doi: 10.1016/j.soildyn.2014.05.001
[9] ZHANG M, ZHAO C L, XU C J. Lateral dynamic response of pile group embedded in unsaturated soil[J]. Soil Dynamics and Earthquake Engineering, 2021, 142: 106559.
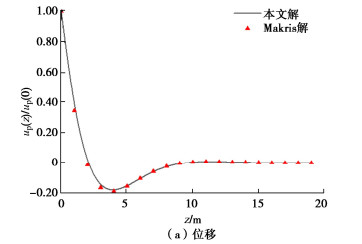
[10] MAKRIS N. Soil-pile interaction during the passage of Rayleigh waves: an analytical solution[J]. Earthquake Engineering & Structural Dynamics, 1994, 23(2): 153-167.



 下载:
下载: