Laws of long-term operation accumulation settlement of deep drainage pipelines in soft soil areas
-
摘要: 深层调蓄管道因长期承受充放水循环荷载导致运营期产生较大沉降，并可能进一步引起管道泄漏、损坏等，从而影响深隧调蓄系统正常运营与环境安全。针对长期充放水循环荷载导致的软土地层管道沉降问题，采用拟静力有限元模拟得到管道满流荷载导致的地基应力分布，并基于分层总和法与软土塑性应变、孔压随加载循环累积的经验公式，提出了管道下方软土地基长期沉降的计算方法。将该法用于上海苏州河段深层调蓄管道长期沉降预测，分析得到了管底地基未加固条件下管道-地基系统长期沉降演化规律。结果表明因充放水循环荷载具有低频重载的特点，地基沉降的绝大部分由于软土的循环累积塑性应变导致，而由孔压消散引起的固结沉降几乎可以忽略。研究成果可为软土地区深隧排水系统设计和运维安全保障提供有益参考。Abstract: The deep drainage pipelines experience significant settlement during operation due to the long-term cyclic loading from water filling and discharge, potentially leading to pipe leakage and damage, consequently affecting the normal operation of the deep tunnel drainage system and environmental safety. To address the settlement issue of pipelines in soft soils caused by the long-term cyclic loading from water filling and discharge, a quasi-static finite element method is employed to simulate the stress distribution in the foundation induced by full-flow loads on the pipeline. Based on the layered summation method and empirical formulas for plastic strain and pore pressure accumulation with loading cycles in soft soils, a method for calculating the long-term settlement of the soft soil foundation beneath the pipeline is proposed. This method is used to predict the long-term settlement of the deep pipelines in the Suzhou River section of Shanghai, and the evolution laws of settlement in the pipeline-foundation system under untreated conditions of the bottom foundation are analyzed. The results indicate that due to the low-frequency heavy loading characteristics of water filling and discharge cycles, the settlement induced by the cumulative plastic strain in the foundation soils accounts for the vast majority. In contrast, the consolidation settlement caused by pore pressure dissipation can be almost ignored. The research findings can provide references for the design and operation safety assurance of deep tunnel drainage systems in soft soil areas.
-
Keywords:
- deep stratum /
- drainage pipeline /
- long-term settlement /
- cyclic loading /
- empirical model
-
0. 引言
近年来，随着“交通强国”战略和“一带一路”倡议的实施，大量的超高层建筑、大跨度桥梁、超长海底隧道等工程项目相继出现，桩基础因其承载力高、稳定性好、变形小等优点[1-2]，在季节性冻土、湿陷性黄土、软土等复杂恶劣地质环境中和山区交通[3-4]、海上风电[5-6]、跨海大桥等重要项目设施中得到了广泛应用，因此，对桩基承载力进行科学评估，并合理选择其设计参数，是目前亟待解决的问题。
传统的桩基载荷试验有两种方法，一种是高应变法[7-8]，另一种是静压法[9-14]。高应变动测分析具有快速方便的特点，但测试时桩身弹性的假定与实际不符，因此得到的Q-S曲线有一定误差[15]。静压法可采用堆载法、锚桩横梁法和拉压锚法，堆载法要解决成百上千吨堆载材料的来源、存储和运输及吊装，费时费力；而锚桩横梁法和拉压锚法由于需要设置多个锚桩、反力梁等，设备成本较高，并且容易受到场地、吨位等因素的制约，在试验过程中，基桩的潜能无法完全被挖掘出来，很难获得可靠的试验数据，从而无法科学、合理地评估基桩的承载力。
桩基自平衡载荷试验是基于改进传统载荷试验的反力系统发展而来的，称之为O-Cell法[16-18]，国内称为自平衡法[19-21]；作为一种新的桩基承载力检测手段，因该技术受场地条件限制较少，故而特别适用于一些特殊工程，如深基坑工程的桩基承载力检测试验。但该测试技术的主要缺陷在于，主要设备荷载箱是一种特别设计可用于加载的设备，造价高昂；使用时焊接在钢筋笼上，试验完毕后无法回收[22]。
本文研发了一种可回收自平衡法桩基承载力检测装置，具有适用范围广、造价低廉、测试周期短等优点，并根据荷载传递特性模型分析了该新型测试装置的工作机理，并通过现场实测结果和三维有限元计算进行了验证，结合桩身荷载沉降、轴力等数据，揭示了可回收自平衡法桩基承载力检测装置的工作机理。
1. 新型检测结构的提出及工作机理
1.1 新型可回收检测结构的提出及构造
针对现有测试技术周期长、受地形影响大等原因，基于自平衡法的测试原理和开瓶器受力方式，从节能减排、绿色低碳等角度出发，提出一种可回收自平衡法桩基承载力检测装置[22]，装置主要包括试验桩、液压千斤顶、反力梁、反力锚筋、反力钢板、位移监测系统，结构原理及装置如图 1所示。
该装置采用分离桩体和加载系统的方式，实现了一种可回收自平衡法桩基承载力检测，主要做法是在桩身中性点下放置反力钢板，上段桩预设孔洞并安设受压钢柱，钢柱顶安装液压千斤顶和反力梁，并通过反力锚筋与桩身连接形成整体测试装置，试验时，液压加载系统控制千斤顶沿垂直方向同时施加荷载，得到上段挖孔桩向上、下段实心桩向下的位移，绘制Q-S曲线，进而得到桩基承载力、桩基沉降等参数。
1.2 工作机理及主要优点
该装置工作的主要技术原理为：①作用力与反作用力原理：在实心桩和挖孔桩交界处设置钢板，将桩身分为上下两部分，液压千斤顶加载时锚筋受向上拉力，同时通过预留孔洞内插入的受压杆对钢板产生向下压力。②检测原理：在作用力与反作用力原理下，液压千斤顶通过受压杆和钢板下压使实心桩产生向下位移，由于锚筋和钢梁组成的反力系统使得挖孔桩产生向上位移，绘制对应的“Q-S曲线”，判断桩基承载力。③回收原理：测量结束以后，拆除钢梁、液压千斤顶、扩大盘，按照设计高度切割锚筋，运用起重设备将受压杆从挖孔桩的预留孔洞中分段吊出回收，拆除各构件以便再次组装利用，上端桩体的预留孔洞内填筑混凝土并振捣填实后可作为承载桩使用。
其主要的优点是：①该装置使用空间小，特别适用于坡地、水上、基坑底、狭窄场地；②该装置利用桩的侧阻力与端阻力互为反力，可清楚区分侧阻力与端阻力分布以及各自的荷载-位移曲线；③该装置使用液压千斤顶提供荷载，费用低，可多根桩同时测试，测试周期短，有利于增加试桩数量，扩大检测范围；④试验结束后，组合钢柱吊出回收再利用，大量节约资源；⑤在试验桩预留孔洞注浆后，试验桩仍可作为工程承载桩使用，经济效益显著。
2. 工作机理分析
2.1 荷载传递函数微分方程
基本假设如下：
（1）桩为弹性体，忽略受压钢柱、反力钢板的变形及反力锚筋与上段桩之间的相对位移。
（2）可由单元上下两面的轴向力和平均截面刚度来计算各单元应变。
（3）桩端承载力-沉降量关系及不同深度的桩侧摩阻力-变形量关系与标准试验方法相同。
新型可回收检测结构的工作机理及微单元受力分析如图 2所示。
由微单元受力可得
$$ \frac{{{\text{d}}{s^2}(z)}}{{{\text{d}}{z^2}}} = \frac{U}{{EA}}q(z) \text{, }\; $$ (1) 式中：$ U $为桩周长；$ E $和$ A $分别为桩的弹性模量和横截面积。根据剪切位移法，假设桩周土的位移为
$$ s(z) = \frac{{q(z){r_0}}}{{{G_{\text{s}}}}}\ln ({r_{\text{m}}}/{r_0}) \text{, }\; $$ (2) 式中：q(z)为桩侧摩阻力；$ {r_0} $为桩半径；$ {r_{\text{m}}} $为有效影响半径，$ {r_{\text{m}}} $=2.5L(1-$ {\nu _{\text{s}}} $)，L为桩长；$ {G_{\text{s}}} $为桩侧土剪切模量；$ {\nu _{\text{s}}} $为土体泊松比。
将式（2）代入式（1）可得
$$ \frac{{{{\text{d}}^2}s(z)}}{{{\text{d}}{z^2}}} - \frac{U}{{EA}} \cdot \frac{{s(z) \cdot {G_{\text{s}}}}}{{{r_0} \cdot \ln ({r_{\text{m}}}/{r_0})}} = 0 。 $$ (3) 令$ k = (2{\rm{ \mathsf{ π} }} \cdot {G_{\text{s}}})/\ln ({r_{\text{m}}}/{r_0}) $，定义为桩土剪切刚度系数，$\alpha = \sqrt {k/EA} $，可得
$$ \frac{{{{\text{d}}^2}s(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2} \cdot s(z) = 0 。 $$ (4) 2.2 上段桩荷载传递规律
自平衡法检测中，上段桩自重对端承载力有一定影响，因此，考虑上段桩自重影响时，其桩侧荷载传递基本微分方程为
$$ \frac{{{\text{d}}{s_1}^2(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2}{s_1}(z) = \frac{\gamma }{E} \text{, }\; $$ (5) 式中，$ \gamma $为桩体重度。
上段桩顶的边界条件为
$$ {Q_1}(z) = - {\left. {EA\frac{{{\text{d}}{s_1}(z)}}{{{\text{d}}z}}} \right|_{z = 0}} = 0 \text{, }\; $$ (6) 上段桩底的边界条件为
$$ {Q_1}(z) = - {\left. {EA\frac{{{\text{d}}{s_1}(z)}}{{{\text{d}}z}}} \right|_{z = {L_1}}} = {Q_{\text{u}}}, {s_1}(z) = {\left. {{s_1}(z)} \right|_{z = {L_1}}} = {s_{\text{u}}} 。 $$ (7) 式中：$ {Q_{\text{u}}} $和$ {s_{\text{u}}} $分别为液压千斤顶施加的向上的荷载与产生的位移。
根据式（5）可得，上段桩的桩身位移和轴力为
$$ \left\{ \begin{array}{l} {s_1}(z) = {C_1}{{\text{e}}^{\alpha z}} + {C_2}{{\text{e}}^{ - \alpha z}} - \frac{\gamma }{{{\alpha ^2}E}} \hfill \\ {Q_1}(z) = - {C_1}EA\alpha {{\text{e}}^{\alpha z}} + {C_2}EA\alpha {{\text{e}}^{ - \alpha z}} \hfill \end{array} \right. \text{, }\; $$ (8) 式中：C1和C2为常数，可由式（6），（7）确定。
将式（8）用矩阵形式表达为
$$ \left\{ {\begin{array}{*{20}{l}} {{s_1}(z)} \\ {{Q_1}(z)} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{{\text{e}}^{\alpha z}}}&{{{\text{e}}^{ - \alpha z}}} \\ { - EA\alpha {{\text{e}}^{\alpha z}}}&{EA\alpha {{\text{e}}^{ - \alpha z}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{C_1}} \\ {{C_2}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} 。 $$ (9) 试验桩侧地基土层按照单元厚度为hi进行划分，可得桩单元顶部的内力和位移表达为
$$ \left\{ {\begin{array}{*{20}{c}} {{s_1}({z_i})} \\ {{Q_1}({z_i})} \end{array}} \right\} = {T^1}(z)\left\{ {\begin{array}{*{20}{l}} {{C_1}} \\ {{C_2}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\; $$ (10) 其中，
$$ {T^1} = \left[ {\begin{array}{*{20}{c}} {\cosh (\alpha {h_i})}&{ - {{(EA\alpha )}^{ - 1}}\sinh (\alpha {h_i})} \\ { - EA\alpha \sinh (\alpha {h_i})}&{\cosh (\alpha {h_i})} \end{array}} \right] 。 $$ (11) 根据位移连续性条件可得：
$$ \left\{ {\begin{array}{*{20}{l}} {{s_1}(z = {L_1})} \\ {{Q_1}(z = {L_1})} \end{array}} \right\} = \left[ {{T^1}} \right]\left\{ {\begin{array}{*{20}{l}} {{s_1}(z = 0)} \\ {{Q_1}(z = 0)} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\; $$ (12) 式中，$ {L_1} $为上段桩长。
荷载试验过程中，上段桩侧土体出现塑性区，第i段桩单元侧摩阻力达到土体剪切强度$ {q_{{f_{\text{u}}}}} $后，假定该单元进入塑性状态后摩阻力保持稳定状态，后期增加的荷载将转移到上部弹性区域的桩单元承担，第i段桩单元微分方程为
$$ \frac{{{\text{d}}{s_1}^2(z)}}{{{\text{d}}{z^2}}} - \frac{U}{{EA}}{q_{{f_{\text{u}}}}} = \frac{\gamma }{E} 。 $$ (13) 求解并表达为增量形式为
$$ \left\{ {\begin{array}{*{20}{l}} {\Delta {s_{1i}}} \\ {{Q_{1i}}} \end{array}} \right\} = \left[ {{T_f}} \right]\left\{ {\begin{array}{*{20}{l}} {\Delta {s_{1i}}} \\ {\Delta {Q_{1i}}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\; $$ (14) 其中，
$$ {\left[ {{T_f}} \right]_i} = \left[ {\begin{array}{*{20}{c}} 1&{ - \frac{{{h_i}}}{{EA}}} \\ 0&1 \end{array}} \right] 。 $$ (15) 2.3 下段桩荷载传递规律
对于下段桩受压加载时，不需要克服桩自重，桩侧受正摩阻力作用，受力特征与传统受压桩相同，同理可得
$$ \frac{{{\text{d}}{s_2}^2(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2}{s_2}(z) = 0 \text{, }\; $$ (16) 式中，s2(z)与Q2(z)分别表示下段桩z位置处的位移与轴力。同理可得
$$ {\left\{ {\begin{array}{*{20}{l}} {{s_2}({z_i})} \\ {{Q_2}({z_i})} \end{array}} \right\}_b} = \left[ {{T^2}({z_i})} \right]\left\{ {\begin{array}{*{20}{l}} {{s_2}({z_i})} \\ {{Q_2}({z_i})} \end{array}} \right\} \text{, }\; $$ (17) 其中，
$$ {T^2}({z_i}) = \left[ {\begin{array}{*{20}{c}} {\cosh (\alpha {h_i})}&{ - {{{\text{(}}EA\alpha {\text{)}}}^{ - 1}}\sinh (\alpha {h_i})} \\ { - EA\alpha \sinh (\alpha {h_i})}&{\cosh (\alpha {h_i})} \end{array}} \right] 。 $$ (18) 2.4 Q-S曲线等效转换方法
以反力钢板位置为起点，将上段桩分割为n个单元，桩身任意处的内力与变形量如下：
$$ Q(i)=Q(0)+\sum\limits_{m=1}^{i}q(m)\{U(m)+U(m+1)\}q(m)/2 \text{, }\; $$ (19) $$ s(i)=s(0)+\sum\limits_{m=1}^{i}\frac{Q(m)+Q(m+1)}{E(m)A(m)+E(m+1)A(m+1)}h(m) 。 $$ (20) 式中：Q(0)为i=0处桩的轴力（kN），即上部液压千斤顶的加载值；s(0)为i=0处桩的位移（m），即上段桩的位移；q(m)为m处的桩侧摩阻力（kPa）。
上段桩等效转换桩顶i=n时的荷载和位移如下：
$$ Q(n)=Q(0)+\sum\limits_{m=1}^{n}q(m)\{U(m)+U(m+1)\}q(m)/2 \text{, }\; $$ (21) $$ \begin{array}{l}s(n)=s(0)+\frac{h(n)}{E(n)A(n)+E(n-1)A(n-1)}\cdot \\ \{2Q(0)+\sum\limits_{m=1}^{n-1}q(m)[U(m)+U(m+1)]h(m)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\begin{array}{*{20}{c}} {} \\ {} \end{array}q(n)[U(n) + U(n - 1)]h(n)/2} \right\} 。 \end{array} $$ (22) 根据上文建立的荷载传递模型，采用MATLAB编程可得到多层地基中上、下段桩的轴力、位移值，根据式（21），（22）将测试结果进行转换，在利用等荷载法将试桩的Q-S曲线转换为传统静压桩的Q-S曲线，可得到试桩的极限承载力：
$$ {Q}_{\text{u}}={Q}_{\text{u}}{}_{上}+{Q}_{\text{u}}{}_{下} 。 $$ (23) 3. 工程对比与数值模拟分析
3.1 工程概况与数值模拟建模
以润扬长江大桥桩基承载力检测工程[23]为参考，基于ABAQUS建立了大型三维有限元分析模型（如图 3），由于篇幅限制，详细参数与测试方法见文献[23]。
3.2 试桩Q-S曲线对比分析
荷载箱加载现场实测结果、数值模拟分析结果与新型检测结构加载时的对比曲线如图 4所示，可以看出，三者上段桩与下段桩的Q-S曲线发展趋势基本一致，加载分为15个等级，每级8000 kN，加载结束后，上段桩位移18.26 mm，下端桩位移7.91 mm，因此取上、下段桩极限承载力分别为62771 kN和56436 kN。就数值大小而言，本文理论计算结果比现场实测结果大0.16%~12.49%，可认为该新型可回收桩基检测结构在合理评价桩基承载力方面具有优势；数值分析结果略小于现场实测结果，可能与现场土层非均匀性、桩-土相对位移、边界条件等的简化分析有关。
3.3 桩身轴力分析
各级加载下，桩身轴力对比如图 5所示，可以看出理论计算结果、数值模拟结果与实测结果均比较吻合；下段桩轴力出现衰减，表明荷载较小时，施加荷载主要由桩身下部土层承担，荷载逐级增大时，上部土层逐渐发挥作用；从曲线疏密程度来看，曲线越稀疏轴力衰减越大，从钢板位置向上25 m范围内曲线较疏，可认为该部分土层承担的荷载较大。
![]()
图 5 各级加载下试桩轴力分布Figure 5. Distribution of axial force of test piles under different loads3.4 等效转换结果分析
从图 6可以看出，现场实测结果、理论计算结果和数值模拟结果基本吻合，现场实测桩基承载力比数值模拟结果大3.5%，本文理论计算结果为119207 kN，可见新型可回收结构检测结果优于荷载箱结构，精度提高3.5%。
4. 结论
本文研发了一种可回收自平衡桩基承载力检测装置，建立了荷载传递模型，分析了新型结构的工作机理，并与现场实测结果、数值模拟结果进行了对比分析，主要结论如下：
（1）通过分离桩体和加载系统的方式，提出一种可回收自平衡法桩基承载力检测装置，主要做法是在桩身中性点下放置反力钢板，替代荷载箱进行加载，特别适用于坡地、水上、基坑底、狭窄场地，结构巧妙，装配化程度高，具备可回收、低耗能等优点，为桩基承载力检测提供了新的思路。
（2）建立了新型结构作用下的桩体荷载传递模型，本文理论结果分析表明，解析模型能够合理反映新型结构作用下的上、下段桩的荷载沉降特性以及桩身轴力等分布规律，与现场实测结果、数值模拟结果吻合程度较好，承载力检测精度提高3.5%，可认为该新型结构具有一定的适用性和推广价值。
（3）本文仅针对新型检测装置作用的等截面试桩进行了荷载传递机理分析，但对湿陷性黄土、冻土等特殊地层桩和变截面桩未进行研究，以待下一步进行现场试验，综合分析该新型结构的工作原理。
-
![]()
图 5 管底地基沉降与循环次数关系
Figure 5. Relationship between settlement of foundation below pipeline and number of cyclies
![]()
图 6 不同循环次数下管道下方地基不同深度处总沉降量
Figure 6. Total settlement at different depths of foundation beneath pipeline for different numbers of cycles
表 1 土层基本参数
Table 1 Basic parameters of soil strata
层序 土名 厚度/
m密度/
(g·cm-3)压缩模量/
MPa泊松比 渗透系数/
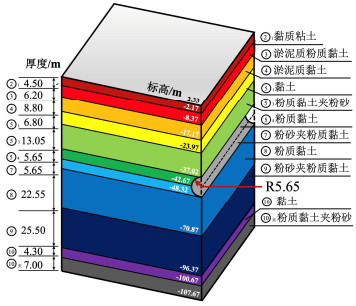
(m·s-1)侧压力系数 孔隙比e 有效内摩擦角φ′/(°) ②1 粉质黏土 4.50 1.85 5.03 0.38 2E-8 0.48 0.926 28.5 ③ 淤泥质粉质黏土 6.20 1.75 3.34 0.41 1E-7 0.50 1.175 29.6 ④ 淤泥质黏土 8.80 1.70 2.68 0.41 1E-8 0.53 1.335 27.9 ⑤1 黏土 6.80 1.76 3.82 0.41 2E-8 0.51 1.127 30.5 ⑤3 粉质黏土夹粉砂 13.05 1.79 5.20 0.38 3E-7 0.47 1.001 31.6 ⑤4 粉质黏土 5.65 1.95 6.36 0.38 1E-8 0.45 0.699 32.4 ⑦ 粉砂夹粉质黏土 5.65 1.94 11.55 0.33 5E-6 0.37 0.694 — ⑧ 粉质黏土 22.55 1.84 5.76 0.35 3E-7 0.47 0.900 32.8 ⑨ 粉砂夹粉质黏土 25.50 2.01 15.56 0.35 5E-4 0.38 0.570 33.0 ⑩ 黏土 4.30 2.00 10.97 0.38 2E-7 0.51 0.641 31.6 ⑩夹 粉质黏土夹粉砂 7.00 1.95 8.67 0.38 5E-5 0.51 0.710 32.0 
下载: 导出CSV
表 2 模型参数
Table 2 Model parameters
a n c b au nu c bu 0.076 1.408 0.5 0.408 0.0385 1.37 0.5 0.32
下载: 导出CSV
-
[1] 仇保兴. 海绵城市(LID)的内涵、途径与展望[J]. 给水排水, 2015, 51(3): 1-7. QIU Baoxing. Connotation, approach and prospect of sponge city (LID)[J]. Water & Wastewater Engineering, 2015, 51(3): 1-7. (in Chinese)
[2] WALKER D E, HEATH G R, LEVY W P. Design of a storage tunnel control strategy to eliminate cso and reduce stormwater discharges to south Boston beaches[J]. Proceedings of the Water Environment Federation, 2006, 2006(4): 226-250. doi: 10.2175/193864706783796402
[3] 何巍伟, 王梦华, 武今巾. 深层排水隧道研究进展[J]. 科技资讯, 2023, 21(3): 59-64, 134. HE Weiwei, WANG Menghua, WU Jinjin. Research progress of deep drainage tunnel[J]. Science & Technology Information, 2023, 21(3): 59-64, 134. (in Chinese)
[4] 刘明, 黄茂松, 李进军. 地铁荷载作用下饱和软黏土的长期沉降分析[J]. 地下空间与工程学报, 2006, 2(5): 813-817. doi: 10.3969/j.issn.1673-0836.2006.05.026 LIU Ming, HUANG Maosong, LI Jinjun. Long-term settlement of saturated soft clay under subway loading[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(5): 813-817. (in Chinese) doi: 10.3969/j.issn.1673-0836.2006.05.026
[5] MONISMITH C L, OGAWA N, FREEME C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. Transportation Research Record, 1975(537): 1-17.
[6] LI D Q, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering, 1996, 122(12): 1006-1013. doi: 10.1061/(ASCE)0733-9410(1996)122:12(1006)
[7] CHAI J C, MIURA N. Traffic-load-induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(11): 907-916. doi: 10.1061/(ASCE)1090-0241(2002)128:11(907)
[8] 黄茂松, 姚兆明. 循环荷载下饱和软黏土的累积变形显式模型[J]. 岩土工程学报, 2011, 33(3): 325-331. http://cge.nhri.cn/article/id/13943 HUANG Maosong, YAO Zhaoming. Explicit model for cumulative strain of saturated clay subjected to cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 325-331. (in Chinese) http://cge.nhri.cn/article/id/13943
[9] HUANG M S, YAO Z M. Effect of the principal stress direction on cyclic cumulative deformation and pore pressure of soft clay[J]. Procedia Engineering, 2016, 143: 811-819. doi: 10.1016/j.proeng.2016.06.132
[10] 姚兆明, 张明慧, 陈军浩. 饱和软黏土循环累积孔压模型及地铁隧道路基长期沉降计算[J]. 铁道学报, 2012, 34(9): 87-92. doi: 10.3969/j.issn.1001-8360.2012.09.015 YAO Zhaoming, ZHANG Minghui, CHEN Junhao. Cyclic accumulative pore pressure explicit model of saturated soft clay and long-term settlement calculation of subway tunnel roadbed[J]. Journal of the China Railway Society, 2012, 34(9): 87-92. (in Chinese) doi: 10.3969/j.issn.1001-8360.2012.09.015
[11] 马霄, 钱建固, 韩黎明, 等. 交通动载下路基长期运营沉降等效有限元分析[J]. 岩土工程学报, 2013, 35(增刊2): 910-913. http://cge.nhri.cn/article/id/15517 MA Xiao, QIAN Jiangu, HAN Liming, et al. Equivalent finite element method for long-term settlement of subgrade induced by traffic load[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 910-913. (in Chinese) http://cge.nhri.cn/article/id/15517
[12] 黄茂松, 宋晓宇, 秦会来. K0固结黏土基坑抗隆起稳定性上限分析[J]. 岩土工程学报, 2008, 30(2): 250-255. doi: 10.3321/j.issn:1000-4548.2008.02.016 HUANG Maosong, SONG Xiaoyu, QIN Huilai. Basal stability of braced excavations in K0-consolidated soft clay by upper bound method[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 250-255. (in Chinese) doi: 10.3321/j.issn:1000-4548.2008.02.016
[13] 毛盘, 张旭东, 叶斌, 等. 特深圆形竖井土压力分布模式及影响因素研究[J]. 地下空间与工程学报, 2022, 18(1): 257-267. MAO Pan, ZHANG Xudong, YE Bin, et al. Study on earth pressure distribution pattern of ultra-deep circular shaft and its influential factors[J]. Chinese Journal of Underground Space and Engineering, 2022, 18(1): 257-267. (in Chinese)
计量
- 文章访问数: 48
- HTML全文浏览量: 13
- PDF下载量: 13
