Dynamic response of a visco-elastic half-space subjected to buried moving loads
-
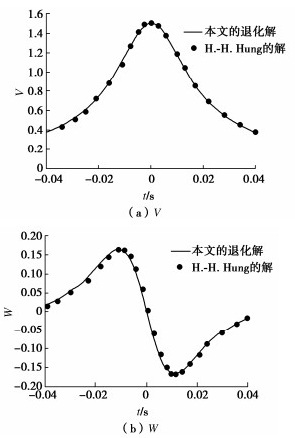
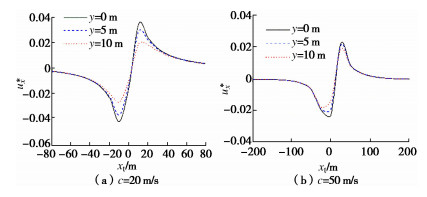
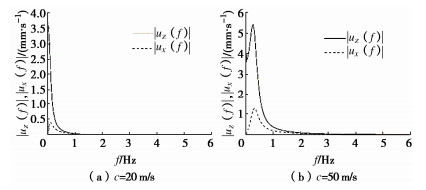
摘要: 采用积分变换方法对埋置移动荷载作用下三维黏弹性半空间地基振动的衰减规律进行了理论研究。首先,基于理想弹性介质的动力Navier方程,利用Helmholtz分解定理及傅里叶变换方法,在直角坐标系中求得了变换域内弹性介质动力响应分量的表达式。结合相应的边界条件及连续条件,得到了埋置移动荷载作用下黏弹性半空间地基动力响应的积分形式解。当荷载埋深为零时,埋置移动荷载退化为地表移动荷载,对比发现退化解结果与已有结果吻合较好。最后,采用IFFT法对地基土体动力响应进行数值求解,分析了移动荷载埋深、速度等因素对地基振动的分布衰减规律以及频谱分布的影响。Abstract: The attenuation of the vibration of a three-dimensional visco-elastic half-space subjected to the embedded moving loads is investigated theoretically. By employing the Fourier integral transform method and the Helmholtz decomposition, the Navier equations for the ideal elastic medium are solved, and the dynamic components in the transformed domain are derived in the Cartesian coordinate. Combined with the boundary conditions and continuity conditions, the analytical solutions to the dynamic response of the viscoelastic half-space due to the embedded moving loads are obtained. When the depth of the moving loads is zero, the results obtained in this study are in good agreement with the published ones. By employing the IFFT method, some numerical examples are selected to discuss the influences of the depth, velocity and viscous damping of the soil on the propagation of the vibration and the amplitude spectra of the displacement.
-
0. 引言
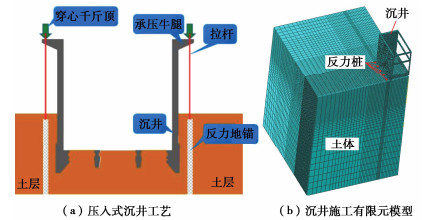
沉井法是一项传统的地下工程施工工艺,在大型桥梁墩台基础、地下工业厂房等场景应用广泛,但传统下沉工艺存在沉井姿态纠偏困难、下沉缓慢等弊端,压入式沉井借助反力装置,将沉井压入土体,可消除土层差异的不利影响,实现下沉全过程的有效控制。
为此,利用压入式连续沉井群构建地下车站成为了可能(如图 1所示)。类似明挖式基坑修建方式,沉井下沉过程会不断扰动周围土体,评估和预测沉井施工对周边环境的影响有助于保护相邻设施,但目前对沉井压入过程环境影响的研究主要集中在现场实测。
徐鹏飞等[1]分析了沉井压沉过程周边土体监测数据,研究了压入式沉井施工对周边环境的影响。邓友生等[2]对比分析监测数据与有限元结果,研究了沉井对邻近建筑物的影响。罗实瀚等[3]分析地锚式沉井施工过程的现场监测数据,探讨了施工对周边环境的影响。上海市地标《地下工程预制装配技术标准》[4]通过总结上述实测数据,推荐了井外地表沉降剖面曲线。
上述研究均未考虑反力桩存在对土体沉降规律的影响,本文以某车站沉井工程为例,通过数值模拟分析压入式沉井施工对环境的影响,进一步研究桩间距对地表沉降的调控作用,并基于抗拔力等效原则,同时探究桩间距和桩径对周边土体沉降变化的影响。
1. 工程概况
如图 1所示,某沉井群工程项目为地下车站,主体长283.4 m,沿纵向分为7节沉井,两个端头井各1节,分别为#1、#7沉井,标准段5节,分别为#2~#6沉井,各沉井相邻纵向净距2.5 m。
车站主体结构7节沉井均采用压入式沉井法施工,如图 2(a)所示,通过千斤顶提供下压力,将沉井压入土体。同时在外侧设置反力桩,用于平衡反力以及控制地表沉降,本工程反力桩沿车站纵向边界布置,桩间距(相邻桩侧至桩侧的距离)3.5 m,桩中心距离井壁边1.5 m,采用桩径1000 mm灌注桩,桩长48 m。
2. 沉井贯入数值模拟
为分析沉井贯入引起的周边地表沉降,采用ABAQUS软件进行数值模拟。取标准段沉井建模,长44.42 m,宽25.5 m,深24.8 m,侧壁厚1 m,内部隔墙厚0.5 m;土体模型长73 m,宽63 m,高96 m。根据结构对称性,建立如图 2(b)所示1/4有限元模型。
除实际工况外,本文还设置14根和20根桩径为1 m的两种工况,以研究桩间距对于地表沉降的调控作用。数值模拟的不同工况参数如表 1所示。
表 1 数值模拟工况介绍Table 1. Case studies for numerical simulation工况 桩径D/m 桩间距s/m 桩数 评述 0 — — — 无反力桩 1 1 3.5 10 实际工况 2 1 2.3 14 桩间距影响 3 1 1.2 20 4 0.5 1.7 20 与工况1抗拔等效 5 0.25 0.85 40 同时,为依据抗拔承载力等效原则分析不同直径反力桩对地表沉降的影响,参考API规范[5]中抗拔桩侧摩阻力计算方法:
f=αc, (1) 式中:α为摩擦因子;c为该点土体不排水抗剪强度。
抗拔承载力,即桩侧总摩阻力,为桩身各点侧摩阻力之和,与桩身侧面积正相关。抗拔力等效原则可近似表述为总桩侧面积相等。基于此获得与实际工程具有一致抗拔承载力的工况4,5,具体参见表 1。
采用罚函数控制沉井-土体、反力桩-土体的接触,设置摩擦系数0.4,通过设置极限剪应力以控制反力桩极限抗拔力;采用“生死单元”模拟井内土开挖过程。
该工程采用不排水下沉施工方式,为确保数值模拟与实际情况相符,土体重度采用有效重度。
在沉井埋深范围内第④层土占比超过50%,且对该层土物理力学性质研究较为深入,故选取该层土进行单一地层模拟,采用ABAQUS内置运动硬化土体本构模型,沉井及反力桩均采用弹性本构模型。沉井、反力桩及土体材料参数见表 2,3。
表 2 沉井、反力桩材料参数Table 2. Material parameters of caissons and uplift piles结构物 弹性模量/GPa 泊松比 沉井、反力桩 30 0.3 表 3 第④层灰色淤泥质黏土材料参数Table 3. Material parameters of gray silty clay of Layer 4材料参数 数值 重度/(kN·m-3) 16.4 弹性模量/kPa 69502 不排水抗剪强度/kPa 27 泊松比 0.49 初始屈服应力A 2.7 运动硬化参数C1 16712 Gamma1 325 3. 沉井贯入环境影响分析
3.1 沉井贯入地表沉降分析
在不考虑反力桩的情况下,沿沉井长边中点、长边角点、短边中点、短边角点4个典型断面,研究沉井下沉到设计标高时地表沉降,结果如图 3所示。
对于单一沉井,上海市地标《地下工程预制装配技术标准(轨道交通工程)》[4]中根据实测结果对地表沉降最大值和下限值进行了拟合:
ΔvmH(%)=0.016(H2t2−1), (2) {ΔvΔvm=−0.95dHc+1 0⩽dHc⩽0.75ΔvΔvm=−0.23dHc+0.46 0.75⩽dHc⩽2。 (3) 式中:d为距井壁距离;H为沉井贯入深度;t为井内土塞高度,本工程取2 m;Δvm为最大地表沉降。
徐鹏飞等[1]根据沉井施工过程的地表沉降监测数据,拟合得到指数型地表沉降分布曲线方程:
ΔvΔvm=e−4.3dH。 (4) 沿4个断面提取地表沉降曲线,并与徐鹏飞等[1]及规范方法[4]进行对比,如图 4所示,其中,Δv为该断面地表沉降;Δvm为该断面最大地表沉降。
由图 4可知,本文地表沉降曲线与徐鹏飞等[1]及规范方法[4]在发展趋势上较为吻合;本文地表沉降最大值55.67 cm与规范方法最大值62.1 cm存在约10%的误差,后者相对更为保守;沉井贯入时长短边引起的地表沉降存在差异;水平方向0~15 m内地表沉降较为明显,大于15 m对地表沉降影响较小,与规范方法设置d/H=0.55为地表沉降曲线分界点较为符合。
3.2 反力桩对沉井贯入地表沉降影响分析
(1)实际工况数值模拟结果
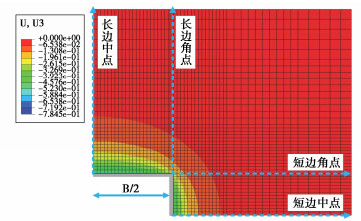
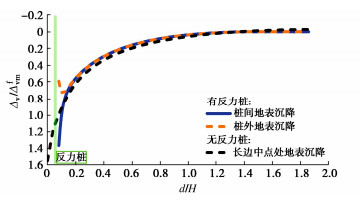
实际施工时,在井外侧均匀布置10根桩径为1 m的反力桩。本文对实际工况进行模拟,位移云图如图 5所示,选取沉井长边中点处提取地表沉降,如图 6所示,其中Δfvm为没有桩基时桩外侧处的土体沉降值。
结合图 5,6可知,反力桩会极大的改变地表沉降的分布规律。由于桩基竖向刚度远大于周围土体,所以桩外侧土体沉降显著减少,又由于实际工况桩间距较大,所以桩间土的沉降规律更接近于不考虑反力桩时的土体沉降,因此沉井外侧的差异沉降较为显著。
(2)桩间距对地表沉降的影响
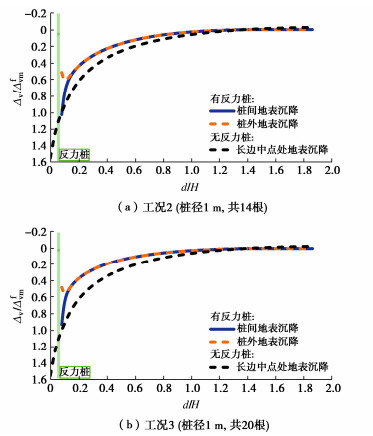
工况2,3在保持桩径不变情况下,将桩数加密,以调查桩间距s对地表沉降的调控作用,选取沉井长边中点处提取地表沉降,如图 7所示。
显然,随着桩数的增加,反力桩的隔离效应更为显著,桩外侧和桩间土体沉降都得到了显著减少,与无反力桩的地表沉降相比,沉降的影响范围也得到显著改善。
(3)抗拔等效下桩径对地表沉降的影响
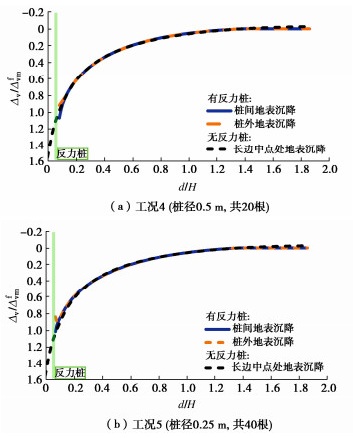
桩基原为提供下压力所设,故在与实际工况抗拔等效前提下讨论桩径对地表沉降的影响。针对工况4,5,选取沉井长边中点处提取地表沉降,如图 8所示。
图 7(b),8(a)对比了同为20根反力桩时桩径1 m和0.5 m时的井外沉降,可见桩径增加可显著改善井外的影响范围,桩径减小会使得沉降剖面更接近无反力桩的情况。
工况1(图 6)、工况4和5(图 8)的沉降剖面对比发现,在抗拔力等效时,井外侧土体沉降趋势基本一致。具体到桩外侧的土体沉降,随着桩径的减小也会显著减少对土体沉降的约束效果。
3.3 沉井压入与反力桩地表沉降归一化响应
为进一步研究桩间距对地表沉降的影响效果,同时分析桩间距和桩径对周边土体沉降的耦合影响,在上述5种工况的基础上补充以下两种工况:
工况6:保持桩径1 m不变,将桩数减少到6根;
工况7:以实际工程中10根桩径为1 m抗拔桩所提供的反力为基准,设置8根桩径1.25 m反力桩。
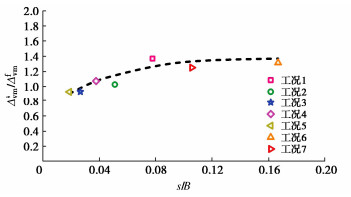
对不同工况下反力桩间地表最大沉降进行归一化处理,如图 9所示。其中,Δsvm为有反力桩情况下桩间土最大沉降;Δfvm为无反力桩情况下桩间土最大沉降所在处对应的地表沉降;B为沉井长边边长。
随着归一化桩间距s/B的减少(桩加密),桩间土体沉降较不考虑反力桩时有所改善,但随桩间距拉大,桩间未受反力桩约束的土体范围随之扩大,由沉井贯入对土体产生的部分拖拽作用从桩周转移至不受约束的桩间土体,使其承受较之前更大的拖拽作用,土体沉降反而会大于不考虑反力桩时的地表沉降,增大的幅度会随着s/B的增加而趋于稳定。当然,值得注意的是,该结论仅在确有一定数量的反力桩时成立,因为随着桩间距不断拉大,沉降的增幅显然会归回至1,即不考虑反力桩时的情况。
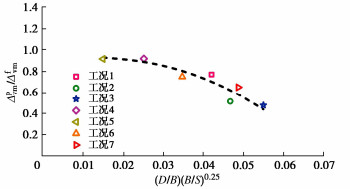
对桩外侧地表最大沉降进行归一化处理,如图 10所示。其中,Δpvm为有反力桩情况下桩外侧土最大沉降;横轴(D/B) (B/S)0.25为同时对桩间距和桩径的归一化形式,它表述了桩径增加或桩间距减小,会减小桩外侧地表最大沉降。图 9,10中的归一化曲线,可结合式(3)或者规范推荐的沉降剖面以预估反力桩对沉井外侧地表沉降的影响,进而通过合理设置反力桩直径和间距,达到调控井外土体沉降的目标。
4. 结论
通过分析压入式沉井外侧反力桩,探究了反力桩对沉井贯入诱发地表沉降的影响,主要得到以下4点结论。
(1)沉井贯入引起的地表沉降在井外壁处最大,最大值在长边中点处。
(2)反力桩会改变地表沉降分布规律。桩外侧土沉降显著减少,而桩间土沉降规律更接近于不考虑反力桩时的结果,因此沉井外侧的差异沉降较为显著。
(3)桩径相同情况下,随桩数增加,反力桩隔离效应更为显著,土体沉降显著减少,沉降影响范围显著改善。桩数相同情况下,桩径增加可改善沉降影响范围,桩径减小会使沉降剖面更接近无反力桩情况。
(4)形成了桩外侧和桩间土体沉降剖面的修正的归一化曲线,为压入式连续沉井群地下车站在高密度城市中心的实施提供参考支撑。
-
-
[1] EASON G. The stresses produced in a semi-infinite solid by a moving surface force[J]. International Journal of Engineering Science, 1965, 2(6): 581-609. doi: 10.1016/0020-7225(65)90038-8
[2] HUNG H H, YANG Y B. Elastic waves in visco-elastic half-space generated by various vehicle loads[J]. Soil Dynamics and Earthquake Engineering, 2001, 21(1): 1-17. doi: 10.1016/S0267-7261(00)00078-6
[3] DE BARROS F C P, LUCO J E. Response of a layered viscoelastic half-space to a moving point load[J]. Wave Motion, 1994, 19(2): 189-210. doi: 10.1016/0165-2125(94)90066-3
[4] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. higher frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 179-191. doi: 10.1121/1.1908241
[5] BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498. doi: 10.1063/1.1728759
[6] JIN B, YUE Z Q, THAM L G. Stresses and excess pore pressure induced in saturated poroelastic halfspace by moving line load[J]. Soil Dynamics and Earthquake Engineering, 2004, 24(1): 25-33. doi: 10.1016/j.soildyn.2003.09.004
[7] 胡安峰, 孙波, 谢康和. 下卧基岩饱和地基在移动荷载作用下的动力响应[J]. 振动与冲击, 2012, 31(4): 151-156. HU Anfeng, SUN Bo, XIE Kanghe. Dynamic response of saturated subgrade with rock substratum subjected to moving loads[J]. Journal of Vibration and Shock, 2012, 31(4): 151-156. (in Chinese)
[8] XU B, LU J F, WANG J H. Dynamic response of an infinite beam overlying a layered poroelastic half-space to moving loads[J]. Journal of Sound and Vibration, 2007, 306(1/2): 91-110.
[9] CAI Y Q, SUN H L, XU C J. Steady state responses of poroelastic half-space soil medium to a moving rectangular load[J]. International Journal of Solids and Structures, 2007, 44(22/23): 7183-7196.
[10] PAK R Y S. Asymmetric wave propagation in an elastic half-space by a method of potentials[J]. Journal of Applied Mechanics, 1987, 54(1): 121-126. doi: 10.1115/1.3172945
[11] SENJUNTICHAI T, RAJAPAKSE R K N D. Dynamic Green's functions of homogeneous poroelastic half-plane[J]. Journal of Engineering Mechanics, 1994, 120(11): 2381-2404. doi: 10.1061/(ASCE)0733-9399(1994)120:11(2381)
[12] 陈胜立, 张建民, 陈龙珠. 饱和地基中埋置点源荷载的动力Green函数[J]. 岩土工程学报, 2001, 23(4): 423-426. doi: 10.3321/j.issn:1000-4548.2001.04.008 CHEN Shengli, ZHANG Jianmin, CHEN Longzhu. Dynamic Green's functions of saturated soils subjected to the internal excitation[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 423-426. (in Chinese) doi: 10.3321/j.issn:1000-4548.2001.04.008
[13] 杜秦文, 朱向荣, 丁伯阳. 埋置点源简谐荷载作用下Gibson土体动力Green函数[J]. 工程力学, 2007, 24(2): 45-49. DU Qinwen, ZHU Xiangrong, DING Boyang. Dynamic Green's function for Gibson soil subjected to internal excitation[J]. Engineering Mechanics, 2007, 24(2): 45-49. (in Chinese)
[14] METRIKINE A V, VROUWENVELDER A C W M. Surface ground vibration due to a moving train in a tunnel: two-dimensional model[J]. Journal of Sound Vibration, 2000, 234(1): 43-66. doi: 10.1006/jsvi.1999.2853
[15] YUAN Z H, BOSTRÖM A, CAI Y Q. Benchmark solution for vibrations from a moving point source in a tunnel embedded in a half-space[J]. Journal of Sound Vibration, 2017, 387: 177-193. doi: 10.1016/j.jsv.2016.10.016
[16] FORREST J A, HUNT H E M. A three-dimensional tunnel model for calculation of train-induced ground vibration[J]. Journal of Sound Vibration, 2006, 294(4/5): 678-705.
[17] ZOU C, WANG Y M, WANG P, et al. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot[J]. The Science of the Total Environment, 2015, 536: 761-773. doi: 10.1016/j.scitotenv.2015.07.123




 下载:
下载: