Spherical cavity expansion-based method for cone factor considering nonlinear characteristics of clay
-
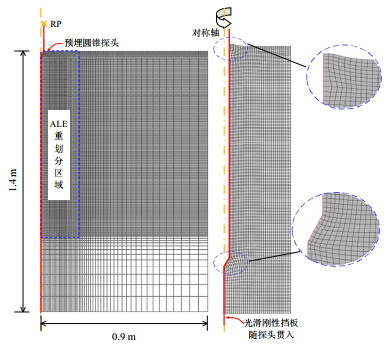
摘要: 当前规范中根据静力触探结果解释黏土不排水剪切强度采用的是推荐的锥尖系数,但该系数存在经验性取值的问题,更重要的是当前锥尖系数均是基于理想弹塑性土体模型导得,未考虑土体应变应变的非线性特性。为此,首先在ABAQUS有限元软件中模拟了圆锥贯入过程,评估锥尖阻力qc,饱和黏土采用双曲线硬化弹塑性模型,并使用ALE重划分技术防止网格发生畸变。有限元结果表明:土体刚度、锥面粗糙度和破坏准则等因素均影响着锥尖系数。同时在有限元中模拟了不排水圆孔扩张过程,得到球孔扩张极限承载系数的表达式。随后建立了锥尖阻力与球孔极限扩孔压力之间的等效换算关系,最后对工程实例进行了计算分析。Abstract: According to the current specifications, the undrained shear strength of clay is interpreted based on the recommended cone factor derived from empirical values. However, this factor has limitations in terms of its empirical nature. Moreover, the existing cone factors are derived from the elastic-perfectly plastic model, without considering the nonlinear characteristics of soil deformation. To tackle these issues, a simulation of the cone penetration process is performed using the finite element software ABAQUS. The cone resistance qc is assessed using the hyperbolic hardening model for clay, and the arbitrary Lagrangian Eulerian (ALE) remeshing technique is employed to prevent grid distortion. The finite element results show that the factors such as soil stiffness, cone roughness and failure criteria affect the cone factor. Furthermore, the undrained expansion for a circular cavity is simulated using the finite element method to obtain the expression for the ultimate bearing capacity factor. Subsequently, an equivalent conversion relationship between the smooth cone tip resistance and the limit expansion pressure of the cavity is established. Finally, a verification against an engineering case is conducted.
-
0. 引言
近年来,中国海洋工程建设与资源开发加速,海上风电场越来越多,截至2019年底,海上风能累计装机容量已达6.7 GW。目前单桩是沿海浅水区风力涡轮机支撑结构最常用的基础形式,约占70%以上,风、波浪、水流和运行荷载主要通过桩侧向传递到土体中。在这些循环荷载作用后,海洋地基土可能产生刚度弱化、强度降低,严重时影响构筑物的使用或安全。据报道[1],地震时多数土工结构的失稳生在震后数小时到24 h,突显了“循环荷载后”土的特性研究的重要性。特别是,海洋结构物长期受到海洋环境中的静载、动载交叉作用,因此单桩设计需要研究循环荷载后土的静力学特性劣化规律及工程效应。
目前已有较多学者研究了循环荷载作用过程中土的动应变、动孔压、动强度发展规律,而对于循环荷载作用后土体静力特性的劣化研究涉及较少。Yasuhara等[2]发现低塑性黏土循环后剪切模量的衰减比不排水强度更显著,建立了其与超固结比的关系。Kargar等[3]试验发现,钙质砂循环荷载后的强度和刚度特性与排水条件、循环产生的超孔压和残余应变有关。Hazirbaba等[4]指出固结有效应力和循环加载引起的超孔压越大,循环后砂土的沉降也越大。国内学者对黏土(王淑云等[5]、黄茂松等[6])、粉土(陈存礼等[7])进行循环荷载后剪切试验,一般认为周期荷载后土的不排水强度及刚度会减小,受固结应力、动应力比、动应变及动孔压等因素影响,应力路径表现出超固结性质。关于循环荷载作用对桩基承载特性的影响,朱斌等[8]通过离心试验研究了砂土中单桩在水平静力和循环荷载作用下的变形特性,在修正API p-y曲线初始刚度的基础上,采用双曲线型p-y曲线分析了水平受荷单桩的内力和变形。Rosquoet等[9]使用离心模型测试了干砂中柔性桩在横向循环载荷下的承载性能,引入折减系数来量化循环荷载对p-y曲线的影响。目前API(2014)规范采用0.9折减系数考虑循环荷载对桩基侧阻极限强度的影响[10]。总体上,对于粉土循环荷载后的特性弱化研究非常欠缺,特别是其对海洋结构物的稳定性影响需要深入研究。
对杭州湾重塑海相粉土进行循环加载后静三轴不排水剪试验,研究循环荷载后粉土刚度和强度等静力特性的弱化规律,结合横向受荷单桩的非线性地基梁数值分析,研究循环荷载后海洋单桩承载特性的劣化规律,以期改进现有API规范中p-y公式对循环荷载的适用性。
1. 粉土的循环后静力特性试验
1.1 重塑土样的基本物性
试验采用饱和重塑试样,取自杭州湾海域,粉土的砂粒含量为27.4%,粉粒含量为52.6 %,黏粒含量为20.0%,其他物理性质指标为:相对质量密度Gs=2.69,液限wL=23%,塑性指数IP=7.9。控制试样干密度ρd=1.63 g/cm3。
1.2 试验方法
采用GDS三轴仪,进行单调不排水剪试验和循环不排水加载+ 单调不排水剪试验。单调加载采用应变控制,剪切速率为0.1%/min;对于循环加载,先以2 kPa/min的速度施加一定的静偏应力qs,然后进行应力控制的循环加载,应力幅值σd = qs,频率为0.1 Hz,波形为正弦波。循环加载结束后迅速降低静偏应力,进行不排水三轴剪切。
循环荷载停止后的轴向应变记为残余应变εa、超静孔压记为残余孔压Δuc,定义循环应力比CSR= σd/σc、超孔压比ru=Δuc/σc,σc为固结压力。参照土工试验方法标准,取试样轴向应变达到15%时破坏,此时偏应力的一半为不排水强度值。前期残余应变εa不计入循环后剪切试验的剪应变。
2. 试验结果分析
2.1 粉土循环荷载下应变和孔压分析
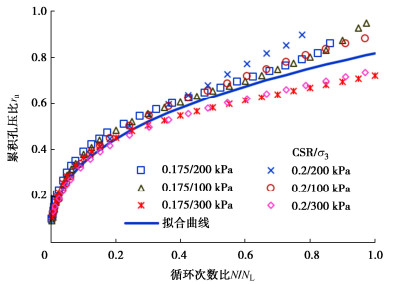
由于粉土在较低的剪应变水平内,孔隙水压力急剧增加,为了防止试样破坏或液化,本文选择超孔压比ru作为评估循环荷载作用的参数。试样累积孔压比ru与循环次数N的关系如图 1所示。
试验表明,在循环应力比水平较高时(CSR > 0.175),累积孔压Δuc随循环次数增加而增大,且很快达到液化(ru > 0.85)。如图 1,将累积孔压和循环次数分别用固结围压、液化次数归一化,发现不同循环应力比的累积孔压比与液化次数比分布集中,可采用乘幂函数描述为:
ru=0.82⋅(NNL)0.37。 (1) 式中:液化循环次数NL = (CSR/0.43)-1/0.15,N为循环加载次数。
在循环应力水平较低时,超孔压后期累积缓慢,表明循环荷载对土样的损伤作用有限,只有足够的循环次数(> 1000),才有可能发生液化。累积超孔压比ru与循环次数N曲线的切线模量与循环应力比相关,采用对数函数描述为
ru=f(CSR)⋅ln(N)+g(CSR)。 (2) 式中:f = 0.82CSR-0.0455,g = 0.244CSR-0.0258。
在实际工程设计计算中,已知循环应力比和循环作用次数时,可以通过类似图 1的试验结果,直接或插值得到超孔压比ru,然后利用ru计算循环荷载对土体强度和刚度的弱化程度。
2.2 粉土循环后不排水强度弱化分析
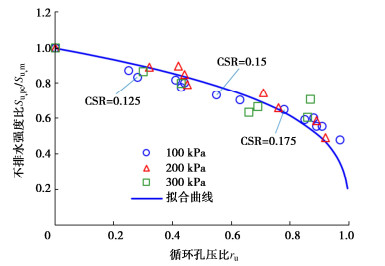
试样在100,200,300 kPa 3种围压下进行单调不排水三轴剪切试验,测得其不排水强度Su, m分别为35,70,112 kPa;由于不排水循环载荷引起粉土颗粒松散程度增加和内部结构的损伤,经历循环加载后,试样的不排水强度Su, pc显著降低,将相同围压下的不排水强度比记为rs = Su, pc/Su, m,3个围压下循环应力比和超孔压比与不排水强度比的对应关系如图 2所示。
从图 2可以看出,不同围压、不同循环应力比的不排水强度比均随残余孔压比Δuc/σc的增大而减小,当超孔压比(> 0.8)较大时,强度急剧降低,但有一定水平的残余强度。图 3中标注了部分循环应力比,全部数据分布在一个很窄的条带内,说明围压和循环应力比的影响很小,本文予以忽略。Yasuhara等[2]指出循环荷载引起的超孔压会使土的有效应力降低,产生“似超固结”现象,导致试样的不排水强度降低。基于似超固结比(固结压力与当前有效应力比)的概念,不排水强度比rs与循环超孔压比的关系可以表达为
Su, pcSu, m=(1−Δucσc)ns。 (3) 式中:ns参数与土体的压缩性有关,图 3中取ns=0.3,可见该公式与试验结果拟合程度较高。
2.3 粉土循环后不排水剪刚度弱化分析
为了简便,工程上经常选择应力应变曲线上峰值抗剪强度一半处的割线模量E50来预测变形,该模量被视为中等水平应变的平均值[11]。对于不排水条件,某些土应力在一半破坏强度下的行为仍然可以被描述为“弹性”,是工程设计重点关注的应力区间特性。本文主要考虑海洋荷载在海床地基引起的中到大应变问题,因而分析试验应力应变曲线的割线模量E50的弱化规律。
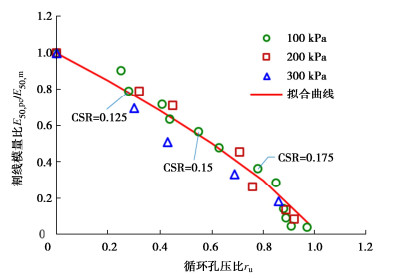
试样在3种围压下进行单调不排水三轴剪切试验,测得其不排水割线模量E50分别为23.9,39.7,45.9 MPa。由于循环载荷对粉土颗粒组构的损伤或破坏,循环加载后试样的不排水剪割线变形模量降低,将re = E50u, pc/E50u, m记为相同围压下的不排水割线模量比,不同围压和循环应力比作用下,不排水割线模量比和循环超孔压比的关系如图 3所示。
与强度衰减规律类似,随循环超孔压比增加,粉土的归一化的割线变形模量弱化规律受围压和循环应力比的影响很小,数据点分布较集中,孔压比大于0.8后,模量衰减较显著,超过0.9后刚度几乎消失。不排水割线模量比re与循环超孔压比的关系可以采用与式(3)相同的形式,即
E50u, pcE50u, m=(1−Δucσc)ne。 (4) 式中:ne参数与粉土的剪切特性有关,取ne=0.75时,上述经验关系与试验结果拟合较好。
3. 循环荷载后单桩的承载特性
以杭州湾某海域为例,水深h=10 m,简谐波波高H=5.5 m(极端情况),波浪周期T=10 s,波长L=100 m,粉土浮重度γ′=10.3 kN/m3,内摩擦角φ=30.5°,黏聚力c′=1.5 kPa,海床表面不排水。经过Biot理论弹性计算的海底剪应力τvh与垂直有效应力σ′v之比幅值随深度变化表达式为[12]
τvhσ′v = πγwγ′H/Lcosh(2πh/L)e−2πZ/L, (5) 对于一定的循环应变或孔压比,三轴试验的循环应力比要高于现场剪应力比,其关系为
CSR = 1crτvhσ′v。 (6) 式中:cr=0.55~0.72,本文取0.65。
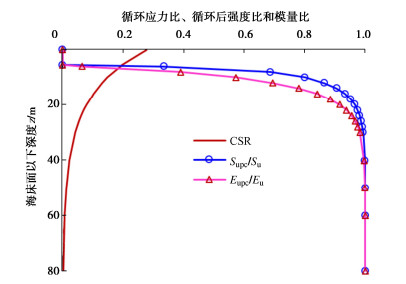
将式(6)的循环应力比代入式(1),(2)计算出累积孔压比ru,进一步通过式(3),(4)计算得到强度和模量衰减随深度的分布如图 4所示,在海床表层约5 m深度,粉土发生液化,不排水强度和模量弱化程度随深度急剧减小,影响深度约为40 m。
根据API(2014)建议,砂土中的桩基础侧向承载特性呈现为非线性,某一深度z处的p-y曲线可近似采用双曲正切函数。本文对粉土采用该p-y公式,并引入循环荷载对强度和刚度的损伤作用,描述为
p=rsψpu⋅tanh(rekzrsψpuy)。 (7) 式中:ψ=3−0.8z/D⩾0.9,D为桩体直径;pu= min,C1,C2和C3为摩擦角的函数;k为土层刚度随深度变化的比例系数。根据粉土摩擦角查表得k=11000 kN/m3,C1=1.91,C2=2.67和C3=28.75。
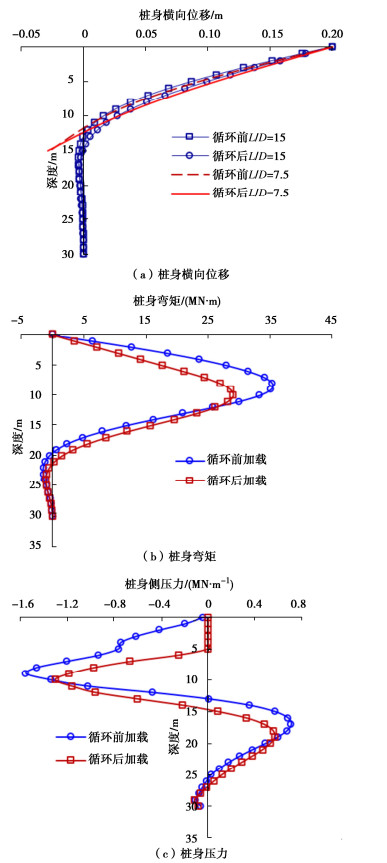
计算取钢管桩直径D=2.0 m,长度L=30 m,抗弯刚度为11.6 GN·m2,采用横向位移控制桩顶加载,最大值ymax=10%D,允许桩头自由转动。分析时沿桩长均分为30个梁单元,在地面以下梁单元节点处设置p-y弹簧支座。考虑前述波浪荷载作用持续1 h对海床中桩身横向位移、弯矩和侧压力的影响,计算结果如图 5所示。
从图 5可以看出,超过20 m深度后,桩身基本没有横向位移,循环后加载的位移较大(图 5(a));桩身弯矩存在反弯点,循环后加载的弯矩较小,最大弯矩减小约17%,且反弯点深度增加约1 m(图 5(b));循环加载后,在海床面以下约5 m深度存在液化现象,桩身侧压力显著减小,总的横向承载力减小约42%(图 5(c))。图 5(a)还显示了桩长15 m(L/D=7.5)的计算结果,可以看出长径比较小时,桩底有踢脚现象,循环荷载后桩的刚性反应更明显。
4. 结论
对杭州湾重塑海相粉土进行了循环三轴不排水剪切及循环后不排水剪试验,研究了循环荷载对粉土不排水强度和变形模量的损伤作用,计算了波浪荷载对单桩横向承载特性的影响,主要得到以下3点结论。
(1)循环荷载作用下,围压归一化的累积孔压与液化次数归一化的循环次数之间可以拟合为乘幂函数关系;循环应力比较小时,累积孔压比为循环次数的对数函数,系数与循环应力比相关。
(2)循环荷载作用后粉土的不排水强度和变形模量降低,可采用似超固结的概念,表述为循环荷载停止时残余孔压比Δua/σ3的指数函数。
(3)在本文的波浪荷载和粉土海床条件下,波浪荷载对海床地基的强度和刚度折减比随深度急剧衰减,影响深度约为40 m,浅部约5 m深度有液化现象,循环荷载后桩身位移增加、最大弯矩减小约17%,横向承载力减小约40%,桩身的刚性反应增强。
-
-
[1] YU H S, MITCHELL J K. Analysis of cone resistance: review of methods[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(2): 140-149. doi: 10.1061/(ASCE)1090-0241(1998)124:2(140)
[2] YU H S, HERRMANN L R, BOULANGER R W. Analysis of steady cone penetration in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(7): 594-605. doi: 10.1061/(ASCE)1090-0241(2000)126:7(594)
[3] MAHMOODZADEH H, RANDOLPH M F. Penetrometer testing: effect of partial consolidation on subsequent dissipation response[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(6): 04014022. doi: 10.1061/(ASCE)GT.1943-5606.0001114
[4] TEH C I, HOULSBY G T. An analytical study of the cone penetration test in clay[J]. Géotechnique, 1991, 41(1): 17-34. doi: 10.1680/geot.1991.41.1.17
[5] LU Q, RANDOLPH M F, HU Y, et al. A numerical study of cone penetration in clay[J]. Géotechnique, 2004, 54(4): 257-267. doi: 10.1680/geot.2004.54.4.257
[6] LIYANAPATHIRANA D S. Arbitrary Lagrangian Eulerian based finite element analysis of cone penetration in soft clay[J]. Computers and Geotechnics, 2009, 36(5): 851-860. doi: 10.1016/j.compgeo.2009.01.006
[7] VESIĆ A S. Expansion of cavities in infinite soil mass[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(3): 265-290. doi: 10.1061/JSFEAQ.0001740
[8] VESIC A S. Design of pile foundations[R]. Washington D C: National Cooperative Highway Research Program, Transportation Research Board, 1977.
[9] LADANYI B, JOHNSTON G H. Behavior of circular footings and plate anchors embedded in permafrost[J]. Canadian Geotechnical Journal, 1974, 11(4): 531-553. doi: 10.1139/t74-057
[10] NASH D F T, POWELL J J M, LLOYD I M. Initial investigations of the soft clay test site at Bothkennar[J]. Géotechnique, 1992, 42(2): 163-181. doi: 10.1680/geot.1992.42.2.163



 下载:
下载: