Influences of ambient temperature on temperature field and mechanical behaviors of underground pipe galleries
-
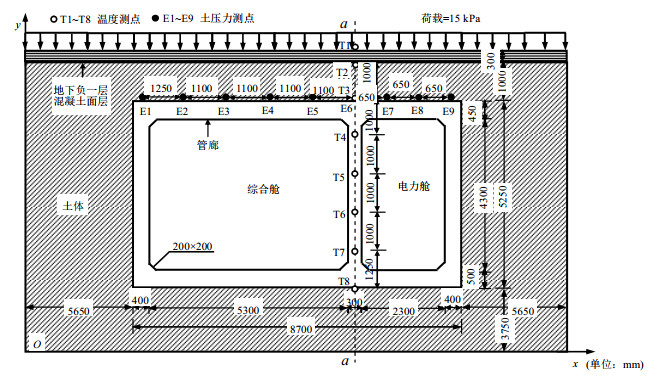
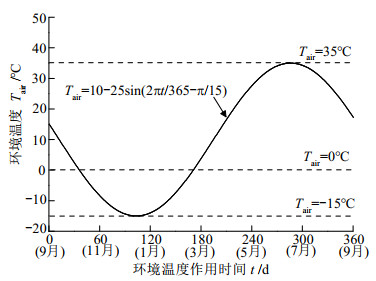
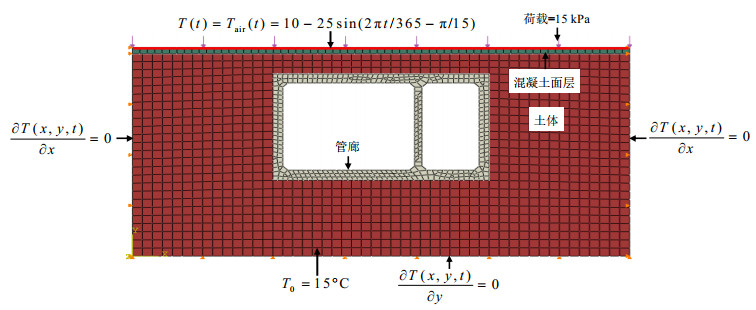
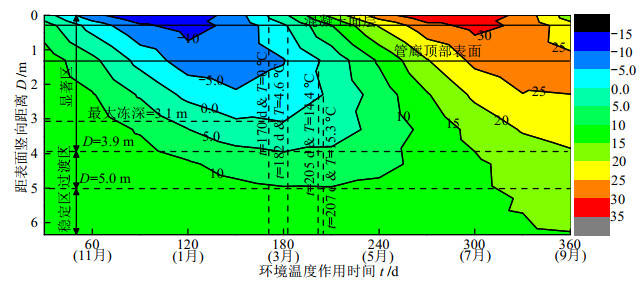
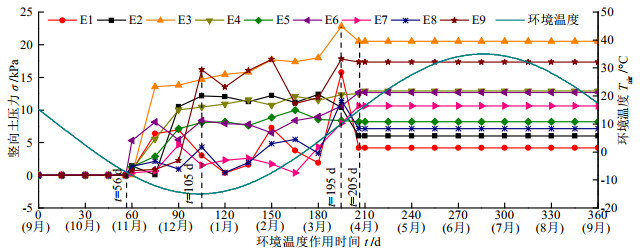
摘要: 季冻区季节性温度变化对地下管廊的工程应用性能产生显著影响,为了研究季冻区环境温度对地下管廊温度场和力学特性的影响,采用ABAQUS有限元数值模拟技术分别研究了季节性环境温度作用下地下管廊温度场和土压力的变化规律。数值分析结果表明:管廊竖向截面最大冻深明显滞后于最低环境温度出现时刻;在升温与降温过程中,管廊上部及附近区域温度场先后出现“冷核区”和“热核区”等特殊现象,随着升温与降温的持续作用而逐渐消失;在降温与升温过程中,管廊顶板土压力先后出现增加与减小趋势;当季节性温度变化作用结束后,管廊顶板土压力显著大于初始状态。Abstract: Seasonal temperature changes in the seasonal frozen areas have a significant impact on the engineering application performance of the underground pipe galleries. To study the effects of ambient temperature in the seasonal frozen areas on the temperature field and mechanical behaviors of the underground pipe galleries, the change laws of temperature field and earth pressure of the underground pipeline galleries under seasonal ambient temperature are studied by conducting the ABAQUS finite element numerical simulation. The numerical analysis results indicate that the occurent moment of the maximum freezing depth of the vertical section inside the pipe gallery is lagged behind that of the lowest ambient temperature. During the process of heating and cooling, the temperature fields inside the upper and nearby areas of the pipe gallery successively exhibit the special phenomena such as "cold core zone" and "hot core zone". These phenomena gradually disappear with the continuous effects of heating and cooling. During the cooling and heating processes, the earth pressure on the roof of the pipe gallery shows an increasing and decreasing tendency. After the influences of seasonal temperature, the earth pressure on the roof is significantly greater than that at the initial state.
-
Keywords:
- ambient temperature /
- temperature field /
- mechanical behavior /
- pipe gallery /
- numerical simulation
-
0. 引言
土体与结构的界面的力学特性分析是解决土体与工程结构相互作用的关键[1-2]。在桩基础、锚杆、大坝、隧道和加筋土挡墙等构筑物中,界面力学特性往往受到结构界面特征和土体性质的共同作用和影响。此外,土体与结构的相互作用机理对工程结构破坏模式和稳定性评价具有重要影响,同时也是土体-结构面本构模型精细化研究的重点。大量土体与结构的界面的研究[3-6]表明界面剪切强度是土体与混凝土结构之间力学作用的重要指标之一。界面剪切强度受材料粗糙度、土壤成分、相对密度、土壤颗粒粒径分布和形态、土壤含水率、正应力大小、剪切速率、剪切方向、循环次数、环境温度等因素的影响[7-9]。
关于土体-混凝土界面本构模型也取得相应的研究。Desai等[10]先通过改变正应力、相对位移、循环次数和初始密度等条件,依据砂土-混凝土界面循环直剪试验修正了Ramberg-Osgood模型参数,提出了土体与刚性界面的界面剪切强度非线性弹性模型;随后,又提出了一种基于扰动状态概念(DSC)的砂土-混凝土界面本构模型,通过循环直剪试验确定了模型参数,并通过有限元对模型进行了验证和比较[11]。Hu等[12]提出了包含粗糙度在内的10个参数的界面本构模型,通过砂土-钢板的直剪试验对参数进行修正,使得模型满足界面剪切硬化、软化等应力应变行为的预测。Liu等[13]将临界状态土力模型(CSSM)引入到界面本构模型,通过将粗糙度系数Rn对极限状态应力系数Mc进行修正,较好的描述了砂土与刚性界面之间的应变硬化、软化、法向膨胀和应力路径等。
综上所述,目前基于粗糙度系数为主要变量,预测黏土-混凝土的界面强度衰减的研究寥寥。可能原因如下:①混凝土相对钢板,其起伏度和不规则程度离散型较大,粗糙度的评价指标无法统一;②黏性土与砂土等无黏性土相比,其力学性能指标具有一定的差异性,通过一种模型覆盖所有土体-混凝土界面强度都是十分困难的。
通过定制的大型界面循环剪切试验装置,开展基于灌注桩桩身粗糙度条件下的饱和黏土-混凝土界面循环剪切试验,研究不同循环周期、循环幅值条件对粉质黏土-混凝土界面强度的衰减的影响。最后,通过对循环稳定后粉质黏土-混凝土界面强度衰减系数进行表征,并结合黏土-混凝土界面剪切强度模型,提出粉质黏土-混凝土界面强度衰减模型。
1. 试验方案
1.1 试验装置
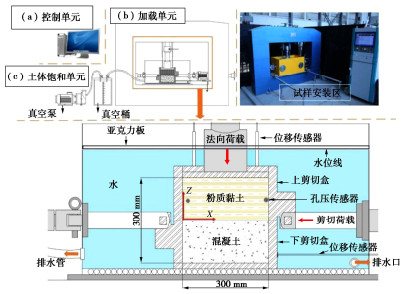
本试验采用大型循环直剪装置,如图 1所示。该装置包含伺服加载系统、数据监测和采集系统、真空饱和系统。上下剪切盒尺寸均为300 mm×300 mm×150 mm,满足SL235—2012[14]中直剪摩擦仪的试样盒尺寸宜大于80 mm×80 mm的规定。装置水平方向最大荷载200 kN,竖向最大荷载200 kN,误差±0.6%;位移范围0~300 mm,试验荷载增量0.0001 kN;位移增量0.001 mm。
1.2 土体材料
武汉临江区域的粉质黏土广泛,埋深厚,抗剪强度低,渗透性能差。本试验土体采集于武汉临江地层地表-8~-21 m。表 1为粉质黏土物理力学参数,测试得到其最大干密度为1.78 g/m3。将土体晒干烘干研磨过筛后再进行装样处理。
表 1 粉质黏土物理力学性质Table 1. Basic physical and mechanical properties of silty clay物理力学性能指标 数值 干重度/(kN·m-3) 15.8 含水率/% 32 最优含水率/% 13 液限/% 37 塑限/% 20 孔隙比 0.82 黏聚力/kPa 44.3 内摩擦角/(°) 15.9 1.3 混凝土界面试件制作
目前,国内通常采用灌砂法[15]来评价试件界面的粗糙度系数,记做Ry:
Ry=VA。 (1) 式中:V为灌入标准砂的体积;A为混凝土试件垂直投影面积。
但灌砂法无法体现界面的各项异性。基于前期研究工作基础[5],在Tatone等[16]评价参数的基础上,提出了改进Grasselli评价参数RMG,见式(2)。其针对规则、不规则的界面的表征更符合客观规律。
RMG=2A0⋅θ∗maxC+1。 (2) 式中:Aθ为剪切方向的有效面积比;θ∗为最大剪切方向视倾角;C为拟合得到的节理表面粗糙度参数。
试验试块采用3D打印的方式还原混凝土桩桩面粗糙度。步骤如下:通过手持3D扫描仪对武汉临江深基坑内裸露的不同深度位置的混凝土桩面进行20组随机扫描取样。再随机选取投影面积为300 mm×300 mm的三维模型制作混凝土试样。选取的三维模型通过3D打印技术制作成混凝土桩面模具,再通过模具制作混凝土试样,混凝土试块尺寸为300 mm(长)×300 mm(宽)×150 mm(高),数据采集及混凝土试块制作流程如图 2所示。试验中,混凝土试块采用硅酸盐水泥(PO32.5)。混凝土试块选用碎石为粗骨料,河沙为细骨料。
1.4 试验流程
直剪试验主应力分别为100,200,300,400 kPa。循环剪切速率为1 mm/min,剪切位移为2,3,4,5 mm,在多次循环积累使得循环拉力稳定后,再进行剪切破坏试验。在试验中,法向应力通过钢柱和钢板传递到上剪切盒的粉质黏土中,再传递到下剪切盒的混凝土试件。竖向变形和水平位移均由直线位移传感器(LVDT)监测。剪切最大位移为试样长度的15%。
2. 试验结果与分析
2.1 循环次数对剪切应力的影响
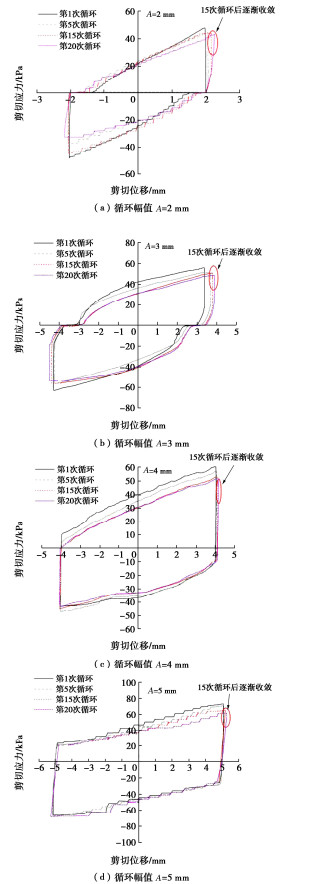
以法向压力200 kN为例,不同剪切循环幅值剪切应力-剪切位移关系如图 3所示,每个循环的剪切应力-应变曲线基本呈现为闭合状态,且闭合环的剪应力的极大值与极小值出现在循环的正负最大位移处,剪切应力的最大值均出现在第1次循环内的最大位移处。随着循环次数增加,剪切应力峰值逐渐降低,加载段与卸载段间曲线夹角也逐渐变小,即封闭的循环圈逐渐变扁平。
此外,随着循环次数的增加,剪切应力峰值减小的速率逐渐降低,并逐渐趋于稳定。第1次循环和第5次循环的剪切应力-剪切位移曲线差异性较大;而在15次循环后,部分循环的剪切位移-剪切应力曲线近似重合,这表明剪切应力-剪切位移曲线特性的差异随着循环次数的增加而减少。
2.2 循环幅值对剪切应力的影响
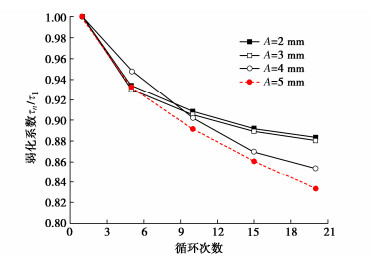
在图 3中,循环次数固定时,当循环剪切幅值从2,3,4,5 mm依次增大,其对应循环圈内剪切应力的峰值也对应增大。Mortara等[17]将第n次循环时循环圈极大值τn与第1次循环时循环圈极大τ1之比定义为弱化系数。不同循环幅值下界面剪切弱化系数(τn/τ1)与循环次数关系见图 4。如图 4所示,随着循环次数的增大,弱化系数比值不断减小,即剪切应力极值的弱化程度变大。此外,随着循环剪切幅值的增大,相同循环次数下剪切应力极值的弱化程度也越大。比较图 4中幅值下弱化系数曲线,可以看出循环幅值越大,曲线越陡,即弱化增量越大,在A=5 mm时,最为明显。这说明循环幅值增大则对土体扰动程度越大,土体在达到下一个稳定阶段时所需要的时间或过程更长。
此外,循环幅值大小对循环圈形状改变较为显著。当循环剪切幅值较小时,剪切阶段与卸载阶段应力-应变曲线均呈现非线性,卸载回弹幅度较大。但当循环幅值逐渐增大,剪切阶段与卸载阶段应力-应变曲线均呈现线性趋势,每个循环圈内加载与卸载的斜率基本保持一致,类似“平行四边形”,卸载回弹位移较小。上述现象可能说明当循环幅值较小时,卸载时桩-土界面为弹塑性状态;而当循环幅值超过一定阈值,其卸载时桩-土界面为塑性状态。
从图 4中还可以观察到,弱化系数τn/τ1与循环次数呈幂函数关系,其随循环幅值的不同平缓程度不同。因此,将τn/τ1作为自变量,循环次数N、循环幅值比为因变量,进行非线性拟合得到弱化系数曲线,见下式:
τn/τ1=N−0.064(A/Amax)。 (3) 式中:N为循环次数;A为循环幅值;Amax为试验中最大循环幅值。
通过式(3)可知,当循环次数大于20次后,弱化系数几乎无变化。因此,随着循环次数增加,弱化系数减小量逐渐减小,其值逐渐趋于稳定。由于室内试验的限制,循环次数无法持续累积,但可通过式(3)进行预测。
2.3 基于衰减系数的循环稳定后界面剪切峰值强度预测
Poulos[18]将循环后峰值剪应力与单调加载中的峰值剪切应力之比定义为应力衰减系数,见下式:
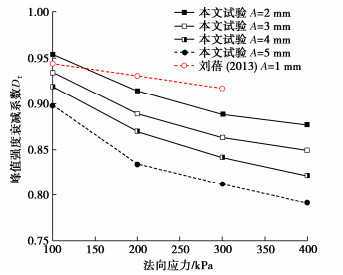
Dτ =τcpτp。 (4) 针对本文试验以及刘蓓[19]开展的循环剪切试验中,不同法向压力下,不同循环幅值的界面峰值强度衰减系数Dτ 见图 5。如图 5所示,相同剪切幅值下,随着法向应力不断增大,循环稳定后峰值强度衰减程度不断增大,且增量不断增大。这表明高法向应力作用下,循环剪切过程的发展对粉质黏土-混凝土界面土体扰动程度更大,导致循环稳定后剪切强度相比单调剪切强度衰减变大。类似地,随着循环幅值的增大,其循环稳定后峰值轻度衰减程度不断增大,这与2.2节循环圈弱化系数规律相同。
由图 5可知,不同工况的循环稳定后界面剪切峰值强度折减系数Dτ存在相同的变化趋势。因此,通过式(4)对本试验以及文献中[19]峰值强度衰减系数Dτ 进行表征。将Dτ 作为因变量,A和σ作为自变量,通过对自变量无量纲表示后通过非线性回归分析,获得循环稳定后黏土-混凝土界面剪切峰值强度折减系数Dτ 预测公式如下:
Dτ =a(AmaxA)b(σmaxσ)c。 (5) 其中,a=0.816,b=0.057,c=0.066为拟合系数,A为循环幅值,Amax为试验中最大循环幅值,a为界面剪切法向应力,σmax为试验中最大法向应力。
将式(5)代入式(4),可得到循环稳定后界黏土-混凝土面剪切峰值强度通过单调剪切界面剪切峰值强度的表示关系:
τcp=Dτ τp=a(AmaxA)b(σmaxσ)cτp。 (6) 根据本研究团队的相关成果[5]中界面剪切极限剪切强度预测公式,见(7),将式(7)代入式(6)可得到循环稳定后黏土-混凝土界面剪切峰值强度τcp预测公式,见式(8)。
τp=Kσtan[φ/(91−RMG)]+c, (7) τcp=a(AmaxA)b(σmaxσ)c{Kσtan[φ/(91−RMG)]+c}。 (8) 其中,RMG=2A0⋅θ∗max/C+1,K=0.98,a=0.816,b=0.057,C=0.066均为拟合系数,a为法向应力,φ为土体摩擦角,c为土体黏聚力。
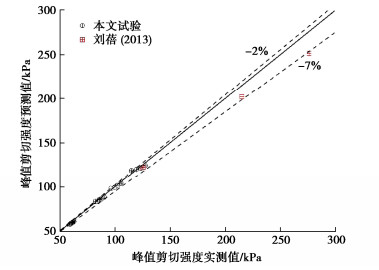
通过式(8)对本章试验和文献中[19]相关数据循环稳定后界面剪切峰值强度τcp进行预测,并与实际值对比见图 6。试验数据与预测值数值十分接近,只有少数数据点表误差约为±7%,而大多数数据误差范围均在±2%以内。因此,式(8)能够对黏土-混凝土界面循环稳定后剪切强度具有较好的预测性。
3. 结论
通过粉质黏土-混凝土界面循环剪切试验,分析不同循环周期、循环幅值对界面强度的衰减影响。通过循环幅值和法向压力无量纲幂函数拟合,对循环稳定后界面强度衰减系数进行表征,提出粉质黏土-混凝土界面强度衰减模型。主要得到以下4点结论。
(1)在一个完整剪切循环内,随着循环次数增加,剪切应力峰值减小的速率逐渐降低,并逐渐趋于稳定。在第15次循环后,大部分循环的剪切位移-剪切应力曲线近似重合,这表明剪切应力-剪切位移曲线特性的差异随着循环次数的增加而减少。
(2)循环幅值大小对循环圈形状改变较为显著。当循环剪切幅值较小时,剪切阶段与卸载阶段应力-应变曲线均呈现非线性,卸载回弹幅度较大。但当循环幅值逐渐增大,剪切阶段与卸载阶段应力-应变曲线均呈现线性趋势,每个循环圈内加载与卸载的斜率基本保持一致,类似“平行四边形”。
(3)弱化系数τn/τ1与循环次数呈幂函数关系,随着循环次数增加,弱化系数减小量逐渐减小,其值趋于稳定。
(4)将峰值剪切强度衰减系数Dτ作为因变量,循环幅值A和法向应力σ作为自变量,通过无量纲非线性回归分析,提出循环稳定后黏土-混凝土界面剪切峰值强度折减系数Dτ表征方法。结合黏土-混凝土界面峰值强度模型,提出粉质黏土-混凝土界面强度衰减模型,具有较高的拟合度。
-
表 1 混凝土面层与管廊的力学与热物理参数
Table 1 Mechanical properties and thermal physical parameters of concrete surface and pipe gallery
参数 值 密度ρ/(g·cm-3) 2.4 弹性模量E/MPa 20000 泊松比 0.25 热传导系数λ/(W/(m·℃)) 1.5 比热容C/(J/(kg·℃)) 970 表 2 土体热膨胀系数
Table 2 Thermal expansion coefficients of soil
T/℃ -20 -10 -3 0 > 0 α/(℃-1) -6×10-4 -7.2×10-4 -9.6×10-4 -1.2×10-3 0 注:负号表示土体在低温作用下体积膨胀,0表示土体在正温作用下体积保持不变。 表 3 土体力学与热物理参数
Table 3 Mechanical and thermal physical parameters of soil
主要参数 值 冻土 融土 黏聚力c/kPa 12 12 内摩擦角ϕ/(°) 22 22 密度ρ/(g·cm-3) 1.89 1.89 弹性模量E/MPa 75 35 泊松比 0.25 0.3 热传导系数λ/(W/(m·℃)) 1.82 1.63 比热容C/(J/(kg·℃)) 2720 3140 -
[1] LAI J X, QIU J L, FAN H B, et al. Freeze-proof method and test verification of a cold region tunnel employing electric heat tracing[J]. Tunnelling and Underground Space Technology, 2016, 60: 56-65. doi: 10.1016/j.tust.2016.08.002
[2] TAN X J, CHEN W Z, YANG D S, et al. Study on the influence of airflow on the temperature of the surrounding rock in a cold region tunnel and its application to insulation layer design[J]. Applied Thermal Engineering, 2014, 67(1/2): 320-334.
[3] LAI Y M, WU Z W, ZHU Y L, et al. Nonlinear analysis for the coupled problem of temperature, seepage and stress fields in cold-region tunnels[J]. Tunnelling and Underground Space Technology, 1998, 13(4): 435-440. doi: 10.1016/S0886-7798(98)00086-8
[4] LIU L L, LI Z, LIU X Y, et al. Frost front research of a cold-region tunnel considering ventilation based on a physical model test[J]. Tunnelling and Underground Space Technology, 2018, 77: 261-279. doi: 10.1016/j.tust.2018.04.011
[5] XIAO C Z, CUI F L, DING L Q, et al. Temperature distributions in geogrid-reinforced soil retaining walls subjected to seasonal freeze-thaw cycles[J]. International Journal of Geomechanics, 2022, 22(12): 04022234. doi: 10.1061/(ASCE)GM.1943-5622.0002595
[6] YARIVAND A, BEHNIA C, BAKHTIYARI S, et al. Performance of geosynthetic reinforced soil bridge abutments with modular block facing under fire scenarios[J]. Computers and Geotechnics, 2017, 85: 28-40. doi: 10.1016/j.compgeo.2016.12.004
[7] 高煜, 刘勇, 石苏意, 等. 泡沫轻质土路堤稳定性分析及材料参数控制标准[J]. 长沙理工大学学报(自然科学版), 2017, 14(1): 24-30, 83. doi: 10.3969/j.issn.1672-9331.2017.01.004 GAO Yu, LIU Yong, SHI Suyi, et al. Foam light weight soil embankment stability analysis and control standard of material parameters[J]. Journal of Changsha University of Science and Technology(Natural Science), 2017, 14(1): 24-30, 83. (in Chinese) doi: 10.3969/j.issn.1672-9331.2017.01.004
[8] 中华人民共和国建设部. 砌体结构设计规范: GB 50003—2001[S]. 北京: 中国建筑工业出版社, 2002. Ministry of Construction of the People's Republic of China. Code for Design of Masonry Structures: GB 50003—2001[S]. Beijing: China Architecture & Building Press, 2002. (in Chinese)
[9] 付晓丹. 季冻区悬臂式支挡路基温度场与应力场数值分析[D]. 兰州: 兰州交通大学, 2019. FU Xiaodan. Numerical Analysis of Temperature and Stress Fields in Subgrade with Cantilever Retaining wall in Seasonally Frozen Regions[D]. Lanzhou: Lanzhou Jiaotong University, 2019. (in Chinese)
[10] LAI Y, WANG Q, NIU F, et al. Three-dimensional nonlinear analysis for temperature characteristic of ventilated embankment in permafrost regions[J]. Cold Regions Science and Technology, 2004, 38(2/3): 165-184.



 下载:
下载: