Influences of iterative algorithms and flexible structures on control performance of centrifugal shaking table
-
摘要: 目前迭代算法和柔性结构对离心机振动台控制性能的影响尚缺乏认识，尤其铰接装置作为柔性连接结构在许多离心机振动台上得到应用，以减小离心力荷载下台面和吊篮变形对作动器安全带来的危险。以一套负载1500 kg离心机振动台为样本，采用不同强度、频带的典型地震波为控制目标，探讨了有无迭代算法、柔性结构条件对离心机振动台的控制性能影响。结果表明：20~200 Hz频宽范围内，迭代算法对最大峰值误差、平均峰值误差、平均谱面积误差的影响可忽略。采用迭代算法前后平均峰值误差分别为5.90%，6.15%，平均谱面积误差分别为5.02%，4.94%。柔性结构对于加速度峰值≤7.5g地震波的复现精度有显著影响，尤其是80~150 Hz高频段；对于加速度峰值≥20g地震波的复现精度影响，在频宽20~120 Hz可忽略，但对于120~170 Hz频段的小幅值成分的复现能力影响不容忽略，逊于无柔性结构条件。同时，在无柔性结构条件下对比了不同负载、同一输入荷载的实测输出波，发现两输出波的峰值误差与谱面积误差均无明显差异，证明了离心机振动台具有良好的重复性和稳定性。研究方法和结论，对提高离心机振动台控制性能的影响因素认识和改进设计方法，具有重要指导价值和科学意义。Abstract: Currently, there is a lack of understanding regarding the impact of iterative algorithms and flexible structures on the control performance of centrifugal shaking table. In particular, the hinge devices, serving as the flexible connecting structures, have been widely applied in many centrifugal shaking tables to diminish the risks posed by deformations of the platform and bucket under centrifugal force loads to the safety of the actuators. Using a centrifugal shaking table with loads of 1500 kg as a sample, the typical seismic waves with different intensities and frequency bands are selected as the control targets. The influences of the iterative algorithms and flexible structures on the control performance of the centrifugal shaking table are investigated. The results indicate that under the frequency bandwidth varying from 20 to 200 Hz, the impact of the iterative algorithms on the maximum peak error, average peak error and average spectral area error can be neglected. The average peak errors before and after using the iterative algorithms are 5.90% and 6.15%, respectively, and the average spectral area errors are 5.02% and 4.94%, respectively. The flexible structures significantly affect the reproduction accuracy of seismic waves with acceleration peaks ≤7.5g, especially in the high-frequency range of 80 to 150 Hz. For the seismic waves with acceleration peaks ≥20g, the impact on reproduction accuracy is negligible in the frequency range of 20 to 120 Hz. However, the influences on the reproduction capability of small-amplitude components in the frequency range of 120 to 170 Hz cannot be ignored, which is inferior to the condition without the flexible structures. Simultaneously, under the condition without the flexible structures, a comparison of the measured platform output waves for the same input load under different loads reveals no significant differences in the peak errors and spectral area errors between the two output waves. This proves the good repeatability and stability of centrifugal shaking table. The research methods and conclusions have significant guiding value and scientific significance for improving the understanding of the influencing factors of the control performance of the centrifugal shaking table and improving the design method.
-
0. 引言
离心机振动台是当前海洋、水利、土木等领域岩土抗震研究的重要科学试验设施之一，其有效性、先进性已为国际共识[1-7]，可较真实地模拟地震荷载下岩土体变形和岩土构筑物破坏的过程。但是，由于离心机振动台运行在高g值离心力场中且与吊篮存在严重的运动学和动力学耦合，又受众多非线性因素影响。因此，如何提高离心机振动台的控制性能是学者们关注和亟需解答的一个重要课题。
目前国内现役离心机振动台仅有9套，分别归属于南京水利科学研究院、中国水利水电科学研究院、清华大学、香港科技大学、同济大学、浙江大学、成都理工大学、交通运输部天津水运工程科学研究所和中国地震局工程力学研究所。其中，张建民等[4]介绍了清华大学离心机振动台的性能指标和功能特色，并基于开展的性能检测试验评价了离心机振动台的系统性能。陈云敏等[5]介绍了浙江大学的离心机振动台的性能指标和结构组成，并基于开展的饱和砂土地基震陷试验对离心机振动台系统的性能进行了初步检验。顾行文等[6]介绍了南京水利科学研究院的NS-2型离心机振动台的性能指标和关键技术，并基于某沥青混凝土墙砂砾石坝试验对离心机振动台系统性能指标进行了初步验证。但这些成果，对迭代算法和柔性结构带给离心机振动台控制性能的影响，鲜见讨论。
本文以中国地震局工程力学研究所1500 kg离心机振动台为样本，介绍了离心机振动台的总体设计和基本组成，通过50g离心加速度下多个典型地震波的输入/输出对比测试，探讨了迭代算法、柔性结构对离心机振动台控制性能的影响，同时检验了不同负载下动力离心试验地震荷载的可重复效果，以期为正在建设和规划的离心机振动台研制提供参考。
1. 离心机振动台系统整体设计
1.1 试验设备与性能指标
中国地震局工程力学研究所与哈尔滨工业大学联合研制的DCIEM-40-300水平单向离心机振动台整体采用吊篮与振动台一体化的方法，如图 1所示。其主要性能指标：离心加速度100g，有效负载3000 kg，最大半径5.5 m，有效吊篮净空1.8 m×1.6 m×1.0 m；振动加速度30g，振动速度1 m/s，振动位移±10 mm，振动负载1500 kg，振动频宽10~300 Hz，平台有效尺寸1.6 m×0.8 m×0.8 m。除此之外，还配备了160 ch动态数据采集仪和自主研发了包括孔压、土压、加速度的各种宽频带高分辨力测量传感器。
![]()
图 1 DCIEM-40-300离心机振动台系统Figure 1. Shaking table test system of DCIEM-40-300 centrifuge1.2 一般问题和设计方案
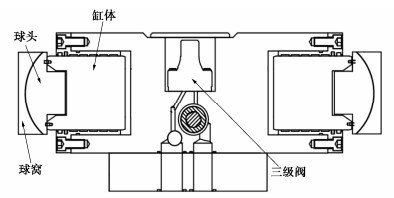
铰接装置作为柔性连接结构在许多离心机振动台上得到应用，以减小离心力荷载下台面和吊篮变形对作动器安全性带来的危险。但是，铰接装置本身存在间隙，且现有离心机振动台多数采用多阀单缸作动器[4-6]，在往返过程中会涉及到力换向的问题，换向过程间隙的存在可能对离心机振动台控制精度和稳定性产生影响。
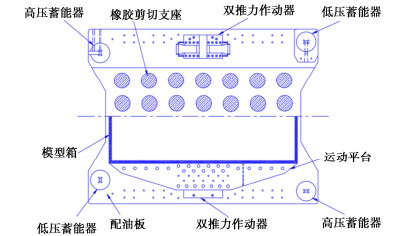
中国地震局工程力学研究所的负载1500 kg离心机振动台，采用了双推力作动器，结构示意图如图 2所示，每个作动器由两条柱塞缸和一个三级伺服阀集成，且柱塞缸内部增设弹簧以使球头、球窝、摩擦板间始终紧密配合形成零间隙连接，避免了柔性结构。振动台总体设计如图 3所示，两个双推力作动器对称布置在运动平台两侧，以使作用线更接近岩土模型质心。运动平台由28个圆形弹性橡胶剪切轴承支撑。每个作动器由安装在配油板上的28 MPa高压蓄能器供油，并通过1.3 MPa低压蓄能器回油。蓄能器主要用作储油和稳压，可满足离心机不停机情况下连续激发多次振动试验的需求。
![]()
图 3 负载1500 kg离心机振动台设计方案与结构组成Figure 3. Design scheme and structural composition of centrifugal shaking table with a load of 1500 kg1.3 试验设计与评价指标
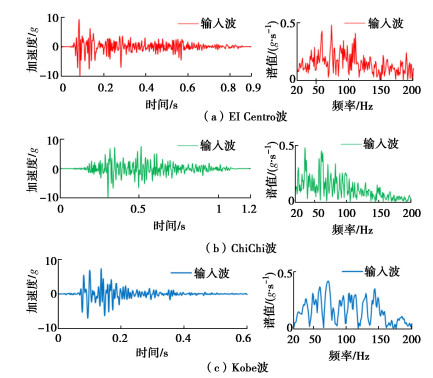
本次试验选用的地震波有El Centro波、ChiChi波和Kobe波，其输入波时程和频谱如图 4所示，均为50g离心加速度下的压缩输入波。迭代算法是通过多次重复激振试验系统来生成正式试验的驱动信号，旨在使振动台的输出信号尽可能接近输入信号，根据最新研究成果，本文研究采用适于高频液压作动器的时域波形复现的迭代算法。此外，由于中国地震局工程力学研究所负载1500 kg离心机振动台作动器与平台间为无间隙连接，需要通过在作动器球窝与平台摩擦板间加入橡胶叠，利用橡胶叠来模拟柔性结构。
2. 迭代算法的影响
2.1 地震动峰值
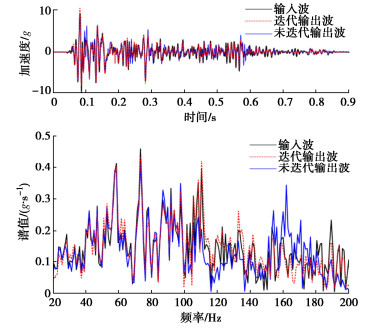
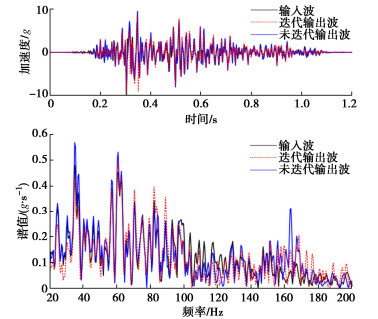
振动台负载1200 kg时，离心加速度50g下，采用迭代算法前后10g El Centro波、10g ChiChi波的输出波时程曲线如图 5，6所示。经计算采用迭代算法后的El Centro波输出波最大峰值误差为5.3%，ChiChi波输出波最大峰值误差为6.5%，平均峰值误差为5.9%；而未采用迭代算法的El Centro波的实测输出波最大峰值误差为7.8%，ChiChi波输出波最大峰值误差为4.5%，平均峰值误差6.15%。迭代算法前后的平均峰值误差相差不明显，即迭代算法基本不影响再现地震动的最大峰值误差、平均峰值误差。
![]()
图 5 迭代算法对10g El Centro波加速度时程及频谱影响Figure 5. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g El Centro waves![]()
图 6 迭代算法对10g ChiChi波加速度时程及频谱影响Figure 6. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g ChiChi waves2.2 地震动频宽
图 5和图 6给出了振动台负载1200 kg时，离心加速度50g下，采用迭代算法前后10g El Centro波、10g ChiChi波的输出波频谱。经计算采用迭代算法后的El Centro波输出波谱面积误差为6.06%，ChiChi波输出波谱面积误差为3.97%，平均谱面积误差为5.02%；而未采用迭代算法的El Centro波的实测输出波谱面积误差为5.98%，ChiChi波输出波谱面积为3.88%，平均谱面积误差4.94%。通过对比前后数据，发现在20~200 Hz频宽变化条件下，迭代算法对谱面积误差影响可忽略。
3. 柔性结构的影响
3.1 地震动峰值
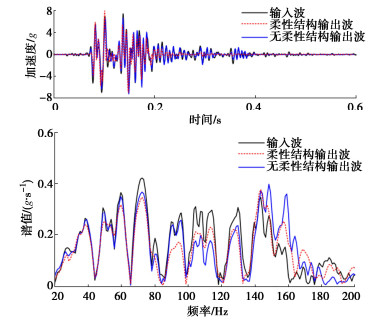
图 7，8给出了振动台负载1200 kg时，离心加速度50g下，在有无柔性结构时7.5g Kobe波、20g El Centro波的输出波时程曲线。经计算柔性结构工况下的7.5g Kobe波输出波最大峰值误差为7.11%，20g El Centro波输出波最大峰值误差为3.63%，平均峰值误差为5.32%；而采用无柔性结构即球头、球窝与摩擦板零间隙连接时Kobe波输出波最大峰值误差为3.51%，El Centro波输出波最大峰值误差为3.07%，平均峰值误差为3.29%；柔性结构对峰值误差影响较小。但在加速度时程图中可明显看出柔性结构在7.5g Kobe波下基本复现不出持时在0.2 s后加速度峰值≤2.5g的波形，而在20g El Centro波下对0.65 s后加速度峰值≤2.5g的波形的复现效果虽比7.5gKobe波下有所改善，但与无柔性结构相比仍存在一定的差距。
![]()
图 7 柔性结构对7.5g Kobe波加速度时程及频谱影响Figure 7. Effects of flexible structure on time history of acceleration and frequency spectrum of 7.5g Kobe waves![]()
图 8 柔性结构对20g El Centro波加速度时程及频谱影响Figure 8. Effects of flexible structure on time history of acceleration and frequency spectrum of 20g El Centro waves3.2 地震动频宽
振动台负载1200 kg时，离心加速度50g下，在有无柔性结构时7.5g Kobe波、20g El Centro波的输出波频谱图对比，如图 7，8所示。经计算柔性结构工况下7.5g Kobe波输出波谱面积误差为8.37%，20g El Centro波输出波谱面积误差为7.95%，平均谱面积误差为8.16%；而采用无柔性结构即无间隙连接时Kobe波输出波谱面积误差为4.89%，El Centro波输出波谱面积误差为8.09%，平均谱面积误差为6.49%；柔性结构对谱面积误差影响较小。但在频谱图中可明显看出柔性结构对于7.5gKobe地震波的复现精度有显著影响，尤其是80~150 Hz的高频段；对于20g El Centro地震波的复现精度影响在频宽20~120 Hz可忽略，但对于120~170 Hz频段的小幅的复现能力影响不容忽略，逊于无柔性结构条件。
4. 不同负载下重复性
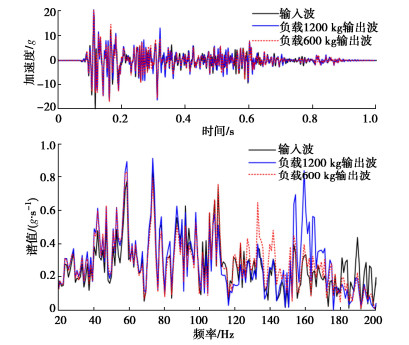
此外，探讨了无柔性结构不同负载下离心振动台的波形重复性。更换不同重量的负载即1200 kg和600 kg，先后输入了两次同一幅值20g El Centro波，加速度时程曲线及频谱如图 9所示。负载1200 kg时，输出波峰值误差为3.07%，谱面积误差为8.09%；负载600 kg时，输出波峰值误差为3.2%，谱面积误差为5.56%。虽然不同负载在120~200 Hz频宽下的振动有所差异，但是从峰值误差和谱面积误差来看影响较小，可以忽略。对比前后两次输出波的峰值误差、谱面积误差，发现其均无明显差异，证明了离心机振动台具有良好的重复性和稳定性。
![]()
图 9 不同负载下20g El Centro波加速度时程及频谱对比Figure 9. Comparison of time history of acceleration of 20g El Centro waves and frequency spectrum with different loads5. 结论
（1）20~200 Hz频宽变化条件下，迭代算法对最大峰值误差、平均峰值误差、平均谱面积误差的影响可忽略。采用迭代算法前后平均峰值误差分别为5.90%，6.15%，平均谱面积误差分别为5.02%，4.94%。
（2）柔性结构对于加速度峰值≤7.5g地震波的复现精度有显著影响，尤其是80~150 Hz的高频段；对于加速度峰值≥20g地震波的复现精度影响在频宽20~120 Hz可忽略，但对于120~170 Hz频段的小幅值成分的复现能力影响不容忽略，逊于无柔性结构条件。
（3）同时，在无柔性结构条件下对比不同负载即1200 kg和600 kg下同一输入荷载的实测台面输出波，发现两输出波的峰值误差与谱面积误差均无明显差异，证明了离心机振动台具有良好的重复性和稳定性，为开展平行模型试验和检验不同抗震设计方法提供了有力条件。
-
![]()
图 1 DCIEM-40-300离心机振动台系统
Figure 1. Shaking table test system of DCIEM-40-300 centrifuge
![]()
图 3 负载1500 kg离心机振动台设计方案与结构组成
Figure 3. Design scheme and structural composition of centrifugal shaking table with a load of 1500 kg
![]()
图 5 迭代算法对10g El Centro波加速度时程及频谱影响
Figure 5. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g El Centro waves
![]()
图 6 迭代算法对10g ChiChi波加速度时程及频谱影响
Figure 6. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g ChiChi waves
![]()
图 7 柔性结构对7.5g Kobe波加速度时程及频谱影响
Figure 7. Effects of flexible structure on time history of acceleration and frequency spectrum of 7.5g Kobe waves
![]()
图 8 柔性结构对20g El Centro波加速度时程及频谱影响
Figure 8. Effects of flexible structure on time history of acceleration and frequency spectrum of 20g El Centro waves
-
[1] KIM D S, LEE S H, CHOO Y W, et al. Self-balanced earthquake simulator on centrifuge and dynamic performance verification[J]. KSCE Journal of Civil Engineering, 2013, 17(4): 651-661. doi: 10.1007/s12205-013-1591-3
[2] NG C W W. The state-of-the-art centrifuge modelling of geotechnical problems at HKUST[J]. Journal of Zhejiang University SCIENCE A, 2014, 15(1): 1-21. doi: 10.1631/jzus.A1300217
[3] WILSON D W, BOULANGER R W, FENG X, et al. The NEES geotechnical centrifuge at UC Davis[C]//Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver. Canada: IEEE Press, 2004.
[4] 张建民, 于玉贞, 濮家骝, 等. 电液伺服控制离心机振动台系统研制[J]. 岩土工程学报, 2004, 26(6): 843-845. http://cge.nhri.cn/cn/article/id/11539 ZHANG Jianmin, YU Yuzhen, PU Jialiu, et al. Development of a shaking table in electro-hydraulic servo-control centrifuge[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845. (in Chinese) http://cge.nhri.cn/cn/article/id/11539
[5] 陈云敏, 韩超, 凌道盛, 等. ZJU400离心机研制及其振动台性能评价[J]. 岩土工程学报, 2011, 33(12): 1887-1894. http://cge.nhri.cn/cn/article/id/14444 CHEN Yunmin, HAN Chao, LING Daosheng, et al. Development of geotechnical centrifuge ZJU400 and performance assessment of its shaking table system[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1887-1894. (in Chinese) http://cge.nhri.cn/cn/article/id/14444
[6] 顾行文, 任国峰, 王年香, 等. NS-2型水平单向离心机振动台研制及性能验证[J]. 岩土工程学报, 2020, 42(增刊2): 72-76. doi: 10.11779/CJGE2020S2002 GU Xingwen, REN Guofeng, WANG Nianxiang, et al. Development and performance tests on NS-2 horizontal unidirectional centrifugal shaker[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(S2): 7-12. (in Chinese) doi: 10.11779/CJGE2020S2002
[7] ILANKATHARAN M, KUTTER B. Modeling input motion boundary conditions for simulations of geotechnical shaking table tests[J]. Earthquake Spectra, 2010, 26(2): 349-369. doi: 10.1193/1.3383214
下载:
计量
- 文章访问数: 82
- HTML全文浏览量: 11
- PDF下载量: 12
