Reliability evaluation of flexibly soft contact earth pressure cell testing based on centrifugal tests on tunnels
-
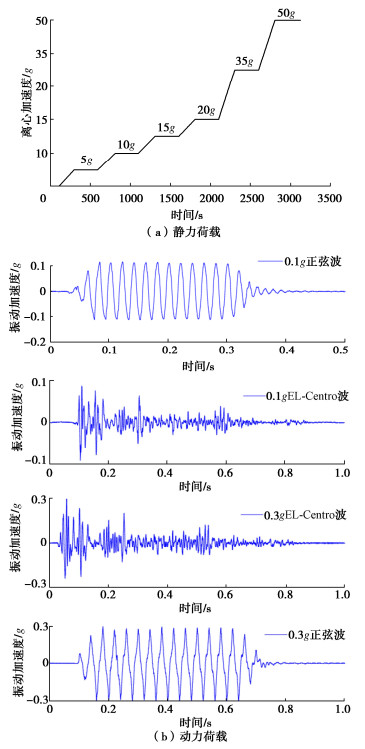
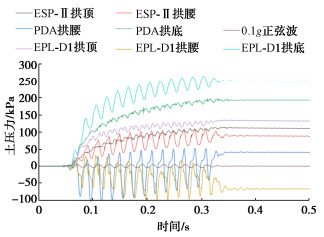
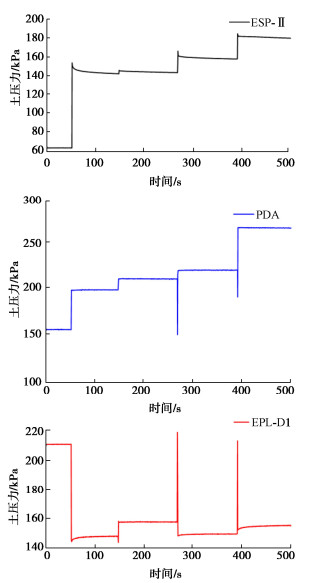
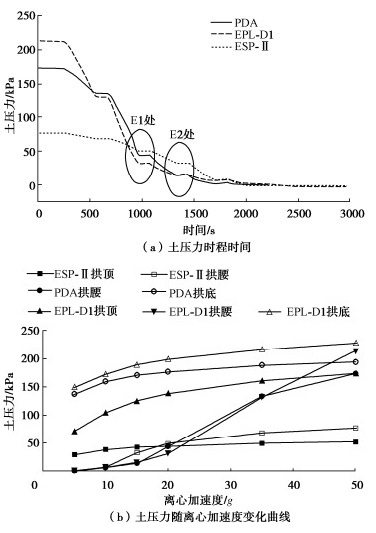
摘要: 开展一系列离心模型试验,选取线性误差、平均幅值误差、响应速率作为指标,基于隧道模型对柔性软接触新型土压计ESP-Ⅱ和两种国际代表性传统土压传感器(PDA、EPL-D1)进行对比评价,验证新研发土压力计测量的可靠性。主要结论如下:①静力状态下,ESP-Ⅱ、PDA、EPL-D1线性误差分别为19.36%,12.7%,21.0%,平均幅值误差为5.79%,48.2%,22.6%,证明ESP-Ⅱ土压力计相比国际两种土压计具有较好静力测试性能。②动力荷载下,ESP-Ⅱ、PDA、EPL-D1土压力计的平均响应速率分别为67.1,51.5,65.8 Hz,ESP-Ⅱ的响应速率略高于其他两种土压力计,具有良好的响应频率;序列地震动荷载下ESP-Ⅱ、PDA测得土压力与EPL-D1不同,呈现一致增量规律,而数值存在一定差异,反映土体具有较强结构性。③卸载过程中,3种土压力计测得数据均呈现不同程度的非线性变化特征,PDA和EPL-D1土压力时程曲线产生了偏折、跳变现象,而ESP-Ⅱ土压力时程曲线保持了较好数据连续性,一定程度说明软接触式设计能实现土压力计与土体的良好接触。Abstract: A series of centrifugal model tests are conducted by selecting the linear error, average amplitude error and response rate as the indice. Based on the tunnel model, a new flexibly soft contact earth pressure cell ESP-Ⅱ and two internationally representative traditional earth pressure sensors (PDA and EPL-D1) are compared and evaluated to verify the reliability of the newly developed earth pressure cell measurement. The main conclusions are as follows: (1) Under the static state, the linear errors of ESP-Ⅱ, PDA and EPL-D1 are 19.36%, 12.7% and 21.0%, respectively, and the average amplitude errors are 5.79%, 48.2% and 22.6%, indicating that the ESP-Ⅱ earth pressure cell has better static testing performance compared to the two international earth pressure cells. (2) Under the dynamic loads, the average response rates of ESP-Ⅱ, PDA and EPL-D1 earth pressure cells are 67.1, 51.5, and 65.8 Hz, respectively. The response rate of ESP-Ⅱ is slightly higher than that of the other two types of earth pressure cells, indicating a good response frequency. The earth pressures measured by ESP-Ⅱ and PDA under sequential seismic loads are different from those of EPL-D1, showing a consistent incremental pattern. However, there are certain differences in the numerical values, indicating that the soils have strong structural characteristics. (3) During the unloading process, the data measured by the three types of earth pressure cell show varying degrees of nonlinear changes. The time-history curves of earth pressures of PDA and EPL-D1 exhibit bending and jumping phenomena, while those of ESP-Ⅱ maintain good data continuity, indicating to some extent that the soft contact design can achieve good contact between the earth pressure cells and the soils.
-
Keywords:
- tunnel /
- centrifugal model test /
- soft contact type /
- earth pressure cell /
- test reliability
-
0. 引言
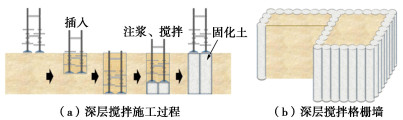
深层搅拌工法因其施工范围小、对周围环境影响弱、适用场地类型多等突出优势,于20世纪70年代开始在世界范围内广泛应用于地基处理[1]。该类工法主要通过将水泥等黏结剂与原位土体进行搅拌混合而形成如图 1(a)所示的柱状固化土。现有研究表明,离散的柱状加固体仅能有限减弱处理地基的震后沉降,但无法有效抑制场地的液化灾害[2-3]。在此基础上,通过将柱状固化土相互重叠组成如图 1(b)所示格栅墙处理地基。格栅墙处理地基的抗液化性能已经多次在地震灾后调研中得到了验证。例如,1995年阪神大地震[4-5]和2011年东日本大地震[1]。相似地,格栅式地下连续墙也常被用作抗液化桥梁基础[6]。格栅墙对于处理地基的抗液化机理可以归纳为以下3点:首先,由于格栅墙相对于未加固土体具有更高的刚度,可以很大程度分担地震导致的剪应力荷载,从而达到抑制场地液化的效果;其次,由于格栅墙由相互重叠的柱形加固体组成,水平方向上不存在渗流通道,可以阻断周围未加固区域的高孔压向被加固区域运移;最后,在周围区域液化发生后,格栅墙处理地基整体可以作为一种挡土结构,从而限制液化大变形的发生(尤其是倾斜场地)。
在长期服役过程中,地下结构的损坏往往具有不可逆的特性,即通过现有技术手段进行地下结构的损伤评估和功能性恢复存在困难。在1995年阪神大地震中,大量地下结构物严重损坏,包括著名的日本大开车站“M”型破坏[7-8],打破了地下结构物在地震中具有较高安全性的传统观念。格栅墙作为一种地基处理手段的同时,其主体部分格栅式形状和高于周围土体的刚度,使其具备了类似于地下结构的地震动响应和破坏形态。相对于混凝土浇筑而成的地下基础以及地下结构,水泥土格栅墙由于其较低的材料强度更容易在地震荷载下发生较大的塑性损伤乃至破坏。
本研究针对自由场地和水泥土格栅墙处理地基开展了两组超重力离心模型试验。试验采用含黏粒砂土和粗砂分别作为易液化层和下卧非液化层。同时通过水泥土材料制作格栅墙模型,对水泥土格栅墙处理地基在多次振动下的长期服役性能进行评价,揭示了格栅墙在强振后的损伤形态和残余抗液化性能。
1. 超重力模型试验
1.1 模型布置图
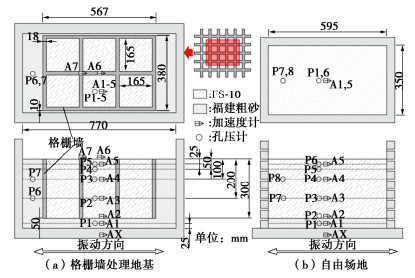
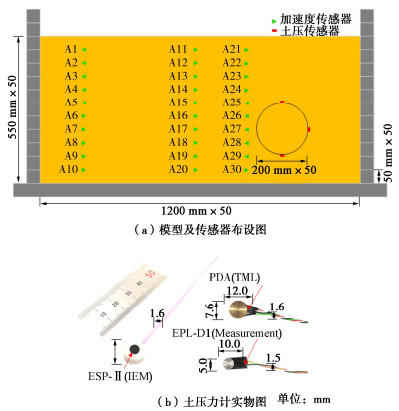
利用浙江大学ZJU400超重力离心机和机载单向振动台,本研究在50g离心加速度下开展了两组超重力振动台试验。其中,1组采用水泥土格栅墙对易液化层进行加固(SC),另1组为未处理自由场地模型(FF)。两组模型在原型尺度下均包含15 m厚的易液化层,下覆2.5 m厚的致密粗砂下卧层,如图 2所示。
在实际工程中,易液化场地通常会采用多格室格栅墙进行抗液化处理。而由于模型试验的有限空间,模型中的单元格室数量存在一定限制。本文采用如图 2所示红色区域中2×3的六格室格栅墙模型作为代表单元。为模拟其较高的刚度边界,水泥土格栅墙处理地基模型在内部尺寸为770 mm(长),400 mm(宽)和500 mm(高)的刚性箱中制作,且格栅墙模型周围布置粗砂,防止其周围土体发生较大程度的软化。格栅墙的内部间距为8.25 m,墙厚为0.9 m,其宽高比为0.55,面积置换率为25%。自由场地模型FF在内部尺寸为595 mm(长),350 mm(宽)和500 mm(高)的剪切模型箱中制作的,其边界条件允许永久剪切变形而更接近半无限自由场地。以上两组模型均采用黏滞系数50倍于水的硅油进行饱和。
1.2 试验材料
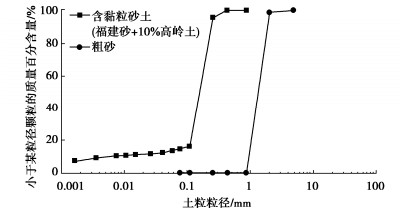
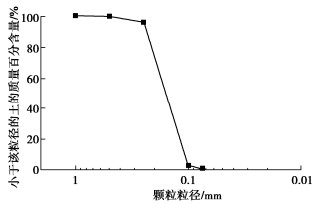
模型中易液化层和下卧非液化层分别采用福建砂+10%高岭土(FS-10)和福建粗砂,且分别通过砂雨法和夯击法制作。易液化层和下卧非液化层的密实度分别为50%和80%,两者的物性参数和颗分曲线分别如表 1和图 3所示。本试验中采用了水泥土材料制作格栅墙模型。水泥土采用福建标准砂、高岭土、水泥(52.5R)和水按照比例1.64∶0.29∶0.572∶1进行混合,并在25℃恒温环境进行养护。其28 d后的无侧限抗压强度约为4 MPa,与实际工况中0.1~1 MPa量级[1]相符。同时,水泥土的强度和小应变剪切刚度间具有统一的对应关系,表明本文采用水泥土的刚度参数也符合实际工况。故本文采用水泥土格栅墙模型为同质缩尺模型,其应力、应变与原型的相似比尺为1,可认为其变形特性及破坏模式与原型相同。
表 1 福建砂+10%高岭土及福建粗砂物性参数表Table 1. Physical properties of Fujian sand with Kaolin clay of 10% and Fujian coarse sand物性参数 符号 单位 FS-10 福建粗砂 土粒密度 ρs g/cm3 2.651 2.648 最大孔隙比 emax — 1.143 0.801 最小孔隙比 emin — 0.60 0.568 细粒含量 Fc % 15 0.2 平均粒径 D50 mm 0.1578 1.31 渗透系数 k m/s 8.04×10-6 7.14×10-3 1.3 输入振动
按照表 2设计的振动序列,对两组超重力离心模型输入频率为1.2 Hz、不同幅值的正弦波。输入正弦波前段为4圈幅值递增的不等幅正弦波,中段为50圈最大幅值的等幅正弦波,后段为4圈幅值递减的不等幅正弦波。本文主要对比模型SC中M2和模型FF中M3两次振动的响应规律。由于振动台输出波形存在一定高频成分,故实际输入加速度幅值(PBA)略高于设计值。而相同设计PBA下的振动波形的阿里亚斯强度(Ia)基本保持一致。
表 2 振动事件Table 2. Shaking events模型 振动顺序 设计PBA/g 实际PBA/g Ia/(m·s-1) SC M1 0.40 0.45 32.8 M2 0.15 0.20 7.8 FF M1 0.15 0.22 7.4 M2 0.40 0.50 34.6 M3 0.15 0.21 7.0 2. 格栅墙振后损伤状态
为了解格栅墙模型的振后损伤状态,在模型试验完成停机后,对模型SC进行振后开挖。通过观测发现,水泥土格栅墙一侧最外部横向墙体(垂直于振动方向)发生破坏。两次振动结束后其顶部共计出现六处显性裂缝;而埋置传感器的中部格室及另一侧格室均保持完好。如图 4所示,破坏侧两面横向墙体在与纵向墙体(平行于振动方向)交界点及其中部位置,均发现有竖向贯穿型裂缝,且其中一面横向墙体还伴随有局部斜向裂缝。该斜向裂缝均未有穿越竖向贯穿裂缝现象,表明斜向裂缝发育后于竖向贯穿裂缝。
3. 格栅墙处理地基强振后残余响应
3.1 加速度
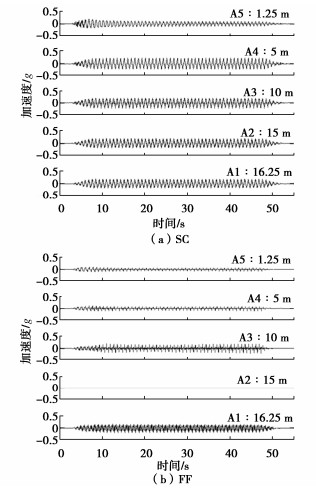
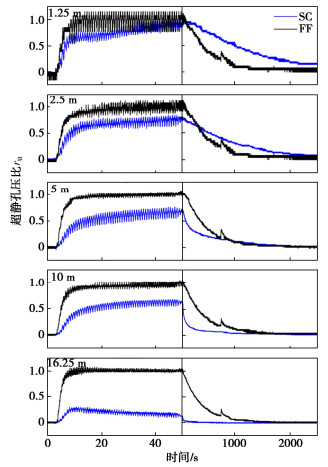
强振历史下,SC(M2)和FF(M3)两组模型在0.15g振动事件中不同深度的加速度时程如图 5所示。在自由场地模型FF中,M3(0.15g)振动下土体表现出显著的振动衰减现象;以及由于强振后土体密实度增加而表现出强烈的剪胀峰。
在强振后格栅墙处理地基SC中,被围束土体由于密实度的增加,其加速度仅在浅层土体(A5)中表现出约50%的幅值衰减;而在其余位置均随深度变浅而表现出非液化场地典型的加速度放大现象。模型SC中被围束土体在5~10 m深度范围相对于粗砂层的加速度放大系数约为1.27。
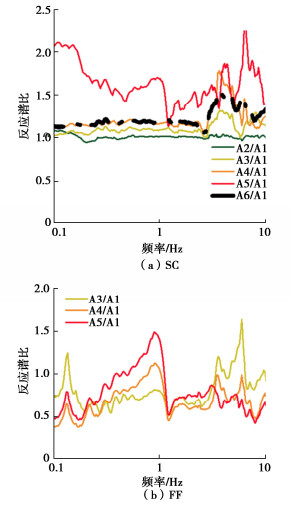
SC(M2)和FF(M23)两组模型易液化层加速度时程相对于粗砂层加速度时程在5%阻尼比下的响应谱比值如图 6所示。自由场地模型FF在M3(0.15g)振动下,随着深度变浅,加速度时程中的高频成分衰减而低频成分被逐渐放大。而强振后的格栅墙处理地基SC加速度响应相对于下卧粗砂层几乎在全频域内表现出放大效应,即反应谱比值始终大于1,且该数值随被围束土体深度变浅而进一步增加。同时,5 m深度处被围束土体(A4)的反应谱比与格栅墙顶部(A6)最为接近。
3.2 超静孔压比
在强振历史后,SC(M2)和FF(M3)两组模型在0.15g振动事件中,不同深度的超静孔压比时程如图 7所示。自由场地模型FF在强震历史后,易液化层仍在全深度发生了严重的液化现象。其超静孔压在消散过程(约750 s)时突增,是由振动台异常脉冲信号导致。在未损伤格栅墙处理地基中,被围束土体的超静孔压比沿深度方向的分布规律通常表现出“束腰效应”[9],即被围束土体超静孔压比在格室中部深度较小,而在两端逐渐增大。而格栅墙处理地基在强振后损伤状态下,其对超静孔压抑制效果随深度增加而逐渐增强,且相对于自由场地表现出良好的抗液化效果。该现象表明格栅墙体损伤后,由于整体质量减小导致惯性力减弱,显著减小易液化层与下卧层间的剪切荷载,进而减弱了处理地基底部超静孔压的发展。
3.3 被围束土体峰值剪应变
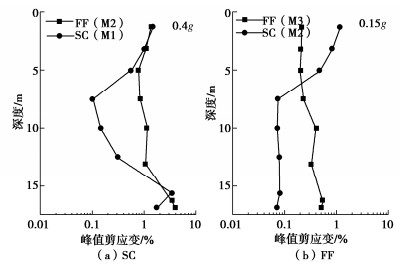
利用加速度时程记录可得,超重力离心模型SC和FF在不同振动中剪应变峰值深度剖面如图 8所示。
在自由场地FF中,易液化层不同深度峰值剪应变较为接近,在M2(0.4g)中约为1%;在M3(0.15g)中,其峰值剪应变减小至约0.3%。格栅墙处理地基SC(M1)在初振下剪应变峰值深度剖面(图 8(a))表现出类似于超静孔压比的“束腰效应”[9]。其中,格栅墙内被围束土体中部深度7.5 m处的峰值剪应变均为全深度最小,约为0.09%,显著低于自由场地。
在强振历史后,SC(M2)模型在0.15g振动事件中,峰值剪应变的深度剖面如图 8(b)所示。被围束土体上半层被围束土体峰值剪应变与SC(M1)相近;而下半层被围束土体峰值剪应变则显著小于SC(M1)工况和自由场地FF(M3)。尤其是格栅墙底部及下卧粗砂层中剪应变均大幅度减小,其16.25 m处的峰值剪应变约为自由场地中的15%。该现象可能由于格栅墙体的塑性损伤及破坏使得处理地基的整体刚度和质量降低,而使得其自身惯性力及与下卧粗砂层间的刚度差异减小,故两者在应力连续条件下的相对变形显著降低。
4. 结论
本研究通过超重力离心模型试验对水泥土格栅墙处理地基在多次振动下的长期服役性能进行研究。首先,通过振后模型开挖的物理观测得到了水泥土格栅墙的损伤形态。其次,对比自由场地和水泥土格栅墙处理地基强振后的加速度、超静孔压比和峰值剪应变等动力响应,揭示了格栅墙在强振后残余抗液化性能。主要得到以下4点结论。
(1)格栅墙在强振下主要的损伤模式主要表现为竖向贯穿型裂缝,并部分伴随有局部斜向裂缝。且外侧格室对于中心格室表现出类似于群桩基础的“遮蔽效应”。
(2)强振后格栅墙处理地基在0.1~10 Hz频域内均表现出放大效应。相比于自由场地中显著的振动衰减,格栅墙内部被围束土体未发生显著软化而仍具有较高的振动幅值。
(3)格栅墙外侧格室发生破坏后,其中心格室仍具有良好的抗液化效果。相比于强振历史后自由场地全深度液化,中心格室内被围束土体仅在浅层1.25 m处出现液化现象。
(4)强振后格栅墙内部被围束土体区别于初振时的“束腰效应”,仅在浅层出现相比于自由场地更大的峰值剪应变。而格栅墙由于整体刚度的削弱,其与下卧粗砂层间的剪切变形显著减小。
-
表 1 原型/模型隧道参数
Table 1 Parameters of prototype/model tunnel
材料参数 原型材料 模型材料 弹性模量/GPa 35.5 71 隧道外径/mm 10000 200 隧道内径/mm 9000 190 衬砌厚度/mm 500 5 隧道长度/mm 20000 400 表 2 3种土压力计静力测量值及计算值
Table 2 Static measurements and calculated values of three types of soil pressure cells
离心加速度/g 土层深度/m 测量值/kPa 计算值/kPa ESP-Ⅱ PDA EPL-D1 5 1.25 9.26 — 37.83 18.13 1.75 4.33 5.82 9.34 11.15 2.25 — 53.01 61.40 34.43 10 2.5 15.66 — 59.52 36.27 3.5 14.10 18.21 25.33 22.30 4.5 — 76.09 83.67 52.57 15 3.75 21.24 — 76.17 54.40 5.25 22.98 33.64 45.13 33.44 6.75 — 94.24 106.14 70.70 20 5 26.14 — 90.65 72.53 7 30.98 51.34 67.03 44.59 9 — 111.45 126.32 88.83 35 8.75 38.52 — 130.59 126.94 12.25 55.01 114.05 142.16 78.04 15.75 — 152.51 178.98 143.24 50 12.5 51.36 — 174.97 181.34 17.5 78.37 174.82 216.41 111.48 22.5 — 191.26 227.81 197.64 -
[1] KARL T. Theoretical Soil Mechanics[M]. New York: J Wiley and Sons Inc, 1943.
[2] 陈若曦, 朱斌, 陈云敏, 等. 基于主应力轴旋转理论的修正Terzaghi松动土压力[J]. 岩土力学, 2010, 31(5): 1402-1406. doi: 10.3969/j.issn.1000-7598.2010.05.009 CHEN Ruoxi, ZHU Bin, CHEN Yunmin, et al. Modified Terzaghi loozening earth pressure based on theory of main stress axes rotation[J]. Rock and Soil Mechanics, 2010, 31(5): 1402-1406. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.05.009
[3] 刘晶波, 刘祥庆, 王宗纲, 等. 土-结构动力相互作用系统离心机振动台模型试验[J]. 土木工程学报, 2010, 43(11): 114-121. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201011018.htm LIU Jingbo, LIU Xiangqing, WANG Zonggang, et al. Dynamic centrifuge model test of a soil-structure interaction system[J]. China Civil Engineering Journal, 2010, 43(11): 114-121. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201011018.htm
[4] WANG J, LIU H Q, LIU H B, et al. Centrifuge model study on the seismic responses of shield tunnel[J]. Tunnelling and Underground Space Technology, 2019, 92: 103036. doi: 10.1016/j.tust.2019.103036
[5] CILINGIR U, GOPAL MADABHUSHI S P. A model study on the effects of input motion on the seismic behaviour of tunnels[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(3): 452-462. doi: 10.1016/j.soildyn.2010.10.004
[6] 芮瑞, 吴端正, 胡港, 等. 模型试验中膜式土压力盒标定及其应用[J]. 岩土工程学报, 2016, 38(5): 837-845. doi: 10.11779/CJGE201605009 RUI Rui, WU Duanzheng, HU Gang, et al. Calibration tests on diaphragm-type pressure cells[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 837-845. (in Chinese) doi: 10.11779/CJGE201605009
[7] 魏永权, 罗强, 张良, 等. 离心力场中微型土压力传感器非线性响应分析[J]. 岩土力学, 2015, 36(1): 286-292. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201501039.htm WEI Yongquan, LUO Qiang, ZHANG Liang, et al. Study of nonlinear response of miniature earth pressure transducer in centrifugal force field[J]. Rock and Soil Mechanics, 2015, 36(1): 286-292. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201501039.htm
[8] 梁波, 厉彦君, 凌学鹏, 等. 离心模型试验中微型土压力盒土压力测定[J]. 岩土力学, 2019, 40(2): 818-826. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902047.htm LIANG Bo, LI Yanjun, LING Xuepeng, et al. Determination of earth pressure by miniature earth pressure cell in centrifugal model test[J]. Rock and Soil Mechanics, 2019, 40(2): 818-826. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902047.htm
[9] 蔡正银, 代志宇, 徐光明, 等. 离心模型试验中界面土压力盒标定方法研究[J]. 水利学报, 2020, 51(6): 695-704. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202006007.htm CAI Zhengyin, DAI Zhiyu, XU Guangming, et al. Study on calibration method of interface soil pressure sensor in centrifugal model test[J]. Journal of Hydraulic Engineering, 2020, 51(6): 695-704. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202006007.htm



 下载:
下载: