Centrifugal mode tests on seismic response of underground structures with pile foundations in soft clay
-
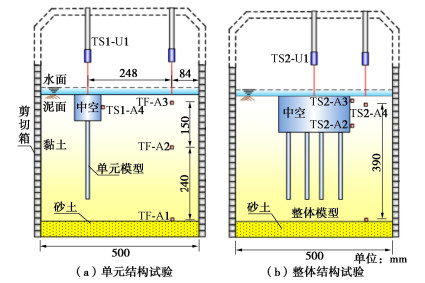
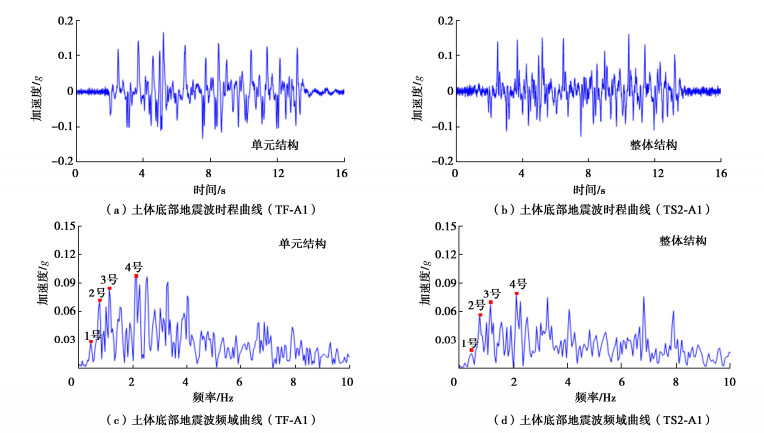
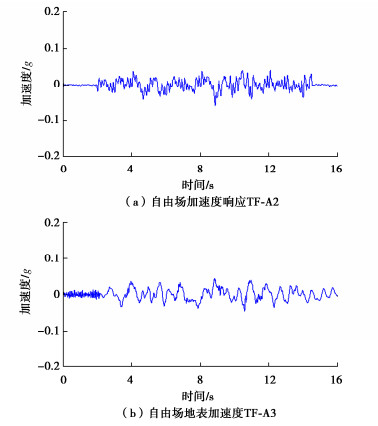
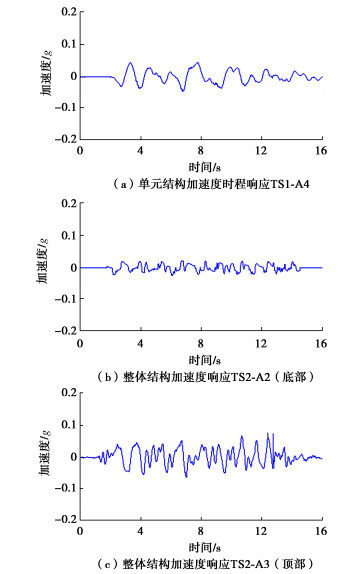
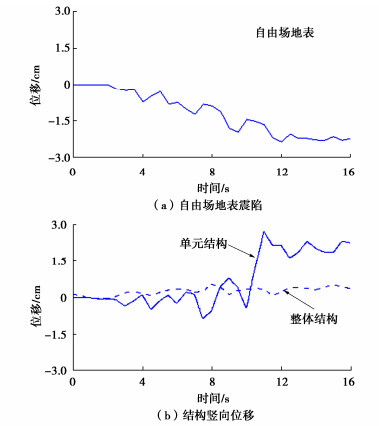
摘要: 针对大空间含桩地下结构（如地下车行系统）在地震作用下的动力响应特性以及场地震陷、结构上浮等危害展开离心振动台试验。试验采用饱和软黏土作为地基土，设计了自由场、整体浅埋地下结构以及等效单元浅埋地下结构3种试验情况，利用层状剪切箱消除边界反射效应，在50g的离心加速度下开展水平地震试验。试验结果表明，不同结构在地震过程中会产生自振在特定的频率区段放大响应，在整体质量、静态浮力及转动惯量等效的前提下，整体结构相对单元结构形式能够降低地震作用下结构的自振效应，且整体结构具有更好地震后抗浮性能。Abstract: The centrifuge shaking table tests are conducted to investigate the dynamic response characteristics of large underground structures with piles, such as underground transportation systems, under seismic loading. In addition, the potential hazards like ground liquefaction and structural buoyancy are examined. The saturated soft clay is used as the foundation soil in the tests, which are designed to represent three scenarios: free field condition, integrated shallowly-buried underground structure, and equivalent single-cell shallowly-buried underground structure. To eliminate the boundary reflection effects, a layered shear box is utilized. The horizontal seismic tests are conducted at 50g centrifugal acceleration. The test results indicate that different structures amplify the response at specific frequency bands associated with their natural vibrations. Under the premise of the equivalent overall mass, static buoyancy and moment of inertia, the integrated structure reduces the effects of the natural vibrations during seismic events compared to the single-cell configuration and exhibits superior post-seismic buoyancy resistance properties.
-
Keywords:
- dynamic centrifuge test /
- pile foundation /
- earthquake /
- interaction /
- frequency characteristic
-
0. 引言
离心机振动台是当前海洋、水利、土木等领域岩土抗震研究的重要科学试验设施之一，其有效性、先进性已为国际共识[1-7]，可较真实地模拟地震荷载下岩土体变形和岩土构筑物破坏的过程。但是，由于离心机振动台运行在高g值离心力场中且与吊篮存在严重的运动学和动力学耦合，又受众多非线性因素影响。因此，如何提高离心机振动台的控制性能是学者们关注和亟需解答的一个重要课题。
目前国内现役离心机振动台仅有9套，分别归属于南京水利科学研究院、中国水利水电科学研究院、清华大学、香港科技大学、同济大学、浙江大学、成都理工大学、交通运输部天津水运工程科学研究所和中国地震局工程力学研究所。其中，张建民等[4]介绍了清华大学离心机振动台的性能指标和功能特色，并基于开展的性能检测试验评价了离心机振动台的系统性能。陈云敏等[5]介绍了浙江大学的离心机振动台的性能指标和结构组成，并基于开展的饱和砂土地基震陷试验对离心机振动台系统的性能进行了初步检验。顾行文等[6]介绍了南京水利科学研究院的NS-2型离心机振动台的性能指标和关键技术，并基于某沥青混凝土墙砂砾石坝试验对离心机振动台系统性能指标进行了初步验证。但这些成果，对迭代算法和柔性结构带给离心机振动台控制性能的影响，鲜见讨论。
本文以中国地震局工程力学研究所1500 kg离心机振动台为样本，介绍了离心机振动台的总体设计和基本组成，通过50g离心加速度下多个典型地震波的输入/输出对比测试，探讨了迭代算法、柔性结构对离心机振动台控制性能的影响，同时检验了不同负载下动力离心试验地震荷载的可重复效果，以期为正在建设和规划的离心机振动台研制提供参考。
1. 离心机振动台系统整体设计
1.1 试验设备与性能指标
中国地震局工程力学研究所与哈尔滨工业大学联合研制的DCIEM-40-300水平单向离心机振动台整体采用吊篮与振动台一体化的方法，如图 1所示。其主要性能指标：离心加速度100g，有效负载3000 kg，最大半径5.5 m，有效吊篮净空1.8 m×1.6 m×1.0 m；振动加速度30g，振动速度1 m/s，振动位移±10 mm，振动负载1500 kg，振动频宽10~300 Hz，平台有效尺寸1.6 m×0.8 m×0.8 m。除此之外，还配备了160 ch动态数据采集仪和自主研发了包括孔压、土压、加速度的各种宽频带高分辨力测量传感器。
![]()
图 1 DCIEM-40-300离心机振动台系统Figure 1. Shaking table test system of DCIEM-40-300 centrifuge1.2 一般问题和设计方案
铰接装置作为柔性连接结构在许多离心机振动台上得到应用，以减小离心力荷载下台面和吊篮变形对作动器安全性带来的危险。但是，铰接装置本身存在间隙，且现有离心机振动台多数采用多阀单缸作动器[4-6]，在往返过程中会涉及到力换向的问题，换向过程间隙的存在可能对离心机振动台控制精度和稳定性产生影响。
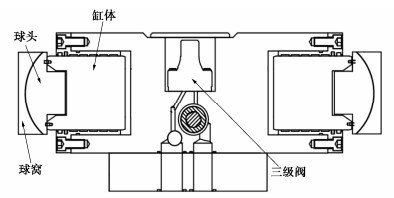
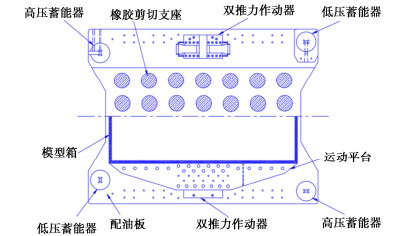
中国地震局工程力学研究所的负载1500 kg离心机振动台，采用了双推力作动器，结构示意图如图 2所示，每个作动器由两条柱塞缸和一个三级伺服阀集成，且柱塞缸内部增设弹簧以使球头、球窝、摩擦板间始终紧密配合形成零间隙连接，避免了柔性结构。振动台总体设计如图 3所示，两个双推力作动器对称布置在运动平台两侧，以使作用线更接近岩土模型质心。运动平台由28个圆形弹性橡胶剪切轴承支撑。每个作动器由安装在配油板上的28 MPa高压蓄能器供油，并通过1.3 MPa低压蓄能器回油。蓄能器主要用作储油和稳压，可满足离心机不停机情况下连续激发多次振动试验的需求。
![]()
图 3 负载1500 kg离心机振动台设计方案与结构组成Figure 3. Design scheme and structural composition of centrifugal shaking table with a load of 1500 kg1.3 试验设计与评价指标
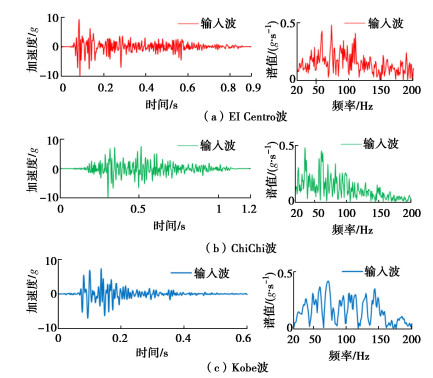
本次试验选用的地震波有El Centro波、ChiChi波和Kobe波，其输入波时程和频谱如图 4所示，均为50g离心加速度下的压缩输入波。迭代算法是通过多次重复激振试验系统来生成正式试验的驱动信号，旨在使振动台的输出信号尽可能接近输入信号，根据最新研究成果，本文研究采用适于高频液压作动器的时域波形复现的迭代算法。此外，由于中国地震局工程力学研究所负载1500 kg离心机振动台作动器与平台间为无间隙连接，需要通过在作动器球窝与平台摩擦板间加入橡胶叠，利用橡胶叠来模拟柔性结构。
2. 迭代算法的影响
2.1 地震动峰值
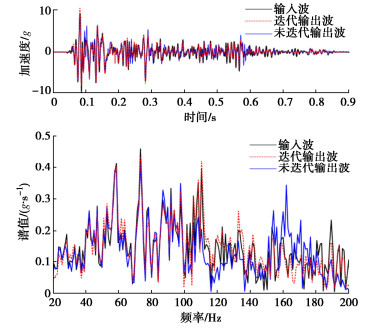
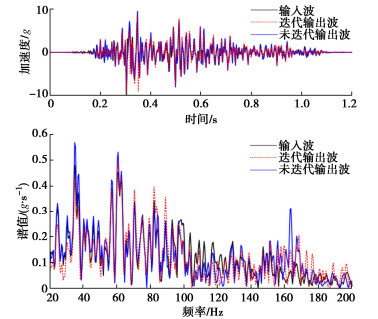
振动台负载1200 kg时，离心加速度50g下，采用迭代算法前后10g El Centro波、10g ChiChi波的输出波时程曲线如图 5，6所示。经计算采用迭代算法后的El Centro波输出波最大峰值误差为5.3%，ChiChi波输出波最大峰值误差为6.5%，平均峰值误差为5.9%；而未采用迭代算法的El Centro波的实测输出波最大峰值误差为7.8%，ChiChi波输出波最大峰值误差为4.5%，平均峰值误差6.15%。迭代算法前后的平均峰值误差相差不明显，即迭代算法基本不影响再现地震动的最大峰值误差、平均峰值误差。
![]()
图 5 迭代算法对10g El Centro波加速度时程及频谱影响Figure 5. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g El Centro waves![]()
图 6 迭代算法对10g ChiChi波加速度时程及频谱影响Figure 6. Effects of iterative algorithm on time history of acceleration and frequency spectrum of 10g ChiChi waves2.2 地震动频宽
图 5和图 6给出了振动台负载1200 kg时，离心加速度50g下，采用迭代算法前后10g El Centro波、10g ChiChi波的输出波频谱。经计算采用迭代算法后的El Centro波输出波谱面积误差为6.06%，ChiChi波输出波谱面积误差为3.97%，平均谱面积误差为5.02%；而未采用迭代算法的El Centro波的实测输出波谱面积误差为5.98%，ChiChi波输出波谱面积为3.88%，平均谱面积误差4.94%。通过对比前后数据，发现在20~200 Hz频宽变化条件下，迭代算法对谱面积误差影响可忽略。
3. 柔性结构的影响
3.1 地震动峰值
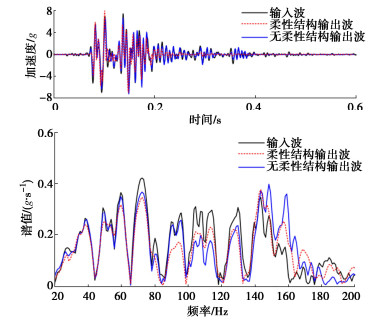
图 7，8给出了振动台负载1200 kg时，离心加速度50g下，在有无柔性结构时7.5g Kobe波、20g El Centro波的输出波时程曲线。经计算柔性结构工况下的7.5g Kobe波输出波最大峰值误差为7.11%，20g El Centro波输出波最大峰值误差为3.63%，平均峰值误差为5.32%；而采用无柔性结构即球头、球窝与摩擦板零间隙连接时Kobe波输出波最大峰值误差为3.51%，El Centro波输出波最大峰值误差为3.07%，平均峰值误差为3.29%；柔性结构对峰值误差影响较小。但在加速度时程图中可明显看出柔性结构在7.5g Kobe波下基本复现不出持时在0.2 s后加速度峰值≤2.5g的波形，而在20g El Centro波下对0.65 s后加速度峰值≤2.5g的波形的复现效果虽比7.5gKobe波下有所改善，但与无柔性结构相比仍存在一定的差距。
![]()
图 7 柔性结构对7.5g Kobe波加速度时程及频谱影响Figure 7. Effects of flexible structure on time history of acceleration and frequency spectrum of 7.5g Kobe waves![]()
图 8 柔性结构对20g El Centro波加速度时程及频谱影响Figure 8. Effects of flexible structure on time history of acceleration and frequency spectrum of 20g El Centro waves3.2 地震动频宽
振动台负载1200 kg时，离心加速度50g下，在有无柔性结构时7.5g Kobe波、20g El Centro波的输出波频谱图对比，如图 7，8所示。经计算柔性结构工况下7.5g Kobe波输出波谱面积误差为8.37%，20g El Centro波输出波谱面积误差为7.95%，平均谱面积误差为8.16%；而采用无柔性结构即无间隙连接时Kobe波输出波谱面积误差为4.89%，El Centro波输出波谱面积误差为8.09%，平均谱面积误差为6.49%；柔性结构对谱面积误差影响较小。但在频谱图中可明显看出柔性结构对于7.5gKobe地震波的复现精度有显著影响，尤其是80~150 Hz的高频段；对于20g El Centro地震波的复现精度影响在频宽20~120 Hz可忽略，但对于120~170 Hz频段的小幅的复现能力影响不容忽略，逊于无柔性结构条件。
4. 不同负载下重复性
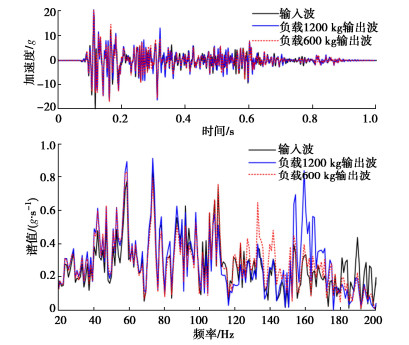
此外，探讨了无柔性结构不同负载下离心振动台的波形重复性。更换不同重量的负载即1200 kg和600 kg，先后输入了两次同一幅值20g El Centro波，加速度时程曲线及频谱如图 9所示。负载1200 kg时，输出波峰值误差为3.07%，谱面积误差为8.09%；负载600 kg时，输出波峰值误差为3.2%，谱面积误差为5.56%。虽然不同负载在120~200 Hz频宽下的振动有所差异，但是从峰值误差和谱面积误差来看影响较小，可以忽略。对比前后两次输出波的峰值误差、谱面积误差，发现其均无明显差异，证明了离心机振动台具有良好的重复性和稳定性。
![]()
图 9 不同负载下20g El Centro波加速度时程及频谱对比Figure 9. Comparison of time history of acceleration of 20g El Centro waves and frequency spectrum with different loads5. 结论
（1）20~200 Hz频宽变化条件下，迭代算法对最大峰值误差、平均峰值误差、平均谱面积误差的影响可忽略。采用迭代算法前后平均峰值误差分别为5.90%，6.15%，平均谱面积误差分别为5.02%，4.94%。
（2）柔性结构对于加速度峰值≤7.5g地震波的复现精度有显著影响，尤其是80~150 Hz的高频段；对于加速度峰值≥20g地震波的复现精度影响在频宽20~120 Hz可忽略，但对于120~170 Hz频段的小幅值成分的复现能力影响不容忽略，逊于无柔性结构条件。
（3）同时，在无柔性结构条件下对比不同负载即1200 kg和600 kg下同一输入荷载的实测台面输出波，发现两输出波的峰值误差与谱面积误差均无明显差异，证明了离心机振动台具有良好的重复性和稳定性，为开展平行模型试验和检验不同抗震设计方法提供了有力条件。
-
![]()
图 6 结构中部加速度频谱对比
Figure 6. Comparison of structure displacements between numerical and centrifugal model
表 1 试验模型相似比
Table 1 Similarity ratios of model
构件 相似常数 EI/(N·m-2) EA/N m/kg J/(kg·m-2) 桩 1︰504
(1︰49.84)1︰502
(1︰502)— — 整体结构 — — 1︰504
(1︰49.64)1︰505
(1︰49.84)
下载: 导出CSV
-
[1] 张虎臣. 淤泥地基地震触变研究[J]. 岩土工程学报, 1989, 11(3): 78-85. http://cge.nhri.cn/cn/article/id/9280 ZHANG Huchen. Study on seismic thixotropy of silt foundation[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(3): 78-85. (in Chinese) http://cge.nhri.cn/cn/article/id/9280
[2] SEED H B, CHAN C K. Clay strength under earthquake loading conditions[J]. Journal of the Soil Mechanics and Foundations Division, 1966, 92(2): 53-78. doi: 10.1061/JSFEAQ.0000867
[3] SEED H B, IDRISS I M. Simplified procedure for evaluating soil liquefaction potential[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(9): 1249-1273. doi: 10.1061/JSFEAQ.0001662
[4] 冯忠居, 王逸然, 蔡杰, 等. 桩-震陷土层耦合作用下变截面单桩动力响应[J]. 振动工程学报, 2023, https://kns.cnki.net/kcms/detail/32.1349.TB.20230328.0904.002.html. FENG Zhongju, WANG Yiran, CAI Jie. Dynamic response characteristics of diameter variable section single pile under the coupling action of pile‑splinter soil layer[J]. Journal of Vibration Engineering, 2023, https://kns.cnki.net/kcms/detail/32.1349.TB.20230328.0904.002.html.(in Chinese)
[5] GOH S H, ZHANG L. Estimation of peak acceleration and bending moment for pile-raft systems embedded in soft clay subjected to far-field seismic excitation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(11): 04017082. doi: 10.1061/(ASCE)GT.1943-5606.0001779
[6] 周燕国, 陈云敏, 社本康广, 等. 软粘土地基上建筑物不均匀震陷离心机试验研究[J]. 中国科学(E辑: 技术科学), 2009, 39(6): 1129-1137. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200906014.htm ZHOU Yanguo, CHEN Yunmin, SHE Benkangguang, et al. Centrifuge experimental study on uneven seismic subsidence of buildings on soft clay foundation[J]. Science in China (Series E (Technological Sciences)), 2009, 39(6): 1129-1137. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200906014.htm
[7] WILSON D W. Soil-pile-superstructure Interaction in Liquefying Sand and Soft Clay[D]. Davis: University of California, Davis. 1998.
[8] 黄茂松, 钟锐, 任青. 层状地基中沉箱加桩复合基础的水平-摇摆振动[J]. 岩土工程学报, 2012, 34(5): 790-797. http://cge.nhri.cn/cn/article/id/14565 HUANG Maosong, ZHONG Rui, REN Qing. Lateral vibration of caisson-pile composite foundation in layered soils[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(5): 790-797. (in Chinese) http://cge.nhri.cn/cn/article/id/14565
[9] 钟锐, 黄茂松. 沉箱加桩复合基础地震响应离心试验[J]. 岩土力学, 2014, 35(2): 380-388. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201402012.htm ZHONG Rui, HUANG Maosong. Centrifuge tests for seismic response of caisson-pile composite foundation[J]. Rock and Soil Mechanics, 2014, 35(2): 380-388. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201402012.htm
[10] 梁发云, 陈海兵, 黄茂松, 等. 结构-群桩基础地震响应离心振动台模型试验[J]. 建筑结构学报, 2016, 37(9): 134-141. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201609017.htm LIANG Fayun, CHEN Haibing, HUANG Maosong, et al. Model test on seismic response of superstructure and pile group[J]. Journal of Building Structures, 2016, 37(9): 134-141. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201609017.htm
[11] 田兆阳, 李平, 朱胜, 等. 强震作用下软土场地桩基负摩阻力振动台试验研究[J]. 岩土工程学报, 2022, 44(3): 550-559. doi: 10.11779/CJGE202203017 TIAN Zhaoyang, LI Ping, ZHU Sheng, et al. Shaking table tests on negative friction of piles in soft soils under strong earthquake motion[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(3): 550-559. (in Chinese) doi: 10.11779/CJGE202203017
[12] 刘鸿哲, 黄茂松. 不同埋深矩形隧道地震响应的离心振动台试验[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3404-3412. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2054.htm LIU Hongzhe, HUANG Maosong. Centrifugal shaking table test of seismic response of rectangular tunnels with different buried depths[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3404-3412. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2054.htm
[13] YANG D, NAESGAARD E, BYRNE P M, et al. Numerical model verification and calibration of George Massey Tunnel using centrifuge models[J]. Canadian Geotechnical Journal, 2004, 41(5): 921-942.
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
