Clay strength in calculation of penetration resistance of offshore wind bucket foundation
-
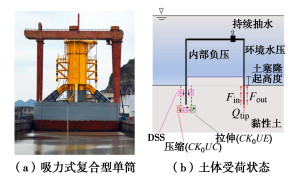
摘要: 沉贯阻力的准确预测对筒型基础成功应用至关重要。单剪(DSS)试验测得的不排水抗剪强度su是沉贯安装设计中的关键土参数,DSS试验考虑了K0固结下土体的应力状态、主应力旋转以及实际工程平面应变状态,与吸力式筒型安装过程中土体的受荷状态相符。研究总结了黏土中筒型基础沉贯阻力计算方法,并分析了各种方法的特点。针对黏土强度取值问题,采用单剪仪对滨海土进行等体积单剪试验,探讨了干密度ρd、法向应力σv'及超固结比(OCR)对su的影响,并分析了su差异产生的原因。最后,提出了基于临界状态理论、强度指标、SHANSEP的3种预测su的计算方法。研究成果为黏土中筒型基础沉贯阻力计算时土体参数取值提供了依据。Abstract: The accurate prediction of penetration resistance is crucial for the successful application of bucket foundations. The undrained shear strength (su) obtained from the direct simple shear (DSS) tests is a key soil parameter in bucket installation design. The DSS tests consider the stress state of the soil under K0 consolidation, the rotation of principal stresses and the actual engineering plane strain state, which corresponds to the loading conditions of the soil during installation of suction bucket. This study summarizes the calculation methods for bucket penetration resistance in clay and analyzes the characteristics of various methods. To address the issue of determination of soil strength, the coastal soil is subjected to consolidated undrained triaxial shear tests using a single shear apparatus. The influences of dry density (ρd), effective normal stress (σv') and overconsolidation ratio (OCR) on su are explored, and the reasons for the differences in values of su are analyzed. Finally, three prediction methods for su based on the critical state theory, strength index and SHANSEP are proposed. The research findings provide a basis for determining soil parameters in calculation of foundations penetration resistance of bucket in clayey soils.
-
0. 引言
某护岸工程采用的大圆筒结构似于无底、无隔墙的圆形沉箱结构,可以直接建在基床上或硬基础上,广泛地应用于岸壁码头、突堤码头及系船柱等港口水工构筑物,主要靠自重和筒壁与内填料的相互作用来抵挡外力,因具有结构简单、用料量少、结构受力条件好、施工速度快、造价低、耐久性好的优点,自20世纪80年代开始进行了一些工程实践[1-2]。
由于大圆筒结构薄壳和曲面受力特征,其与土体相互作用更加复杂,众多学者在室内模型试验、离心模型试验及数值模拟方面均取得了较多的科研成果。刘建起等[3]采用小型室内模型试验对非沉入式无底圆筒内填料压力与结构倾覆过程中内填料摩擦力、结构基底应力及抗倾稳定性进行了研究;竺存宏等[4]进行了外径为1.2 m的圆筒模型试验,分析了大圆筒结构在倾覆失稳过程中作用在筒内外壁上的土压力变化特征。徐光明等[5]针对软黏上地基上深埋式大圆筒码头结构进行了离心机模型试验,就大圆筒的深高比、径高比和筒壁摩擦作用对结构工作性状的影响规律进行了初步探讨。陈福全等[6]采用三维有限元对某实际工程采用的大圆筒码头结构进行了分析,筒体采用8节点非协调元离散,筒土界面采用三维刚塑性接触面单元模拟,研究了大直径圆筒码头的工作性状。
已有的研究主要集中在沉入式大圆筒结构与软土地基相互作用,较少涉及到基床式大圆筒结构,尤其是对于波浪荷载作用下大直径圆筒结构稳定性认识不足,本文采用水位差法等效模拟波浪荷载,通过离心模型试验技术研究某护岸工程大圆筒结构位移性状、内力反应及土压力变化规律,验证大圆筒结构在设计波浪荷载作用下稳定性。
1. 试验方案
1.1 试验设备
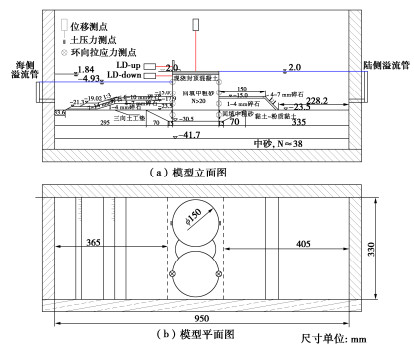
试验在南京水利科学研究院NHRI60g·t中型土工离心机上开展,如图 1。该机的有效半径2 m,最大加速度200g,最大负荷300 kg,离心机容量(最大离心加速度与最大负荷乘积)达60 g·t。试验用模型箱的内部有效尺寸为950 mm×450 mm×330 mm(长×高×宽),其一侧面为有机玻璃窗口,便于监控试验过程。大直径钢圆筒护岸和防波堤结构的水平位移和竖向沉降以及筒侧土压力采用图 2所示的激光位移计和图 3所示的薄片式土压力盒测量。
1.2 模型布置
根据大直径钢圆筒护岸结构断面几何尺寸,并结合模型布置、模型制作、模型测量等因素,选定模型比尺n = 200,模型布置见图 4。
1.3 材料模拟
一般来说,离心模型试验中所有材料应该选用应与原型相同,因此,模型结构物仍采用与原型相同的材料进行制作。
原型护岸结构物为大直径钢圆筒,其直径30 m、高度为32.5 m、壁厚22 mm,经过计算,相应的模型圆筒结构直径为150 mm、高度为162.5 mm。采用与原型同样材质的钢或不锈钢(其弹模与钢材接近),其壁厚0.11 mm。
试验土料取自现场,将上部淤泥②1、粉质黏土③1、粉质黏土③2、粉质黏土④2、黏土④2、粉质黏土④3和黏土④3合并,成为厚度18.20 m黏土-粉质黏土合并层,以地基强度指标作为主要模拟量,合并层地基不排水强度目标值为90 kPa。对于模型中砂层,控制其密实度制作而成。黏土层物理力学指标见表 1。
块石等大体积护坡材料,按模型相似比计算后制作模拟,三向土工垫用土工滤膜进行模拟,原型现浇封顶混凝土层用铝合金圆盘制作模拟。
表 1 土的物理力学性质指标Table 1. Physical properties of soils土名 厚度/m 含水率/% 密度/(g·cm-3) 不排水强度/kPa 淤泥②1 1.10 35.2 1.86 3.0 粉质黏土③1 2.00 25.1 1.99 37.0 粉质黏土③2 3.40 23.2 2.02 75.8 粘土-粉质黏土④2 4.30 26.8 1.96 83.1 粘土-粉质黏土④3 7.40 24.5 1.99 128.5 1.4 测试技术
位移测量采用了激光位移传感器,在大直径钢圆筒模型顶部设置了一个铝合金片光靶,钢圆筒模型筒体水位面以上位置可作为一个光靶,共布置了2个侧向位移测点;沉降测点位于钢圆筒顶部铝合金圆盘伸出部位。
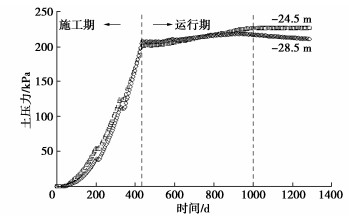
土压力测量采用了进口薄片式微型土压力盒,如图 4所示,共布置了4个土压力测点,海侧筒壁面上2个,陆侧筒壁面上2个,其位置分别对应于原型标高-24.5,-28.5 m。
为了掌握和控制大直径钢圆筒护岸模型两侧水位,采用微型孔隙水压力计进行水压力测量,如图 4所示,共布置了4个水压力测点,海陆两侧各2个测点。
同时在大直径钢圆筒模型筒体4个高度位置处设置了环向正应力测点,如图 4所示,从上至下,4个测点位置分别对应于原型标高-5.0,-12.2,-19.4,-26.6 m。
1.5 水位差法等效模拟波浪荷载
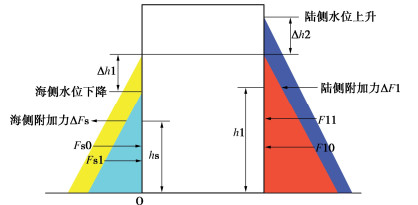
大直径钢圆筒护岸所承受的波浪荷载作用,具体可用各种最不利工况中波峰或波谷时所对应的波压力和波吸力进行表征,无论波压力还是波吸力,对大圆筒产生的力学效应均可归结为一个侧向滑动力和一个转动力矩,使大圆筒发生侧向滑动和倾转。因此,可在模型试验中,通过调整大圆筒海侧和陆侧的水位,产生一个等效的侧向滑动力和一个等效的转动力矩,使大圆筒发生侧向滑动和倾转。基于上述分析,图 5为水位差法模拟等效波浪荷载的原理示意图,鉴于筒体在波浪荷载作用下的稳定性主要体现在其力矩作用所产生的转动效应上,因此,水位控制模拟法中优先考虑力矩等效,再考虑滑动力等效,需要说明的是,该方法将波浪荷载作为集中荷载考虑,且并未涉及波浪荷载对地基强度弱化效应的影响。具体做法是提高陆侧水位高度,高度增加值为Δh2,陆侧作用力由F10增加至F11,陆侧附加力为ΔF1=F11-F10;同时降低海侧水位高度,减小值为Δh1,海侧作用力由FS0减小至FS1,海侧附加力为ΔFS=FS0−FS1。假设圆筒模型在波浪荷载作用下绕图 5中所示o点转动,海陆侧附加力对应o点力臂分别为hs和hl。调整后的总附加滑动力ΔF和总附加滑动力矩ΔM分别如下所示:
ΔF=ΔF1+ΔFS, (1) ΔM=ΔF1×h1+ΔFS×hS。 (2) 1.6 试验程序
试验准备:制作结构物。
制作模型:制备地基,放置模型结构物,筒内回填,埋设和安装传感器,设置溢流孔。
恢复自重应力:按施工速率控制离心机加速度上升速率至200g,并运行1 h,期间进行数据采集。
模型试验:筒内放入回填料,两侧放置护底块石,按施工速率控制离心机加速度上升速率至200g,并稳速运行30 min,相当于模拟了原型运行期833 d,期间慢慢升高护岸陆侧的水位直至达到设计水位;试验中,离心机加速阶段,相当于实际工程的施工期;离心机稳速阶段,即代表工程进入运行期。
2. 试验结果分析
本文给出的试验结果均已换算至原型。
2.1 水位控制过程
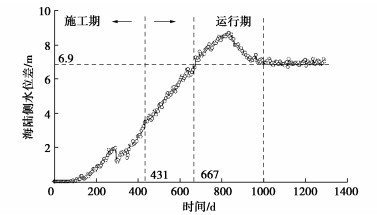
大直径钢圆筒护岸模型置于离心机吊篮中,启动离心机升高其模型加速度,同时缓慢升高护岸陆侧的水位,如图 6所示,约在431 d时,模型达到设计加速度200g,约在667 d,两侧水位差达到6.9 m,约在1000 d后,两侧水位差回落至6.9 m,并维持在6.9 m上下。当模型护岸两侧水位差满足筒前海侧水位面为-4.91 m,筒后陆侧水位面为2.0 m,这就等于给大直径钢圆筒护岸结构施加了等效波浪力荷载,即25 a一遇波吸力荷载。
2.2 位移性状
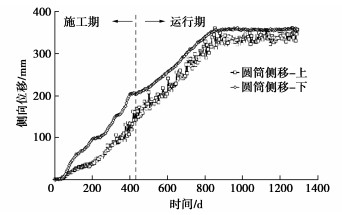
图 7给出了大直径钢圆筒护岸模型加速度升高和两侧水位差增大过程中筒体侧向位移随时间的发展过程曲线,其中上测点高出模型筒顶15 mm,下测点低于模型筒顶15 mm。从图可见,伴随着加速度的升高和大直径钢圆筒护岸模型两侧水位差逐渐增大,筒顶上测点和下测点两处侧向位移读数发展迅速。对应于两侧水位差作用于钢圆筒护岸上波吸力荷载达到最大时,两个测点侧向位移读数也达到最大,分别约为343,357 mm。之后钢圆筒侧向位移渐渐趋于稳定值,分别为346,360 mm。由于大直径钢圆筒筒顶上下两各测点处侧向位移量相近,因此,在波吸力荷载作用下,筒体侧向位移模式近似为平移,位移量约353 mm。
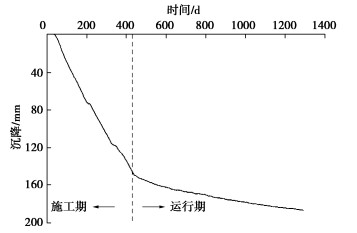
图 8是大直径钢圆筒护岸模型在加速度升高和施工期波吸力荷载作用下筒体顶部沉降发展曲线。同样,伴随着加速度的升高,大直径钢圆筒两侧作用的水压力差逐渐增大,筒顶测点的沉降数值迅速增大。当加速度达到设计值200g时,此时护岸两侧水位差尚未达到最大,但沉降增长速率明显减小,沉降曲线出现一个明显的转折点。即筒体护岸竣工时,此时波浪荷载虽未达到设计值,但其沉降已基本完成,达到147 mm,之后缓慢增长,两年多(833 d)时间内沉降累计仅增加了约40 mm。对比图 7,8可知,大直径钢圆筒护岸两侧水位差对其筒体沉降的影响程度,远小于对筒体侧向位移的影响程度。
2.3 结构内力反应
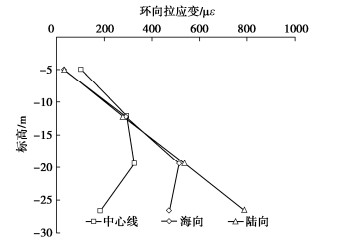
环向拉应变随标高的分布如图 9所示,沿大直径钢圆筒海向和中心线高度方向布置的环向拉应变测点,筒壁标高在-19.4 m位置处的环向拉应变最大,即在筒身1/3高度部位的筒壁环向拉应变最大;沿陆向高度方向布置的环向拉应变测点,筒壁在-26.6 m位置处的环向拉应变最大。沿大直径钢圆筒圆周方向,3个位向筒壁处环向拉应变大小差别不大,只是在筒壁底部,陆向筒壁环向拉应变测值比海向和中心线出的大。
根据应变测量值推算筒壁环向拉应力在10~170 MPa,其均值约为90 MPa,处于钢圆筒材料允许应力范围内;筒壁内外压力差在10~250 kPa,其均值约为130 kPa。
2.4 土压力性状
图 10给出了筒体下部侧壁上的海侧两个测点土压力发展过程曲线。随着模型加速度的升高和大直径钢圆筒两侧水压力差的增大,两个测点处的土压力数值均迅速增大。当模型加速度达到设计值200g后一段时间,两侧水位差达到峰值并渐趋稳定后,两个测点土压力值也增大至最大并同时趋于稳定值。约1000天时,海侧标高-24.5 m和-28.5 m测点土压力分别达227 kPa和219 kPa,之后土压力数值基本稳定,这与结构位移变化规律基本一致,停机前,这两个测点土压力测值分别为227 kPa和211 kPa。筒壁土压力是由筒壁与周围邻近土体间挤密程度决定的,土压力趋于恒定值,表明筒体与周围邻近土体之间没有新的相对位移趋势,即筒体在波浪荷载作用下位移变形已经稳定,因此,从土压力发展变化角度看,大直径钢圆筒护岸结构在波浪荷载作用下是稳定安全的。
图 11给出了大直径钢圆筒护岸海侧两个测点的土压力-标高分布,同时图中给出了这两个测点之间的被动动土压力和2/3被动动土压力分布,计算公式如下:
pzp=σ′vKp+pw, (3) p2/3zp=2/3⋅σ′vKp+pw。 (4) 式中:pzp为计算点处朗肯被动土压力;p2/3zp为计算点处2/3朗肯被动土压力;σ′v为筒前海侧有效竖向应力。计算时,水下土体重度取9 kN/m3;Kp为朗肯被动土压力系数,是计算点处所在细砂土体内摩擦角的函数。计算时,中粗砂内摩擦角取34°;pw为计算点处海侧水压力。
从图 11可见,位于换填中粗砂土层中大直径钢圆筒护岸海侧两个测点处土压力,其实测值与朗肯被动土压力分布相去甚远,与2/3朗肯被动土压力分布也不完全相近,因此,位于换填中粗砂土层内大直径钢圆筒部分筒壁土压力分布规律尚需进一步的研究。
3. 结论
(1)大直径钢圆筒护岸结构在施工期25 a一遇波吸力荷载作用下,筒体近似平移,侧向位移量约353 mm,筒顶沉降约为187 mm,钢圆筒整体稳定。
(2)大直径钢圆筒侧向位移发展主要是由两侧水位差即波浪力荷载大小所决定,而筒体沉降则主要是由护岸自重所控制
(3)筒壁环向拉应力在10~170 MPa,其均值约为70 MPa,处于钢圆筒材料允许应力范围内。
(4)位于换填中粗砂土层中大直径钢圆筒护岸海侧两个测点处土压力随水位差增大至峰值后趋于稳定,表明筒体与周围邻近土体之间没有新的相对位移趋势。
(5)结果表明,大直径钢圆筒护岸结构在施工期25 a一遇波吸力荷载作用下是稳定安全的,满足使用要求,设计方案合理、可行。
-
表 1 基于不排水抗剪强度su的计算方法
Table 1 Methods based on undrained shear strength su
方法分类 计算公式 API-RP-2GEO[2] R=(Ao+Ai)hαsu+Atip9su Houlsby等[8] V′+sAin=Aohαosu1+Aihαisu1+ Atip(γ′h−s+su2Nc) DNV-RP-E303[3] Rb=(Ao+Ai)hαsavu,D+Atip(Ncsavu,tip+γ′h) 注:R为筒型基础贯入阻力;AO,Ai,Atip,Ain,h分别为筒裙外部周长、筒裙内部周长、筒端部面积、筒内顶盖面积、筒型基础贯入深度;α为黏合系数,α=1/st,st为黏土的灵敏度;γ′为土体有效重度;V’为有效竖向荷载(考虑基础入水及浮力);s为筒型基础贯入所需吸力;su1为贯入深度内土体不排水抗剪强度平均值;su2为贯入深度处土体不排水抗剪强度;Nc为承载力系数;savu,D为DSS不排水抗剪强度平均值;savu,tip为三轴压缩、三轴拉伸、DSS不排水抗剪强度平均值。 表 2 基于su的沉贯阻力计算方法属性
Table 2 Properties of su-based methods for penetration resistance
方法分类 自重沉贯 吸力沉贯 土参数 经验系数 API √ × γ’, su α Houlsby & Byrne √ √ γ’, su1, su1, st αi, αo, Nc DNV √ √ γ’, savu,D, savu,tip, st α, Nc 表 3 滨海土物性指标及力学参数
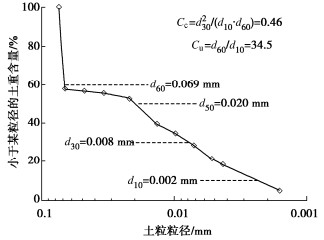
Table 3 Physical parameters and mechanical parameter of coastal clay
土质 数值 土粒相对质量密度Gs 2.73 液限wL/% 64.00 塑限wp/% 27.76 塑性指数Ip 36.24 饱和密度ρsat/(g·cm-3) 1.68 含水率w /% 52.62 孔隙比e 1.39 注:取76 g锥入土深度为10 mm所对应的含水率为液限。 表 4 试验方案
Table 4 Test design
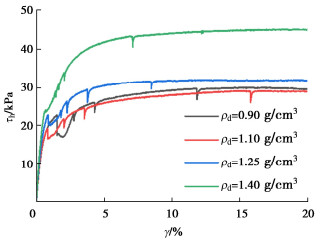
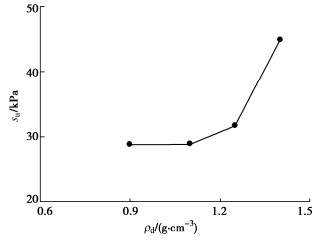
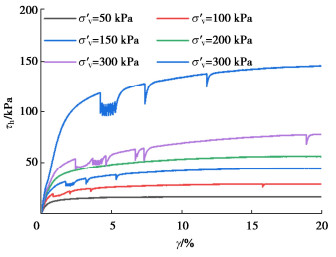
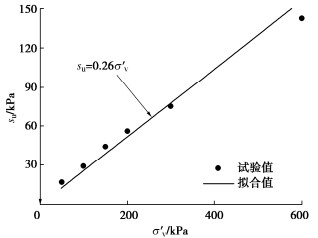
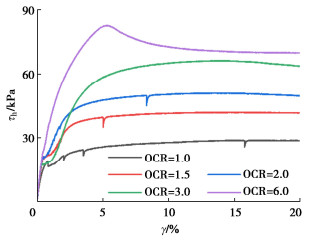
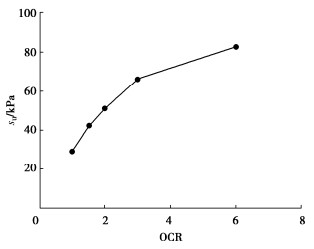
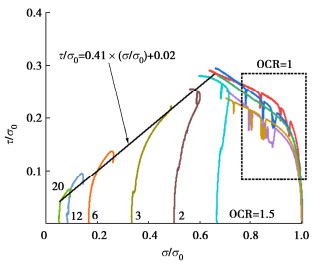
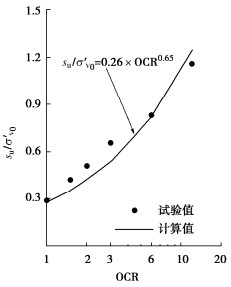
ρd/(g·cm-3) σ′v /kPa OCR 0.90 100 1 1.25 100 — 1.10 50,100,150,200,300,600 1 1.40 100 — 1.10 100 1.5,2,3,6 1.10 50 12 -
[1] MENG X C, YANG X, LIANG C, et al. Research on the calculation method of penetration resistance of bucket foundation for offshore wind turbines[J]. Marine Structures, 2023, 91: 103474. doi: 10.1016/j.marstruc.2023.103474
[2] American Petroleum Institute. PR-2GEO Geotechnical and Foundation Design Considerations[S]. 2014.
[3] Det Norske Veritas. DNVGL-RP-E303 Geotechnical Design and Installation of Suction Anchors in Clay[S]. 2017.
[4] International Organization for Standardization. ISO/DIS 19901-4 Geotechnical Design Considerations[S]. 2022.
[5] LADD C C. Stability evaluation during staged construction[J]. Journal of Geotechnical Engineering, 1991, 117(4): 540-615.
[6] 李作勤. 扭转三轴试验综述[J]. 岩土力学, 1994, 15(1): 80-93. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX401.013.htm LI Zuoqin. Summary of torsional triaxial test[J]. Rock and Soil Mechanics, 1994, 15(1): 80-93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX401.013.htm
[7] HANZAWA H, NUTT N, LUNNE T, et al. A comparative study between the NGI direct simple shear apparatus and the mikasa direct shear apparatus[J]. Soils and Foundations, 2007, 47(1): 47-58. doi: 10.3208/sandf.47.47
[8] HOULSBY G T, BYRNE B W. Design procedures for installation of suction caissons in clay and other materials[J]. Geotechnical Engineering, 2005, 158(2): 75-82.
[9] MAYNE P W. Piezocone profiling of clays for maritime site investigations[C]//Proceedings of the Proceedings of the 11th Baltic Sea Geotechnical Conference, Gdansk, 2008.
[10] MAYNE P W. Stress anisotropy effects on clay strength[J]. Journal of Geotechnical Engineering, 1985, 111(3): 356-366.




 下载:
下载: