0.   引言

土体是非均匀介质，其固相颗粒从黏粒到块石的尺度变化范围很大，且形状和接触关系复杂，其强度与变形特性与土体内部的微细观结构有密切关系，其破坏表现为形成明显的应变局部化区域，即剪切带。无论是传统的土力学理论，还是现代的试验和模拟方法^[1]，在解释土体多尺度力学特性及变形物理机制方面均有待深入研究。考虑土体的尺度效应，可以更准确地理解其散体特性，为工程设计提供可靠的力学参数，对预测土体变形和破坏过程具有重要理论意义。

房营光等^[2]提出具有多尺度理论框架的基体-加强颗粒模型，深入研究土体强度特性的尺度效应现象。Shi等^[3]研究了剪切过程中颗粒压碎，探讨了潜在的宏观-微观联系。Hu等^[4]使用代表体积单元（RVE）的响应对冲刷和非冲刷试样的宏观剪切响应进行了基准测试。Luo等^[5]计算不同应力水平下的峰前输入应变能、弹性应变能和耗散应变能。Dong等^[6]将地质材料各向异性与应力的大小和方向联系，考虑主应力影响给出各向异性强度的一般描述。Tang等^[7]实现并研究一种依赖于等效塑性应变的内部特征长度演化关系。

本文基于系列土工试验结果，探讨土体介质基于有效应力的强度与变形的颗粒尺度效应规律。首先以不同尺度的石英砂作为加强颗粒，进行三轴压缩试验研究，验证土体的尺度效应，以土体胞元模型理论为基础求得不同尺度加强颗粒内禀尺度；其次，通过数值模拟的方法对土体破坏过程及强度进行计算与试验对比验证；最后，引入宏观参数平均能量释放系数来描述土体宏观的能量转换情况。为量化土体尺寸效应及代表性单元确定提供理论和实践参考。

1.   土体内禀尺度

参考土体胞元模型^[8]，将粒径小于0.075 mm的颗粒作为基体，大于0.075 mm的颗粒作为加强颗粒，假设基体材料形成均匀连续的介质，则不同大小的加强颗粒可视为球体均布在基体中，与水结合构成土体骨架的细观单元——土体胞元。在三维应力状态条件下，剪切带上流动剪应力可表示为

式中，$\varphi$为土体的内摩擦角。

通过应变梯度理论来描述土体胞元内部因加强颗粒与其邻近基体变形性状差异引起的细观性状畸变。土体胞元的应变梯度可由应变的一阶差分近似表示，即

式中：${\eta _{\text{k}}}$为对应加强颗粒粒径为${D_{\text{k}}}$的土体胞元的应变梯度；${A_{{\text{sce}}}}$为土体胞元的面积，${A_{{\text{sce}}}} = {L^2}$；${A_D}$为加强颗粒的面积，${A_D} = {\text{π }}D_{\text{k}}^2/4$。

假设在复杂应力状态下，屈服应力可以表示为：

式中：${l_{\text{e}}}$为内禀尺度；${\sigma _{\text{s}}}$为含有加强颗粒试件的屈服应力；${\sigma _{{\text{ref}}}}$为基体试件的屈服应力；$f(\varepsilon )$为基体试件应变函数。

由式（3），（4）可知，只需基体材料的应力-应变关系以及加强颗粒的粒径、级配和体分比，则可计算出包含加强颗粒的土体的内禀尺度。

2.   三轴试验研究

2.1   试验方案

采用TAW-2000微机控制三轴试验机开展三轴压缩试验，以3 mm/min的加载速率施加轴向荷载直至试样破坏。基体颗粒材料采用钠基膨润土，加强颗粒材料为商用石英砂。以相似级配的原则对加强颗粒进行配比，其中加强颗粒粒径分为5组，分别为0.1~0.2 mm、0.4~0.8 mm、1~2 mm、2~4 mm、5~10 mm。制样过程参照土工试验方法标准（GB_T50123—2019)，试样为50 mm⊆100 mm的圆柱体，围压条件分别为0，0.1，0.5，1 MPa。

2.2   试验结果

本组试验有效试样共20个，破坏模式中剪切带为单一型5个、X型3个、平行型3个、V型3个，鼓胀型2个，其他型4个。

根据理论公式（4）以及试验结果，可以求得内禀尺度如表 1所示，从屈服强度结果可见含有石英砂加强颗粒的土体强度均大于基体的强度，说明掺入的石英砂对膨润土基质有加强作用；石英砂粒径越小，对膨润土基质的强化作用越大。内禀尺度与最大粒径呈正相关趋势，而内禀尺度与试样最大粒径之比随加强颗粒尺度增大而减小。

表  1  内禀尺度计算及参数

Table  1.  Intrinsic scale calculation and parameters

围压/kPa	加强粒径/mm	基体强度/MPa	屈服强度/MPa	内禀尺度/mm	内禀尺度与粒径比
100	0.1~0.2	1.54	4.58	16.81	84.05
	0.4~0.8		2.73	18.36	22.95
	1.0~2.0		2.35	28.45	14.23
	2.0~4.0		2.18	43.08	10.77
	5.0~10		1.88	52.20	5.20
500	0.1~0.2	2.18	6.08	14.52	72.60
	0.4~0.8		4.24	23.84	29.80
	1.0~2.0		3.88	46.42	23.21
	2.0~4.0		3.21	50.36	12.59
	5.0~10		3.21	125.61	12.50
1000	0.1~0.2	2.91	6.81	9.59	6.99
	0.4~0.8		4.82	14.94	18.68
	1.0~2.0		4.78	36.36	18.18
	2.0~4.0		4.72	69.99	17.49
	5.0~10		4.68	170.59	17.10

下载: 导出CSV 

| 显示表格

3.   数值模拟研究

模拟试样的尺寸为50 mm×100 mm，单元尺寸为粒径的1/3~1/2，最小为0.05 mm，类型为CEP4R，应力加载，端部约束，计算参数依据试验结果，本构模型分别使用摩尔-库伦（M-C）和塑性损伤模型（CDP）。

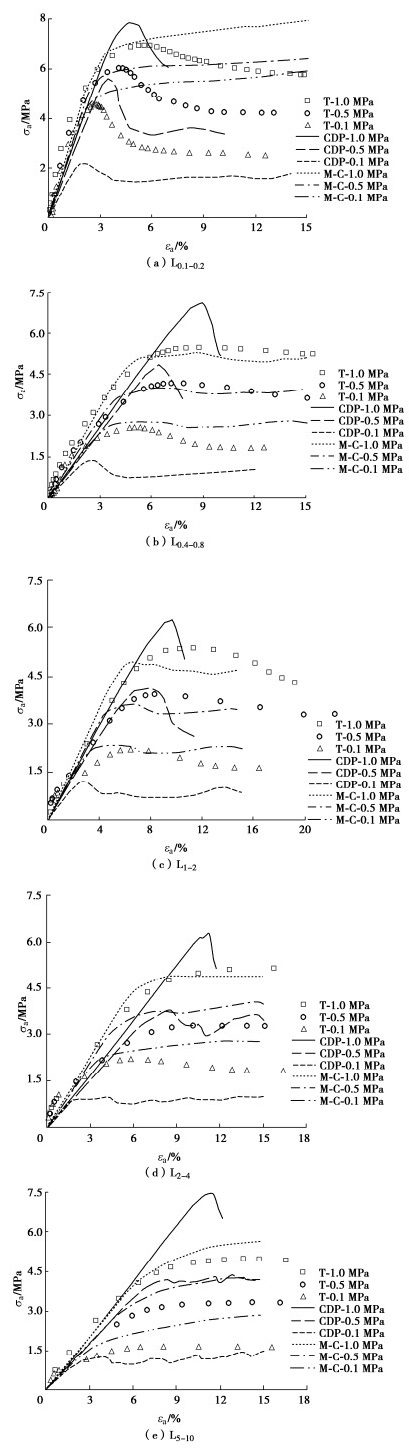
多尺度试验的模拟与试验结果对比如图 1所示，图例中T表示试验结果，不同模型计算与试验结果基本吻合。从不同尺寸加强颗粒试验的应力应变曲线结果可见均表现出明显压硬性，且同一围压条件下应力峰值随加强颗粒粒径增大而减小。加强颗粒粒径0.1~0.2 mm的CDP模型计算优于M-C模型，随着粒径增大，M-C模型与试验吻合更好。

图  1  数值模拟与试验竖向应力-竖向应变曲线对比

Figure  1.  Comparison of vertical stress-vertical strain curves between numerical simulations and tests

下载: 全尺寸图片 幻灯片

数值模拟及试验破坏模式如图 2所示，剪切带的形成和发展是土体剪胀特性、孔隙水在土体内的移动、边界约束的联合作用，通过试验和数值模拟可见，端部约束为主导的情况下倾向于形成两条剪切带，端部约束相对较弱的情况下倾向于形成一条，如图 2（a）所示；图 2（b）和（c）形成了非对称的双带，一条主导剪切带，另一条与主导剪切带平行或者相交的次要剪切带；图 2（d）的破坏模式为V型，是没有形成试样内部上下贯通的一种局部剪切带模式。

图  2  试样破坏模式

Figure  2.  Damage modes of samples

下载: 全尺寸图片 幻灯片

4.   剪切带形成机理讨论

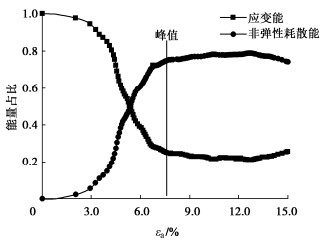
图 3为应变能及非弹性耗散能占土体总体能量的比例。第一阶段为弹性压缩阶段，非弹性耗散能基本为0，即外力做的功全部转化为应变能，在细观层中胞元的基体仅发生弹性压缩；第二阶段，应变到达1.6%后，非弹性耗散能开始增长，应变能占比开始下降，说明土体发生塑性变形，剪切带开始形成，细观层面中胞元中的协调微裂纹开始产生不可逆的扩张；第三阶段，应变到达7.3%后，应变能、非弹性耗散能占比趋于稳定，随着应变增加会产生更多协调微裂纹及均匀微裂纹，进而形成宏观层面的完整剪切带。

图  3  能量与占比曲线

Figure  3.  Curves of energy and percentage

下载: 全尺寸图片 幻灯片

基体与加强颗粒交界处存在原生协调微裂纹。加强颗粒的弹性模量比基体大，压缩过程中加强颗粒周围易产生应力集中现象，胞元内基体和加强颗粒交界面发生变形的不均匀导致产生应变梯度，直至塑性变形区域扩张。加强颗粒较为集中的区域交界面较多，密集的原生协调微裂纹更易吸收能量而进一步扩展，若干相邻土体胞元即产生连续的塑性变形。

土体变形过程中涉及土颗粒的黏聚、碰撞、摩擦等与能量释放和耗散相关的微细观变形和运动细节，即：

式中：U为产生单位表面积微裂纹脆性固体释放的应变能；$\xi$为产生单位表面积微裂纹土体释放的能量；S为剪应力达到剪切流动应力时裂纹密度；$\tau _{\text{s}}^{}$为土体的流动剪应力；$\beta$为能量释放系数，a为非线性系数。

从宏观层面引入平均应变能释放系数，该系数表征试样在到达峰值应力之后试样整体的应变能转化情况，如式（6）所示。在试样整体能量到达峰值之后所释放的能量占峰值应变能的比例，如式（7）所示。

式中：$\kappa$为围压影响系数，$\kappa = 26.21 + 19.14\sigma \chi$；$\overline {{\eta _0}} = 44.81 + 7.48\sigma \chi - 4.36{(\sigma \chi )^2}$，其中$\overline {{\eta _0}}$为初始释放系数，$\chi$=26.21+19.14$\sigma$，$\chi$取为1 kPa^-1，t为粒径影响系数，一般取1~4 mm^-1之间；${\sigma _c}$为残余应力；${\sigma _{\max }}$为应力峰值。

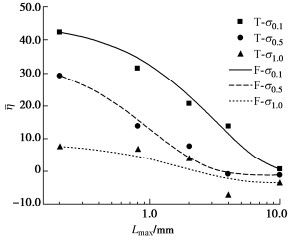
平均应变能系数计算结果如图 4所示，F表示计算结果，T表示试验结果，两者相符。随着加强颗粒粒径和围压的增大，计算得到的值呈现减小趋势，值越小表示软化效果越明显，为负值时，应力应变曲线为硬化型。其原因是加强颗粒较小时，接触面的协调微裂纹较多，土体进入塑性应变时，较多的协调微裂纹扩张，从而在加载过程中引发更多的局部破坏，释放能量大于吸收能量，试样整体表现为释放能量，所以其强度曲线表现为软化。在较高的围压条件下，各处主应力均增加，导致接触面上的协调微裂纹被压缩减小，土体具有更强的储存弹性应变能力，不容易发生较多的局部破坏。在这种情况下，土体吸收大于释放的能量，使得试样整体呈现为吸收外界能量的状态，所以强度曲线更倾向于硬化型。

图  4  计算结果与试验结果对比

Figure  4.  Comparison between calculated and test results

下载: 全尺寸图片 幻灯片

5.   结论

本文针对土体内部特征参数对宏观变形和强度的影响，开展了基于胞元模型思想的系列试验，主要得到以下3点结论：

（1）不同尺度加强颗粒试样的三轴试验破坏模式出现了单一型、“X”型、“V”型、平行型等多种剪切带模式，并在数值模拟中得到验证。不同尺寸的加强颗粒试验说明土体具有尺寸效应，土体强度与粒径呈现反比趋势；在加强颗粒粒径较小时，土体表现为应变软化，且粒径越小软化效果越明显；与数值模拟结论一致。通过胞元模型理论计算出内禀尺度与土体最大粒径呈现正相关。

（2）从能量角度验证了剪切带的竞争过程。土体剪切带的形成是一个渐进的过程，弹性压缩阶段，外力做的功全部转化为应变能；在到达应力峰值点之前非弹性耗散能开始增长，土体发生塑性变形，扩展成应变局部化区域，在土体达到应力峰值之前，多条局部化区域启动，竞争过程产生应力峰值，过峰值后主导形式确定，宏观剪切带形成并贯通。

（3）在胞元模型理论的基础上从宏观层面引入平均应变能释放系数，该系数表征试样在到达峰值应力之后试样整体的应变能转化情况，经试验验证合理。