Centrifugal model tests on influences of anchor dropping on offshore pipelines
-
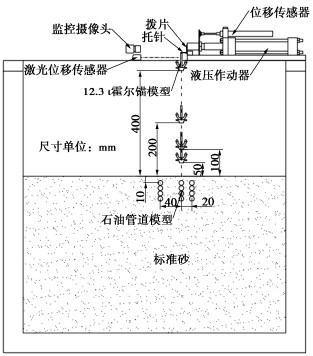
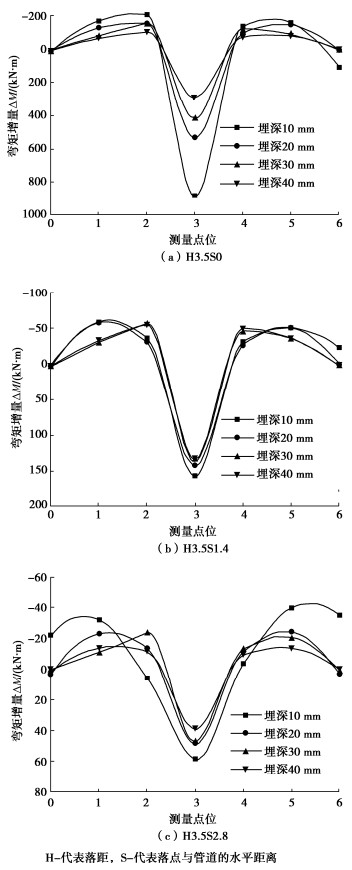
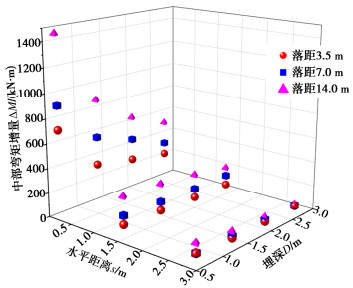
摘要: 锚击是影响海底管道安全运营的重要因素之一。采用天科院TK-C500土工离心机以及新开发的抛锚试验装置开展了抛锚离心模型试验，测量了海底管道的受力变化，分析了抛锚作业对浅埋海底管道的影响。试验结果表明，落距对管道弯矩的变化有着普遍性的影响，管道弯矩增量与落点的水平距离和管道埋深呈现明显的非线性特征。当12.3 t霍尔锚落在ϕ630管道正上方时，各种不同落距各种不同管道埋深工况，管道弯矩增量都远大于其塑性屈服弯矩，管道的安全运行已经受到了严重威胁。当落距小于3.5 m、水平距离大于1.4 m时和当落距增大到7 m、水平距离大于2.8 m时，管道弯矩增量不会超过塑性屈服弯矩；随着落距继续增大，锚落于管道一定范围内时，都将对管道安全运行产生严重威胁。Abstract: Anchoring is one of the important factors affecting the safe operation of submarine pipelines. The centrifugal model tests are carried out by using the TK-C500 geotechnical centrifuge and the newly developed anchor dropping test devices. The force changes of the submarine pipelines are measured, and the influences of the anchor dropping operation on the shallowly buried submarine pipelines are analyzed. The test results show that the dropping distance has a universal influence on the change of the bending moment of the pipelines, and the increment of the bending moment of the pipelines has obvious nonlinear characteristics with the horizontal distance of the dropping point and the buried depth of the pipelines. When the Hall anchor of 12.3 t falls directly above the pipelines with ϕ630, the bending moment increment of the pipelines is much larger than its plastic yield bending moment regardless of the different dropping distance or the buried depth of the pipelines, and the safe operation of the pipelines is seriously threatened. When the dropping distance is less than 3.5 m and the horizontal distance is greater than 1.4 m, and the dropping distance increases to 7 m and the horizontal distance is greater than 2.8 m, the increment of bending moment of the pipelines will not exceed the plastic yield bending moment. As the dropping distance continues to increase, when the anchor falls within a certain range of the pipelines, it will pose a serious threat to the safe operation of the pipelines.
-
0. 引言
钙质砂是一种分布于热带海洋的特殊岩土介质，由于其成因和组构上的特殊性导致其工程力学性质与普通的陆源砂有明显区别。目前国内外针对钙质砂地基应力变化及破坏模式等研究很少，其工程特征及地基性能尚无明确统一的说法，这给基础设施的设计、施工建设带来很大的困难，因此需要研究钙质砂类岩土的应力特性和承载机理。
钙质砂的应力特性，国内外已作了一些研究。文哲等[1]采用中国南沙某岛礁吹填珊瑚钙质砂，在级配和组分分析的基础上，研究不同密实度、含水率条件下轴向荷载钙质砂的剪切力学特性。王刚等[2]进行钙质砂不破碎三轴剪切过程的数值试验，以确定临界状态与固定级配的对应关系。相盈盈[3]采用三轴固结不排水剪切试验，对南海海区岛礁饱和钙质砂进行剪切特性分析。张季如等[4]为了研究不同应力路径对钙质砂的颗粒破碎和力学性质的影响，对不同固结压力的钙质砂进行了5种应力路径下的排水三轴压缩试验。Lade等[5]针对珊瑚砂的时间变量开展了三轴压缩试验，提出了应力下降原因。Yamamuro等[6]开展了钙质砂三轴排水试验，考虑了不同的围压状态和相对密实度，抗剪强度与轴向应变的变化规律。其他学者[7-9]对钙质砂的工程承载特性进行了部分研究。
由以上研究可以发现，针对钙质珊瑚砂的力学工程特性性质已经已有一定基础，与其他砂类试验对比分析，结果显示钙质砂是一种天然特殊砂，钙质砂在高压条件下发生颗粒破碎，其破碎性质也会引起钙质砂的力学性质发生改变，其性质与普通砂存在很大差异，工程中不能使用普通砂的成果分析。目前有关三轴试验剪切速率的影响因素相关研究较少，本文在不同围压下采用不同剪切速率对高低围压下钙质砂进行三轴固结排水试验，分析围压、剪切速率对钙质砂应力影响分析。
1. 三轴排水剪切试验
1.1 试验材料
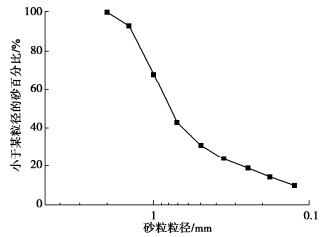
试验采用的试样取自中国海南省三沙市西沙群岛，试样中存在大块的砂砾和尖锐的贝壳，见图 1，为避免戳破橡胶膜影响试验，对原试样进行烘干、筛分、按一定比例进行配比后使用见图 2，试验筛除大于2 mm颗粒的钙质砂，将钙质砂分为9个粒径范围，不同粒径含量见表 1。颗粒级配见图 3，试验用钙质砂基本物理参数见表 2。
表 1 试样粒径范围Table 1. Grain-size ranges of sample粒径/mm 1.45~2 1~1.45 0.71~1 0.5~0.71 0.355~0.5 百分比/% 7 25 25 12 7 粒径/mm 0.25~0.355 0.18~0.25 0.125~0.18 0.075~0.125 百分比/% 5 4.5 4.5 10 表 2 试样基本物理参数Table 2. Basic physical parameters of sampleGS emax emin D60/mm D30/mm D10/mm 2.80 0.58 1.07 0.9 0.49 0.125 1.2 试验仪器
试验采用英国GDS公司生产的自动三轴试验系统GDSTAS完成（图 4）。应变控制速率从0.00001~9.99999 mm/min。压力室最大承受压力为3.5 MPa，2 MPa孔隙水压力传感器精度为全量程的0.15%，内置水下荷重传感器精度为全量程的0.1%。3 MPa/ 200 mm3标准围压/体积控制器（围压控制），具有自动压力和体积溢出保护，测量精度为量测值的0.25%，压力精度为全量程的0.1%，体积变化测量和显示分辨率为1 mm3。3 MPa/200 mm3标准反压/体积控制器（反压控制），具有自动压力和体积溢出保护，测量精度为量测值的0.25%，压力精度为全量程的0.1%，体积变化测量和显示分辨率为1 mm3。
1.3 试验方案
试验方案如表 3所示。试验为三轴固结排水试验，试样相对密实度为70%，有效围压为300，600 kPa。剪切应变速率分别为0.15%，0.035%，0.0045%/min，研究钙质砂在不同围压、不同剪切速率下的应力变化特性。试样直径为50 mm，高度100 mm。
表 3 试验方案Table 3. Test schemes相对密实度Dr 有效围压/kPa 剪切应变速率/(%·min-1) 0.70 300，600 0.0045，0.035，0.15 试验采用干法制样，将配比好的试样按一定质量分层装入模具，因钙质砂的特性导致内部空隙较多，试验中利用CO2、水头饱和、反压饱和相结合的方法对试样进行饱和，提高试样的饱和度。首先从试样底部缓慢通入CO2，从试样顶部排出，通气时间为2 h，此过程置换试样内部的空气。然后水头饱和，从试样底部缓慢进水，从试样顶部排水，控制水流速度，时间为2 h，此过程置换试样中的CO2。最后进行反压分级饱和，并监测试样饱和度，直到饱和度大于95%。接下来进行试样固结，实时监测孔隙水压力变化，直到孔隙水压力消散，有效围压达到预定值。按照设定的剪切速率进行三轴排水试验，轴向位移达到20%试验停止。
2. 结果分析
2.1 围压与剪切速率对偏应力影响
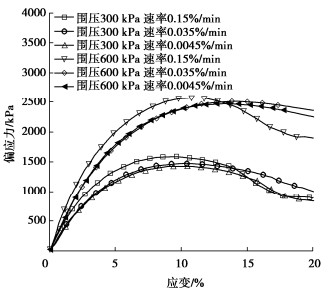
不同围压下各剪切速率的偏应力应变曲线，见图 5。偏应力曲线趋势相同，剪切初期偏应力上升较快，当应变超过5%时偏应力增长变缓，低围压下应变达到10%左右时偏应力出现峰值，高围压下应变达到12%左右时偏应力出现峰值，随后偏应力开始下降，高围压偏应力峰值出现的较晚。
不同围压下剪切速率对峰值的影响规律相同，偏应力峰值随剪切速率的增大而增大，剪切速率越快应力峰值越大，应力下降也越快应力下降比越大，可见剪切速率对应力的峰值大小及残余剪切强度有一定影响。低围压下不同剪切速率最大偏应力峰值差比为11%，且在低围压约束力下剪切速率减小时试样颗粒发生重组后再剪切，因此速率0.035%，0.0045%/min的偏应力峰值软化后又会出现硬化趋势；高围压下不同剪切速率最大偏应力峰值差比为4%，可见低围压下剪切速率对偏应力峰值影响更大。这与福建标准砂的性质不同，周杰[10]对不同应力下福建标准砂进行5种剪切速率试验，表明在低应力下砂的抗剪强度与剪切速率基本无关，高围压下，砂的抗剪强度随剪切速度增大而减小。
2.2 围压与剪切速率对偏应力比影响
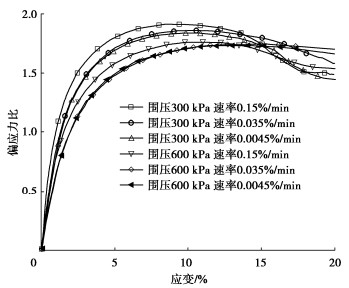
不同围压下各剪切速率的偏应力比曲线，见图 6。偏应力比曲线趋势相同先增大后减小趋于稳定。围压越小偏应力比上升越快、偏应力比越大，可见低围压下的剪切效果更明显，偏应力和峰值的变化情况相对于平均有效应力的变化更大，因为围压越低对颗粒束缚较小，钙质砂的越容易发生错动导致偏应力上升。应力应变分析中低围压下剪切速率越小时偏应力出现峰值然后减小有又硬化的趋势，因此在低围压下剪切速率越小偏应力比峰值后减小有又上升趋势。
相同围压下剪切速率越大，偏应力增长越快、偏应力比越大，剪切时砂粒之间重组排列，高剪切速度使得砂粒之间迅速咬合偏应力快速上升导致试样破坏，钙质砂的结构特征使得对剪切速率更加敏感。但是相对于0.15%/min的剪切速度，0.035%/min和0.0045%/min的速度偏应力比的变化几乎相同，可见当剪切速率低于一定速率时，偏应力比的变化并不受剪切速度的影响。
2.3 围压与剪切速率对应力路径影响
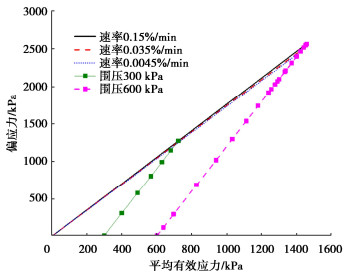
固结排水试验的偏应力-平均有效应力曲线，见图 7。不同围压条件下，偏应力-平均有效应力关系曲线都是斜率为3的直线，是因为剪切时排水条件使得孔压保持稳定值不变，且围压为一定值，根据平均有效应力为p′=[2(σ3−μ)+(σ1−μ)]/3，σ3为围压，σ1为轴向应力，μ为孔隙水压力，经计算相邻点有效应力变化为p′=（σ11−σ12）/3，即为轴向应力差除以3，相邻点偏应力为q′=σ11−σ12，即为轴向应力差，所以曲线斜率为q′/p′=3。
不同剪切速率下的破坏线q′=Mp′趋势相同，由应力应变分析可以看出偏应力峰值随剪切速率的增大而增大，破坏线是关系偏应力峰值与圆点的连线，可见剪切速率越大破坏线角度越大，三条线的M值近似为1.75，由公式φ=arcsin（3M/(6+M)）=42°，钙质砂的内摩擦角近似为42°。这由钙质砂的结构特性决定，钙质砂形状不规则且尖锐，颗粒之间咬合错动，剪切破坏角较大，内摩擦角较大。
2.4 围压与剪切速率对孔隙比影响
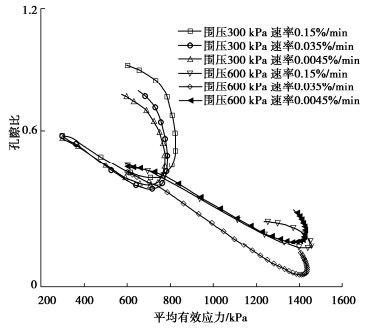
不同围压及剪切速率条件下，孔隙比-平均有效应力关系曲线，见图 8。偏应力峰值以前平均有效应力逐渐增大，偏应力峰值以后平均有效应力逐渐变小，且偏应力峰值以前不同围压下孔隙比相对于平均有效应力的下降速率相近呈线性变化，可见孔隙比与平均有效应力的变化趋势在剪切初始阶段不受剪切速率的变化影响。偏应力峰值以后孔隙比相对于平均有效应力变化呈曲线增大状态。
剪切过程中试样体积先减小后增大，孔隙比表现为先减小后增大，拐点发生在偏应力峰值的前后，剪切过程表现为密砂的特征。不同围压孔隙比下降速率相近，低围压剪缩阶段剪切速率对孔隙比的影响不明显，剪缩阶段颗粒之间位置调整砂粒发生相互错动重新排列压实，试样体积减小，孔隙比减小。剪胀阶段剪切速率对孔隙比的影响较大，剪切速率越大，孔隙比增大越快，随着剪切阶段颗粒间的作用力逐渐小于颗粒的抗剪强度试样破坏，尖利不规则的砂粒重新组合排列试样体积增大，孔隙比增大。
3. 结论
本文开展了钙质砂三轴排水剪切试验速率对应力特性影响研究，分析不同围压、不同剪切速率状态下钙质砂剪切过程中应力的变化规律，得出以下4点结论。
（1）偏应力应变曲线趋势相同，偏应力曲线均出现峰值，高围压偏应力峰值出现比低围压偏应力峰值出现的晚。剪切速率越快，偏应力峰值越大，偏应力下降越快，剪切速率对偏应力峰值大小及残余剪切强度有一定影响，低围压下剪切速率对偏应力峰值影响更大。
（2）偏应力比应变曲线趋势相同先增大后减小趋于稳定。围压越小偏应力比上升越快，偏应力比越大，相同围压下剪切速率越大，偏应力比增长越快偏应力比越大。当剪切速率低于一定速度时，偏应力比的变化并不受剪切速度的影响。
（3）不同围压下偏应力平均有效应力的关系是斜率为3的直线，不同速率下的破坏线趋势相同，偏应力峰值随剪切速率的增大而增大，破坏线是关系偏应力峰值与圆点的连线，因此剪切速率越大破坏线角度越大，破坏线的斜率近似为1.75，钙质砂内摩擦角近似为42°。
（4）偏应力峰值以前平均有效应力逐渐增大，偏应力峰值以后平均有效应力逐渐变小，且偏应力峰值以前不同围压下孔隙比相对于平均有效应力的下降速率相近。低围压剪缩阶段剪切速率对孔隙比下降速率的影响不明显，剪胀阶段剪切速率越大，孔隙比的增长越大。
-
![]()
图 6 落距7.0 m时不同水平距离的管道弯矩变化
Figure 6. Variation of bending moment of pipelines with different horizontal distances under falling distance of 7.0 m
![]()
图 7 不同因素影响的管道中部弯矩增量
Figure 7. Increment of bending moment in middle of pipelines affected by different factors
表 1 模型参量比例常数（模型/原型）
Table 1 Ratios of similitude parameters
参量 比例常数 参量 比例常数 离心加速度 70 应变 1 线性尺度 1∶70 位移 1∶70 应力 1 密度 1 弹性模量 1 抗弯刚度 1∶704 
下载: 导出CSV
表 2 模型管道参数
Table 2 Parameters of model pipelines
类别 外径/mm 壁厚/mm 弹模/GPa 抗弯刚度/
(N·mm-2)原型 630 25 210 4.46×1011 模型 9 1.5 69 1.86×104
下载: 导出CSV
-
[1] 杨秀娟, 修宗祥, 闫相祯, 等. 海底管道受坠物撞击的三维仿真研究[J]. 振动与冲击, 2009, 28(11): 47-50, 69, 202. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200911012.htm YANG Xiujuan, XIU Zongxiang, YAN Xiangzhen, et al. 3D simulation of submarine pipeline impacted by dropped objects[J]. Journal of Vibration and Shock, 2009, 28(11): 47-50, 69, 202. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200911012.htm
[2] PALMER A, TOUHEY M, SI H. Full-scale impact tests on pipelines[J]. International Journal of Impact Engineering, 2006, 32(8): 1267-1283. doi: 10.1016/j.ijimpeng.2004.09.003
[3] 雷震名, 谭红莹, 龚海潮, 等. 基于能量法的跨航道海底管线抗落锚实验研究[J]. 水道港口, 2015, 36(3): 272-276. https://www.cnki.com.cn/Article/CJFDTOTAL-SDGK201503024.htm LEI Zhenming, TAN Hongying, GONG Haichao, et al. Energy method-based experimental research on crossing sub-sea pipeline protection by rockfill against anchors[J]. Journal of Waterway and Harbor, 2015, 36(3): 272-276. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDGK201503024.htm
[4] 孙翠梅, 李效民, 郭海燕, 等. 不同水深和铺设条件下海底管道受坠物锚击损伤的研究[J]. 中国造船, 2018, 59(4): 142-151. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201804016.htm SUN Cuimei, LI Xiaomin, GUO Haiyan, et al. Study on damage of submarine pipeline impacted by dropped objects under different water depth and laying conditions[J]. Ship Building of China, 2018, 59(4): 142-151. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201804016.htm
[5] 王振宁. 应急抛锚载荷作用下海底管道埋深数值模拟研究[D]. 武汉: 武汉理工大学, 2016. WANG Zhenning. Numerical Simulation Research of Submarine Pipeline Depth against Emergency Anchor Loading[D]. Wuhan: Wuhan University of Technology, 2016. (in Chinese)
[6] 王彦頔, 任宇晓, 庄道坤, 等. 海床中落锚问题的模型试验和大变形有限元研究[J]. 岩土工程学报, 2020, 42(增刊2): 202-207. doi: 10.11779/CJGE2020S2036 WANG Yandi, REN Yuxiao, ZHUANG Daokun, et al. Study on anchor dropping in seabed based on model tests and large deformation finite element method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(S2): 202-207. (in Chinese) doi: 10.11779/CJGE2020S2036
[7] 李建东, 张宇亭, 裴文斌. 土工离心机水平垂直双向振动台[J]. 水道港口, 2020, 41(1): 107-112. https://www.cnki.com.cn/Article/CJFDTOTAL-SDGK202001016.htm LI Jiandong, ZHANG Yuting, PEI Wenbin. Horizontal-vertical bi-axial shaker for geotechnical centrifuge[J]. Journal of waterway and Harbor, 2020, 41(1): 107-112. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDGK202001016.htm
[8] 牛爱军, 毕宗岳, 张高兰. 海底管线用管线钢及钢管的研发与应用[J]. 焊管, 2019, 42(6): 1-6. https://www.cnki.com.cn/Article/CJFDTOTAL-HGZZ201906001.htm NIU Aijun, BI Zongyue, ZHANG Gaolan. Development and application of pipeline steel and steel pipe for offshore pipeline in China[J]. Welded Pipe and Tube, 2019, 42(6): 1-6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HGZZ201906001.htm
[9] ISHIHARA K. Liquefaction and flow failure during earthquakes[J]. Géotechnique, 1993, 43(3): 351-451. doi: 10.1680/geot.1993.43.3.351
[10] JÁKY J. The coefficient of earth pressure at rest[J]. Journal for the Society of Hungarian Architects and Engineers, 1944, 7: 355-358.
[11] 宣凯. 抛锚作业对海底管线损害研究[D]. 大连: 大连海事大学, 2012. XUAN Kai. The Study on Anchoring Damage to Subsea Pipelines[D]. Dalian: Dalian Maritime University, 2012. (in Chinese)
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
