0.   引言

土是天然生成的具有碎散性、多相性等特殊性质的材料，其物理力学性质最为复杂^[1]。尽管人类工程活动从一开始就需考虑地基土的性质，但直到20世纪20年代太沙基《土力学》（Erdbaumechanik）的出版，土力学才成为一门独立的学科。一百年来土力学学科在理论与技术方面均取得很大发展，但其理论体系至今仍有较大发展完善的空间。

改革开放以来，伴随国家社会经济发展及大规模工程建设，中国的土力学及基础工程学科取得举世瞩目的成就，特别是在岩土工程施工技术、施工设备方面突飞猛进，完成了大量世界级的高难度复杂工程。但是，纵观国内外的土力学学科，相对于数值方法、计算技术、施工技术及设备来看，工程设计分析普遍需要的基本理论、方法方面的发展相对非常缓慢。中国土力学及岩土工程领域的研究人员，在国内外发表的论著数量惊人，其中不乏在理论上很有创新的成果，但由于这样或那样的原因，不少新理论、新方法还未能得到行业的较广泛认同。工程设计分析中广泛采用的某些理论方法多年来已被注意到不尽合理；为解决某些复杂工程问题所提出的一些设计计算方法在理论方面存在争议。其中最突出的是基坑工程中几乎所有的规范规程（比如文献[2，3]等）对黏性土不排水计算采用固结不排水指标和土水合算，业内虽有不少讨论，但截至目前尚未形成主流的一致看法。此外，基础工程中地基沉降这一基本问题的计算方法，多年以来一直是采用压缩模量进行计算的分层总和法^[4]，地基承载力的计算一直推崇的是太沙基在20世纪40年代提出的近似计算公式，等等。由于这些基本理论与方法的缺陷，使一些工程问题的计算有较大误差甚至错误，由此导致不少工程技术人员完全不相信土力学的基本理论。

笔者多年研究土力学及岩土工程的计算理论与方法，包括土的弹塑性、渗流、固结、地下结构抗震、多场耦合等多方面^[5-6]，同时注意紧密结合诸如地基基础、复合地基、深基坑、高填方、路基冻胀变形等多方面的工程问题。因此也很关注实际工程问题的设计计算方法。本文着重就笔者近年来一直关注的饱和土不排水计算进行讨论。

本文内容包含以下4个部分：①讨论土体不排水计算的总应力法与有效应力法及各自的局限性，并从有限元基本方程阐述孔隙水压的处理，指出不管采用有限元法还是工程简化计算方法均应注意区分两类孔隙水压和两种总应力。②审视Skempton-Henkel超静水压计算公式对不同应力路径的适用性与计算准确性，进而将该计算式与莫尔库仑强度准则（MC强度准则）相结合构建了一种饱和土不排水强度模型，对等向固结与不等向固结下饱和土不排水强度特性进行了分析，以对实际工程计算中强度参数的选取提供参考；建议对饱和土的不排水计算采用广义Tresca强度准则，并针对采用MC强度准则按有效应力法进行不排水计算会产生较大误差的问题，除指出应直接输入不排水强度外，还给出一种采用等代强度参数的处理方法。③分析固结不排水强度指标（CU强度指标）直接用于土体强度计算的缺陷，指出仅当土中总应力路径与测定CU指标的试验中相同时，用此指标直接计算才能给出准确的结果，特别是对地基承载力问题直接用此指标计算会给出严重偏危险的结果。还对基坑工程中主动、被动土水压力采用CU指标并土水合算的问题进行了分析，建议了合理计算方法及相应公式；对发生不排水极限土压力时的滑移面倾角这一基本理论问题也进行了较深入的探讨。④针对饱和地基承载力及短期沉降计算，剖析业内多年所用方法的问题，在深入解读有关因素影响机理基础上给出新的计算方法，并展示了其应用。最后，结合上述一系列问题的讨论，谈了个人就开展有关工程计算分析理论与方法研究的体会与看法。

1.   饱和土不排水计算的基本方法

当饱和土承受荷载时其孔隙水与土骨架共同作用，孔隙水压大小自然要影响有效应力的大小，从而影响土的强度和变形。根据土的渗透性与加载速率的相对大小，饱和土的计算近似分为排水、不排水和部分排水（固结）3种情况，其中固结计算与不排水计算均涉及水压与土体变形的耦合，较之排水计算更为复杂。本文集中讨论不排水计算的有关问题，讨论中借助不排水计算的有限元基本方程对有关理论进行阐述，以求得出对有限元计算与工程计算均适用的结论。

1.1   要区分两类孔隙水压与两种总应力

设想拟对水位之下的饱和土层进行新加荷载下的计算分析，而在施加荷载前土中已存在稳定的孔隙水压以及与土体有效重度对应的自重有效应力。当施加荷载时，土体发生剪切变形，并有发生体积压缩的趋势。因孔隙中含水饱和，这体积压缩趋势首先使孔隙水压增长，这新增长的孔隙水压称为超静水压，此前的孔隙水压称为静水压或稳态水压。因此，土中任一点的总应力应写为^[6-7]

其中向量$\{ \boldsymbol{m}\}$中与正应变对应的元素为1，其余为0。式（1）将有效应力原理中的孔隙水压明确写为稳态水压${p_{{\text{st}}}}$与超静水压${p_{{\text{ex}}}}$两部分。${p_{{\text{st}}}}$是与静水位或不排水加载前已存在的稳态渗流对应的水压，在施加荷载之前即可由水位或稳态渗流进行计算；而孔隙超静水压与有效应力则需考虑土的变形性质进行计算。在计算拟加荷载引起变形的有限元计算中，将式（1）表示的总应力代入有限元平衡方程，有

随后，因为稳态水压已知，故应移到方程右侧，得

此时式（3）的右端项由此前土的饱和重度与地面水压及其他荷载计算的等效节点力，变成由土的有效重度及其他荷载计算的等效节点力，当有渗流时还有渗透力对应的等效节点力。可以理解，事先给定的水位高低，亦即稳态水压的大小，不会改变式（3）的右端项，因水位的高低并不影响任一土颗粒上下、左右的水压之差。不管水位是在地面还是高出地面上千米，式（3）的右端是相同的，亦即计算给出的有效应力与超静水压之和将是相同的。受静水压影响的变形已经发生，拟计算的变形与静水压大小无关。

由上可见包含孔隙水压的总应力也有两种：①包含全部孔隙水压的总应力；②仅包含超静水压的总应力。由于两类孔隙水压的性质及计算方法不同，两种总应力显然也有必要予以区分，笔者分别称它们为平衡总应力与本构总应力^[8]。包含全部孔隙水压的平衡总应力如式（1）所示，是与全部外荷载平衡的总应力，而本构总应力为有效应力与超静水压之和，即

其中的有效应力和超静水压的计算均需用到土和水的应力应变关系，即本构模型。平衡总应力和本构总应力的引入应有助于明晰有关概念。

当对饱和土进行不排水条件下的计算时，如采用总应力法直接求解的总应力是本构总应力，求解中所用总应力强度指标对应的总应力也是本构总应力。

如将总应力法直接用于求解平衡总应力，即

也就是要将饱和土的总应力-应变关系，包括强度准则，用于平衡总应力$\{ {\sigma _{\text{e}}}\}$进行“土水合算”，则会得出与式（3）矛盾的错误结果。特别是当把饱和土的强度准则用于平衡总应力，则相当于如下计算土的抗剪强度：

当总应力对应的强度指标$\varphi$大于零，则水位高低直接影响土的强度，对处于深水之下的土将给出严重夸大的强度，显然是错误。

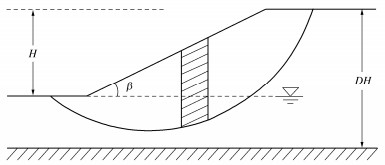
上述原理虽是利用有限元方程阐释的，但其本质是平衡与本构，具有普遍适用性，对饱和土的其他任何计算方法都是成立的。比如，当采用条分法对图 1所示黏性土坡进行稳定分析时，对于水下滑移面的抗剪强度计算，必须从土条总重对滑移面的法向压力中扣除静水压，再利用总应力强度指标计算抗滑力。计算水位下的地基承载力时，必须用地基土的有效重度是同样的道理。

图  1  有地下水影响的边坡稳定问题

Figure  1.  Slope stability under influences of groundwater

下载: 全尺寸图片 幻灯片

1.2   不排水计算的有效应力法与总应力法

（1）有效应力法

根据太沙基有效应力原理，土的强度和变形直接决定于有效应力。所以较准确的分析应该分别计算出有效应力和超静水压，亦即采用有效应力法。为计算超静水压自然须考虑孔隙水的压缩性。

对于饱和土，当忽略土颗粒的压缩性而仅考虑孔隙水的压缩性时，土体积的压缩近似等于孔隙水的压缩，由此可得到孔隙超静水压的计算式^{[6, 9]}：

式中：K_f为水的体积变形模量，其数值一般比土骨架的体积模量大得多；n为土的孔隙率；$\{ \boldsymbol{\varepsilon} \}$与${\varepsilon} _{\text{v}}$分别为土的应变向量和体积应变；向量$\{ \boldsymbol{m}\}$中与正应变对应的元素为1，其余为0。这样，本构总应力为

其中

将式（8）代入式（3），并利用有限元的节点位移$\{\hat{\boldsymbol{u}}\}$表达应变$\{\boldsymbol{\varepsilon}\}$则有

亦即只需把与水的刚度[D_f]加入到原来的弹性矩阵[D]，即可实现饱和土的有效应力的计算。由式（10）求出有限元的节点位移后，再由几何方程求应变，由土的本构模型计算有效应力，由式（7）计算超静水压。当考虑土的弹塑性时，则需用弹塑性矩阵[D_ep]代替[D]并分步加载迭代求解

其中，

这里对土的弹性或弹塑性矩阵加入水的刚度，实际只是大幅度提高了饱和土在不排水条件下的体积变形模量，而未改变其剪切模量。由此可计算出饱和土不排水条件下的等效泊松比为一个很接近0.5的值。

上述计算中K_f的取值不可过大，否则整体刚度矩阵的数值性态劣化，使计算困难。一般可取K_f为土的体积变形模量K的1000倍。这样，尽管K_f的取值较实际值可能偏小很多，使计算的体积应变偏大，但这偏大的体积应变相对于剪切应变仍可忽略，所计算的结构变形仍有足够的精度。同时，由式（7）可见，此时计算的超静水压及相应的有效应力仍误差不大^[5-6]。

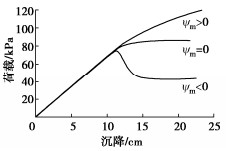
因总体积应变${\text{d}}{\varepsilon _{\text{v}}}$为弹性体积应变${\text{d}}\varepsilon _{\text{v}}^{\text{e}}$与塑性体积应变${\text{d}}\varepsilon _{\text{v}}^{\text{p}}$之和，而饱和土不排水条件下的总体积应变${\text{d}}{\varepsilon _{\text{v}}} \approx {\text{0}}$，所以有${\text{d}}\varepsilon _{\text{v}}^{\text{e}} \approx - {\text{d}}\varepsilon _{\text{v}}^{\text{p}}$。如土体无塑性体积变化，亦即无剪胀剪缩变形，则弹性体积应变为零，亦即有效正应力的均值不变；如发生塑性体积压缩，则有效正应力均值减小，超静水压增大，土的抗剪强度降低；反之，则有效正应力均值增大，超静水压减小，土的抗剪强度增大。亦即，如土的剪胀角大于零，则不排水条件下的土工结构将呈现硬化的性质，反之则软化^[5]（图 2）。

图  2  不同剪胀角计算的地基荷载沉降曲线^[5]

Figure  2.  Load-displacement curves calculated under different dilation angles

下载: 全尺寸图片 幻灯片

如上进行饱和土不排水条件下的计算，对于弹性问题其计算的准确性可以保证。但对弹塑性问题，则需采用能够很好计算土的剪胀或剪缩过程的本构模型。否则，体积应变的微小误差会引起超静水压和有效应力的较大误差，从而给出错误的变形和强度。但到目前还很少有本构模型能够很好计算土体剪胀的过程。以岩土有限元软件Plaxis^[10]中业内公认能较好计算土的强度和变形的硬化土模型来说，其中的剪胀角基本按Rowe公式计算^[11]：

式中：${\psi _{\text{m}}}$为与机动摩擦角${\varphi _{\text{m}}}$对应的机动剪胀角；${\varphi _{\text{f}}}$为土颗粒材料固有的摩擦角。研究表明土体剪切的初始阶段，式（13）给出负值剪胀角的绝对值偏大，近似处理办法是将其人为置零；而当${\varphi _{\text{m}}}$达到摩擦角的最大值$\varphi$时，剪胀角保持恒定的最大值，在不排水条件不能计算土体的破坏，所以需要在土的孔隙率达到设定的最大值时将剪胀角人为置零。这些处理显然是很简化的。

再看采用广泛应用的莫尔库仑模型（MC模型）按有效应力法进行的计算。因它假定土在屈服破坏之前为弹性，不能考虑土的剪胀或剪缩，计算的变形和强度都会有较大误差。如图 3所示，在不排水条件下采用MC模型的计算将给出竖直的有效应力路径，而实际上当土为正常固结或轻度超固结，在较小剪应力水平时即发生剪缩，产生超静水压，其有效应力路径将向左上弯曲，故此时的计算将高估土的强度。而对超固结土，当剪应力水平较高时剪胀，超静水压为负，有效应力路径向右上弯曲，故此时的计算将低估土的强度。因此，饱和土不排水条件下的计算，即便仅关注土的强度，也不可采用常规的MC模型；但可输入摩擦角φ=0，黏聚力c=c_u，实际是直接输入土的不排水强度，改用Tresca模型^{[6, 10]}。当然，这一做法仍是近似的（见下节）。实际上，采用Tresca模型时，也可按总应力法计算，但按有效应力法的计算，近似给出超静水压，可与固结计算相衔接。

图  3  MC模型计算应力路径与实际应力路径的差异

Figure  3.  Differences between actual stress path and that calculated by MC model

下载: 全尺寸图片 幻灯片

（2）不排水计算的总应力法

由上可见，不排水计算的有效应力法需要能够较好模拟土的剪胀及强度的本构模型，目前尚无简单实用且能较好满足计算精度的模型。此外，实际工程的地勘报告也不能提供用于先进复杂本构模型的参数。所以，工程计算多采用总应力法，即直接计算本构总应力，而不企求分别计算超静水压与有效应力。

此时由于不能计算土的有效应力，而基于本构总应力的本构模型更是难以构建，所以更不能企求准确计算土的弹塑性变形。对于弹性参数，此时可给出剪切模量G或变形模量E=3G，再给出取值接近0.5的泊松比$\nu$。土的强度则如上直接输入土的不排水强度c_u，采用Tresca强度准则或下一节将要讨论的广义Tresca准则。但也有人认为可以采用MC之类的模型、输入固结不排水指标进行计算，但此种做法须很慎重，有关讨论见本文第3节。

2.   饱和土不排水强度理论与计算

饱和土在不排水条件下的强度取决于土骨架与孔隙水的相互作用，较排水条件下的强度有着不同的复杂性。理解土的不排水强度特性的首要基础理论是众所周知的有效应力原理和MC强度准则，以及20世纪五六十年代Skempton^[12-13]、Henkel^[14-16]、Schofield等^[17]等众多学者所做的杰出工作。国内沈珠江^[18-20]、李广信^[21]对饱和土的不排水强度同样有深入的研究。近年来的有关研究在文献[22]中有较全面的综述，这里仅就工程应用层面的基本理论进行讨论。下面首先考虑不排水剪切时的超静水压计算，之后将超静水压计算公式与三主应力表达的MC强度准则结合给出一个土的不排水强度模型，继而用它讨论饱和黏性土不排水强度的一些特性。最后简要介绍用于实际工程计算的广义Tresca模型，以及采用MC模型按有效应力法进行计算时的等效强度指标。

2.1   不排水剪切产生的超静水压

Skempton^[12]于1954年即提出著名的超静水压计算公式：

式中：$\Delta {\sigma _i}$为土在不排水条件下所受总应力的增量；A，B为超静水压系数。一般认为A主要与土的类别及不排水剪切前的应力历史有关，对于黏性土主要与其灵敏度及超固结度有关。对正常固结土A值较大，对超固结土A值较小，甚至为负值。B是与土的饱和度有关的系数，对于饱和土为1，对于非饱和土小于1。

关于土在不排水剪切时的超静水压计算，国内外的土力学教材中也多是给出式（14）。但笔者经分析认识到，此式并不能用于三轴压剪之外的应力路径。因为，当土仅有弹性变形时，对于不排水三轴压剪，系数A理论上应为1/3，而对于三轴拉剪则应为2/3。也就是说，当A取同一值时，式（14）不可能既适用于三轴压剪又适用于三轴拉剪。实际上Skempton在发表式（14）数年后的1960年又以给编辑部信函的形式给出式（14）的改进形式^[13]：

式中：$\alpha = (A - 1/3)/\sqrt 2$。式（15）是Skempton依据他本人及Henkel等多人所完成的大量精细试验，包括重塑土和一些原状土样的试验归纳总结的，可用于多种不同的不排水剪切路径。Henkel^[15]在同年发表的一篇国际会议论文也给出同样的计算公式。

对式（15），研究人员多认为它主要是考虑了中主应力的影响，也有文献提出进一步的改进建议^[21]。笔者认为，此式除适用于多种不同应力路径外，还有很重要的一点，即它把平均总压应力引起的超静水压，即第一项，与剪切引起的超静水压，即第二项，清晰地分开了。第一项不引起有效正应力均值的变化，而第二项则使有效正应力均值变化，笔者建议称第一项为弹性超静水压，第二项为塑性超静水压（或剪胀超静水压），分别写为

此区分有助于清晰理解饱和土的不排水强度特性。

此外，笔者认为式（15）对土体经受不排水剪切到破坏时的超静水压计算还是较准确的。剪切过程中系数A的值显然是不断变化的，因为土在排水条件下的剪胀角是随应力水平变化的。但土的不排水强度是一定的，所以超静水压系数A也有其确定值。随后采用此式进行分析所得结果的合理性也在一定程度上支持上述观点。由于这里是讨论土的不排水强度，系数A应写为A_f，但为录入方便简写为A。土的有效摩擦角除特别说明外均写为φ。

现考察3种典型应力路径下式（15）的具体形式。对于三轴压剪应力状态，不管是加载、减载还是等p压剪，其超静水压按式（15）计算为

亦即可以写成与原来相同的形式。而对于各种形式的三轴拉剪，按式（15）其超静水压计算式为

此时，A同样取1/3即可给出弹性情况下三轴拉剪的超静水压。对于平面应变问题，注意到饱和土不排水条件下平面外应力增量$\Delta {\sigma _2}$=$0.5(\Delta {\sigma _1} + \Delta {\sigma _3})$，有

由式（20）可见，对于平面应变问题，如仍采用原来的式（14），则其孔压系数A，现记为A_pl，与新公式中系数A的关系为

这与Scott给出的系数相同（见文献[23]，380页）。由式（20），（21）可见，平面应变剪切时的总超静水压要较三轴压剪中的大一些，但塑性超静水压要小一些。由此可预料，同样条件下平面应变状态下的不排水强度会较三轴应力状态下的大一些。

由上可见，如采用式（14）计算超静水压，不同的不排水应力路径将有不同A值，而写成式（15）的形式则可用任一种试验确定A值，之后可用于各种不同的应力路径。这样，可采用较容易做的三轴压剪试验测定孔压系数A，再利用式（15）计算不同应力路径下的超静水压。

2.2   土的不排水强度模型

将上述超静水压计算公式与MC强度准则相结合即可确定土的不排水强度。但常用形式的MC强度准则是采用大小两有效主应力之和确定土的强度，而任意两主应力和与具体荷载情况有关，是不确定的。因此，需将MC强度准则写成由三主应力表达的形式。

由有效应力表达的土的MC强度准则：

这里的c、$\varphi$均为有效强度指标。

再设应力为三轴压剪状态，即${\sigma '_1} > {\sigma '_2} = {\sigma '_3}$，并记${p'_{}} = ({\sigma '_1} + {\sigma '_2} + {\sigma '_3})/3$，则式（22）即可写为

对于正常固结土或到临界状态时的土，c=0，这样式（23）即与土的临界状态方程相同，右端$p'$前的系数即为临界状态线的斜率M。

又在同一$\pi$平面上（图 4），三轴压剪点与拉剪点对应的最大剪应力之比为

图  4  应力空间的莫尔库仑屈服面

Figure  4.  Mohr-Coulomb yield surface in stress space

下载: 全尺寸图片 幻灯片

为能同时表达压剪、拉剪，进而近似表达其中间各应力状态下的抗剪强度，将式（23）写为

其中$\omega$符合下列条件：

式（25）即为有效应力表达的MC强度准则的三维形式。

在不排水条件下，由前面对超静水压计算式的讨论，式（25）中的平均有效应力$p'$应等于初始平均有效应力${p'_0}$减去塑性超静水压$\Delta {u_{\text{p}}}$，即

而式（25）左端可改用总应力表示，从而有

对于正常固结土，黏聚力c=0，式（28）成为

这样，将式（28）与式（15）结合，就构成一个饱和土不排水强度模型。用此强度模型可对饱和土在不同加载路径和不同固结应力状态下的强度特性进行分析。

2.3   土的不排水强度特性分析

（1）等向固结土在不同剪切路径下的强度

首先考察各种不同三轴压剪应力路径下的饱和土不排水强度。如土在不排水剪切前为等向固结，则不管是加载压剪、减载压剪还是等p压剪，式（28）左端均可写为

可见此时的极限偏差应力与计算塑性超静水压的偏差应力增量相同。由式（28）可知，对于组分与应力历史相同的土，不管三轴不排水压剪的具体应力路径如何，最终将得到相同的不排水强度。

类似地，对于三轴不排水拉剪与不排水平面剪切，可以得到相同的结论，即对给定类型的剪切路径，不管具体不排水剪切应力路径如何，极限状态时的超静水压和强度都相同。

但对不同类型的剪切方式，即便是固结应力相同的同种土，其到极限状态时的塑性超静水压不同，强度也不同。

首先比较三轴不排水拉剪与不排水压剪。设两土样均为等向固结，且固结应力相等，则由式（28），（17）可知，压剪与拉剪的极限偏差应力q_c、q_e将分别符合

式中：$\bar \omega$为式（26）所示的$1 + \omega$，$\bar A = A - 1/3$。由式（31），（32）可得出两强度比为

显然，当A>1/3，两强度比将小于$\bar \omega$，亦即q_e与q_c的比值要较同一$\pi$平面上拉剪与压剪的比值大一些。其原因是拉剪对应的塑性水压较小，这使相同固结应力下的拉剪点最终位于较压剪点高一些的$\pi$平面上，这与Henkel^{[14, 16]}文中试验结果吻合。

类似地，可以将等向固结土的不排水平面应变剪切强度与三轴压剪强度进行比较。此时平面外主应力增量$\Delta {\sigma _2}$=$0.5(\Delta {\sigma _1}{\text{ + }}\Delta {\sigma _3})$，所得两极限偏差应力比与式（33）形式相同，只需将其中的$\bar \omega$换为1+$\omega$/2，将$\bar A$换为$0.5\sqrt 3 (A - 1/3)$。

由上可见，对3类不同的不排水剪切试验，即便初始平均固结应力相同，但不排水剪切到极限状态时，所产生的超静水压不同，其强度也不再符合同一$\pi$平面上不规则六边形显示的相对大小关系（见图 4），而是后两种试验的强度有所增大。

Henkel^[14-16]曾进行了大量的固结不排水三轴剪切试验，包括压剪和拉剪，而压剪和拉剪试验中又都包括加载剪切、减载剪切和等p剪切。其试验结果表明对固结应力相同的同种土，所有压剪的强度相同，所有拉剪试验的强度相同，拉剪强度小于压剪强度，但拉剪试验到破坏时的平均有效正应力稍大于压剪试验（见文[16]中图 5）。本文前述的所有分析结论均与Henkel的结论一致，这在表明本文分析方法正确的同时，也从侧面证明了Skempton-Henkel超静水压计算公式（15）的适用性和准确性。

（2）非等向固结土的不排水强度

非等向固结土在不排水剪切时会呈现明显的非各向同性。文献中多是针对K₀固结土进行分析，文献[24~26]都是假定土在K₀固结过程中发生机动硬化，K₀固结线成为屈服面的中心轴线，用此屈服面相应的弹塑性模型分析饱和土不排水剪切试验中大主应力在竖直方向和在水平方向时的强度及其比值。文献[27]则是采用基于细观层次上的热力学分析所建立的本构模型进行类似的分析。这里将展示利用式（29）结合式（17）可以方便地进行同样的分析，包括三轴剪切与平面应变剪切的分析。

先看平面应变剪切。不排水剪切前的固结应力，对NC土也是初始有效应力，为

设不排水加载使大主应力仍在竖直方向，各总应力分量的增量为

由式（17）有所产生的塑性超静水压为

式中，${\bar A_{{\text{pl}}}} = 0.866A - 0.289$。

将上列各主应力的初始值与增量值之和以及式（36）代入式（29），解得

式中，${\varpi _{{\text{pl}}}} = 1 + 0.5\omega$。

于是得出K₀固结土的平面应变剪切试验中大主应力在竖向时的极限偏差应力：

类似推导可给出K₀固结土在同类试验中大主应力在水平方向时的极限偏差应力：

由式（38），（39）即可给出K₀固结土受平面应变剪切时大主应力在竖直方向和水平方向时的不排水强度比。当给定摩擦角$\varphi$与系数A的值，M，$\omega$，${\varpi _{{\text{pl}}}}$，K₀及${\bar A_{{\text{pl}}}}$的值可按前述有关公式由$\varphi$或A计算，再由式（38）、（39）即可得出相应的不排水强度及其比值。比如，当$\varphi$=20°，A=0.8，相应的K₀=1-sinφ=0.66，M=0.77，两向不排水强度比为1.4。计算分析还知，K₀及A值越大，两向强度的比值越大。当仅有弹性超静水压时，即A=1/3时，两向强度比恒等于1；当A>1/3，两向强度比大于1，反之则小于1。两向强度比随$\varphi$增大而增大，设A=0.8，$\varphi$=20°时为1.40，$\varphi$=25°时为1.55。两向强度系数的均值，即不排水强度均值与初始竖向有效应力${\sigma '_{{\text{v0}}}}$的比值，随$\varphi$增大而增大，比如A=0.8，$\varphi$=20°时强度系数为0.22，$\varphi$=25°时为0.25。当等向固结应力与K₀固结的大小两主应力均值相同时，其不排水强度等于K₀固结条件下两向强度的均值。所有这些对理解土的不排水强度特性、对依据室内试验选取实际工程分析所需强度参数有重要参考价值。

通过同样的分析，可给出三轴剪切时大主应力分别在竖向（三轴压剪）和水平向（三轴拉剪）时的不排水强度：

由式（40），（41）即可给出K₀固结土在不排水剪切时两向强度的比值。当K₀=1时可以得出与式（33）相同的结果。

对于三轴剪切的不排水强度，计算表明，如塑性超静水压可忽略时，即A=1/3时，两向强度比等于(3+$\sin \varphi$)/(3-$\sin \varphi$)，即与排水条件下的相同；如A>1/3，则两向强度比大于此值，反之则小于此值。两向强度比随$\varphi$增大而增大，比如，设A=0.8，当$\varphi$= 20°时，比值为1.80，25°时为2.2，30°时为2.6。不排水强度系数也随$\varphi$增大而增大，如设A=0.8，20°时不排水强度系数为0.21，25°时为0.23。此时的强度系数较平面应变条件下稍小，因给定系数A的值，后一条件下的塑性超静水压较小。当等向固结应力与K₀固结的三正应力均值相同时，其不排水强度近似等于K₀固结条件下两向强度的均值，A=1/3时才准确相等。这一点与平面应变剪切时也稍有不同。

比较平面应变状态与三轴应力状态下的两向强度比可见，后者的两向强度比明显大于前者。但应注意，即便在三轴排水剪切试验中，亦即无不排水剪切引发的各向异性时，两向强度比(3+$\sin \varphi$)/(3-$\sin \varphi$)也是大于1的。将三轴剪切的两向不排水强度比除以排水强度比之后，三轴不排水剪的两向强度比较平面应变状态下的两向强度比只是稍大。比如，当A=0.8，$\varphi$= 20°时，三轴不排水两向强度比值为1.8，而此时(3+$\sin \varphi$)/(3-$\sin \varphi$)为1.26，1.8除以1.26为1.43，而对应的平面应变强度比为1.40。此外，实际土工结构中的应力状态多在压剪与拉剪之间，或说在平面应变对应的应力状态附近，故一般工程近似计算中可取两向强度的均值。

上述分析给出的强度系数、强度比及平面应变剪切与三轴剪切强度的相对大小等结果与文献[24~26]给出的结果基本吻合，表明本文采用所构建不排水强度模型进行有关问题的分析是可行的。

同时，本文的分析还直观显示了不排水强度非各向同性的原因：对K₀固结土，当大主应力在水平向时，不排水剪切的路径较长，产生的塑性超静水压较大，所以强度较低。由此可知不排水强度是与大主应力（或小主应力）方向而非滑移面方向对应的，因为大主应力在竖直方向和水平方向时的滑移面可能相同（见3.4节）。这后一点又意味着，饱和土不排水强度的非各向同性主要不是因为土骨架本身性质的差异引起的。由此又会引出对不排水强度各向异性之分析方法的思考。

这里或许会有的一点疑问是，在水平应力增大的初始阶段土中剪应力是减小的，此种情况下可否由式（17）计算塑性超静水压。但深入思考可理解这与采用机动硬化后的屈服面进行分析隐含了本质上近乎相同的假定。

工程实践中一般是将三轴等向固结压剪试验测得的不排水强度用于各种实际工程，包括平面应变问题。因此需回答，等向固结应力取何值时抗剪强度等于平面应变状态下的两向强度均值。采用上列公式取多组不同参数计算发现，三轴试验中等向固结应力取大小两固结正应力均值时，所得两向均值接近但略小于平面应变条件下的两向强度均值，差异约为3%。但如取等向固结压剪结果，则固结应力取三正应力均值时，所得不排水强度更接近但稍小于平面应变条件下的两向强度均值；如取等向固结应力等于大小两主应力均值，对常见典型土体参数，三轴压剪试验的结果比平面应变状态下两向强度的均值大约7%。

由上述讨论可清晰认识土的不排水强度与排水强度的显著差异。在排水条件下，荷载产生的压应力直接提高土的强度，土的强度直接决定于当前压应力的大小，而与初始应力状态无关。比如，计算地基在排水条件下的承载力时，根本不需要知道K₀的值。而在不排水条件下，饱和土受到的平均正压应力全部被孔隙水承受，对土的强度没有直接的显著影响，只有剪应力引起的剪胀或剪缩及相应的塑性超静水压使土中初始有效压应力改变从而影响土的强度。饱和土的强度决定于不排水剪前的初始有效应力（包括K₀的大小）及应力历史，是在不排水剪切之前就已确定的。荷载对土的不排水强度的影响只是其所产生主应力的方向与此前固结主应力的差异情况。

上述讨论用土力学中最基本的知识说明了貌似很深奥的饱和土不排水强度特性，比起采用基于临界土力学理论并考虑机动硬化的本构模型的推导更易于被工程师理解。

2.4   不排水强度计算及等代强度指标

（1）一般三维应力状态下的强度计算

2.2节将MC强度准则与塑性超静水压计算公式结合给出的不排水强度模型，还不便于直接用于土的不排水强度计算，因一般不易测定土的超静水压系数A。较方便的是直接测定给定固结应力下的不排水强度，这样式（28）应改写为

式中：$S_{\text{u}}^{\text{c}}$为给定固结应力状态及不排水剪切方向的不排水压剪强度；${\omega _{\text{u}}}$为与同条件下压剪-拉剪强度比对应的系数，

式（43）中${\omega _{\text{u}}}$不同于式（28）中的$\omega$，因据上节的讨论，不排水条件下此系数与摩擦角不再有原来$\omega$与摩擦角所符合的关系。换句话解释，$\omega$对应于土体破坏时的有效应力状态点在同一$\pi$平面时压剪强度与拉剪强度的比值，而${\omega _{\text{u}}}$对应于初始固结应力状态点在同一$\pi$平面时不排水压剪强度与拉剪强度的比值。

由式（28）右端的表达式可以理解，式（42）中的$S_{\text{u}}^{\text{c}}$可写为如下形式：

式中：a，b应与土是否为等向固结、非等向固结时固结应力的罗德角以及不排水剪切时大主应力与固结应力的相对方向有关。同样，${\omega _{\text{u}}}$一般来说也是随这些因素变化的。但实际工程计算中，一般都需简化，多可采用平均压剪和拉剪强度进行计算，或取等向固结下的不排水压剪强度。当实际土工结构在不排水加载时其内各点的大主应力方向各不相同，采用平均强度或压剪强度进行计算并要求合适的计算安全系数应是可行的。当然，对于固结应力状态及不排水加载时大主应力方向均明确的问题，比如主动土压和被动土压的计算，参照2.2节的讨论确定土的不排水强度作为输入值可使计算更为准确。

简化的形如式（42）的不排水强度公式，文献中称为广义Tresca强度准则^[28]，其屈服面为柱面而非锥面，在$\pi$平面的形状与MC屈服面相同。采用此强度准则进行土的不排水强度计算，可按总应力法或有效应力法，因有效应力与总应力的Lode角相同。对有限元软件输入的模型参数可为a、b及${\omega _{\text{u}}}$，当软件内不能进行式（44）的计算时，则需直接输入每个单元的压剪强度和拉剪强度。对水平土层，还可输入土层顶面处的不排水强度及其随深度的增长率。

（2）MC模型的应用及等代强度指标

前文已述，当采用MC模型按有效应力法进行土的不排水计算时，不能正确给出土的不排水强度。因此，岩土有限元软件Plaxis中建议此时直接输入土的不排水强度S_u，亦即c_u，同时取${\varphi _{\text{u}}}$=0。但须注意，此时所采用的实际是Tresca模型，它不能考虑压剪与拉剪强度的区别。所以，在实际工程计算中需考虑所分析问题的特点，据有关讨论适当选取强度参数。

此外，当直接输入土的不排水强度进行计算时，由于不排水强度随固结应力的增大而增大，而固结应力的分布又无简单规律的情况下，则需逐个单元输入。当计算软件中无逐个单元输入强度的功能时，则无法进行计算。为此，笔者基于对不排水强度及有关计算模型理解的基础上，针对平面应变问题提出采用等代强度指标的方法^[29]，可采用MC模型按有效应力法实现实际复杂工程的固结不排水计算。

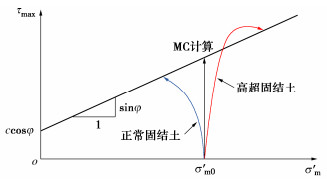
平面应变问题的大小主应力均在计算平面内，按有效应力法计算时，弹性阶段的有效应力路径，亦即有效应力莫尔圆顶点的轨迹在图 5所示坐标平面内为竖直线①。因此时计算平面内的平均总压应力和弹性超静水压的增量均为$(\Delta {\sigma _1} + \Delta {\sigma _3})/2$，即平均有效压应力计算值保持不变。故当采用MC模型按有效应力法进行计算时，屈服前的有效应力路径是竖直的。而屈服之后，对平面应变问题，当输入剪胀角为零，处于塑性状态的应力也不会沿屈服面移动。因为不排水条件下当剪胀角为零，塑性超静水压为零，3个有效正应力和不变，而出平面方向的有效正应力是由面内两个有效主应力决定的，故面内两个有效主应力之和在屈服后也保持不变。

图  5  由MC模型按有效应力法计算的弹性有效应力路径

Figure  5.  Elastic effective stress path calculated by MC model

下载: 全尺寸图片 幻灯片

由上可知，当采用MC模型按有效应力法进行土的不排水计算时，从面内平均有效正应力点竖直向上的有效应力路径与破坏线交点处的剪应力即为计算的极限剪应力。令此剪应力等于由试验直接或间接确定的不排水强度c_u，反求出相应的强度指标，则可采用MC模型按有效应力法计算，从而实现任意固结应力下不排水强度的准确计算。这反求的强度指标称为“等代强度指标”。这样，由图 5有

将不排水强度c_u表示为

联立式（45），（46）解得

如已知土的固结不排水强度指标，还可由下式确定a和b^[29]：

下面给出两个算例，一方面对等代强度指标进行检验，另一方面展示其应用。

a）算例1：等代强度指标的检验

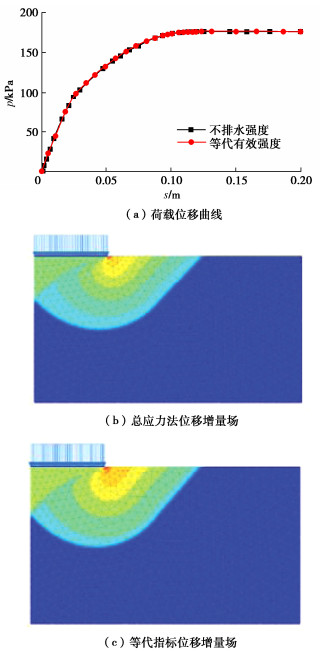
此例计算一条形基础下饱和黏性土地基的极限承载力。基础宽10 m，土层参数为φ_cu=15.0°，c_cu= 20.0 kPa，K₀=0.6，γ'=10.0 kN/m³。

这里是水平土层，其不排水强度c_cu随深度线性增大，可由CU强度指标c_cu、φ_cu结合K₀和γ'按文献[29]或3.2节所给公式计算给出地面处的不排水强度c₀=26.1 kPa、不排水强度随深度的增长率c_inc=2.81 kPa/m，输入有限元软件按总应力法计算。同时，又可由CU强度指标按式（47），（48）给出等代强度指标c_eq=27.8 kPa，φ_eq=20.4°，采用MC模型按有效应力法计算。

前一方法计算给出地基极限承载力p_u=175.4 kPa，后一方法给出p_u=176.3 kPa，荷载-位移曲线的对比如图 6所示，两曲线几乎重合，表明上述等代指标的准确性。

图  6  条基承载力问题用两种方法计算结果的对比

Figure  6.  Comparison of bearing capacities of strip footing calculated by two methods

下载: 全尺寸图片 幻灯片

进行上述计算时需注意，两计算中的等效模量要准确相同，即剪切模量G相同，总应力法输入的泊松比与有效应力法中的等效不排水泊松比准确相等。此外，采用等代强度指标按有效应力法的计算中不应采用拉伸截断，因为当有效应力的某分量为拉时将其人为置零，就使平均有效压应力增大，从而高估土的强度。这实际是不排水计算与排水计算的又一区别。排水计算中不拉伸截断会高估土的强度，而不排水计算中却相反。但在不排水计算中三个有效主应力之和小于零时则应置零。不过，这种情况在这里的计算中不会发生，因这里塑性超静水压为零，而初始3个有效主应力和是大于零的。还有，进行不排水计算时，材料不可压缩，需采用合适的单元以避免网格闭锁^[6]。

b）算例2：等代强度指标的应用展示

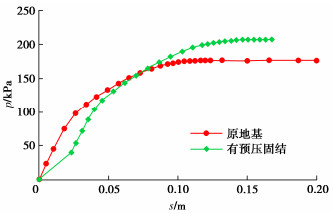
此例所有参数同算例1，但先施加40 kN/m²的荷载令地基充分固结，这里是做排水计算；之后再快速加载，即按不排水计算。因预压固结后地基中固结应力分布不规则，就不能再简单输入两个不排水强度参数c₀和c_inc，而需采用等代强度指标。计算给出有预压固结的地基极限承载力为p_u=207.0 kPa，相比无预压固结时增大18%。荷载-位移曲线的对比见图 7。

图  7  有无预压固结的荷载-位移曲线对比

Figure  7.  Load-displacement curves with and without preloading

下载: 全尺寸图片 幻灯片

需说明的是，等代强度指标的应用严格说仅限于平面应变问题。对于非平面应变应力状态，其弹性有效应力路径在图 5坐标系中不再是竖直的。比如轴对称问题中的三轴压剪点，虽然其大小主应力恒在计算平面内，但面内弹性总正应力增量均值为$(\Delta {\sigma _1} + \Delta {\sigma _3})/2$，超静水压增量为$(\Delta {\sigma _1} + 2\Delta {\sigma _3})/3$，故面内平均有效正应力的增量为$(\Delta {\sigma '_1} + \Delta {\sigma '_3})/2$= $(\Delta {\sigma _1} - \Delta {\sigma _3})/6$，而最大剪应力增量为$(\Delta {\sigma _1} - \Delta {\sigma _3})/2$，故计算的弹性有效应力路径斜率为3（图 5中路径②）。类似分析可知轴对称问题中的三轴拉剪点在不排水剪切时的弹性有效应力路径斜率为-3（图 5中路径③）。同时，当弹性有效应力路径非竖直时，其与破坏线的交点位置还与初始剪应力有关。再者，即使在轴对称问题中，一般只有少部分点的应力一直处于三轴应力状态，大部分点的应力属于一般三维应力状态。对一般三维应力状态，当采用理想弹塑性模型按有效应力法进行强度计算时，在3个有效主应力和不变的条件下，其大小两主应力和会据荷载情况而调整变化，亦即弹性有效应力路径不能事先确定，屈服后的有效应力状态还会沿屈服面移动。如3个主应力调整为一大两小的三轴压剪状态，则会给出最大的极限剪应力；如调整为两大一小的三轴拉剪应力状态，则给出最小的极限剪应力。

所以，对于非平面应变问题，应采用广义Tresca模型进行计算。但当所分析结构在极限状态时，塑性区域的应力状态均为三轴压剪或拉剪时，可仿照前述的推导，令相应弹性有效应力路径与破坏线交点对应的剪应力等于不排水强度，由此确定等代强度指标进行计算。比如，圆形基础在中心荷载下的承载力问题，其塑性区域的应力均为三轴压剪状态，在不考虑非各向同性的情况下可用对应的等代强度指标计算。

3.   固结不排水强度指标的缺陷及其正确应用

由前述讨论知道，对于饱和土的不排水计算目前工程实用的方法是总应力法，计算重点是土体的稳定。进行这种计算分析时，中国工程界多采用固结不排水强度指标（CU强度指标）${\varphi _{{\text{cu}}}}$、${c_{{\text{cu}}}}$直接代入诸如地基承载力、土压力等计算公式进行计算，这相当于用下式计算土在总应力$\sigma$作用下的极限剪应力：

虽然这种做法很早就在北美应用^[30]，但在理论上是有缺陷的，欧洲无这种强度指标^{[23, 31]}，欧洲研发机构开发的岩土有限元软件，比如Plaxis^[10]、Optum^[32]也都没有这种指标。应用CU指标直接进行计算需注意其应用条件。但在中国的工程实践中，CU指标的应用又扩大到土水合算，这在理论上是不正确的。本节着重对CU强度指标的缺陷进行分析，最后结合基坑工程中土压力的计算，对土水合算的误差情况进行一些讨论。

3.1   固结不排水强度指标的缺陷分析

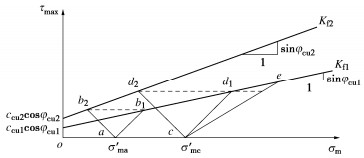
考察测定CU强度指标的三轴试验过程，即可看出直接采用这种指标进行强度计算的缺陷^{[6, 8]}。图 8给出试验过程中的总应力路径，即大小两总主应力决定的莫尔应力圆顶点移动的轨迹。图 8中坐标系的横轴为大小两主应力均值，纵轴为最大剪应力。

图  8  三轴加载应力路径及相应强度指标

Figure  8.  Stress paths and corresponding strength indices under triaxial loading

下载: 全尺寸图片 幻灯片

首先看常用三轴固结不排水压剪试验，即对试样施加围压使其等向固结之后，再在不排水条件下逐步增大竖向应力直至试样破坏。这种加载过程中，大小总主应力的均值与剪应力的增量均为竖向总应力增量$\Delta {\sigma _1}$的二分之一，故总应力路径的斜率为1。设试样1、2的固结围压分别为${\sigma '_{{\text{ma}}}}$，${\sigma '_{{\text{mc}}}}$，当施加竖向总应力，总应力路径向右上发展，两试样分别到b₁点和d₁点时破坏。由于土的破坏线近似为直线，过b₁、d₁点的直线即为试验确定的破坏线${K_{{\text{f1}}}}$。该线是试样破坏时总应力莫尔圆顶点的连线，其斜率和截距分别为sin${\varphi _{{\text{cu}}}}$和${c_{{\text{cu}}}}\cos {\varphi _{{\text{cu}}}}$（见土力学教材，比如文献[33]）。这样，由三轴压剪试验就测得了CU强度指标${\varphi _{{\text{cu}}}}$和${c_{{\text{cu}}}}$。

之后，再对同种土的两个试样分别施加与前相同的围压进行三轴固结不排水压剪试验。但此时的压剪试验是在不排水条件下逐步减小围压的试验，剪切过程中总应力路径的斜率为-1，亦即向左上方倾斜。而根据2.3节的讨论，或根据Henkel试验发现的土的含水率-固结应力-抗剪强度唯一性关系^[14]，或根据临界土力学原理^[17]，当试样的组分相同、正常固结应力相同，其不排水强度相同。这样，试样1的总应力路径达到与b₁点相同剪应力的b₂点破坏，试样2达到与d₁点相同剪应力的d₂点破坏。这样连结b₂点与d₂点得破坏线${K_{{\text{f2}}}}$，它给出另一组与此前差异很大的CU强度指标。

以上情况说明，不同加载路径将给出不同的CU强度指标，此前已有不少学者指出这一点（比如文献[34]）。所以，CU强度指标不是一种客观指标，按某一加载路径的试验测定的指标只能用于相同斜率总应力路径的抗剪强度计算。由于破坏线向右上倾斜，所以当实际总应力路径较测定强度指标的试验路径平缓时，也就是同样大小剪应力对应的正应力增量相对较大时，直接用式（49）计算极限剪应力将夸大土的强度，反之将低估土的强度。由于实际土工结构受载时其内各点的总应力路径往往各不相同，故大部分部位的强度计算将有误差，甚至有些部位的误差还会很大，按上述的总应力路径斜率判别法，不难进行分析判断。

式（49）的理论缺陷实际上是很显然的。按式（49），土中任一点的总应力$\sigma$越大则该点的抗剪强度越大，这显然错误。因为可以对土中固结应力给定的点在不排水条件施加很大的压力，从而使得总应力$\sigma$很大，但不排水条件下施加的压应力不会使饱和土的强度发生变化。

固结不排水试验给出的${\varphi _{{\text{cu}}}}$之所以大于零，图 8中的破坏线之所以向右上倾斜，是因为对同种土的多个试样分别施加了大小不同的固结应力，从而得出大小不同的极限剪应力。亦即，${\varphi _{{\text{cu}}}}$大于零是在反映不同试样因其固结应力不同而具有强度的不同。但是，强度指标应反映土中给定点在受载过程中的强度性质。而饱和土在经受不排水剪切之前其任一给定点的固结应力是给定的，强度是已给定的，施加给任一点的总压应力不会改变其强度，也就是相应的“摩擦角”为零。式（49）实际上是把土中不同点表现出的强度差异错误地施加到了同一给定点。这是一种因似是而非的感觉导致的逻辑错误。

分析式（49）理论缺陷的另一视角是前已述及的一个道理，即饱和土不排水强度与其前期固结应力是密切关联的，而式（49）显然是说，土中任一点的强度是由当前总应力决定的，不需要其固结应力的任何信息。

3.2   固结不排水强度指标的正确应用

以上清楚说明了CU强度指标的缺陷，并指出直接用此指标进行土体稳定分析何时会高估强度、何时会低估强度。在工程计算中一般不宜采用此种指标直接进行计算，而应采用土的不排水强度并取不排水摩擦角${\varphi _{\text{u}}}$=0°进行计算^[35-38]。

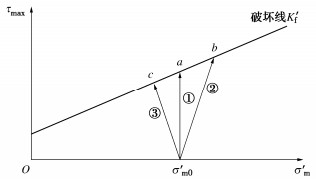
但CU强度指标给出了不排水强度的信息，可由它计算不同固结应力下土的不排水强度c_u，之后采用c_u并取${\varphi _{\text{u}}}$=0°进行分析。为从CU强度指标计算不排水强度c_u，仍可利用图 8方便地进行。比如由图 8中试样1的加载三轴剪切试验，由于不排水阶段的总应力路径ab₁的斜率为1，而总应力路径端点对应的剪应力即为不排水强度c_u，再注意${K_{\text{f}}}$线的斜率为$\sin {\varphi _{{\text{cu}}}}$，截距为${c_{{\text{cu}}}}\cos {\varphi _{{\text{cu}}}}$，则有方程

由此解出c_u为

式（51）与沈珠江^[36]给出的公式相同，但沈珠江^[36]推导此式的过程似有忽略不排水剪切过程中剪切所产生超静水压的假定。

按上述推导方法还可以得到用三轴减载压剪试验测得的CU强度指标$\tilde{\varphi}_{\mathrm{cu}}, \tilde{c}_{\mathrm{cu}}$表示的不排水强度，即

式（52）与式（51）的区别只是这里分式的分母中为加号。进而还可从上述一种指标计算另一种指标。

此外，实际土层往往为K₀固结而非等向固结，根据2.3节的讨论，K₀固结会引发土不排水强度的非各向同性，但当等向固结应力与K₀固结的大小两主应力均值相同时，三轴压剪试验给出的不排水强度一般仅稍大于平面应变状态下两向强度的均值。李广信^[39]据临界土力学理论分析认为，在平均固结应力相同的条件下，可认为等向固结不排水剪与K₀固结不排水剪的强度近似相等。故在一般工程计算中可近似采用等向固结不排水剪测得的CU强度指标，取式（51）中的固结应力${\sigma '_{{\text{ma}}}}$为$(1 + {K_0})\gamma 'z/2$来计算K₀固结土的平均不排水强度c_u，这也与沈珠江^[36]的建议相同。由此得出利用CU强度指标计算K₀固结土层不排水强度的公式：

其中，

式中：${c_{\text{0}}}$为不排水强度在土层顶面的值；${c_{{\text{inc}}}}$为不排水强度随深度的增加率。

顺便说说强度增长的计算，即大小固结主应力均值${\sigma '_{\text{m}}}$增大$\Delta {\sigma '_{\text{m}}}$时，土的不排水强度的增长$\Delta {S_{\text{u}}}$。由式（51）显然有

文献中有采用$\Delta {S_{\text{u}}} = \Delta {\sigma '_{\text{m}}}\tan {\varphi _{{\text{cu}}}}$，明显偏低。魏汝龙等^[40]曾指出此问题并建议采用固结快剪指标，认为可近似将$\tan {\varphi _{{\text{cu}}}}$乘以1+$\sin {\varphi _{{\text{cu}}}}$，但较式（56）的值还是稍小。

计算土层的不排水强度时还需水平应力系数K₀，对正常固结土层的K₀可用经验公式K₀=1-$\sin \varphi$。但地勘报告一般不提供有效强度指标$\varphi$，而多提供${\varphi _{{\text{cu}}}}$。如按K₀=1-$\sin {\varphi _{{\text{cu}}}}$计算将给出偏大的K₀值，偏于不安全。考虑到较大深度处的不排水强度近似等于${c_{{\text{inc}}}}z$，而相应深度处的最大剪应力0.5$(1 - {K_0})\gamma 'z$应小于${c_{{\text{inc}}}}z$，由此给出K₀值的下限为1-2$\sin {\varphi _{{\text{cu}}}}$。据此建议用下式近似估计K₀值：

当对超静水压系数A的值有较好估计时，可利用系数A计算式（28）中的塑性超静水压，再令式（28）计算的三轴压剪强度与式（51）计算的c_u相等，即可给出确定有效摩擦角$\varphi$的公式如下：

由式（58）可见，当A>0，则$\varphi > {\varphi _{{\text{cu}}}}$；反之则$\varphi < {\varphi _{{\text{cu}}}}$。还可分析给定${\varphi _{{\text{cu}}}}$时A的取值上限等，限于篇幅，不再展开。

利用CU强度指标计算土的不排水强度时，可方便地考虑土的欠固结，即当土为欠固结时，将计算c_u时所用固结应力乘以实际固结系数即可。这在采用CU指标直接计算时是无法考虑的。

不排水强度${c_{\text{u}}}$属于总应力强度，实际应用时稳态水压严格说也应单独考虑。但因其对应的摩擦角为零，故可用饱和重度直接计算平衡总应力，并用此总应力进行平衡和强度分析。

3.3   地基不排水承载力的计算对比

为了解采用CU指标直接进行计算所引起误差的大小，笔者课题组进行了多种工程问题的计算对比，发现对于地基承载力问题，直接用CU指标进行计算普遍会高估承载力。指标${\varphi _{{\text{cu}}}}$越大，误差越大，比换算为不排水强度再行计算可高出1倍甚至2倍多^[8]。

这里仅给出一典型算例。此例中设地基为正常固结饱和黏性土，有关参数为：${\varphi _{{\text{cu}}}}$=15°，c_cu=20 kPa，${\gamma _{{\text{sat}}}}$=20 kN/m³；基础为宽6 m的条形，不考虑埋深。采用前述公式从CU强度指标计算的不排水强度为c_u =26.1+2.81z（kPa）。

图 9给出利用有限元软件Plaxis计算给出的基础荷载-位移关系曲线，其中用不排水强度计算的极限承载力为164 kPa，而直接用CU指标计算给出的极限承载力为300 kPa，后者大了将近1倍。如CU摩擦角再大一些，误差还会更大，甚至可超过200%。需指出，这里地下水位在地面附近，当采用CU强度指标直接计算时，这里是采用土的有效重度。如用饱和重度，即土水合算，会更严重高估地基的承载力。

图  9  两种参数计算的浅基础荷载-位移曲线

Figure  9.  Load-displacement curves calculated by using different types of parameters

下载: 全尺寸图片 幻灯片

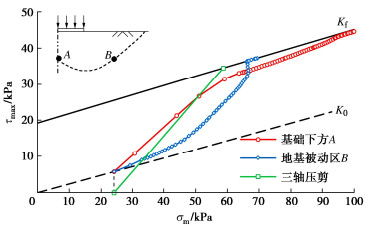
采用CU指标直接计算之所以会严重高估地基承载力，其原因就是前已指出的，因在加载过程中地基中每一点的总应力路径都比测定CU强度指标的三轴试验中平缓得多。先看基底下的主动破坏区，随荷载增大竖向总应力增大使地基受剪，同时水平压应力也在增大，而三轴剪切试验中在竖向应力增大的过程中围压保持不变，所以基底下主动区的总应力路径，尽管有初始剪应力，总地来看其总应力路径还是要比试验中的路径平缓（见图 10）。图 10中还给出被动区一点的总应力路径，可见它同样比三轴压剪试验中的平缓。

图  10  地基中两点随荷载增大时的总应力路径

Figure  10.  Total stress paths at two points in soils

下载: 全尺寸图片 幻灯片

实际上张在明^[41]早在1995年就指出上述两种参数计算地基承载力的巨大差异，随后修订的北京地区地基基础勘察设计规范就已建议采用土的不排水强度计算饱和黏性土地基的极限承载力^[42]。天津岩土工程技术规范也明确规定对正常固结黏性土采用自重应力下预固结的不固结不排水强度进行土体稳定计算^[43]。

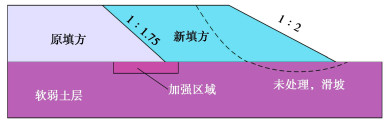
现在再看一个软土场地上填筑边坡的工程实例，这同样属于在软基上加载的承载力问题。该填筑边坡是20世纪90年代贵州某机场填方工程的一部分。其一期填筑坡比1∶1.75（见图 11），设计验算安全系数足够，但施工中填了滑，再填再滑，最后将坡脚下软土采用碎石加固后才完成填筑。当时的技术人员得到的认识是，软土场地上填筑边坡的稳定性按土力学的计算是靠不住的。数年后二期填筑，坡比1∶2，坡度更小了，计算安全系数足够，直接填筑，又是屡填屡滑，只好请教一期的技术负责人，再次加固坡脚下软土才完成填筑，也再次强化了按土力学计算无用的认识。

图  11  软土地基上填筑边坡实例

Figure  11.  Filled slope on soft soil layer

下载: 全尺寸图片 幻灯片

现在重新审视该工程可以理解，当时的计算是采用CU指标直接计算的。根据一些不很完整的资料，这里构造一个算例。设原地基参数${\varphi _{{\text{cu}}}}$=13.5°，c_cu= 9 kPa，${\gamma _{{\text{sat}}}}$= 19 kN/m³，地下水位接近地表。填筑体材料参数φ=38°，c=2 kPa，γ= 20 kN/m³；坡高5 m，坡比1∶2。直接用CU强度指标计算得安全系数K=1.61。折算为不排水强度c_u=c₀+c_incz，其中c₀=11.42 kPa，c_inc= 2.31 kPa/m。计算c_inc时取K₀=1-1.5sinφ_cu=0.65。计算给出K=1.08，不满足要求。这才是软基上填筑边坡“计算靠不住”的真正原因。但当时问题原因没搞清楚，以致有关技术人员得出岩土问题只能靠经验的认识。类似现象在中国工程界具有较大的普遍性。由此看到探究、普及岩土力学基本理论的必要性。

3.4   基坑工程中土压力的计算对比

基坑开挖对于饱和黏性土来说同样属于快速加载，基坑支护挡土构件所受土压力一般应按不排水计算。根据前述有关讨论，饱和土不排水条件下的主动土压和被动土压计算在理论上合理的做法应是采用不排水强度c_u并取${\varphi _{\text{u}}}$=0〫进行计算，魏汝龙早在1995年就建议如下计算^[44]：

式中：p_au为采用不排水强度计算的主动土压与水压之和；p_pu为按同样思路计算的被动土压与水压之和。其中的不排水强度${c_{\text{u}}}{\text{ = }}{c_{\text{0}}}{\text{ + }}{c_{{\text{inc}}}}z$对同一土层随深度线性增大，可按式（53）从CU强度指标和相应深度处的固结应力计算，还可考虑K₀固结引发的强度非各向同性。

但中国几乎所有关于基坑支护技术的规范规程一直以来均采用CU强度指标进行土水合算，已有多位学者指出其在理论上的不合理^[45-46]。以地下水位接近地表的情况为例，按现行规范规程方法，挡土构件在深度z处所受土水压力的计算式为

式中：${p_{{\text{ac}}}}$和为主动土压与水压之和；${p_{{\text{pc}}}}$为被动土压与水压之和。

式（61）~（64）提出的工程背景是：最初采用CU强度指标进行土水分算得出主动区的总土水压力明显偏大，为此先是提出水压折减，后改为土水合算。如此计算的结果与实测较为接近，因此对被动区总土水压力的计算也采取同样的思路。

显然，按前述讨论，规范规程方法有如下问题：①静水压未单独考虑；②采用CU强度指标直接计算；③计算公式无固结应力的信息，特别是未用到K₀。虽然就主动区来看，该方法给出的结果误差不大，但理论上的缺陷有碍此方法的推广应用，也不利于从工程实践总结经验。下面分别就一般主动区和被动区以及坑底被动区对规范规程方法的问题进行分析。

（1）主动区土水压力的计算分析

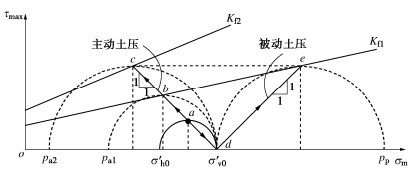
基坑挡土构件所受主动土压是开挖卸载情况下发生的，故应取卸载强度指标，业内多位学者持此观点（比如文献[47]）。这里通过应力路径分析及相应公式推导来论证这一点。图 12给出K₀固结土的总应力（本构总应力）路径从初始点a分别沿主动和被动方向移动的轨迹。主动土压应力路径的斜率为-1，按前述讨论，应采用卸载压剪试验所测强度指标进行计算，亦即极限状态对应于卸载压剪破坏线K_f2上的c点。而现行规范规程方法采用一般加载压剪所测强度指标进行计算，亦即认为应力路径发展到加载破坏线K_f1上的点b破坏，从而低估了土的强度，得出偏大的主动土压。而土水合算，相当于水压折减，又使计算的水压偏小。综合两部分结果才使得总主动土水压力误差不大。

图  12  K₀固结土发生不排水极限土压时的总应力路径

Figure  12.  Total stress paths in K₀-consolidated soil at undrained ultimate earth pressure

下载: 全尺寸图片 幻灯片

如将静水压单独写出，即土水分算，将式（61）改写为

再采用卸载压剪指标${\tilde \varphi _{{\text{cu}}}}$，亦即取主动土压系数K_ac及$\sqrt {{K_{{\text{ac}}}}}$分别为

将式（66）代入式（65）有

式（67）右端括号内表达式恰是式（53）表示的不排水强度${c_{\text{u}}}$，只是需取K₀=1。亦即，直接用CU指标计算主动土压并土水分算，等于取等向固结应力为竖向应力计算不排水强度，再用此不排水强度进行计算，这由图 12也可看出。所以，如取K₀=1，则式（67）即可写为与式（59）相同的形式：

式（68）与式（59）的区别：①式（59）中的不排水强度${c_{\text{u}}}$对K₀固结土是用大小两有效主应力的均值作为固结应力计算的，即所用固结应力较小些，还可以考虑土的欠固结；②式（59）中的不排水强度取值可考虑K₀固结土主动破坏时的强度与等向固结不排水剪切试验所测值的差异，一般是前者稍大一些。但此两点差异对主动土压力计算结果的影响相反，对于正常固结土最终引起的总差异应不大。下面给出一个算例展示几种不同计算的差异情况。

设水位下黏土层，${\varphi _{{\text{cu}}}}$=15°，c_cu=15 kPa，${\gamma _{{\text{sat}}}}$= 20 kN/m³，超静水压系数A=0.8，由前述公式有$\varphi$=26.2°，K₀=0.56，相应此K₀值的c_u=19.55+2.81z（kPa）。由2.3节理论计算还知这里K₀固结土的平面压剪强度应由三轴压剪强度乘以1.15。这样可以采用理论上较准确的不排水强度按式（59）得出总主动土水压力的理论准确值。

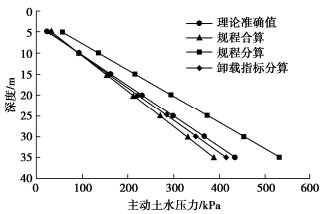
图 13给出4种方法计算的主动土压力与水压的总压力值随深度的分布，其中包括按式（56）得出的理论准确值、按式（61）采用CU指标合算（规程合算）的土水压力、采用CU指标分算（规程分算）的土水压力，以及采用卸载强度指标分算的土水压力。卸载剪切强度指标可据式（51），（52）给出其由加载强度指标计算的公式：

图  13  4种方法计算的总主动土水压力比较

Figure  13.  Active soil water pressures calculated by four methods

下载: 全尺寸图片 幻灯片

由图 13可见规程合算方法给出的结果总体误差不大，但5 m深度处偏大51%，随深度增大合算值变为偏小，即偏于危险。用加载压剪CU指标分算（规程分算）结果确实严重偏大，与理论准确值最接近的是采用卸载强度指标分算的结果，其土水总压力在5 m深度处偏大不到10%，而深度到30 m时偏小仅约4%。

但须指出，上述计算比较是仅考虑土水自重引起的总主动土水压力，未考虑地面荷载。当地面有新加荷载时，由3.1节的分析知道，即便采用加载压剪试验给出的CU指标，也会高估荷载作用下土的强度，低估荷载引起的主动土压力。

所以，最合理的做法是将CU强度指标转换为不排水强度再行计算。这样，在确定不排水强度时还可考虑诸如上述土的欠固结、测试CU强度指标的试验中应力路径与地基中实际应力路径的差异、K₀固结土的非各向同性等。

（2）被动区土水压力的计算分析

由图 12，被动土压总应力路径的de段斜率为1，与三轴压剪试验中相同，故可采用三轴压剪试验测定的CU强度指标直接计算。这样，对于被动土水压力的计算，式（63）的问题主要是土水合算，将静水压乘以了大于1的被动土压力系数，夸大了水的抗力。由图 12可见的另一问题是，该式相当于以竖向自重应力为固结应力均值，也就是按K₀=1计算，也高估了被动土压力。由此再次看到不排水强度与排水强度的区别：本来在排水条件下完全正确的计算，对不排水强度计算却有问题。更严格地审视式（63）的问题是，它未考虑K₀固结土的不排水强度的非各向同性。对于被动土压力，大主应力在水平方向，K₀固结土的不排水强度要比等向固结土的低一些。但最大的问题还是土水合算。

如将静水压单独写出，即土水分算，将式（63）改写为

再将被动土压力系数K_pc及$\sqrt {{K_{{\text{pc}}}}}$的下列计算式

代入式（71）则有

由计算不排水强度c_u的式（53）可见，式（73）右侧括号内表达式在取K₀=1时又恰好是不排水强度c_u，这样式（73）可写为与采用c_u计算的式（60）相同的形式：

只是这里的不排水强度对应于K₀=1。

据上可理解，对于总被动土水压力的计算，只要进行分算，即可得出与正确方法相近的计算结果。当然，采用不排水强度c_u的计算，可考虑各种因素的影响来确定c_u的取值，从而使计算更为准确。

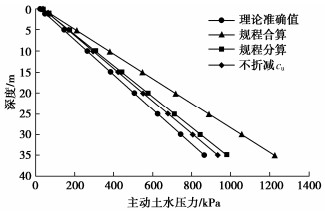
这里给出一个算例对理论准确方法、规程合算及规程分算的结果进行对比。有关参数同主动土压力的计算对比算例，只是对被动土压力的计算，需由前述理论将三轴等向固结压剪试验确定的不排水强度予以折减，以考虑K₀固结对不排水强度的影响。经计算对此例折减系数近似为0.72。

图 14给出4种方法计算结果的比较。由图 14可见，规程合算方法计算的结果明显偏大，各深度处基本均偏大约42%，即偏于不安全；而规程分算的结果到深35 m处才偏大13.6%，从工程角度看误差不大。因此对总被动土水压力，可采用CU指标分算。但同样需注意，新加地面荷载对应的被动土压仍是采用不排水强度的计算方法才能较准确地考虑。

图  14  4种方法计算的总被动土水压力比较

Figure  14.  Passive soil water pressures calculated by four methods

下载: 全尺寸图片 幻灯片

图 14中还给出不考虑K₀固结使土的不排水被动强度的降低，即不折减c_u进行的计算，对此算例如此计算的精度也完全满足要求。可见，对K₀固结土考虑其不排水强度的非各向同性予以修正并非总是必要。K₀固结土的强度随大主应力方向变化，而对极限土压力问题大主应力方向是明确的，应该也容易对不排水强度进行修正。但强度c_u仅影响计算公式的一部分，不予修正也不会引起最终结果的较大误差。同理，K₀值的近似计算对计算结果影响也不大，因它在计算公式中的影响范围更小。

（3）坑底被动土水压力计算

基坑工程中被动土压力的计算多是针对坑底被动区。当坑底以下土层为饱和黏性土，基坑开挖过程及之后的运行期较短，饱和黏土的固结度很低，一般应按不排水计算。此种条件下，可近似认为坑底土中负值超静水压未消散，式（60）中的不排水强度采用开挖前的有效固结应力计算。以场地为均一土层的情况为例，设H为坑深，坑底往下深度z处的不排水强度为

故坑深越大，不排水强度越高，计算被动土压力也越大。

如果考虑基坑开挖过程及之后的运行时间较长，坑底往下一定厚度范围内的土发生了显著的固结，那么土的不排水强度应按超固结土计算，较公认的计算公式为^{[35, 48-49]}

式中：m$\approx$1-C_s/C_c，C_s和C_c的分别为土的回弹指数与压缩指数。m的值按文献[35]中表 2给出的几种土，对压剪强度为0.83~1.0，对拉剪为0.74~1.0。考虑20 m深基坑坑底下4 m处的不排水强度，设固结几乎完成，则此处应力的超固结度OCR=6，竖向有效应力减小为开挖前的1/6，如取m=1，则不排水强度不变；如保守地取m=0.74，则此处的不排水强度变为原来的63%，而非采用CU指标计算的1/6。当然，为稳妥起见，可以取小些的m值。

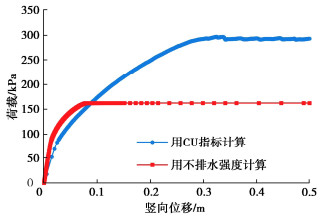
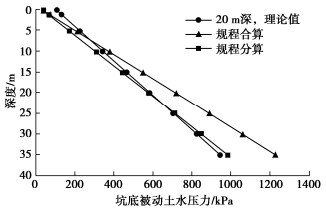
但如按规程公式计算，则计算的被动土压力与坑深无关，且在坑底往下一定深度范围内计算值严重偏小。而土水合算又使计算的总土水压力随深度快速增大，偏于危险（见图 15）。如由坑外主动土压、坑内被动土压力来分析基坑挡土构件嵌固段是否会踢脚破坏并发生坑底隆起，则对小嵌深的情况则计算安全系数严重偏小，而对大嵌深的情况计算安全系数又会严重偏大。

图  15  坑底被动土压的计算比较

Figure  15.  Calculated passive soil pressures on bottom of excavation

下载: 全尺寸图片 幻灯片

由上面对坑壁主动土压力和坑底被动土压力的讨论可以理解，对于饱和黏性土层中开挖边坡的稳定分析，由于其倾角介于直立与水平之间，如采用CU指标合算，会低估其稳定性，而采用卸载强度指标又会高估其稳定性，准确计算还是应采用土的不排水强度。限于篇幅不再给出算例。

此外，基坑支护的整体稳定及坑底抗隆起验算的现行做法也是采用CU强度指标并土水合算。有关规范规程中建议的坑底抗隆起稳定安全系数的简化计算方法仍有改进余地，主要是按地基承载力的验算应明确仅适用于挡土构件嵌深小的情形，且应考虑地基承载力的宽度项；圆形滑移面法适用于嵌深较大的情况，如按上海规范的计算方法，在嵌深不超过笔者提出的临界嵌深时所计算安全系数在排水条件下是较准确的^[50]。改进的验算方法对饱和地基不排水条件下的计算误差则主要来自于采用CU强度指标土水合算。笔者课题组的研究表明，由于采用CU指标土水合算夸大了坑外土的强度，同时低估了坑内土的强度，所计算的安全系数误差对常见基坑在-30%~+30%范围内，而分算的安全系数则偏小很多^[51]。说明土水合算在这里又是一个以错抵错的做法。具体计算对比见文献[51]。

（4）不排水极限土压滑移面倾角探究

由上可见，饱和土不排水极限土压力可用CU强度指标计算，也可用不排水强度并取${\varphi _{\text{u}}}$=0计算，当然还可用有效强度指标与超静水压系数等多种方式进行计算。由此对发生极限土压时的滑移面倾角也有不同看法。但滑移面倾角是确定的，不会因计算所用强度参数的不同而改变。

据有效应力原理，土的强度与变形从根本上是由有效应力决定。又因为土是摩擦材料，其强度最终应服从MC准则，即有效应力莫尔圆与库仑强度包线相切为极限条件。由此来看，滑移面应是切点处应力所在的面，也就是45°$\pm$$\varphi$/2。但对此尚有进一步探究的必要。

首先，笔者认为滑移面倾角不会由CU指标的摩擦角${\varphi _{{\text{cu}}}}$确定。这可从至少3个不同角度来论证：①CU指标非客观指标，测定该指标的试验加载路径不同则会得出不同的指标，故不可能由${\varphi _{{\text{cu}}}}$确定滑移面倾角；②用CU指标确定的强度线上每一点分别对应于土中固结应力不同的点而非给定点，给定点的总应力圆与该线的切点无真实物理意义；③如按式（65）或式（71）土水分算，将CU指标代入计算的土压力是有误差的，由求解土压力的极限平衡理论可知，其对应的滑移面也就不是真实滑移面。

再看滑移面的倾角是否由${\varphi _{\text{u}}}$=0确定，亦即滑移面倾角是否为45°。首先从以上3个角度考察不排水强度参数均无问题：①它是客观指标，给定土的应力历史即可给出${c_{\text{u}}}$、${\varphi _{\text{u}}}$的确定值；②由每一具体c_u值和${\varphi _{\text{u}}}$=0°确定的强度线，确实反映土中对应点在不同总应力下的强度；③将c_u、${\varphi _{\text{u}}}$代入土压力计算公式，即式（59）或式（60），给出的结果理论上是精确的，因式（59）与（60）实际均为${\sigma _1}$-${\sigma _3}$=2c_u的等价变化形式，所以${\varphi _{\text{u}}}$=0°对应的滑移面倾角45°也应是正确的。

同时，有限元计算给出的滑移面倾角是45°。图 16给出平面应变被动土压问题由有限元计算给出的滑移面，还计算了不排水三轴压剪、拉剪试验的滑移面，均近似为45°。这里的计算是采用有效应力法有限元，输入土的有效强度指标，采用MC强度准则进行的。计算中虽未考虑土的剪胀剪缩，但有超静水压，同样反映有效应力在45°面上未到极限状态却在45°面滑移的现象。还有，前面2.4节在检验笔者提出的等代强度指标时，分别做了用等效强度指标按有效应力法的计算和输入不排水强度按总应力法的计算，两种计算不但给出几乎重合的荷载-位移曲线，所给破坏阶段的增量位移云图也很难看出差别。这也表明输入有效摩擦角计算的滑移面与大小主应力的夹角为45°。再者，Davis等^[52]在用数值滑移线法求解饱和地基不排水极限承载力时，直接就采用了与大小主应力夹角为45°的滑移线，得出的结果与笔者所做有限元极限分析的结果也很吻合。再看Prandtl、Reissner、太沙基等在分析地基承载力时所用滑移线，在摩擦角为零的情况下与大小主应力的夹角也是45°，而这零值摩擦角显然是总应力对应的摩擦角，因为不存在有效摩擦角为零的土。郑颖人等^[53]讲到饱和黏性土的滑移线时也用45°。所有上述表明，理论计算给出的滑移面倾角是45°，按45°倾角计算不排水地基承载力、土压力也都未发现错误。因此，笔者目前倾向于认为饱和土不排水条件下的滑移面倾角是由${\varphi _{\text{u}}}$=0°决定的。

图  16  有效应力法有限元计算的被动土压滑移面倾角

Figure  16.  Slip surface at passive earth pressure calculated by effective stress FEM ($\varphi$=${30^ \circ }$, $\psi = {0^ \circ }$, c=10 kPa)

下载: 全尺寸图片 幻灯片

为理解上述计算结果，需要再次深刻认识饱和土的抗剪强度特性。如前所述，饱和土的强度是在承受不排水剪切之前就给定的，在剪切时只要最大剪应力达到其强度c_u，土即破坏，而与总压应力大小无关。设想以某种应力路径分别对排水和不排水条件下的两土样加载到濒临破坏，此刻及时施加压应力，—当然是总应力的压应力，因为不能直接干预有效应力，但排水条件下的总应力等同于有效应力—，那么排水条件下的土样就会远离破坏状态，而不排水条件下的土样则无可挽回。再就是须注意到，对饱和土进行不排水加载时，有效应力莫尔圆与库仑强度线相切总是与最大剪应力达到c_u同时发生或同时不发生，所以在对饱和土进行不排水计算时可以输入有效强度指标按有效应力法计算，也可以输入不排水强度${c_{\text{u}}}$和零值${\varphi _{\text{u}}}$按总应力法计算，得到的极限荷载是相同的，滑移面也应该是相同的。很难想象得到完全相同的极限荷载，却给出截然不同的滑移面。

不过，滑移面倾角45°确实难以很好解释，文献[54]报道，在对一种有效摩擦角约为32°的饱和粉质黏土进行的三轴不排水压剪试验中，观察到滑移面倾角很接近45°+$\varphi$/2。但文献[55]对伦敦黏土的不排水剪切试验则表明，试样的破裂面倾角有很大的离散性，具体与试样的局部缺陷、应变局部化以及相应的局部渗流等因素有关。所以对滑移面倾角的试验验证，还需更多的工作。笔者理解，前述的45°应是较均匀的大尺度土体在不排水条件下破裂面倾角的统计平均值。如果试验给出破坏滑移面倾角是由有效摩擦角决定，则说明有效应力法有限元计算的滑移面倾角错误，但极限承载力正确，那也是很难理解的。

明确滑移面的倾角大小不但是个重要的理论问题，同时也有重要的工程意义，比如确定基坑支护中背拉锚杆的自由段长度时就需要知道滑移面的倾角。

4.   饱和地基承载力与沉降计算方法

地基承载力与沉降计算，自然也包括饱和地基在不排水条件下的计算，是土力学基础工程的基本课题。但饱和地基的不排水强度随深度线性增大，对此种地基的极限承载力的计算尚未见其他文献中提出相应的公式。饱和地基短期沉降的简化计算在文献中也讨论很少。虽然这些问题均可采用有限元计算，但对一般工程人们还是希望采用相对简便的计算方法。简便计算方法的研究也有助于加深对有关作用机理的理解。采用简便方法计算也便于进行方案比选，积累工程经验，快速评估数值计算结果。

地基在不排水条件下的计算与排水条件下的计算是紧密联系的，其主要方面是相通的。由于排水条件下的地基沉降与地基极限承载力计算的现行方法仍有较明显的不足，为较好解决不排水地基承载力与沉降的简化计算问题，需首先对现行排水条件下的计算方法进行剖析，以求给出排水与不排水条件下的统一改进方法。

4.1   地基承载力的计算

（1）存在的问题

地基极限承载力计算公式的研究始自20世纪20年代。Prandtl在1920年针对无埋深基础、不考虑地基土重度情况下给出计算公式的第一项，随后Reissner考虑埋深给出计算公式的第二项，到1943年太沙基考虑地基土重度与基底摩擦给出地基承载力的完整解答^[56]。极限承载力计算公式包括如下3项：

其中，系数${N_\gamma }$是以图表形式给出。

因式（77）中第三项中承载力系数${N_\gamma }$是近似的且无解析计算式，众多学者继续进行研究，其中Hansen^[57]给出${N_\gamma }$的近似计算公式${N_\gamma } = a({N_q} - 1)\tan \varphi$在欧洲广泛应用。但此${N_\gamma }$仍有较大误差，为保守起见，其中的系数a由最初的2.0先后改为1.8，1.5。显然，由于${N_\gamma }$的不精确，第三项的误差随基础宽度增大而增大。

针对地基承载力计算，笔者注意到的问题是第三项仅与B、$\gamma$和$\varphi$等3个参数有关，此项与Prandtl-Reissner解叠加给出地基承载力的完整解。叠加的做法不符合塑性问题求解的基本原理。实际上，太沙基当时就已指出为考虑地基土的自重，应采用同一破坏滑移面进行计算，但因这样的滑移面难以找到，故在当时只能近似处理。

（2）新思路与新方法

为改进地基承载力的计算，笔者深入分析了地基承载的机理，发现了各因素间的内在联系^[58]，从而为提出改进的计算公式提供了可能。笔者先是注意到地基极限承载力计算公式中第二项与第一项的关系：

两项之间的这一关系无论是从Prandtl-Reissner公式，还是从太沙基公式均可得出。笔者对此给出如下解读：q对承载力的贡献首先是使地基承载力提高一倍q值，进而在$\varphi$>0的情况下又使地基承载力提高$(q\tan \varphi ){N_c}$。基础周围超载q首先使地基承载力提高一倍q值，其力学机理是，这q与基底压力中等于一倍q的压力共同构成满布于整个持力层表面的均布压力，这种压力绝对不会造成地基的破坏。而当$\varphi$>0时，这满布的均布压力q又会使地基承载力提高$(q\tan \varphi ){N_c}$。这意味着$q\tan \varphi$与土的黏聚力c等效。这种解读同时也清晰说明了N_q与地基承载力深度修正系数的下限为何是1。由于N_c、N_q两个系数在理论上是精确的，上述结论具有理论正确性。

理解了q的上述本质作用之后，进一步思考又可理解土体重度$\gamma$与$\tan \varphi$的积相当于黏聚力c随深度的增长率。由此可知，当土的摩擦角为零，则γ对承载力的贡献为零；而基础宽度是以与γ相乘的形式出现在承载力计算公式中，这就又可解释为何对于软土地基承载力的宽度修正系数为零。

为验证上述解读的正确、准确性，笔者课题组采用有限元极限分析法对地基极限承载力进行了两种参数输入下的计算对比：一种计算中如实输入地基土强度指标c、φ及重度$\gamma$，另一计算中将土体重度γ设为零，同时取地基土的黏聚力为c+$\gamma z\tan \varphi$。所完成的多个计算均取得准确相同的结果。

基于上述理解，可以将基础埋深超载q及地基土自重均统一归结为黏聚力，这为给出统一考虑各因素的承载力计算公式提供了可能。由于前人的大量研究表明，对此问题很难给出准确的解析解答，笔者采用理论分析与数值拟合相结合的方法。注意到上述等效关系，地基承载力影响参数仅有基础宽度、摩擦角和随深度线性增大的黏聚力。计算地基承载力的很自然的一个思路是：采用滑移面最大深度Z_max一半处的黏聚力乘以摩擦角$\varphi$决定的承载力系数N_c，再考虑一数值拟合确定的修正系数$\beta$即可给出地基的极限承载力^[58]，即

滑移面深度Z_max应在Prandtl滑移面深度基础上修正得出，而Prandtl滑移面是黏聚力为常值时的滑移面，所以修正系数应与黏聚力的深度增长率有关，且黏聚力随深度增长越快滑移面应越浅。而黏聚力随深度增长的快慢是相对的，相对于体系内的某个尺度，考虑体系内各量的量纲，自然想到如下的无量纲参数：

式中：分子是一倍基础宽度的深度内的黏聚力增长量，而分母是地基中等效黏聚力的稳定值。

由力学原理可以理解，随后的大量计算对比也证明，此无量纲参数的构建是正确的，它确实能综合反映其中几个参数的影响，不管其中的各个参数如何变化，只要k值不变，地基承载力值相同。

此外，摩擦角$\varphi$也应作为一个独立的影响参数。尽管无量纲参数k中已含有$\varphi$，但它是与$\gamma$相乘以反映等效黏聚力随深度增长的。在忽略$\gamma$的情况下，k不变化，而不同的$\varphi$会给出不同的滑移面深度，所以滑移面深度的修正系数应由k和$\varphi$两个参数决定。

参数$\beta$实际是考虑滑移面形状变化的一个修正系数，所以它也应由k和$\varphi$两个参数决定。

如上的理论分析保证了独立影响参数确定的准确性，而无量纲参数的正确引入，将影响参数的数量大幅度减少，从而为随后数值拟合的高效和高精度提供了可能。

经数值拟合给出滑移面深度

其中，Z_PR为Prandtl滑移面深度^[33]：

滑移面形状修正系数$\beta$为

这样便得出排水条件下地基承载力的计算公式。经与有限元极限分析的结果对比，式（81）~（83）具有很高的计算精度，误差不超过5%，具体见文献[58]。

对不排水条件下的地基承载力可方便地由式（81）~（83）得出。前已指出，$\gamma \tan \varphi$在力学本质上是地基中黏聚力随深度的增长率。因此，不排水地基的c_inc与排水条件下的$\gamma \tan \varphi$是等价的，而不排水地基的c₀对应于公式中的黏聚力c。所以，将式（81）~（83）中的$\gamma \tan \varphi$与c分别用c_inc和c₀替换，并将$\varphi$=0代入，即给出不排水条件下的地基极限承载力计算公式^[59]：

与有限元极限分析计算给出的高精度结果对比表明，式（81）~（83）同样具有很高的计算精度^[51]。同时，此套计算公式具有解析解的性质。比如，当c₀=0 kPa，无量纲参数k为无限大，计算式成为零乘以无限大的形式，此时用罗必塔法则求极限得出的计算公式与Davis等^[52]针对此特殊情况给出的公式准确相同。这些从多方面证明了上述思路及方法的正确性。

以上是针对条形基础发生整体剪切破坏时的地基承载力计算公式。当地基土相对很软或埋深相对较大情况下，地基可能发生局部剪切破坏，此时建议仍按太沙基的做法，采用折减的强度指标进行计算^[33]。

对于其他形状的基础、荷载倾斜、地面倾斜等情况，建议暂仍近似采用Hansen等给出的修正系数^[33]，因为所提出的公式仍可如经典公式那样写成3项，比如式（79）可写为

但目前的第三项与所有输入参数有关。

对于偏心荷载下的地基承载力计算，笔者发现Meyerhof^[60]提出的方法简便而精确，即把远离荷载合力作用点一侧的基础面积减小使成为中心荷载作用的基础，再用此折减面积后的基础计算地基承载力。但据笔者对基础埋深超载作用机理的解读，当荷载偏心距较大，致使基底最小压力值小于埋深对应超载q时，埋深对地基承载力的贡献如仍如常计算将给出偏大的计算值，有限元极限分析的结果验证了这一推测^[61]。

（3）工程应用简介

地基承载力较准确的计算在不少情况下很有必要，比如一些不需严格控制沉降的临时性工程，准确计算地基承载力对保证工程安全而又经济就很必要。

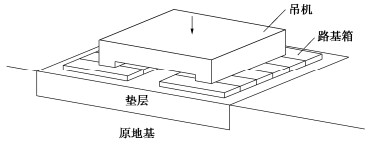
石化行业建造大型加工设施过程中，常需吊装一些质量超千吨的大型设备。所采用的重型履带吊机本身质量在两三千吨，还需一定的配重以保持吊装中吊机的平衡。这就需要对吊机站位处的地基进行处理。目前一般采用换土垫层，再在垫层之上沿吊机履带各铺设一排路基箱（图 17）。

图  17  吊装换填地基示意图

Figure  17.  Sketch of replacement foundation for hoisting

下载: 全尺寸图片 幻灯片

对此换填地基的验算方法此前一直沿用建筑地基处理规范建议的方法^[62]，在垫层承载力有保证的前提下，取一侧履带与路基箱及其下垫层、地基进行验算。荷载由路基箱传给垫层，再按一定扩散角扩散到下卧层，要求下卧层的承载力特征值大于扩散后的附加压力与原自重应力之和。对下卧地基的承载力特征值按地基处理规范是取塑性区发展到1/4基础宽的深度时的荷载${p_{1/4}}$。该方法的安全系数取值不甚明确，更大的问题是基础宽度较大时误差很大，故规范规定基础宽度大于6 m取6 m^[4]。但路基箱的宽度多为7，8 m，所以更合理的做法是按极限状态设计，即采用极限承载力除以安全系数的方法。

目前国内外多采用太沙基公式或汉森公式计算地基的极限承载力，安全系数一般取2.0。而由上述讨论，这两公式的计算有较大误差。笔者课题组以国内基础宽度取上限6 m的情况进行计算对比，发现其计算误差有正有负，具体误差大小与相关参数的组合有关，而正误差可达+30%^[58]，当基础宽度大于6m时误差更大。而本文公式计算精度很高，故在同样可靠度条件下可要求计算安全系数不小于2.0/1.3≈1.55，目前初步确定不小于1.5~1.6。这样，当采取原公式计算的误差小于+30%，甚至为负时，用新公式计算的设计方案就较原方案经济。

比如，广西华谊某吊装项目^[64]，采用4000 t级吊车主吊，车身质量2050 t，所吊设备连同吊具质量为2000 t，再加配重总质量达5550 t。场地浅层为厚度较大的砂性填土，强度指标c=10 kPa，φ=15°。采用2 m厚混凝土碎块垫层，上铺双排路基箱，每排长19.6 m，宽8 m。用汉森公式（其中a取2.0）计算的安全系数为1.92，小于要求达到的2.0；而按新公式计算安全系数1.96，已显著大于所要求的1.5~1.6。实际情况是吊装顺利成功。此例中按Hansen公式计算的承载力稍偏小。

而对于沿海饱和黏性土地基，此前常有采用CU强度指标计算安全系数已大于2.0，但吊装中又不得不临时采取加固措施的情况。按新公式采用不排水强度计算就能较准确计算地基的极限承载力，从而保证安全。以浙江镇海典型吊装场地为例，场地浅层以黏性填土和粉质黏土为主，CU强度指标典型值约为c_cu=17.6 kPa，φ_cu=11.3°。吊装总荷载及路基箱铺设方案与上例相同。但这里采用固化土垫层，7 d龄期无侧限抗压强度不小于1 MPa。垫层厚度如取2 m，采用CU强度指标c_cu、φ_cu直接计算下卧层的承载力安全系数为2.07，已大于2.0，但按以往经验知道此厚度明显偏小。用新公式计算的安全系数仅为1.38，确实不满足。取垫层厚2.5 m，用新公式计算的安全系数1.51，可认为满足要求，实际吊装也满足。

4.2   地基沉降计算

（1）目前方法存在的问题

对地基基础的沉降计算，国内建筑地基基础规范一直是采用分层总和法^[4]。这种方法利用布氏解计算基底中心下地基不同深度处由基底平均压力引起的竖向附加应力，再由各土层的竖向附加应力和侧限压缩模量计算其压缩量，将影响深度内各土层压缩量累加给出基础的沉降量。

显然，因采用侧限压缩模量，这种方法不能计算饱和地基的短期沉降。即便对于永久沉降，该方法计算的沉降值一般都误差很大，故在规范中建议对计算值按经验进行修正。在国家地基基础规范中修正系数$\psi$从硬土地基的0.2到软土地基的1.4，取值范围很大。如此修正后与实际沉降仍有较大差异，故各地区的地基基础规范又各提出不同的修正系数。比如，北京地区地基基础勘察设计规范中^[42]，对高层建筑地基的修正系数则从对硬土小荷载下的1.0到软土大荷载下的0.3。上海地基基础设计规范中^[65]的修正系数则从相对较好地层较小荷载下的0.3到软土较大荷载下的2.5。这里除修正系数大小有显著差异外，北京规范所建议的修正系数与国家规范中修正系数的取值规律还正相反。这些情况说明计算方法本身也很需要改进。

考察该方法不难看出其假定与实际情况有多方面的差异：①按基底附加压力均布计算附加应力，未考虑基础及上部结构刚度的影响；②采用布氏解计算实际分层地基的附加应力，含有地基为均质、各向同性、线弹性半无限体的假定，还忽略了基础的埋深；③采用侧限压缩模量，而实际上即便对中心受载基础其形心下的地基也非侧限压缩。

对地基沉降的简化计算方法已有很多研究，提出多种不同的计算方法^[21]，但直至目前国内工程界所应用的主流方法仍是分层总和法。近年来杨光华^[66]针对分层总和法的改进做了大量工作，其提出的方法是，对于硬土改用现场荷载板试验反算的随荷载增大而折减的变形模量；对于软土则采用3个正应力分量，按胡克定律并分解为侧限压缩和实际水平应力与侧限应力之差对应的压缩沉降两部分进行计算。对前一部分仍采用试验给出的压缩曲线计算，对后一部分则用邓肯张模型确定的切线变形模量计算。但对一般工程，特别是在初步设计阶段，不便做荷载板试验；而采用3个正应力的计算，则因实际非均匀地基的水平应力会与布氏解有较大差异^{[33, 49]}而带来误差。

（2）改进思路及新方法

改进方法力求克服现行方法的缺陷。针对基底附加压力的计算，为考虑基础及上部结构刚度的影响，可对常见类型的建筑通过实测或数值分析了解基底压力分布规律，据以对基础平面适当分区，给出各区块的压力系数。对埋深的影响，当埋深较大情况下可改用Mindlin解计算地基的附加应力。

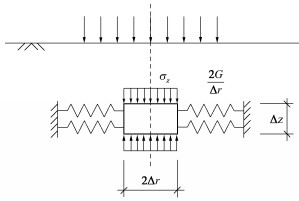
这样问题就归结为是仅用竖向应力还是同时用水平应力，以及用什么模量进行计算。实际上，分层总和法最初是太沙基针对黏性土层提出的。之所以仅采用布氏竖向应力是因为对于实际非均匀地基，其竖向应力与布氏竖向应力差异相对不大，而水平应力的差异要明显大一些。而侧限压缩模量又相对较易测试，且在附加应力不大且在排水条件下与有一定侧向约束时的等效竖向模量在数值上相差不大，故太沙基采用侧限压缩模量。基于此，笔者认为对于浅基础仍应采用布氏竖向应力计算，但模量不可采用侧限模量，也不能采用完全无侧限的变形模量。经反复思考，笔者想到曾针对地下结构地震反应有限元分析所研究的黏弹性传输边界^{[6, 67]}，想到用黏弹性边界的弹簧来模拟周围土体对拟计算沉降部位土柱体的约束作用，从而使计算的等效竖向模量及沉降接近实际。这样就提出图 18所示的计算模型。

图  18  地基沉降计算模型

Figure  18.  Computational model for foundation settlement

下载: 全尺寸图片 幻灯片

模型中，水平弹簧的刚度取2G/$\Delta r$，其中G为土的剪切模量^[6]，$\Delta r$为弹簧作用点与计算点的距离，这里应取一微小值。由于模型中压缩层的侧面既非自由也非完全侧限，故此模型可称为沉降计算的半侧限模型，相应计算方法为半侧限分层总和法。

现给出相应的计算公式。先考虑圆形或方形基础。设图中微元在竖向附加应力作用下两侧向外位移$\Delta u$，则水平正应变${\varepsilon _x}$，${\varepsilon _y}$与分布弹簧的力亦即水平正应力${\sigma _x}$，${\sigma _y}$分别为

又由广义胡克定律有

于是解得

利用各向同性材料变形模量与剪切模量的关系$E =$ $2(1 + \nu )G$，式（92）可写为

式（93）显示，对于布氏地基本文模型实际是用E/(1-${\nu ^2}$)代替侧限压缩模量。

显然，当地基土不可压缩时利用此式仍可能计算沉降值。计算时，可将地基压缩层划分为多个薄层，由式（93）计算各层的压缩量，再累加给出地基沉降值。

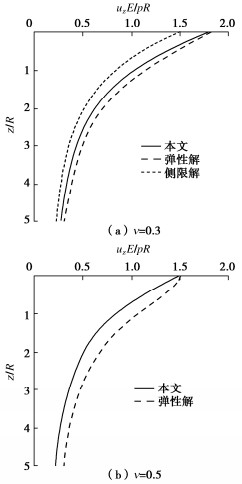
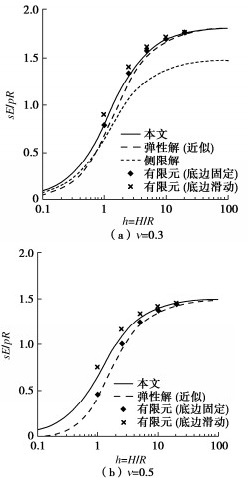
对于弹性地基上简单形状基础的沉降在文献中可找到解析解^[68]。将布氏竖向应力解（可见土力学教材，比如文献[33]）代入式（93）积分即给出本文模型的解，其与解析解吻合情况还较满意。图 19给出半无限体表面半径为R的圆形均布压力p作用下，其中心点下不同深度处的沉降计算对比，可见本文模型计算沉降在地基内偏小一些，但在地表处与解析解相等，总体上比采用侧限压缩模量的计算要好。

图  19  圆形均布荷载下布氏地基的沉降计算对比

Figure  19.  Calculated settlements of Boussinesq foundation under circular uniform loads

下载: 全尺寸图片 幻灯片

实际地基往往下卧坚硬土层甚至岩层。图 20给出本文模型仍采用布氏竖向应力计算的不同厚度覆土层上受均布荷载的圆形柔性基础的沉降与弹性近似解析解及有限元计算结果的对比。对此类问题弹性解析解是近似的，故还做了弹性有限元计算，计算中底边界分别按完全固定和可水平滑动两种情况考虑。有限覆盖层内的竖向应力较半无限体内的要大一些^[33]，但同时其水平应力也大，本文模型仍采用布氏竖向应力计算，计算结果与有限元吻合良好。

图  20  有限压缩层上圆形均布荷载中心点沉降计算对比

Figure  20.  Calculated settlements of finite compressive layers under circular uniform loads

下载: 全尺寸图片 幻灯片

利用本文模型还做了有限压缩层分为上硬下软和上软下硬两个分层情况下，圆形柔性基础的沉降与有限元计算结果的对比。还对方形基础进行了与上同样的几种计算。所有计算结果均较为令人满意。

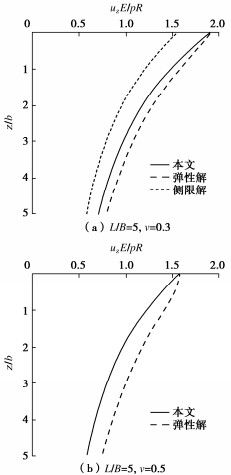
进而又对长宽不等的矩形和条形基础进行了类似计算。对于条形基础只能考虑有限压缩层地基，因为在理论上，对于沉降计算，半无限地基上没有条形基础。对于矩形基础和条形基础，两水平正应力${\sigma _x}$、${\sigma _y}$是不相等的，由此会产生上述模型是否仍然有效的疑问。但考察竖向应变的计算式（90）可见，此计算方法并不要求水平应力${\sigma _x}$和${\sigma _y}$都接近实际，而只需两者之和误差不大即可。随后的计算对比也表明计算结果同样令人满意。图 21给出长宽比为5的矩形基础下地基内不同深度处的计算沉降对比。

图  21  矩形均布荷载下布氏地基的计算沉降对比

Figure  21.  Calculated settlements of Boussinesq foundation under rectangular uniform loads

下载: 全尺寸图片 幻灯片

综上可见，笔者提出的计算模型具有较好的应用前景。但用于实际工程计算的关键是模型参数的取值，以下给出参数取值方法及相应的沉降计算步骤。

以往的大量研究表明直接采用地勘报告提供的模量会给出严重偏大的计算沉降。文献[66]所给一例显示，室内试验给出压缩模量为5~8 MPa的土，由原位压板试验反求的变形模量可达30~40 MPa。笔者认为这很大的差异，不仅仅是因为试样被扰动，还有实际地基中较深部位及周围土的小应变刚度的影响。

因此，笔者建议从土的小应变刚度出发考虑应变水平对小应变模量予以折减得到计算所需要的模量。当按小应变模量公式计算的模量达到其下限时，再改用邓肯张模型（DC模型）考虑土的塑性对模量进行折减，也就是将DC模型应力应变曲线的开始一段改用小应变的应力应变曲线。对小应变时的初始模量G₀可利用动测所给波速计算，或由压缩模量利用经验关系式估计。控制模量衰减过程的剪应变${\gamma _{0.7}}$的经验取值也已有很多文献可参考，比如文献[10，69]。

小应变阶段的割线剪切模量G_s随剪应变$\gamma$的衰减可按下式计算^{[6, 10]}：

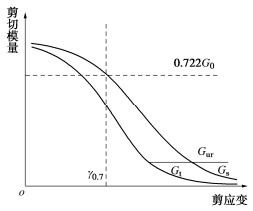
式中：${\gamma _{0.7}}$为剪切模量衰减到初始值的72.2%的剪应变值。小应变模量随应变增大而衰减的下限是相应的切线模量衰减到卸载模量G_ur（图 22），即当剪应变达到${\gamma _{{\text{cut}}}}$

图  22  土的小应变剪切模量衰减曲线

Figure  22.  Shear modulus-strain curves of soils

下载: 全尺寸图片 幻灯片

在小应变阶段，土为弹性，变形模量E与计算弹簧刚度的模量G应同时随应变增大而减小，此时水平应力计算值不变，故可由G_s$\gamma$=$0.5({\sigma _z} - {\sigma _x})$求解相应的剪应变及割线模量，代入式（92）并注意此时$\nu$取0.5即可得出由附加应力${\sigma _z}$计算竖向应变的公式：

当如上的计算超出小应变的范围，对应的剪应变大于式（95）计算的${\gamma _{{\text{cut}}}}$，亦即

对超出${\sigma _{z{\text{,cut}}}}$的部分考虑土的弹塑性进行计算。此时土的切线变形模量E_t按DC模型如下折减：

其中，破坏比R_f可取0.9，极限剪应力τ_f等于不排水强度c_u，剪应力仍近似由附加应力计算，即$\tau =$ $0.5({\sigma _z} - {\sigma _x})$，E_i据大、小应变阶段切线模量应连续的要求确定：

但在弹塑性阶段，随塑性变形发展水平应力会有所增大，故在此情况下弹簧刚度不应与土的变形模量等幅度折减。因为等幅度折减时，弹簧提供的约束应力不变。目前的简化做法是，当按式（98）计算的E_t值大于G_ur时，认为剪应力水平不高，弹簧刚度取2G_ur，否则取2E_t。计算表明如此处理能兼顾不同荷载水平下计算的准确性。

在用切线刚度计算时，需将竖向附加应力超出${\sigma _{z{\text{,cut}}}}$的部分分成数个小的增量逐步计算累加。

此外，在考虑塑性变形对模量折减时，应注意基础对其下一定范围内土的约束作用，对这部分土的模量折减幅度适当减小。这部分土的厚度在基底形心下设为1/8~1/4基础宽度，随离开形心的水平距离增大而减小，到基础边缘下为零。折减幅度则为基础底面处不折减，到此厚度的下界面处正常折减。这部分土体类似于太沙基分析地基承载力时所考虑的弹性核。

小应变模量G₀可由动测给出的波速计算，当勘察报告未提供波速数据时，可从侧限压缩模量估计卸载模量，进而给出初始剪切模量的参考值。常用经验关系式有^{[6, 10]}：$E_{{\text{ur}}}^{{\text{ref}}} = (3{\text{~}}4)E_{{\text{oed}}}^{{\text{ref}}}$，$G_{\text{0}}^{{\text{ref}}} = (1{\text{~2}})E_{{\text{ur}}}^{{\text{ref}}}$。顾晓强等^[69]对上海土层做了大量试验及实测研究，发现类似经验关系式中的倍数更大一些。

综上所述，本文所提出简化计算方法的要点为：①对于浅基础仍仅采用布氏竖向附加应力计算，但对较大的基底面积考虑基础与上部结构刚度的影响，分区给出压力系数，再用角点法计算附加应力；②在拟计算压缩沉降的土柱体侧面附加黏弹性人工边界的弹簧来考虑周围土的约束作用；③对变形模量取值建议从小应变刚度出发考虑应变水平进行折减得出，当折减模量小于卸载模量时按DC模型计算土的折减模量。

（3）初步应用

现将上述半侧限分层总和法用于中石化天津南港某吊装换填地基的短期沉降计算。场地地基近似水平分层，各层土厚度及部分力学参数见表 1。所采用的主吊车为自身质量为2320 t的4000吨级履带式吊机，所吊设备连同吊具质量为1734 t，再加个配重总质量约为6000 t。

表  1  地层参数

Table  1.  Soil parameters

序号	地层名称	层厚/m	重度γ/(kN·m-3)	黏聚力c/kPa	内摩擦角φ/(°)	压缩模量Es1-2/MPa
①	填土	3	19.0	13.6	17.2	—
⑥1	粉土	2	19.9	11.6	26.8	6.5
⑥2	黏土	11	17.8	16.0	14.1	2
	粉质黏土	9	19.5	16.0	16.0	3.5~10

下载: 导出CSV 

| 显示表格

地基处理采用换土垫层，垫层采用厚2.5 m，7 d龄期无侧限抗压强度不低于1.5 MPa的固化土。在吊机两履带下各横铺7块规格为8 m×2.8 m的路基箱，路基箱靠内侧端头间净距s=6.4 m。固化土垫层对附加压力的扩散角按θ=30°计算，由路基箱端往外扩出t=1.44 m，固化土垫层的水平尺寸稍超出扩散范围。计算中考虑的平面尺寸为长X=25.29 m，宽Y= 22.79 m。

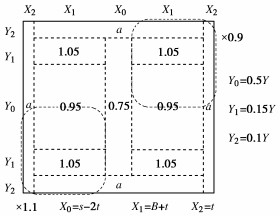
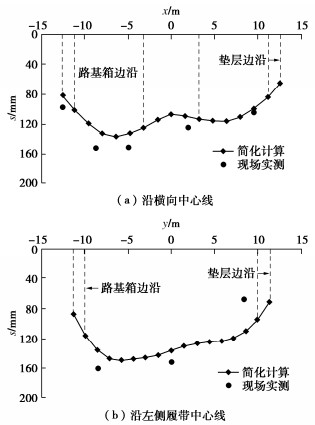
计算给出平均附加压力为p_m=104.6 kPa。但路基箱与固化土刚度有限，垫层底附加压力与刚性基础下有所不同。这里据粗略的有限元计算结合实测将垫层平面区域分区（图 23），每区块内假定压力均布，以便利用角点法计算任一点下不同深度的附加应力。吊装过程中，吊臂回转角在与纵轴成顺时针51°角方向，偏心距约为0.41 m，从而使图中左下区域的压力有所增大（乘以1.1），右上部分的压力减小（乘以0.9）。最终粗略确定的各区块附加压力系数如图 23所示，其中B=8 m，边缘压力系数α=1.12。

图  23  各区块下卧层顶附加压力系数

Figure  23.  Load pressure coefficients on underlying layer in each sub-area

下载: 全尺寸图片 幻灯片

据有关参数取值经验，考虑地勘取样等扰动对表 1所给E_s1-2适当放大（乘以1.5）。参考压力100 kPa下的各模量参考值：黏土取$E_{{\text{ur}}}^{{\text{ref}}}$=4E_s1-2，$G_{\text{0}}^{{\text{ref}}}$=2$E_{{\text{ur}}}^{{\text{ref}}}$；粉土及粉质黏土取$E_{{\text{ur}}}^{{\text{ref}}}$=3.5E_s1-2，$G_{\text{0}}^{{\text{ref}}}$=1.5$E_{{\text{ur}}}^{{\text{ref}}}$。在此基础上再按幂律考虑实际围压下的模量，幂指数对粉土取0.75，黏土取0.95，γ_0.7均取2×10^-4。上述参数取值中是用理论上稍大的E_s1-2近似作为$E_{{\text{oed}}}^{{\text{ref}}}$。

图 24给出沿横向中心线和沿左侧履带的沉降计算值，计算结果与现场实测吻合较好，多数点相对误差低于20%。计算与实测均显示，履带前后和左右履带之间的沉降差均小于吊机允许的0.5%。

图  24  计算沉降与实测对比

Figure  24.  Comparison between calculated and measured settlements

下载: 全尺寸图片 幻灯片

上述计算表明所提出的计算模型和方法可用于实际工程计算，但还需更多的计算检验与完善，特别是在模型参数取值方面需积累更多的经验。

此外，所提出的半侧限沉降计算方法同样可用于排水条件下的沉降计算，亦即长期沉降计算，相关的计算检验在进行中。但也须指出，对此类高度简化的计算模型期望过高也是不现实的，它只能作为初步设计中粗略估计沉降的一种便捷手段。

5.   结论

本文针对岩土工程中普遍需要的饱和土强度及变形计算理论与方法进行了系统的讨论，得到以下10点结论。

（1）饱和土不排水计算无论采用总应力法还是有效应力法，均应注意区分静水压与超静水压，区分包含全部孔隙水压的平衡总应力与不包含静水压的本构总应力。静水压在理论上总应单独计算，亦即“土水分算”，总应力法中直接计算的是本构总应力。

（2）Skempton与Henkel所提出的超静水压改进计算公式适用于不同的应力路径，其突出优点还在于将土在不排水条件下所产生的超静水压清晰地分为两部分，笔者分别称它们为弹性超静水压和塑性超静水压，前者不引起土内有效压应力均值的改变，而后者要改变土内有效压应力均值从而影响土的不排水强度。

（3）将Skempton-Henkel超静水压计算公式与MC强度准则相结合所构成的饱和土不排水强度模型，可用于分析饱和土的不排水强度特性。对等向固结与K₀固结土在平面应变剪切与三轴压剪、拉剪强度特性的分析结果，与文献中已有实测及理论分析结果基本吻合，表明所构建强度模型的合理性，也证明了Skempton-Henkel超静水压计算公式用于不同应力路径的适用性和准确性。

（4）饱和土不排水强度与排水强度的显著差异是，前者在土经受不排水剪切之前已基本确定，只要荷载所产生总应力的Lode角相同，则不管具体总应力路径如何，最大剪应力到一定值时土便破坏；而后者是与所加荷载密切相关的，荷载所产生总应力大小及具体应力路径不同，土的排水强度也不同。

（5）非等向固结土在不排水剪切时呈现非各向同性的原因是，当荷载引起的总应力使固结应力的小主应力发展为大主应力时，其不排水剪切路径长，产生的塑性超静水压大。

（6）进行土工结构的不排水稳定分析时，应考虑不排水强度的非各向同性，合理选择强度参数。不排水稳定分析的基本模型不再是排水条件下采用的MC模型，而应采用广义Tresca模型，输入与固结应力对应的不排水压剪和拉剪强度。采用MC模型按有效应力法计算不能准确计算土的不排水强度，应直接输入土的平均强度，对平面应变问题还可采用笔者提出的等代强度指标进行计算。

（7）固结不排水强度指标不是客观指标，将此种强度指标直接用于土工结构的稳定分析，仅当结构内各部位在不排水加载时的总应力路径与测试该强度指标的试验中相同时才是准确的。特别是对于地基承载力问题，用固结不排水指标直接计算会给出严重偏大的结果。合理的做法是按文中所建议的公式将此种强度指标转换为不排水强度再行计算。

（8）基坑工程中极限土压力也宜采用不排水强度并取${\varphi _{\text{u}}}$=0进行计算。如用固结不排水指标直接计算，则应土水分算，且对主动土压采用卸载压剪对应的固结不排水强度指标，对被动土压采用加载压剪强度指标。从加载压剪强度指标计算卸载压剪强度指标可采用本文建议的公式。

（9）目前常用地基极限承载力计算公式，无论太沙基公式还是汉森公式，均包含了叠加计算的近似，误差较大。通过深入分析埋深超载及地基土重度对地基承载力影响的内在机理，给出综合各因素影响的地基承载力计算的统一公式，对排水和不排水条件下的承载力计算均可给出较经典公式更准确的结果，从而能更好保证设计方案的安全和经济。

（10）本文提出的计算地基沉降的半侧限模型，克服了基础工程中一直应用的分层总和法采用侧限模量计算的缺陷，可以计算饱和地基的短期沉降，对地基的排水沉降也可望取得较好的结果，值得进一步发展完善。

以上是笔者就饱和土不排水强度及变形计算理论及方法的一些思考，希望能够对有关研究及工程应用以及规范规程的修订提供参考。由于问题的复杂性，还有不少方面需要进一步深入研究，希望引起同行的关注与讨论，推进中国土力学及岩土工程基本理论的发展与进步。笔者认为，正是因为土力学及岩土工程问题的高度复杂性，才更需要清晰的概念和严谨而辩证的思维。对于复杂问题可以在尽力理解清楚的基础上近似，而不可概念错误。按以错抵错的思路提出的方法不能推广，不利于总结经验、发展理论。