Shear wave velocity-based evaluation of liquefaction resistance of in-situ sand with aging effects
-
摘要: 剪切波速是评价饱和砂土抗液化强度的常用指标之一。在基于初始液化标准的砂土抗液化强度剪切波速表征模型（即“周-陈模型”）的基础上，进一步引入考虑沉积时间效应的修正系数，分别对原位测得的剪切波速和重塑砂土抗液化强度进行修正，使得“周-陈模型”能适用于原位砂土抗液化强度评价。针对云南巧家县某工程场地，进行原位剪切波速测试、现场取样并开展室内单元体试验，得到了“周-陈模型”的关键表征参数，据此建立了相应的地震液化剪切波速判别方法。利用该判别方法对该工程场地砂土层不同钻孔土层进行了地震液化判别，并与国内外其它液化判别方法进行比较，发现判别结果基本一致。本文发展的考虑沉积时间效应的剪切波速表征模型为评价实际工程场地原位砂土抗液化强度提供了有效手段。Abstract: The shear wave velocity is one of the commonly used parameters to evaluate liquefaction resistance of sandy soils. In this study, based on the initial liquefaction criterion-based shear wave velocity characterization model (i.e., the "Zhou-Chen model"), two correction parameters are intruduced to consider the aging effects to correct the field measured shear wave velocity and the liquefaction resistance of reconstituted sand, respectively, so that the "Zhou-Chen model" can be used to evaluate the liquefaction resistance of in-situ sandy soils. In an engineering case from Qiaojia County, Yunnan Province, both field measurements of shear wave velocity and laboratory testings are conducted to determine the parameters of the "Zhou-Chen model", and then a simplified procedure to evaluate liquefaction potential using the field shear wave velocity measurement is established. This simplified procedure is then used to evaluate the liquefaction potential of the engineering site, and the results are consistesnt with those by other methods. The proposed characterization model with further consideration of the aging effects provides a promising way to evaluate the liquefaction resistance of in-situ sandy soils with the ageing effects.
-
Keywords:
- liquefaction resistance /
- in-situ sand /
- aging effect /
- shear wave velocity /
- characterization model
-
0. 引言
钙质砂是由珊瑚骨骼、贝类、虫黄藻类等海洋生物残骸沉积而成，其主要组成成分是碳酸钙[1-3]，是我国南海岛礁吹填的主要材料。因其生成环境、成因以及物质组成等因素影响，钙质砂具有颗粒易破碎、形状极不规则、内孔隙发育、微观结构复杂等显著区别于陆源石英砂的特点[4-6]。随着“一带一路”国家战略和建设“海洋强国”政策方针的推进，研究钙质砂工程力学特性具有重要意义[7-9]。
钙质砂作为填方工程的天然材料，其应力状态复杂多变，土体受到各向异性应力状态影响而产生初始静剪应力，在建（构）筑物的自重和动荷载（波浪、地震和交通荷载等）作用下，易引起地基强度降低、变形过大以及液化失稳等灾害。实际上，动荷载作用下剪切应力做功将导致材料损伤效应的累积，不排水条件下表现为孔压增长。因此，可以将孔压的升高与土体颗粒在运动或重排过程中所耗损的能量建立关联。损耗能作为标量，相较于应力、应变等矢量，可直接数学叠加，大幅度降低分析难度。Nemat-Nasser等[10]首先提出了耗散能量的概念，建立其与残余孔压的关系，来有效地评估孔隙水压力的产生和发展过程。Kokusho[11]和Pan等[12]提出了土骨架破坏产生的单位体积耗散能与应变和残余孔压累积直接相关，为评价砂土在不规则循环应力条件下的抗液化能力提供了有效方法。总体而言，上述研究主要针对石英砂，能否适用于钙质砂仍需进一步探究。
本文以饱和钙质砂为研究对象，开展不排水条件下循环剪切三轴试验，探究相对密实度、初始静剪应力以及循环应力对其孔压发展的影响；同时，引入能量法，建立钙质砂孔压与损耗能之间联系，提出基于能量损耗的液化评价方法，为钙质砂地基稳定性分析提供理论依据和技术支撑。
1. 试验材料与方案
1.1 试验材料
本文试验材料为中国南海某岛礁的天然钙质砂，颗粒多呈灰白色，形状有片状、块状、棒状等，颗粒内孔隙多、微观结构复杂，如图 1所示。
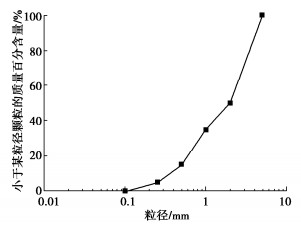
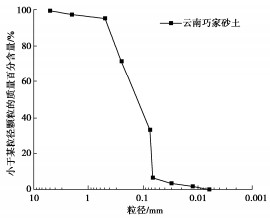
经过现场取材、清水冲洗、烘干等过程后，对粒径大于5 mm的颗粒进行剔除，处理后颗粒分布级配曲线如图 2所示，主要基本物理性质参数见表 1。不难发现，试样基本不含0.1 mm以下的细颗粒，不均匀系数和曲率系数分别为6.84和0.78，属于不良级配砂土。
表 1 钙质砂物理性质指标Table 1. Physical properties of calcareous sand相对质量密度 d50/
mm不均匀系数 曲率系数 最大孔隙比 最小孔隙比 2.79 2.0 6.84 0.78 1.15 0.87 1.2 试验方案
结合实际工况，采用CKC三轴试验系统模拟复杂应力条件下饱和钙质砂循环剪切试验，先进行有效围压为100 kPa的等向固结后再根据试验设计的初始静偏应力状态进行非等向固结，具体方案如表 2所示。初始静剪应力比SSR和循环应力比CSR可通过式（1）和（2）计算。
表 2 不排水循环剪切试验方案Table 2. Summary of undrained cyclic triaxial tests试验系列 相对密实度
Drqs/
kPaqcyc/
kPaSSR CSR Nf Ⅰ 70%
（密砂）0 20 0 0.1 232 0 25 0 0.125 74 0 30 0 0.15 17 0 40 0 0.2 6 20 30 0.1 0.15 168 20 45 0.1 0.225 19 20 50 0.1 0.25 3 50 50 0.25 0.25 53 50 60 0.25 0.3 11 50 70 0.25 0.35 6 80 70 0.4 0.35 14 80 80 0.4 0.4 7 -10 25 -0.05 0.125 78 -10 30 -0.05 0.15 39 -10 35 -0.05 0.175 8 -20 20 -0.1 0.1 210 -20 25 -0.1 0.125 11 -20 30 -0.1 0.15 8 -40 20 -0.2 0.1 57 -40 25 -0.2 0.125 16 -40 30 -0.2 0.15 8 Ⅱ 30%
（松砂）0 15 0 0.075 943 0 20 0 0.1 120 0 25 0 0.125 37 0 30 0 0.15 18 24 30 0.12 0.15 61 24 35 0.12 0.175 16 24 40 0.12 0.2 5 40 15 0.2 0.075 175 40 20 0.2 0.1 9 50 12.5 0.25 0.0625 17 50 15 0.25 0.075 2 -10 12.5 -0.05 0.0625 382 -10 15 -0.05 0.075 180 -10 20 -0.05 0.1 11 -20 10 -0.1 0.05 246 -20 12.5 -0.1 0.0625 202 -20 15 -0.1 0.075 12 -40 5 -0.2 0.025 104 -40 7.5 -0.2 0.0375 13 -40 10 -0.2 0.05 2 SSR=qs2p′0， (1) CSR=qcyc2p′0。 (2) 式中：qs为初始静剪偏应力；qcyc为循环偏应力；p′0为平均有效正应力。
2. 试验结果与分析
2.1 孔压特性发展规律
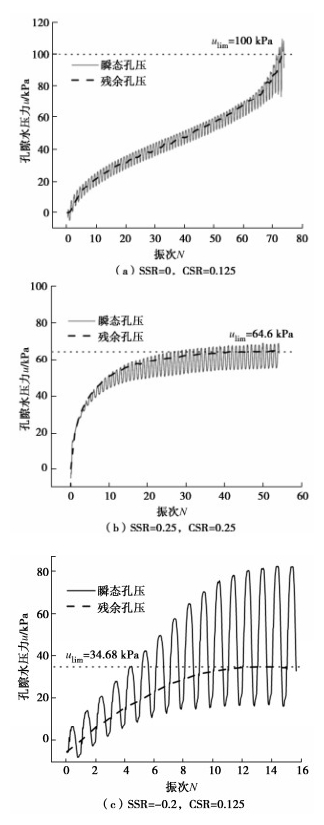
图 3给出不同初始偏应力作用下饱和密砂的孔压发展规律曲线。孔隙水压力可分为两类：①随着循环荷载作用实时变化的孔压，即实线所示的瞬态孔压，这种孔压会随着循环荷载的卸载而快速消散；②每个循环加载结束，试样未及时恢复的孔压，即虚线所示的残余孔压。从图 3（a）中可以看出，对于等向固结的试样，残余孔压在前期随着荷载的施加而逐渐累积，而在后期快速增长，直至达到荷载施加前的有效围压，ulim=100 kPa。如图 3（b）所示，在压缩静偏应力作用下，孔压在加载初期迅速累积，随着循环荷载持续进行，残余孔压逐渐趋于稳定，ulim=64.6 kPa。在拉伸静偏应力作用下，孔压发展与压缩静偏应力时有类似的变化趋势，孔压在加载初期累积较快而后基本保持不变，ulim=34.68 kPa。
同时，通过式（3）和（4）定义固结应力比Kc和残余孔压比ur。
Kc=σv0σh0， (3) ur=uσh0。 (4) 式中：σv0和σh0分别为初始有效竖向应力和水平应力，u为残余孔压。
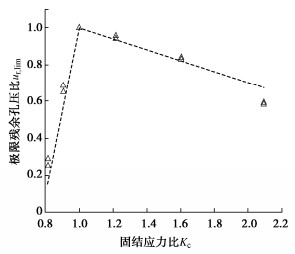
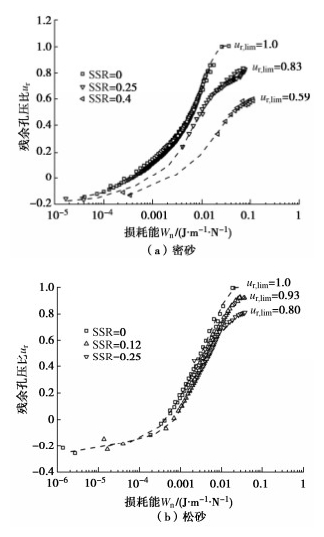
图 4给出了饱和密砂的极限残余孔压比和固结应力比的关系曲线。从图中可以看出，饱和密砂的极限残余孔压比随着固结应力比的增大呈先增大后减小的趋势，在Kc=1（等向固结）时，极限残余孔压比达到最大值ur, lim=1，且大致上呈线性分布，与循环应力幅值大小无明显关系。
![]()
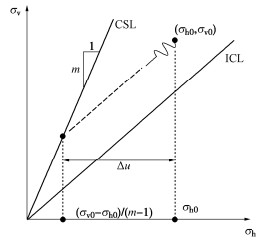
图 4 极限残余孔压比与固结应力比的关系Figure 4. Relationship between ultimate residual pore pressure ratio and consolidation stress ratio对于同一材料的砂土，其在循环荷载作用下有效应力路径将沿着平行于等向固结线（ICL）的方向逐渐靠近临界状态线（CSL），而与循环应力幅值无关，如图 5所示。因此，对于给定的初始应力状态（σh0，σv0），会与临界状态线相交于一点，且理论上初始应力点与最终应力点之间的水平距离Δu为试验中的极限残余孔压，如式（5）所示。根据ur和Kc定义，可得到两者关系如式（6），符合图 4所示的线性关系。
ulim=Δu=σh0−σv0−σh0m−1， (5) ur, lim=ulimσh0=1−Kc−1m−1。 (6) ![]()
图 5 初始静剪应力状态对残余孔压影响示意图Figure 5. Influences of initial static shear stress on residual pore pressure2.2 损耗能演化规律
动荷载作用下饱和砂土损耗的能量主要用于颗粒的相对运动和重新排列。因此，引入能量法，提出基于损耗能的砂土液化评价方法。循环加载过程中一个振次的损耗能W可用应力-应变滞回圈的面积表示，即：
W=n−1∑i=112(qi+1+qi)(εa, i+1−εa, i)。 (7) 式中：n为计算增量的总个数，qi和εa, i分别为第i个增量的偏应力和轴向应变。
图 6分别给出饱和钙质砂在不同初始静偏应力作用下残余孔压比与正交化损耗能的内在关系，正交化损耗能Wn为损耗能W与初始有效水平正应力σh0的比值。结果显示：饱和密砂的残余孔压初期增长缓慢，随着Wn的增大而较快增长，最后趋于稳定；在饱和松砂中也观察到类似的变化趋势。这说明残余孔压与损耗能的关系主要取决于初始应力条件。
![]()
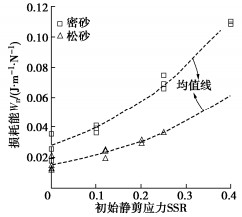
图 6 残余孔压比与损耗能的关系Figure 6. Relationship between residual pore pressure ratio and dissipated energy从图 7可以看出，饱和钙质砂在失稳破坏时所积累的损耗能随着初始静剪应力的增加而增加；对于同一初始应力状态，密砂所需能量始终大于松砂。研究表明[13-14]，饱和砂土在循环荷载作用下损耗能主要与初始应力和相对密实度有关，受循环荷载幅值影响极小，具体可用式（8）表示：
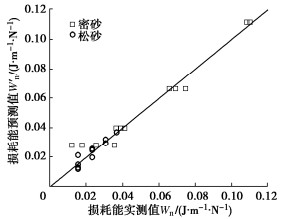
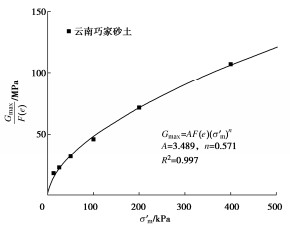
W′n=10a(Dr−0.78)10b(SSR−1.0)。 (8) ![]()
图 7 损耗能与初始静剪应力比的关系Figure 7. Relationship between dissipated energy and initial static shear stress ratio式中：a和b为经验参数，根据本次试验数据可分别取0.65，1.5。图 8对损耗能的试验实测值与通过式（8）所得的预测值进行对比，发现两者基本落在斜率为1的对角线两侧，表明能量模型可较好地预测不同试验条件下饱和钙质砂的损耗能。
3. 结论
（1）饱和钙质砂的极限残余孔压比随固结应力比呈先增大后减小的趋势，在Kc=1时存在最大值，临界状态理论可以解释此现象。
（2）不排水循环加载条件下饱和钙质砂的损耗能与试样的初始静剪应力比和相对密实度有关，受循环应力比影响极小，可通过构建的能量模型较好地预测不同试验条件下饱和钙质砂所累积的损耗能。
-
![]()
图 6 钻孔QFK01实测剪切波速Vs, M和估计剪切波速Vs, E
Figure 6. Values of Vs, M and Vs, E for borehole QFK01
![]()
图 7 钻孔QFK01内CSR和CRR随深度的变化
Figure 7. Variation of CSR and CRR with depth for borehole QFK01
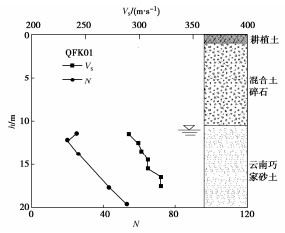
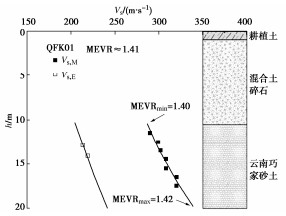
表 1 不同钻孔的沉积时间效应参数MEVR
Table 1 Values of aging effect parameter MEVR for different boreholes
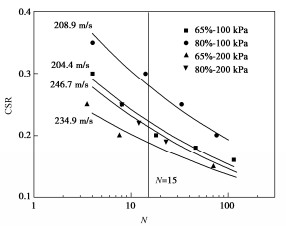
钻孔编号 测量波速Vs, M 估算波速Vs, E MEVR QFK01 312 m/s 221 m/s 1.41 QFK07 245 m/s 183 m/s 1.34 QFK17 288 m/s 191 m/s 1.51 QFK23 278 m/s 209 m/s 1.33 平均值/标准差 — — 1.40 / 0.07 
下载: 导出CSV
表 2 不同液化判别方法的地震液化判别结果
Table 2 Results of liquefaction evaluation by different methods
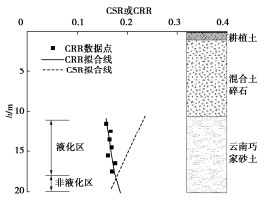
钻孔编号 砂层埋深/m 液化区深度/m 本研究方法 中国建规法 美国NCEER法 QFK01 10.5~20.0 10.5~18.4 10.5~19.0 10.5~18.1 QFK03 1.0~7.5 1.0~7.5 1.0~7.5 1.0~2.1 QFK04 2.7~8.4 2.7~8.4 2.7~8.4 2.7~8.4 QFK07 2.6~7.6 2.6~7.6 2.6~7.6 2.6~7.6 QFK17 5.3~11.8 6.2~11.8 5.3~11.8 7.5~11.8 QFK23 6.5~17.7 6.5~17.7 6.5~17.7 6.5~11.8 FZK312 14.5~17.5 无 无 无 FZK318 9.8~15.9 9.8~14.8 9.8~15.9 9.8~15.9
下载: 导出CSV
-
[1] SEED H B, IDRISS I M, ARANGO I. Evaluation of liquefaction potential using field performance data[J]. Journal of Geotechnical Engineering, 1983, 109(3): 458-482. doi: 10.1061/(ASCE)0733-9410(1983)109:3(458)
[2] YOUD T L, IDRISS I M. Liquefaction resistance of soils: summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(4): 297-313. doi: 10.1061/(ASCE)1090-0241(2001)127:4(297)
[3] 曹振中, 袁晓铭. 砂砾土液化的剪切波速判别方法[J]. 岩石力学与工程学报, 2010, 29(5): 943-951. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201005013.htm CAO Zhenzhong, YUAN Xiaoming. Shear wave velocity-based approach for evaluating gravel soils liquefaction[J]. Chinese Journal of Rock Mechanics and Engineering. 2010, 29(5): 943-951. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201005013.htm
[4] 陈国兴, 孙苏豫, 吴琪, 等. 基于剪切波速的砂砾土地震液化评价新方法[J]. 岩土工程学报, 2022, 44(10): 1763-1771. doi: 10.11779/CJGE202210001 CHEN Guoxing, SUN Suyu, WU Qi, et al. Shear wave velocity-based new procedure for assessing seismic liquefaction triggering of sand-gravel soils[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(10): 1763-1771. (in Chinese) doi: 10.11779/CJGE202210001
[5] 孙锐, 袁晓铭. 适于不同深度土层液化的剪切波速判别公式[J]. 岩土工程学报, 2019, 41(3): 439-447. doi: 10.11779/CJGE201903005 SUN Rui, YUAN Xiaoming. Depth-consistent vs-based approach for soil liquefaction evaluation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 439-447. (in Chinese) doi: 10.11779/CJGE201903005
[6] CHEN G X, WU Q, ZHAO K, et al. A binary packing material–based procedure for evaluating soil liquefaction triggering during earthquakes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(6): 04020040. doi: 10.1061/(ASCE)GT.1943-5606.0002263
[7] ZHOU Y G, CHEN Y M. Laboratory investigation on assessing liquefaction resistance of sandy soils by shear wave velocity[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(8): 959-972. doi: 10.1061/(ASCE)1090-0241(2007)133:8(959)
[8] ZHOU Y G, CHEN Y M, SHAMOTO Y. Verification of the soil-type specific correlation between liquefaction resistance and shear-wave velocity of sand by dynamic centrifuge test[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1): 165-177. doi: 10.1061/(ASCE)GT.1943-5606.0000193
[9] 赵倩玉, 孙锐. 适用于新疆场地的剪切波速液化判别公式[J]. 岩土工程学报, 2013, 35(增刊2): 383-388. http://cge.nhri.cn/cn/article/id/15413 ZHAO Qianyu, SUN Rui. A shear-wave velocity discrimination formula for liquefaction applicable to Xinjiang region[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 383-388. (in Chinese) http://cge.nhri.cn/cn/article/id/15413
[10] CHEN G X, KONG M Y, KHOSHNEVISAN S, et al. Calibration of Vs-based empirical models for assessing soil liquefaction potential using expanded database[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 945-957. doi: 10.1007/s10064-017-1146-9
[11] 周燕国, 丁海军, 陈云敏, 等. 基于原位测试指标的砂土时间效应定量表征初步研究[J]. 岩土工程学报, 2015, 37(11): 2000-2006. doi: 10.11779/CJGE201511009 ZHOU Yanguo, DING Haijun, CHEN Yunmin, et al. Characterization of ageing effect of sands based on field testing indices[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2000-2006. (in Chinese) doi: 10.11779/CJGE201511009
[12] 陈光仔, 蔡袁强, 王军, 等. 时间效应对砂土小应变动力特性影响及其细观机制研究[J]. 岩石力学与工程学报, 2013, 32(增刊2): 4215-4223. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2151.htm CHEN Guangzai, CAI Yuanqiang, WANG Jun, et al. Research of dynamic properties changes and microscopic mechnism of aging sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 4215-4223. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2151.htm
[13] 丁海军. 砂土液化时间效应的剪切波速表征研究[D]. 杭州: 浙江大学, 2015. DING Haijun. Shear Wave Velocity-Based Characterization of Aging Effect on Soil Liquefaction[D]. Hangzhou: Zhejiang University, 2015. (in Chinese)
[14] 周燕国, 沈涛, 王越, 等. 基督城易液化场地震后小应变剪切刚度演化规律研究[J]. 岩土工程学报, 2020, 42(8): 1411-1417. doi: 10.11779/CJGE202008005 ZHOU Yanguo, SHEN Tao, WANG Yue, et al. Post-earthquake evolution of small-strain shear stiffness at liquefiable deposit in Christchurch[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1411-1417. (in Chinese) doi: 10.11779/CJGE202008005
[15] LEON E, GASSMAN S L, TALWANI P. Accounting for soil aging when assessing liquefaction potential[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(3): 363-377. doi: 10.1061/(ASCE)1090-0241(2006)132:3(363)
[16] ANDRUS R D, HAYATI H, MOHANAN N P. Correcting liquefaction resistance for aged sands using measured to estimated velocity ratio[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 735-744. doi: 10.1061/(ASCE)GT.1943-5606.0000025
[17] BWAMBALE B, ANDRUS R D. State of the art in the assessment of aging effects on soil liquefaction[J]. Soil Dynamics and Earthquake Engineering, 2019, 125: 105658. doi: 10.1016/j.soildyn.2019.04.032
[18] ANDRUS R D, STOKOE K H. Liquefaction resistance of soils from shear-wave velocity[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(11): 1015-1025. doi: 10.1061/(ASCE)1090-0241(2000)126:11(1015)
[19] 袁晓铭, 卢坤玉, 林颖, 等. 哈尔滨地区砂土层N-V关系特征曲线及对比研究[J]. 地震工程与工程振动, 2020, 40(6): 1-15. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202006001.htm YUAN Xiaoming, LU Kunyu, LIN Ying, et al. The N-V relationship curve of sand layers in Harbin region and its comparison with those in other regions of China[J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(6): 1-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202006001.htm
[20] BRADLEY K, MALLICK R, ANDIKAGUMI H, et al. Earthquake-triggered 2018 Palu Valley landslides enabled by wet rice cultivation[J]. Nature Geoscience, 2019, 12(11): 935-939. doi: 10.1038/s41561-019-0444-1
[21] 董菲蕃, 陈国兴, 金丹丹. 福建沿海3个盆地的土层剪切波速与深度的统计关系[J]. 岩土工程学报, 2013, 35(增刊2): 145-151. http://cge.nhri.cn/cn/article/id/15372 DONG Feifan, CHEN Guoxing, JIN Dandan. Statistical relation between shear wave velocity and depth of soils in three basins in coastal area of Fujian province[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 145-151. (in Chinese) http://cge.nhri.cn/cn/article/id/15372
[22] 王琦, 刘红帅, 郑桐, 等. 天津地区覆盖土层剪切波速与埋深的相关性分析[J]. 地震工程与工程振动, 2018, 38(6): 190-201. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201806022.htm WANG Qi, LIU Hongshuai, ZHENG Tong, et al. Correlation analysis between shear wave velocity and depth of covering soils in Tianjin[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(6): 190-201. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201806022.htm
[23] LIAO S S C, WHITMAN R V. Overburden correction factors for SPT in sand[J]. Journal of Geotechnical Engineering, 1986, 112(3): 373-377. doi: 10.1061/(ASCE)0733-9410(1986)112:3(373)
[24] 中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2016[S]. 北京: 中国建筑工业出版社, 2016. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for Investigation of Geotechnical Engineering: GB 50021—22001[S]. Beijing: China Architecture and Building Press, 2016. (in Chinese)
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
