饱和砂-黏及砂-粉-黏混合土动孔压特性

李涛; 唐小微; 曾铃; 杨钢

doi:10.11779/CJGE2023S20044

饱和砂-黏及砂-粉-黏混合土动孔压特性 English Version

李涛^{1, 2,},
唐小微²,
曾铃¹,
杨钢²

1.
长沙理工大学土木工程学院, 湖南长沙 410114
2.
大连理工大学海岸和近海工程国家重点实验室, 辽宁大连 116024

基金项目:

国家自然科学基金项目 52308339

海岸和近海工程国家重点实验室开放基金项目 LP2110

桥梁工程安全控制教育部重点实验室开放基金项目 23ZDXK10

湖南省教育厅一般项目 22C0143

详细信息

作者简介:
李涛(1989—)，男，博士，讲师，主要从事混合砂土液化试验及理论等方面的研究工作。E-mail: litao@csust.edu.cn

中图分类号: TU435
计量
- 文章访问数: 122
- HTML全文浏览量: 25
- PDF下载量: 26
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Dynamic pore water pressure characteristics of saturated sand-clay and sand-silt-clay mixtures

1.
School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China
2.
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China

摘要

摘要: 含细粒砂土在吹填土中广泛分布，其在长期服役过程中可能经受波浪及车辆荷载的循环作用，掌握含细粒砂土动孔隙水压力的变化特性对于评价吹填土在循环荷载作用下的安全性及稳定性尤为重要。通过对饱和重塑砂-黏混合土及砂-粉-黏混合土开展室内固结不排水循环三轴试验，研究了不同黏粒含量、细粒含量、黏粉比和孔隙比下砂-黏混合土及砂-粉-黏混合土动孔压的发展特征。结合不同混合土内部颗粒赋存状态光学显微镜图像及颗粒赋存状态理论，揭示了黏粒含量、细粒含量、黏粉比和孔隙比对混合土动孔压发展的影响规律及影响机理。试验结果表明：对于砂骨架孔隙比与孔隙比恒定的砂-黏混合土来说，随着黏粒含量的增加，动孔压在振动后期的波动性增长趋势分别增强、减弱；对于砂-粉-黏混合土来说，随着细粒中粉粒含量增多（黏粒含量减少），FC=5%试样动孔压在振动后期的波动性增长趋势呈现非单调变化规律，不同孔隙比下FC=10%试样动孔压在振动后期的波动性增长趋势单调增强；提出了适用于砂-黏混合土以及砂-粉-黏混合土动孔压发展的Mod-Baziar模型，该模型不仅扩展了动孔压的预测范围，而且具有更高的预测精度，其可以更好反映动孔压的整体发展趋势以及孔压在振动后期的细节变化；当采用Mod-Baziar模型分别对不同孔隙比下的纯砂、砂-黏混合土以及砂-粉-黏混合土动孔压进行预测时，模型中各个参数的取值范围依次增大。初步分析认为上述试验结果是由不同颗粒间复杂的黏结、摩擦及填充作用所致。
- 混合土 /
- 黏粒含量 /
- 细粒含量 /
- 黏粉比 /
- 动三轴试验 /
- 动孔压模型
Abstract: The sand-fines mixtures are widely distributed in hydraulic fill soil and may be subjected to the cyclic action of wave and vehicle loads during their long-term service. It is very important to know the dynamic pore water pressure changing characteristics of the sand-fines mixtures for evaluating the safety and stability of hydraulic fill soil under cyclic loading. The consolidated undrained cyclic triaxial tests are carried out on the saturated reconstituted sand-clay and sand-silt-clay mixtures to investigate the development features of dynamic pore water pressure of mixed soil with different clay contents, fines contents, clay silt ratios and void ratios. By combining with the optical microscope images of soil particles and the theory of soil particles occurrence modes, the influence laws and mechanisms of clay content, fines content, clay silt ratio and void ratio on the dynamic pore water pressure of mixed soils are revealed. It is find that for the sand-clay mixtures (constant e and constant e_s), with the increasing clay contents, the fluctuation growth trend of dynamic pore water pressure at the later stage of vibration increases and weakens respectively. For the sand-silt-clay mixtures, with the increasing silt contents (decreasing clay contents), the fluctuation growth trend of the dynamic pore water pressure at the later stage of vibration of specimens with FC of 5% changes nonmonotonously. While the fluctuation growth trend of the dynamic pore water pressure at the later stage of vibration of specimens with FC of 10% increases monotonically under different void ratios. The Mod-Baziar model applied to the development of dynamic pore water pressure of sand-clay mixtures and sand-silt-clay mixtures is proposed, which extends the prediction range of dynamic pore water pressure and has higher prediction accuracy. The Mod-Baziar model can better reflect the overall development trend and detail change at the later stage of dynamic pore water pressure. By comparing the values of each parameter in the Mod-Baziar model, it is found that when the Mod-Baziar model is used to predict the dynamic pore water pressure of sand, sand-clay mixtures and sand-silt-clay mixtures with different void ratios respectively, the value range of each parameter in the model increases successively. The preliminary analysis suggests that the above results are attributed to the complex bonding, friction and filling between different particles.
- mixed soil /
- clay content /
- fines content /
- clay silt ratio /
- dynamic triaxial test /
- dynamic pore water pressure model

HTML全文

0. 引言

众多吹砂填海造地工程以及人工岛填筑工程中用到了大量含细粒砂土，这些场地中的土体在波浪和车辆等荷载的循环往复作用下，土中孔隙水压力不断累积和发展，继而进一步影响土体的变形和强度，最终导致土体发生液化。众多液化灾害表明^[1]，发生液化的砂土中很大一部分都包含一定量的细粒（黏粒和粉粒），而对动孔压进行精准预测已成为液化研究领域的关键问题之一。针对饱和砂土动孔压的发展特征，Seed等^[2]发现饱和砂土动孔压在振动全周期内的增长速率不固定，并提出了反正弦经验公式对孔压的发展过程进行模拟，随后将该模型推广到了含粉粒砂土动孔压的预测中；Booker等^[3]对Seed所提动孔压模型进行简化，给出了形式更为简单的动孔压模型；Baziar等^[4]进一步对Booker所提动孔压模型进行完善，扩展了动孔压模型的适用范围。国内在纯净砂土动孔压研究方面，许成顺等^[5]对不同密实度福建标准砂进行了不同振动频率的循环扭剪试验，发现动孔压受加载频率影响；董青等^[6]基于饱和砂土不排水循环三轴试验，提出了可以同时模拟循环加载作用下孔压增长以及卸载时孔压减小的模型。针对含细粒砂土动孔压发展特征，王桂萱等^[7]发现细粒含量越低，动孔压上升幅度速度越快，细粒含量越高，动孔压上升速度越慢；吴琪等^[8]通过对饱和珊瑚砂进行不排水循环扭剪试验后得出细粒含量增加会导致动孔压随循环振次发展速率增大的结论。关于动孔压发展的内在机理方面，张伏光等^[9]通过三维离散元模拟，发现颗粒间胶结的存在能够抑制孔压的发展，并且给出随着动应力的增加，颗粒间胶结先破坏，摩擦后起作用的结论；而王志华等^[10]通过多组不排水循环三轴试验，证实了液化过程中土体内部结构破坏过程与动孔压累积增长过程存在等价关系，并指出动孔压累积是触发可液化土体内部网状结构渐进破坏的原因。

总体来看，目前绝大多数动孔压模型主要适用于饱和砂土、粉土以及砂中掺杂非塑性粉粒的砂-粉混合土，可以考虑黏粒黏性影响的动孔压发展预测模型还未见诸于报道。为此本文分别以砂骨架孔隙比e_s和孔隙比e为制样控制参数，对黏粒含量CC=0（纯砂）、5%，10%的砂-黏混合土，细粒含量FC=5%，10%，黏粉比CS（黏粒含量与粉粒含量之比）=0.25，1，4的砂-粉-黏混合土进行固结不排水循环三轴试验。结合混合土细观观测结果，提出颗粒状态赋存理论；基于该理论，考虑本文动孔压发展特征，建立适用于砂-黏混合土和砂-粉-黏混合土动孔压发展的预测模型。

1. 试验概况

1.1 土体参数

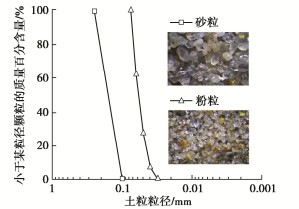
试验所用砂粒为粒径在0.1~0.25 mm的福建标准砂，其平均粒径d₅₀=0.158；粉粒提取自大连某建筑场地粉土，其粒径范围为0.02~0.075 mm，平均粒径d₅₀=0.058；黏粒为钙基商用膨润土，其液限w_L=104%，塑限w_P=52%，塑性指数I_P=52。图 1为试验所用砂粒和粉粒的颗粒级配曲线以及光学显微镜视角下的细观形貌特征，可以发现，这两种颗粒的细观形貌特征比较相近，只是在颗粒粒径大小方面存在较大差别。

图 1 试验所用砂粒和粉粒的颗粒级配曲线

Figure 1. Grain-size distribution curves of sand and silt

下载: 全尺寸图片幻灯片

1.2 试样制备及试验方法

试样尺寸为39.1 mm×80 mm（直径×高度）。为了保证其均匀性，首先对每一份（共四份）粗细粒混合土样在干燥状态下进行充分拌和，然后再分别向每份拌和好的干燥土样中加入6%的无气水，随后对含水土样进行充分拌和，按照分层湿装法对四份已拌合均匀的土样进行击实。之后采用机器饱和法对三轴试样进行饱和，当孔隙水压力系数B＞0.95时，即认为试样达到饱和。为了初步反映波浪或车辆荷载对土体液化的影响，本文首先采用CKC全数字闭环控制气动式三轴仪对试样进行等压固结（ ${\sigma _3}$ =200 kPa），然后对完成固结的试样继续施加只有压应力形式的竖向半正弦循环荷载 ${\sigma _{\text{d}}}$ ，加载频率f=0.5 Hz，试验结束标准为：动轴向应变 ${\varepsilon _{\text{a}}}$ =30%。全程记录试验过程中孔隙水压力数据。以上试验操作流程均按照《土工试验方法标准》^[11]执行，试验具体设计方案见表 1。同时为了探究混合土动孔压变化的内在机理，采用土颗粒染色与光学显微镜观测相结合的方法对表 1中试样的细观特征进行观测，具体观测流程如图 2所示。

表 1 试验设计方案

Table 1. Design schemes of dynamic tests

试验编号	细粒含量FC/%	细粒中黏、粉占比/%		黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
试验编号	细粒含量FC/%	黏粒	粉粒	黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
D1	0	－	－	－	200	0.9800	0.9800
D2	5	20	80	0.25	200	0.9800	0.8823
D3		50	50	1	200	0.9800	0.8823
D4		80	20	4	200	0.9800	0.8823
D5		100	0	－	200	0.9800	0.8823
D6	10	20	80	0.25	200	0.9800	0.7967
D7		50	50	1	200	0.9800	0.7967
D8		80	20	4	200	0.9800	0.7967
D9		100	0	－	200	0.9800	0.7967
D10	0	－	－	－	200	0.8823	0.8823
D11	10	20	80	0.25	200	1.0704	0.8823
D12		50	50	1	200	1.0704	0.8823
D13		80	20	4	200	1.0704	0.8823
D14		100	0	－	200	1.0704	0.8823

下载: 导出CSV

| 显示表格

图 2 混合土细观特征观测流程

Figure 2. Observation process of micro-characteristics of mixed soil

下载: 全尺寸图片幻灯片

1.3 试验结果与分析

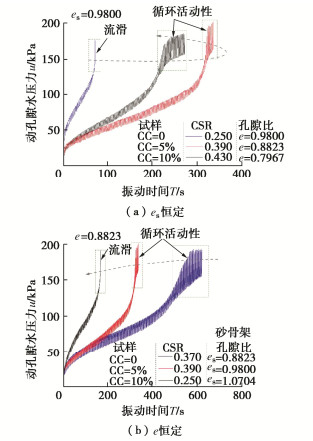
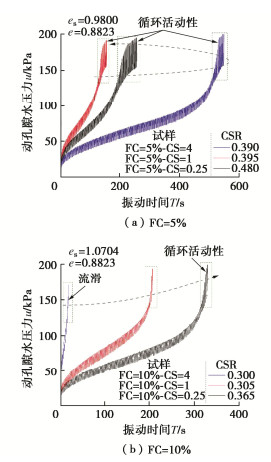
图 3为砂-黏混合土动孔压试验结果。可以看到当e_s恒定时，随着CC增加，动孔压在振动后期的波动性增长趋势逐渐增强（图 3（a）），试样液化破坏形式由流滑^[5]（纯砂）向循环活动性^[12]（CC=5%及CC=10%）转变。相反，当e恒定时，随着CC增加，动孔压在振动后期的波动性增长趋势逐渐减弱（图 3（b）），试样液化破坏形式由循环活动性（纯砂和CC=5%）向流滑（CC=10%）转变。图 4为砂-黏混合土细观特征图像，图中透明颗粒为砂粒，红色颗粒为染色黏粒。从图中可以看到，砂粒与黏粒均匀分布，黏粒含量较低时（CC=5%），黏粒分布在砂颗粒表面、填充于砂颗粒孔隙之中，黏粒含量较高时（CC=10%），除了上述的黏粒外，较多黏粒聚集成团，填充于砂颗粒孔隙之中并胶结砂颗粒。

图 3 砂-黏混合土动孔压试验结果

Figure 3. Dynamic pore water pressures of sand-clay mixtures

下载: 全尺寸图片幻灯片

图 4 砂-黏混合土细观特征图像

Figure 4. Microscopic feature images of sand-clay mixtures

下载: 全尺寸图片幻灯片

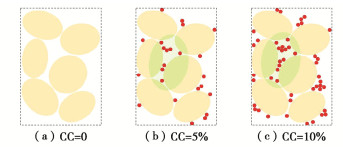
具体从细观角度分析，当e_s恒定时，试样内部砂颗粒间的距离几乎一致（图 5），当CC=5%时，一部分黏粒附着于砂颗粒表面，一部分黏粒填充在砂颗粒孔隙之中，还有一部分黏粒散落在砂颗粒之间的接触点位上（图 5（b））；当CC=10%时，土中黏粒含量总体增多，更多黏粒填充在砂颗粒孔隙之中、附着于砂颗粒表面以及散落在砂颗粒之间的接触点位上，此时接触点位上的黏粒逐渐聚集成直径较大的黏粒聚集体，对砂粒起黏结作用（图 5（c））。黏粒的堵塞、黏结阻滞了孔压的增长，这使得动孔压在振动后期波动性增长趋势增强，该发现与张伏光等^[9]得出的颗粒间胶结能够抑制土体孔压发展的结论相类似。

图 5 砂-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 5. Contact states of sand-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

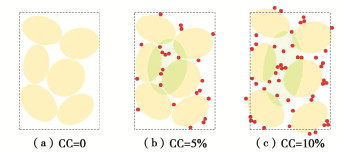
当e相同时，试样内部粗细颗粒间距离几乎一致（图 6）。在砂-黏混合土中，黏粒同样分别填充在砂颗粒孔隙之中、附着于砂颗粒表面以及散落在砂颗粒之间的接触点位上。当CC=5%时，为了使粗细颗粒间距离（孔隙）维持恒定，此时单位体积内砂颗粒数量减少，砂粒与砂粒之间的接触减少，土体骨架作用降低（图 6（b）），继而土体抵抗变形能力减弱，因此CC=5%试样动孔压在振动后期表现出较快的增长趋势（较低的波动性增长趋势）。CC=10%试样中黏粒含量更高，其内部砂粒质量更少，虽然该试样中较多的黏粒使颗粒间黏结效应更强，但更多黏粒的加入也无法有效弥补砂颗粒骨架作用的损失（图 6（c）），因此土体抵抗变形的能力最弱，最终致使CC=10%试样动孔压在振动后期增长趋势最快（波动性增长趋势最弱）。

图 6 砂-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 6. Contact states of sand-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

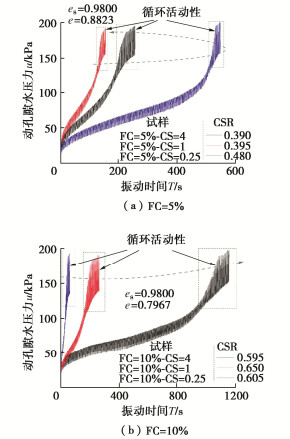
图 7和图 8为砂-粉-黏混合土动孔压试验结果。可以看到，当FC=10%时，无论e_s恒定或是e恒定时，随着CS减小，振动后期动孔压波动性增长趋势逐渐增强，试样在液化时循环活动性特征逐渐增强亦或液化模式逐渐由流滑向循环活动性转变。当FC=5%时，随着CS减小，振动后期动孔压波动性增长趋势并非单调变化。

图 7 砂-粉-黏混合土动孔压试验结果（e_s恒定）

Figure 7. Dynamic pore water pressures of sand-silt-clay mixtures (constant e_s)

下载: 全尺寸图片幻灯片

图 8 砂-粉-黏混合土动孔压试验结果（e恒定）

Figure 8. Dynamic pore water pressures of sand-silt-clay mixtures (constant e)

下载: 全尺寸图片幻灯片

图 9^[13]为砂-粉-黏混合土细观特征图像，图中透明颗粒为砂粒，红色颗粒为染色黏粒，蓝色颗粒为染色粉粒。从图中可以看出，在砂-粉-黏混合土中，各种粗细颗粒均匀分布；黏粒和粉粒对砂粒的填充、黏结及骨架作用同时存在，随着细粒中黏粒与粉粒相对含量的变化，上述作用呈现出不同的主导地位；当黏粒含量较低时，黏粒主要分布在砂颗粒或粉颗粒表面，当黏粒含量较高时，除了分布在粗颗粒表面的黏粒外，黏粒或聚集成团，或包裹砂粒或粉粒。当粉粒含量较低时，粉粒主要分散在砂颗粒孔隙之中，当粉粒含量较高时，除了分散在孔隙之中的粉粒外，粉粒还与砂粒共同起到土体骨架作用。FC=5%试样中细粒含量整体偏少，此时细粒主要填充在砂颗粒孔隙之中（图 10）。在FC=5%-CS=1试样中，黏粒和粉粒“含量相当”，此时这两种细粒填充在砂颗粒孔隙之中并相互黏结，只有极少数细粒扮演土骨架作用或黏附于砂颗粒表面（图 9（b）和图 10（b））；在FC=5%-CS=4和FC=5%-CS=0.25试样中，黏粒与粉粒分别相对过剩，而这些细粒中“含量相当”的黏粒与粉粒填充在砂颗粒孔隙之中并相互黏结。FC=5%-CS=0.25试样中部分“剩余”粉粒扮演土骨架角色，同时粉粒也增强了砂颗粒之间的摩擦作用，该作用不断抑制颗粒之间的相互移动（图 9（a）和图 10（a）），进而延缓了土体结构崩塌的速度，从而在振动后期该试样动孔压波动性增长趋势较为强烈；而在FC=5%-CS=4试样中，“剩余”的黏粒散落在砂颗粒表面及接触点位上，这些黏粒一定程度上增强了砂颗粒间的黏结作用，进而不断抑制颗粒之间的相互移动（图 9（c）和图 10（c）），从而在振动后期该试样动孔压波动性增长趋势也较为显著。由于土属于摩擦型材料，因此可以合理推断，粉粒对砂颗粒的摩擦作用强于黏粒对砂颗粒的黏结作用，从而FC=5%-CS=0.25试样在振动后期动孔压波动性增长趋势比FC=5%-CS=4试样更为明显。与此同时相比于FC=5%-CS=1试样来说，FC=5%-CS=0.25试样及FC=5%-CS=4试样中，除了“含量相当”的黏粒与粉粒相互黏结外，“剩余”粉粒和黏粒对土体强度也会起到增强作用，这些因素都使得这两种试样在振动后期动孔压波动性增长趋势强于FC=5%-CS=1试样。对于具有相同e_s的FC=10%试样（图 11）来说，其细粒含量高于FC=5%试样，此时细粒对砂颗粒的摩擦及黏结作用总体上超过细粒对砂颗粒孔隙的填充作用，同时同样由于粉粒对砂颗粒的摩擦作用强于黏粒对砂颗粒的黏结作用，因此随着CS降低，振动后期试样动孔压波动性增长趋势单调增强。同样的分析也适用于e恒定条件下的FC=10%试样（图 12）。此外，通过观察图 7和图 8可以发现，FC=10%-e_s=0.9800试样在振动后期动孔压波动性增长趋势较FC=10%-e= 0.8823试样更为明显。通过图 11及图 12分析可知，虽然两种试样的细粒含量相同，但FC=10%-e_s=0.9800试样孔隙比更小（0.7967），粗细颗粒间接触更紧密，单位体积内黏粒和粉粒对砂骨架的影响更大，从而直接影响动孔压在振动后期的增长模式，最终表现出FC=10%-e_s=0.9800试样在振动后期动孔压波动性增长趋势强于FC=10%-e=0.8823试样。

图 9 砂-粉-黏混合土细观特征图像^[13]

Figure 9. Microscopic feature images of sand-silt-clay mixtures^[13]

下载: 全尺寸图片幻灯片

图 10 砂-粉-黏混合土颗粒接触状态示意图

Figure 10. Contact states of sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

图 11 砂-粉-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 11. Contact states of sand-silt-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

图 12 砂-粉-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 12. Contact states of sand-silt-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

2. 混合土动孔压模型

研究动荷载作用下孔隙水压力的变化规律对土体液化预测和评价尤为重要。从图 3、图 7和图 8中可以看到，本文所有动孔压数据均表现出反正弦函数特征，但在振动后期动孔压增长模式又有所区别：动孔压直接达到围压；动孔压交替式达到围压。截止目前，众多学者提出多种动孔压模型对具有反正弦特征的动孔压试验结果进行预测和分析，其中Seed^[2]反正弦函数预测模型最为经典。接下来首先对包括Seed模型在内的三种经典动孔压模型进行回顾，之后以其为基础并结合本文动孔压的发展特征，经过一定的数学推导，提出一个更为准确、有效的适用于砂-黏混合土以及砂-粉-黏混合土动孔压发展的预测模型。

2.1 经典动孔压模型回顾

上文指出，基于对纯砂和含粉粒砂土动孔压发展规律的认识，Seed提出了反正弦动孔压模型（式（1））；Booker和Baziar在此基础上进行简化并提出各自的动孔压模型（式（2）和（3））。

（1）Seed模型

$u/{\sigma '_{\text{c}}} = 1/2 + 1/{\rm{\mathsf{π}}}\arcsin [2{(N/{N_{\text{f}}})^{\frac{1}{\theta }}} - 1] \text{；}$

(1)

（2）Booker模型

$u/{\sigma '_{\text{c}}} = 2/{\rm{\mathsf{π}}}\arcsin {(N/{N_{\text{f}}})^{\frac{1}{{2\theta }}}} \text{；}$

(2)

（3）Baziar模型

$u/{{\sigma }^{\prime }}_{\text{c}}=2/{\rm{\mathsf{π}}}\mathrm{arcsin}{(N/{N}_{\text{f}})}^{\frac{1}{2\theta }}+\beta \sqrt{\left[1-{\text{(2}\cdot (N/{N}_{\text{f}})-1\text{)}}^{2}\right]}。$

(3)

式中：u为动孔压； ${\sigma '_{\text{c}}}$ 为初始有效围压；N为循环振次；N_f为循环破坏振次；θ、β为模型参数。

经验证发现，Seed和Booker模型的预测结果几乎相同，Baziar模型与Seed和Booker模型之间差异较大。此外上述三种动孔压模型主要适用于纯砂或含粉粒砂土，当向砂中掺入塑性细粒（黏粒）时，上述模型是否依然适用有待商榷。本文随机选取两组动孔压试验结果，以动孔压比R_u=0.9作为试样破坏标准，对上述三种动孔压模型预测效果进行综合评估。由于Seed和Booker模型预测结果几乎相同，这里选用形式较为简单的Booker模型与Baziar模型对所选取的两组动孔压试验结果进行拟合，结果如图 13所示。

图 13 三模型对混合土动孔压的拟合结果

Figure 13. Fitting results of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

从图 13可以看出，Booker和Baziar模型对CC=5%及FC=10%-CS=1试样动孔压的整体发展趋势拟合效果较为一般，其中Baziar模型的拟合效果稍好一些。进一步观察可知，这两种动孔压模型都较难精确描述动孔压在振动后期的细节变化，因此建立适用于本文动孔压发展的预测模型显得尤为重要。

2.2 混合土动孔压模型建立

下面结合本文混合土动孔压发展特征，以Baziar模型为基础，经过一定数学推导和分析，提出适用于砂-黏混合土及砂-粉-黏混合土动孔压发展的预测模型，并将其命名为Mod-Baziar模型，其表达式如下：

$u/{\sigma '_{\text{c}}} = 2/{\rm{\mathsf{π}}}\arcsin {(N/{N_{\text{f}}})^{\frac{1}{{2\theta }}}} + \beta \sqrt {\left[ {1 - {{(2 \cdot (N/{N_{\text{f}}}) - 1)}^2}} \right]} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\gamma ({{\text{e}}^{N/{N_{\text{f}}}}} - 1)/{{\text{e}}^{\omega \cdot (N/{N_{\text{f}}})}} 。$

(4)

式中：u为动孔压； ${\sigma '_{\text{c}}}$ 为初始有效围压；N为循环振次；N_f为循环破坏振次； $\theta ,{\text{ }}\beta ,{\text{ }}\gamma ,{\text{ }}\omega$ 均为模型参数。

可以看出，Mod-Baziar模型可退化为Baziar和Booker模型。下一步采用Mod-Baziar模型再次对图 13的动孔压试验结果进行拟合，为了便于比较，将三种动孔压模型拟合结果绘制在同一坐标下，如图 13所示。由图 13可知，相比于Booker和Baziar模型，Mod-Baziar模型可以对动孔压整体发展趋势和振动后期的细节变化做出更为准确的预测。接下来采用上述三种动孔压模型对本文所有动孔压试验结果进行拟合，具体拟合度结果如图 14所示，从图 14可以看到，Mod-Baziar模型对各试样动孔压的拟合度最高。

图 14 三模型对各个试样动孔压的拟合度

Figure 14. R-squared of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

图 15为本文所有混合土动孔隙水压力比与归一化循环振次的关系。可以看到，拟合度相对较高的Baziar模型（图中阴影部分）在描述土体动孔压发展特征时还稍显不足，尤其当动孔压接近围压时，该模型预测结果与真实孔压相差较多。而Mod-Baziar模型（图中蓝色虚线所示）对动孔压的整体发展趋势及细节变化都能给出较好的反映，由此可以看出该模型可以对本文土体动孔压发展给出更为满意的预测结果。

图 15 饱和砂-黏、砂-粉-黏混合土动孔压发展

Figure 15. Development of dynamic pore water pressure for saturated sand-clay and sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

表 2列出了不同类型混合土动孔压试验结果采用Mod-Baziar模型预测后的参数取值范围。可以看到，当采用Mod-Baziar模型对表 1中不同土体动孔压试验结果进行拟合时，参数θ取值范围为1.2~2.5，参数β取值范围为0~-0.5，参数 $\gamma$ 取值范围为-0.6~1.9；参数ω取值范围为-2.9~3.9。

表 2 Mod-Baziar模型拟合参数取值范围

Table 2. Fitting parameter ranges of Mod-Baziar model

土体	模型参数
土体	θ	β	γ	ω
纯砂	1.5430~2.0362	-0.0057~-0.2760	0.1152 ~0.5637	0.4136~1.9222
砂-黏	1.3227~2.3576	-0.1089~-0.4709	0.0132~1.4852	-2.0889~2.7362
砂-粉-黏	1.2490~2.4263	-0.0510~-0.4252	-0.5369~1.8854	-2.8496~3.8353

下载: 导出CSV

| 显示表格

此外通过进一步对比可以发现，纯砂试样的4个模型参数分布范围最小，砂-黏混合土模型参数分布范围有所扩大，砂-粉-黏混合土模型参数分布范围最大（见图 16）。由此可以看出，砂中随着黏粒和粉粒的加入，基于Mod-Baziar模型得到的模型参数范围有所扩大，这也间接表明了在动荷载作用下，黏粒和粉粒的加入对土体孔压发展的影响在逐步扩大。

图 16 Mod-Baziar模型中各个参数取值范围

Figure 16. Value ranges of each parameter in Mod-Baziar model

下载: 全尺寸图片幻灯片

3. 结论

本文对砂-黏混合土以及砂-粉-黏混合土进行了室内固结不排水循环三轴试验，初步探讨了这两类混合土的动孔压发展特性，并提出可以准确描述其动孔压变化的预测模型。主要得出以下结论：

（1）随着CC增加，e_s与e恒定时的砂-黏混合土在振动后期动孔压波动性增长趋势分别增强、减弱；随着CS减小，FC=5%砂-粉-黏混合土在振动后期动孔压波动性增长趋势呈现出非单调变化规律，而不同e下FC=10%砂-粉-黏混合土在振动后期的动孔压波动性增长趋势单调增强。

（2）当采用Mod-Baziar模型依次对纯砂、砂-黏混合土以及砂-粉-黏混合土动孔压进行预测时，模型中各个参数的取值范围逐渐增大。这一规律间接表明黏粒和粉粒的加入对土体动孔压发展的影响在逐步扩大。目前关于这种影响的内在机理研究还不够深入，未来拟继续从颗粒细观角度定量分析Mod-Baziar模型参数的演化规律。

图 1 试验所用砂粒和粉粒的颗粒级配曲线

Figure 1. Grain-size distribution curves of sand and silt

下载: 全尺寸图片幻灯片

图 2 混合土细观特征观测流程

Figure 2. Observation process of micro-characteristics of mixed soil

下载: 全尺寸图片幻灯片

图 3 砂-黏混合土动孔压试验结果

Figure 3. Dynamic pore water pressures of sand-clay mixtures

下载: 全尺寸图片幻灯片

图 4 砂-黏混合土细观特征图像

Figure 4. Microscopic feature images of sand-clay mixtures

下载: 全尺寸图片幻灯片

图 5 砂-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 5. Contact states of sand-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

图 6 砂-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 6. Contact states of sand-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

图 7 砂-粉-黏混合土动孔压试验结果（e_s恒定）

Figure 7. Dynamic pore water pressures of sand-silt-clay mixtures (constant e_s)

下载: 全尺寸图片幻灯片

图 8 砂-粉-黏混合土动孔压试验结果（e恒定）

Figure 8. Dynamic pore water pressures of sand-silt-clay mixtures (constant e)

下载: 全尺寸图片幻灯片

图 9 砂-粉-黏混合土细观特征图像^[13]

Figure 9. Microscopic feature images of sand-silt-clay mixtures^[13]

下载: 全尺寸图片幻灯片

图 10 砂-粉-黏混合土颗粒接触状态示意图

Figure 10. Contact states of sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

图 11 砂-粉-黏混合土颗粒接触状态示意图（e_s=0.9800）

Figure 11. Contact states of sand-silt-clay mixtures(e_s=0.9800)

下载: 全尺寸图片幻灯片

图 12 砂-粉-黏混合土颗粒接触状态示意图（e=0.8823）

Figure 12. Contact states of sand-silt-clay mixtures(e=0.8823)

下载: 全尺寸图片幻灯片

图 13 三模型对混合土动孔压的拟合结果

Figure 13. Fitting results of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

图 14 三模型对各个试样动孔压的拟合度

Figure 14. R-squared of Booker, Baziar and Mod-Baziar models for dynamic pore water pressure of mixtures

下载: 全尺寸图片幻灯片

图 15 饱和砂-黏、砂-粉-黏混合土动孔压发展

Figure 15. Development of dynamic pore water pressure for saturated sand-clay and sand-silt-clay mixtures

下载: 全尺寸图片幻灯片

图 16 Mod-Baziar模型中各个参数取值范围

Figure 16. Value ranges of each parameter in Mod-Baziar model

下载: 全尺寸图片幻灯片

表 1 试验设计方案

Table 1 Design schemes of dynamic tests

试验编号	细粒含量FC/%	细粒中黏、粉占比/%		黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
试验编号	细粒含量FC/%	黏粒	粉粒	黏粉比CS	固结压力σ₃/kPa	初始砂骨架孔隙比e_s	初始孔隙比e
D1	0	－	－	－	200	0.9800	0.9800
D2	5	20	80	0.25	200	0.9800	0.8823
D3		50	50	1	200	0.9800	0.8823
D4		80	20	4	200	0.9800	0.8823
D5		100	0	－	200	0.9800	0.8823
D6	10	20	80	0.25	200	0.9800	0.7967
D7		50	50	1	200	0.9800	0.7967
D8		80	20	4	200	0.9800	0.7967
D9		100	0	－	200	0.9800	0.7967
D10	0	－	－	－	200	0.8823	0.8823
D11	10	20	80	0.25	200	1.0704	0.8823
D12		50	50	1	200	1.0704	0.8823
D13		80	20	4	200	1.0704	0.8823
D14		100	0	－	200	1.0704	0.8823

下载: 导出CSV

表 2 Mod-Baziar模型拟合参数取值范围

Table 2 Fitting parameter ranges of Mod-Baziar model

土体	模型参数
土体	θ	β	γ	ω
纯砂	1.5430~2.0362	-0.0057~-0.2760	0.1152 ~0.5637	0.4136~1.9222
砂-黏	1.3227~2.3576	-0.1089~-0.4709	0.0132~1.4852	-2.0889~2.7362
砂-粉-黏	1.2490~2.4263	-0.0510~-0.4252	-0.5369~1.8854	-2.8496~3.8353

下载: 导出CSV

参考文献(13)

[1]	SASAKI Y, TOWHATA I, MIYAMOTO K, et al. Reconnaissance report on damage in and around river levees caused by the 2011 off the Pacific coast of Tohoku earthquake[J]. Soils and Foundations, 2012, 52(5): 1016-1032. doi: 10.1016/j.sandf.2012.11.018
[2]	SEED H B, MARTIN P P, LYSMER J. Pore-water pressure changes during soil liquefaction[J]. Journal of the Geotechnical Engineering Division, 1976, 102(4): 323-346. doi: 10.1061/AJGEB6.0000258
[3]	BOOKER J R, RAHMAN M S, SEED H B. Gadflea: a computer program for the analysis of pore pressure generation and dissipation during cyclic or earthquake loading[R]. Berkeley, CA: Earthquake Engineering Research Center, University of California, 1976.
[4]	BAZIAR M, SHAHNAZARI H, SHARAFI H. A laboratory study on the pore pressure generation model for Firouzkooh silty sands using hollow torsional test[J]. International Journal of Civil Engineering, 2011, 9: 126-134.
[5]	许成顺, 王冰, 杜修力, 等. 循环加载频率对砂土液化模式的影响试验研究[J]. 土木工程学报, 2021, 54(11): 109-118. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202111011.htm XU Chengshun, WANG Bing, DU Xiuli, et al. Experimental study on effect of cyclic loading frequency on liquefaction mode of sand[J]. China Civil Engineering Journal, 2021, 54(11): 109-118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202111011.htm
[6]	董青, 周正华, 苏杰, 等. 基于对数动骨架考虑可逆孔压的有效应力本构研究[J]. 岩土工程学报, 2020, 42(12): 2322-2329. doi: 10.11779/CJGE202012020 DONG Qing, ZHOU Zhenghua, SU Jie, et al. Constitutive model for effective stress based on logarithmic skeleton curve considering reversible pore pressure[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2322-2329. (in Chinese) doi: 10.11779/CJGE202012020
[7]	王桂萱, 桑野二郎, 竹村次朗. 循环荷载下砂质混合土孔隙水压力特性研究[J]. 岩土工程学报, 2004, 26(4): 541-545. doi: 10.3321/j.issn:1000-4548.2004.04.023 WANG Guixuan, JiRO Kuwano, JIRO Takemura. Study on excess pore water pressures of sands mixed with clays under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 541-545. (in Chinese) doi: 10.3321/j.issn:1000-4548.2004.04.023
[8]	吴琪, 王路阳, 刘启菲, 等. 基于剪切应变特征的饱和珊瑚砂超静孔压发展模型试验研究[J]. 岩土工程学报, 2023, 45(10): 2091-2099. doi: 10.11779/CJGE20220956 WU Qi, WANG Luyang, LIU Qifei, et al. Experimental study on development model of excess pore pressure for saturated coral sand based on shear strain characteristics[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(10): 2091-2099. (in Chinese) doi: 10.11779/CJGE20220956
[9]	张伏光, 聂卓琛, 陈孟飞, 等. 不排水循环荷载条件下胶结砂土宏微观力学性质离散元模拟研究[J]. 岩土工程学报, 2021, 43(3): 456-464. doi: 10.11779/CJGE202103008 ZHANG Fuguang, NIE Zhuochen, CHEN Mengfei, et al. DEM analysis of macro- and micro-mechanical behaviors of cemented sand subjected to undrained cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 456-464. (in Chinese) doi: 10.11779/CJGE202103008
[10]	王志华, 何健, 高洪梅, 等. 基于触变流体理论的可液化土体振动孔压模型[J]. 岩土工程学报, 2018, 40(12): 2332-2340. doi: 10.11779/CJGE201812023 WANG Zhihua, HE Jian, GAO Hongmei, et al. Dynamic pore water pressure model for liquefiable soils based on theory of thixotropic fluid[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2332-2340. (in Chinese) doi: 10.11779/CJGE201812023
[11]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[12]	刘洋, 吴顺川, 周健. 循环荷载下砂土变形的细观数值模拟Ⅱ: 密砂试验结果[J]. 岩土工程学报, 2007, 29(11): 1676-1682. doi: 10.3321/j.issn:1000-4548.2007.11.014 LIU Yang, WU Shunchuan, ZHOU Jian. Micro-numerical simulation of cyclic biaxial test Ⅱ: results of dense sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1676-1682. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.11.014
[13]	LI T, TANG X W. Influences of low fines content and fines mixing ratio on the undrained static shear strength of sand-silt-clay mixtures[J]. European Journal of Environmental and Civil Engineering, 2022, 26(9): 3706-3728. doi: 10.1080/19648189.2020.1813206