地铁行车荷载作用下地层和重叠隧道变形数值模拟研究

胡垚; 李明帅; 郭飞; 许英刚; 雷华阳; 吴筱; 陈学俭

doi:10.11779/CJGE2023S20041

地铁行车荷载作用下地层和重叠隧道变形数值模拟研究 English Version

胡垚^{1, 2,},
李明帅²,
郭飞³,
许英刚⁴,
雷华阳⁴,
吴筱²,
陈学俭^5, ,

1.
地质灾害防治与地质环境保护国家重点实验室(成都理工大学), 四川成都 610059
2.
成都理工大学环境与土木工程学院, 四川成都 610059
3.
中交(天津)生态环保设计研究院有限公司, 天津 300220
4.
天津大学建筑工程学院, 天津 300350
5.
武汉大学水利水电学院, 湖北武汉 430072

基金项目:

国家自然科学基金项目 42307260

国家自然科学基金项目 52378363

四川省自然科学基金项目 2023NSFSC0882

地质灾害防治与地质环境保护国家重点实验室开发基金项目 SKLGP2023K024

北京交通大学隧道及地下工程教育部工程研究中心开放课题 TUC2022-03

详细信息

作者简介:
胡垚(1994—)，男，博士，副研究员，主要从事岩土与地下工程方面的教学和科研工作。E-mail：hyjiaoliu@163.com

通讯作者:
陈学俭，E-mail: chenxj@whu.edu.cn

中图分类号: TU753;U231
计量
- 文章访问数: 155
- HTML全文浏览量: 37
- PDF下载量: 16
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Numerical simulation of deformation of strata and stacked tunnels under traffic loads of subway

1.
State Key Laboratory of Geological Disaster Prevention and Geological Environment Protection, Chengdu University of Technology, Chengdu 610059, China
2.
College of Environment and Civil Engineering, Chengdu University of Technology, Chengdu 610059, China
3.
CCCC (Tianjin) Eco-Environmental Protection Design & Research Institute Co., Ltd., Tianjin 300220, China
4.
School of Civil Engineering, Tianjin University, Tianjin 300350, China
5.
College of Water Resources and Hydropower, Wuhan University, Wuhan 430072, China

摘要

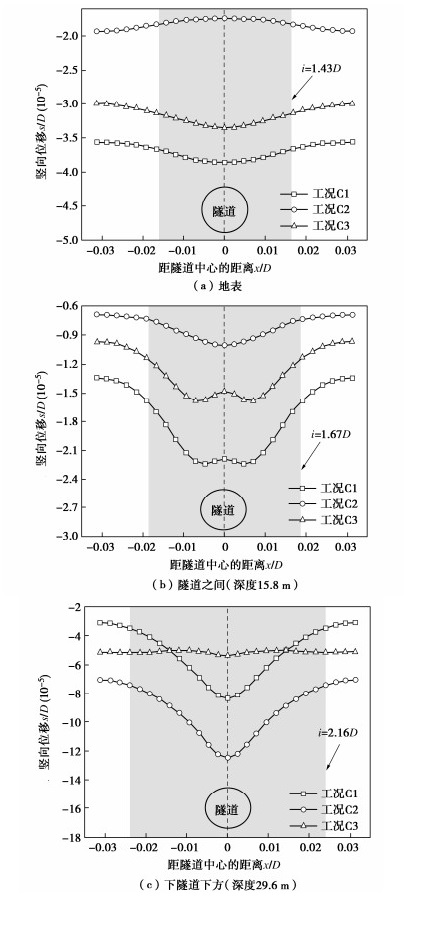
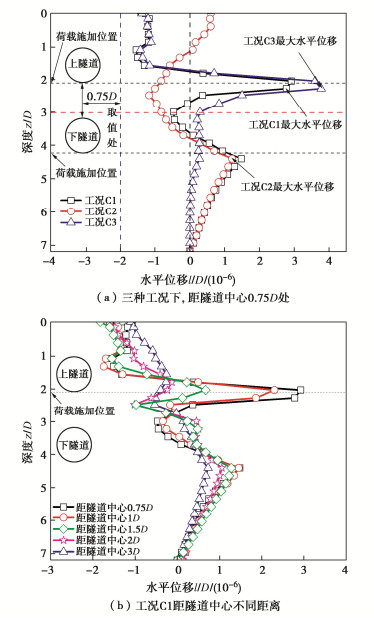
摘要: 地铁列车运行时产生的行车荷载对地层和重叠隧道有显著影响。然而，现有研究很少聚焦重叠隧道变形响应，且缺乏行车荷载施加位置的影响。选取天津某重叠隧道工程，采用激振力函数确定行车荷载，开展地铁行车荷载作用下地层及重叠隧道变形数值模拟。结果表明：地铁行车荷载的施加位置会对地层位移和隧道变形产生明显影响。S_max值和i值均与数据提取位置相关。距隧道中心1.5D为地铁行车荷载引起地层水平位移的临界影响范围。三种工况作用下，隧道纵向变形均表现为整体下沉。行车荷载仅施加于上或下隧道时，施加荷载的隧道横向变形较大；同时施加于两隧道时，两隧道均在底部产生变形。
- 重叠隧道 /
- 行车荷载 /
- 激振力函数 /
- 数值模拟 /
- 变形特性
Abstract: The traffic loads of subway have a significant impact on the strata and stacked tunnels. However, the existing studies have rarely focused on the deformation response of stacked tunnels and consider the influences of the location of the traffic loads. By selecting a stacked tunnel project in Tianjin, the excitation force function is used to determine the traffic loads, and numerical simulations are conducted to analyze the deformation of stacked tunnels under the traffic loads of subway. The results demonstrate that the position where the traffic loads of subway are applied significantly affects the displacement of strata and deformation of tunnels. Both S_max and i values are related to the location of data extraction. The critical influence range of lateral displacement caused by the traffic loads of subway is 1.5D from the center of the tunnel. Under the three conditions, the longitudinal deformations of the tunnels are overall downward. When the traffic loads of subway are applied only to the upper or the lower tunnel, the transverse deformation of the tunnel under the loads is large. When the loads are applied to two tunnels synchronously, both the two tunnels deform at the bottom.
- stacked tunnel /
- traffic load /
- excitation force function /
- numerical simulation /
- deformation characteristic

HTML全文

0. 引言

钙质砂是由珊瑚骨骼、贝类、虫黄藻类等海洋生物残骸沉积而成，其主要组成成分是碳酸钙^[1-3]，是我国南海岛礁吹填的主要材料。因其生成环境、成因以及物质组成等因素影响，钙质砂具有颗粒易破碎、形状极不规则、内孔隙发育、微观结构复杂等显著区别于陆源石英砂的特点^[4-6]。随着“一带一路”国家战略和建设“海洋强国”政策方针的推进，研究钙质砂工程力学特性具有重要意义^[7-9]。

钙质砂作为填方工程的天然材料，其应力状态复杂多变，土体受到各向异性应力状态影响而产生初始静剪应力，在建（构）筑物的自重和动荷载（波浪、地震和交通荷载等）作用下，易引起地基强度降低、变形过大以及液化失稳等灾害。实际上，动荷载作用下剪切应力做功将导致材料损伤效应的累积，不排水条件下表现为孔压增长。因此，可以将孔压的升高与土体颗粒在运动或重排过程中所耗损的能量建立关联。损耗能作为标量，相较于应力、应变等矢量，可直接数学叠加，大幅度降低分析难度。Nemat-Nasser等^[10]首先提出了耗散能量的概念，建立其与残余孔压的关系，来有效地评估孔隙水压力的产生和发展过程。Kokusho^[11]和Pan等^[12]提出了土骨架破坏产生的单位体积耗散能与应变和残余孔压累积直接相关，为评价砂土在不规则循环应力条件下的抗液化能力提供了有效方法。总体而言，上述研究主要针对石英砂，能否适用于钙质砂仍需进一步探究。

本文以饱和钙质砂为研究对象，开展不排水条件下循环剪切三轴试验，探究相对密实度、初始静剪应力以及循环应力对其孔压发展的影响；同时，引入能量法，建立钙质砂孔压与损耗能之间联系，提出基于能量损耗的液化评价方法，为钙质砂地基稳定性分析提供理论依据和技术支撑。

1. 试验材料与方案

1.1 试验材料

本文试验材料为中国南海某岛礁的天然钙质砂，颗粒多呈灰白色，形状有片状、块状、棒状等，颗粒内孔隙多、微观结构复杂，如图 1所示。

图 1 典型钙质砂颗粒电镜扫描（SEM）图像

Figure 1. SEM image of typical calcareous sand particles

下载: 全尺寸图片幻灯片

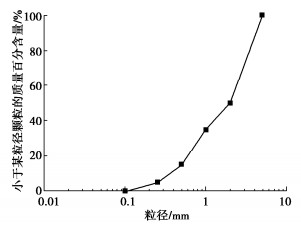
经过现场取材、清水冲洗、烘干等过程后，对粒径大于5 mm的颗粒进行剔除，处理后颗粒分布级配曲线如图 2所示，主要基本物理性质参数见表 1。不难发现，试样基本不含0.1 mm以下的细颗粒，不均匀系数和曲率系数分别为6.84和0.78，属于不良级配砂土。

图 2 钙质砂颗分级配曲线

Figure 2. Grain-size distribution curve of calcareous sand

下载: 全尺寸图片幻灯片

表 1 钙质砂物理性质指标

Table 1. Physical properties of calcareous sand

相对质量密度	d₅₀/ mm	不均匀系数	曲率系数	最大孔隙比	最小孔隙比
2.79	2.0	6.84	0.78	1.15	0.87

下载: 导出CSV

| 显示表格

1.2 试验方案

结合实际工况，采用CKC三轴试验系统模拟复杂应力条件下饱和钙质砂循环剪切试验，先进行有效围压为100 kPa的等向固结后再根据试验设计的初始静偏应力状态进行非等向固结，具体方案如表 2所示。初始静剪应力比SSR和循环应力比CSR可通过式（1）和（2）计算。

表 2 不排水循环剪切试验方案

Table 2. Summary of undrained cyclic triaxial tests

试验系列	相对密实度 D_r	${q_{\text{s}}}$ / kPa	${q_{{\text{cyc}}}}$ / kPa	SSR	CSR	N_f
Ⅰ	70% （密砂）	0	20	0	0.1	232
		0	25	0	0.125	74
		0	30	0	0.15	17
		0	40	0	0.2	6
		20	30	0.1	0.15	168
		20	45	0.1	0.225	19
		20	50	0.1	0.25	3
		50	50	0.25	0.25	53
		50	60	0.25	0.3	11
		50	70	0.25	0.35	6
		80	70	0.4	0.35	14
		80	80	0.4	0.4	7
		-10	25	-0.05	0.125	78
		-10	30	-0.05	0.15	39
		-10	35	-0.05	0.175	8
		-20	20	-0.1	0.1	210
		-20	25	-0.1	0.125	11
		-20	30	-0.1	0.15	8
		-40	20	-0.2	0.1	57
		-40	25	-0.2	0.125	16
		-40	30	-0.2	0.15	8
Ⅱ	30% （松砂）	0	15	0	0.075	943
		0	20	0	0.1	120
		0	25	0	0.125	37
		0	30	0	0.15	18
		24	30	0.12	0.15	61
		24	35	0.12	0.175	16
		24	40	0.12	0.2	5
		40	15	0.2	0.075	175
		40	20	0.2	0.1	9
		50	12.5	0.25	0.0625	17
		50	15	0.25	0.075	2
		-10	12.5	-0.05	0.0625	382
		-10	15	-0.05	0.075	180
		-10	20	-0.05	0.1	11
		-20	10	-0.1	0.05	246
		-20	12.5	-0.1	0.0625	202
		-20	15	-0.1	0.075	12
		-40	5	-0.2	0.025	104
		-40	7.5	-0.2	0.0375	13
		-40	10	-0.2	0.05	2

下载: 导出CSV

| 显示表格

${\text{SSR}} = \frac{{{q_{\text{s}}}}}{{2{{p'}_0}}}\text{，}$

(1)

${\text{CSR}} = \frac{{{q_{{\text{cyc}}}}}}{{2{{p'}_0}}}。$

(2)

式中： ${q_{\text{s}}}$ 为初始静剪偏应力； ${q_{{\text{cyc}}}}$ 为循环偏应力； ${p'_0}$ 为平均有效正应力。

2. 试验结果与分析

2.1 孔压特性发展规律

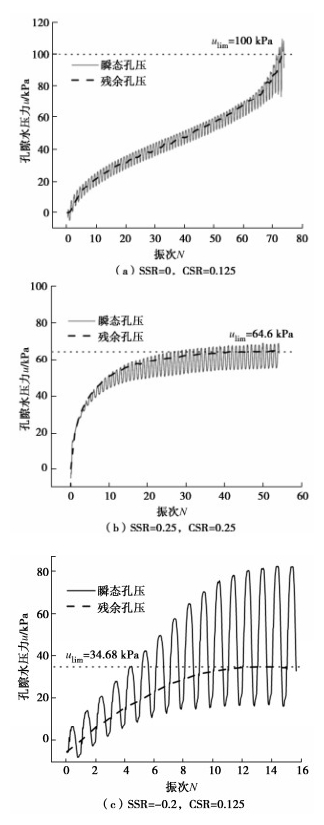
图 3给出不同初始偏应力作用下饱和密砂的孔压发展规律曲线。孔隙水压力可分为两类：①随着循环荷载作用实时变化的孔压，即实线所示的瞬态孔压，这种孔压会随着循环荷载的卸载而快速消散；②每个循环加载结束，试样未及时恢复的孔压，即虚线所示的残余孔压。从图 3（a）中可以看出，对于等向固结的试样，残余孔压在前期随着荷载的施加而逐渐累积，而在后期快速增长，直至达到荷载施加前的有效围压，u_lim=100 kPa。如图 3（b）所示，在压缩静偏应力作用下，孔压在加载初期迅速累积，随着循环荷载持续进行，残余孔压逐渐趋于稳定，u_lim=64.6 kPa。在拉伸静偏应力作用下，孔压发展与压缩静偏应力时有类似的变化趋势，孔压在加载初期累积较快而后基本保持不变，u_lim=34.68 kPa。

图 3 钙质砂孔压增长变化规律

Figure 3. Development of pore water pressure of calcareous sand

下载: 全尺寸图片幻灯片

同时，通过式（3）和（4）定义固结应力比K_c和残余孔压比u_r。

${K_{\text{c}}} = \frac{{{\sigma _{{\text{v}}0}}}}{{{\sigma _{{\text{h}}0}}}}\text{，}$

(3)

${u_{\text{r}}} = \frac{u}{{{\sigma _{{\text{h}}0}}}}。$

(4)

式中： ${\sigma _{{\text{v}}0}}$ 和 ${\sigma _{{\text{h}}0}}$ 分别为初始有效竖向应力和水平应力，u为残余孔压。

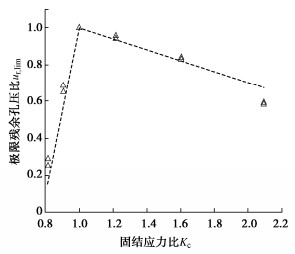
图 4给出了饱和密砂的极限残余孔压比和固结应力比的关系曲线。从图中可以看出，饱和密砂的极限残余孔压比随着固结应力比的增大呈先增大后减小的趋势，在K_c=1（等向固结）时，极限残余孔压比达到最大值u_{r, lim}=1，且大致上呈线性分布，与循环应力幅值大小无明显关系。

图 4 极限残余孔压比与固结应力比的关系

Figure 4. Relationship between ultimate residual pore pressure ratio and consolidation stress ratio

下载: 全尺寸图片幻灯片

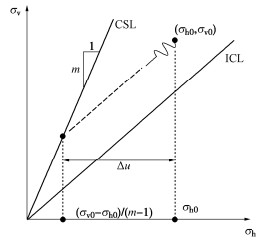
对于同一材料的砂土，其在循环荷载作用下有效应力路径将沿着平行于等向固结线（ICL）的方向逐渐靠近临界状态线（CSL），而与循环应力幅值无关，如图 5所示。因此，对于给定的初始应力状态（σ_h0，σ_v0），会与临界状态线相交于一点，且理论上初始应力点与最终应力点之间的水平距离 $\Delta u$ 为试验中的极限残余孔压，如式（5）所示。根据u_r和K_c定义，可得到两者关系如式（6），符合图 4所示的线性关系。

${u_{\lim }} = \Delta u = {\sigma _{{\text{h}}0}} - \frac{{{\sigma _{{\text{v}}0}} - {\sigma _{{\text{h}}0}}}}{{m - 1}}\text{，}$

(5)

${u_{{\text{r, lim}}}} = \frac{{{u_{\lim }}}}{{{\sigma _{{\text{h0}}}}}} = 1 - \frac{{{K_{\text{c}}} - 1}}{{m - 1}}。$

(6)

图 5 初始静剪应力状态对残余孔压影响示意图

Figure 5. Influences of initial static shear stress on residual pore pressure

下载: 全尺寸图片幻灯片

2.2 损耗能演化规律

动荷载作用下饱和砂土损耗的能量主要用于颗粒的相对运动和重新排列。因此，引入能量法，提出基于损耗能的砂土液化评价方法。循环加载过程中一个振次的损耗能W可用应力-应变滞回圈的面积表示，即：

$W = \sum\limits_{i = 1}^{n - 1} {\frac{1}{2}} ({q_{i + 1}} + {q_i})({\varepsilon _{{\text{a, }}i + 1}} - {\varepsilon _{{\text{a, }}i}}) 。$

(7)

式中：n为计算增量的总个数， ${q_i}$ 和 ${\varepsilon _{{\text{a, }}i}}$ 分别为第i个增量的偏应力和轴向应变。

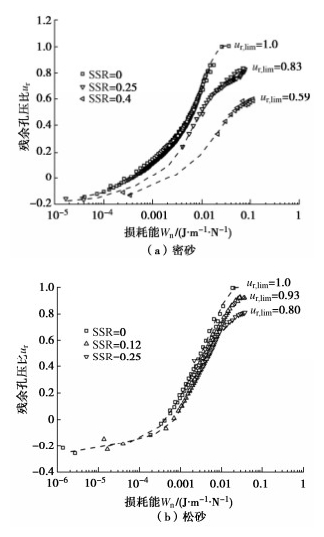
图 6分别给出饱和钙质砂在不同初始静偏应力作用下残余孔压比与正交化损耗能的内在关系，正交化损耗能W_n为损耗能W与初始有效水平正应力 ${\sigma _{{\text{h0}}}}$ 的比值。结果显示：饱和密砂的残余孔压初期增长缓慢，随着W_n的增大而较快增长，最后趋于稳定；在饱和松砂中也观察到类似的变化趋势。这说明残余孔压与损耗能的关系主要取决于初始应力条件。

图 6 残余孔压比与损耗能的关系

Figure 6. Relationship between residual pore pressure ratio and dissipated energy

下载: 全尺寸图片幻灯片

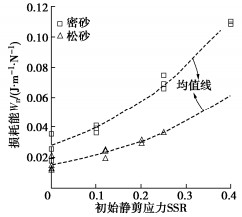
从图 7可以看出，饱和钙质砂在失稳破坏时所积累的损耗能随着初始静剪应力的增加而增加；对于同一初始应力状态，密砂所需能量始终大于松砂。研究表明^[13-14]，饱和砂土在循环荷载作用下损耗能主要与初始应力和相对密实度有关，受循环荷载幅值影响极小，具体可用式（8）表示：

${W'_{\text{n}}} = {10^{a\left( {{D_{\text{r}}} - 0.78} \right)}}{10^{b\left( {{\text{SSR}} - 1.0} \right)}}。$

(8)

图 7 损耗能与初始静剪应力比的关系

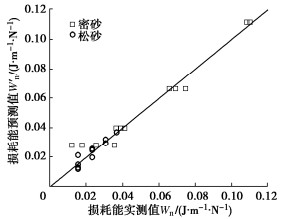
Figure 7. Relationship between dissipated energy and initial static shear stress ratio

下载: 全尺寸图片幻灯片

式中：a和b为经验参数，根据本次试验数据可分别取0.65，1.5。图 8对损耗能的试验实测值与通过式（8）所得的预测值进行对比，发现两者基本落在斜率为1的对角线两侧，表明能量模型可较好地预测不同试验条件下饱和钙质砂的损耗能。

图 8 损耗能实测值与预测值

Figure 8. Measured and predicted values of dissipated energy

下载: 全尺寸图片幻灯片

3. 结论

（1）饱和钙质砂的极限残余孔压比随固结应力比呈先增大后减小的趋势，在K_c=1时存在最大值，临界状态理论可以解释此现象。

（2）不排水循环加载条件下饱和钙质砂的损耗能与试样的初始静剪应力比和相对密实度有关，受循环应力比影响极小，可通过构建的能量模型较好地预测不同试验条件下饱和钙质砂所累积的损耗能。

图 1 天津某双线重叠隧道工程概况图

Figure 1. Project overview of twin stacked tunnels in Tianjin

下载: 全尺寸图片幻灯片

图 2 前1 s内地铁行车荷载时程曲线

Figure 2. Time-history curves of traffic loads of subway within first 1 s

下载: 全尺寸图片幻灯片

图 3 沿Y轴切割一半的模型（工况C1）

Figure 3. Half-cut model along Y axis (case C1)

下载: 全尺寸图片幻灯片

图 4 地层竖向位移

Figure 4. Vertical displacements of strata

下载: 全尺寸图片幻灯片

图 5 地层水平位移

Figure 5. Lateral displacements of strata

下载: 全尺寸图片幻灯片

图 6 隧道纵向变形

Figure 6. Longitudinal deformations of tunnel

下载: 全尺寸图片幻灯片

图 7 隧道横向变形

Figure 7. Transverse deformations of tunnel

下载: 全尺寸图片幻灯片

表 1 土层参数

Table 1 Parameters of soil strata

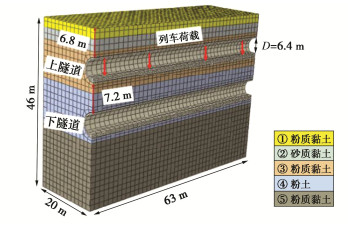
土层	重度/(kN·m^-3)	塑性体积模量对数	应力比	渗透系数/(m·d^-1)	孔隙比	体积模量对数	泊松比
①粉质黏土	18.4	0.058	0.86	0.00018	0.776	0.0072	0.32
②砂质粉土	17.9	0.031	1.03	0.00050	0.742	0.0039	0.35
③粉质黏土	10.3	0.055	0.89	0.00031	0.764	0.0069	0.35
④粉土	12.2	0.020	1.37	2.00000	0.595	0.0025	0.30
⑤粉质黏土	18.0	0.047	0.90	0.00485	0.683	0.0059	0.35

下载: 导出CSV

表 2 模拟方案

Table 2 Simulation schemes

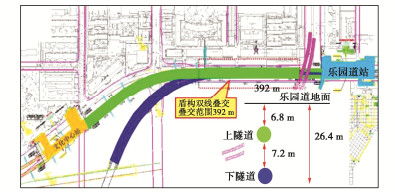
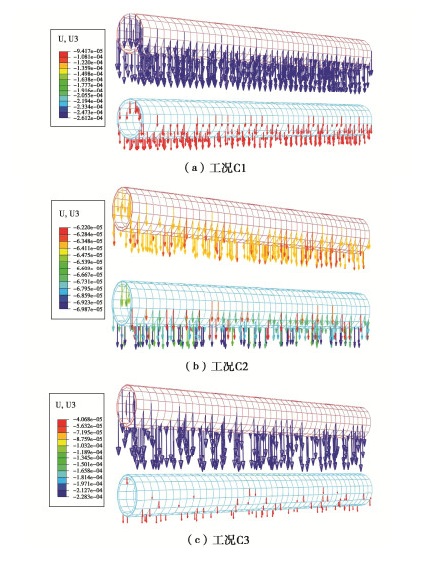
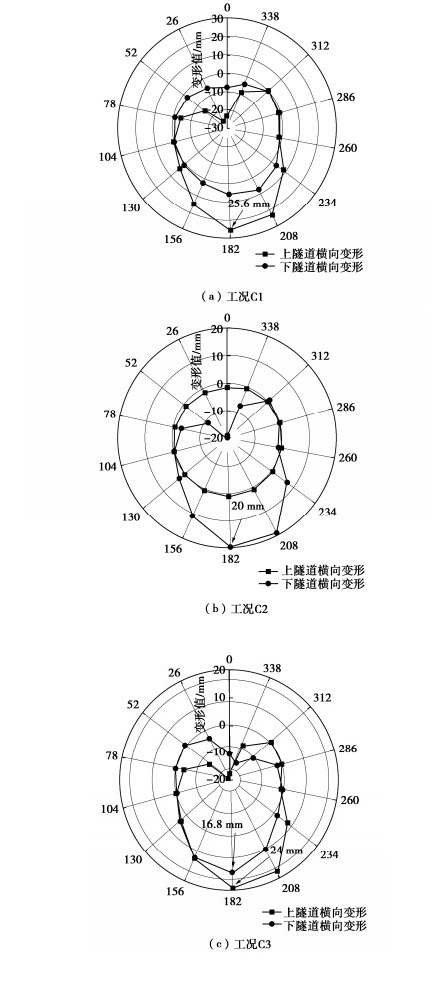
工况	地铁行车荷载施加位置
工况	上隧道	下隧道
C1	√	×
C2	×	√
C3	√	√

下载: 导出CSV

参考文献(15)

[1]	张曦, 唐益群, 周念清, 等. 地铁振动荷载作用下隧道周围饱和软黏土动力响应研究[J]. 土木工程学报, 2007, 40(2): 85-88. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200702016.htm ZHANG Xi, TANG Yiqun, ZHOU Nianqing, et al. Dynamic response of saturated soft clay around a subway tunnel under vibration load[J]. China Civil Engineering Journal, 2007, 40(2): 85-88. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200702016.htm
[2]	雷华阳, 张磊, 许英刚, 等. 快速地铁列车荷载下软土地基沉降数值模拟研究[J]. 岩土工程学报, 2019, 41(增刊1): 45-48. doi: 10.11779/CJGE2019S1012 LEI Huayang, ZHANG Lei, XU Yinggang, et al. Numerical simulation of settlement of soft soil foundation under fast metro train loads[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 45-48. (in Chinese) doi: 10.11779/CJGE2019S1012
[3]	胡垚, 雷华阳, 雷峥, 等. 三向地震作用下叠交隧道地震响应振动台试验研究[J]. 岩土力学, 2022, 43(增刊2): 104-116, 129. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2022S2011.htm HU Yao, LEI Huayang, LEI Zheng, et al. Shaking table test study on seismic response of overlapping tunnels under three-dimensional earthquake[J]. Rock and Soil Mechanics, 2022, 43(S2): 104-116, 129. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2022S2011.htm
[4]	安俊杰, 黄飞, 黄小亮, 等. 施工车辆荷载对隧道内煤系地层的影响规律研究[J]. 能源与环保, 2023, 45(3): 263-269. https://www.cnki.com.cn/Article/CJFDTOTAL-ZZMT202303045.htm AN Junjie, HUANG Fei, HUANG Xiaoliang, et al. Research on influencing law of construction vehicle load on coal measures strata in tunnels[J]. China Energy and Environmental Protection, 2023, 45(3): 263-269. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZZMT202303045.htm
[5]	郑海忠, 严武建, 石玉成, 等. 重复列车荷载作用下季节性冻土区桥墩-基础场地振动特性变形分析[J]. 工程地质学报, 2020, 28(4): 907-915. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202004024.htm ZHENG Haizhong, YAN Wujian, SHI Yucheng, et al. Vibration characteristics and long-term deformation analysis of bridge piers-foundation sites in seasonal frozen soil region under repeated train load[J]. Journal of Engineering Geology, 2020, 28(4): 907-915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202004024.htm
[6]	陈凡, 王士民, 谢金池, 等. 液化砂土地层加固措施研究与盾构隧道列车振动响应分析[J]. 铁道标准设计, 2021, 65(4): 110-117. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202104020.htm CHEN Fan, WANG Shimin, XIE Jinchi, et al. Research on strengthening measures of liquefiable sandy. ground and analysis of train vibration response of shield tunnel[J]. Railway Standard Design, 2021, 65(4): 110-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202104020.htm
[7]	葛世平, 姚湘静, 叶斌, 等. 列车振动荷载作用下隧道周边软黏土长期沉降分析[J]. 岩石力学与工程学报, 2016, 35(11): 2359-2368. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201611020.htm GE Shiping, YAO Xiangjing, YE Bin, et al. Analysis of long-term settlement of soft clay under train vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(11): 2359-2368. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201611020.htm
[8]	莫海鸿, 邓飞皇, 王军辉. 营运期地铁盾构隧道动力响应分析[J]. 岩石力学与工程学报, 2006, 25(增刊2): 3507-3512. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2024.htm MO Haihong, DENG Feihuang, WANG Junhui. Dynamic response analysis of subway shield tunnel during operation period[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3507-3512. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2024.htm
[9]	杨文波, 邹涛, 涂玖林, 等. 高速列车振动荷载作用下马蹄形断面隧道动力响应特性分析[J]. 岩土力学, 2019, 40(9): 3635-3644. YANG Wenbo, ZOU Tao, TU Jiulin, et al. Analysis of dynamic response characteristics of horseshoe shaped cross-section tunnel under vibration load of high-speed train[J]. Rock and Soil Mechanics, 2019, 40(9): 3635-3644. (in Chinese)
[10]	高峰, 关宝树, 仇文革, 等. 列车荷载作用下地铁重叠隧道的响应分析[J]. 西南交通大学学报, 2003, 38(1): 38-42. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200301009.htm GAO Feng, GUAN Baoshu, QIU Wenge, et al. Dynamic responses of overlapping tunnels to passing trains[J]. Journal of Southwest Jiaotong University, 2003, 38(1): 38-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200301009.htm
[11]	潘昌实, PANDE G N. 黄土隧道列车动荷载响应有限元初步数定分析研究[J]. 土木工程学报, 1984, 17(4): 19-28, 18. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC198404001.htm PAN Changshi, PANDE G N. Preliminary deterministic finite element study on a tunnel driven in loess subjected to train loading[J]. China Civil Engineering Journal, 1984, 17(4): 19-28, 18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC198404001.htm
[12]	胡昭艳, 齐静, 高峰. 高速铁路列车振动荷载的分析[J]. 四川建筑, 2008, 28(1): 65-66. https://www.cnki.com.cn/Article/CJFDTOTAL-SCJI200801028.htm HU Zhaoyan, QI Jing, GAO Feng. Analysis of vibration load of high-speed railway trains[J]. Sichuan Architecture, 2008, 28(1): 65-66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCJI200801028.htm
[13]	韩俊艳, 万宁潭, 赵密, 等. 地铁振动荷载作用下场地动力响应及振动衰减规律研究[J]. 防灾减灾工程学报, 2022, 42(1): 191-199. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202201021.htm HAN Junyan, WAN Ningtan, ZHAO Mi, et al. Research on site dynamic response and vibration attenuation under the vibration loading of subway[J]. Journal of Disaster Prevention and Mitigation Engineering. 2022, 42(1): 191-199. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202201021.htm
[14]	HU Y, LEI H Y, ZHENG G, et al. Assessing the deformation response of double-track overlapped tunnels using numerical simulation and field monitoring[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2022, 14(2): 436-447.
[15]	孙凤明. 小近距并行盾构隧道的掘进相互影响分析[D]. 浙江大学, 2015. SUN Fengming. Analysis of Interaction between Small-Spacing Parallel Shield Tunnel Excavations[D]. Hangzhou: Zhejiang University, 2015. (in Chinese)