基于不同原位试验的土壤液化判别模型保守性评估

沈梦芬; 鲍丽春; 孙宏磊; 蔡袁强

doi:10.11779/CJGE2023S20036

基于不同原位试验的土壤液化判别模型保守性评估 English Version

浙江工业大学土木工程学院, 浙江杭州 310014

基金项目:

国家自然科学基金项目 42007236

国家自然科学基金项目 U2239251

浙江省自然科学基金项目 LY24D020001

浙江省自然科学基金项目 LQ20D020002

详细信息

作者简介:
沈梦芬(1988—)，女，博士，副教授，主要从事土壤液化灾害评估、抗液化地基处理、岩土与地质工程风险分析和稳健性优化设计。E-mail：mshen@zjut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 175
- HTML全文浏览量: 39
- PDF下载量: 35
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Assessment of model bias of SPT, V_s and CPT-based liquefaction models

Zhejiang University of Technology, Hangzhou 310014, China

摘要

摘要: 基于现场原位试验和地震液化案例库建立的液化判别模型是一种常见的场地液化判别方法。然而，场地液化判别模型存在着准确性因测试手段而异的问题，即判别模型存在偏差；同时基于同一原位试验建立的液化判别模型的准确性因地震场地而异，即存在地震场地变异性。为评估基于SPT，V_s和CPT建立的液化判别模型的保守性特点，研究汇编了同时含有3种原位试验的地震液化案例库，分别含88，176，107个案例，涉及6次地震事件和场地。根据汇编的案例库采用贝叶斯分层建模法(BHM)标定了SPT-Youd模型、V_s-AS模型和CPT-RW模型的偏差系数，建立了分地震场地的液化判别模型。结果表明：CPT-RW模型的场地液化判别结果最为保守，SPT-Youd模型存在高估多个地震场地的抗液化能力而偏于危险的情况，V_s-AS模型的保守性则介于两者之间；基于汇编的CPT案例库，运用BHM法分地震场地建立的液化判别模型能够有效地修正CPT-RW模型的保守性，且不同地震场地的修正程度不同。研究工作可在工程师采用多种原位试验结果评估同一场地的液化势时提供有效的先验信息。
- 地震液化 /
- 标准贯入试验(SPT) /
- 剪切波速测试(V_s) /
- 静力触探试验(CPT) /
- 模型偏差系数 /
- 贝叶斯分层建模
Abstract: The liquefaction models established through the in-situ tests and liquefaction case histories are widely adopted in the liquefaction evaluation of a site. However, it is reported that the model accuracy varies with the in-situ test methods (i.e., model bias), as well as the earthquake sites (i.e., seismic site variability). To assess the model bias of SPT-Youd model, V_s-AS model and CPT-RW model, a database of liquefaction case histories containing all these three in-situ tests is compiled firstly, containing 88, 176 and 107 cases, respectively, and involving sites from six seismic events. Based on the compiled database, the Bayesian hierarchical modeling (BHM) method is adopted to correct the model bias of the three models, and liquefaction models for each of the seismic sites are established. It is found that the CPT-RW model is the most conservative model, and the liquefaction resistance calculated by the SPT-Youd model is overestimated in several seismic sites, and the conservatism of the V_s-AS model is between them according to the complied database. Using the complied CPT database, the seismic site-specific liquefaction models established by the BHM method can effectively correct the conservatism of the original CPT-RW model, and the levels of correction vary from one seismic site to another. This study provides effective priori information for engineers to assess the liquefaction potential of a site using multiple in-situ tests.
- earthquake-induced soil liquefaction /
- standard penetration test /
- shear wave velocity test /
- cone penetration test /
- model uncertainty /
- Bayesian hierarchical modeling

HTML全文

0. 引言

基于震后液化案例和现场原位试验发展起来的场地液化判别模型是一种在国内外工程实践中被广泛应用的液化判别方法^[1]，如基于Youd等^[2]的SPT液化判别模型(SPT-Youd模型)，基于Andrus等^[3]的V_s液化判别模型(V_s-AS模型)和基于Robertson等^[4]的CPT液化判别模型(CPT-RW模型)。由于现场原位试验的测量误差及测试手段的差异，场地液化判别模型存在着准确性因测试手段而异的问题^[5-6]，即在同一个场地开展多种原位试验计算的抗液化安全系数F_s可能存在较大差别，甚至相反。因此有必要评估基于这3种原位试验的液化判别模型的保守性，为工程师采用多种原位试验结果开展液化判别提供一定的先验信息。

另一方面，由于地震液化案例库是根据地震事件和所在场地汇编的，基于同一原位试验的液化判别模型的准确性因地震场地而异^[7-9]。已有研究利用贝叶斯分层建模法(BHM)修正了CPT-RW模型和SPT-Youd模型的模型偏差，发现基于全球案例库建立的液化判别模型运用在不同地震场地时具有不同的预测精度，即存在地震场地变异性^[7-9]。贝叶斯分层建模法为评价基于不同原位试验的液化判别模型及其在不同地震场地的保守性提供了新思路。

综上，为评估SPT-Youd模型、V_s-AS模型和CPT-RW模型的保守性特点，通过汇编同时含有SPT、V_s和CPT的地震液化案例库，采用BHM法修正上述3种模型，评价3种模型在同一场地进行液化判别时的保守性特点，以及同一判别模型在不同地震场地的变异性特征。

1. 液化判别模型

一般用抗液化安全系数(F_s)评价土体的液化势，定义为循环抗力比(CRR)与循环应力比(CSR)的比值：

${F_{\text{s}}} = \frac{{{\text{CRR}}}}{{{\text{CSR}}}} 。$

(1)

当F_sc≤1时，土壤发生液化；当F_sc > 1时，土壤不发生液化。其中，循环应力比CSR为

${\text{CSR}} = \frac{{{\tau _{{\text{av}}}}}}{{{{\sigma '}_{\text{v}}}}} = 0.65\left( {\frac{{{a_{\max }}}}{g}} \right)\left( {\frac{{{\sigma _{\text{v}}}}}{{{{\sigma '}_{\text{v}}}}}} \right){r_{\text{d}}} 。$

(2)

式中： ${\tau _{{\text{av}}}}$ 为地震引起的平均循环剪应力；a_max为地表峰值加速度，单位为g（重力加速度）； ${\sigma _{\text{v}}}$ ， ${\sigma '_{\text{v}}}$ 分别为上覆总应力和上覆有效应力（kPa）；r_d为应力折减系数。

1.1 SPT-Youd模型

SPT-Youd模型的计算安全系数F_sc定义为CRR_7.5/CSR_7.5，即规准化到震级为7.5时的修正循环抗力比与修正循环应力比的比值。CRR_7.5的表达式^[2]为

${\text{CRR}}_{\text{7}\text{.5}}=\frac{1}{34-{({N}_{1})}_{\text{60cs}}}+\frac{{({N}_{1})}_{\text{60cs}}}{135}+\frac{50}{{\left[10\cdot {({N}_{1})}_{\text{60cs}}+45\right]}^{2}}-\frac{1}{200}。$

(3)

式中：(N₁)_60cs为等效洁净砂的修正标贯击数；CSR_7.5的表达式为

${\text{CS}}{{\text{R}}_{{\text{7}}{\text{.5}}}}{\text{ = }}\frac{{{\text{CSR}}}}{{{\text{MSF}}}} 。$

(4)

1.2 V_s-AS模型

V_s-AS模型中CRR计算的公式为^[3]

${\text{CRR = }}\left[ {a{{\left( {\frac{{{K_{\text{c}}}{V_{{\text{s1}}}}}}{{100}}} \right)}^2} + b\left( {\frac{1}{{V_{{\text{s1}}}^{\text{*}} - {K_{\text{c}}}{V_{{\text{s1}}}}}} - \frac{1}{{V_{{\text{s1}}}^*}}} \right)} \right]{\text{MSF}} 。$

(5)

式中：a，b为曲线拟合参数，其中a=0.022，b=2.8；K_c为考虑土体胶结老化引起V_s1值偏高的修正系数，若待评估的土壤是未固结的，且年龄小于10000 a，K_c的值可以假定等于1^[3]；V_s1为修正的剪切波速（m/s）；V_s1为循环液化发生的V_s1上限值，当细粒土含量FC≤5% 时，V_s1＝215 m/s；5% < FC≤35% 时，V_s1＝215-0.5×（FC-5）m/s；FC > 35% 时，V_s1＝200 m/s。

1.3 CPT-RW模型

CPT-RW模型的CRR计算公式为^[4]

$\text{CRR=}\left\{ \begin{array}{l}0.833\text{(}{q}_{\text{t1N, cs}}/1000\text{)}+0.05\text{ }（{q}_{\text{t1N, cs}} < 50）\\ 93\text{(}{q}_{\text{t1N, cs}}/1000\text{)}+0.08\text{ }（50 < {q}_{\text{t1N, cs}} < 160）\end{array} \right. 。$

(6)

式中：q_{t1N, cs}为归一化锥尖阻力，修正静力触探试验成果得到^[2]。

2. 模型偏差修正方法

本文采用BHM法修正液化判别模型的模型偏差，并建立基于地震场地的液化概率判别模型。由于基于现场原位试验建立的液化判别模型存在模型偏差，故式（1）获得的F_s为土体的计算安全系数F_sc，而非真实的安全系数F_sa。本文定义F_sc与F_sa的比值为模型偏差系数c，则F_sa可由下式求解：

${F_{{\text{sa}}}} = \frac{{{F_{{\text{sc}}}}}}{c} 。$

(7)

式中：c < 1表示判别模型计算的F_sc因低估了土体的抗液化能力而偏于保守，c≥1则表示计算的F_sc因高估了土体的抗液化能力而偏于危险。

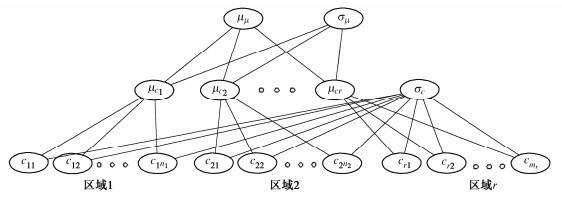
由于液化判别模型在不同地震场地的模型偏差系数存在差异，故可将不同地震场地的c视为随机变量。在BHM法中（图 1），令c_ij表示第i个地震场地第j个案例的模型偏差系数，μ_ci表示第i个地震场地所有模型偏差系数的均值。由于μ_ci是非负的，因此可假定μ_ci服从均值为μ_μ、标准差为σ_μ的对数正态分布^[7]，即

$f({\mu _{{\text{c}}i}}|{\mu _{{\mathsf{μ}}}}, {\sigma _{{\mathsf{μ}}}}) = \frac{1}{{\sqrt {2{\mathsf{π}} } {\mu _{{\text{ci}}}}\sqrt {\ln (1 + \sigma _{{\mathsf{μ}}}^2/\mu _{{\mathsf{μ}}}^2)} }} \cdot\\ \;\;\; \exp \left\{ {\frac{{ - {{(\ln {\mu _{{\text{c}}i}} - \ln {\mu _{{\mathsf{μ}}}} + 0.5\ln (1 + \sigma _{{\mathsf{μ}}}^2/\mu _{{\mathsf{μ}}}^2))}^2}}}{{2\ln (1 + \sigma _{{\mathsf{μ}}}^2/\mu _{{\mathsf{μ}}}^2)}}} \right\} 。$

(8)

图 1 基于贝叶斯分层建模法的液化判别模型修正流程图

Figure 1. Flow chart for modification of liquefaction model by BHM method

下载: 全尺寸图片幻灯片

令x_ij表示第i个地震场地的第j个案例，则x_ij=1表示液化案例，x_ij=0表示非液化案例。基于对数正态假设，场地的液化概率和不液化概率可分别为^[9]

${P_{{\text{L}}ij}} = P({x_{ij}} = 1{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) = P({F_{{\text{sa}}ij}} \leqslant 1{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) \\ \;\;\;\;\;\;= P({c_i} \geqslant {F_{{\text{sc}}ij}}{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) = P(\ln {c_i} \geqslant \ln {F_{{\text{sc}}ij}}{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) \\ \;\;\;\;\;\;= 1 - P(\ln {c_i} \leqslant \ln {F_{{\text{sc}}ij}}{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) \\ \;\;\;\;\;\;= 1 - {\mathit{\Phi}} \left( {\frac{{\ln {F_{{\text{sc}}ij}} - \ln {\mu _{{\text{c}}i}} + 0.5\ln (1 + \sigma _{\text{c}}^{\text{2}}/\mu _{{\text{c}}i}^2)}}{{\sqrt {\ln (1 + \sigma _{\text{c}}^{\text{2}}/\mu _{{\text{c}}i}^{\text{2}})} }}} \right) \text{，}$

(9)

$P({x_{ij}} = 0{\text{|}}{\mu _{{\text{c}}i}}, {\sigma _{\text{c}}}) = 1 - {P_{{\text{L}}ij}}\\ \;\;\;\;\;\;\;\; = {\mathit{\Phi}} \left( {\frac{{\ln {F_{{\text{sc}}ij}} - \ln {\mu _{{\text{c}}i}} + 0.5\ln (1 + \sigma _{\text{c}}^{\text{2}}/\mu _{{\text{c}}i}^{\text{2}})}}{{\sqrt {\ln (1 + \sigma _{\text{c}}^{\text{2}}/\mu _{{\text{c}}i}^{\text{2}})} }}} \right) 。$

(10)

式中：Φ为标准正态分布的累积分布函数。根据式（9）即可建立基于各个地震场地的液化概率判别公式，接下来介绍该模型参数的标定方法。

给出了上述随机变量与不同地震场地之间的关系。在BHM中，μ_μ从平均意义上表征模型预测结果的偏差程度， ${\sigma _{{\mathsf{μ}}}}$ 表征c在不同地震场地的变异性大小， ${\sigma _{\text{c}}}$ 表征c在地震场地内的变异性。则式（9）包含的待标定参数 $\theta$ ={μ_μ， ${\sigma _{{\mathsf{μ}}}}$ ， ${\sigma _{\text{c}}}$ ，μ_c1，μ_c2，...，μ_ci}。假设第i个地震场地共包含n_i个案例，并且令x_i={x_i1, x_i2, …, x_ini }表示第i个地震场地的所有案例，则来自r个地震场地的所有案例可表示为X={x₁，x₂，…，x_r}。令 $f({\mu _{{\mathsf{μ}}}})$ ， $f({\sigma _{{\mathsf{μ}}}})$ 和 $f({\sigma _{\text{c}}})$ 分别表示μ_μ， ${\sigma _{{\mathsf{μ}}}}$ 和 ${\sigma _{\text{c}}}$ 的先验分布，则根据贝叶斯定理^[10]， $\theta$ 的后验分布可表示为

$f(\theta |X) \propto f({\mu _{{\mathsf{μ}}}})f({\sigma _{{\mathsf{μ}}}})f({\sigma _{\text{c}}})\prod\limits_{i{\text{ = 1}}}^r {f({\mu _{{\text{c}}i}}|{\mu _{{\mathsf{μ}}}}, {\sigma _{{\mathsf{μ}}}})} \cdot\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \prod\limits_{i{\text{ = 1}}}^r {\left[ {\prod\limits_{j{\text{ = 1}}}^{{n_{{\text{L}}i}}} {{P_{{\text{L}}ij}}^{{w_{{\text{L}}i}}}\prod\limits_{j{\text{ = 1}}}^{{n_{\text{N}}}_{{\text{L}}i}} {{{\left( {1 - {P_{{\text{L}}ij}}} \right)}^{{w_{{\text{NL}}i}}}}} } } \right]} 。$

(11)

式中：n_Li，n_NLi分别为第i个区域的液化案例数和非液化案例数；w_Li，w_NLi分别为第i个区域中液化案例和非液化案例的权重因子，用于考虑第i个区域取样偏差的影响。w_Li，w_NLi可分别按下式计算^[9]：

${w_{{\text{L}}i}} = \frac{{{Q_{\text{p}}}}}{{{Q_{{\text{s}}i}}}} \text{，}$

(12)

${w_{{\text{NL}}i}} = \frac{{1 - {Q_{\text{p}}}}}{{1 - {Q_{{\text{s}}i}}}} 。$

(13)

式中：Q_si为标定案例库中第i个区域液化案例的比例；Q_p为现实中液化案例的真实比例，可取为0.456^{[7, 9]}。为获得待标定参数 $\theta$ ，需要确定μ_μ， ${\sigma _{{\mathsf{μ}}}}$ 和 ${\sigma _{\text{c}}}$ 的先验分布。本研究假设μ_μ， ${\sigma _{{\mathsf{μ}}}}$ 和 ${\sigma _{\text{c}}}$ 遵循范围为0至3的均匀分布。 $f({\mu _{{\mathsf{μ}}}})$ ， $f({\sigma _{{\mathsf{μ}}}})$ 和 $f({\sigma _{\text{c}}})$ 分别表示各自的先验分布，其值分别为1/3，1/3，1/3。采用马尔可夫链蒙特卡罗（Markov Chain Monte Carlo, MCMC）模拟从 $\theta$ 的后验分布中抽取样本，即可计算求解 $\theta$ 的后验分布^{[7, 9]}。

由于μ_μ， ${\sigma _{{\mathsf{μ}}}}$ 和 ${\sigma _{\text{c}}}$ 的值具有不确定性，且μ_ci，σ_c的不确定性将进一步传播到c_i中。所以令E(c_i)，Std(c_i)表示c_i的均值和标准差，计算公式为^{[7, 9]}

$E({c_i}) = E({\mu _{{\text{c}}i}}) \text{，}$

(14)

${\text{Std}}({c_i}) = \sqrt {{E^2}({\sigma _{\text{c}}}) + {\text{St}}{{\text{d}}^2}({\mu _{{\text{c}}i}}) + {\text{St}}{{\text{d}}^2}({\sigma _{\text{c}}})} 。$

(15)

令c_N表示标定案例库以外新区域的模型偏差系数，则E(c_N)表示该新区域的模型偏差系数的均值。对于不在标定案例库中的新区域，对c_N的估算只能通过其分布假定，即c_N服从均值为μ_μ标准差为σ_μ的对数正态分布。μ_μ和σ_μ中的不确定性也会传播到c_N中，在这种情况下，新区域的E(c_N)，Std(c_N)可分别按下式计算^{[7, 9]}：

$E({\mu _{{\text{cN}}}}) = E({\mu _{{\mathsf{μ}}}}) \text{，}$

(16)

${\text{Std}}({\mu _{{\text{cN}}}}) = \sqrt {{E^2}({\sigma _{{\mathsf{μ}}}}) + {\text{St}}{{\text{d}}^2}({\mu _{{\mathsf{μ}}}}) + {\text{St}}{{\text{d}}^2}({\sigma _{{\mathsf{μ}}}})} 。$

(17)

3. 结果分析

3.1 案例库汇编

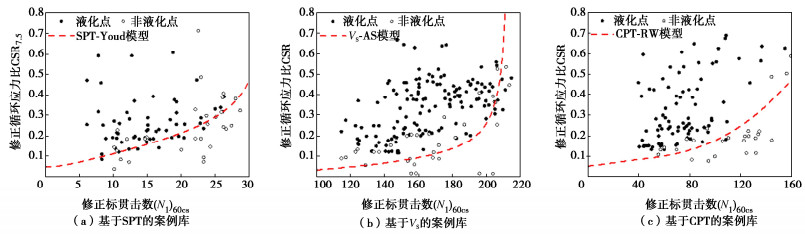
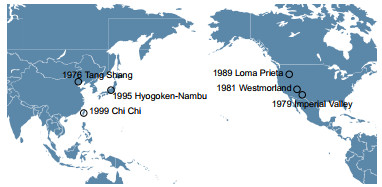
本研究汇总了目前较完整的地震液化案例库，即含252个SPT的案例库^[11]，含415个V_s的案例库^[12]和含165个CPT的案例库^[13]，从3个案例库中筛选出同时包含SPT，V_s和CPT试验数据的6个地震场地，并剔除其中32个(N₁)_60cs≥30，25个V_s1 > 215，6个q_{t1N, cs} > 160的案例，以及1个边缘液化案例，汇总得到基于SPT试验的案例88个，基于V_s试验的案例176个，基于CPT试验的案例107个，结果汇总在表 1。图 2为收集到的各地震案例在对应液化判别模型下的液化触发曲线。可观察到汇编的案例库中，基于CPT的液化和非液化案例区分度最高，基于SPT和V_s的案例库存在较多相互交错的液化案例数和非液化案例，区分度更差。图 3为表 1中汇编的地震场地分布情况，可见这6次地震事件对应的场地横跨亚洲和美洲，因此下文对基于3种原位试验的液化判别模型的地震场地变异性进行标定。

表 1 汇编的地震液化案例库

Table 1. Compiled liquefaction database

地震事件	SPT案例库^[11]			V_s案例库^[12]			CPT案例库^[13]
地震事件	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数
1976 Tangshan地震	7.6	5	1	8	15	1	7.8	9	2
1979 Imperial Valley地震	6.53	4	3	6.5	4	7	6.5	2	3
1981 Westmorland地震	5.9	3	4	5.9	6	5	5.9	3	2
1989 Loma Prieta地震	6.93	15	7	7	41	15	7	37	16
1995 Hyogoken-Nambu地震	6.9	26	10	7	64	5	7.2	17	2
1999 Chi Chi地震	7.6	6	4	7.6	12	1	7.6	14	0
合计	—	59	29	—	142	34	—	82	25

下载: 导出CSV

| 显示表格

图 2 液化案例及其液化触发曲线图

Figure 2. Case histories and their liquefaction boundary curves

下载: 全尺寸图片幻灯片

图 3 汇编的地震液化案例场地及其分布图

Figure 3. Distribution of earthquake sites complied in liquefaction database

下载: 全尺寸图片幻灯片

3.2 模型修正结果

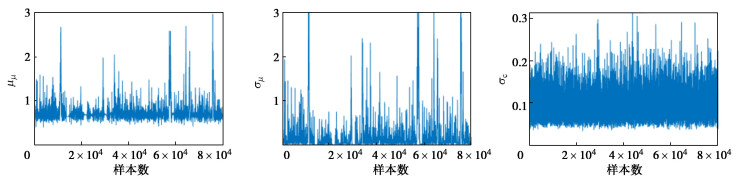
以液化和非液化案例区分度更高的CPT数据为例，将表 1中的原始数据和先验分布带入式(11)，采用MCMC模拟（图 4）可以获得μ_μ，σ_μ和σ_c的样本分布。基于汇总案例库采用上述方法分别对3个模型进行修正，结果见表 2，分析可知：

图 4 基于CPT案例库的MCMC模拟法的样本抽样图

Figure 4. Trace plot of samples generated with MCMC simulation through CPT-based database

下载: 全尺寸图片幻灯片

表 2 经BHM法修正后液化判别模型参数的后验分布

Table 2. Posterior distribution of liquefaction model parameters corrected by BHM method

地震场地	SPT-Youd模型^[2]				V_s-AS模型^[3]				CPT-RW模型^[4]
地震场地	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)
μ_μ	1.21	0.31	—	—	1.04	0.36	—	—	0.75	0.20	—	—
σ_μ	0.42	0.47	—	—	0.49	0.66	—	—	0.18	0.37	—	—
σ_c	1.03	0.64	—	—	0.68	0.24	—	—	0.10	0.03	—	—
案例库外的区域	1.21	0.70	1.21	1.40	1.04	0.90	1.04	1.15	0.75	0.46	0.75	0.47
1976 Tangshan	1.18	0.30	1.18	1.25	0.74	0.14	0.74	1.44	0.67	0.06	0.67	0.12
1979 Imperial Valley	1.04	0.30	1.04	1.24	0.77	0.16	0.77	1.13	0.67	0.07	0.67	0.12
1981 Westmorland	1.28	0.34	1.28	1.25	1.07	0.34	1.07	1.13	0.76	0.14	0.76	0.18
1989 Loma Prieta	1.16	0.25	1.16	1.23	0.81	0.11	0.81	1.17	0.72	0.03	0.72	0.11
1995 Hyogoken-Nambu	1.06	0.23	1.06	1.23	0.84	0.11	0.84	1.13	0.64	0.07	0.64	0.12
1999 Chi Chi	0.89	0.29	0.89	1.24	1.21	0.54	1.21	1.13	0.78	0.30	0.78	0.32

下载: 导出CSV

| 显示表格

（1）SPT-Youd模型、V_s-AS模型和CPT-RW模型都存在模型偏差，即从平均意义上表征模型保守性的E(μ_μ)值不等于1；同时，这3个模型均存在地震场地变异性，即地震场地相应的E(c_i)值不等于1。

（2）CPT-RW模型标定的E(μ_μ)值和E(c_i)值均小于1，说明通过该模型计算的F_sc值在各个地震场地均偏于保守；SPT-Youd模型标定的E(μ_μ)值为1.21，且6个地震场地中有5个的E(c_i)值均大于1，说明由该模型计算的F_sc高估了这5个场地的抗液化能力，因而偏于危险；V_s-AS模型的E(μ_μ)值为1.04，判别模型的保守性总体介于CPT-RW模型和SPT-Youd模型之间。

（3）CPT-RW模型标定的E(σ_μ)值为0.18，大于E(σ_c)值0.10，说明其地震场地间的变异性大于区域内变异性；SPT-Youd模型和V_s-AS模型则与CPT-RW模型相反，即E(σ_μ)值小于E(σ_c)值，该现象可能与案例库中的液化和非液化案例的区分度相关，需进一步开展相关工作证实。

3.3 分地震场地的液化判别模型

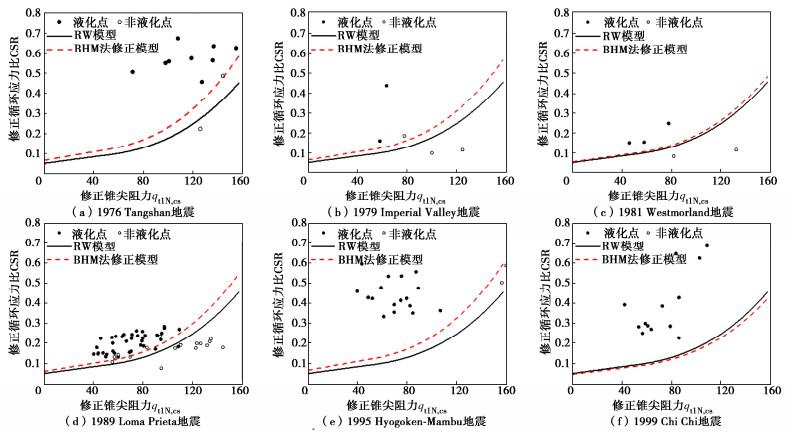
图 5为分地震场地绘制的CPT-RW模型和经BHM法修正后模型的液化触发曲线图，其中BHM法绘制的是P_L=30%的结果。CPT-RW模型对应的液化触发曲线在多个地震场地都存在把不液化的案例划分为液化的现象，总的来说该模型偏于保守；经BHM法修正后的液化触发曲线在CPT-RW模型的上方（图（5a）~（5e）），且不同地震场地的修正程度不同，表明BHM法可以有效修正原始CPT-RW模型的保守性；由于在1999 Chi Chi地震中缺乏非液化案例（图 5（f）），因此BHM修正模型对应的液化触发曲线位于原始CPT-RW模型的下方。

图 5 基于CPT案例库分地震场地建立的液化触发曲线

Figure 5. Seismic site-specific liquefaction boundary curves using CPT-based liquefaction case histories

下载: 全尺寸图片幻灯片

4. 结论

为评价SPT-Youd模型、V_s-AS模型和CPT-RW模型的保守性特点，本研究汇编了同时含有SPT、V_s和CPT的地震液化案例库，采用BHM法修正并探究了3种液化判别模型在同一地震场地的保守性特点和在不同地震场地的变异性特征，得出3点结论。

（1）本研究汇编了同时含有基于SPT，V_s和CPT的地震液化案例库，分别含88，176，107个案例，涉及6次地震事件的场地；受试验本身不确定性的影响，SPT和V_s案例库中液化和非液化案例重合度高，CPT案例库的液化和非液化案例区分度较高；SPT-Youd模型、V_s-AS模型和CPT-RW模型均存在模型偏差，需要修正。

（2）采用基于不同原位试验的液化判别模型在判别同一个地震场地时，其保守性存在差异。其中，CPT-RW模型计算的F_sc最为保守，SPT-Youd模型计算的F_sc因高估了多个地震场地的抗液化能力而偏于危险，V_s-AS模型的保守性介于两者之间。

（3）采用BHM法分地震场地建立的液化概率模型能够有效地修正原始判别模型的保守性，且不同地震场地的修正程度不同。

本研究工作可在工程师采用多种原位试验结果评估同一场地的液化势时提供有效的先验信息。必须指出，上述结论受案例库的影响较大，随着更多地震液化案例的收集，可提高本工作结论的普适性。

图 1 基于贝叶斯分层建模法的液化判别模型修正流程图

Figure 1. Flow chart for modification of liquefaction model by BHM method

下载: 全尺寸图片幻灯片

图 2 液化案例及其液化触发曲线图

Figure 2. Case histories and their liquefaction boundary curves

下载: 全尺寸图片幻灯片

图 3 汇编的地震液化案例场地及其分布图

Figure 3. Distribution of earthquake sites complied in liquefaction database

下载: 全尺寸图片幻灯片

图 4 基于CPT案例库的MCMC模拟法的样本抽样图

Figure 4. Trace plot of samples generated with MCMC simulation through CPT-based database

下载: 全尺寸图片幻灯片

图 5 基于CPT案例库分地震场地建立的液化触发曲线

Figure 5. Seismic site-specific liquefaction boundary curves using CPT-based liquefaction case histories

下载: 全尺寸图片幻灯片

表 1 汇编的地震液化案例库

Table 1 Compiled liquefaction database

地震事件	SPT案例库^[11]			V_s案例库^[12]			CPT案例库^[13]
地震事件	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数
1976 Tangshan地震	7.6	5	1	8	15	1	7.8	9	2
1979 Imperial Valley地震	6.53	4	3	6.5	4	7	6.5	2	3
1981 Westmorland地震	5.9	3	4	5.9	6	5	5.9	3	2
1989 Loma Prieta地震	6.93	15	7	7	41	15	7	37	16
1995 Hyogoken-Nambu地震	6.9	26	10	7	64	5	7.2	17	2
1999 Chi Chi地震	7.6	6	4	7.6	12	1	7.6	14	0
合计	—	59	29	—	142	34	—	82	25

下载: 导出CSV

表 2 经BHM法修正后液化判别模型参数的后验分布

Table 2 Posterior distribution of liquefaction model parameters corrected by BHM method

地震场地	SPT-Youd模型^[2]				V_s-AS模型^[3]				CPT-RW模型^[4]
地震场地	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)
μ_μ	1.21	0.31	—	—	1.04	0.36	—	—	0.75	0.20	—	—
σ_μ	0.42	0.47	—	—	0.49	0.66	—	—	0.18	0.37	—	—
σ_c	1.03	0.64	—	—	0.68	0.24	—	—	0.10	0.03	—	—
案例库外的区域	1.21	0.70	1.21	1.40	1.04	0.90	1.04	1.15	0.75	0.46	0.75	0.47
1976 Tangshan	1.18	0.30	1.18	1.25	0.74	0.14	0.74	1.44	0.67	0.06	0.67	0.12
1979 Imperial Valley	1.04	0.30	1.04	1.24	0.77	0.16	0.77	1.13	0.67	0.07	0.67	0.12
1981 Westmorland	1.28	0.34	1.28	1.25	1.07	0.34	1.07	1.13	0.76	0.14	0.76	0.18
1989 Loma Prieta	1.16	0.25	1.16	1.23	0.81	0.11	0.81	1.17	0.72	0.03	0.72	0.11
1995 Hyogoken-Nambu	1.06	0.23	1.06	1.23	0.84	0.11	0.84	1.13	0.64	0.07	0.64	0.12
1999 Chi Chi	0.89	0.29	0.89	1.24	1.21	0.54	1.21	1.13	0.78	0.30	0.78	0.32

下载: 导出CSV

参考文献(13)

[1]	段伟, 蔡国军, 赵泽宁, 等. 基于CPTU测试的砂质与粉质土液化概率模型与评价方法研究[J]. 岩土工程学报, 2023, 45(1): 66-74. doi: 10.11779/CJGE20210645 DUAN Wei, CAI Guojun, ZHAO Zening, et al. CPTU-based probabilistic model and evaluation method for liquefaction of sandy and silty soils[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(1): 66-74. (in Chinese) doi: 10.11779/CJGE20210645
[2]	YOUD T L, IDRISS I M. Liquefaction resistance of soils: summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(4): 297-313. doi: 10.1061/(ASCE)1090-0241(2001)127:4(297)
[3]	ANDRUS R D, STOKOE K H. Liquefaction resistance of soils from shear-wave velocity[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(11): 1015-1025. doi: 10.1061/(ASCE)1090-0241(2000)126:11(1015)
[4]	ROBERTSON P K, WRIDE C F. Evaluating cyclic liquefaction potential using the cone penetration test[J]. Canadian Geotechnical Journal, 1998, 35(3): 442-459. doi: 10.1139/t98-017
[5]	HU J L. Integration of double-weighted Bayesian and simplified methods for predicting seismic liquefaction based on multiple databases[J]. International Journal of Geomechanics, 2023, 23(12): 04023214. doi: 10.1061/IJGNAI.GMENG-8548
[6]	ROLLINS K, AMOROSO S, HRYCIW R. Comparison of DMT, CPT, SPT, and V_s based liquefaction assessment on Treasure Island during the Loma Prieta earthquake[C]//Proc 3rd Int Conf on the Flat Dilatometer. London, 2015.
[7]	ZHANG J, JUANG C H, MARTIN J R, et al. Inter-region variability of Robertson and Wride method for liquefaction hazard analysis[J]. Engineering Geology, 2016, 203: 191-203. doi: 10.1016/j.enggeo.2015.12.024
[8]	XIAO S H, ZHANG J, YE J M, et al. Establishing region-specific N–V_s relationships through hierarchical Bayesian modeling[J]. Engineering Geology, 2021, 287: 106105. doi: 10.1016/j.enggeo.2021.106105
[9]	ZHANG J, XIAO S H, HUANG H W, et al. Calibrating a standard penetration test based method for region-specific liquefaction potential assessment[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(10): 5185-5204. doi: 10.1007/s10064-020-01815-w
[10]	GE Y X, ZHANG J, ZHU L W, et al. Developing region-specific liquefaction assessment criterion for Bachu region, China[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2020, 6(3): 04020026. doi: 10.1061/AJRUA6.0001070
[11]	BOULANGER R, IDRISS I M. CPT-based liquefaction triggering procedure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142: 04015065. doi: 10.1061/(ASCE)GT.1943-5606.0001388
[12]	KAYEN R, MOSS R E S, THOMPSON E M, et al. Shear-wave velocity–based probabilistic and deterministic assessment of seismic soil liquefaction potential[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(3): 407-419. doi: 10.1061/(ASCE)GT.1943-5606.0000743
[13]	KU C S, JUANG C H, CHANG C W, et al. Probabilistic version of the Robertson and Wride method for liquefaction evaluation: development and application[J]. Canadian Geotechnical Journal, 2012, 49(1): 27-44. doi: 10.1139/t11-085