基于不同原位试验的土壤液化判别模型保守性评估

沈梦芬; 鲍丽春; 孙宏磊; 蔡袁强

doi:10.11779/CJGE2023S20036

基于不同原位试验的土壤液化判别模型保守性评估 English Version

浙江工业大学土木工程学院, 浙江杭州 310014

基金项目:

国家自然科学基金项目 42007236

国家自然科学基金项目 U2239251

浙江省自然科学基金项目 LY24D020001

浙江省自然科学基金项目 LQ20D020002

详细信息

作者简介:
沈梦芬(1988—)，女，博士，副教授，主要从事土壤液化灾害评估、抗液化地基处理、岩土与地质工程风险分析和稳健性优化设计。E-mail：mshen@zjut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 174
- HTML全文浏览量: 39
- PDF下载量: 34
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Assessment of model bias of SPT, V_s and CPT-based liquefaction models

Zhejiang University of Technology, Hangzhou 310014, China

摘要

摘要: 基于现场原位试验和地震液化案例库建立的液化判别模型是一种常见的场地液化判别方法。然而，场地液化判别模型存在着准确性因测试手段而异的问题，即判别模型存在偏差；同时基于同一原位试验建立的液化判别模型的准确性因地震场地而异，即存在地震场地变异性。为评估基于SPT，V_s和CPT建立的液化判别模型的保守性特点，研究汇编了同时含有3种原位试验的地震液化案例库，分别含88，176，107个案例，涉及6次地震事件和场地。根据汇编的案例库采用贝叶斯分层建模法(BHM)标定了SPT-Youd模型、V_s-AS模型和CPT-RW模型的偏差系数，建立了分地震场地的液化判别模型。结果表明：CPT-RW模型的场地液化判别结果最为保守，SPT-Youd模型存在高估多个地震场地的抗液化能力而偏于危险的情况，V_s-AS模型的保守性则介于两者之间；基于汇编的CPT案例库，运用BHM法分地震场地建立的液化判别模型能够有效地修正CPT-RW模型的保守性，且不同地震场地的修正程度不同。研究工作可在工程师采用多种原位试验结果评估同一场地的液化势时提供有效的先验信息。
- 地震液化 /
- 标准贯入试验(SPT) /
- 剪切波速测试(V_s) /
- 静力触探试验(CPT) /
- 模型偏差系数 /
- 贝叶斯分层建模
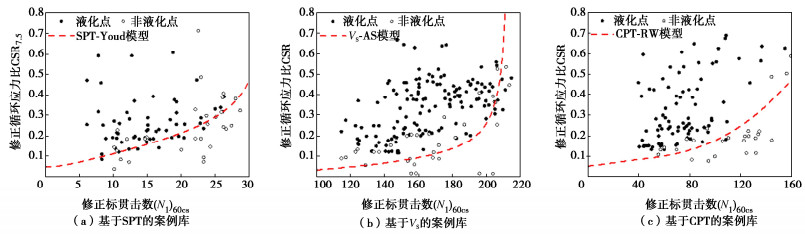
Abstract: The liquefaction models established through the in-situ tests and liquefaction case histories are widely adopted in the liquefaction evaluation of a site. However, it is reported that the model accuracy varies with the in-situ test methods (i.e., model bias), as well as the earthquake sites (i.e., seismic site variability). To assess the model bias of SPT-Youd model, V_s-AS model and CPT-RW model, a database of liquefaction case histories containing all these three in-situ tests is compiled firstly, containing 88, 176 and 107 cases, respectively, and involving sites from six seismic events. Based on the compiled database, the Bayesian hierarchical modeling (BHM) method is adopted to correct the model bias of the three models, and liquefaction models for each of the seismic sites are established. It is found that the CPT-RW model is the most conservative model, and the liquefaction resistance calculated by the SPT-Youd model is overestimated in several seismic sites, and the conservatism of the V_s-AS model is between them according to the complied database. Using the complied CPT database, the seismic site-specific liquefaction models established by the BHM method can effectively correct the conservatism of the original CPT-RW model, and the levels of correction vary from one seismic site to another. This study provides effective priori information for engineers to assess the liquefaction potential of a site using multiple in-situ tests.
- earthquake-induced soil liquefaction /
- standard penetration test /
- shear wave velocity test /
- cone penetration test /
- model uncertainty /
- Bayesian hierarchical modeling

HTML全文

0. 引言

非饱和状态下的土体具有很高的强度^[1]，然而遇水湿化强度会迅速降低，局部可能达到饱和，该状态下的土压力值与非饱和条件下的值差别很大。多名学者统计显示大部分基坑事故都与水有关，此外，2019年6月8日南宁绿地中心基坑塌陷也是因为场地管道爆裂，非饱和土遇水湿化，作用在支护结构的土压力增大^[2]。因此，亟需定量评估浸湿作用对非饱和土侧向土压力的影响，提出计算方法，减少此类事故发生。

目前，对非饱和土压力研究获得了很大进展，但现有研究多从理论出发进行公式推导，1961年Coleman等^[3]提出双变量理论，Fredlund便得到净应力与吸力的双变量理论，之后得到了扩展的朗肯土压力理论，但是在平时的设计和研究中，仍然采用朗肯土压力理论^[4]计算非饱和土压力。姚攀峰等^[5]提出了与扩展型朗肯土压力不同的计算方法广义朗肯土压力计算方法，陈铁林等^[6]解决水位变化及降水条件下的土压力计算问题，根据K₀定义推导K₀求解式。任传健等^[7]结合Fredlund非饱和土抗剪切与强化准则和经典的朗肯土压计算公式，得出考虑降水变化的土压计算公式。汪丁建等^[8]在饱和土朗肯土压力分析基础上，推导出降雨条件下非饱和朗肯土压力。王晓亮等^[9]将降雨和蒸发对基质吸力的影响引入到非饱和土抗剪强度公式中，得到K₀随降雨定性变化，但没有定量结果。

已有的大量研究充分表明水对静止土压力的影响不可忽略，但已有的计算公式复杂不实用，结果有待验证。导致现有非饱和土体仍采用饱和土理论的计算结果加安全储备来设计计算^[10]，安全系数是否足够不明确。为了使湿化条件下静止土压力增量的演化规律更明确，本文通过室内试验确定了其相关的变化规律、建立相应的计算模型，减小对安全施工的威胁。

1. 试验材料与方法

1.1 土料特性

取北京延庆地区原状粉质黏土进行烘干、碾碎、过0.25 mm筛备用，进行基本物理性质测试，依据《土工试验方法标准：GB/T50123—2019》^[11]，结果见表 1。

表 1 土的基本物理性质

Table 1. Basic physical properties of soil

最大干密度/ (g·cm^-3)	最优含水率/%	液限 w_L/%	塑限w_P/%	塑性指数I_P	土粒相对密度G_S
1.80	16.5	30.7	15.2	15.5	2.73

下载: 导出CSV

| 显示表格

1.2 试验方案

选择干密度1.53 g/cm³（压实度0.85）、高度40 mm的标准环刀试样开展K₀压缩试验，设5个不同的初始饱和度与4个不同的上覆荷载，具体方案见表 2。

表 2 浸水条件下非饱和粉质黏土试验方案

Table 2. Test schemes under water immersion conditions

上覆荷载/kPa	加载过程	初始饱和度
100/200/ 300/400	100(200/300/400)kPa→湿化→逐级加载至1600kPa	0.2/0.3/0.4/ 0.5/0.6

下载: 导出CSV

| 显示表格

1.3 试验过程

（1）仪器标定。本文采用JCY型K₀固结仪来完成K₀压缩试验，在气囊中充入与试样等体积的水，利用水各向等压特性标定仪器在竖向压力下对土压力的测量，根据试验数据拟合得到两仪器的标定系数^[12]。

（2）制样并养护得到不同初始含水率试样。用饱和再风干的土样模拟经过了干湿循环的天然非饱和土，通过7 d密闭养护保证孔隙水分布均匀，见图 1。

图 1 准备不同初始含水率的试样

Figure 1. Preparation of samples with different initial moisture contents

下载: 全尺寸图片幻灯片

（3）加上覆荷载待稳定后进行湿化饱和，湿化稳定后养护7 d，再完成后续设定加载至试验结束。

（4）卸压并整理仪器装置，将不同初始饱和度湿化前与湿化压缩后试样进行对比，如图 2所示。

图 2 试验前后对比图

Figure 2. Comparison of soil samples before and after tests

下载: 全尺寸图片幻灯片

2. 试验结果及规律

K₀固结仪连接压力传感器采集数据，得到侧压力随时间变化关系^[12]，从而得到粉质黏土在5个不同初始饱和度S_r和4个不同上覆荷载P作用下发生湿化与湿化后继续加载的水平静止土压力-竖向压力的关系曲线，见图 3，因篇幅关系只展示S_r=0.2结果^[12]。对于非饱和土一般采用水土合算计算土压力，此时侧压力传感器测量得到的相当于水土合算下的土压力。

图 3 静止土压力随竖向压力变化关系(S_r=0.2)

Figure 3. Variation of static earth pressure with vertical pressure (S_r=0.2)

下载: 全尺寸图片幻灯片

湿化静止土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 统计见表 3，计算式为

$\Delta {\sigma _{{\text{h}}}} = {\sigma _{{\text{w}}}} - {\sigma _{{\text{d}}}} 。$

(1)

表 3 湿化静止土压力增量计算值统计

Table 3. Statistics of calculated increment static earth pressure

初始饱和度S_r	0.2	0.3	0.4	0.5	0.6
100 kPa下增量值	35.14	25.10	17.41	12.5	3.53
200 kPa下增量值	68.95	48.38	33.32	22.97	6.31
300 kPa下增量值	95.01	68.95	47.86	29.99	8.98
400 kPa下增量值	118.02	90.00	60.99	35.97	10.11

下载: 导出CSV

| 显示表格

式中： ${\sigma _{{\text{d}}}}$ 为上覆荷载作用下湿化前静止土压力大小； ${\sigma _{{\text{w}}}}$ 湿化饱和后静止土压力大小。

3. 静止土压力增量计算模型

3.1 湿化过程中静止土压力演变规律

不同初始饱和度湿化过程的增湿水平不同，可使用湿化前初始饱和度表示增湿水平，即：S_r=1的增湿水平为0，S_r越小增湿水平越大。

由表 3可以看到湿化时静止土压力都有不同程度的增大，且初始饱和度S_r越低或上覆荷载P越大，静止土压力增量越大。图 3数据显示，湿化后继续加载呈线性且斜率基本一致，表明K₀值大小近似一致，S_r与P的不同不会影响湿化饱和后K₀大小。可能原因是：静止土压力系数主要由有效内摩擦角决定，饱和后有效内摩擦角接近，因此湿化饱和后K₀近似一致。

土体强度理论认为土颗粒间存在综合作用，包括吸力、胶结作用、德华力以及化学键等^[4]，非饱和土研究学者^[13]一般认为土骨架受压为保证完整性依靠两部分力平衡：一是土颗粒间的基质吸力，取决于土体的含水量；另外是土颗粒间的胶结力，取决于土体内部的黏粒微量物质。静止土压力增量是由颗粒间胶结作用的减弱和基质吸力减小两方面原因引起的^[14]。为推导计算模型引出中间变量0.65-S_r，如图 4所示，初始饱和度越小，湿化导致基质吸力减少量就越大，静止土压力增量就越大；湿化饱和后上覆荷载越大，对土体胶结力破坏就越大，如图 5所示，湿化饱和后的静止土压力增量，随上覆荷载增加而变大。

图 4 静止土压力增量与初始饱和度关系

Figure 4. Variation of increment of static earth pressure increment with initial saturation

下载: 全尺寸图片幻灯片

图 5 静止土压力增量与上覆荷载关系

Figure 5. Variation of increment of static earth pressure with load

下载: 全尺寸图片幻灯片

3.2 湿化过程中静止土压力增量计算模型

土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 与上覆荷载P，初始饱和度S_r都呈线性关系，双线性模型见式（2），P和S_r确定时有一次函数式（3），（4）。当变量 $n=（{S}_{\text{r}}{\text{+}}{b}_{1}）{\text{=0}}{\text{.65}}-{S}_{{\text{r}}}$ 时，土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 与n成正比例， ${k_1}{k_2}m$ 为斜率，见图 4。

$\Delta {\sigma _{{\text{h}}}} = {k_1}n \times {k_2}m {\text{，}}$

(2)

${k}_{1}n={k}_{1}（{S}_{{\text{r}}}{\text{+}}{b}_{1}） {\text{，}}$

(3)

${k}_{2}m={k}_{2}（P{\text{+}}{b}_{2}）。$

(4)

P与其对应的 ${k_1}{k_2}m$ 拟合得 ${k_1}{k_2}m{{\text{ = 0}}}{{\text{.60}}}P + {{\text{19}}}{{\text{.76}}}$ ，再将 $n$ 代入式（2）中，得到式（5）。当初始饱和度S_r较大接近饱和土时，静止土压力增量为0，观察式（5），当饱和度S_r＞0.65时，湿化不会引起静止土压力增加。

$\Delta {\sigma _{{\text{h}}}} = \left\{ \begin{array}{l} (0.60P{{\text{ + 19}}}{{\text{.76}}}){{\text{(}}}0.65 - {S_{{\text{r}}}}{{\text{)}}} \;\;\;\;{{\text{(}}}{S_{{\text{r}}}} \leqslant 0.65{{\text{)}}} \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\text{ (}}}{S_{{\text{r}}}} > 0.65{{\text{)}}} \hfill \\ \end{array} \right. 。$

(5)

为了更直观的表现增量的含义，将 $\Delta {S_{{\text{r}}}} = 1 - {S_{{\text{r}}}}$ 代入式（5），得到最终的增量表达式如下：

$\begin{equation} \Delta \sigma_{\mathrm{h}}=\left\{\begin{array}{ll} (0.60 P+19.76)\left(\Delta S_{\mathrm{r}}-0.35\right) & \left(\Delta S_{\mathrm{r}} \geqslant 0.35\right) \\ 0 & \left(\Delta S_{\mathrm{r}}<0.35\right) \end{array}\right. 。 \end{equation}$

(6)

4. 挡土墙静止土压力计算案例分析

以延庆某深基坑为背景，结合勘察数据，对上文的模型进行试算。该基坑开挖深度23 m，上表面有8 kPa的均布荷载，施工阶段饱和度0.25，已勘测到自然地面以下34 m地层特性，土体基本为粉质黏土。

根据划分土层的重度与厚度计算出土层下表面荷载，并根据K₀算出湿化前静止土压力 ${\sigma _{{\text{h}}}}_i$ ，K₀按经验值取0.3。根据式（6）算出静止土压力增量 $\Delta {\sigma _{{\text{h}}}}_i$ ，接着计算出湿化后静止土压力 ${\sigma _{{\text{w}}}}_i$ 和 ${\sigma _{{\text{w}}}}_i$ / ${\sigma _{{\text{h}}}}_i$ 比值，计算值随深度变化绘制在图 6中，发现比值随深度增大而减小，但始终大于1.8，说明湿化对静止土压力影响较大。

图 6 不同累计深度处静止土压力与其相关计算值关系

Figure 6. Static earth pressures and their correlation with depth

下载: 全尺寸图片幻灯片

由于本文采用重塑土进行试验，和天然土体湿化时侧压力变化结果不同，特别是黄土等结构性非饱和土，其湿化可能发生湿陷等行为，导致土压力演化较为复杂。本文研究结果仅适用于非结构性的非饱和土。

5. 结论

本文通过开展室内试验，定量评估浸湿作用对非饱和土侧向土压力的影响，实测浸湿饱和作用下静止土压力增量的变化规律，建立相应的计算模型，通过应用发现设计时必须重视湿化的影响，并得到以下3点结论。

（1）湿化饱和后，土体的静止土压力系数K₀值与初始饱和度、上覆荷载无关。推测土体静止土压力系数K₀值主要由有效内摩擦角决定，饱和后有效内摩擦角基本一致，故K₀值大小近似一致。

（2）湿化前的初始饱和度越低，湿化饱和后的静止土压力增量越大；且湿化饱和后的静止土压力增量，随湿化时的上覆荷载增加而变大。

（3）基于试验数据和机理分析，得到了湿化条件下考虑上覆荷载与初始饱和度的双线性土压力增量计算模型；将其应用于某支挡工程，发现湿化后的土压力可达初始土压力1.8倍以上，设计时必须予以重视。

图 1 基于贝叶斯分层建模法的液化判别模型修正流程图

Figure 1. Flow chart for modification of liquefaction model by BHM method

下载: 全尺寸图片幻灯片

图 2 液化案例及其液化触发曲线图

Figure 2. Case histories and their liquefaction boundary curves

下载: 全尺寸图片幻灯片

图 3 汇编的地震液化案例场地及其分布图

Figure 3. Distribution of earthquake sites complied in liquefaction database

下载: 全尺寸图片幻灯片

图 4 基于CPT案例库的MCMC模拟法的样本抽样图

Figure 4. Trace plot of samples generated with MCMC simulation through CPT-based database

下载: 全尺寸图片幻灯片

图 5 基于CPT案例库分地震场地建立的液化触发曲线

Figure 5. Seismic site-specific liquefaction boundary curves using CPT-based liquefaction case histories

下载: 全尺寸图片幻灯片

表 1 汇编的地震液化案例库

Table 1 Compiled liquefaction database

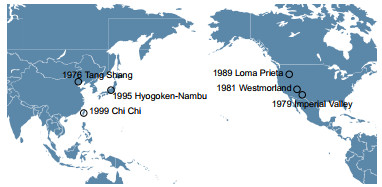
地震事件	SPT案例库^[11]			V_s案例库^[12]			CPT案例库^[13]
地震事件	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数	震级	液化案例数	非液化案例数
1976 Tangshan地震	7.6	5	1	8	15	1	7.8	9	2
1979 Imperial Valley地震	6.53	4	3	6.5	4	7	6.5	2	3
1981 Westmorland地震	5.9	3	4	5.9	6	5	5.9	3	2
1989 Loma Prieta地震	6.93	15	7	7	41	15	7	37	16
1995 Hyogoken-Nambu地震	6.9	26	10	7	64	5	7.2	17	2
1999 Chi Chi地震	7.6	6	4	7.6	12	1	7.6	14	0
合计	—	59	29	—	142	34	—	82	25

下载: 导出CSV

表 2 经BHM法修正后液化判别模型参数的后验分布

Table 2 Posterior distribution of liquefaction model parameters corrected by BHM method

地震场地	SPT-Youd模型^[2]				V_s-AS模型^[3]				CPT-RW模型^[4]
地震场地	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)	E()	Std()	E(c_i)	Std(c_i)
μ_μ	1.21	0.31	—	—	1.04	0.36	—	—	0.75	0.20	—	—
σ_μ	0.42	0.47	—	—	0.49	0.66	—	—	0.18	0.37	—	—
σ_c	1.03	0.64	—	—	0.68	0.24	—	—	0.10	0.03	—	—
案例库外的区域	1.21	0.70	1.21	1.40	1.04	0.90	1.04	1.15	0.75	0.46	0.75	0.47
1976 Tangshan	1.18	0.30	1.18	1.25	0.74	0.14	0.74	1.44	0.67	0.06	0.67	0.12
1979 Imperial Valley	1.04	0.30	1.04	1.24	0.77	0.16	0.77	1.13	0.67	0.07	0.67	0.12
1981 Westmorland	1.28	0.34	1.28	1.25	1.07	0.34	1.07	1.13	0.76	0.14	0.76	0.18
1989 Loma Prieta	1.16	0.25	1.16	1.23	0.81	0.11	0.81	1.17	0.72	0.03	0.72	0.11
1995 Hyogoken-Nambu	1.06	0.23	1.06	1.23	0.84	0.11	0.84	1.13	0.64	0.07	0.64	0.12
1999 Chi Chi	0.89	0.29	0.89	1.24	1.21	0.54	1.21	1.13	0.78	0.30	0.78	0.32

下载: 导出CSV

参考文献(13)

[1]	段伟, 蔡国军, 赵泽宁, 等. 基于CPTU测试的砂质与粉质土液化概率模型与评价方法研究[J]. 岩土工程学报, 2023, 45(1): 66-74. doi: 10.11779/CJGE20210645 DUAN Wei, CAI Guojun, ZHAO Zening, et al. CPTU-based probabilistic model and evaluation method for liquefaction of sandy and silty soils[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(1): 66-74. (in Chinese) doi: 10.11779/CJGE20210645
[2]	YOUD T L, IDRISS I M. Liquefaction resistance of soils: summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(4): 297-313. doi: 10.1061/(ASCE)1090-0241(2001)127:4(297)
[3]	ANDRUS R D, STOKOE K H. Liquefaction resistance of soils from shear-wave velocity[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(11): 1015-1025. doi: 10.1061/(ASCE)1090-0241(2000)126:11(1015)
[4]	ROBERTSON P K, WRIDE C F. Evaluating cyclic liquefaction potential using the cone penetration test[J]. Canadian Geotechnical Journal, 1998, 35(3): 442-459. doi: 10.1139/t98-017
[5]	HU J L. Integration of double-weighted Bayesian and simplified methods for predicting seismic liquefaction based on multiple databases[J]. International Journal of Geomechanics, 2023, 23(12): 04023214. doi: 10.1061/IJGNAI.GMENG-8548
[6]	ROLLINS K, AMOROSO S, HRYCIW R. Comparison of DMT, CPT, SPT, and V_s based liquefaction assessment on Treasure Island during the Loma Prieta earthquake[C]//Proc 3rd Int Conf on the Flat Dilatometer. London, 2015.
[7]	ZHANG J, JUANG C H, MARTIN J R, et al. Inter-region variability of Robertson and Wride method for liquefaction hazard analysis[J]. Engineering Geology, 2016, 203: 191-203. doi: 10.1016/j.enggeo.2015.12.024
[8]	XIAO S H, ZHANG J, YE J M, et al. Establishing region-specific N–V_s relationships through hierarchical Bayesian modeling[J]. Engineering Geology, 2021, 287: 106105. doi: 10.1016/j.enggeo.2021.106105
[9]	ZHANG J, XIAO S H, HUANG H W, et al. Calibrating a standard penetration test based method for region-specific liquefaction potential assessment[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(10): 5185-5204. doi: 10.1007/s10064-020-01815-w
[10]	GE Y X, ZHANG J, ZHU L W, et al. Developing region-specific liquefaction assessment criterion for Bachu region, China[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2020, 6(3): 04020026. doi: 10.1061/AJRUA6.0001070
[11]	BOULANGER R, IDRISS I M. CPT-based liquefaction triggering procedure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142: 04015065. doi: 10.1061/(ASCE)GT.1943-5606.0001388
[12]	KAYEN R, MOSS R E S, THOMPSON E M, et al. Shear-wave velocity–based probabilistic and deterministic assessment of seismic soil liquefaction potential[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(3): 407-419. doi: 10.1061/(ASCE)GT.1943-5606.0000743
[13]	KU C S, JUANG C H, CHANG C W, et al. Probabilistic version of the Robertson and Wride method for liquefaction evaluation: development and application[J]. Canadian Geotechnical Journal, 2012, 49(1): 27-44. doi: 10.1139/t11-085