Analytical solutions for scattering of plane waves by a cylindrical lined cavity in unsaturated poroelastic media
-
摘要: 采用波函数展开法求解了非饱和多孔弹性介质中无限长圆柱形衬砌洞室对平面波的二维散射问题。将非饱和孔隙弹性介质视为利用界面混合物理论建立的孔隙弹性模型，并将控制方程解耦为4个亥姆霍兹方程。衬砌结构视为单相弹性介质，并解耦为两个亥姆霍兹方程。利用边界条件求解波函数中待定系数，分别得到平面P波和SV波在非饱和多孔弹性介质中圆柱形衬砌洞室周围散射问题的解析解。利用该解析解，考虑饱和度对剪切模量的影响，数值计算分析了不同入射频率下饱和度对洞室周围动应力集中系数的影响。Abstract: In this study, two-dimensional scattering of plane waves by a cylindrical lined cavity embedded in an infinite unsaturated poroelastic medium is solved by the wave function expansion method. The unsaturated poroelastic medium is simulated as a poroelastic model formulated using the theory of mixture with interfaces, and the governing equations are solved by reduction to four Helmholtz equations. The lining structure is considered as a single-phase elastic medium and decoupled into two Helmholtz equations. Using the boundary conditions to solve the undetermined coefficients in the wave function, the analytical solutions are obtained for the scattering problem of plane P-waves and SV-waves around cylindrical lined cavities in unsaturated porous elastic media. Using the analytical solutions, numerical calculations are conducted to analyze the effects of factors such as saturation on the dynamic stress concentration coefficient around the lined cavity.
-
0. 引言
地下洞室对弹性波的散射问题在地震工程、地下结构抗爆、地球物理勘探等领域有着广泛的应用。近年来，许多研究人员基于波函数展开法[1-2]对单相介质中衬砌结构的动力响应进行了探讨。然而，土和岩石具有多孔性和多相性，单相弹性连续介质无法准确描述实际情况。因此，波在两相介质中的传播和动力响应问题受到广泛关注。应用Biot饱和多孔介质波动理论，周香莲等[3]求解了全空间圆柱形衬砌洞室对平面波散射的解析解。Jiang等[4]引入大圆弧假设，解决了平面P波入射下饱和多孔弹性半空间中圆形衬砌洞室周围的散射问题。为了更符合实际工程，张海等[5]使用辅助函数配合波函数展开法和傅立叶级数展开方法，进一步研究了SH波入射下含直边界半圆形衬砌洞室的动力响应。Ding等[6]利用波函数展开法，给出了平面P波入射下饱和多孔弹性介质中复合衬砌动应力集中的解析解。Hasheminejad等[7]解析分析P波和SV波作用下饱和多孔弹性介质中变壁厚内衬的圆柱形洞室的动应力集中问题。Liu等[8]基于平面复变理论得到了多孔弹性半空间中衬砌洞室对P1和SV波散射的解析解。徐长节等[9]，Xu等[10]基于非局部弹性理论分析了孔径效应和孔隙动力学效应对饱和土中圆柱形衬砌动力响应的影响。Ding等[11]基于非局部Biot理论得到了平面P波入射下饱和多孔介质中浅埋复合衬砌洞室动力响应的解析解。
综上，饱和多孔介质中衬砌洞室的动力响应已经得到了广泛而充分的研究。可实际上，土是一种三相介质，即使地下水位以下的土，也可能存在不完全饱和的情况。Li等[12]总结了众多非饱和孔隙弹性模型以及非饱和多孔介质波动特性的研究，表明由于气相的存在，非饱和介质的动态响应在许多方面与传统饱和多孔介质的动态反应显著不同。然而，目前有关非饱和多孔介质中衬砌洞室对地震波散射问题的研究还较为匮乏。Li等[13]研究了非饱和多孔介质中圆形洞室在内部荷载作用下的动力响应。Tan等[14]研究了无限非饱和多孔弹性介质中不完全接触的衬砌洞室对平面P波的散射问题。以考虑混合物理论的非饱和多孔介质动力理论为基础，采用波函数展开法和分离变量法，分别推导了平面P波和SV波入射时衬砌洞室周围位移应力的解析解。分析了不同入射频率下饱和度对衬砌洞室周围动应力集中系数的影响。
1. 分析模型
1.1 数学模型和基本方程
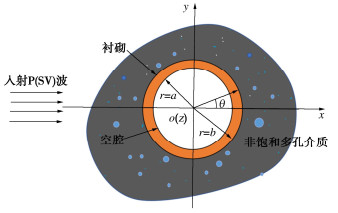
为了简化研究模型，把非饱和多孔介质中圆柱形衬砌洞室，视为无限非饱和多孔介质全空间中一个无限长度的衬砌洞室（图 1）。
衬砌洞室的内径为a，外径为b。本研究基于Wei等[15]提出的非饱和多孔介质动力学理论。控制方程表示为
$$ \left. \begin{array}{l}{n}_{0}^{\rm{S}}{\rho }_{0}^{\rm{S}}{\ddot{u}}^{\rm{S}}=({M}_\text{SS}+G)\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{S}}+G\mathit{\nabla }\cdot \mathit{\nabla }{u}^{\rm{S}}+{M}_\text{SW}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{W}}+\\ \;\;\;\;\;\;\;\;\;\;{M}_\text{SN}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{N}}+ {\widehat{\mu }}^{\rm{W}}({\dot{u}}^{\rm{W}}-{\dot{u}}^{\rm{S}})+ {\widehat{\mu }}^{\rm{N}}({\dot{u}}^{\rm{N}}-{\dot{u}}^{\rm{S}})\text{，}\\ {n}_{0}^{\rm{W}}{\rho }_{0}^{\rm{W}}{\ddot{u}}^{\rm{W}}={M}_\text{SW}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{S}}+{M}_\text{WW}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{W}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;{M}_\text{WN}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{N}}-{\widehat{\mu }}^{\rm{W}}({\dot{u}}^{\rm{W}}-{\dot{u}}^{\rm{S}})\text{，}\\ {n}_{0}^{\rm{N}}{\rho }_{0}^{\rm{N}}{\text{u ¨}}^{\rm{N}}={M}_\text{SN}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{S}}+{M}_\text{WN}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{W}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M}_{\text{NN}}\mathit{\nabla }\mathit{\nabla }\cdot {u}^{\rm{N}}-{\widehat{\mu }}^{\rm{N}}({\dot{u}}^{\rm{N}}-{\dot{u}}^{\rm{S}})。\end{array} \right\} $$ (1) 式中：上角标$ S，W，N $分别为非饱和介质中的固体骨架部分、液相部分和气相部分；G为非饱和多孔介质的剪切模量；$ n_0^\alpha ,\rho _0^\alpha ,{u^\alpha } $分别为各相的初始体积分数、初始密度和初始位移；$ {M_\text{SS}} $，$ {M_\text{WW}} $，$ {M_\text{NN}} $，$ {M_\text{SW}} $，$ {M_\text{SN}} $，$ {M_\text{WN}} $为与体积模量、剪切模量及模量间耦合相关的弹性系数；$ {\hat \mu ^f} $为渗透率相关的系数，$ f = \text{W,N} $。Wei等[15]给出了相关参数的表达式。采用Van等[16]提出的土水特征曲线V-G模型。
非饱和多孔介质中的本构关系表示为
$$ \left. \begin{array}{l}\boldsymbol{\sigma }^{\rm{S}}=({M}_\text{SS}\mathit{\nabla }\cdot {u}^{\rm{S}}+{M}_\text{SW}\mathit{\nabla }\cdot {u}^{\text{W}}+{M}_{\text{SN}}\mathit{\nabla }\cdot {u}^{\text{N}})\boldsymbol{I}+\\ \;\;\;\;\;\;\;\;2G\left[\mathit{\nabla }{u}^{\text{S}}+{(\mathit{\nabla }{u}^{\text{S}})}^{T}\right]\text{，}\\ \boldsymbol{\sigma }^{\text{w}}=({M}_\text{SW}\mathit{\nabla }\cdot {u}^{\rm{S}}+{M}_\text{WW}\mathit{\nabla }\cdot {u}^{\text{W}}+{M}_{\text{WN}}\mathit{\nabla }\cdot {u}^{\text{N}})\boldsymbol{I}\text{ }\text{，}\\ \boldsymbol{\sigma }^{\rm{N}}=({M}_\text{SN}\mathit{\nabla }\cdot {u}^{\rm{S}}+{M}_\text{WN}\mathit{\nabla }\cdot {u}^{\text{W}}+{M}_{\text{NN}}\mathit{\nabla }\cdot {u}^{\text{N}})\boldsymbol{I}\text{ }。\end{array} \right\} $$ (2) 式中：${\boldsymbol{\sigma }^\alpha }$为各相的应力张量，$ \alpha = \text{S,W,N} $；I为单位张量矩阵。
衬砌介质被视为连续、各向同性的单相弹性介质，衬砌介质位移为$ {u^{\text{L}}} $，衬砌介质的拉梅常数为$ {\lambda }_\text{L}，{\mu }_\text{L} $，衬砌密度为${\rho _{\rm{L}}}$。
1.2 动力学方程的求解
根据亥姆霍兹(Helmholtz)矢量分解原理，非饱和多孔介质方程中的位移可以表示为两部分：
$$ {u^\alpha }{\text{ = }}\mathit{\nabla }{\varphi ^\alpha }{\text{ + }}\mathit{\nabla } \times {\varPsi ^\alpha }\;\;\;\;\;\;(\alpha = \text{S,W,N}) 。 $$ (3) 式中：$ {\varphi ^\alpha },{\varPsi ^\alpha } $分别为非饱和多孔介质中$ \alpha $相的标量势函数和矢量势函数。
本文考虑简谐波入射，势函数可表示为$ \varphi = $ $ \varphi (x,y,z){{\text{e}}^{ - {\text{i}}\omega t}} $。将式（3）代入方程（1）可得
$$ \left. \begin{array}{l}({\mathit{\nabla }}^{2}-{k}_{j}^{2}){\varphi }_{j}^{\rm{S}}=0\text{，}\\ {\varphi }_{j}^{\rm{W}}={\delta }_{j}^{\rm{W}}{\varphi }_{j}^{\rm{S}}\text{，}\\ {\varphi }_{j}^{\rm{N}}={\delta }_{j}^{\rm{N}}{\varphi }_{j}^{\rm{S}}\left(j=1,2,3\right)\text{，}\end{array} \right\} $$ (4a) $$ \left. \begin{array}{l}({\mathit{\nabla }}^{2}-{k}_{4}^{2}){\varPsi }^{\rm{S}}=0\text{，}\\ {\varPsi }_{}^{\rm{W}}={\zeta }_{}^{\rm{W}}{\varPsi }_{}^{\rm{S}}\text{，}\\ {\varPsi }_{}^{\rm{N}}={\zeta }_{}^{\rm{N}}{\varPsi }_{}^{\rm{S}}。\end{array} \right\} $$ (4b) 从式（4a），（4b）中可以看出非饱和多孔介质中有3种压缩波1种剪切波，${k_i}$为3种压缩波波数, $i = 1,2,3$，$ {k_4} $为剪切波的波数，$ {\delta }_{j}^{\rm{W}}，{\delta }_{j}^{\rm{N}} $分别为液相、气相压缩波参与系数，$j = 1,2,3$; $ {\zeta }_{}^{\rm{W}}，{\zeta }_{}^{\rm{N}} $分别为液相、气相剪切波参与系数。详细表达式参见文献[13]。
将式（4a），（4b）中固相波函数转换到圆柱坐标系下并使用分离变量法求解，可得固体骨架的标量势函数和矢量势函数的通解为
$$ \varphi _j^{\rm S}(r,\theta ) = \sum\limits_{n = 0}^\infty {{A_{n,j}}{{\text{K}}_n}} ({k_j}r)\cos n\theta {\text{ }}(j = 1,2,3) \text{，} $$ (5) $$ {\varPsi ^{\rm S}}(r,\theta ) = \sum\limits_{n = 0}^\infty {{B_n}{{\text{K}}_n}} ({k_4}r)\sin n\theta 。 $$ (6) 式中：$ {A_{n,j}} $，$ {B_n} $为待定系数；$ {{\text{K}}_n} $为第二类修正Bessel函数，下标n代表阶数。
同理可以得到衬砌介质中标量势函数和矢量势函数的通解：
$$ {\varphi _{\text{L}}}(r,\theta ) = \sum\limits_{n = 0}^\infty {(A_n^{^{(1)}}{{\text{I}}_n}({k_{{L_1}}}r) + A_n^{^{(2)}}{{\text{K}}_n}({k_{{L_1}}}r))} {\text{e}^{\text{i}n\theta }} \text{，} $$ (7) $$ {\varPsi _{\text{L}}}(r,\theta ) = \sum\limits_{n = 0}^\infty {(B_n^{^{(1)}}{{\text{I}}_n}({k_{{L_2}}}r) + B_n^{^{(2)}}{{\text{K}}_n}({k_{{L_2}}}r))} {\text{e}^{\text{i}n\theta }} 。 $$ (8) 式中：$ {\varphi _{\rm{L}}} $，$ {\varPsi _{\rm{L}}} $分别表示衬砌介质中的标量势函数和矢量势函数；$ A_n^{^{(1)}} $，$ A_n^{^{(2)}} $，$ B_n^{^{(1)}} $和$ B_n^{^{(2)}} $为待定系数，分别表示P和$ {\text{SV}} $波的振幅；$ {{\text{I}}_n} $为第一类虚宗量Bessel函数，下标n代表阶数。
2. 波场分析与求解
2.1 波场分析
假设具有圆频率的平面谐波P1或SV波沿x轴正方向传播，用贝塞尔-傅立叶级数表示为
$$ 入射\text{P}_{1}波： {\varphi ^{\rm{i}}} = {\varphi _{\text{0}}}\sum\limits_{n = 0}^\infty {{\varepsilon _n}} {i^n}{{\text{J}}_n}({k_{\text{0}}}r){\text{cos }}n\theta {\text{e}^{ - \text{i}\omega t}} \text{，} $$ (9) $$ 入射\text{SV}波： {\varPsi ^{\rm{i}}} = {\varPsi _{\text{0}}}\sum\limits_{n = 0}^\infty {{\varepsilon _n}} {i^n}{{\text{J}}_n}({k_{\text{0}}}r){\text{cos }}n\theta {\text{e}^{ - \text{i}\omega t}} 。 $$ (10) 式中：$ {k_0} = \omega /{c_\text{p}} $(入射P1波)或者$ {k_0} = \omega /{c_s} $(入射SV波)表示入射波的波数，$ {\varphi _0} $($ {\varPsi _0} $)表示入射波振幅，$ {{\text{J}}_n}\left( . \right) $表示第一类n阶贝塞尔函数，若$ n = 0 $则$ {\varepsilon _n} = 1 $，若$ n \geqslant 1 $则$ {\varepsilon _n} = 2 $且$ i = \sqrt { - 1} $，t表示时间，$ {\text{e}^{ - \text{i}\omega t}} $为时间因子将从后续表达式中省略。
入射平面波进入非饱和多孔介质，由于衬砌洞室的存在，会在非饱和多孔介质中产生散射波，在衬砌介质中产生透射波和内表面的反射波。以P1波入射为例，非饱和多孔介质中的波场可表示为
$$ \left. \begin{array}{l}{\varphi }^{\text{S}}={\varphi }_{0}{\displaystyle \sum _{n=0}^{\infty }{\varepsilon }_{n}}{i}^{n}{\text{J}}_{n}({k}_{\text{0}}r)\text{cos }n\theta \text{+}{\displaystyle \sum _{n=0}^{\infty }{A}_{n,j}{\text{K}}_{n}}({k}_{j}r)\cos n\theta \text{，}\\ {\varphi }^{\rm{W}}={\delta }_{1}^{\rm{W}}{\varphi }_{0}{\displaystyle \sum _{n=0}^{\infty }{\varepsilon }_{n}}{i}^{n}{\text{J}}_{n}({k}_{\text{0}}r)\text{cos }n\theta \text{+}\\ \;\;\;\;\;\;\;\;{\displaystyle \sum _{j=1}^{3}{\delta }_{j}^{\rm{W}}{\displaystyle \sum _{n=0}^{\infty }{A}_{n,j}{\text{K}}_{n}}({k}_{j}r)\cos n\theta }\text{，}\\ {\varphi }^{\rm{N}}={\delta }_{1}^{\rm{N}}{\varphi }_{0}{\displaystyle \sum _{n=0}^{\infty }{\varepsilon }_{n}}{i}^{n}{\text{J}}_{n}({k}_{\text{0}}r)\text{cos }n\theta \text{+}\\ \;\;\;\;\;\;\;\;{\displaystyle \sum _{j=1}^{3}{\delta }_{j}^{\rm{N}}{\displaystyle \sum _{n=0}^{\infty }{A}_{n,j}{\text{K}}_{n}}({k}_{j}r)\cos n\theta \text{ }}\text{，}\end{array} \right\} $$ (11a) $$ \left. \begin{array}{l}{\varPsi }^{\rm{S}}={\displaystyle \sum _{n=0}^{\infty }{B}_{n}{\text{K}}_{n}}({k}_{4}r)\sin n\theta \text{，}\\ {\varPsi }^{\rm{W}}={\zeta }^{\rm{W}}{\varPsi }^{\rm{S}}\text{，}\\ {\varPsi }^{\rm{N}}={\zeta }^{\rm{N}}{\varPsi }^{\rm{S}}。\end{array} \right\} $$ (11b) 衬砌介质中的总波场可表示为
$$ \left. \begin{array}{l}{\varphi }_\text{L}={\displaystyle \sum _{n=0}^{\infty }\left({A}_{n}^{{}^{(1)}}{\text{I}}_{n}({k}_{\text{L}_{1}}r)+{A}_{n}^{{}^{(2)}}{\text{K}}_{n}({k}_{\text{L}_{1}}r)\right)}\cos n\theta \text{，}\\ {\varPsi }_\text{L}={\displaystyle \sum _{n=0}^{\infty }\left({B}_{n}^{{}^{(1)}}{\text{I}}_{n}({k}_{\text{L}_{2}}r)+{B}_{n}^{{}^{(2)}}{\text{K}}_{n}({k}_{\text{L}_{2}}r)\right)}\sin n\theta 。\end{array} \right\} $$ (12) 2.2 边界条件
当$ r = a $时，在衬砌介质中：
$$ \left. \begin{array}{l}{\sigma }_{rr}^{\text{L}}=0\text{，}\\ {\sigma }_{r\theta }^{\text{L}}=0。\end{array} \right\} $$ (13) 当$ r = b $时，非饱和多孔介质与衬砌介质满足连续变形条件与界面不透水边界条件：
$$ \left. \begin{array}{l}{u}_{r}{}^{\rm L}={u}_{r}{}^{\rm{S}}={u}_{r}{}^{\rm{W}}={u}_{r}{}^{\rm{N}}\text{，}\\ {u}_{\theta }{}^{\rm L}={u}_{\theta }{}^{\rm{S}}\text{，}\\ {\sigma }_{r\theta }{}^{\text{L}}={\sigma }_{r\theta }{}^{\rm{S}}\text{，}\\ {\sigma }_{rr}{}^{\text{L}}={\sigma }_{rr}{}^{\rm{S}}+{\sigma }^{\rm{W}}+{\sigma }^{\rm{N}}。\end{array} \right\} $$ (14) 式中：$ u_{^r}^\alpha $，$ u_\theta ^\alpha $分别为非饱和多孔介质各相位移法向和切向分量，$ \alpha = \text{S,W,N} $；$ {u_r}^{\rm L} $，$ {u_\theta }^{\rm L} $分别为衬砌的法向、切向位移分量；$ {\sigma _{rr}}^{\rm S} $，$ {\sigma _{r\theta }}^{\rm S} $分别为非饱和多孔介质固相法向、切向应力分量；$ {\sigma ^{\rm W}} $，$ {\sigma ^{\rm N}} $分别为非饱和多孔介质的孔隙水压力和孔隙气压力；$ {\sigma _{rr}}^{\text{L}} $，$ {\sigma _{r\theta }}^{\text{L}} $分别为衬砌法向和切向应力分量。
2.3 求解
将非饱和多孔介质和衬砌介质中总波场势函数的式（11），（12），代入应力和位移的式（2）中，根据边界条件，可得到波场中未知幅值系数的方程：
$$ \left[\begin{array}{llllllll} G_1 & G_2 & G_3 & G_4 & G_5 & G_6 & G_7 & G_8 \\ H_1 & H_2 & H_3 & H_4 & H_5 & H_6 & H_7 & H_8 \\ T_1 & T_2 & T_3 & T_4 & 0 & 0 & 0 & 0 \\ U_1 & U_2 & U_3 & U_4 & 0 & 0 & 0 & 0 \\ V_1 & V_2 & V_3 & V_5 & -\left.D_1\right|_{r=b} & -\left.D_2\right|_{r=b} & -\left.D_3\right|_{r=b} & -\left.D_4\right|_{r=b} \\ Y_1 & Y_2 & Y_3 & Y_5 & -\left.F_1\right|_{r=b} & -\left.F_2\right|_{r=b} & -\left.F_3\right|_{r=b} & -\left.F_4\right|_{r=b} \\ 0 & 0 & 0 & 0 & \left.D_1\right|_{r=a} & \left.D_2\right|_{r=a} & \left.D_3\right|_{r=a} & \left.D_4\right|_{r=a} \\ 0 & 0 & 0 & 0 & \left.F_1\right|_{r=a} & \left.F_2\right|_{r=a} & \left.F_3\right|_{r=a} & \left.F_4\right|_{r=a} \end{array}\right]\left[\begin{array}{l} A_{n, 1} \\ A_{n, 2} \\ A_{n, 3} \\ B_n \\ A_n^{(1)} \\ A_n^{(2)} \\ B_n^{(1)} \\ B_n^{(2)} \end{array}\right]=\left[\begin{array}{l} G_9 \\ H_9 \\ T_5 \\ U_5 \\ -V_4 \\ -Y_4 \\ 0 \\ 0 \end{array}\right] . $$ (15) 系数$ {G}_{i}，{H}_{i}，{D}_{i}，{F}_{i}，{T}_{i}，{U}_{i}，{V}_{i}和{Y}_{i} $的表达式由上述公式计算得出，表达式略。通过求解式（15），得到未知波幅系数，以确定非饱和多孔介质和衬砌中的波场，从而获得其中位移和应力的解析解答。
3. 验证和算例
3.1 退化验证
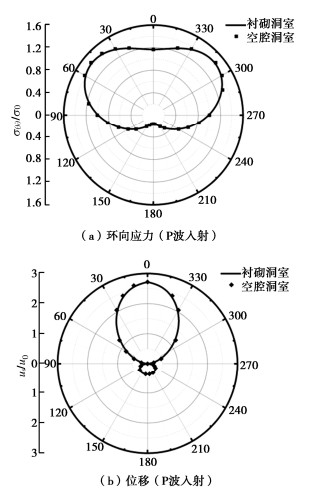
将衬砌外内半径之比取1.000001，其结果将会退化为非饱和多孔介质中无衬砌洞室的情况。与文献[13]计算结果对比，取参数（n0=0.34，Sr=0.6），图 2给出了P波入射下衬砌洞室与空腔洞室动应力集中因子对比结果。从图 2中可以看出，当衬砌很薄时，衬砌洞室退化后的结果与洞室的计算结果一致。
![]()
图 2 非饱和多孔介质中衬砌外内半径之比为1.000001时衬砌洞室与空腔洞室集中因子对比结果Figure 2. Comparison results of concentration factors between cavity and lining cavity with 1.000001 of ratio of outer radius to inner radius in unsaturated porous media3.2 算例分析
工程抗震研究的重点是衬砌的动应力集中因子(dynamic stress concentration factor，简称DSCF)，本文中考虑介质中环向应力与入射波产生的环向应力的比值，表达式为$ {\sigma _{\theta \theta }}^{\rm S}/{\sigma _0} $，其中
$$\begin{align} {\sigma _{\theta \theta }}^{\rm S} =& \left( {{M_\text{SS}}{\mathit{\nabla }^2}{\varphi ^{\rm S}} + {M_\text{SW}}{\mathit{\nabla }^2}{\varphi ^{\rm W}} + {M_{\rm{SN}}}{\mathit{\nabla }^2}{\varphi ^{\rm N}}} \right) + \\ &\frac{{2G}}{r}\left( {\frac{{\partial {\varphi ^{\rm S}}}}{{\partial r}} + \frac{1}{r}\frac{{{\partial ^2}{\varphi ^{\rm S}}}}{{\partial {\theta ^2}}}} \right) - 2G\left[ {\frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{{\partial {\varPsi ^{\rm S}}}}{{\partial \theta }}} \right)} \right] \text{，} \end{align} $$ (16) $$\begin{array}{c} {\sigma _0} = [2G + {M_\text{SS}} + {M_\text{SW}} + {M_\text{SN}} + \delta _1^{\rm W}({M_\text{WW}} + {M_\text{SW}} + {M_\text{WN}}) + \\ {\delta }_{1}^{\rm{N}}\left({M}_\text{SN}+{M}_\text{WN}+{M}_\text{NN}\right)]{k}_{1}^{2}\text{ (P}波入射\text{)} \text{，} \end{array} $$ (17a) $$ {\sigma _0} = Gk_4^2\;\;\;\;\;\; (\text{SV}波入射) 。 $$ (17b) 从应力表达式中可以看到动剪切模量是一个关键因素，在以往的研究中很少将饱和度作为动剪切模量的考量，实际饱和度的变化对土中动剪切模量影响很大[17]。采用下式计算非饱和土动剪切模量[17]：
$$ G = {G_0} + \frac{{2050}}{\alpha }\ln (\sqrt {{{({S_e})}^{ - 2}} - 1} + {({S_e})^{ - 1}})\tan \phi ' 。 $$ (18) 式中：$ {G_0} $为土体饱和时动剪切模量；$ \phi ' $为土体饱和时内摩擦角。
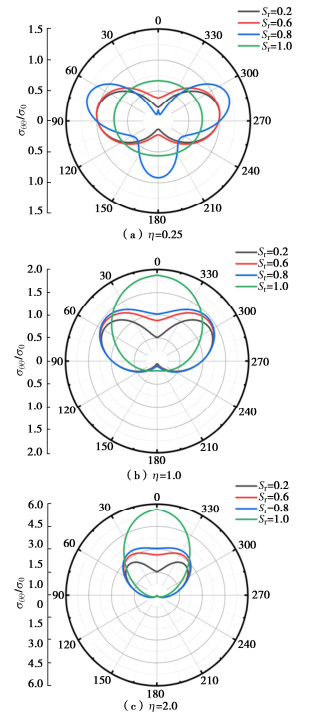
本文分别分析P波和SV波入射时，不同频率下饱和度对衬砌洞室周围动应力集中因子的影响。为避免孔洞尺寸对分析结果的影响采用无量纲频率$ \eta = a \times {k_0} $，式中a为衬砌内半径，k0为入射波波数。衬砌介质的参数取$ {\lambda _{\rm{L}}} = $3.5×107 kPa，$ {\mu _{\rm{L}}} = $3.5×107 kPa，$ {\rho _{\rm{L}}} = 2500{\text{ }}\rm kg/{m^3} $。非饱和多孔介质的材料参数及土水特征曲线参数$ \alpha $，$ d $，$ {S_{r\rm{W}}}{\text{ }} $，$ {S_{r\rm{N}}}{\text{ }} $，如表 1所示[13, 17]。
表 1 非饱和多孔介质材料参数Table 1. Material parameters of unsaturated porous medium孔隙率$ {n_0} $ $\rho _0^{\rm S}$/(kg·m-3) $\rho _0^{\rm W}$/(kg·m-3) $\rho _0^{\rm N}$/(kg·m-3) ${K_\rm{S}}/\rm kPa$ 0.36 2650 1000 1.1 3.6×107 ${K_\rm{W}}/\rm kPa$ ${K_\rm{N}}/\rm kPa$ ${\nu ^{\rm W}}$$ /(\rm Pa \cdot s) $ ${\nu ^{\rm N}}$$ /(\rm Pa \cdot s) $ $ {G_0}/\rm kPa $ 2×106 110 1.0×10-3 1.8×10-5 9.23×107 $ \widehat K{\text{/}} $kPa $ \kappa $/($\rm m \cdot {\rm s^{ - 1}} $) $ {\alpha _\text{B}} $ $ {S_{r\rm{W}}}{\text{ }} $ $ {S_{r\rm{N}}}{\text{ }} $ $2.0 \times {10^5}$ $2.5 \times {10^{ - 12}}$ 1 0.05 1 $ \upsilon $ d $ \alpha $ $ \phi ' $/(°) 0.3 2 $2.0 \times {10^{ - 5}}$ 20 取衬砌外内半径之比为$ \vartheta = 1.1 $，分别计算$ \eta $为0.25，1.0，2.0情况下饱和度为Sr为0.2，0.6，0.8，1.0时衬砌外壁动应力集中因子分布情况。图 3，4分别给出了P波和SV波入射时衬砌洞室周边动力集中因子分布曲线。从图中可以看出，P波和SV波入射时衬砌周边的应力均对称分布在入射波两侧，饱和介质与非饱和介质中动应力分布有明显差异。P波入射时，饱和度变化对动应力分布形状影响较大，饱和时动应力分布形状与非饱和状态时有显著不同；SV波入射时，饱和度变化对动应力分布形状影响较小，饱和时动应力大于非饱和状态。P波入射下，当$ \eta $=0.25时，Sr < 1.0动应力集中因子的最大值随饱和度的增加逐渐增大，在Sr为0.2，0.6时分布形式较一致呈“8”字形，最大值出现在80°，280°；在Sr=0.8时图像分布形式变为3个凸起，最大值出现在70°，180°和290°。Sr=1.0时动应力集中因子呈椭圆形沿洞中均匀分布，最大值角度出现在80°，280°。当$ \eta $=1.0时，Sr < 1.0动应力集中因子最大值随饱和度的增加逐渐增大，动应力集中因子分布呈“豌豆状”，随饱和度增加逐渐饱满。Sr=1.0时动应力集中因子呈椭圆形分布在坐标系的中上部，最大值出现在0°，360°。当$ \eta $=2.0时，动应力集中因子最大值随饱和度的增加逐渐增大，曲线集中分布在坐标系的上半部分，随饱和度增加最大值出现位置逐渐向0°坐标轴靠拢。P波入射时，最小值位置出现在入射面和入射背面，基本不受饱和度和入射频率的影响。
![]()
图 3 P波入射时考虑饱和度对剪切模量的影响下衬砌洞室周边动力集中因子分布曲线Figure 3. Curves of dynamic stress concentration factors around lining cavity considering influences of saturation on shear modulus under incidence of P-waves![]()
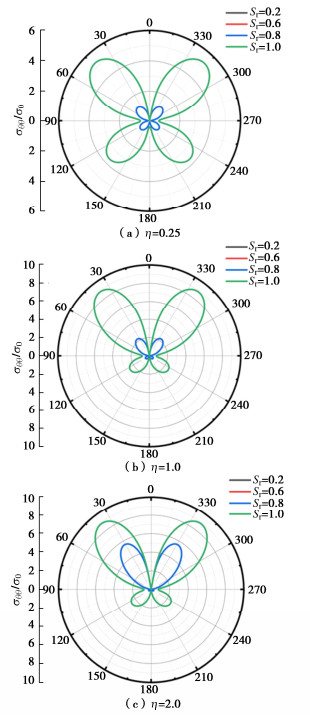
图 4 SV波入射时考虑饱和度对剪切模量的影响下衬砌洞室周边动力集中因子分布曲线Figure 4. Curves of dynamic stress concentration factors around lining cavity considering influences of saturation on shear modulus under SV-waves由于P波与SV波入射的振动形式不同，衬砌洞室周边动应力集中因子分布不同，在SV波入射时动应力集中因子呈蝶状分布。对比图 3，4可以发现不同相对频率下，饱和时动应力集中因子最大值要大于入射$ {P_{}} $波时的动应力集中因子。在图 4中可以发现，SV波入射时，饱和与非饱和情况存在明显差异，相比于Sr=1.0，Sr < 1.0时环向应力数值更小。在Sr < 1.0时饱和度对动应力集中因子影响较小，但随相对频率变化动应力集中因子变化明显，整体上随着入射频率的增加衬砌周边动应力逐渐增加，由于Sr=1.0与Sr < 1.0增幅不一致，在相对频率为2.0时饱和与非饱和动应力集中因子最接近。Sr < 1.0时最大值出现角度不变为40°，320°；Sr=1时最大值出现角度变化为50°，310°；30°，330°；20°，340°。$ SV $波入射时最小值出现在轴线上。
4. 结论
推导了平面P波和SV波入射下非饱和多孔介质中内嵌圆柱形衬砌洞室的动力响应解析解。考虑了饱和度对剪切模量的影响，求解并分析了饱和度和频率对圆柱形衬砌洞室动应力集中因子的影响，得到3点结论。
（1）饱和度对动应力集中因子的影响不容忽视，无论P波还是SV波入射，饱和时动应力分布与非饱和时有显著不同。且P波入射时，饱和度对动应力集中因子的分布形式影响较大，随着饱和度增加，动应力因子最大值出现角度逐渐向0°偏移，动应力集中因子最大值逐渐增加；SV波入射下，饱和度小于1时，饱和度对动应力集中因子影响较小。
（2）由于P波与SV波的振动形式不同，衬砌洞室周边动应力集中因子分布不同。P波入射时，动应力集中因子分布更多呈椭圆形或“豌豆”状；SV波入射时，动应力集中因子分布呈蝶状。
（3）入射频率主要影响动应力集中因子的大小。随着入射频率的增加，P波和SV波入射下洞室周边动应力集中因子最大值均逐渐增加。
-
![]()
图 2 非饱和多孔介质中衬砌外内半径之比为1.000001时衬砌洞室与空腔洞室集中因子对比结果
Figure 2. Comparison results of concentration factors between cavity and lining cavity with 1.000001 of ratio of outer radius to inner radius in unsaturated porous media
![]()
图 3 P波入射时考虑饱和度对剪切模量的影响下衬砌洞室周边动力集中因子分布曲线
Figure 3. Curves of dynamic stress concentration factors around lining cavity considering influences of saturation on shear modulus under incidence of P-waves
![]()
图 4 SV波入射时考虑饱和度对剪切模量的影响下衬砌洞室周边动力集中因子分布曲线
Figure 4. Curves of dynamic stress concentration factors around lining cavity considering influences of saturation on shear modulus under SV-waves
表 1 非饱和多孔介质材料参数
Table 1 Material parameters of unsaturated porous medium
孔隙率n0 ρS0/(kg·m-3) ρW0/(kg·m-3) ρN0/(kg·m-3) KS/kPa 0.36 2650 1000 1.1 3.6×107 KW/kPa KN/kPa νW/(Pa⋅s) νN/(Pa⋅s) G0/kPa 2×106 110 1.0×10-3 1.8×10-5 9.23×107 ˆK/kPa κ/(m⋅s−1) αB SrW SrN 2.0×105 2.5×10−12 1 0.05 1 υ d α ϕ′/(°) 0.3 2 2.0×10−5 20 
下载: 导出CSV
-
[1] PAO Y H, MOW C C, ACHENBACH J D. Diffraction of elastic waves and dynamic stress concentrations[J]. Journal of Applied Mechanics, 1973, 40(4): 872.
[2] LIU Q J, ZHAO M J, WANG L H. Scattering of plane P, SV or Rayleigh waves by a shallow lined tunnel in an elastic half space[J]. Soil Dynamics and Earthquake Engineering, 2013, 49: 52-63. doi: 10.1016/j.soildyn.2013.02.007
[3] 周香莲, 周光明, 王建华. 饱和土中圆形衬砌结构对弹性波的散射[J]. 岩石力学与工程学报, 2005, 24(9): 1572-1576. doi: 10.3321/j.issn:1000-6915.2005.09.017 ZHOU Xianglian, ZHOU Guangming, WANG Jianhua. Scattering of elastic wave by circular cavity with lining in saturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1572-1576. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.09.017
[4] JIANG L F, WANG J H, ZHOU X L. Scattering of elastic compression waves by circular lining in half-space saturated soils [J]. Geotechnics. 2008, 29(2): 315-320. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT202401012.htm [5] 张海, 杨国岗, 刘中宪, 等. 弹性半空间中含直边界半圆形衬砌隧道对SH波的散射解析解[J]. 应用力学学报, 2017, 34(2): 243-249, 401. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201702009.htm ZHANG Hai, YANG Guogang, LIU Zhongxian, et al. An analytical solution to scattering of plane SH waves by a semi-circle lined tunnel in elastic half-space boundary[J]. Chinese Journal of Applied Mechanics, 2017, 34(2): 243-249, 401. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201702009.htm
[6] DING H B, TONG L H, XU C J, et al. Aseismic performance analysis of composite lining embedded in saturated poroelastic half space[J]. International Journal of Geomechanics, 2020, 20(9): 04020156. doi: 10.1061/(ASCE)GM.1943-5622.0001787
[7] HASHEMINEJAD S M, KAZEMIRAD S. Dynamic response of an eccentrically lined circular tunnel in poroelastic soil under seismic excitation[J]. Soil Dynamics and Earthquake Engineering, 2008, 28(4): 277-292. doi: 10.1016/j.soildyn.2007.06.007
[8] LIU Q J, YUE C, ZHAO M J. Scattering of harmonic P1 and SV waves by a shallow lined circular tunnel in a poroelastic half-plane[J]. Soil Dynamics and Earthquake Engineering, 2022, 158: 107306. doi: 10.1016/j.soildyn.2022.107306
[9] 徐长节, 丁海滨, 童立红, 等. 基于非局部Biot理论下饱和土中深埋圆柱形衬砌对平面弹性波的散射[J]. 岩土工程学报, 2018, 40(9): 1563-1570. doi: 10.11779/CJGE201809001 XU Changjie, DING Haibin, TONG Lihong, et al. Scattering waves generated by cylindrical lining in saturated soil based on nonlocal Biot theory[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(9): 1563-1570. (in Chinese) doi: 10.11779/CJGE201809001
[10] XU C J, DING H B, TONG L H, et al. Scattering of a plane wave by shallow buried cylindrical lining in a poroelastic half-space[J]. Applied Mathematical Modelling, 2019, 70: 171-189. doi: 10.1016/j.apm.2019.01.029
[11] DING H B, TONG L H, XU C J, et al. Dynamic responses of shallow buried composite cylindrical lining embedded in saturated soil under incident P wave based on nonlocal-Biot theory[J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 40-56. doi: 10.1016/j.soildyn.2019.02.018
[12] LI W H, ZHENG J, TRIFUNAC M D. Saturation effects on ground motion of unsaturated soil layer-bedrock system excited by plane P and SV waves[J]. Soil Dynamics and Earthquake Engineering, 2018, 110: 159-172. doi: 10.1016/j.soildyn.2018.04.005
[13] LI W H, YANG Z, ZHANG A C, et al. Scattering of plane waves by cylindrical cavity in unsaturated poroelastic medium[J]. Applied Sciences, 2022, 13(1): 494. doi: 10.3390/app13010494
[14] TAN Y, YANG M S, LI X Y. Dynamic response of a circular lined tunnel with an imperfect interface embedded in the unsaturated poroelastic medium under P wave[J]. Computers and Geotechnics, 2020, 122: 103514. doi: 10.1016/j.compgeo.2020.103514
[15] WEI C F, MURALEETHARAN K K. A continuum theory of porous media saturated by multiple immiscible fluids: I. Linear poroelasticity[J]. International Journal of Engineering Science, 2002, 40(16): 1807-1833. doi: 10.1016/S0020-7225(02)00068-X
[16] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated Soils1[J]. Soil Science Society of America Journal, 1980, 44(5): 892. doi: 10.2136/sssaj1980.03615995004400050002x
[17] 徐明江. 非饱和土地基与基础的动力响应研究[D]. 广州: 华南理工大学, 2010. XU Mingjiang. Investigation on Dynamic Response of Unsaturated Soils and Foundation[D]. Guangzhou: South China University of Technology, 2010. (in Chinese)
计量
- 文章访问数: 130
- HTML全文浏览量: 46
- PDF下载量: 13
